Abstract
We study union types and recursive types in the setting of a gradually typed lambda calculus. Our goal is to obtain a foundational account for languages that enable recursively defined data structures to be passed between static and dynamically typed regions of a program. We discuss how traditional sum types are not appropriate for this purpose and instead study a form of “true” union in the tradition of soft typing (Cartwright and Fagan, 1991) and occurrence typing (Tobin-Hochstadt and Felleisen, 2008). Regarding recursive types, our formulation is based on the axiomatization of subtyping by Brand and Henglein (1998).
This paper defines three artifacts. First, in the context of the simply typed lambda calculus, we define the semantics of our unions and integrate them with equi-recursive types. Second, we add a dynamic type \(\star \) to obtain a gradually typed lambda calculus. Its semantics is defined by translation to the third artifact, a blame calculus (Wadler and Findler, 2009) extended with unions and equi-recursive types.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
Amadio, R.M., Cardelli, L.: Subtyping recursive types. ACM Trans. Program. Lang. Syst. 15(4), 575–631 (1993)
Brandt, M., Henglein, F.: Coinductive axiomatization of recursive type equality and subtyping. Fundam. Inf. 33(4), 309–338 (1998)
Cartwright, R., Fagan, M.: Soft typing. In: Conference on Programming Language Design and Implementation, PLDI, pp. 278–292. ACM Press (1991)
Castagna, G., Nguyen, K., Xu, Z., Im, H., Lenglet, S., Padovani, L.: Polymorphic functions with set-theoretic types: part 1: syntax, semantics, and evaluation. In: Symposium on Principles of Programming Languages, POPL, pp. 5–17. ACM (2014)
Cimini, M., Siek, J.G.: The gradualizer: a methodology and algorithm for generating gradual type systems. In: Symposium on Principles of Programming Languages, POPL, January 2016
Flatt, M., and PLT.: The Racket reference 6.0. Technical report, PLT Inc. (2014). http://docs.racket-lang.org/reference/index.html
Frisch, A., Castagna, G., Benzaken, V.: Semantic subtyping: dealing set-theoretically with function, union, intersection, and negation types. J. ACM 55(4), 19: 1–19: 64 (2008)
Kelsey, R., Clinger, W., Rees, J.: Revised\(^5\) report on the algorithmic language scheme. High.-Order Symbolic Comput. 11(1), 7–105 (1998)
Pierce, B.C.: Programming with intersection types, union types, and polymorphism. Technical report CMU-CS-91-106, Carnegie Mellon University (1991)
Pierce, B.C.: Types and Programming Languages. MIT Press, Cambridge (2002)
Siek, J.G., Taha, W.: Gradual typing for objects. In: Ernst, E. (ed.) ECOOP 2007. LNCS, vol. 4609, pp. 2–27. Springer, Heidelberg (2007)
Siek, J.G., Thiemann, P., Wadler, P.: Blame and coercion: together again for the first time. In: Conference on Programming Language Design and Implementation, PLDI, June 2015
Tobin-Hochstadt, S., Felleisen, M.: The design and implementation of Typed Scheme. In: Symposium on Principles of Programming Languages, January 2008
Tobin-Hochstadt, S., Felleisen, M.: Logical types for untyped languages. In: International Conference on Functional Programming, ICFP, pp. 117–128. ACM (2010)
Vouillon, J.: Subtyping union types. In: Marcinkowski, J., Tarlecki, A. (eds.) CSL 2004. LNCS, vol. 3210, pp. 415–429. Springer, Heidelberg (2004)
Wadler, P., Findler, R.B.: Well-typed programs can’t be blamed. In: Castagna, G. (ed.) ESOP 2009. LNCS, vol. 5502, pp. 1–16. Springer, Heidelberg (2009)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendix
A Appendix
1.1 A.1 Type Safety of \(\lambda _{\mu \cup }\)
Lemma 1
(Subtyping Substitution). If \(\mu X .\;P <: \mu X .\;Q\), then \([X{:=}\mu X .\;P]P <: [X{:=}\mu X .\;Q] Q\).
Lemma 2
(Canonical Forms).
-
Suppose \(\emptyset \vdash V : P\).
-
1.
If \(P=\iota \) then \(V=k\) and \(\varDelta (k)=\iota \) for some constant k.
-
2.
If \(P=A \times B\) then \(V=(V_1,V_2)\) for some \(V_1\) and \(V_2\).
-
3.
If \(P=A \rightarrow B\) then \(V=\lambda x{:}A' .\; M\) for some x, \(A'\), and M.
-
4.
If \(P=\cup \,\mathcal {C}\) then \(\emptyset \vdash V : \mathcal {C}(c)\) for some \(c \in \mathrm {dom}(\mathcal {C})\).
-
1.
-
Suppose \(\emptyset \vdash V : \mu X .\;P\). Then \(\emptyset \vdash V : [X{:=}\mu X .\;P]P\) and the first part of this proposition can be applied.
Proof
The proof is by mutual induction on the derivation of \(\emptyset \vdash V : P\) and \(\emptyset \vdash V : \mu X .\;P\). The cases for constants, pairs, and abstraction are immediate.
Case 
From \(\emptyset \vdash V : \mu X .\;P\) we have \(\emptyset \vdash V : [X{:=}\mu X .\;P]P\) by induction. Then again by induction we conclude.
Case 
Let \(A=\mu X .\;P\) and \(B=\mu X .\;Q\). By induction we have \(\emptyset \vdash V : [X{:=}A]P\). From \(A <: B\) we have \([X{:=}A]P <: [X{:=}B]Q\) by Lemma 1. Thus we conclude that \(\emptyset \vdash V : [X{:=}\mu X .\;Q]Q\)
Case 
The rest of the typing rules don’t apply to values. \(\square \)
Lemma 3
(Preservation). If \(\emptyset \vdash M : A\) and \(M \longrightarrow N\), then \(\emptyset \vdash N : A\).
Proof
The proof is by induction on the derivation of \(M \longrightarrow N\). All of the reduction rules are standard except for the reduction rule for case.
Case  We have \(\emptyset \vdash V : \cup \,\mathcal {C}\), \(\emptyset \vdash M' : \mathcal {C}(c) \rightarrow A\), and \(\emptyset \vdash N' : (\cup \,\mathcal {C}-c) \rightarrow A\). We have two subcases to consider.
We have \(\emptyset \vdash V : \cup \,\mathcal {C}\), \(\emptyset \vdash M' : \mathcal {C}(c) \rightarrow A\), and \(\emptyset \vdash N' : (\cup \,\mathcal {C}-c) \rightarrow A\). We have two subcases to consider.
-
Subcase \( tycon (V) = c\). From \(\emptyset \vdash V : \cup \,\mathcal {C}\), canonical forms (Lemma 2), and \( tycon (V) = c\), we have \(\emptyset \vdash V : \mathcal {C}(c)\). We conclude that \(\emptyset \vdash M' \;V : A\).
-
Subcase \( tycon (V) \ne c\). From \(\emptyset \vdash V : \cup \,\mathcal {C}\), canonical forms (Lemma 2), and \( tycon (V) \ne c\), we have \(\emptyset \vdash V : \cup \,(\mathcal {C}-c)\). We conclude that \(\emptyset \vdash N' \;V : A\).
Lemma 4
(Progress). If \(\emptyset \vdash M : A\) then either M is a value or \(M \longrightarrow N\) for some N.
Proof
The proof is by induction on the derivation of \(\emptyset \vdash M : A\). The only novel case in the proof is for the typing rule of case.
Case 
By induction, either L is a value or \(L \longrightarrow L'\). In the later case we conclude immediately using the frame reduction rule. Suppose L is a value. From canonical forms (Lemma 2) we have \(\emptyset \vdash L : \mathcal {C}(c')\) for some \(c' \in \mathrm {dom}(\mathcal {C})\). We have two cases to consider.
-
Subcase \(c = c'\). We have \(\emptyset \vdash L : c(\bar{B})\) so by cases on the canonical forms, we have \( tycon (L)=c\). Therefore the following reduction applies:
$$\begin{aligned} (\texttt {case} \,c?(L) \,\texttt {then} \,M' \,\texttt {else} \,N') \longrightarrow M' \;L \end{aligned}$$ -
Subcase \(c \ne c'\). We have \(\emptyset \vdash L : c'(\bar{B})\) so by cases on the canonical forms, we have \( tycon (L)\ne c\). Therefore the following reduction applies:
$$\begin{aligned} (\texttt {case} \,c?(L) \,\texttt {then} \,M' \,\texttt {else} \,N') \longrightarrow N' \;L \end{aligned}$$
1.2 A.2 Correctness of Algorithmic Type System for \(\lambda ^{\star }_{\mu \cup }\)
Figure 10 defines the meet-join and meet-meet operators.
1.3 A.3 Translation to \(\lambda \textsf {B} _{\mu \cup }\) Preserves Types
Lemma 5
(Merge and Subtyping). If \(A \lesssim B\) then \(A <: (A \mathrel {\rightharpoonup }B)\).
Lemma 6
(Merge and Compatibility). \((A \mathrel {\rightharpoonup }B) \sim B\)
Lemma 7
(Meet-Join and Compatible-Subtype). \(A \lesssim (A \mathrel {\triangledown }B)\) and \(B \lesssim (A \mathrel {\triangledown }B)\).
Lemma 13
(Cast Insertion Preserves Types). If \(\varGamma \vdash M : A \leadsto M'\) then \(\varGamma \vdash M' : A\).
Proof
The proof is by induction on the derivation of \(\varGamma \vdash M : A \leadsto M'\).
-
Case
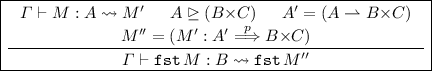
By the induction hypothesis, we have \(\varGamma \vdash M' : A\). From \(A \mathrel {\trianglerighteq }(B{\times }C)\) we have \(A \lesssim (B{\times }C)\). Then by Lemma 5, we have \(A <: A'\), so \(\varGamma \vdash M' : A'\). By Lemma 6 we have \(A' \sim B{\times }C\) and therefore \(\varGamma \vdash M'' : B{\times }C\). We conclude that \(\varGamma \vdash \texttt {fst} \,M'' : B\).
-
Case
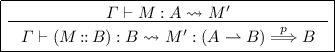
By the induction hypothesis, we have \(\varGamma \vdash M' : A\). From \(A \lesssim B\) we have \(A <: (A \mathrel {\rightharpoonup }B)\). So \(\varGamma \vdash M' : (A \mathrel {\rightharpoonup }B)\). Also, we have \((A \mathrel {\rightharpoonup }B) \sim B\).
$$\begin{aligned} \varGamma \vdash (M' : (A\mathrel {\rightharpoonup }B) \mathop {\Longrightarrow }\limits ^{p} B) : B \end{aligned}$$ -
Case
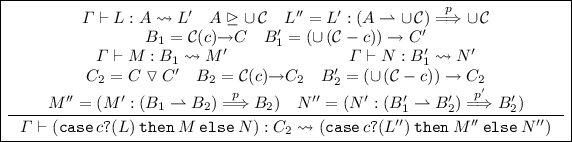
From \(C_2 = C \mathrel {\vartriangle }C'\) we have \(C \lesssim C_2\) (Lemma 7) and so \(C <: (C \mathrel {\rightharpoonup }C_2)\). Similarly, we have \(C' <: (C' \mathrel {\rightharpoonup }C_2)\). Also, we have \((C \mathrel {\rightharpoonup }C_2) \sim C_2\) and \((C'\mathrel {\rightharpoonup }C_2) \sim C_2\) (Lemma 6). Thus, with the induction hypotheses for M and N, we have \(\varGamma \vdash M'' : B_2\) and \(\varGamma \vdash N'' : B'_2\). Similarly, we also have \(\varGamma \vdash L'' : \cup \,\mathcal {C}\). Therefore, we have
$$\begin{aligned} \varGamma \vdash (\texttt {case} \,c?(L'') \,\texttt {then} \,M'' \,\texttt {else} \,N'') : C_2 \end{aligned}$$The rest of the cases are similar. \(\square \)
1.4 A.4 Type Safety of \(\lambda \textsf {B} _{\mu \cup }\)
Lemma 8
If \(\mu X .\;P \sim \mu Y .\;Q\) then \([X{:=}\mu X .\;P]P \sim [Y{:=}\mu Y .\;Q]Q\).
Lemma 15
(Preservation). If \(\emptyset \vdash M : A\) and \(M \longrightarrow N\), then \(\emptyset \vdash N : A\).
Proof
The proof is by induction on the derivation of \(M \longrightarrow N\). We only consider the novel cases.
-
Case

By canonical forms (Lemma 14) and because \( tycon (V)=c\), we have \(\emptyset \vdash V : \mathcal {C}(c)\). Also, because \(\cup \,\mathcal {C} \sim \cup \,\mathcal {C'}\), we have \(\mathcal {C}(c) \sim \mathcal {C}'(c)\). So \(\emptyset \vdash (V : \mathcal {C}(c) \mathop {\Longrightarrow }\limits ^{p} \mathcal {C'}(c)) : \mathcal {C}'(c)\). Finally, because \(\mathcal {C'}(c) <: \cup \,\mathcal {C'}\) we conclude that
$$\begin{aligned} \emptyset \vdash (V : \mathcal {C}(c) \mathop {\Longrightarrow }\limits ^{p} \mathcal {C'}(c)) : \cup \,\mathcal {C'} \end{aligned}$$ -
Case

By canonical forms (Lemma 14) we have \(\emptyset \vdash V : [X{:=}\mu X .\;P]P\). Also, because \(\mu X .\;P \sim \mu Y .\;Q\) we have \([X{:=}\mu X .\;P]P \sim [Y{:=}\mu Y .\;Q]Q\) (Lemma 8). Thus, we have
$$\begin{aligned} \emptyset \vdash (V : [X{:=}\mu X .\;P]P \mathop {\Longrightarrow }\limits ^{p} [Y{:=}\mu Y .\;Q]Q) : [Y{:=}\mu Y .\;Q]Q \end{aligned}$$ -
Case

We have \(\emptyset \vdash V : G\) and \(G <: H\), so \(\emptyset \vdash V : H\). \(\square \)
Lemma 16
(Progress). If \(\emptyset \vdash M : A\) then either M is a value or \(M \longrightarrow N\) for some N.
Proof
The proof is by induction on the derivation of \(\emptyset \vdash M : A\). All of the cases in the proof are standard except for the case for cast.
-
Case

By the induction hypothesis, either \(M'\) is a value or \(M' \longrightarrow N'\). In the later case we can conclude immediately by applying the reduction rule for frames. Suppose \(M'\) is a value. We proceed by cases on \(A' \sim A\).
-
Subcase
 We have $$\begin{aligned} M' : \star \mathop {\Longrightarrow }\limits ^{p} \star \longrightarrow M' \end{aligned}$$
We have $$\begin{aligned} M' : \star \mathop {\Longrightarrow }\limits ^{p} \star \longrightarrow M' \end{aligned}$$ -
Subcase
 By canonical forms (Lemma 14), \(M' = V : G \mathop {\Longrightarrow }\limits ^{q} \star \). Now if Q is a ground type (let it be H), then we have either $$\begin{aligned} V : G \mathop {\Longrightarrow }\limits ^{q} \star \mathop {\Longrightarrow }\limits ^{p} H \longrightarrow V \quad \text { or }\quad V : G \mathop {\Longrightarrow }\limits ^{q} \star \mathop {\Longrightarrow }\limits ^{p} H \longrightarrow \texttt {blame} \,p \end{aligned}$$
By canonical forms (Lemma 14), \(M' = V : G \mathop {\Longrightarrow }\limits ^{q} \star \). Now if Q is a ground type (let it be H), then we have either $$\begin{aligned} V : G \mathop {\Longrightarrow }\limits ^{q} \star \mathop {\Longrightarrow }\limits ^{p} H \longrightarrow V \quad \text { or }\quad V : G \mathop {\Longrightarrow }\limits ^{q} \star \mathop {\Longrightarrow }\limits ^{p} H \longrightarrow \texttt {blame} \,p \end{aligned}$$depending on whether \(G <: H\) or not.
-
Subcase
 If P is a ground type, then \(M' : P \mathop {\Longrightarrow }\limits ^{p} \star \) is a value. Otherwise, we have $$\begin{aligned} M' : P \mathop {\Longrightarrow }\limits ^{p} G \mathop {\Longrightarrow }\limits ^{p} \star \end{aligned}$$
If P is a ground type, then \(M' : P \mathop {\Longrightarrow }\limits ^{p} \star \) is a value. Otherwise, we have $$\begin{aligned} M' : P \mathop {\Longrightarrow }\limits ^{p} G \mathop {\Longrightarrow }\limits ^{p} \star \end{aligned}$$where G is the unique ground type compatible with P.
-
Subcase
 We have $$\begin{aligned} M' : \iota \mathop {\Longrightarrow }\limits ^{p} \iota \longrightarrow M' \end{aligned}$$
We have $$\begin{aligned} M' : \iota \mathop {\Longrightarrow }\limits ^{p} \iota \longrightarrow M' \end{aligned}$$ -
Subcase
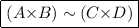 By canonical forms (Lemma 14), we have \(M' = (V,W)\). So $$\begin{aligned} (V,W) : A {\times } B \mathop {\Longrightarrow }\limits ^{p} C {\times } D \longrightarrow (V : A \mathop {\Longrightarrow }\limits ^{p} C, W : B \mathop {\Longrightarrow }\limits ^{p} D) \end{aligned}$$
By canonical forms (Lemma 14), we have \(M' = (V,W)\). So $$\begin{aligned} (V,W) : A {\times } B \mathop {\Longrightarrow }\limits ^{p} C {\times } D \longrightarrow (V : A \mathop {\Longrightarrow }\limits ^{p} C, W : B \mathop {\Longrightarrow }\limits ^{p} D) \end{aligned}$$ -
Subcase
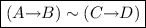 We have $$\begin{aligned} M' : A {\rightarrow }B \mathop {\Longrightarrow }\limits ^{p} C {\rightarrow }D \longrightarrow \lambda x{:}C .\; M' \;(x : C \mathop {\Longrightarrow }\limits ^{\overline{p}} A) : B \mathop {\Longrightarrow }\limits ^{p} D \end{aligned}$$
We have $$\begin{aligned} M' : A {\rightarrow }B \mathop {\Longrightarrow }\limits ^{p} C {\rightarrow }D \longrightarrow \lambda x{:}C .\; M' \;(x : C \mathop {\Longrightarrow }\limits ^{\overline{p}} A) : B \mathop {\Longrightarrow }\limits ^{p} D \end{aligned}$$ -
Subcase
 Let \(c= tycon (M')\). We have $$\begin{aligned} M' : \cup \,\mathcal {C} \mathop {\Longrightarrow }\limits ^{p} \cup \,\mathcal {C'} \longrightarrow M' : \mathcal {C}(c) \mathop {\Longrightarrow }\limits ^{p} \mathcal {C'}(c) \end{aligned}$$
Let \(c= tycon (M')\). We have $$\begin{aligned} M' : \cup \,\mathcal {C} \mathop {\Longrightarrow }\limits ^{p} \cup \,\mathcal {C'} \longrightarrow M' : \mathcal {C}(c) \mathop {\Longrightarrow }\limits ^{p} \mathcal {C'}(c) \end{aligned}$$ -
Subcase
 We have $$\begin{aligned} M' : \mu X .\;P \mathop {\Longrightarrow }\limits ^{p} \mu X .\;Q \longrightarrow M' : [X{:=}\mu X .\;P]P \mathop {\Longrightarrow }\limits ^{p} [X{:=}\mu X .\;Q]Q \end{aligned}$$
We have $$\begin{aligned} M' : \mu X .\;P \mathop {\Longrightarrow }\limits ^{p} \mu X .\;Q \longrightarrow M' : [X{:=}\mu X .\;P]P \mathop {\Longrightarrow }\limits ^{p} [X{:=}\mu X .\;Q]Q \end{aligned}$$
-
\(\square \)
1.5 A.5 Blame Safety
Figure 11 defines the positive and negative subtype relations used to define blame safety in Sect. 4.3.
Lemma 9
(Unfolding Positive and Negative Subtyping).
-
1.
If \(\mu X .\;P \mathrel {<:}^{+}\mu X .\;Q\) then \([X{:=}\mu X .\;P]P \mathrel {<:}^{+}[X{:=}\mu X .\;Q]Q\)
-
2.
If \(\mu X .\;P \mathrel {<:}^{-}\mu X .\;Q\) then \([X{:=}\mu X .\;P]P \mathrel {<:}^{-}[X{:=}\mu X .\;Q]Q\)
Theorem 12
(Blame Safety).
-
1.
If \(M \mathrel {\textsf {safe} }p\) and \(M \longrightarrow N\) then \(N \mathrel {\textsf {safe} }p\).
-
2.
If \(M \mathrel {\textsf {safe} }p\) then \(M \not \longrightarrow \texttt {blame} \,p\).
Proof
-
1.
The proof of the first part is by induction on the derivation \(M \longrightarrow N\). The interesting cases involve the reduction of casts.
-
Case
 where \(c= tycon (V)\)
where \(c= tycon (V)\)
We have \(V \mathrel {\textsf {safe} }p\) and \((\cup \,\mathcal {C} \mathop {\Longrightarrow }\limits ^{p} \cup \,\mathcal {C'}) \mathrel {\textsf {safe} }p\). There are three cases to consider:
-
(a)
Subcase \(q=p\): So \(\cup \,\mathcal {C} \mathrel {<:}^{+}\cup \,\mathcal {C'}\) and therefore \(\mathcal {C}(c) \mathrel {<:}^{+}\mathcal {C'}(c)\). Thus
$$\begin{aligned} (V : \mathcal {C}(c) \mathop {\Longrightarrow }\limits ^{p} \mathcal {C'}(c)) \mathrel {\textsf {safe} }p \end{aligned}$$ -
(b)
Subcase \(q=\overline{p}\): So \(\cup \,\mathcal {C} \mathrel {<:}^{-}\cup \,\mathcal {C'}\) and therefore \(\mathcal {C}(c) \mathrel {<:}^{-}\mathcal {C'}(c)\). Thus
$$\begin{aligned} (V : \mathcal {C}(c) \mathop {\Longrightarrow }\limits ^{\overline{p}} \mathcal {C'}(c)) \mathrel {\textsf {safe} }p \end{aligned}$$ -
(c)
Subcase \(q\ne p, q \ne \overline{p}\): We immediately have
$$\begin{aligned} (V : \mathcal {C}(c) \mathop {\Longrightarrow }\limits ^{q} \mathcal {C'}(c)) \mathrel {\textsf {safe} }p \end{aligned}$$
-
(a)
-
Case

We have \(V \mathrel {\textsf {safe} }p\) and \((\mu X .\;P \mathop {\Longrightarrow }\limits ^{p} \mu X .\;Q) \mathrel {\textsf {safe} }p\). There are three cases to consider:
-
(a)
Subcase \(q=p\): So \(\mu X .\;P \mathrel {<:}^{+}\mu X .\;Q\) and therefore \([X{:=}\mu X .\;P]P \mathrel {<:}^{+}[X{:=}\mu X .\;Q]Q\) (Lemma 9). Thus
$$\begin{aligned} (V : [X{:=}\mu X .\;P]P \mathop {\Longrightarrow }\limits ^{p} [X{:=}\mu X .\;Q]Q) \mathrel {\textsf {safe} }p \end{aligned}$$ -
(b)
Subcase \(q=\overline{p}\): So \(\mu X .\;P \mathrel {<:}^{-}\mu X .\;Q\) and therefore \([X{:=}\mu X .\;P]P \mathrel {<:}^{-}[X{:=}\mu X .\;Q]Q\) (Lemma 9). Thus
$$\begin{aligned} (V : [X{:=}\mu X .\;P]P \mathop {\Longrightarrow }\limits ^{\overline{p}} [X{:=}\mu X .\;Q]Q) \mathrel {\textsf {safe} }p \end{aligned}$$ -
(c)
Subcase \(q\ne p, q \ne \overline{p}\): We immediately have
$$\begin{aligned} (V : [X{:=}\mu X .\;P]P \mathop {\Longrightarrow }\limits ^{q} [X{:=}\mu X .\;Q]Q) \mathrel {\textsf {safe} }p \end{aligned}$$
-
(a)
-
The rest of the cases are the same as for the original blame calculus.
-
-
2.
The proof of the second part is by induction on \(M \longrightarrow \texttt {blame} \,p\) and we seek to reach a contradiction. The only reduction rule that triggers blame is
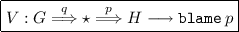 where \(G \not <: H\)
where \(G \not <: H\) We have \((\star \mathop {\Longrightarrow }\limits ^{p} H) \mathrel {\textsf {safe} }p\) so \(\star \mathrel {<:}^{+}H\). Thus \(H=\star \) but \(\star \) is not a ground type, hence a contradiction. \(\square \)
Rights and permissions
Copyright information
© 2016 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Siek, J.G., Tobin-Hochstadt, S. (2016). The Recursive Union of Some Gradual Types. In: Lindley, S., McBride, C., Trinder, P., Sannella, D. (eds) A List of Successes That Can Change the World. Lecture Notes in Computer Science(), vol 9600. Springer, Cham. https://doi.org/10.1007/978-3-319-30936-1_21
Download citation
DOI: https://doi.org/10.1007/978-3-319-30936-1_21
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-30935-4
Online ISBN: 978-3-319-30936-1
eBook Packages: Computer ScienceComputer Science (R0)



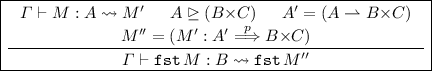
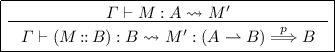
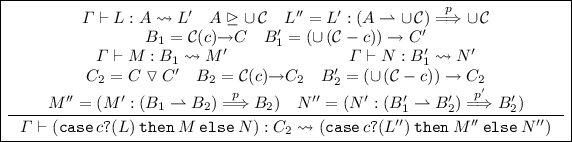




 We have
We have  By canonical forms (Lemma
By canonical forms (Lemma  If P is a ground type, then
If P is a ground type, then  We have
We have 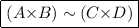 By canonical forms (Lemma
By canonical forms (Lemma 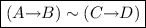 We have
We have  Let
Let  We have
We have 
 where
where 
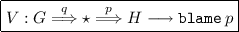 where
where