Abstract
The representation of Lie groups is closely related to the representation of their Lie algebras, and we shall discuss them later in this chapter. In the case of compact groups, however, there is a well developed representation theory, which we shall consider in the first section. Before discussing compact groups, let us state a definition and a proposition that hold for all Lie groups.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
This can always be done by rescaling the volume element.
- 2.
When a symmetric group is considered as an abstract group—as opposed to a group of transformations—we may multiply permutations (keep track of how each number is repeatedly transformed) from left to right. However, since the permutations here act on vectors on their right, it is more natural to calculate their products from right to left.
- 3.
We use the word “local” to mean the collection of all points that can be connected to the identity by a curve in the Lie group G. If this collection exhausts G, then we say that G is connected. If, furthermore, all closed curves (loops) in G can be shrunk to a point, we say that G is simply connected. The word “local” can be replaced by “simply connected” in what follows.
- 4.
Recall that the rank of \(\mathfrak{g}\) is the dimension of the Cartan subalgebra of \(\mathfrak{g}\).
- 5.
Sometimes we use
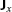 ,
,  , and
, and 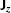 instead of
instead of 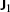 ,
,  , and
, and  .
. - 6.
Please make sure to differentiate between the pair (M ij ,P k ) (which acts on p) and the pair
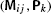 , which acts on the state vectors in the Hilbert space of representation.
, which acts on the state vectors in the Hilbert space of representation. - 7.
This “angular momentum” includes ordinary rotations as well as the Lorentz boosts.
- 8.
The reader should be warned that although such a rotation does not change p, the rotation operator may change the state |ψ p 〉. However, the resulting state will be an eigenstate of the
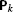 ’s with eigenvalue p.
’s with eigenvalue p. - 9.
We are using the fact that O(p,n−p) is transitive (see Problem 30.15).
- 10.
We use units in which c=1.
References
Barut, A., Raczka, R.: Theory of Group Representations and Applications. World Scientific, Singapore (1986)
Fulton, W., Harris, J.: Representation Theory. Springer, Berlin (1991)
Hamermesh, M.: Group Theory and Its Application to Physical Problems. Dover, New York (1989)
Mackey, G.: Induced Representations. Benjamin, Elmsford (1968)
Miller, W.: Lie Theory and Special Functions. Academic Press, New York (1968)
Varadarajan, V.: Lie Groups, Lie Algebras and Their Representations. Springer, Berlin (1984)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Representation of Lie Groups and Lie Algebras. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_30
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_30
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


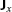 ,
,  , and
, and 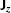 instead of
instead of 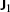 ,
,  , and
, and  .
.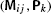 , which acts on the state vectors in the Hilbert space of representation.
, which acts on the state vectors in the Hilbert space of representation.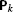 ’s with eigenvalue p.
’s with eigenvalue p.