Abstract
In many physical applications, a vector space  has a natural “product”, i.e., a binary operation
has a natural “product”, i.e., a binary operation  , which we call multiplication. The prime example of such a vector space is the vector space of matrices. It is therefore useful to consider vector spaces for which such a product exists.
, which we call multiplication. The prime example of such a vector space is the vector space of matrices. It is therefore useful to consider vector spaces for which such a product exists.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
We shall, for the most part, abandon the Dirac bra-and-ket notation in this chapter due to its clumsiness; instead we use boldface roman letters to denote vectors.
- 2.
It should be clear that the algebra of polynomials cannot be finite dimensional.
- 3.
It is more common to use ϕ,ψ etc. instead of
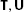 , etc. for linear maps of algebras.
, etc. for linear maps of algebras. - 4.
In keeping with our notation, we use ι for the identity homomorphism of the algebra
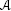 .
. - 5.
The reader is advised to show that \(\{\mathbf{f}_{i}\}_{i=1}^{4}\) is a linearly independent set of vectors.
- 6.
The index p has no significance in the final answer because all the e pq with varying p but a fixed q generate the same matrices.
- 7.
Recall that
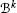 is the collection of products
is the collection of products 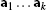 of elements in
of elements in 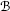 .
. - 8.
Note that
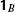 is not the identity of
is not the identity of  . It satisfies
. It satisfies 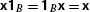 only if
only if 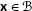 .
. - 9.
Since \(\mathbb{C}\) is a subalgebra of \(\mathbb{H}\), the tensor product is actually redundant. However, in the classification of the Clifford algebras discussed later in the book, \(\mathbb{C}\) is sometimes explicitly factored out.
- 10.
This is equivalent to replacing
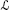 with
with 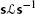 , which is allowed by Theorem 3.2.7 and the non-uniqueness clause of Theorem 3.5.27.
, which is allowed by Theorem 3.2.7 and the non-uniqueness clause of Theorem 3.5.27. - 11.
A proof of the theorem can be found in Sect. 10.5.
References
Benn, I.M., Tucker, R.W.: An Introduction to Spinors and Geometry with Applications in Physics. Adam Hilger, Bristol (1987)
Blyth, T.: Module Theory. Oxford University Press, Oxford (1990)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Algebras. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_3
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


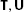 , etc. for linear maps of algebras.
, etc. for linear maps of algebras.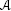 .
.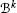 is the collection of products
is the collection of products 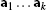 of elements in
of elements in 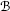 .
.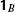 is not the identity of
is not the identity of  . It satisfies
. It satisfies 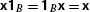 only if
only if 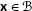 .
.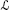 with
with 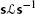 , which is allowed by Theorem 3.2.7 and the non-uniqueness clause of Theorem 3.5.27.
, which is allowed by Theorem 3.2.7 and the non-uniqueness clause of Theorem 3.5.27.