Abstract
The familiar two- and three-dimensional vectors can easily be generalized to higher dimensions. Representing vectors by their components, one can conceive of vectors having N components. This is the most immediate generalization of vectors in the plane and in space, and such vectors are called N-dimensional Cartesian vectors. Cartesian vectors are limited in two respects: Their components are real, and their dimensionality is finite. Some applications in physics require the removal of one or both of these limitations. It is therefore convenient to study vectors stripped of any dimensionality or reality of components. Such properties become consequences of more fundamental definitions. Although we will be concentrating on finite-dimensional vector spaces in this part of the book, many of the concepts and examples introduced here apply to infinite-dimensional spaces as well.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
Keep in mind that \(\mathbb{C}\) is the set of complex numbers and \(\mathbb{R}\) the set of reals.
- 2.
Complex numbers, particularly when they are treated as variables, are usually denoted by z, and we shall adhere to this convention in Part III. However, in the discussion of vector spaces, we have found it more convenient to use lower case Greek letters to denote complex numbers as scalars.
- 3.
A detailed discussion of tensor products and tensors in general is given in Chap. 26.
- 4.
A function that is linear in both of its arguments is called a bilinear function.
- 5.
In our present discussion, we are avoiding situations in which a nonzero vector can have zero “length”. Such occasions arise in relativity, and we shall discuss them in Part VIII.
- 6.
In some books, particularly in the mathematical literature, the second argument is chosen to be conjugate linear.
- 7.
This uniqueness holds up to a certain equivalence of inner products that we shall not get into here.
- 8.
The positive definiteness must be relaxed in the space-time of relativity theory, in which nonzero vectors can have zero “length”.
- 9.
The first property follows from this by letting α=0.
- 10.
It is convenient here to use the notation
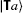 for
for  . This would then allow us to write the dual (see below) of the vector as
. This would then allow us to write the dual (see below) of the vector as  , emphasizing that it is indeed the bra associated with
, emphasizing that it is indeed the bra associated with 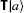 .
. - 11.
Since
 is a set, we should write the equality as
is a set, we should write the equality as  , or at least as
, or at least as  . However, when there is no danger of confusion, we set {|0〉}=|0〉=0.
. However, when there is no danger of confusion, we set {|0〉}=|0〉=0. - 12.
Recall that the dimension of a vector space depends on the scalars used in that space. Although we are dealing with two different vector spaces here, since they are both over the same set of scalars (complex or real), no confusion in the concept of dimension arises.
- 13.
The word “isomorphism”, as we shall see, is used in conjunction with many algebraic structures. To distinguish them, qualifiers need to be used. In the present context, we speak of linear isomorphism. We shall use qualifiers when necessary. However, the context usually makes the meaning of isomorphism clear.
- 14.
Matrices will be taken up in Chap. 5. Here, we assume only a nodding familiarity with elementary matrix operations.
- 15.
Do not confuse this “*” with complex conjugation.
- 16.
The significance of this notation will become clear in Sect. 4.3.
References
Axler, S.: Linear Algebra Done Right. Springer, Berlin (1996)
Friedman, A.: Foundations of Modern Analysis. Dover, New York (1982)
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2013 Springer International Publishing Switzerland
About this chapter
Cite this chapter
Hassani, S. (2013). Vectors and Linear Maps. In: Mathematical Physics. Springer, Cham. https://doi.org/10.1007/978-3-319-01195-0_2
Download citation
DOI: https://doi.org/10.1007/978-3-319-01195-0_2
Publisher Name: Springer, Cham
Print ISBN: 978-3-319-01194-3
Online ISBN: 978-3-319-01195-0
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


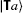 for
for  . This would then allow us to write the dual (see below) of the vector as
. This would then allow us to write the dual (see below) of the vector as  , emphasizing that it is indeed the bra associated with
, emphasizing that it is indeed the bra associated with 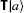 .
. is a set, we should write the equality as
is a set, we should write the equality as  , or at least as
, or at least as  . However, when there is no danger of confusion, we set {|0〉}=|0〉=0.
. However, when there is no danger of confusion, we set {|0〉}=|0〉=0.