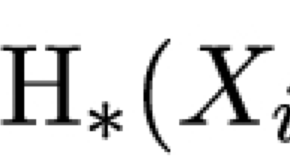
Collection
Rationality Problems
- Submission status
- Closed
This special issue of the Rendiconti del Circolo Matematico di Palermo is devoted to a venerable topic in algebraic geometry, namely “Rationality Problems”. The concept of a rational variety is very old, it goes back to the very beginnings of algebraic geometry and rationality problems are landmarks in the development of algebraic geometry. It is may be useful to quicky recall what all this is about. An irreducible algebraic variety X of dimension n is said to be rational if it is birationally equivalent to the projective space Pn of dimension n. A curve X is rational if and only if its genus is 0. For a surface X the famous rationality criterion by Guido Castelnuovo (1894) says that X is rational if and only if two birational invariants of X, the bigenus P2 and the irregularity q, are both zero. So for curves and surfaces it is possible to check rationality by the vanishing of some birational numerical invariants. This is no longer the case for higher dimensional varieties, at least so far. Moreover, recognizing rationality is a hard, often untractable, problem in general.
An equally older but weaker notion than rationality is the one of unirationality. A variety X as above is said to be unirational if there is a rational dominant map Pn → X. It is an old result due to Jacob Lüroth (1876) that a unirational curve is also rational. Castelnuovo’s rationality criterion implies that if a surface is unirational then it is also rational. Again, this is no longer true for higher dimensional varieties. It has been a longstanding conjecture that a smooth complex cubic hypersurface in P4, which is known to be unirational since Noether’s times, is not rational: this has been proven to be in fact the case by H. Clemens and Ph. Griffiths only in 1972. At the same time, other examples of unirational, non–rational, varieties of dimension 3 have been given by V. A. Iskovski and Y. Manin and by M. Artin and D. Mumford. As for rationality, also unirationality is hard to recognize since no numerical birational invariant of varieties has been discovered so far, useful to detect unirationality.
In the course of the years, various other notions, weaker than rationality and unirationality, have been introduced. Among these the notions of stable rationality, uniruledness, rational connectedness play today a very important role. A variety X is said to be stably rational if there is an integer m such that X×Pm is rational. If a variety is stably rational then it is also unirational. A variety is said to be uniruled if it is covered by a family of rational curves. A variety X is rationally connected if two general points of X are connected by a rational curve contained in X. A beautiful theorem by S. Boucksom, J.– P. Demailly, M. Paun, T. Peternell (valid over the complex field), says that a variety X is uniruled if and only if its canonical class KX is not pseudoeffective (2013). It is a long-standing conjecture, usually attributed to S. Mori, that a variety X is uniruled if and only if the Kodaira dimension of X is negative. Moreover, it is still an open conjecture, due to D. Mumford, that a variety is rationally connected if and only if H0(X,(ΩX)⊗n) = 0 for all positive integers n. This conjecture is true if X has dimension at most 3.
The research on rationality problems of this sort, or related problems, is in general very active and an enormous variety of great and beautiful geometric ideas have been displayed in this field.
The present issue contains seven papers whose authors are among the best specialists in the field.
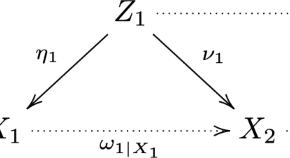
In their paper, Ch. Böhning, H. C. Graf von Bothmer and M. van Garrel introduce, for a simple normal crossing variety, the concepts of prelog Chow ring and saturated prelog Chow group, as well as their counterparts for numerical equivalence. After proving basic properties of these objects, they explain how they can be used in a possible further development of the degeneration method by C. Voisin et al. to prove stable irrationality of very general fibres of certain families of varieties.
I. Cheltov’s paper deals with a nice classical topic, namely Kummer quartic double solids and their equivariant birational geometry. By definition a Kummer quartic double solid is a finite double covering π : X → P3 branched on a complex Kummer quartic surface. As is well known such an X is rational and it is birationally not rigid. The paper deals with a deep and exhaustive study of the equivariant birational rigidity of X, with respect to a fixed subgroup G of Aut(X).
The paper by J.– L. Colliot–Thélène and F. Scavia, investigates a version of the integral Tate conjecture for 1-cycles on the product of a curve and a surface over a finite field, under the assumption of geometrical CH0–triviality of the surface. This means that, over any algebraically closed field extension, the degree map on the zero dimensional Chow group of the surface is an isomorphism. The authors prove, under suitable hypotheses, various interesting properties of natural maps in cohomology for the product of a curve and a surface that is geometrical CH0–trivial.
Toric varieties form an important class of rational varieties. A. Kresch and Y. Tschinkel study in their paper G-equivariant birational geometry of toric varieties, for G is a finite group.
The paper of M. Mella deals with the classical concept of Cremona equivalence of projective varieties: he extends some known results to reducible varieties and proves a very interesting and very general contractibility result for unions of rational subvarieties.
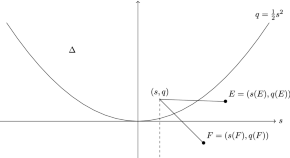
L. Pertusi and P. Stellari survey in their paper some recent results concerning the Categorical Torelli problem, i.e., a way of reconstructing a smooth projective variety up to isomorphism, by using properties of some subcategories of the bounded derived category of coherent sheaves of such a variety. They focus in particular on Enriques surfaces, and on prime Fano threefolds, in particular cubic hypersurfaces in P5. These latter varieties are very interesting from the point of view of rationality, since they are unirational. Some of them are rational, but in general they are conjectured to be not rational, though this conjecture is widely open.
Fano varieties play an extremely important role in the general classification of varieties. J. Kollár, Y. Miyaoka and S. Mori showed that a smooth Fano variety over an algebraically closed field is rationally connected. In his paper Y. Prokhorov deals with the classification of non–rational Fano varieties X of dimension 3, with terminal Gorenstein singularities, such that the rank of the Picard group is 1, the rank of the class group is at most 2 and (-KX)3 ≥ 8.
In conclusion, we hope that the scientific community will appreciate our effort of collecting in this issue this set of beautiful papers, that offers a quite interesting cross section of the research in the field.
Please note: Due to a mistake made during production, two articles belonging to this special issue were accidentally published in regular issues: Cheltsov, I.: Kummer quartic double solids (published in volume 72; issue 3; pages 1993-2024) and Prokhorov, Y.: Rationality of Fano threefolds with terminal Gorenstein singularities, II (published in volume 72; issue 3; pages 1797-1822). Springer regrets this mistake and offers sincere apologies to the affected authors. This topical collection aims to provide a page where all of the "Rationality Problems" special issue articles can be found, including those that were accidentally omitted from the special issue.
Editors
-
Alessandro Verra
Università Roma Tre
-
Ciro Ciliberto
Università di Roma Tor Vergata
Articles (8 in this collection)
-

-
Introduction to the special issue on “Rationality Problems” of the Rendiconti del Circolo Matematico di Palermo
Authors
- C. Ciliberto
- A. Verra
- Content type: Editorial
- Published: 03 June 2023
- Pages: 2857 - 2859
-
Sur la conjecture de Tate entière pour le produit d’une courbe et d’une surface \(CH_{0}\)-triviale sur un corps fini
Authors
- Jean-Louis Colliot-Thélène
- Federico Scavia
- Content type: OriginalPaper
- Published: 27 April 2023
- Pages: 2895 - 2927
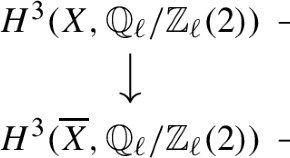
-
Equivariant Burnside groups and toric varieties
Authors
- Andrew Kresch
- Yuri Tschinkel
- Content type: OriginalPaper
- Published: 15 November 2022
- Pages: 3013 - 3039
-
Categorical Torelli theorems: results and open problems
Authors
- Laura Pertusi
- Paolo Stellari
- Content type: OriginalPaper
- Open Access
- Published: 15 September 2022
- Pages: 2949 - 3011
-
Kummer quartic double solids
Authors
- Ivan Cheltsov
- Content type: OriginalPaper
- Open Access
- Published: 11 July 2022
- Pages: 1993 - 2023
-
Rationality of Fano threefolds with terminal Gorenstein singularities, II
Authors
- Yuri Prokhorov
- Content type: OriginalPaper
- Published: 24 June 2022
- Pages: 1797 - 1821
-
Prelog Chow rings and degenerations
Authors
- Christian Böhning
- Hans-Christian Graf von Bothmer
- Michel van Garrel
- Content type: OriginalPaper
- Open Access
- Published: 23 May 2022
- Pages: 2861 - 2894