Skip to main content
SpringerLink
Log in

From Ohkawa to Strong Generation via Approximable Triangulated Categories—A Variation on the Theme of Amnon Neeman’s Nagoya Lecture Series

  • Conference paper
  • First Online:
Bousfield Classes and Ohkawa's Theorem (BouCla 2015)

Part of the book series: Springer Proceedings in Mathematics & Statistics ((PROMS,volume 309))

  • 538 Accesses

Abstract

This survey stems from Amnon Neeman’s lecture series at Ohakawa’s memorial workshop. Starting with Ohakawa’s theorem, this survey intends to supply enough motivation, background and technical details to read Neeman’s recent papers on his “approximable triangulated categories” and his \({{\,\mathrm{\mathbf {D}}}}^{b}_{\mathrm {coh}}(X)\) strong generation sufficient criterion via de Jong’s regular alteration, even for non-experts.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 129.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 169.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 169.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    The author also would like to thank Professors Mitsunori Imaoka, Takao Matumoto, Takeo Ohsawa, Katsumi Shimomura, and Masayuki Yamasaki, for coorganizing the workshop.

  2. 2.

    Actually, the author thought even such a short list is exciting.

  3. 3.

    Concerning this sentence, Professor Morava communicated the following thoughts to the author: “When I read it I was reminded of a quotation from the English writer Sir Thomas Browne (from ‘Urn Burial’, in 1658):

    What song the Sirens sang, or what name Achilles assumed when he hid himself among women, though puzzling questions, are not beyond all conjecture...

    I believe understanding the structure of Ohkawa’s set (perhaps by defining something like a topology on it) is very important, not just for homotopy theory but for mathematics in general. An analogy occurs to me, to other very complicated objects (like the Stone-Čech compactification of the rationals or the reals, or maybe the Mandelbrot set) which are very mysterious but can approached as limits of more comprehensible objects. Indeed I wonder if this is what Neeman’s theory of approximable triangulated categories points toward.” 

  4. 4.

    Let us briefly recall the localization in the abelian category setting: [41, III, 1] [43, p. 122, Exer. 9]. Just as we may start with thick triangulated categories for Verdier quotients, which we will see in Remark 2.3 (iii), to localize an abelian category \(\mathcal {A}\) by its full subcategory \(\mathcal {B},\) we start with assuming \(\mathcal {B}\) is a \(\underline{Serre\,\,subcategory}\), i.e.

    $$\begin{aligned} \text {for any exact sequene}\ 0 \rightarrow B' \rightarrow B \rightarrow B'' \rightarrow 0 \ \text {in}\, \mathcal {A},\qquad \left( B\in \mathcal {B}\iff ( B' \in \mathcal {B}\, \text {and}\, B'' \in \mathcal {B}) \right) \end{aligned}$$

    Then the \(\underline{ quotient~ category~ \mathcal {A}/\mathcal {B}, ~in~ the~ sense~ of~ Gabriel, ~Grothendieck, and ~ Serre}\), is of the following form:

    $$\begin{aligned} \begin{aligned} {\text {Ob}} \mathcal {A}/\mathcal {B}:= {\text {Ob}} \mathcal {A}; \qquad {\text {``}\!{{\,\mathrm{Hom}\,}}\!\text {''}}_{\mathcal {A}/\mathcal {B}} ( A, A' ) := \varinjlim _{\underline{A},\underline{A'} \ \text {s.t.}\ A/\underline{A} \in \mathcal {B}, \underline{A'} \in \mathcal {B}} \ {{{\,\mathrm{Hom}}}_{\mathcal {A}}} \left( \underline{A}, A'/\underline{A'} \right) \end{aligned} \end{aligned}$$

    Thus, an element of \({{\,\mathrm{Hom}}}_{\mathcal {A}/\mathcal {B}}( A, A' )\) is of the following form:

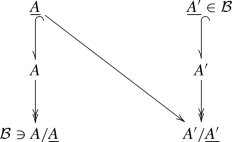
    However, if we consider a similar diagram in the setting of derived categories, we may take the homotopy pullback \(\widetilde{\underline{A}}\) as in the following diagram:

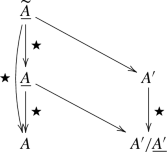
    Here, arrows with \(\bigstar \) are local maps, and so, this gives a pair of maps \(( A \xleftarrow {\bigstar } \widetilde{ \underline{A} } \rightarrow A' ),\) which is a typical element in the “\({{\,\mathrm{Hom}\,}}\)” class in the Verdier quotient.

  5. 5.

    WARNING!: In this article, we follow the convention of [111, Def. 1.5.1] [78, 4.5] for a \(\underline{ triangulated~ subcategory}\), which is automatically full by this convention. On the other hand, it is not so in the convention of [131, p. 3,1.1].

  6. 6.

    Verdier quotient does not necessarily have small \({{\,\mathrm{Hom}\,}}\)-sets.

  7. 7.

    If \(\mathcal {T}\) is essentially small, this result also follows immediately from a general result reviewed later in Proposition 4.3.

  8. 8.

    We dot not require \(\mathcal {T}\) to have small coproducts in this definition.

  9. 9.

    This is an adjoint pair of functors between ordinary categories, and we are not considering any triangulated structure.

  10. 10.

    Goes back at least to Verdier.

  11. 11.

    Let us recall the following precursor of this result in the setting of abelian categories, which goes back at least to Gabriel (see also [126, Lem. 3.2]): If an exact functor \(F : \mathcal {A}\rightarrow \mathcal {B}\) between abelian categories has a fully faithful right adjoint G (i.e. the adjunction \(F\circ G \rightarrow {\text {Id}}_{\mathcal {B}}\) is an isomorphism, then \({{\,\mathrm{Ker}\,}}F\) is Serre subcategory of \(\mathcal {A},\) and F induces the following equivalence of abelian categories: \(\mathcal {A}/ {{\,\mathrm{Ker}\,}}F \ \xrightarrow {\cong } \ \mathcal {B},\) where the left hand side is the abelian quotient category in the sense of Gabriel, Grothendieck, and Serre.

  12. 12.

    We do not require \(\mathcal {T}\) to have small coproducts.

  13. 13.

    An arrow above is left adjoint to the arrow below.

  14. 14.

    A Bousfield colocalization functor means its opposite functor is a Bousfield localization functor [54, Def. 3.1.1] [78, 2.8]. WARNING: This terminology is not consistent with that of Bousfield [21] (see [54, Rem. 3.1.4]).

  15. 15.

    Strictly speaking, the definition here is slightly differently from Krause’s, but essentially the same.

  16. 16.

    This claim itself is a special case of Corollary 2.17.

  17. 17.

    This “perfectly generated” condition is used to apply Brown representability (Theorem 2.15) to construct two right adjoints in the recollement.

  18. 18.

    For the precise definition of recollement, consult [15, 1.4].

  19. 19.

    Strictly speaking, this is the telescope conjecture without smash (tensor) product, but coincides with the original Ravenel’s telescope conjecture for \(\mathcal {T}=\mathcal {S}\mathcal {H},\) and more generally for rigidly compactly generated tensor triangulated categories [54, Def. 3.3.2, Def. 3.3.8] (see also Proposition 2.28).

  20. 20.

    For a serious treatment of the definition of “tensor triangulated category,” consult [92].

  21. 21.

    For a concise summary of the academic life of Professor Tetsusuke Ohkawa, see [91] in this proceedings.

  22. 22.

    For short reviews of the Morel-Voevodsky stable homotopy category, cosult [72, 94] for instance.

  23. 23.

    If \(x\in \mathcal {T}\) is strongly dualizable, i.e. rigid, the natural map \(x \rightarrow D^2x\) is an isomorphism [81, Chapter III] [54, Th. A.2.5.(b)].

  24. 24.

    In a rigidly compactly generated tensor triangulated category, any compact object is rigid, for, by Proposition 2.23, any compact object is seen to be isomorphic to a direct summand of a finite extensions of finite coproducts of rigid elements. In particular, in a rigidly compactly generated tensor triangulated category, \(\mathbbm {1}\) is both rigid and compact.

  25. 25.

    Recall in this case \(\mathcal {T}\) becomes distributive, because for any objects \(x_{\lambda }\ (\lambda \in \Lambda ), y, z\) in \(\mathcal {T},\) \( {{\,\mathrm{Hom}\,}}\left( ( \oplus _{\lambda } x_{\lambda } ) \otimes y, z \right) \cong {{\,\mathrm{Hom}\,}}\left( \oplus _{\lambda } x_{\lambda }, \underline{{{\,\mathrm{Hom}\,}}}(y,z) \right) \cong \prod _{\lambda } {{\,\mathrm{Hom}\,}}\left( x_{\lambda }, \underline{{{\,\mathrm{Hom}\,}}}(y,z) \right) \cong \prod _{\lambda } {{\,\mathrm{Hom}\,}}( x_{\lambda }\otimes y, z ) \cong {{\,\mathrm{Hom}\,}}\left( \oplus _{\lambda } x_{\lambda }\otimes y, z \right) .\)

  26. 26.

    Conjecture 2.32 should be taken more seriously. In fact, Professor Peter May is very glad to see Conjecture 2.32 is advertised here.

  27. 27.

    Our presentation of “supports” in this definition and next proposition is somewhat different from those given in [2, Proof of Th. 4.12] [61, App. A], but the author hopes this would be more transparent to the reader.

  28. 28.

    So, should had been known to Verdier.

  29. 29.

    Let us recall the following precursor of this result in the setting of abelian category of quasi-coherent sheaves, which should go back at least to Gabriel (see e.g. [126, In the proof of Prop. 3.1]): \( {{\,\mathrm{QCoh}\,}}(X) \big / {{\,\mathrm{QCoh}}}_Z (X) \ \xrightarrow [\cong ]{\overline{j^*}} \ {{\,\mathrm{QCoh}\,}}(U), \) where the left hand side is the abelian quotient category in the sense of Gabriel, Grothendieck, and Serre.

  30. 30.

    Unlike Theorem 2.37 stated under the noetherian assumption, (14) is stated under more general quasicompact, quasiseparated assumption. Therefore, in this equality \(\left( {{{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}} \right) _Z (X) := \left\{ Y \in {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X) \ \mid \ {{\,\mathrm{Supp}\,}}Y \subseteq Z \right\} = \mathrm {Ker}\ {\mathbf {L}}j^*,\) we may not replace \({{\,\mathrm{Supp}\,}}\) with \({{\,\mathrm{supp}\,}}.\) In fact, without the noetherian hypothesis, Theorem 2.37 becomes very bad as was shown in [107]. The author is grateful to Professor Neeman for this reference.

  31. 31.

    Such a property is not usually satisfied for general triangulated categories. So, most effort to generalize the Hopkins–Smith theorem for a general triangulated category \(\mathcal {T}\) aim at a classification of thick (tensor) ideals of \(\mathcal {T}^c.\)

  32. 32.

    This telescope conjecture is equivalent to the telescope conjecture without product Conjecture 2.22 via Propositions 2.28 and 2.29.

  33. 33.

    A trend here is to apply the higher algebra technique of Lurie [85, 86] to understand chromatic phenomena [13, 133], where the latter contains a concise review of higher algebra technology. Different kinds of applications of Lurie’s higher algebra technique can be seen in [89, 90].

  34. 34.

    This splitting conjecture implies, for any p-completed finite spectrum F and any infinite subset \(\{ n_i \}_{i=1}^{\infty } \subseteq \mathrm {N},\) the natural map \(F \rightarrow \prod _{i=1}^{\infty } L_{K(n_i)}F\) is split injective. For this and much more, consult [9, 51].

  35. 35.

    It appears that [97, p. 4, Corollary] should be modified as in (27).

  36. 36.

    Strickland’s theorem for \(G=\mathbb {Z}/2\) has recently been generalized to arbitrary finite group G by Balmer–Sanders [8].

  37. 37.

    See Defjnition 4.22 for this concept.

  38. 38.

    Or, researchers might prefer “\(\heartsuit \)-felt” \({{\,\mathrm{\mathbf {D}}}}^{b}_{\mathrm {coh}}(X) \cong \mathcal {D}^b( {{\,\mathrm{Coh}\,}}(X) )\) (although separated, not mere quasi-separated, assumption is needed for this equivalence) over simply formal \({{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}(X) \cong {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X)^c\)...

  39. 39.

    Having arbitrary small coproducts was an indispensable assumption for Brown representability and Bousfield localization (Theorem 2.15, Corollary 2.16).

  40. 40.

    If we apply (29) in order to obtain the isomorphism (32), we must require the extra “separated” assumption, for then we should also use the isomorphism:

    $$\begin{aligned} {{\,\mathrm{\mathbf {D}}}}^{b}_{\mathrm {coh}}(X) = \mathcal {D}^b( {{\,\mathrm{Coh}\,}}(X) ), \end{aligned}$$
    (32)

    which requires the “separated” assumption of X. This fact, and the above approach to use (30) was communicated to the author by Professor Neeman.

  41. 41.

    Professor Takeo Ohsawa is the AMS Stefan Bergman Prize 2014 recipient. His survey paper [114] in this proceedings is a concise summary of his work for which this prize was awarded. It was his Bergman Prize money which enabled us to invite distinguished lecturers to Ohkawa’s memorial conference at Nagoya University in the summer of 2015. Takeo Ohsawa was also Tetsusuke Ohkawa’s highschool classmate at Kanazawa University High School in Kanazawa, Japan.

  42. 42.

    X being proper over \({{\,\mathrm{Spec}\,}}(\mathbb {C})\) implies (as part of the definition of properness) that it is separated, hence \({{\,\mathrm{\mathbf {D}}}}^b ({{\,\mathrm{Coh}\,}}(X)) = {{\,\mathrm{\mathbf {D}}}}^{b}_{\mathrm {coh}}(X).\) Hence, these two isomorphisms are trivial consequences of the isomorphism \(\phi ^* : {{\,\mathrm{Coh}\,}}(X) \xrightarrow {\cong } {{\,\mathrm{Coh}\,}}(X^{\text {an}}).\) These two isomorphism are supplied just for reader’s information.

  43. 43.

    Of course, there are many other mathematical approaches to physics. For instance, some of Costello’s approach to quantum field theory via Lurie’s higher algebra [85, 86] point of view are touched upon in Matsuoka’s surveys [89, 90] in this proceedings.

  44. 44.

    Theorem 4.5 is reduced to Theorem 2.33 for \({{\,\mathrm{QCoh}\,}}(X) \cong {\text {Ind}} {{\,\mathrm{Coh}\,}}(X)\) under the Noetherian hypothesis [84, Lem. 3.9]. See also [25, p. 2] [121].

  45. 45.

    As we shall briefly review later, Bridgeland’s space of stability conditions is a kind of moduli space of “enriched hearts” of a triangulated category.

  46. 46.

    WARNING! We had already introduced the same notation \({{\,\mathrm{supp}\,}}\) back in Definition 2.35. However, from Proposition 2.36, Theorem 4.11, these two usages of \({{\,\mathrm{supp}\,}}\) coincide for the most fundamental example of \(\mathcal {K}= {{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}(X).\)

  47. 47.

    Let us recall the following related result in the setting of abelian category of quasi-coherent sheaves, which should go back at least to Gabiriel (see e.g. [126, Prop. 3.1]): \( {{\,\mathrm{Coh}\,}}(X) \big / {{\,\mathrm{Coh}}}_Z (X) \ \xrightarrow [\cong ]{\overline{j^*}} \ {{\,\mathrm{Coh}\,}}(U), \) where the left hand side is the abelian quotient category in the sense of Gabriel, Grothendieck, and Serre.

  48. 48.

    The following interesting historical account on the difficulty of generalizing statements in \({{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}\) (14) (15):

    $$\begin{aligned} {\left\{ \begin{array}{ll} {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X) \big / \left( {{{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}} \right) _Z (X) \ \xrightarrow [\cong ]{\overline{{\mathbf {L}}j^*}} \ {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(U) \\ L = {\mathbf {R}}j_* {\mathbf {L}}j^* = \left( {\mathbf {R}}j_*\mathcal {O}_U \right) \otimes _{\mathcal {O}_X}^{{\mathbf {L}}} - : \ {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X) \ \rightarrow \ {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X) \big / \left( {{{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}} \right) _Z (X) \ \xrightarrow [\cong ]{\overline{{\mathbf {L}}j^*}} \ {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(U) \xrightarrow {{\mathbf {R}}j_*} {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X) \end{array}\right. } \end{aligned}$$

    and the precursor in the setting of abelian categories reviewed in footnote 27:

    $$\begin{aligned} {{\,\mathrm{QCoh}\,}}(X) \big / {{\,\mathrm{QCoh}}}_Z (X) \ \xrightarrow [\cong ]{\overline{j^*}} \ {{\,\mathrm{QCoh}\,}}(U) \end{aligned}$$

    to the setting of \({{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}},\) has been communicated to the author by Professor Neeman:

    ... But the right adjoints \(j_* : {{\,\mathrm{QCoh}\,}}(U) \rightarrow {{\,\mathrm{QCoh}\,}}(X)\) and \({\mathbf {R}}j_* : {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(U) \rightarrow {{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X)\) fail to preserve the finite subcategories \({{\,\mathrm{Coh}\,}}(-)\) and \({{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}(- ).\) For these categories some work is needed. Especially in the case of \({{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}( - )\); for a long time all that was known was that \({\mathbf {L}}j^* : {{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}(X) \rightarrow {{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}(U)\) isn’t surjective on objects, hence the natural map

    $$\begin{aligned} \frac{ {{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}(X) }{ {{\,\mathrm{Ker}\,}}({\mathbf {L}}j^*) } \ \longrightarrow {{\,\mathrm{\mathbf {D}}}}^{\mathrm {perf}}(U) \ \end{aligned}$$

    couldn’t be an equivalence. So the assumption was that this map had to be worthless.

    Thomason’s ingenious insight was that the old counterexamples were a red herring. Up to idempotent completion this map is an equivalence, and in particular induces an isomorphism in higher K-theory. This of course required proof. Thomason gave a rather involved proof, following SGA6, and I noticed that the proof simplifies and generalizes when one uses the methods of homotopy theory.

    It was an amusing role reversal: Thomason, the homotopy theorist, had the brilliant idea but gave a clumsy proof using the techniques of algebraic geometry, while I, the algebraic geometer, simplified the argument with the techniques of homotopy theory.

  49. 49.

    This is the involved part of this proof, for the existence of recollement there requires Brown representability.

  50. 50.

    For the fact that the idempotent completion of a triangulated category has a natural structure of a triangulated category, there is a proof in Balmer–Schlichting [6].

  51. 51.

    The weaker reconstruction just as a topological space was already shown by Thomason (see Theorem 4.11) in the course of his establishing a \({{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X)\) analogue of the Hopkins–Smith theorem (see Theorems 4.12 and 4.10).

  52. 52.

    It was Neeman’s insight to notice surprising usefullness of introducing related categories \(\mathopen {\langle }\mathcal {A}\mathclose {\rangle }_{l}^{[m,n]}\) and \(\overline{\mathopen {\langle }\mathcal {A}\mathclose {\rangle }}_{l}^{[m,n]}\) as well.

  53. 53.

    The author is grateful to Professor Neeman for this reference.

  54. 54.

    Unlike (14) and Theorem 4.17, the general case (where X is quasicompact and quasiseparated) is still open—see [104, Just above Lem. 3.5].

  55. 55.

    There is some subtlety here. See e.g. [108, footnote 4 in Proof of Lem. 5; Sketch 7.19.(i)].

  56. 56.

    In fact, when X is affine, strong generation of \({{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X)\) has been proved by Iyengar and Takahashi [60] under different hypotheses, and using quite different techniques, from Neeman’s Theorem 5.16. And they give examples where strong generation fails; see [60] and references therein.

  57. 57.

    (Gabber’s strengthening [40] of) de Jong’s alteration is now widely used in the Morel–Voevodsky motivic stable homotopy theory. See e.g. [55, 71]. For an introductory review of de Jong’s alteration, consult Oort’s [117] for instance.

  58. 58.

    This proof does not directly use the approximability of \({{\,\mathrm{\mathbf {D}}}}_{\mathrm {qc}}(X),\) the approximability enters only indirectly, when we appeal to Theorem 5.10. What we want to highlight here, following a strong suggestion of Professor Neeman, is “the pivotal role that the homotopy-theoretical ideas of Bousfield, Ohkawa, Hopkins–Smith and many others play in the reduction.”

  59. 59.

    \(\underline{\mathrm{WARNING!}}\) In [109, Proof that Theorem 2.3 follows from Theorem 2.4], Neeman concluded the existence of an honest map \(H \rightarrow {\mathbf {R}}f_* \left( \mathcal {O}_Y \oplus \varSigma \mathcal {O}_Y\right) \) corresponding to (56). However, this is quite problematic, and usually, such an honest map \(H \rightarrow {\mathbf {R}}f_* \mathcal {O}_Y \oplus \varSigma {\mathbf {R}}f_* \mathcal {O}_Y\) does not exist. Thus, some sort of patch is needed. The “patch” presented above was communicated to the author by Professor Neeman, and the author replaced his own patch, which concentrates on \(\widetilde{R}\) (see (63)), with Professor Neeman’s “patch” , which concentrates on \(\widetilde{H}\) (see (63)), because Professor Neeman’s patch delivers a simple message how to read [109, Proof that Theorem 2.3 follows from Theorem 2.4]: just replace H with \(\widetilde{H}\) and pretend the map \(\widetilde{\psi }' : \widetilde{H} \rightarrow {\mathbf {R}}f_* \left( \mathcal {O}_Y \oplus \varSigma \mathcal {O}_Y \right) \) obtained in (63) as our “honest map” \(H \rightarrow {\mathbf {R}}f_* \left( \mathcal {O}_Y \oplus \varSigma \mathcal {O}_Y \right) ,\) and then, just proceed as is written in [109, Proof that Theorem 2.3 follows from Theorem 2.4].

    According to Professor Neeman, this leap and omission of justification is standard. So, the reader is required to come up with this kind of patch spelled out in terms of elementary Bousfield (or Miller’s finite) localization instantaneously at the top of his or her head. Thus, homotopy theoretical insight is prerequisite to read Professor Neeman’s papers!

  60. 60.

    In Neeman’s corresponding calculation [109, 1st paragraph in p. 24], the extension length of \({\text {Coprod}}\) was doubled to be \(2(M+N)\) rather than \(M+N\) given in (73). However, the author does not see such a need, and so, the author opted to present as in (73).

References

  1. Alonso Tarrío, L., Jeremías López, A., Souto Salorio, M.J.: Construction of t-structures and equivalences of derived categories. Trans. Am. Math. Society. 355(6), 2523–2543 (2003) MR1974001 (2004c:18020)

    Google Scholar 

  2. Alonso Tarrío, L., Jeremías López, A., Souto Salorio, M.J.: Bousfield localization on formal schemes. J. Algebra 278(2), 585–610 (2004). MR2071654 (2005g:14037)

    Google Scholar 

  3. Balmer, P.: The spectrum of prime ideals in tensor triangulated categories. J. Reine Angew. Math. 588, 149–168 (2005). MR2196732

    Google Scholar 

  4. Balmer, P.: Supports and filtrations in algebraic geometry and modular representation theory. Am. J. Math. 129(5), 1227–1250 (2007). MR2354319 (2009d:18017)

    Google Scholar 

  5. Balmer, P.: Tensor triangular geometry. In: Proceedings of the International Congress of Mathematicians, vol. II, pp. 85–112. Hindustan Book Agency, New Delhi (2010). MR2827786 (2012j:18016)

    Google Scholar 

  6. Balmer, P., Schlichting, M.: Idempotent completion of triangulated categories. J. Algebra 236(2), 819–834 (2001). MR1813503 (2002a:18013)

    Google Scholar 

  7. Balmer, P., Favi, G.: Generalized tensor idempotents and the telescope conjecture. Proc. Lond. Math. Soc. (3) 102(6), 1161–1185 (2011). MR2806103 (2012d:18010)

    Google Scholar 

  8. Balmer, P., Sanders B.: The spectrum of the equivariant stable homotopy category of a finite group. Invent. Math. 208(1), 283–326 (2017). MR3621837

    Google Scholar 

  9. Barthel, T.: A short introduction to the telescope and chromatic splitting conjectures, in this proceedings

    Google Scholar 

  10. Barthel, T., Heard, D., Valenzuela, G.: The algebraic chromatic splitting conjecture for Noetherian ring spectra. Math. Z. 290(3–4), 1359–1375 (2018). MR3856857

    Google Scholar 

  11. Beaudry, A.: The chromatic splitting conjecture at \(n = p = 2\), Geom. Topol. 21(6), 3213–3230 (2017). MR3692966

    Google Scholar 

  12. Beaudry, A., Goerss, P.G., Henn, H.-W.: Chromatic splitting for the \(K(2)\)-local sphere at \(p=2\). arXiv:1712.08182

  13. Behrens, M., Rezk, C.: Spectral algebra models of unstable \(v_n\)-periodic homotopy theory, in this proceedings

    Google Scholar 

  14. Beĭlinson, A.A., Bernstein, J., Deligne, P.: Faisceaux pervers. Analysis and Topology on Singular Spaces, I (Luminy, 1981). Astérisque, vol. 100, pp. 5–171. Société Mathématique de France, Paris (1982). MR0751966 (86g:32015)

    Google Scholar 

  15. Benson, D. J., Carlson, J.F., Rickard, J., Complexity and varieties for infinitely generated modules. II, Math. Proc. Cambridge Philos. Soc. 120(4), 597–615 (1996). MR1401950 (97f:20008)

    Google Scholar 

  16. Benson, D., Iyengar, S.B., Krause, H., Pevtsova, J.: Stratification for module categories of finite group schemes. J. Am. Math. Society. 31(1), 265–302 (2018). MR3718455

    Google Scholar 

  17. Bökstedt, M., Neeman, A.: Homotopy limits in triangulated categories. Compos. Math. 86(2), 209–234 (1993). MR1214458 (94f:18008)

    Google Scholar 

  18. Bondal, A., Orlov, D.: Reconstruction of a variety from the derived category and groups of autoequivalences. Compos. Math. 125(3), 327–344 (2001). MR1818984 (2001m:18014)

    Google Scholar 

  19. Bondal, A., Orlov, D.: Derived categories of coherent sheaves. In: Proceedings of the International Congress of Mathematicians, Beijing, 2002, vol. II, pp. 47–56. Higher Education Press, Beijing (2002). MR1818984

    Google Scholar 

  20. Bondal, A., Van den Bergh, M.: Generators and representability of functors in commutative and noncommutative geometry. Mosc. Math. J. 3(1), 1–36, 258 (2003). MR1996800 (2004h:18009)

    Google Scholar 

  21. Bousfield, A.K.: The localization of spectra with respect to homology. Topology, 18(4), 257–281 (1979). MR551009 55N20 (55N15 55P60)

    Google Scholar 

  22. Bridgeland, T.: Stability conditions on triangulated categories. Ann. Math. (2) 166(2), 317–345 (2007). MR2373143 (2009c:14026)

    Google Scholar 

  23. Buan, A.B., Krause, H., Solberg, Ø.: Support varieties: an ideal approach. Homol. Homotopy Appl. 9(1), 45–74 (2007). MR2280286 (2008i:18007)

    Google Scholar 

  24. Burke, J., Neeman, A., Pauwels, B.: Gluing approximable triangulated categories. arxiv.1806.05342

  25. Calabrese, J., Groechenig, M.: Moduli problems in abelian categories and the reconstruction theorem. Algebr. Geom. 2(1), 1–18 (2015). MR3322195

    Google Scholar 

  26. Casacuberta, C.: Depth and simplicity of Ohkawa’s argument, in this proceedings

    Google Scholar 

  27. Casacuberta, C., Rosický, J.: Combinatorial homotopy categories, in this proceedings

    Google Scholar 

  28. Casacuberta, C., Gutiérrez, J.J., Rosický, J.: A generalization of Ohkawa’s theorem. Compos. Math. 150(5), 893–902 (2014). MR3209799 55N20 18G55 55P42 55U40

    Google Scholar 

  29. Christensen, J.D.: Ideals in triangulated categories: phantoms, ghosts and skeleta. Adv. Math. 136(2), 284–339 (1998). MR1626856 (99g:18007)

    Google Scholar 

  30. Dao, H., Takahashi, R.: The dimension of a subcategory of modules. Forum Math. Sigma 3, e19 (2015) 31 pp. MR3482266

    Google Scholar 

  31. Dao, H., Takahashi, R.: Upper bounds for dimensions of singularity categories. Comptes Rendus Math. Acad. Sci. (Paris) 353(4), 297–301 (2015). MR3319124

    Google Scholar 

  32. de Jong, A.J.: Smoothness, semi-stability and alterations. Inst. Ht. Études Sci. Publ. Math. (83), 51–93 (1996). MR1423020 (98e:14011)

    Google Scholar 

  33. de Jong, A.J.: Families of curves and alterations. Ann. Inst. Fourier (Grenoble) 47(2), 599–621 (1997). MR1450427 (98f:14019)

    Google Scholar 

  34. Dell’Ambrogio, I., Stevenson, G.: On the derived category of a graded commutative Noetherian ring. J. Algebra 373, 356–376 (2013). MR2995031

    Google Scholar 

  35. Devinatz, E.S., Hopkins, M.J., Smith, J.H.: Nilpotence and stable homotopy theory. I. Ann. Math. (2) 128(2), 207–241 (1988). MR0960945 (89m:55009)

    Google Scholar 

  36. Douglas, M.R.: Dirichlet branes, homological mirror symmetry, and stability. In: Proceedings of the International Congress of Mathematicians, Beijing, 2002, vol. III, pp. 395–408. Higher Education Press, Beijing (2002). MR1957548

    Google Scholar 

  37. Dwyer, W.G., Palmieri, J.H., Ohkawa’s theorem: there is a set of Bousfield classes, Proc. Amer. Math. Soc. 129(3), 881-886 (2001). MR1712921 (2001f:55015)

    Google Scholar 

  38. Fukaya, K., Oh, Y.-G., Ohta, H., Ono, K.: Lagrangian Intersection Floer Theory: Anomaly and Obstruction. Part II. AMS/IP Studies in Advanced Mathematics, vol. 46.2. American Mathematical Society, Providence; International Press, Somerville (2009). xii+396 pp. MR2548482 (2011c:53218)

    Google Scholar 

  39. Fukaya, K., Oh, Y.-G., Ohta, H., Ono, K.: Lagrangian Intersection Floer Theory: Anomaly and Obstruction. Part I. AMS/IP Studies in Advanced Mathematics, vol. 46.1. American Mathematical Society, Providence; International Press, Somerville (2009). xii+396 pp. MR2553465 (2011c:53217)

    Google Scholar 

  40. Gabber, O.: Finiteness theorems for tale cohomology of excellent schemes. In: Conference in honor of P. Deligne on the occasion of his 61st birthday, IAS, Princeton, October 2005, p. 45 (2005)

    Google Scholar 

  41. Gabriel, P.: Des catégories abéliennes. Bull. Soc. Math. Fr. 90, 323–448 (1962). MR0232821 (38 #1144)

    Google Scholar 

  42. Gabriel, P., Zisman, M.: Calculus of fractions and homotopy theory. Ergebnisse der Mathematik und ihrer Grenzgebiete, vol. 35. Springer, New York (1967) x+168 pp. MR0210125 (35 # 1019)

    Google Scholar 

  43. Gelfand, S.I., Manin, Y.I.: Methods of Homological Algebra. Springer Monographs in Mathematics, 2nd edn. Springer, Berlin (2003). xx+372 pp. MR1950475 (2003m:18001)

    Google Scholar 

  44. Grothendieck, A.: Éléments de géométrie algébrique. III. Étude cohomologique des faisceaux cohérents. I. Ins. Ht. Études Sci. Publ. Math. 11, 5–167 (1961)

    Google Scholar 

  45. Grothendieck, A., Raynaud, M.: Revêtements étales et groupe fondamental, Séminaire de Géométrie Algébrique. I.H.E.S (1963)

    Google Scholar 

  46. Hall, J.: GAGA theorems. arXiv:1804.01976

  47. Hall, J., Rydh, D.: The telescope conjecture for algebraic stacks. J. Topol. 10(3), 776–794 (2017). MR3797596

    Google Scholar 

  48. Hopkins, M.: Global methods in homotopy theory. Homotopy Theory (Durham, 1985). London Mathematical Society Lecture Note Series, vol. 117, pp. 73–96. Cambridge University Press, Cambridge (1987). MR0932260 (89g:55022)

    Google Scholar 

  49. Hopkins, M.J., Gross, B.H.: The rigid analytic period mapping, Lubin-Tate space, and stable homotopy theory. Bull. Am. Math. Soc. (N.S.) 30(1), 7686 (1994). MR1217353 (94k:55009)

    Google Scholar 

  50. Hopkins, M.J., Smith, J.H.: Nilpotence and stable homotopy theory. II. Ann. Math. (2) 148(1), 1–49 (1998). MR1652975 (99h:55009)

    Google Scholar 

  51. Hovey, M.: Bousfield localization functors and Hopkins’ chromatic splitting conjecture. The Čech centennial, Boston, MA, 1993. Contemporary Mathematics, vol. 181, pp. 225–250. American Mathematical Society, Providence, RI (1995). MR1320994 (96m:55010)

    Google Scholar 

  52. Hovey, M.: Cohomological Bousfield classes. J. Pure Appl. Algebra 103(1), 45–59 (1995). MR1354066 (96g:55008)

    Google Scholar 

  53. Hovey, M., Palmieri, J.H.: The structure of the Bousfield lattice. Homotopy Invariant Algebraic Structures, Baltimore, MD, 1998, pp. 175–196. Contemporary Mathematics, vol. 239, 1999. MR1718080 (2000j:55033)

    Google Scholar 

  54. Hovey, M., Palmieri, J.H., Strickland, N.P.: Axiomatic Stable Homotopy Theory. Memoirs of the American Mathematical Society, vol. 128 (610), x+114 pp. (1997). MR1388895 (98a:55017)

    Google Scholar 

  55. Hoyois, M., Kelly, S., Østvær, P.A.: The motivic Steenrod algebra in positive characteristic. J. Eur. Math. Soc. (JEMS) 19(12), 3813–3849 (2017). MR3730515

    Google Scholar 

  56. Huybrechts, D.: Fourier-Mukai transforms in algebraic geometry. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, Oxford (2006). viii+307 pp. MR2244106 (2007f:14013)

    Google Scholar 

  57. Huybrechts, D., Lehn, M.: The geometry of moduli spaces of sheaves. Cambridge Mathematical Library, 2nd edn. Cambridge University Press, Cambridge (2010). xviii+325 pp. MR2665168 (2011e:14017)

    Google Scholar 

  58. Iyengar, S.B., Krause, H.: The Bousfield lattice of a triangulated category and stratification. Math. Z. 273(3–4), 1215–1241 (2013). MR3030697

    Google Scholar 

  59. Iyengar, S.B., Takahashi, R.: Annihilation of cohomology and decompositions of derived categories. Homol. Homotopy Appl. 16(2), 231–237 (2014). MR326389

    Google Scholar 

  60. Iyengar, S.B., Takahashi, R.: Annihilation of cohomology and strong generation of module categories. Int. Math. Res. Not. IMRN 2016(2), 499–535 (2016). MR3493424

    Google Scholar 

  61. Iyengar, S.B., Lipman, J., Neeman, A.: Relation between two twisted inverse image pseudofunctors in duality theory. Compos. Math. 151(4), 735–764 (2015). MR3334894

    Google Scholar 

  62. Joachimi, R.: Thick ideals in equivariant and motivic stable homotopy categories, in this proceedings

    Google Scholar 

  63. Jørgensen, P.: A new recollement for schemes. Houst. J. Math. 35(4), 1071–1077 (2009). MR2577142 (2011c:14048)

    Google Scholar 

  64. Kapustin, A.N., Li, Y.: Topological correlators in Landau-Ginzburg models with boundaries. Adv. Theor. Math. Phys. 7(4), 727–749 (2003). MR2039036 (2005b:81179a)

    Google Scholar 

  65. Kashiwara, M., Schapira, P.: Sheaves on manifolds. With a chapter in French by Christian Houzel. Corrected reprint of the 1990 original. Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 292. Springer, Berlin (1994). x+512 pp. MR1299726 (95g:58222)

    Google Scholar 

  66. Kato, R., Okajima, H., Shimomura, K.: Notes on an algebraic stable homotopy category, in this proceedings

    Google Scholar 

  67. Kawamata, Y.: \(D\)-equivalence and \(K\)-equivalence. J. Differ. Geom. 61(1), 147–171 (2002). MR1949787 (2004m:14025)

    Google Scholar 

  68. Kawamata, Y.: Birational geometry and derived categories. arXiv:1710.07370

  69. Keller, B.: A remark on the generalized smashing conjecture. Manuscr. Math. 84(2) (1994). 193198 MR1285956 (95h:18014)

    Google Scholar 

  70. Kelly, G.M.: Chain maps inducing zero homology maps. Proc. Camb. Philos. Soc. 61, 847–854 (1965). MR0188273 (32 # 5712)

    Google Scholar 

  71. Kelly, S.: Triangulated categories of motives in positive characteristic. Ph.D. thesis, University of Paris 13; Australian National University (2013). arXiv:1305.5349v2

  72. Kelly, S.: Some observations about motivic tensor triangulated geometry over a finite field, in this proceedings

    Google Scholar 

  73. Kollár, J., Mori, S.: Birational geometry of algebraic varieties, With the collaboration of C. H. Clemens and A. Corti; Translated from the 1998 Japanese original, Cambridge Tracts in Mathematics, vol. 134. Cambridge University Press, Cambridge, 1998, viii+254pp, MR1658959 (2000b:14018)

    Google Scholar 

  74. Kontsevich, M.: Homological algebra of mirror symmetry. In: Proceedings of the International Congress of Mathematicians, Zurich, 1994, vol. 1, 2, pp. 120–139. Birkhauser, Basel (1995). MR1403918 (97f:32040)

    Google Scholar 

  75. Kontsevich, M., Soibelman, Y.: Stability structures, motivic Donaldson-Thomas invariants and cluster transformations (2008). arXiv:0811.2435

  76. Krause, H.: Smashing subcategories and the telescope conjecture–an algebraic approach. Invent. Math. 139(1), 99–133 (2000). MR1728877 (2000k:55016)

    Google Scholar 

  77. Krause, H.: A Brown representability theorem via coherent functors. Topology 41(4), 853–861 (2002). MR1905842 (2003c:18011)

    Google Scholar 

  78. Krause, H.: Localization theory for triangulated categories. Triangulated Categories. London Mathematical Society Lecture Note Series, vol. 375, pp. 161–235 (2010). MR2681709 (2012e:18026)

    Google Scholar 

  79. Krause, H.: Completing perfect complexes. arXiv:1805.10751

  80. Krause, H., Šťovíček, J.: The telescope conjecture for hereditary rings via Ext-orthogonal pairs. Adv. Math. 225(5), 2341–2364 (2010). MR2680168 (2011j:16013)

    Google Scholar 

  81. Lewis Jr., L.G., May, J.P., Steinberger, M.: Equivariant stable homotopy theory. With contributions by J. E. McClure. Lecture Notes in Mathematics, vol. 1213. Springer, Berlin (1986). x+538 pp. MR0866482 (88e:55002)

    Google Scholar 

  82. Lipman, J.: Notes on derived functors and Grothendieck duality. Foundations of Grothendieck duality for diagrams of schemes. Lecture Notes in Mathematics, vol. 1960, pp. 1–259. Springer, Berlin (2009). MR2490557 (2011d:14029)

    Google Scholar 

  83. Lipman, J., Neeman, A.: Quasi-of the twisted inverse image functor perfect scheme-maps and boundedness. Ill. J. Math. 51(1), 209–236 (2007). MR2346195 (2008m:14004)

    Google Scholar 

  84. Lurie, J.: Tannaka duality for geometric stacks. arXiv:math/0412266v2

  85. Lurie, J.: Higher Topos Theory. Annals of Mathematics Studies, vol. 170. Princeton University Press, Princeton (2009). MR2522659 (2010j:18001)

    Google Scholar 

  86. Lurie, J.: Higher algebra. www.math.harvard.edu/~lurie/ (2016)

  87. Mahowald, M., Ravenel, D., Shick, P.: The triple loop space approach to the telescope conjecture. Homotopy Methods in Algebraic Topology, Boulder, CO, 1999. Contemporary Mathematics, vol. 271, pp. 217–284. American Mathematical Society, Providence, RI (2001). MR1831355 (2002g:55014)

    Google Scholar 

  88. Matsuki, K.: Introduction to the Mori Program. Universitext. Springer, New York (2002). xxiv+478, MR1875410 (2002m:14011)

    Google Scholar 

  89. Matsuoka, T.: Koszul duality for \(E_n\)-algebras in a filtered category, in this proceedings

    Google Scholar 

  90. Matsuoka, T.: Some technical aspects of factorization algebras on manifolds, in this proceedings

    Google Scholar 

  91. Matumoto, T.: Memories on Ohkawa’s mathematical life in Hiroshima, in this proceedings

    Google Scholar 

  92. May, J.P.: The additivity of traces in triangulated categories. Adv. Math. 163(1), 3473 (2001). MR1867203 (2002k:18019)

    Google Scholar 

  93. Miller, H.: Finite localizations. Papers in honor of Jos Adem Bol. Soc. Mat. Mex. (2) 37(1–2), 383–389 (1992). MR1317588 (96h:55009)

    Google Scholar 

  94. Minami, N.: A topologist’s introduction to the motivic homotopy theory for transformation group theorists–1, Geometry of transformation groups and combinatorics, RIMS Kôkyûroku Bessatsu. Res. Inst. Math. Sci. (RIMS), Kyoto, B39, 63–107 (2013). MR3156820

    Google Scholar 

  95. Miyaoka, Y., Peternell, T.: Geometry of Higher-Dimensional Algebraic Varieties. DMV Seminar, vol. 26. Birkhuser Verlag, Basel, 1997. vi+217 pp. MR1468476 (98g:14001)

    Google Scholar 

  96. Morava, J.: Noetherian localisations of categories cobordism comodules. Ann. Math. (2) 121, 1–39 (1985). MR0782555 (86g:55004)

    Google Scholar 

  97. Morava, J.: A remark on Hopkins’ chromatic splitting conjecture. arXiv:1406.3286,

  98. Morava, J.: Operations on integral lifts of \(K(n)\), in this proceedings

    Google Scholar 

  99. Morava, J.: Toward a fundamental groupoid for the stable homotopy category. In: Proceedings of the Nishida Fest, Kinosaki, 2003. Geometry and Topology Monographs, vol. 10, pp. 293–318. Geometry & Topology Publications, Coventry (2007). MR2402791 (2009e:55018)

    Google Scholar 

  100. Morel, F., Voevodsky, V.: \({\bf A}^1\)-homotopy theory of schemes. Inst. Ht. Études Sci. Publ. Math. 90, 1999, 45–143 (2001), MR1813224 (2002f:14029)

    Google Scholar 

  101. Mukai, S.: Duality between \(D(X)\) and \(D(\hat{X})\) with its application to Picard sheaves. Nagoya Math. J. 81, 153–175 (1981). MR0607081 (82f:14036)

    Google Scholar 

  102. Nayak, S.: Compactification for essentially finite-type maps. Adv. Math. 222(2), 527–546 (2009)

    Google Scholar 

  103. Neeman, A.: The chromatic tower for \(D(R)\). Topology 31(3), 519–532 (1992). With an appendix by Marcel Bökstedt. MR1174255 (93h:18018)

    Google Scholar 

  104. Neeman, A.: Triangulated categories with a single compact generator and a Brown representability theorem. arXiv:1804.02240

  105. Neeman, A.: The connection between the \(K\)-theory localization theorem of Thomason, Trobaugh and Yao and the smashing subcategories of Bousfield and Ravenel. Ann. Sci. l’Ecole Norm. Supér. (4) 25(5), 547–566 (1992). MR1191736 (93k:18015)

    Google Scholar 

  106. Neeman, A.: The Grothendieck duality theorem via Bousfield’s techniques and Brown representability. J. Am. Math. Soc. 9(1), 205–236 (1996). MRMR1308405

    Google Scholar 

  107. Neeman, A.: Oddball Bousfield classes. Topology 39(5), 931–935 (2000). MR1763956 (2001c:18007)

    Google Scholar 

  108. Neeman, A.: Approximable triangulated categories. arXiv:1806.06995

  109. Neeman, A.: Strong generators in \(D^{perf}(X)\) and \(D^b_{coh}(X)\). arXiv:1703.04484

  110. Neeman, A.: The categories \({\cal{T}}^c\) and \({\cal{T}}^b_c\) determine each other. arXiv:1806.06471

  111. Neeman, A.: Triangulated Categories. Annals of Mathematics Studies, vol. 148. Princeton University Press, Princeton (2001). MR1812507 (2001k:18010)

    Google Scholar 

  112. Neeman, A.: The K-theory of triangulated categories. Handbook of K-theory, vol. 1, 2, pp. 1011–1078 (2005). MR2181838 (2006g:19004)

    Google Scholar 

  113. Noguchi, J.: Analytic Function Theory of Several Variables. Elements of Oka’s Coherence. Springer, Singapore (2016). xvi+397 pp. MR3526579

    Google Scholar 

  114. Ohsawa, T.: A role of the \(L^2\) method in the study of analytic families, in this proceedings

    Google Scholar 

  115. Ohkawa, T.: The injective hull of homotopy types with respect to generalized homology functors. Hiroshima Math. J. 19(3), 631–639 (1989). MR1035147

    Google Scholar 

  116. Ohsawa, T.: \(L^2\) Approaches in Several Complex Variables. Development of Oka-Cartan Theory by \(L^2\) Estimates for the \(\overline{\partial }\) Operator. Springer Monographs in Mathematics. Springer, Tokyo (2015). MR3443603

    Google Scholar 

  117. Oort, F.: Alterations can remove singularities. Bull. Am. Math. Soc. (N.S.) 35(4), 319–331 (1998). MR1638306 (99i:14021)

    Google Scholar 

  118. Orlov, D.O.: Triangulated categories of singularities and D-branes in Landau-Ginzburg models. (Russian. Russian summary) Tr. Mat. Inst. Steklova 246 (2004), Algebr. Geom. Metody, Svyazi i Prilozh, 240–262; translation in Proc. Steklov Inst. Math. 2004, no. 3(246), 227–248. MR2101296 (2006i:81173)

    Google Scholar 

  119. Orlov, D.O.: Matrix factorizations for nonaffine LG-models. Math. Ann. 353(1), 95–108 (2012). MR2910782 14F05 18E30

    Google Scholar 

  120. Orlov, D.: Smooth and proper noncommutative schemes and gluing of DG categories. Adv. Math. 302, 59–105 (2016). MR3545926 14F05 (16E45 18E30)

    Google Scholar 

  121. Perego, A.: A Gabriel theorem for coherent twisted sheaves. Math. Z. 262(3), 571–583 (2009). MR2506308 (2011a:14032)

    Google Scholar 

  122. Ravenel, D.C.: Localization with respect to certain periodic homology theories. Am. J. Math. 106(2), 351–414 (1984). MR0737778 (85k:55009)

    Google Scholar 

  123. Ravenel, D.C.: Nilpotence and periodicity in stable homotopy theory. Ann. Math. Stud. 128, Appendix C by Jeff Smith (1992) xiv+209 MR1192553 (94b:55015)

    Google Scholar 

  124. Rosenberg, A.: Spectra of ‘Spaces’ Represented by Abelian Categories. MPIM Preprints, 2004-115

    Google Scholar 

  125. Rouquier, R.: Dimensions of triangulated categories. J. K-Theory 1(2), 193–256 (2008). MR2434186

    Google Scholar 

  126. Rouquier, R.: Derived categories and algebraic geometry. Triangulated Categories. London Mathematical Society Lecture Note Series, vol. 375, pp. 351–370. Cambridge University Press, Cambridge (2010). MR2681712 (2011h:14022)

    Google Scholar 

  127. Seidel, P., Thomas, R.: Braid group actions on derived categories of coherent sheaves. Duke Math. J. 108(1), 37–108 (2001). MR1831820 (2002e:14030)

    Google Scholar 

  128. Serre, J.P.: Géométrie algébrique et géométrie analytique. Ann. l’institut Fourier (Grenoble) 6, 1–42 (1955–1956). MR0082175 (18,511a)

    Google Scholar 

  129. The Stacks Project, Part 1: Preliminaries, Chapter 17: Sheaves of modules, Section 17.9: Modules of finite type

    Google Scholar 

  130. Thomason, R.W., Trobaugh, T.: Higher algebraic K-theory of schemes and of derived categories. The Grothendieck Festschrift, Volume III. Progress in Mathematics, vol. 88, pp. 247–435. Birkhuser Boston, Boston (1990). MR1106918 (92f:19001)

    Google Scholar 

  131. Thomason, R.W.: The classification of triangulated subcategories. Compos. Math. 105(1), 1–27 (1997). MR1436741 (98b:18017)

    Google Scholar 

  132. Toda, Y.: Limit stable objects on Calabi-Yau 3-folds. Duke Math. J. 149(1), 157–208 (2009). MR2541209 (2011b:14043)

    Google Scholar 

  133. Torii, T.: On quasi-categories of comodules and Landweber exactness, in this proceedings

    Google Scholar 

  134. Uehara, H.: An example of Fourier-Mukai partners of minimal elliptic surfaces. Math. Res. Lett. 11(2–3), 371–375 (2004). MR2067481 (2005g:14073)

    Google Scholar 

  135. Verdier, J.-L.: Catégories dérivées: quelques résultats (état 0). Cohomologie étale. Lecture Notes in Mathematics, vol. 569, pp. 262–311. Springer, Berlin (1977). MR3727440

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Nagoya Institute of Technology, Gokiso, Showa-ku, Nagoya, 466-8555, Japan

    Norihiko Minami

Authors
  1. Norihiko Minami
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Norihiko Minami .

Editor information

Editors and Affiliations

  1. Graduate School of Mathematics, Nagoya University, Nagoya, Aichi, Japan

    Takeo Ohsawa

  2. Department of Computer Science, Nagoya Institute of Technology, Nagoya, Japan

    Norihiko Minami

Rights and permissions

Reprints and permissions

Copyright information

© 2020 Springer Nature Singapore Pte Ltd.

About this paper

Check for updates. Verify currency and authenticity via CrossMark

Cite this paper

Minami, N. (2020). From Ohkawa to Strong Generation via Approximable Triangulated Categories—A Variation on the Theme of Amnon Neeman’s Nagoya Lecture Series. In: Ohsawa, T., Minami, N. (eds) Bousfield Classes and Ohkawa's Theorem. BouCla 2015. Springer Proceedings in Mathematics & Statistics, vol 309. Springer, Singapore. https://doi.org/10.1007/978-981-15-1588-0_3

Download citation

Publish with us

Policies and ethics

Search

Navigation