Keywords

1 Introduction

In advanced social network environment, multimedia signal sequences of big data streams are composed of time series processes. Quantum experiments in quantum satellite using quantum key distribution (QKD) systems [1] is the most advanced ICT development to establish ultra-secure quantum communications. For a QKD system, a truly random number generator [2] play a key role. From an analysis viewpoint, it is necessary to test stationary randomness in time variations. In this section, a list of relevant schemes: pseudo/truly random sequences, P_value, statistical probability distribution, optical statistics, stationary properties, and variant maps, are discussed.

1.1 Pseudo/True Random Sequences

1.1.1 Pseudorandom Sequences

Traditional stream ciphers [3] on linear feedback shift register structure (LFSR) are used as pseudorandom number generators. The LFSR stream ciphers are the core in classical stream ciphers.

The new generation of stream ciphers has being shifted from LFSR [3] to nonlinear modes: NLFSR, clock control [4] and nonlinear functions, etc. It is difficult to use nonlinear mathematical theories, recursive models, descriptive tools, and implementing schemes in nonlinear dynamic environments.

1.1.2 True Random Sequences

Differently from pseudorandom sequences generated by stream ciphers, high-quality stochastic oscillators of truly random sequences are generated from special hardware devices such as laser photonics [5], nonlinear optics, quantum optics [6], quantum noises, thermal noise, chaos, and fractal nonlinear dynamics [7].

1.2 Testing Schemes

1.2.1 P_value Schemes

Various statistic testing packages measure randomness properties on a given random sequence. NIST 800-22 package [8] is a typical representative to provide more than 15 testing schemes. Using the package, it is essential to check whether P_value >0.01 for the sequence. Since such measuring scheme provides a static condition, it is difficult to use only P_value parameter to express complex dynamic behaviors involved in random sequences.

1.2.2 Multiple Statistical Probability Distributions

Measuring random sequences under segment conditions, multiple statistical probability schemes are useful to create various distributions to illustrate complex spatial relationships.

Multivariate normal probability distributions are the most important and powerful tools to test stochastic characteristics of a random data sequence under the framework of probability, stochastic process and statistics [9] for nonlinear problems. In this kind of measuring models, when a data sequence is sufficiently long, the high dimensional probability distribution of the sequence [10] is converged to a continuous Gaussian distribution. Multivariate Gaussian probability distributions support various schemes to analyze complex stochastic data set of measuring sequences in continuous conditions.

1.2.3 Photon Statistic in Quantum Optics

Photon statistics is the theoretical and experimental approach on the statistical distributions in photon counting experiments to analyze the statistical nature of photons in a light source.

Three types of distributions can be obtained by the light source [11]: Poissonian, super-Poissonian, and sub-Poissonian. The variance and average number of photon counts are identified for the corresponding distribution. Both Poissonian and super-Poissonian light are described by a semi-classical theory in which the light source is modeled as an electromagnetic wave and the atom is modeled by quantum mechanics. In contrast, sub-Poissonian light requires the quantization of the electromagnetic field for a proper description and is a direct measure of the particle nature of light.

1.2.4 Stationary Properties

In mathematics and statistics, a stationary process is a stochastic process [12] whose joint probability distribution does not change when shift operations performed. Consequently, parameters such as mean and variance, if they are present, also do not change over time. Stationarity is an interesting property in time series analysis.

In applied mathematics, the Wiener–Khinchin theorem [13], states that the Autocorrelation Function (ACF) of a wide-sense stationary process has a spectral decomposition given by the power spectrum of the process. One of the effective ways for identifying stationary times series is the ACF plot [14]. For a stationary time series, the ACF will drop to zero relatively quickly.

1.3 Quantum Random Resources

Quantum random numbers can be generated from a physical quantum source of a coherent laser light to be splitting a beam of light into two beams and then measuring the power in each beam. Due to the light intensity in each beam fluctuates about the mean. Those fluctuations can be converted into a source of random numbers [15,16,17] being a stationary Poisson distribution.

1.3.1 ANU Resource

The ANU Quantum Random Numbers Server is an open website [18] to offer true random numbers to anyone on the internet. Such random numbers are generated in real-time by measuring the quantum fluctuations of the vacuum. The electromagnetic field of the vacuum exhibits random fluctuations in phase and amplitude at all frequencies. By carefully measuring these fluctuations, ultra-high bandwidth random numbers can be generated.

About 1 GB data streams are downloaded and 100 MB data streams are used for the testing.

1.3.2 USTC Resource

In the Key Laboratory of Quantum Information, USTC, and CAS, true random number sequences are generated [16]. This type of true random sequences supports advanced quantum communication devices of QKD systems [19].

More than 20 GB quantum random number sequences are provided by USTC for random streams testing. Two data sequences are represented as USTC\(_0\) (initial) and USTC (secure), respectively. About 100 MB data streams are selected for each sequence.

1.3.3 Refined Properties

From an analysis viewpoint, a Toeplitz hash algorithm has used to get an initial sequence USTC\(_0\) as input and USTC sequence as output. Checking such refined variations, this is an interesting property for us to make a detailed identification.

From a random testing viewpoint, initial sequences have some difficulties to pass NIST tests and secure sequences are ensured to pass NIST tests. Some refined differences on random characteristics could be distinguished.

1.4 Variant Framework

Various schemes following the top-down strategy are explored to use multiple measures to partition special phase spaces from a top state set to multiple bottom states via multilevels of a hierarchy in combinatorial algorithms [20], image analysis and processing for many years.

The conjugate classification [21] is proposed to apply seven measures in a hierarchy to partition the kernels of four regular plane lattices on \(n=\{4,5,7,9\}\) cases for 2D binary images. For 1D cellular automata sequences, global random behaviors are visualized in 2D maps.

For n-tuple bit vectors, the variant logic framework [22] is proposed, various applications are explored: 3D visual method on random number sequences [23], variant Pseudorandom Number Generator (PRNG) [24], computational simulation on quantum interactions [25], noncoding DNA analysis, bat echolocation [26], and stationary randomness [27].

1.5 Proposed Scheme

For the convenience of testing stationary randomness on random sequences, we propose a testing system for a stationary random sequence with length N, multiple segments M are divided from the sequence by a given length m, a 2-tuple pair of measures can be extracted from a 0-1 segment that are the number of 1 element and the number of 1 pattern in the segment. All paired measures are composed of a sequence of M pairs of measures as an ordered measuring set with M elements.

The pairs of the measuring sequence are directly separated as two independent measuring sequences to keep each parameter in the same order. A total of three sequences of distinct measures are constructed including two sequences on single measures and one sequence on 2-tuple measures.

Following this approach, two sets of single measuring sequences are sorted as two 1D numeric arrays as statistical histograms corresponding to 1D maps and the 2-tuple measuring sequence is sorted as a 2D integer array as statistic histograms being a 2D map. Under the controlling operations on the changes of shift displacement, multiple results of the three measuring sequences are transformed into 1D statistic histograms and 2D pseudo-color maps to show effective patterns from the generated sequence under various positions and conditions on a list of shift operations.

1.6 Organization of the Chapter

This chapter uses a testing system for a stationary random sequence on the system architecture in Sect. 2. In Sect. 3, test results are provided for two quantum random sequences. From the results of the visual maps in Sect. 3, result analysis and brief comparison are described in Sect. 4. And finally in Sect. 5, the main results are summarized.

Fig. 1
figure 1

The architecture of testing stationary random sequences

Full size image

2 Testing System

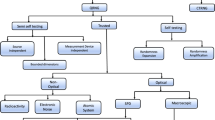
To describe the testing system, diagrams are shown in Fig. 1.

2.1 System Architecture

This system is composed of five parts: Input, Shifted Transformation (ST), Segment Measurement (SM), Combinatorial Projection (CP), and Output.

The input of the testing system is a selected 0-1 sequence and its output is composed of three maps, two in 1D and one in 2D for visual distributions, and three maximals to be processed by ST, SM, and CP modules, respectively.

Further technical details are described in Chapter. Stationary Randomness of Three Types of Six Random Sequences on Variant Maps of this book.

3 Testing Results

Three quantum random sequences are selected from ANU and USTC resources.

Typical results of testing stationary properties for three sequences in nine maps are shown in Fig. 2. Three sets of results are shown in Fig. 3a, b. In Fig. 3a, six values of \(r=\{0, 16, 32, 96, 112, 128\}\) are selected to show three pairs of corresponding maps: 1DP, 2DPQ, and 1DQ for three sequences on the top part. Nine 2D maps of maximal curves for \(r=0-128\) are shown to illustrate refined properties in stationary random curves on the bottom column. In Fig. 3b, three maximal curves on three 2D maps are compared. In Fig.  4a–c, three larger maps on \(r=\{48,64,80\}\) are shown corresponding to (a) 1DP, (b) 2DPQ, and (c) 1DQ for three cases. Three larger maps of three maximal curves are shown in Fig. 5.

Fig. 2
figure 2

ANU, USTC and USTC\(_0\) random sequences on 1DP, 2DPQ, and 1DQ maps

Full size image
Fig. 3
figure 3

ANU, USTC and USTC\(_0\) random sequences on three maps and maximals (a), (b); a Three pairs of nine variant maps in six groups and three pairs of nine maximal maps; b Three 2D maps of three maximal curves for ANU, USTC, and USTC\(_0\)

Full size image
Fig. 4
figure 4figure 4

ANU, USTC, and USTC\(_0\) random sequences random sequences on enlarged maps, \(r=\{48,64,80\}\); a 1DP; b 2DPQ; c 1DQ

Full size image
Fig. 5
figure 5

Three enlarged 2D maps of three maximal curves for ANU, USTC, and USTC\(_0\)

Full size image

3.1 Quantitative Measurements

For a G map, let \(G_x\) be an average variation, \(\varDelta G_x\) be a region of variations and \( G_x^R = \varDelta G_x/G_x\) be a variation ratio. In convenient in comparison, let {Max, Min} be the {largest, smallest} value on a maximal curve; Max-Min is its difference and \(|ANU-USTC|\) is an absolute difference between ANU and USTC measures. Let \((Max-Min)/|ANU-USTC|\) be a relative ratio between (Max-Min) and \(|ANU-USTC|\).

4 Result Analysis

Nine maps in Fig. 2 are in three columns. Three 1DP maps have similar distributions in bell shapes to illustrate Poissonian distributions. Three 2DPQ maps are 2D distributions and there are different symmetric distributions. Maximal elements in ANU, USTC, and USTC\(_0\) maps show stronger vertical oriented features. Three maps have a symmetry on left/right directions and have a broken symmetry on up/down directions. Pseudo-color pixels on three maps are shown in 3D shapes. Compared with three 1DP maps, three 1DQ maps have similar distributions and more narrow bell shapes to illustrate sub-Poissonian distributions.

Six groups of results on shift \(r:\{0,16,32, 96,112,\) \(128\}\) are shown in Fig. 3a on the top columns and each group contains nine distributions in three columns. Three random sequences have stronger stationary randomness that makes all maps in the similar style with minor changes on shift operations. Larger maps on \(r=\{48,64,80\}\) in Fig. 4a–c provide refined visual information to show their variations in details. Enlarged and larger maximal curves are shown in Figs. 3b and 5 for \(r:0-128\) as nine 2D maps with values of average variation and region of variations. From the maximal and minimal stationary regions, there are 1–2% variation ratios for 1DP and 1DQ and \(5\%\) variation ratios for 2DPQ observed. Three curves of maximals on three 2D maps are illustrated in Figs. 3b and 5.

4.1 Relative Ratios on Differences

Details of three maximal measures are compared in Table 1. Three parameters \(\{Q_x, \varDelta Q_x, Q_x^R\}\) on 1DQ maps have 1 values on Max-Min and \(|ANU-USTC|\) ratios; there are 81 on \(P_x\) and 1.6 on \(P_x^R\) and there are 65 on \(PQ_x\) and 7.9 on \(PQ_x^R\) observed.

From this set of testing results, two samples of ANU and USTC are showing similar stationary properties and USTC\(_0\) with different stationary properties among the three sequences. Significant differences of relative ratios are observed from 2DPQ variation measurements.

5 Conclusion

It is feasible to evaluate stationary randomness for a random sequence using the testing system. From three maps {1DP, 1DQ, 2DPQ}, maximals are identified for shift \(r:0-m\). Three 2D maps of maximal curves provide refined characteristics to evaluate stationary randomness. Further explorations and applications are required to check the testing system on other applications.

Table 1 Comparisons on three measures for ANU, USTC, and USTC\(_0\) samples
Full size table