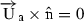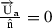Panel Methods

Abstract

The panel methods are the numerical techniques for solving incompressible potential flows over thick two- and three-dimensional geometries by replacing them with mathematical models comprising of sources and vortex panels. The surface to be analyzed will be depicted by the panels consisting of sources and vortices, in turn, these methods are referred to as source panel and vortex panel methods, respectively. In this chapter, we will discuss both source and vortex panel methods along with their applications.

Appendices

Summary

The fluid flow characteristics around any complex three-dimensional vehicle configurations such as an aircraft, automobile, etc., can be determined using the panel methods. The aerospace industry has pioneered in developing and adopting these methods which are ideal for comparatively easy surface modeling and analysis due to their time effective calculations. They show superior performance in modeling fully attached, high Reynolds number subsonic flows. Also, they are proficient in calculating the lift and form drag on the wing and/or over an entire aircraft as long as viscous effects are negligibly small. Although, the panel methods were originally conceived for incompressible flows $\mathrm {\left( M<\text {0.3}\right) }$ only, however, by incorporating compressibility corrections they can be extended to high subsonic speeds $\mathrm {\left( \text {0.3}<M<\text {1}\right) }$.

The panel methods are indeed powerful tools in analyzing the complex incompressible flow configurations, but they experience serious limitations in some situations. They are incapable of modeling the viscous effects, boundary layer characteristics and the phenomena where the flow separates. The lack of modeling the viscosity leads to further constraint; they cannot be used in modeling the forced vortices and/or rotational flows. The panel methods are incapable in modeling the flows at supersonic and hypersonic Mach numbers.

Exercises

1.1 Descriptive Type Questions

• 1. For the constant strength source distribution, calculate the $\mathrm {x}$-component of velocity by the direct integration of Eq. (7.20).

• 2. Using Hess and Smith method, show that the velocities at midpoints of each panel can be obtained by superimposing the contributions from all the sources and the vortices.

• 3. Consider a vortex panel of constant strength, $\mathrm {\zeta =}$ 2 $\mathrm {\mathrm {mm}^{2}\, s^{-1}}$. Find the stream function for the given conditions; $\mathrm {\lambda =\text {9}}$ $\mathrm {mm}$, $\mathrm {r_{1}=\text {5.83}}$ $\mathrm {mm}$, $\mathrm {r_{2}=\text {5}}$ $\mathrm {mm}$, $\mathrm {\theta _{1}=}$ 30.96$\mathrm {^{o}}$ and $\mathrm {\theta _{2}=}$ 36.86$\mathrm {^{o}}$, and evaluate its value at an arbitrary point P (5 mm, 3 mm).

• 4. For a flat plate at an angle of attack $\mathrm {\left( \alpha \right) }$, calculate the influence coefficient matrix $\mathrm {a_{ij}}$ by using the lumped vortex element. To solve the problem divide the chord into five panels of equal lengths and assume the collocation point to be located at $\mathrm {\mathrm {\mathrm {\frac{1}{4^{th}}}}}$ of chord from the trailing edge.

• 5. Consider the fluid flow between two parallel plates separated by a distance $\mathrm {l}$, due to a source of strength $\mathrm {k\left( s\right) }$. Find the complex potential, if the source is located at a distance 0.3$\mathrm {l}$ from the bottom plate.

• 6. Consider a vortex panel with linearly varying vortex strength. Find the value of vortex strength at a point, where the local velocity $\left( \mathrm {u_{S}}\right)$ is 10 $\mathrm {ms^{-1}}$ and $\mathrm {\theta _{2}-\theta _{1}=}$ 5$\mathrm {^{o}}$.

• 7. In a fluid flow, the freestream velocity and the local velocity due to source distribution are 10 and 4 $\mathrm {ms^{-1}}$, respectively. Using the linear perturbation theory with suitable assumptions, find the pressure coefficient.

• 8. Consider the vortex panel of constant strength $\mathrm {\mathrm {\zeta =}}$ 5 $\mathrm {ms^{-1}}$. Find the $\mathrm {y}$-component of velocity if $\mathrm {\frac{r_{2}}{r_{1}}=}$ 0.75.

• 9. For a panel with vortex distribution, the $\mathrm {x}$-component of velocity over the panel is 12 $\mathrm {ms^{-1}}$. If $\mathrm {\mathrm {\theta _{1}=}}$ 120$\mathrm {^{o}}$ and $\mathrm {\theta _{2}=}$ 50$\mathrm {^{o}}$, then calculate the vortex strength of the panel.

• 10. Consider a two-dimensional body of chord 15 mm with source distribution in the direction along the $\mathrm {x}$-axis. Derive an expression for the $\mathrm {x}$-component of induced velocity at a generic point P (25 mm, 30 mm).

1.2 Multiple Choice Questions

• 1. Panel methods are ideal for computing

  • (a) incompressible viscous flows

  • (b) compressible viscous flows

  • (c) compressible inviscid flows

  • (d) incompressible inviscid flows

• 2. The vortex panel method for an airfoil assumes that

  • I. The strength of each panel varies linearly over the panel.

  • II. There exists a component of velocity perpendicular to the airfoil.

  • III. The strength of the panel is continuous across the panel joints.

  • IV. The strength of the panel is discontinuous at the trailing edge.

  Choose the correct option from the following.

  • (a) I and III

  • (b) II only

  • (c) I, II and III

  • (d) II and IV

• 3. Consider an airfoil system with $\mathrm {N}$ control points giving $\mathrm {N}$ equations for the $\mathrm {N+1}$ strengths. The final equation to solve this system is obtained by

  • (a) Kutta condition

  • (b) Helmholtz method

  • (c) The system can be solved without a final.

  • (d) Kelvin’s circulation theorem

• 4. The solution of the panel method becomes invalid when

  • (a) the flow develops local supersonic flow

  • (b) when the flow is tangential to the panels

  • (c) when Neumann boundary conditions are applied

  • (d) the solution is always valid

• 5. It is more accurate to compute the wing lift on the wing body interface using

  • (a) constant vortex panels

  • (b) line sources

  • (c) constant pressure panels

  • (d) line doublets

• 6. In order to simulate a closed body, the sum of the strengths of all the sources should be the sum of all the sink’s strength.

  • (a) equal to

  • (b) more than

  • (c) less than

  • (d) cannot say

• 7. For a constant strength source distribution, the induced velocity at $\mathrm {\mathrm {x=0}}$ or $\mathrm {\mathrm {x=c}}$ has a

  • (a) linear singularity

  • (b) logarithmic singularity

  • (c) parabolic singularity

  • (d) hyperbolic singularity

• 8. For a body in uniform flow, the velocity potential $\mathrm {\left( \phi _{\mathrm {v}}\right) }$ created by by the distribution of vortices is

  • (a) $\mathrm {\mathrm {-\int \frac{\zeta \left( s\right) }{2\pi }\theta ds}}$

  • (b) $\mathrm {\mathrm {\int \frac{\zeta \left( s\right) }{2\pi }\theta ds}}$

  • (c) $\mathrm {\mathrm {-\int \frac{\zeta \left( s\right) }{2\pi }ds}}$

  • (d) $\mathrm {\mathrm {\int \frac{\zeta \left( s\right) }{2\pi }ds}}$

• 9. In vortex panel method, which of the following boundary condition must be satisfied at points?

  • (a)
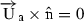
  • (b)
  • (c)
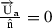
  • (d)

• 10. For a panel with source distribution, the freestream velocity and the pressure coefficient are 50 $\mathrm {ms^{-1}}$ and 0.9, respectively. The perturbation velocity component due to source distribution will be

  • (a) 12.5 ms$^{-1}$

  • (b) 18.5 ms$^{-1}$

  • (c) 22.5 ms$^{-1}$

  • (d) 35.5 ms$^{-1}$

1.2.1 Keys

• 1. (d)

• 2. (b)

• 3. (a)

• 4. (a)

• 5. (c)

• 6. (a)

• 7. (b)

• 8. (a)

• 9. (b)

• 10. (c)