Finite Wing Theory

Abstract

One of the most vital uses of potential flow theory was the analysis of lifting surfaces such as the wings of an aircraft, since the boundary conditions on a complicated geometry can substantially muddle the attempt to solve the problem by analytical means which, in turn, necessitates some simplifying assumptions to obtain the solution. In this chapter, these assumptions will be linked to the definition of the three-dimensional thin wing problems.

Appendices

Summary

The properties associated with an airfoil section which are indeed the same as the properties of a wing of infinite span. These properties are different for the wings of finite span attached to a real aircraft. This is because, unlike an airfoil which is a two-dimensional object, a wing is essentially a three-dimensional body, that is, there will be a component of flow in the spanwise direction. That is, the flow over the wings is three-dimensional in nature and hence their aerodynamic properties are quite different from those of its airfoil sections.

The downwash produced by shedding trailing edge vortices from the wing tips and its effect on the inclination of the local relative wind has two major consequences on the local airfoil section. The actual angle of attack as seen by the airfoil locally is, in fact, lower than the geometric angle of attack $\mathrm {\left( \alpha \right) }$. This angle of attack is referred to as effective angle of attack $\mathrm {\left( \alpha _{eff}\right) }$ for a three-dimensional wing. That is,

$$ \mathrm {\alpha _{eff}=\alpha -\alpha _{i}} $$

Also, the effective freestream velocity $\mathrm {\left( U_{eff}\right) }$ will now become

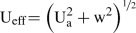
However, for small downwash $\mathrm {\left( w\approx 0\right) }$

$$\begin{aligned} \mathrm {U_{eff}}&\mathrm {\approx U_{a}} \end{aligned}$$

Besides, the downwash induced by these trailing edge vortices from the wing tips leads to an additional component of drag known as induced drag.

The concepts of vortex sheets and vortex filaments are advantageous in evaluating the aerodynamic characteristics of wings of finite span. From a directed line segment $\mathrm {\left( dl\right) }$ of a vortex filament, the induced velocity can be calculated by using the below mentioned Biot–Savart law.

$$\begin{aligned} \mathrm {\mathrm {\overrightarrow{\mathrm {v}}\left( r\right) }}\,&\mathrm {=\mathrm {\frac{\Gamma }{4\pi }\int }\left( \frac{\overrightarrow{\mathrm {dl}}\times \left( \overrightarrow{\mathrm {r}}-\overrightarrow{\mathrm {s}}\right) }{\left| \overrightarrow{\mathrm {r}}-\overrightarrow{\mathrm {s}}\right| ^{3}}\right) } \end{aligned}$$

The velocity induced by a straight vortex filament of the finite length is given as

$$\begin{aligned} \mathrm {v_{i}}\,&\mathrm {=\frac{\Gamma }{4\pi d}\left( \cos \theta _{1}-\cos \theta _{2}\right) } \end{aligned}$$

In the lifting line model, developed by Ludwig Prandtl, a wing is numerically described by an infinite number of horseshoe vortices and these bound vortices pass through the aerodynamic centers of the airfoils, which in turn creates the lifting line. Besides, the trailing edge vortices starting at the lifting line and shed downstream toward the infinity are basically responsible for inducing the downwash at the lifting line, and consequently, modify the local angles of attack. The circulation distribution $\mathrm {\Gamma \left( y\right) }$ is calculated from the accompanying relation

$$ \mathrm {\alpha \left( \beta \right) =}\mathrm {\frac{\Gamma \left( \beta \right) }{\pi U_{a}c\left( \beta \right) }+\alpha _{L=0}\left( \beta \right) +\frac{1}{4\pi U_{a}}\intop _{-b}^{b}\frac{\left[ \frac{d\Gamma \left( y\right) }{dy}\right] dy}{\left( \beta -y\right) }} $$

For the symmetric aerodynamic load distribution, defined as $\mathrm {\Gamma \left( y\right) =\Gamma _{max}\left[ 1-\left( \frac{y}{b}\right) ^{2}\right] ^{\frac{1}{2}}}$, a summary of important relations is described below.

For a symmetric elliptical lift distribution over the wingspan, both induced downwash and induced angle are constant along the span.

$$ \mathrm {w_{i}\left( \theta \right) =-\frac{\Gamma _{max}}{4b}} $$

$$ \mathrm {\alpha _{i}=\frac{\Gamma _{max}}{4bU_{a}}} $$

The total lift acting on the complete wingspan for a symmetric elliptic lift distribution is

$$\begin{aligned} \mathrm {L}\,&\mathrm {=\frac{\pi b}{4}\rho U_{a}\Gamma _{max}} \end{aligned}$$

and the expression for $\mathrm {C_{L}}$ is

$$\begin{aligned} \mathrm {C_{L}}&\mathrm {=\frac{\pi }{2}\frac{b}{S}\frac{\Gamma _{max}}{U_{a}}} \end{aligned}$$

The overall induced drag for a symmetric elliptical loading is given by

$$\begin{aligned} \mathrm {D_{i}}\,&\mathrm {=\frac{\pi }{8}\rho \Gamma _{max}^{2}} \end{aligned}$$

In addition, the coefficient of induced drag is

$$\begin{aligned} \mathrm {C_{D_{i}}}\,&\mathrm {=\frac{\pi }{4}\frac{\Gamma _{max}^{2}}{SU_{a}^{2}}=\frac{1}{\pi }\frac{S}{b^{2}}C_{L}^{2}} \end{aligned}$$

This relation can also be written as

$$\begin{aligned} \mathrm {C_{D_{i}}}\,&\mathrm {=\frac{C_{L}^{2}}{\pi AR}} \end{aligned}$$

where $\mathrm {AR=\frac{b^{2}}{S}}$ is the aspect ratio of a finite wing.

For the symmetric general aerodynamic load distribution, given by , a summary of important relations is described as follows.

The generalized expression for the induced angle $\mathrm {\left( \alpha _{i}\right) }$ is

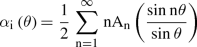
For a wing of finite span, the lift coefficient is given by

$$\begin{aligned} \mathrm {C_{L}}\,&\mathrm {=\pi A_{1}AR} \end{aligned}$$

and the coefficient of induced drag is

$$\begin{aligned} \mathrm {C_{D_{i}}}\,&\mathrm {=\pi AR\sum _{n=1}^{\infty }nA_{n}^{2}=\frac{C_{L}^{2}}{\pi AR}\left( 1+\delta \right) =\frac{C_{L}^{2}}{\pi eAR}} \end{aligned}$$

where $\mathrm {\delta =\sum _{n=2}^{\infty }n\left( \frac{A_{n}^{2}}{A_{1}^{2}}\right) }$ and $\mathrm {e=\left( \frac{1}{1+\delta }\right) }$ is the span efficiency factor.

Exercises

1.1 Descriptive Type Questions

• 1. Show that the integral on the right-hand side of Kelvin’s circulation theorem vanishes, if the fluid is barotropic.

• 2. Prove that the elliptical spanwise lift distribution leads to a constant downwash along the span.

• 3. Consider a vortex sheet, where the velocities above and below the sheet are 6 and 4 $\mathrm {ms^{-1}}$, respectively. The element of this vortex sheet is 0.4 $\mathrm {m}$ wide, which rolled up into a line vortex after some time. Calculate the strength of the vortex.

• 4. Determine the wing loading of an aircraft weighing 2000 $\mathrm {kg}$, if the wing planform area is 18 $\mathrm {m^{2}}$.

• 5. Plot the curve between the induced drag coefficient and the lift coefficient for an elliptical load distribution over the wing of aspect ratio 7.5.

• 6. If the aspect ratio of a glider, having elliptical planform wing, is 6.5. Calculate the change in minimum angle of glide, if the aspect ratio is doubled. Assume $\mathrm {C_{D}=\text {0.03}+\text {0.07}C_{L}^{2}}$.

• 7. An airplane is flying at 150 $\mathrm {ms^{-1}}$ in a steady level flight. If the aircraft weighs 80 $\mathrm {kN}$ and have elliptical wing of span 16 $\mathrm {m}$, determine the induced drag.

• 8. Describe the motion of a vortex pair (a) when their circulations are equal and in the same direction, and (b) when their circulations are equal but in opposite directions.

• 9. Determine the flow field due to (a) a vortex filament, which is in the form of a circular ring (vortex ring), (b) a plane vortex sheet, which is formed by a distribution of horseshoe vortex filament, and (c) an infinite row of point vortices of equal strength distributed along a straight line at equal intervals.

• 10. Find the path of a vortex bounded by two walls perpendicular to each other.

1.2 Multiple Choice Questions

• 1. According to Prandtl’s lifting line theory, which of the following shape of the wing has minimum induced drag?

  • (a) elliptical

  • (b) straight rectangular

  • (c) straight tapered

  • (d) tapered sweptback

• 2. For a wing of finite span, if the lift coefficient is doubled then the induced drag coefficient

  • (a) will remain same

  • (b) will be increased two times

  • (c) will be increased three times

  • (d) will be increased four times

• 3. For an aircraft with tapered straight wing, the root chord and tip chord are 0.9 and 0.5 $\mathrm {m}$, respectively. If the total wingspan is 14 $\mathrm {m}$, then the aspect ratio of wing will be

  • (a) 10

  • (b) 20

  • (c) 0.1

  • (d) 30

• 4. The wing sweep back in an aircraft provides which type of static stability?

  • (a) longitudinal stability

  • (b) lateral stability

  • (c) directional stability

  • (d) both (b) and (c)

• 5. If the aspect ratio of a wing of finite span is increased, the lift curve slope will

  • (a) decrease

  • (b) increase

  • (c) remain same

  • (d) cannot say

• 6. When the “flap” of a wing is deflected, then the lift curve slope will

  • (a) increase

  • (b) decrease

  • (c) remain same

  • (d) increase or decrease depending upon the shape of the flap.

• 7. For any given length, the swept back wings experience lift than the straight wings.

  • (a) less

  • (b) more

  • (c) same

  • (d) cannot say

• 8. Different types of aircraft have different stalling characteristics. Which of the following is TRUE in a “benign stall”?

  • (a) One wing stalls slightly before the other.

  • (b) The nose drops gently and the wings remain level throughout.

  • (c) The nose rises, pushing the wing deeper into the stalled state.

  • (d) All the above are FALSE.

• 9. In the normal cruise motion (straight level flight) of an aircraft, if the cruise speed is increased by three times then the induced drag will be

  • (a) increased by three times

  • (b) increased by nine times

  • (c) $\frac{1}{3{\mathrm {rd}}}$of the original

  • (d) $\frac{1}{9{\mathrm {th}}}$of the original

• 10. For a finite wing, if the coefficient of lift is doubled while the aspect ratio is reduced to half then the induced drag will be

  • (a) doubled

  • (b) four times the original

  • (c) eight times the original

  • (d) $\frac{1}{8{\mathrm {th}}}$of the original

1.2.1 Keys

• 1. (a)

• 2. (c)

• 3. (b)

• 4. (d)

• 5. (b)

• 6. (c)

• 7. (a)

• 8. (b)

• 9. (d)

• 10. (c)