Abstract
It is well known that the Cramer’s rule for the solution \(\mathbf {x}\) of a nonsingular equation
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
References
S.M. Robinson, A short proof of Cramer’s rule. Math. Mag. 43, 94–95 (1970). Reprinted in Selected Papers on Algebra (S. Montgomery et al. eds.) Math. Assoc. Amer. 313–314 (1977)
A. Ben-Israel, A Cramer rule for least-norm solution of consistent linear equations. Linear Algebra Appl. 43, 223–226 (1982)
Y. Chen, A Cramer rule for solution of the general restricted linear equation. Linear Multilinear Algebra 34, 177–186 (1993)
Y. Chen, Expressions and determinantal formulas for solution of a restricted matrix equation. Acta Math. Appl. Sinica 18(1), 65–73 (1995)
J. Ji, An alternative limit expression of Drazin inverse and its applications. Appl. Math. Comput. 61, 151–156 (1994)
W. Sun, Cramer rule for weighted system. J. Nanjing Univ. 3, 117–121 (1986). in Chinese
G.C. Verghes, A "Cramer rule" for least-norm least-square-error solution of inconsistent linear equations. Linear Algebra Appl. 48, 315–316 (1982)
G. Wang, A Cramer rule for minimum-norm\((T)\) least-squares\((S)\) solution of inconsistent equations. Linear Algebra Appl. 74, 213–218 (1986)
G. Wang, A Cramer rule for finding the solution of a class of singular equations. Linear Algebra Appl. 116, 27–34 (1989)
G. Wang, On extensions of cramer rule. J. Shanghai Normal Univ. 21, 1–7 (1992)
G. Wang, Z. Wang, More condensed determinant representation for the best approximate solution of the matrix equation \(AXH=K\). J. Shanghai Normal Univ. 19, 27–31 (1990). in Chinese
H.J. Werner, When is \(B^-A^-\) a generalized inverse of \(AB\)? Linear Algebra Appl. 210, 255–263 (1994)
G. Wang, On the singularity of a certain bordered matrix and its applications to the computation of generalized inverses. J. Shanghai Normal Univ. 18, 7–14 (1989). in Chinese
H.J. Werner, On extensions of Cramer’s rule for solutions of restricted linear systems. Linear Multilinear Algebra 15, 319–330 (1984)
Y. Chen, B. Zhou, On g-inverses and the nonsingularity of a bordered matrix
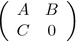 . Linear Algebra Appl. 133, 133–151 (1990)
. Linear Algebra Appl. 133, 133–151 (1990)Y. Wei, A characterization and representation of the generalized inverse \(A_{T, S}^{(2)}\) and its applications. Linear Algebra Appl. 280, 87–96 (1998)
R. Penrose, On best approximate solution of linear matrix equations. Proc. Cambridge Philos. Soc. 52, 17–19 (1956)
J. Ji, The cramer rule for the best approximate solution of the matrix equation \(AXB=D\). J. Shanghai Normal Univ. 14, 19–23 (1985). in Chinese
M. Marcus, M. Minc, A Survey of Matrix Theory and Matrix Inequalities (Mass, Allyn and Bacon, Boston, 1964)
G. Wang, The Generalized Inverses of Matrices and Operators (Science Press, Beijing, 1994). in Chinese
G. Wang, Weighted Moore-Penrose, Drazin, and group inverses of the Kronecker product \(A \otimes B\) and some applications. Linear Algebra Appl. 250, 39–50 (1997)
J. Ji, Explicit expressions of the generalized inverses and condensed cramer rules. Linear Algebra Appl. 404, 183–192 (2005)
Y. Wei, A characterization for the W-weighted Drazin inverse and Cramer rule for W-weighted Drazin inverse solution. Appl. Math. Comput. 125, 303–310 (2002)
R.A. Brualdi, H. Schneider, Determinantal: gauss, schur, cauchy, sylvester, kronecker, jacobi, binet, laplace, muir and cayley. Linear Algebra Appl. 52, 769–791 (1983)
A. Ben-Israel, Minors of the Moore-Penrose inverse. Linear Algebra Appl. 195, 191–207 (1993)
A. Ben-Israel, A volume associated with \(m \times n\) matrices. Linear Algebra Appl. 167, 87–111 (1992)
G. Wang, J. Sun, J. Gao. Minors of the weighted Moore-Penrose inverse. Numer. Math., J. Chinese Univ. 19(4), 343–348 (1997). in Chinese
R.A. Horn, C.R. Johnson, Matrix Analysis, 2nd edn. (Cambridge University Press, Cambridge, 2012)
J. Miao, Reflexive generalized inverses and their minors. Linear Multilinear Algebra 35, 153–163 (1993)
G. Wang, J. Gao, J. Sun, Minors of Drazin inverses. J. Shanghai Normal Univ. 28, 12–15 (1998). in Chinese
G. Wang, J. Gao, Minors of the generalized inverse \(A_{T, S}^{(2)}\). Math. Numer. Sinica 23(4), 439–446 (2001). in Chinese
Y. Yu, The generalized inverse \(A_{T,S}^{(2)}\) on an associative ring: theory and computation. Ph.D. thesis, Shanghai Normal University, China, 2006. in Chinese
Y. Chen, Finite algorithm for the \((2)\)-generalized inverse \(A_{T, S}^{(2)}\). Linear Multilinear Algebra 40, 61–68 (1995)
R.B. Bapat, A. Ben-Israel, Singular values and maximum rank minors of generalized inverses. Linear Multilinear Algebra 40, 153–161 (1995)
R.E. Hartwig, Singular value decomposition and the Moore-Penrose inverse of bordered matices. SIAM J. Appl. Math. 31, 31–41 (1976)
R.E. Hartwig, Block generalized inverses. Arch Rational Mech. Anal. 61, 197–251 (1976)
J. Miao, Representations for the weighted Moore-Penrose inverse of a partitioned matrix. J. Comput. Math. 7, 320–323 (1989)
J. Miao, Some results for computing the Drazin inverse of a partitioned matrix. J. Shanghai Normal Univ. 18, 25–31 (1989). in Chinese
M. Wei, W. Guo, On g-inverses of a bordered matrix: revisited. Linear Algebra Appl. 347, 189–204 (2002)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2018 Springer Nature Singapore Pte Ltd. and Science Press
About this chapter
Cite this chapter
Wang, G., Wei, Y., Qiao, S. (2018). Generalization of the Cramer’s Rule and the Minors of the Generalized Inverses . In: Generalized Inverses: Theory and Computations. Developments in Mathematics, vol 53. Springer, Singapore. https://doi.org/10.1007/978-981-13-0146-9_3
Download citation
DOI: https://doi.org/10.1007/978-981-13-0146-9_3
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-13-0145-2
Online ISBN: 978-981-13-0146-9
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


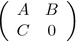 . Linear Algebra Appl. 133, 133–151 (1990)
. Linear Algebra Appl. 133, 133–151 (1990)