Abstract
We sketch a geometric proof of the classical theorem of Atiyah, Bott, and Shapiro [3] which relates Clifford modules to vector bundles over spheres. Every module of the Clifford algebra \(Cl_k\) defines a particular vector bundle over \(\mathord {\mathbb S}^{k+1}\), a generalized Hopf bundle, and the theorem asserts that this correspondence between \(Cl_k\)-modules and stable vector bundles over \(\mathord {\mathbb S}^{k+1}\) is an isomorphism modulo \(Cl_{k+1}\)-modules. We prove this theorem directly, based on explicit deformations as in Milnor’s book on Morse theory [8], and without referring to the Bott periodicity theorem as in [3].
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
\(s(P) \subset \hat{G}\) is a connected component of the set \(\{g\in \hat{G}: g^{-1} = g\}\). When we choose a symmetric metric on \(\hat{G}\) such that \(g\mapsto g^{-1}\) is an isometry, s(P) is a reflective submanifold and hence totally geodesic, thus symmetric.
- 2.
A deck transformation of \(\pi : P\rightarrow \bar{P}\) is an isometry \(\delta \) of P with \(\pi \circ \delta = \pi \).
- 3.
Consider a symmetric space P and a covering \(\pi :P\rightarrow P/\varDelta \) for some discrete freely acting group \(\varDelta \) of isometries on P. Then \(P/\varDelta \) is again symmetric if and only if each symmetry \(s_p\) of P maps \(\varDelta \)-orbits onto \(\varDelta \)-orbits. Thus for each \(\delta \in \varDelta \) we have \(s_p(\delta x) = \tilde{\delta }s_p(x)\) for all \(x\in P\), and \(\tilde{\delta }\in \varDelta \) is independent of x, by discreteness. Thus \(s_p\delta = \tilde{\delta }s_p\), in particular \(s_p\delta s_p = \tilde{\delta }\in \varDelta \). For any other symmetry \(s_q\) we have the same equation \(s_q\delta = \tilde{\delta }s_q\) with the same \(\tilde{\delta }\in \varDelta \), again by discreteness. Thus \(\delta ^{-1}s_ps_q\delta = s_p\tilde{\delta }^{-1}\tilde{\delta }s_q = s_ps_q\), and \(\delta \) commutes with the transvection \(s_ps_q\) (see also [14, Theorem 8.3.11]).
- 4.
\(H^1\) means that \(\lambda \) has a derivative almost everywhere which is square integrable. Replacing any path \(\lambda \) by a geodesic polygon with N vertices, we may replace \(\varLambda \) by a finite dimensional manifold, cf. [8].
- 5.
- 6.
Putting \(S_n = (J_1\dots J_n)^2\) we have
$$S_n = J_1\dots J_nJ_1\dots J_n = (-1)^{n-1}S_{n-1}J_n^2 = (-1)^nS_{n-1},$$thus \(S_n = (-1)^sI\) with \(s = n+(n-1)+\dots +1 = \frac{1}{2} n(n+1)\). When \(n = k-1 \equiv 1\mod 4\), then s is odd, hence \(S_n = -I\).
- 7.
Any one-parameter subgroup \(\gamma \) in \(SO_n\) is a family of planar rotations in perpendicular planes. When \(\gamma (1) = -I\), all rotation angles are odd multiples of \(\pi \). The squared length of \(\gamma \) is the sum of the squared rotation angles. Thus the length is minimal if all rotation angles are just \(\pm \pi \).
- 8.
The clutching map \(\phi : \mathord {\mathbb S}^k\rightarrow SO_{n}\) splits into components \(\phi _j : \mathord {\mathbb S}^k \rightarrow SO(V_j)\). The domain \(\mathord {\mathbb S}^k\) is the union of totally geodesic spherical \((k-1)\)-discs \(D_v\), \(v\in \mathord {\mathbb S}^1\), centered at v and perpendicular to \(\mathord {\mathbb S}^1\). All \(D_v\) have a common boundary \(\mathord {\mathbb S}^{k-2}\). Since \(\phi _0|_{D_v}\) is constant in v, it is contractable along \(D_v\) to a constant map.
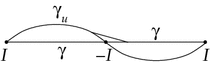
- 9.
In fact, both \({\mathscr {V}}_k\) and \({\mathscr {A}}_k\) are abelian groups with respect to direct sums, not just semigroups, and \(\alpha \) is a group homomorphism. Using the tensor product, \({\mathscr {V}}= \sum _k {\mathscr {V}}_k\) and \({\mathscr {A}}= \sum _k {\mathscr {A}}_k\) become rings and \(\alpha \) a ring homomorphism, see [3].
References
Atiyah, M.: K-Theory. Benjamin (1967)
Atiyah, M., Bott, R.: On the periodicity theorem for complex vector bundles. Acta Math. 112, 229–247 (1964)
Atiyah, M., Bott, R., Shapiro, A.: Clifford modules. Topology 3, 3–38 (1964)
Bott, R.: The stable homotopy of the classical groups. Proc. Nat. Acad. Sci. U.S.A. 43, 933–935 (1957)
Bott, R.: The stable homotopy of the classical groups. Ann. Math. 70, 313–337 (1959)
Chen, B.-Y., Nagano, T.: Totally geodesic submanifolds of symmetric spaces II. Duke Math. J. 45, 405–425 (1978)
Lawson, H.B., Michelson, M.-L.: Spin Geometry. Princeton University Press, Princeton (1989)
Milnor, J.: Morse Theory. Princeton University Press, Princeton (1963)
Mitchell, S.A.: The Bott filtration of a loop group. Springer Lect. Notes Math. 1298, 215–226 (1987)
Mitchell, S.A.: Quillen’s theorem on buildings and the loops on a symmetric space. Enseign. Math. (II) 34, 123–166 (1988)
Nagano, T.: The involutions of compact symmetric spaces. Tokyo J. Math. 11, 57–79 (1988)
Quast, P.: Complex structures and chains of symmetric spaces, Habilitationsschrift Augsburg (2010) (available from the author)
Quast, P.: Centrioles in Symmetric Spaces. Nagoya Math. J. 211, 51–77 (2013)
Wolf, J.A.: Spaces of Constant Curvature, 5th edn. Publish or Perish, Wilmington (Delaware) (1984)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer Nature Singapore Pte Ltd.
About this paper
Cite this paper
Eschenburg, J., Hanke, B. (2017). Bott Periodicity, Submanifolds, and Vector Bundles. In: Suh, Y., Ohnita, Y., Zhou, J., Kim, B., Lee, H. (eds) Hermitian–Grassmannian Submanifolds. Springer Proceedings in Mathematics & Statistics, vol 203. Springer, Singapore. https://doi.org/10.1007/978-981-10-5556-0_25
Download citation
DOI: https://doi.org/10.1007/978-981-10-5556-0_25
Published:
Publisher Name: Springer, Singapore
Print ISBN: 978-981-10-5555-3
Online ISBN: 978-981-10-5556-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)


