Keywords

1 Introduction

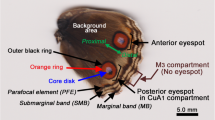
Eyespots, concentric bands of pigment patterning, constitute one of the most studied pattern elements on the wings of butterflies (c.f., Fig. 6.3 for an example). Each eyespot develops around a focus, a small group of cells that sends out a morphogenetic signal that determines the synthesis of circular patterns of pigments in their surroundings. In this work, we consider a model that provides a possible mechanism underlying the determination of the number and locations of eyespots on the wing surface. The model we consider, first described by Sekimura et al. (2015), provides a mechanism that places the foci around which eyespots form in various locations on the entire wing surface. We do not address here subsequent stages of eyespot formation that occurs after the development of the foci.

The model we consider is based on that of Nijhout (1990). The main novelty of the work in Sekimura et al. (2015) was to illustrate that simply changing the conditions assumed to hold at the proximal veins was sufficient to determine whether or not an eyespot formed in a given wing cell. In the present work, we extend the investigations of the models proposed in Sekimura et al. (2015). We show that it is possible to determine the location of eyespots within a wing cell simply by changing the conditions that are assumed to hold at the lateral wing veins that bound the wing cell. Furthermore, we illustrate that it is possible, using a two-stage model, to recapitulate the results of artificial selection experiments in terms of selection and location of eyespots in butterfly wings.

2 Modelling

In this section, we describe the mathematical model for focus point formation that we consider in the present work.

2.1 Setting

As butterfly wing patterns form in two layers that are thought to be separated completely by the middle tissue (e.g. Sekimura et al. 1998), we assume that the formation of eyespots takes place in a single layer of the wing disc. Hence, we model the domain in which eyespot formation occurs as a two-dimensional region. Furthermore, we assume that this two-dimensional region consists of several wing cells, regions bounded by the wing veins, and we consider a region of up to seven wing cells sufficient to represent the entire surface (front or back) of the wing disc. For the sake of simplicity, we assume that each of the wing cells is of the same shape and size.

The model we consider for the formation of focus points is based on that proposed by Nijhout (1990) and consists of a reaction-diffusion system of activator-inhibitor type (Gierer and Meinhardt 1972) posed in each wing cell with time-independent Dirichlet boundary conditions (i.e. a source of chemicals) on the wing veins and Neumann (zero flux) boundary conditions (i.e. no flux of chemicals) at the wing margin.

2.2 Mathematical Model

We denote by n seg the number of wing cells. We denote by Ω i the ith wing cell with boundaries Γ m , i (wing margin), Γ v , i  , Γ v , i + 1 (veins) and Γ p , i (proximal boundary). The boundary conditions for the activator (a 1) are Dirichlet (fixed) on the proximal boundary Γ p , i and the wing veins Γ v , i  , Γ v , i + 1 and Neumann (zero flux) on the wing margin Γ m , i (c.f., Fig. 6.1). The boundary conditions for the inhibitor (a 2) are zero flux on all four boundaries of each wing cell. The Dirichlet boundary condition on each vein Γ v , i is the same for each vein. We take the initial data for both activator and inhibitor to be the positive spatially homogeneous steady state of the Gierer-Meinhardt (GM) equation. Thus, our model for focus pattern formation consists of n seg-independent GM equations. The model system equations may be stated as follows:

Fig. 6.1
figure 1

A sketch of the domain on which we model the formation of eyespot focus points

Full size image

For i = 1 ,  …  , n seg, find \( \overrightarrow{a}\left(\overrightarrow{x},t\right) \),\( \left(\overrightarrow{x},t\right)\in \Omega \times \left(0,T\right) \), such that

$$ {\displaystyle \begin{array}{ll}{\partial}_t\overrightarrow{a}\left(\overrightarrow{x},t\right)-D\Delta \overrightarrow{a}\left(\overrightarrow{x},t\right)=\overrightarrow{f}\left(\overrightarrow{a}\left(\overrightarrow{x},t\right)\right)& \left(\overrightarrow{x},t\right)\in {\Omega}_i\times \left(0,T\right)\\ {}{a}_1\left(\overrightarrow{x},t\right)=u\left(\overrightarrow{x}\right)&\ \overrightarrow{x}\in \partial {\Omega}_i/{\Gamma}_{m,i}\\ {}\nabla {a}_1\left(\overrightarrow{x},t\right)\cdot \overrightarrow{n}\left(\overrightarrow{x},t\right)=0& \left(\overrightarrow{x},t\right)\in {\Gamma}_{m,i}\times \left(0,T\right)\\ {}\nabla {a}_2\left(\overrightarrow{x},t\right)\cdot \overrightarrow{n}\left(\overrightarrow{x},t\right)=0& \left(\overrightarrow{x},t\right)\in \partial {\Omega}_i\times \left(0,T\right)\\ {}\overrightarrow{a}\left(\overrightarrow{x},t\right)={\overrightarrow{a}}^{ss}&\ \overrightarrow{x}\in {\Omega}_i,\end{array}} $$
(6.1)

where D is a diagonal matrix of positive diffusion coefficients and the reaction kinetic vector \( \overrightarrow{f}\left(\overrightarrow{v}\right) \) is given by \( {f}_1\left(\overrightarrow{v}\right)=\alpha \left(\left({\kappa}_1{v}_1^2/{v}_2\right)-{\kappa}_2{v}_1\right) \) and \( {f}_2\left(\overrightarrow{v}\right)=\alpha \left({\kappa}_1{v}_1^2-{\kappa}_3{v}_2\right) \), with κ 1 , κ 2 , κ 3 > 0. The choice of kinetics yields that the corresponding ODE system has a positive steady \( {\overrightarrow{a}}^{ss}=\left({\kappa}_2/{\kappa}_2,{\kappa}_1{\kappa}_3/{\kappa}_2\right)\hat{\mkern6mu} T \).

Nijhout (1990, 1994) showed that the above model was capable of generating source profiles consistent with the formation of an eyespot focus within a wing cell. In Sekimura et al. (2015), we showed that changes in the Dirichlet boundary condition for a 1 at the proximal boundary Γ p , i alone were sufficient to determine whether or not an eyespot focus forms in a wing cell. For the proximal boundary profile, we consider two different cases firstly, prescribed boundary conditions, and secondly, in order to propose a full model, we consider that the boundary profiles are themselves generated by a patterning mechanism that is posed along the entire proximal boundary, i.e. the curved surface Γ p  ≔ ∪ i Γ p , i . For this one-dimensional patterning mechanism, for consistency with the two-dimensional model above, we consider a surface reaction-diffusion system which for illustrative purposes we choose to be the activator-depleted substrate model of Schnakenberg (1979), stated as follows:

Find \( \overrightarrow{u}\left(\overrightarrow{x},t\right) \) such that

$$ {\partial}_t\overrightarrow{u}\left(\overrightarrow{x},t\right)-{D}_u{\Delta}_{\varGamma}\overrightarrow{u}\left(\overrightarrow{x},t\right)=\overrightarrow{h}\left(\overrightarrow{u}\left(\overrightarrow{x},t\right)\right)\kern1.5em \mathrm{on}\ {\Gamma}_p, $$
(6.2)

where D u is a diagonal matrix of positive diffusion coefficients, ΔΓ is the Laplace-Beltrami operator (the analogue to the usual Cartesian Laplacian on the surface) and the function \( \overrightarrow{h}\left(\overrightarrow{u}\right) \) is given by \( {h}_1\left(\overrightarrow{u}\right)=\gamma \left(\overrightarrow{x}\right)\left(a-{u}_1+{u}_1^2{u}_2\right) \) and \( {h}_2\left(\overrightarrow{u}\right)=\gamma \left(\overrightarrow{x}\right)\left(b-{u}_1^2{u}_2\right), \) with a , b > 0. u 1 and u 2 are the concentrations of two chemicals (the activator and substrate, respectively). The function γ can be thought of as a reaction rate and is typically taken to be constant in most studies that employ such systems to model biological pattern formation. However, if such an approach is adopted, patterns with a constant wavelength across Γ p are to be expected. In the present context, this would be insufficient to explain butterfly wing patterning in which the distribution of eyespots occurs with differing frequency in different parts of the wing. For this reason, we allow the reaction rate to be a function of space, which appears to provide sufficient freedom to generate the necessary source profiles from this one-dimensional model that produces any arbitrary eyespot configuration observed on butterfly wings. The resulting model is a two-stage model for focus point formation in which the first stage corresponds to solving the Schnakenberg surface reaction-diffusion system Eq. (6.2) to steady state and in the second stage the solution u 2 to this model is used to determine the proximal boundary profiles for a 1 in the eyespot reaction-diffusion system model Eq. (6.1) within each of the wing cells.

3 Computational Approximation

For the approximation of the eyespot reaction-diffusion system models posed within each of the wing cells, we employ an implicit-explicit finite element method developed and analysed in Lakkis et al. (2013). An advantage of such an approach is that arbitrary, potentially evolving, geometries can be considered. In particular, one does not need to assume that the wing cells are rectangular, and indeed using open-source meshing software, it is even possible to solve the systems on geometries obtained from image data, which may be a worthwhile extension. For the approximation of the surface reaction-diffusion system, we employ the surface finite element method (Dziuk and Elliott 2013). We refer to the above two references for further details on the numerical approach.

4 Results

4.1 Gradients in Source Strength on the Wing Veins Can Determine Eyespot Location in the Wing Cell

We start by illustrating that in the eyespot focus point formation model of Sect. 6.2, it is possible to change the location of eyespots by allowing the Dirichlet boundary condition at the wing veins to vary in space. To this end, we suppose that the wing cells are trapezoidal with parallel sides corresponding to the proximal and marginal boundaries that are chosen to be of length 1.5 and 2.5, respectively and are such that the height (proximal-marginal) is 3. We set the proximal boundary condition to be a convex profile of the form \( u\left(\overrightarrow{x}\right)=2{a}_1^{ss}\left(1-{\mathrm{sin}}^2\left(\pi d\left(\overrightarrow{x}\right)/1.5\right)\right) \) where \( d\left(\overrightarrow{x}\right) \) is the distance from the boundary points of the proximal boundary. The boundary condition thus takes the value \( 2{a}_1^{ss} \) at the boundary points of Γ p , i and decays to 0 at the centre of the proximal boundary. For the wing veins, we consider a gradient in the Dirichlet boundary condition by considering a linear boundary condition of the form \( u\left(\overrightarrow{x}\right)=2{a}_1^{ss}\left(1-{s}_1{x}_2/3\right), \) where x 2 denotes the distance in the proximal-distal direction from the wing margin and s 1 > 0 is a parameter that governs the magnitude of the gradient. Thus the boundary condition takes the value \( 2{a}_1^{ss} \) at the point where the vein meets the marginal boundary and decays towards the proximal boundary with slope given by s 1 > 0. The remaining parameter values we select are given in Table 6.1. For the discretisation we used linear finite elements on a grid with 2145 degrees of freedom (DOFs) and a time step of 0.01. The system was solved until the discrete solution was (approximately) at steady state.

Table 6.1 Parameter values for simulations of Sect. 6.4.1
Full size table

Figure 6.2a–d shows snapshots of the activator a 1 concentration at different times for different values of s1. In each of the subfigures, the value of s 1 = 0 , 0.15 , 0.25 , 0.35 , 0.45 , 0.5 reading from left to right. We see that in the case of constant boundary conditions or if the gradient is small (s 1 = 0 , 0.15 , 0.25 , 0.35), the centreline peak, characteristic of the Nijhout model, does not extend very far from the margin. The focus point forms near the middle of the wing cell and migrates towards the wing margin with the steady state corresponding to a single focus near the margin. For larger values of the gradient (s 1 = 0.45 , 0.5), the centreline peak extends much further, almost reaching the proximal boundary, and the resulting focus point forms close to the proximal boundary. The focus point migrates downwards only until around the centre of the wing cell, and the resulting steady state is a single focus point around the centre of the wing cell.

Fig. 6.2
figure 2

Eyespot focus point formation on a trapezoidal domain. On the wing veins we take a Dirichlet boundary condition of the form \( u\left(\overrightarrow{x}\right)=2{a}_1^{ss}\left(1-{\mathrm{s}}_1{x}_2/3\right). \) In each of the subfigures, the gradient in the Dirichlet boundary condition is increasing with s 1 = 0 , 0.15 , 0.25 , 0.35 , 0.45 , 0.5 reading from left to right. Thus the leftmost snapshot in each subfigure corresponds to constant Dirichlet boundary conditions on the wing veins, whilst the rightmost snapshot in each subfigure corresponds to the steepest linear gradient with \( u\left(\overrightarrow{x}\right)=2{a}_1^{ss} \) at the point where the wing veins meet the margin and \( u\left(\overrightarrow{x}\right)={a}_1^{ss} \) at the point where the wing veins meet the proximal boundary. In all the subfigures, we only display snapshots of the activator a 1 concentration; the inhibitor concentrations are in phase with those of the activator and are thus omitted. For remaining parameter values, see text. (a) t=0.1. (b) t= 0.2. (c) t=0.5. (d) Steady state

Full size image

4.2 A Surface Reaction-Diffusion System Model with Piecewise Constant Reaction Rate Generates Boundary Profiles and Resulting Eyespot Foci Recapitulate Those Observed in Artificial Selection

We now report on simulations in which we illustrate that the two-stage model proposed in Sect. 6.2 (see also, Sekimura et al. 2015) is capable of reproducing the differing selection of dorsal forewing eyespots observed in artificial selection experiments on Bicyclus anynana. Beldade et al. (2002) showed that, through artificial selection, it is possible to generate different phenotypes of B. anynana with either zero, one (anterior or posterior) or two forewing eyespots (anterior and posterior) (c.f., Fig. 6.3). To investigate whether our two-stage model is capable of reproducing these observations, we consider a wing as shown in Fig. 6.4. The proximal (Γ p ) and marginal (Γ m ) boundaries are curves corresponding to a portion of the circumference of two concentric circles of radius 9 and 12, respectively. The wing veins (Γ v , i ) are assumed to be radial and of length 3, whilst the proximal and marginal boundaries of each of the wing cells are approximately of length 1.88 and 3.35, respectively. We consider the two-stage model described in Sect. 6.2. In the first stage, we solve the surface reaction-diffusion system with the Schnakenberg kinetics to steady state. We select Dirichlet (prescribed) boundary conditions for u 1 with u 1 = u 1 ss on one boundary and u 1 = 2u 1 ss at the other boundary point. For u 2 we set zero-flux boundary conditions. The initial data is taken to be the steady state value for both u 1 and u 2. We consider the case that the function γ is piecewise constant (e.g. McMillan et al. 2002); in particular, we allow it to take two distinct values on either side of the midpoint (anterior-posterior) of the proximal boundary curve. The remaining parameter values we employed are shown in Table 6.2. After solving the Schnakenberg system to steady state, we assume the Dirichlet boundary condition at the proximal boundary for the reaction-diffusion system posed in each wing cell is of the form

$$ {a}_1\left(\overrightarrow{x},t\right)=1.9{\overline{u}}_2\left(\overrightarrow{x}\right){a}_1^{SS}\overrightarrow{x}\in {\Gamma}_{p,i}, $$

where \( {\overset{-}{u}}_2\left(\overrightarrow{x}\right) \) is the spatially inhomogeneous steady state of the substrate in the Schnakenberg equation. At the veins, we set Dirichlet boundary conditions for the activator equal to twice the steady state value. The remaining parameter values are given in Table 6.2. We note that each wing cell in this simulation is slightly larger in area than those considered in Sect. 6.4.1, and it is due to this fact that we require a slightly larger activator diffusivity, D 1, than that which was used in Sect. 6.4.1.

Fig. 6.3
figure 3

Eyespot phenotypes of B. anynana produced in artificial selection experiments (Beldade et al. 2002) (Figure reproduced with permission of the publisher)

Full size image
Fig. 6.4
figure 4

Sketch of the geometry used to model the entire region of the wing disc on which eyespot formation occurs for the experiments of Sect. 6.4.2

Full size image
Table 6.2 Parameter values for simulations of Sect. 6.4.2
Full size table

For the numerical parameters, we used a mesh with 3927 DOFs to represent the entire wing disc. The surface reaction-diffusion system was solved on the trace mesh corresponding to the boundary edges of the bulk mesh; the corresponding one-dimensional mesh had 1793 DOFs. We used a piecewise linear finite element method for both the surface and bulk reaction-diffusion systems with a time step of 0.05, and we solved the system until the concentration profiles were (approximately) at steady state. Figure 6.5 shows the steady state values obtained for simulations in which we vary the value of the piecewise constant reaction rate γ. We see that when γ is zero in both the anterior and posterior, as expected the substrate concentration (that satisfies zero-flux boundary conditions) in the one-dimensional system simply converges to a constant. Using this profile in the proximal boundary conditions for the model posed in each wing cell, we generate a wing with no foci similar to the ap case of Fig. 6.3. If we allow γ to be large on one half of the proximal boundary and small on the other half, then we generate boundary profiles from the one-dimensional system that results in a single eyespot in the half of the wing in which γ is large, similar to the Ap and aP phenotypes of Fig. 6.3. Finally, if γ is large and constant across the entire proximal boundary, we generate a profile that leads to both the anterior and posterior foci forming as in the AP phenotype of Fig. 6.3. The choice of Dirichlet boundary conditions for u 1 leads the substrate troughs to form in the correct locations for the eventual eyespots dependent on whether they are anterior or posterior; as for zero-flux or symmetric Dirichlet boundary conditions, we would expect solutions that are symmetric along the midpoint of the proximal boundary. We note that this asymmetry need not be through Dirichlet boundary conditions and could be the result of differences between individual wing cells or some other aspect which is thus far neglected in the modelling.

Fig. 6.5
figure 5

Simulations of eyespot focus point formation using a two-stage model. Initially a reaction-diffusion system with the Schnakenberg kinetics is solved to steady state on the curved proximal boundary using a piecewise constant value for the parameter γ, Dirichlet boundary conditions for u 1 and zero-flux boundary conditions for u 2 (see text for further details). The Dirichlet boundary condition on the proximal boundary is taken to be proportional to the substrate concentration u 2 of the Schnakenberg equation. The remaining boundary conditions and parameter values are given in the text. (a) Steady state values of u 2 and a 1 for constant γ = 0, corresponding to no eyespot foci. (b) Steady state values of u 2 and a 1 for piecewise constant γ = 500 on one half of the wing and γ = 10 on the other half, corresponding to one eyespot focus on the half of the wing with increased γ. (c) Steady state values of u 2 and a 1 for piecewise constant γ = 10 on one half of the wing and γ = 500 on the other half, corresponding to one eyespot focus on the half of the wing with increased γ. (d) Steady state values of u 2 and a 1 for constant γ = 500, corresponding to two eyespot foci

Full size image

5 Discussion

In this study, we reported on further investigations of a model for the selection and distribution of eyespot foci, originally presented in the paper (Sekimura et al. 2015). The basic idea of the model is that whether an eyespot focus forms in a given wing cell and its eventual position in the wing cell can be determined through changing only the boundary conditions that are assumed to hold at the veins. Furthermore, we considered a two-stage model consisting of two related pattern-forming mechanisms, one posed along the proximal vein and the other posed in each wing cell. The two-stage model appears capable of reproducing the results of artificial selection experiments in terms of eyespot selection. A hypothesis within the two-stage model is that patterning in the first stage could be governed by a reaction-diffusion mechanism in which the reaction rate is dependent on the spatial position. Such an assumption is consistent with assuming different levels of gene activation in different regions of the wing (e.g. McMillan et al. 2002). We note however that the present model is still sensitive to changes in the parameter values and crucially, changes in the geometry. In particular, the naturally observed variations in wing cell size across butterflies appear too large for the present model to be applicable. Hence a potentially attractive avenue for future studies is to investigate Turing systems with a degree of scale invariance as has been attempted in other contexts (e.g. Othmer and Pate 1980).