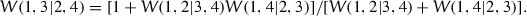Abstract
We consider a transformation from a model on lattice
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
They also feature in the real-space renormalization group method of Chap. 15. There the aim is to obtain an exact, or approximate, transformation for which \({\mathcal {N}}\) and
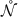 are lattices of the same type with \(n_0<1\). Repeated application of this transformation preserves the critical properties associated with the couplings and leads to trajectories in the space of couplings for which the fixed points can be used to determine critical exponents.
are lattices of the same type with \(n_0<1\). Repeated application of this transformation preserves the critical properties associated with the couplings and leads to trajectories in the space of couplings for which the fixed points can be used to determine critical exponents. - 2.
Although these models were solved independently, it is an interesting and by no means trivial problem (Lavis 1996) to derived the Ising model partition function from that of the eight-vertex model.
- 3.
We shall also use the graph theory terminology of Sect. 16.1.
- 4.
This condition can be easily relaxed for specific lattices to include a small number of different kinds of subsets of sites.
- 5.
As Wegner says (op.cit. p. 571), “the total class of systems to which the transformation can be applied with meaningful results is not known”.
- 6.
We showed in Sect. 16.1.2 that the number of independent cycles for a section graph is the cyclomatic number, which for a planar graph is the number of faces; in this case it is the number of dual lattice sites.
- 7.
It should be noted that
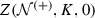 is the partition function for the case where the boundary states have a particular specified value (without loss of generality \(\sigma =0\)). If we had simply chosen the condition that all the boundary states were the same the factor
is the partition function for the case where the boundary states have a particular specified value (without loss of generality \(\sigma =0\)). If we had simply chosen the condition that all the boundary states were the same the factor 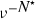 in (9.2.23) would be replaced by
in (9.2.23) would be replaced by 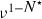 .
. - 8.
The limit of a large lattice is in the sense of van Hove; see Sect. 8.1.
- 9.
That this is the case is evident from Onsager’s solution of the model (see Sect. 12.2.7.3).
- 10.
Hence the name of this transformation.
- 11.
See the footnote concerning the relationship between toroidal boundary conditions and lattice orientation on p. 60. This function is essentially the same as that defined in Sect. 3.8.1 except that here it is more convenient to take the argument values \(0,1\) rather than \(-1,+1\).
- 12.
If the direction rule were used the transformation would correspond to \((\varsigma _1,\varsigma _2,\varsigma _3,\varsigma _4)\rightarrow (-\varsigma _4,\varsigma _1,-\varsigma _2,\varsigma _3)\) giving
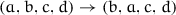 .
. - 13.
For convenience we refer to the different significant subsets of the regions I, II, III and IV as ‘zones’ and ‘subzones’.
- 14.
The special case of the six-vertex model, where
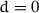 , is discussed below.
, is discussed below. - 15.
For which
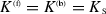 ,
, 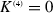 , yielding, from (3.8.11),
, yielding, from (3.8.11),  .
. - 16.
A disorder point in a system is defined to be one, for finite temperature, at which all correlation functions between the states on pairs of sites are zero, as they would be at infinite temperature.
- 17.
Every ratio function is either the negative or reciprocal of one of
 ,
, 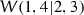 and
and 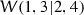 , with
, with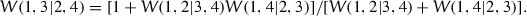
- 18.
Although Wegner (1973) has shown that a version of his transformation can be used to transform the triangular lattice directly into itself.
- 19.
Toroidal boundary conditions are assumed, although the analysis applies equally well to a bounded lattice with an equal number of white and black sites.
- 20.
The labels \(({\mathbf {r}}_1,{\mathbf {r}}_2,{\mathbf {r}}_3)\) in Fig. 9.3 for the neighbours of site \({\mathbf {r}}_{\!\circ }\) are relative to \({\mathbf {r}}_{\!\circ }\) and are not sublattice labels which can be attached with the same orientation to the black sites in Fig. 16.14. However the coupling designations are applicable to all the downward pointing triangles in Fig. 16.14.
- 21.
The derivation given by Hindermann et al. is for \(\nu \ge 4\), but, as remarked by Wu (1982), since it agrees with the \(\nu =2\) (Ising) result (Onsager 1944, see also the comment at the end of Sect. 9.4.2.1), “it is expected the [it] is also exact for \(\nu =3\)”.
- 22.
This notation, not all of which is needed immediately, will be used throughout this and the following section.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Lavis, D.A. (2015). Transformation Methods. In: Equilibrium Statistical Mechanics of Lattice Models. Theoretical and Mathematical Physics. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9430-5_9
Download citation
DOI: https://doi.org/10.1007/978-94-017-9430-5_9
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-017-9429-9
Online ISBN: 978-94-017-9430-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


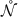 are lattices of the same type with
are lattices of the same type with 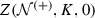 is the partition function for the case where the boundary states have a particular specified value (without loss of generality
is the partition function for the case where the boundary states have a particular specified value (without loss of generality 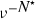 in (
in (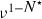 .
.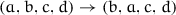 .
.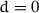 , is discussed below.
, is discussed below.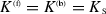 ,
, 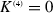 , yielding, from (
, yielding, from ( .
. ,
, 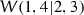 and
and 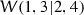 , with
, with