Abstract
It is convenient to use the generic term transform to refer to both the discrete (series) and continuous (integral) cases.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
It is sometimes convenient to use the notation
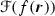 to denote the Fourier transform.
to denote the Fourier transform. - 2.
In one dimension the conditions that \(f({\varvec{r}})\) and \(f^*({\varvec{k}})\) are dependent only on the magnitudes of the vectors reduce to them being even functions. \({\mathcal {S}}_0(q)\) has just two points and can be defined as
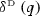 , when (18.1.33) and (18.1.34) reduce to (18.1.31) and (18.1.32).
, when (18.1.33) and (18.1.34) reduce to (18.1.31) and (18.1.32). - 3.
We assume without loss of generality that this ordering of vertices is anticlockwise round the parallelogram.
- 4.
See the footnote on p. 161 for the usage of the term ‘analytic’ for complex-valued functions. Clearly a doubly-periodic function which is analytic in and on the boundary of \(\mathbb {W}(\omega ,\omega ')\) is an entire function.
- 5.
Liouville’s theorem in complex variable theory (not to be confused with his proof of the conservation of measure under a Hamiltonian flow which plays an important role in statistical mechanics) states that, if a function is entire and bounded, it is constant.
- 6.
Here and elsewhere in this section it is assumed that multiple poles and zeros are counted according to their multiplicity and that, if necessary, the period parallelogram is displaced slightly so that no poles or zeros lie on its boundary.
- 7.
A version of the second part of this theorem is proved by Akhiezer (1990, pp. 8–9).
- 8.
\(\frac{1}{2}(1-\tau \bar{\tau })\) and \(\frac{1}{2}(2-\tau -\bar{\tau })\) have the same parity.
- 9.
The other two theta functions, which are avoided in this text, are
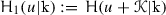 and
and  . In the interests of clarity it should be observed that the notation \(\vartheta _i(u)\), \(i=1,\ldots ,4\), used in many texts for the theta functions, is related to this notation by
. In the interests of clarity it should be observed that the notation \(\vartheta _i(u)\), \(i=1,\ldots ,4\), used in many texts for the theta functions, is related to this notation by 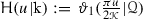 ,
, 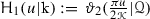 ,
, 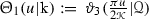 ,
, 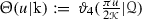 .
. - 10.
In the case of
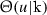 it must be displaced slightly so that the zero at
it must be displaced slightly so that the zero at 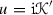 does not lie on the boundary.
does not lie on the boundary. - 11.
It should be noted, for use in Chap. 12, that the expression for \(\mathrm {sn}(u|\mathrm {k})\), but not \(\mathrm {cn}(u|\mathrm {k})\) and \(\mathrm {dn}(u|\mathrm {k})\), takes the same form in terms of Baxter’s modified theta functions.
- 12.
This function just gives the \(2^{2n_2-1}\)-dimensionally degenerate eigenvalues of the matrix given in (12.2.60).
- 13.
Note that \(\prod _{j=1}^{2n_2}\exp \left( 2\,\mathrm{i}\,\psi _j^{(s)}\right) =s\).
- 14.
The \(n=0\) term is understood as the result of taking the limit \(n\rightarrow 0\).
- 15.
In all that follows \(\sigma \) (and all its primed and subscripted versions) is a Potts variable with integer values in the range \([0,\nu -1]\).
- 16.
This is a repetition of (14.2.37).
- 17.
This is a repetition of (14.2.42).
- 18.
These observations are useful because they predict a factor of \(\nu -2\) in all the general computations of cases which would yield zero for \(\nu =2\).
- 19.
This result is derived by proving by induction that
$$ \prod _{k=1}^n \triangle (\nu ;\sigma _k-\sigma )=B_n +\sum _{k=1}^n (-1)^{k+1}A_{k,n}\triangle (\nu ;\sigma _k-\sigma )$$and then summing over the values of \(\sigma \).
- 20.
The state \(\sigma =0\) is excluded by the links to the boundary vertices.
- 21.
See the notation defined in Sect. 16.4.4.
- 22.
For an historical account of the development of Padé approximants see Brezinski (1996, pp. 311–313) and for a comprehensive account of the modern theory see Baker and Graves-Morris (1996).
- 23.
This is the Baker definition (Baker and Graves-Morris 1996, p. 21). The condition \(q_0\ne 0\) originally replaced \(q_0=1\).
- 24.
Notation: \(g(w)=\mathrm {O}(w^k)\) if \(g({{w}})/w^k\) tends to a finite limit as \(w\rightarrow 0\). If \(g(w)=\mathrm {O}(w^k)\) then \(g(w)=\mathrm {O}(w^{k'})\) for \(k'\le k\).
- 25.
Adopting the notation that for any square matrix \({\varvec{W}}\), \(W:=\mathrm {Det}\{{\varvec{W}}\}\).
- 26.
Initially called the ‘recurrence relation method’.
- 27.
\([0/m_0,\ldots ,m_k]_{{{\text { D}}}{{\text {A}}}}\) is the case \(B(w)=b_0\).
- 28.
The
 -functions take care of the zero terms since, for any integer \(n\), if \(1<n\le r-1\),
-functions take care of the zero terms since, for any integer \(n\), if \(1<n\le r-1\), 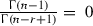 . Also if \(n\le 1\),
. Also if \(n\le 1\), 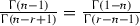 .
. - 29.
With \(c_{0j}:=0\) for \(j>n_0\).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Lavis, D.A. (2015). Analysis. In: Equilibrium Statistical Mechanics of Lattice Models. Theoretical and Mathematical Physics. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9430-5_18
Download citation
DOI: https://doi.org/10.1007/978-94-017-9430-5_18
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-017-9429-9
Online ISBN: 978-94-017-9430-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


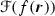 to denote the Fourier transform.
to denote the Fourier transform.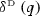 , when (
, when (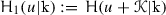 and
and  . In the interests of clarity it should be observed that the notation
. In the interests of clarity it should be observed that the notation 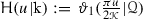 ,
, 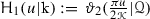 ,
, 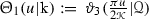 ,
, 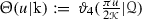 .
.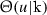 it must be displaced slightly so that the zero at
it must be displaced slightly so that the zero at 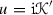 does not lie on the boundary.
does not lie on the boundary. -functions take care of the zero terms since, for any integer
-functions take care of the zero terms since, for any integer 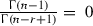 . Also if
. Also if 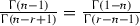 .
.