Abstract
A graph \({\mathfrak {g}}\) is a set of vertices (points) some or all of which are connected by edges (lines).
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In this section we present only those elements of graph theory needed for the discussion of statistical mechanical lattice systems. For more general presentations see, for example, Berge (1962) or Wilson and Watkins (1990). In the case of graphs which are lattices (Sect. 16.2) or parts of lattices (Sect. 16.4) the vertices are usually referred to as ‘sites’ and the edges are ‘first-neighbour pairs’ or ‘second-neighbour pairs’ etc., according to whether they are represented by lines joining closest or next-closest sites. The term bond is also used in our discussion in Sect. 14.3 of the case where a number of bonds replace a single edge of a graph. For the moment we shall suppose that a pair of vertices is connected by at most one edge.
- 2.
Of course, if the chain is finite this condition does not apply to the last vertex.
- 3.
The term ‘simple’ is sometimes used here for both chains and cycles in place of ‘elementary’. We follow the usage of Berge (1962) who uses ‘simple’ for the weaker condition which just disallows repeated edges along the ordering of vertices.
- 4.
There is unfortunately some variation in the literature in the definition of a tree. Thus Lavis and Bell (1999b, Sect. A.7.2) define a tree to be any connected graph, which is not a star. According to this definition a tree is composed of stars connected at articulation points. Then a tree with no closed cycles of edges is called a Cayley tree. To complicate things further the term ‘Cayley tree’ is sometimes used to signify the graph which we have called a Bethe lattice.
- 5.
In the case of a finite lattice this definition is modified by excluding from the valency condition sites of valency one (sometimes called leaves), which terminate the lattice.
- 6.
In fact Berge defines the cyclomatic number by (16.1.1) and then proves it equal to the number of independent cycles.
- 7.
For all the regular lattices, except the dice lattice (Sect. 16.2.2.1), each lattice site has the same coordination number. The dice lattice has sites of coordination numbers three and six.
- 8.
Essentially those is which the van Hove thermodynamic limit (Sect. 8.1) can be taken.
- 9.
Variations of this where more than one site is added to a face or edge, or a site is added to only a translationally invariant subset of the edges or faces is obviously possible. A case where sites are added to only the downward-pointing triangles of a triangular lattice is described in Sect. 16.2.2.4 and used in the star-triangle transformation of Sect. 9.4.
- 10.
It is assumed that the lattices are finite with the cases of different boundary conditions considered below.
- 11.
The case of three-dimensional lattices is discussed below.
- 12.
See Sect. 16.3 for an explication of rapidity lines and lattices.
- 13.
The relationship (16.2.9) between the coordination numbers of interior sites of a lattice and its dual has, of course, general validity.
- 14.
Toroidal boundary conditions can be applied to the honeycomb and kagomé lattices only when \(N\) is divisible by two and three respectively and this will be assumed, where necessary, in all future discussion.
- 15.
Which, as indicated above, carries the assumption for the honeycomb and kagomé lattices that \(N\) is divisible by two and three respectively.
- 16.
Although, of course, forms of decoration which are not edge-decoration can be devised and used for higher-dimensional lattices. Indeed, one might regard both the body-centered cubic lattice of Fig. 16.8 and the face-centred cubic lattice of Fig. 16.9 as decorations of the simple cubic lattice of Fig. 16.7.
- 17.
As would be the case where every line of \({\mathfrak {g}}^\circledast \) is parallel to at least one other line.
- 18.
It should be noted that our definitions of the variables are formulated to achieve consistency with Baxter (1978). They differ from those used in Baxter (1986) and Costa-Santos (2006). Specifically the difference involves the interchange \(\alpha _{ij} \leftrightarrow \lambda -\alpha _{ij}\), corresponding to an interchange between the edge variables of the dual lattice edges passing through every site of \({\mathfrak {g}}^\circledast \). This leads to the replacement of \((m-2)\lambda \) by \(2\lambda \) in the statement of Theorem 16.3.1 (see Baxter 1986, Eq. (8.2)).
- 19.
A rhombic embedding (also called a isoradial embedding) of quadratic graph is a continuous displacement of its vertices and edges which, while leaving all the edge/vertex connections unchanged, transforms every edge into a straight line of unit length; meaning that every face becomes a rhombus.
- 20.
Although it is convenient to allow the topological equivalence between the triangular lattice and a square lattice with edges between all second-neighbour pairs with one of the two orientations.
- 21.
In some cases, like for example in the discussion of graphs on the body-centred cubic lattice in Example 16.4.7, the account given here is generalized to the case where there are two different kinds of edges, corresponding to first-neighbour and second-neighbour pairs of sites. A section graph is then one which has edges connecting all of its first-neighbour and second-neighbour pairs.
- 22.
In this terminology, rather unfortunately, strong embeddings are subclasses of weak embeddings.
- 23.
The significance of this way of labeling graphs is described below.
- 24.
The ‘shape of a graph’ is, in the case of a multi-component graph, taken to mean the shapes of all the components.
- 25.
We simplify the case of graphs placed on the whole lattice to
 . In the case where \({\mathfrak {g}}\) is
. In the case where \({\mathfrak {g}}\) is  or
or  we denote the lattice constants (on \({\mathcal {N}}\)) by
we denote the lattice constants (on \({\mathcal {N}}\)) by  and
and 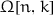 , respectively.
, respectively. - 26.
The term ‘lattice constant’ will whenever the meaning is clear be used to refer to ‘per site’ quantities.
- 27.
This includes the case where \({\mathfrak {g}}'\) and \({\mathfrak {g}}\) are isomorphic; when this is not the case we write \({\mathfrak {g}}'\subset {\mathfrak {g}}\) and say that \({\mathfrak {g}}'\) is a proper subgraph of \({\mathfrak {g}}\).
- 28.
Permutations of the last five lines of the table give other partial orderings.
- 29.
We discuss the details of methods of generating such a sequence below.
- 30.
In the case where
 is a function of other variables, for example those of a thermodynamic system, then that dependence is carried over into the set \(\{\theta _i\}\).
is a function of other variables, for example those of a thermodynamic system, then that dependence is carried over into the set \(\{\theta _i\}\). - 31.
The use of both round and square brackets in this equation indicates that, whereas the members of
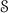 are section graphs, this has not been assumed for \({\mathfrak {g}}'\).
are section graphs, this has not been assumed for \({\mathfrak {g}}'\). - 32.
- 33.
This involves the generalization of the notion of a graph to the case of two types of edges mentioned in a footnote on p. 637.
- 34.
We are for simplicity, at this stage, excluding sublattice ordering of the type described in Sect. 16.4.7.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Lavis, D.A. (2015). Graphs and Lattices. In: Equilibrium Statistical Mechanics of Lattice Models. Theoretical and Mathematical Physics. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9430-5_16
Download citation
DOI: https://doi.org/10.1007/978-94-017-9430-5_16
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-017-9429-9
Online ISBN: 978-94-017-9430-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


 . In the case where
. In the case where  or
or  we denote the lattice constants (on
we denote the lattice constants (on  and
and 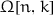 , respectively.
, respectively. is a function of other variables, for example those of a thermodynamic system, then that dependence is carried over into the set
is a function of other variables, for example those of a thermodynamic system, then that dependence is carried over into the set 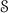 are section graphs, this has not been assumed for
are section graphs, this has not been assumed for  as given in Tables
as given in Tables