Abstract
In this chapter we discuss methods for obtaining coefficients in the expansions of partition functions and free energies, or their derivatives, in a series of powers of temperature-dependent variables.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
As is discussed in Sect. 14.6, in the case of high-temperature series, a singularity on the negative real axis also corresponds to a critical temperature.
- 2.
Thus, for example, for \(F(w):=(0.5-w)^{-0.25}\), although the convergence is for a monotonically increasing sequence, the estimate for \(w_\mathrm {c}\) from \(F_{1000}(w)\) still differs from \(w_\mathrm {c}=0.5\) by \(0.0031577523\). Making the same point Guttmann (1989) considers the susceptibility of the spin-\(\frac{1}{2}\) Ising model for which Nickel has derived 54 terms of the high-temperature series. In this case the estimate from \(F_{54}(w)\) is higher than the exact \(w_\mathrm {c}=1+\sqrt{2}\) by about \(5.4\,\%\).
- 3.
Knowing of course that the spin-\(\frac{1}{2}\) Ising model can be recovered as the special case \(\nu =2\) (Sect. 3.6.4).
- 4.
Rather confusingly, this quantity is often simple called ‘the partition function’ (see, for example Briggs et al. 1994).
- 5.
The order parameter \(\widetilde{\rho }\), which Briggs et al. (1994) call the magnetization, differs from that used (with \(\nu =3\)) in the Landau expansion in Sect. 5.4.2 by a factor of \(2/\sqrt{3}\).
- 6.
The response function
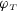 , which Briggs et al. call the susceptibility, differs from the compressibility defined by (1.4.12) by a factor of \(1/(k_{{\text {B}}}T\rho ^2)\). We shall for the sake of maintaining neutrality between lattice-fluid and magnetic interpretations refer to it as the ‘field-response function’. \(c_\rho \) is, of course, the heat capacity at constant density. However, since we shall be concerned solely with calculating it for zero \(\mu \) (\({\mathfrak {Z}}=1\)) it will be the same as the constant \(\mu \) heat capacity.
, which Briggs et al. call the susceptibility, differs from the compressibility defined by (1.4.12) by a factor of \(1/(k_{{\text {B}}}T\rho ^2)\). We shall for the sake of maintaining neutrality between lattice-fluid and magnetic interpretations refer to it as the ‘field-response function’. \(c_\rho \) is, of course, the heat capacity at constant density. However, since we shall be concerned solely with calculating it for zero \(\mu \) (\({\mathfrak {Z}}=1\)) it will be the same as the constant \(\mu \) heat capacity. - 7.
Item (ii) needs qualification if high-temperature moment series in terms of the inverse temperature are derived. These give rise to multi-bonded graphs (see Lavis and Bell 1999b, Sect. 7.6) and have led to the proposal for a finite-cluster moment method by de Neef (1975, Sect. 2.3).
- 8.
We exclude the case of a linear lattice (
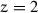 ), for which no phase transition occurs for non-zero temperature.
), for which no phase transition occurs for non-zero temperature. - 9.
A case where such an expansion is useful is in the investigation of the zero-field first-order transition in the Ising model (see Sect. 14.7 and Enting and Baxter 1980).
- 10.
In view of the following discussion it is convenient to include explicit linear \(N\)-dependence of the coefficients in (14.2.4). However, that does not exclude further non-linear dependence.
- 11.
Of course, for all lattices,
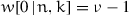 .
. - 12.
For simplicity we regard an isolated site as a tree (and also a chain) with no edges.
- 13.
Notation: \(g(u)=\mathrm {O}(u^k)\) if \(g(u)/u^k\) tends to a finite limit as \(u\rightarrow 0\). If \(g(u)=\mathrm {O}(u^k)\) then \(g(u)=\mathrm {O}(u^{k'})\) for \(k'\le k\).
- 14.
Although there is a Kosterlitz-Thouless transition which can be analysed using a high-temperature series expansion (Oitmaa et al. 2006, Chap. 3).
- 15.
The distinction is sometimes made between ‘magnetic graphs’ with two odd vertices and ‘hyper-magnetic graphs’ with more than two odd vertices; for simplicity we shall refer to all graphs with odd vertices simply as magnetic.
- 16.
The question of what graphs contribute to the \(\mu \ne 0\) series is more complicated, as is illustrated by the examples is Sect. 18.4.
- 17.
Graphs with type B and C articulation points give a zero contribution and those with a type A articulation point can be considered as cases of disconnected components.
- 18.
See the remarks at the end of Sect. 16.2.2.1.
- 19.
Of course, it will then need to be multiplied by the appropriate lattice constant and the number of equivalent locations for the like pairs.
- 20.
The variables \({\mathfrak {Z}}\) and \(q\) are reintroduced when the analysis is particularized, respectively, to the low- and high-temperature cases.
- 21.
The function \(f({\varvec{x}})\) of the vector \({\varvec{x}}\) can be expressed in the form
\(f({\varvec{\delta }}{\varvec{x}})={[\exp ({\varvec{\delta }}{\varvec{x}} {\varvec{\nabla }})f({\varvec{x}})]}_{{\varvec{x}}={\varvec{0}}}\)
at a point \({\varvec{\delta }}{\varvec{x}}\) near the origin. The expansion in powers of the components of \({\varvec{\delta }}{\varvec{x}}\) is then obtained by using the power-series expansion of the exponential.
- 22.
- 23.
In quantum systems these operators will not, in general, commute, but here we are concerned only with classical systems.
- 24.
All chains of the same length but different topologies can be grouped together (e.g. graphs \((3,1)\)–\((3,4)\) in Table 16.1), since they have the same free energies and cluster functions.
- 25.
The comparative lengths of the series, illustrates the greater difficulty in obtaining high-temperature series, something which we shall see again with the finite-lattice method.
- 26.
A different expansion variable, equivalent to \(\nu \, v/(1-v)\), was used in their calculations.
- 27.
For which the argument can easily be extended to the simple cubic lattice.
- 28.
For a \(d\)-dimensional hypercubic lattice the formula is
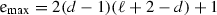 , with the meaning of \(\ell \) generalized in the obvious way.
, with the meaning of \(\ell \) generalized in the obvious way. - 29.
For a \(d\)-dimensional hypercubic lattice the respective formulae are
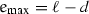 and
and 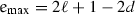 .
. - 30.
A modification of the honeycomb case can be made by reformulating the transfer matrices into ones between vertical rows of sites. This reduces the order but increases the number of matrix multiplications, still leaving the honeycomb case more expensive in computing time than the square and triangular cases.
- 31.
See the list of papers in Enting (1996).
- 32.
And also, although we have not discussed this, on the kagomé lattice for \(\nu =3\) (up to \(u^{66}\)) and \(\nu =4\) (up to \(u^{56}\)).
- 33.
Rather less attention has been given to the way that series analysis can be used to detect first-order transitions and we shall turn to that topic in Sect. 14.7.
- 34.
For more detailed accounts the reader is referred to the review articles by Gaunt and Guttmann (1965) and Guttmann (1989).
- 35.
Excluding models like those discussed in Sect. 10.4 which have upper- and lower-critical temperatures.
- 36.
There may, of course, be other singularities on the circle \(|w|={r}\).
- 37.
This provides a ‘simple’ method for obtaining \(w_\mathrm {c}\) but, as we have shown by examples in Sect. 14.1, convergence is often very slow, leading to the need for the more sophisticated methods described below.
- 38.
The combination of this transformation with a Padé approximant is the Dlog Padé approximant.
- 39.
This terminology is not related to the exponent renormalization described in Sect. 10.2.1.
- 40.
This conjectures that, for a function \(F(w)\) meromorphic in the unit disc, there is a subsequence of the diagonal approximants which converges to \(F(w)\) locally uniformly for all poles in the unit disc.
- 41.
They cannot, of course, exactly coincide since \(P_{n}^{(m)}({{w}})\) and \(Q_{m}^{(n)}({{w}})\) are coprime.
- 42.
- 43.
Linear in the sense that the index variable appear linearly.
- 44.
This work by Dr. Sykes is reported by Guttmann (1989) and elsewhere, but does not seem to have been published.
- 45.
See (12.3.280) for the Ising model, (12.3.322) for the 3-state Potts model and (13.2.2) for the honeycomb dimer model. The case of the eight-vertex model is exceptional since the exponents
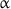 ,
, 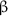 ,
, 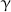 and
and 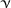 vary through irrational values (Sect. 12.3.8). However, see the results of the application of the proposal of weak universality given in (12.3.326).
vary through irrational values (Sect. 12.3.8). However, see the results of the application of the proposal of weak universality given in (12.3.326). - 46.
Although it is noted by Briggs et al. (1994) that even “with an essential singularity [at the transition point] it may be possible to define the thermodynamic functions in the metastable region by analytic continuation in the complex plane passing around the singularity”.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2015 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Lavis, D.A. (2015). Series Expansions. In: Equilibrium Statistical Mechanics of Lattice Models. Theoretical and Mathematical Physics. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9430-5_14
Download citation
DOI: https://doi.org/10.1007/978-94-017-9430-5_14
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-017-9429-9
Online ISBN: 978-94-017-9430-5
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


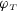 , which Briggs et al. call the susceptibility, differs from the compressibility defined by (
, which Briggs et al. call the susceptibility, differs from the compressibility defined by (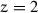 ), for which no phase transition occurs for non-zero temperature.
), for which no phase transition occurs for non-zero temperature.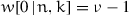 .
.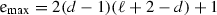 , with the meaning of
, with the meaning of 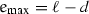 and
and 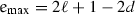 .
. and
and  , implying, contrary to our assumption for Padé approximants that
, implying, contrary to our assumption for Padé approximants that  and
and  .
.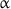 ,
, 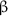 ,
, 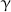 and
and 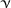 vary through irrational values (Sect.
vary through irrational values (Sect.