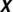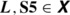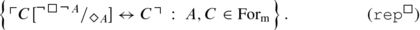Abstract
Jaśkowski’s logic D 2 is usually understood as a set of discussive formulae. Studying Jaśkowski’s paper one can also find a consequence relation (the D 2 -consequence). The logic D 2 was meant to express this consequence relation. Since the logic D 2 was formulated with the help of a modal logic, the consequence relation is also defined in the modal language. It is known that the logic D 2 can be defined by other modal logics than S5. A similar question arises as regards the consequence relation. In Nasieniewski and Pietruszczak (On modal logics defining Jaśkowski’s D2-consequence. In: Tanaka K, Berto F, Mares E, Paoli F (eds) Paraconsistency: logic and applications. Logic, epistemology and the unity of science, chap 8, vol 26. Springer, Dordrecht/New York, pp 141–161, 2013) there are given modal logics other than S5 which define exactly the same consequence relation. In the present paper we try to develop a more general method of defining modal logics which also allow to define the D 2 -consequence.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The term ‘modal logic’ is here always understood as a set of modal formulae. In Appendix we recall the standard notation, chosen basic facts and notions concerning modal logics.
- 2.
In Nasieniewski and Pietruszczak (2013) the D 2 -consequence was defined and the smallest normal and regular modal logics defining the D 2 -consequence were given (see Sect. 6.3). In Nasieniewski and Pietruszczak (2011) some general method of axiomatizing modal logics defining the logic D 2 was proposed. In the current paper this method has been adopted for the case of the D 2 -consequence.
- 3.
As it is known { ◊ A •: A ∈ Π} ⊢ S5 ◊ B • iff for some A 1, …, A n ∈ Π, \(n\geqslant 0\), we have that \(\ulcorner \lozenge A_{1}^{\bullet }\rightarrow (\ldots \rightarrow (\lozenge A_{n}^{\bullet } \rightarrow \lozenge B^{\bullet })\ldots )\urcorner \in \mathbf{S5}\), or equivalently \(\ulcorner (\lozenge A_{1}^{\bullet } \wedge \ldots \wedge \lozenge A_{n}^{\bullet })\rightarrow \lozenge B^{\bullet }\urcorner \in \mathbf{S5}\) (see Lemma 22).
- 4.
By Fact 3(iii) in the case of congruential logic this requirement follows from the condition that \(\boldsymbol{L}\) defines D 2 . Moreover, as we will see in Theorem 8, all considered logics define D 2 and are included in S5 (also non-congruential ones).
- 5.
Notice that this logic exists, because the set of logics in
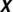
defining \(\mathbf{D}_{\mathbf{2}}\) is closed under arbitrary intersections and \(\mathbf{S5}\) belongs to this set.
- 6.
By Fact 7, the logic

exists, since
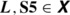
and \(\boldsymbol{L} \cup \{ (\mathtt{C})\} \subseteq \mathbf{S5}\).
- 7.
\(\mathbf{CD45}\mathbf{(1)}\) is the smallest regular logic which contains (D), (4), and (5 \(\mathtt{(1)}\)), i.e. \(\ulcorner \square \top \rightarrow (\mathtt{5})\urcorner \). Also \(\mathbf{CD45}\mathbf{(1)} = \mathbf{CN}^{\mathbf{1}}\mathbf{5}_{\mathbf{c}}\mathbf{5}\mathbf{(1)}\), where (N1 ) is ‘□(p→p)→□□(p→p)’.
- 8.
Notice that for any \(\mathcal{A}\) and \(\mathcal{R}\), the logic \(\boldsymbol{L}^{\lozenge \square }\) exists.
- 9.
- 10.
Again notice that for any \(\mathcal{A}\) and \(\mathcal{R}\) , the logic \(\boldsymbol{L}^{\lozenge \square \star }\) exists.
- 11.
See Footnote 9.
- 12.
For formulae having other forms one can take whatever as value of v. However, by the given restrictions we have that for any A ∈ Form: v( □ ¬A) = 1 iff \(\ulcorner \lozenge A\urcorner \notin \mathbf{S5}\).
- 13.
Notice that in Nasieniewski and Pietruszczak (2008, pp. 202–203) it was proved that \(\ulcorner \lozenge \square (\mathtt{5})\urcorner \in \mathbf{r}\mathbf{S5}^{\mathbf{M}}\) and r S5 M is closed under (mp) ◊ □ and \((\mathrm{cut}_{\lozenge }^{\lozenge \square \lozenge })\); so \(\mathbf{r}\mathbf{S5}_{\vdash }^{\mathbf{M}} \subseteq \mathbf{CD45}\mathbf{(1)}\). Of course, the reverse inclusion can be shown elementarily.
- 14.
- 15.
We can also consider quite weak modal logics in which we use (df ◊ ) instead of (rep □ ). In some logics the symbol ‘ ◊ ’ has not to behave as an abbreviation of ‘¬ □ ¬’, although we can have there the thesis (df □ ) (cf. Remark 2). For example, the formula ‘ □ ◊ p ↔ □ ¬ □ ¬p’ has not to be a thesis of such logics.
- 16.
In Segerberg (1971), Segerberg also puts \(\mathbf{D5}: = \mathbf{CN}^{\mathbf{1}}\mathbf{D4}\mathbf{B}\mathbf{(1)} = \mathbf{CD4B}\mathbf{(1)}\). So we have D5 = E5.
References
Bull, R. A., & Segerberg, K. (1984). Basic modal logic. In D. Gabbay & F. Guenthner (Eds.), Handbook of philosophical logic (Vol. II, pp. 1–88). Dordrecht: Reidel.
Chellas, B. F. (1980). Modal logic: An introduction. Cambridge: Cambridge University Press.
Jaśkowski, S. (1948). Rachunek zdań dla systemów dedukcyjnych sprzecznych. Studia Societatis Scientiarum Torunensis, Sect. A, I(5), 57–77. The first English version: Propositional calculus for contradictory deductive systems. Studia Logica, 24, 143–157 (1969).
Jaśkowski, S. (1999a). A propositional calculus for inconsistent deductive systems. Logic and Logical Philosophy, 7, 35–56. The second English version of Rachunek zdań dla systemów dedukcyjnych sprzecznych.
Jaśkowski, S. (1999b). On the discussive conjunction in the propositional calculus for inconsistent deductive systems. Logic and Logical Philosophy, 7, 57–59. The English version of O koniunkcji dyskusyjnej w rachunku zdań dla systemów dedukcyjnych sprzecznych, Studia Societatis Scientiarum Torunensis, Sect. A, Vol. I, no. 8, 171–172 (1949).
Lemmon, E. J., & Scott, D. (1977). “Lemmon Notes”: An introduction to modal logic (American philosophical quarterly monograph series). Oxford: Basil Blackwell.
Nasieniewski, M., & Pietruszczak, A. (2008). The weakest regular modal logic defining Jaśkowski’s logic D2. Bulletin of the Section of Logic, 37(3/4), 197–210.
Nasieniewski, M., & Pietruszczak, A. (2009). New axiomatizations of the weakest regular modal logic defining Jaśkowski’s logic D2. Bulletin of the Section of Logic, 38(1/2), 45–50.
Nasieniewski, M., & Pietruszczak, A. (2011). A method of generating modal logics defining Jaśkowski’s discussive logic D2. Studia Logica, 97(1), 161–182.
Nasieniewski, M., & Pietruszczak, A. (2012). On the weakest modal logics defining Jaśkowski’s logic D2 and the D2-consequence. Bulletin of the Section of Logic, 41(3/4), 215–232.
Nasieniewski, M., & Pietruszczak, A. (2013). On modal logics defining Jaśkowski’s D2-consequence. In K. Tanaka, F. Berto, E. Mares, & F. Paoli (Eds.), Paraconsistency: Logic and applications (Logic, epistemology and the unity of science, chap. 8, Vol. 26, pp. 141–161). Dordrecht/New York: Springer.
Perzanowski, J. (1975). On M-fragments and L-fragments of normal modal propositional logics. Reports on Mathematical Logic, 5, 63–72.
Segerberg, K. (1971). An essay in classical modal logic (Vols. 1 and 2). Uppsala: Department of Philosophy, Uppsala University.
Acknowledgements
We would like to thank both anonymous referees for their valuable remarks on an earlier version of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix: Some Facts from Modal Logic
Appendix: Some Facts from Modal Logic
As in Chellas (1980) modal formulae are formed in the standard way from propositional letters: ‘p’, ‘q’, ‘p 0’, ‘p 1’, ‘p 2’, …; truth-value operators: ‘¬’, ‘∨’, ‘∧’, ‘ → ’, and ‘ ↔ ’ (connectives of negation, disjunction, conjunction, material implication, and material equivalence, respectively); modal operators: the necessity sign ‘ □ ’ and the possibility sign ‘ ◊ ’; and brackets. By Form we denote the set of modal formulae. Of course, the set Form includes the set of all classical formulae (without ‘ □ ’ and ‘ ◊ ’); let Taut be the set of all classical tautologies. Besides, for any A, B, C ∈ Form, let C[A∕ B ] be any formula that results from C by replacing one or more occurrences of A, in C, by B.
For any subset \(\Phi \) of Form we put \(\square \Phi: =\{ \ulcorner \square A\urcorner: A \in \Phi \}\) and \(\lozenge \Phi: =\{ \ulcorner \lozenge A\urcorner: A \in \Phi \}\).
Modal logics are certain sets of formulae. As in Bull and Segerberg (1984), we define a modal logic as a set \(\boldsymbol{L}\) of modal formulae satisfying the following conditions:
-
\(\mathbf{Taut} \subseteq \boldsymbol{ L}\),
-
\(\boldsymbol{L}\) includes the following set of formulae
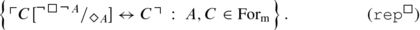
-
\(\boldsymbol{L}\) is closed under the following two rules: modus ponens for ‘ → ’:

and uniform substitution:

where sA is the result of uniform substitution of formulae for propositional letters in A.
Of course, by (sb), every modal logic includes the set PL of modal formulae which are instances of classical tautologies (i.e. instances of elements of Taut).
All members of a logic are called its theses. By (rep □ ), every modal logic has the following thesis:

Remark 2.
In Bull and Segerberg (1984) the symbol ‘ ◊ ’ is only an abbreviation of ‘¬ □ ¬’. In the present paper ‘ ◊ ’ is a primary symbol, thus we have to add the set of axioms (rep □ ). The use of this set corresponds to the applying of the formula (df ◊ ) as a definition together with the definitional rule. Formulae from (rep □ ) allow to replace one or more occurrences of ‘¬ □ ¬’ with ‘ ◊ ’ and vice versa. □
Lemma 8.
A logic contains the formula:

iff it contains its dual version:

We say that a modal logic \(\boldsymbol{L}\) is rte-logic iff \(\boldsymbol{L}\) is closed under replacement of tautological equivalents, i.e., for any A, B, C ∈ Form

A modal logic is rte-logic iff it includes the following set

In any thesis of any rte-logic we can replace one or more occurrences of ‘¬ □ ¬’ (resp. ‘ □ ¬’, ‘¬ □ ’, ‘¬ ◊ ¬’, ‘¬ ◊ ’, ‘ ◊ ¬’) by ‘ ◊ ’ (resp. ‘¬ ◊ ’, ‘ ◊ ¬’,‘ □ ’, ‘ □ ¬’, ‘¬ □ ’) and vice versa. Thus, every rte-logic has the following thesis

Lemma 9.
An rte-logic contains, respectively, the following formulae:






iff it contains, respectively, theirs dual versions:






In Bull and Segerberg (1984) a modal logic is called classical modal Footnote 14 (cm-logic for short) iff it is rte-logic which contains (K) and

Thus, all cm-logics include the set □ PL.
We say that a modal logic is congruential iff it is closed under the congruence rule

A modal logic is congruential iff it is closed under replacement:

iff it contains (df □ ) and is closed under the following rule

Lemma 10.
Every modal logic closed under (rep) includes the set (rep PL ); so every congruential logic is an rte-logic.
Besides (N), we use the following formulae


Lemma 11.
For any congruential logic \(\boldsymbol{L}\) the following conditions are equivalent:
-
(a)
\(\boldsymbol{L}\) has a pair of theses of the form B and \(\ulcorner \square B\urcorner \) (resp. \(\ulcorner \lozenge B\urcorner \), \(\ulcorner \lozenge \square B\urcorner \) ),
-
(b)
\(\boldsymbol{L}\) has a thesis of the form \(\ulcorner \square T\urcorner \) (resp. \(\ulcorner \lozenge T\urcorner \), \(\ulcorner \lozenge \square T\urcorner \) ), where \(T \in \mathbf{PL}\),
-
(c)
\(\boldsymbol{L}\) contains ( \(\mathtt{N}\) ) (resp. (P), (\(\mathtt{PN}\))).
Lemma 12.
If a congruential logic contains ( \(\mathtt{N}\) ) (resp. (P), (\(\mathtt{PN}\))), then it is closed under the necessity (resp. possibility, possibility-necessity) rule:



Lemma 13.
If a congruential logic has theses ( \(\mathtt{5}\) ) and either
-
A theses of the form \(\ulcorner \lozenge B\urcorner \) , or
-
(T),
then it is closed under the rule (nec).
It is known (cf. e.g. Chellas 1980) that while defining congruential logics one uses (df ◊ ) instead of (rep □ ), i.e., treats them as subsets of Form which contain Taut and (df ◊ ), and are closed under the rules (mp), (sb) and (cgr).Footnote 15
Lemma 14.
Let \(\boldsymbol{L}\) be any modal logic closed under (nec), and containing (\(\mathtt{T}\)) and (\(\mathtt{5}\)). Then for any A ∈ Form : \(A \in \boldsymbol{ L}\) iff \(\ulcorner \lozenge \square A\urcorner \in \boldsymbol{ L}\).
Lemma 15.
Let \(\boldsymbol{L}\) be any modal logic containing ( \(\mathtt{T}\) ), ( \(\mathtt{5}\) ), \((\mathtt{5}^{\diamond})\), (4) and (4 ◇). Then for any sequences of modal operators \(\mathcal{M}\) and \(\mathcal{M}^{\prime}\), and any A ∈ Form : \(\ulcorner \mathcal{M}\lozenge A\urcorner \in \boldsymbol{ L}\) iff \(\ulcorner \lozenge A\urcorner \in \boldsymbol{ L}\) iff \(\ulcorner \mathcal{M}^{\prime}\lozenge A\urcorner \in \boldsymbol{ L}\).
We say that a modal logic is monotonic iff it is closed under the monotonicity rule:

Of course, every monotonic logic is closed under (rep) and under the dual form of (mon):

Lemma 16.
For any monotonic logic the following conditions are equivalent:
-
(a)
It has at least one thesis of the form \(\ulcorner \square B\urcorner \) (resp. \(\ulcorner \lozenge B\urcorner \), \(\ulcorner \lozenge \square B\urcorner \) ),
-
(b)
It contains ( \(\mathtt{N}\) ) (resp. (P), (\(\mathtt{PN}\))).
We say that a modal logic is regular iff it is closed under the regularity rule:

A modal logic is regular iff it contains (K) and is closed under (mon) iff it contains (R) and is closed under (cgr). Every regular logic has the theses (R◇ ) and

By (R◇ □ ) we obtain.
Lemma 17.
For any regular logic the following conditions are equivalent:
-
(a)
It has at least one thesis of the form \(\ulcorner \lozenge B\urcorner \),
-
(b)
It contains (P),
-
(c)
It contains the following formula

A modal logic is normal iff it contains (K) and is closed under (nec) iff it is regular and contains (N) iff it contains (N) and (K) and is closed under (cgr). Thus, all normal logics are cm-logics.
Let K (resp. C2) be the smallest normal (resp. regular) modal logic. Using names of the above formulae, to simplify notation of normal (resp. regular) logics we write the Lemmon code KX 1 … X n (resp. CX 1 … X n ) to denote the smallest normal (resp. regular) logic containing the formulae (X 1), …, (X n ) (see Bull and Segerberg 1984; Chellas 1980; Segerberg 1971). Besides, let for any formula A ∈ Form, KX 1 … X n ⊕ A (resp. CX 1 … X n ⊕ A) be the smallest normal (resp. regular) logic which includes KX 1 … X n (resp. CX 1 … X n ) and contains A.
Lemma 18.
-
(i)
\((\mathtt{D}) \in \mathbf{C}\mathbf{5}_{\mathbf{c}} \subseteq \mathbf{K5}_{\mathbf{c}}\).
-
(ii)
\((\mathtt{5}_{\mathtt{c}}) \in \mathbf{CD4} \subseteq \mathbf{KD4}\).
-
(iii)
\(\mathbf{KD4} = \mathbf{K5}_{\mathbf{c}}\mathbf{4}\) and \(\mathbf{CD4} = \mathbf{C5}_{\mathbf{c}}\mathbf{4}\).
Proof.
-
(i)
‘ ◊ (p → □ p)’ belongs to C 5 c , by (R◇ □ ). So, we use Lemma 17.
- (ii)
-
(iii)
By (i) and (ii). □
The logic CF, called falsum, is the smallest regular logic containing the following formula

We have \(\ulcorner \lozenge A\urcorner \in \mathbf{CF}\), for any A ∈ Form.
We standardly put T: = KT, S4: = KT4 and \(\mathbf{S5}: = \mathbf{KT5} = \mathbf{KT4B} = \mathbf{KD4B} = \mathbf{KD5B}\). As it is known, T ⊊ S4 ⊊ S5, CD5 = KD5, CD45 = KD45 and \(\mathbf{CT5} = \mathbf{KT5} =:\mathbf{S5}\). Thus, to avoid “normalization” of regular logics one has to use some special formulae. We adopt a convention from Segerberg (1971, p. 206) and for any formula (X) we put \((\mathtt{X(1)}): = \ulcorner \square (p\rightarrow p)\rightarrow (\mathtt{X})\urcorner \). Notice that in all monotonic logics, any formula of the form \(\ulcorner \square A\rightarrow B\urcorner \) is equivalent to \(\ulcorner \square (p\rightarrow p)\rightarrow (\square A\rightarrow B)\urcorner \). Thus, the formulae (T), (D), (4) and (5c ) are respectively equivalent to (T(1)), (D(1)), (4(1)) and (5c (1)).
Lemma 19.
The following formulae:
belong to S5 , as well as for any n > 0 the following formula:
Lemma 20.
If (C), i.e. ‘◊(◊p→q)→(◊p→◊q)’, belongs to \(\boldsymbol{L}\), then for any n > 0 the following formula belongs to \(\boldsymbol{L}\):
Proof.
By induction on the number of propositional letters in a formula. It the case of two letters we just have (C). For the inductive step, by (C) and (sb) we have also:
By the inductive hypothesis we have
The thesis follows by PL. □
Lemma 21 (Segerberg 1971, vol. II, Corollary 2.4).
\(\mathbf{CN}^{\mathbf{1}}\mathbf{X}_{1}\mathbf{(1)}\ldots \mathbf{X}_{n}\mathbf{(1)} = \mathbf{CF} \cap \mathbf{KX}_{1}\ldots \mathbf{X}_{n}\) , where

In Segerberg (1971), Segerberg puts E5: = CN 1 T4 B (1). So \(\mathbf{E5} = \mathbf{CF} \cap \mathbf{KT4B} = \mathbf{CF} \cap \mathbf{S5}\), by Lemma 21. Notice that E5 = CT4B (1), since (N1 ) is an instance of (4). We have also E5 = CN 1 T 5 (1) and \(\mathbf{E5} = \mathbf{CF} \cap \mathbf{KT4B} = \mathbf{CF} \cap \mathbf{KD4B} = \mathbf{CD4B}\mathbf{(1)}\).Footnote 16 Moreover, notice that \(\mathbf{CD4}\mathbf{5}\mathbf{(1)} = \mathbf{CN}^{\mathbf{1}}\mathbf{D4}\mathbf{5}\mathbf{(1)} = \mathbf{CF} \cap \mathbf{KD45}\).
For any modal logic \(\boldsymbol{L}\) we define the relation of consequence \(\vdash _{\boldsymbol{L}}\) with the help of modus ponens for ‘ → ’ as the only rule of inference, i.e., \(\vdash _{\boldsymbol{L}}\) is the pure modus-ponens-style inference relation based on \(\boldsymbol{L}\). For any \(\varPi \subseteq \mathrm{ For}_{\mathrm{m}}\) and B ∈ Form:
Lemma 22 (Lemmon and Scott 1977).
\(\varPi \vdash _{\boldsymbol{L}}B\) iff for some n⩾0 and for some A 1 , …, A n ∈Π we have \(\ulcorner A_{1}\rightarrow (\ldots \rightarrow (A_{n}\rightarrow B)\ldots )\urcorner \in \boldsymbol{L}\) , or equivalently \(\ulcorner (A_{1} \wedge \ldots \wedge A_{n})\rightarrow B\urcorner \in \boldsymbol{L}\).
Rights and permissions
Copyright information
© 2014 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Nasieniewski, M., Pietruszczak, A. (2014). A Method of Generating Modal Logics Defining Jaśkowski’s Discussive D2 Consequence. In: Weber, E., Wouters, D., Meheus, J. (eds) Logic, Reasoning, and Rationality. Logic, Argumentation & Reasoning, vol 5. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-9011-6_6
Download citation
DOI: https://doi.org/10.1007/978-94-017-9011-6_6
Published:
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-017-9010-9
Online ISBN: 978-94-017-9011-6
eBook Packages: Humanities, Social Sciences and LawPhilosophy and Religion (R0)