Skip to main content
SpringerLink
Log in
Book cover

Formal Approaches to Semantics and Pragmatics pp 31–64Cite as

Meta-Lambda Calculus and Linguistic Monads

  • Chapter

  • 844 Accesses

Part of the book series: Studies in Linguistics and Philosophy ((SLAP,volume 95))

Abstract

Meta-lambda calculus (MLC) is a two-level typed lambda calculus with meta-level types and terms. MLC has been adopted in the analyses of natural language semantics and pragmatics by means of monads and monadic translation (Bekki 2009; Bekki and Asai 2010), however, the soundness of the equational theory in Bekki (2009) has not been fully proven with respect to the categorical semantics in Bekki (2009). In this article, we introduce a revised syntax and an equational theory of MLC with base-level/meta-level substitution and \(\alpha /\beta /\eta \)-conversions, and prove their soundness with respect to a revised categorical semantics of MLC.

Our sincere thanks to the participants at LENLS5 and LENLS6, especially Elin McCready, Robert van Rooij, Kei Yoshimoto, Masahiko Sato, and the late Norry Ogata, and also to the participants at FLOPS2010, especially Olivier Danvy, Ian Zerney, Chung-chieh Shan, Oleg Kiselyov, Yukiyoshi Kameyama for their valuable comments. Our special thanks go to Kenichi Asai for many discussions in our research group. We also thank the anonymousss reviewers for their insightful comments. Daisuke Bekki is partially supported by a Grant-in-Aid for Young Scientists (A) (No. 22680013) from the Ministry of Education, Science, Sports and Culture

This is a preview of subscription content, log in via an institution.

Chapter
USD   29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD   84.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD   109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD   109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Learn about institutional subscriptions

Notes

  1. 1.

    This definition of raw terms is a slightly revised version of that in Bekki (2009) and Bekki and Asai (2010).

  2. 2.

    The length of a base-level unit \(\langle \rangle \) and a meta-level unit \(\left\langle \left\langle {}\right\rangle \right\rangle \) is defined to be 0, and a base-level finite product of the form \(\langle M_1,\dots ,M_n \rangle \) and a meta-level finite product of the form \(\left\langle \left\langle {M_1,\dots ,M_n}\right\rangle \right\rangle \) is defined to be n.

  3. 3.

    See Theorem 9 in Bekki (2009).

  4. 4.

    See, for example, Lambek (1980), Lambek and Scott (1986), and Crole (1993).

  5. 5.

    See MacLane (1997), p. 60 for a proof of Proposition 2.

  6. 6.

    See MacLane (1997), p. 34. \(Y(\llbracket \varGamma \rrbracket _{}) = \mathcal {C}(\llbracket \varGamma \rrbracket _{},-): \mathcal {C} \longrightarrow \mathcal {S}et\) maps a morphism \(f: A \longrightarrow B\) in \(\mathcal {C}\) to the morphism \(\mathcal {C}(\llbracket \varGamma \rrbracket _{},f): \mathcal {C}(\llbracket \varGamma \rrbracket _{},A) \longrightarrow \mathcal {C}(\llbracket \varGamma \rrbracket _{},B)\) in \(\mathcal {S}et\). \(Y(\llbracket \varGamma \rrbracket _{})(f) = \mathcal {C}(\llbracket \varGamma \rrbracket _{},f)\) is also written as \(f_*\) and called “composition with f on the left” or “the map induced by f.” It then maps a morphism \(a: \llbracket \varGamma \rrbracket _{} \longrightarrow A\) in \(\mathcal {C}(\llbracket \varGamma \rrbracket _{},A)\) to \(f \circ a: \llbracket \varGamma \rrbracket _{} \longrightarrow B\) in \(\mathcal {C}(\llbracket \varGamma \rrbracket _{},B)\). The two morphisms \(\mathcal {C}(\llbracket \varGamma \rrbracket _{},f)\) and \(\mathcal {C}(\llbracket \varGamma \rrbracket _{},g)\) induced by two composable morphisms \(f: A \longrightarrow B\) and \(g: B \longrightarrow C\) are also composable in \(\mathcal {S}et\), as indicated in the following diagram.

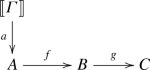
  7. 7.

    See MacLane (1997), p.116 for “Theorem 1” and its proof.

  8. 8.

    For the definition of \(S_{\varGamma ,x:\alpha }\), see Definition 14.

  9. 9.

    The proof is the revised version of what we presented in Masuko and Bekki (2011).

  10. 10.

    Using meta-level \(\eta \)-conversion in the proof is not prohibited since the proof of the conversion is independent of this lemma.

References

  • Bekki, D. (2009). Monads and meta-lambda calculus. In H. Hattori, T. Kawamura, T. Ide’, M. Yokoo & Y. Murakami (Eds.), New Frontiers in Artificial Intelligence Conference and Workshops, (JSAI 2008), Asahikawa, Japan, June 2008, Revised Selected Papers from LENLS5 (Vol. LNAI 5447, pp. 193–208), Springer.

    Google Scholar 

  • Bekki, D., & Asai, K. (2010). Representing covert movements by delimited continuations. In K. Nakakoji, Y. Murakami & E. McCready (Eds.), New Frontiers in Artificial Intelligence JSAI-isAI 2009 Workshops, Tokyo, Japan, November 2009, Selected Papers from LENLS7 (Vol. LNAI 6284, pp. 161–180). Heidelberg: Springer.

    Google Scholar 

  • Crole, R. L. (1993) Categories for types. Cambridge: Cambridge University Press.

    Google Scholar 

  • Danvy, O., & Filinski, A. (1990) Abstracting control. LFP90, the 1990 ACM Conference on Lisp and Functional Programming (pp. 151–160).

    Google Scholar 

  • Hayashishita, J. R., & Bekki, D. (2011). Conjoined nominal expressions in Japanese: Interpretation through monad, In The Eighth International Workshop on Logic and Engineering of Natural Language Semantics (LENLS8) (pp. 139–152). JSAI International Symposia on AI 2011, Takamatsu, Kagawa, Japan.

    Google Scholar 

  • Kock, A. (1970). Strong functors and monoidal monads. Various Publications Series 11, Aarhus Universitet, August 1970.

    Google Scholar 

  • Lambek, J. (1980). From \(\lambda \)-calculus to cartesian closed categories. In: J. P. Seldin & J. R. Hindley (Eds.), To H. B. Curry: Essays on combinatory logic, lambda calculus and formalism. New York: Academic Press.

    Google Scholar 

  • Lambek, J., & Scott, P. J. (1986). Introduction to higher order categorical logic. Cambridge: Cambridge University Press.

    Google Scholar 

  • MacLane, S. (1997). Categories for the working mathematician. Graduate texts in mathematics (2nd ed.). New Yok: Springer.

    Google Scholar 

  • Masuko, M., & Bekki, D. (2011). Categorical semantics of meta-lambda calculus. The 13th JSSST Workshop on Programming and Programming Languages (PPL2011) (in Japanese) (pp. 60–74), Joozankei, Japan.

    Google Scholar 

  • Moggi, E. (1989). Computational lambda-calculus and monads. Fourth Annual IEEE Symposium on Logic in Computer, Science (pp. 14–23).

    Google Scholar 

  • Ogata, N. (2008). Towards computational non-associative lambek lambda-calculi for formal pragmatics. The Fifth International Workshop on Logic and Engineering of Natural Language Semantics (LENLS2008) in Conjunction with the 22nd Annual Conference of the Japanese Society for Artificial Intelligence (pp. 79–102), Asahikawa, Japan.

    Google Scholar 

  • Shan, C. C. (2001). Monads for natural language semantics. In K. Striegnitz (Ed.), The ESSLLI-2001 student session (13th European summer school in logic, language and information, 2001). pp. 285–298.

    Google Scholar 

  • Unger, C. (2011). Dynamic semantics as monadic computation. The Eighth International Workshop on Logic and Engineering of Natural Language Semantics (LENLS8) (pp. 153–164). JSAI International Symposia on AI 2011, Takamatsu, Kagawa, Japan.

    Google Scholar 

  • Wadler, P. (1992). Comprehending monads. Mathematical structure in computer science (Vol. 2, pp. 461–493). Cambridge: Cambridge University Press. (an ealier version appears in Conference on Lisp and Functional Programming, Nice, France, ACM, June 1990).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ochanomizu University, Graduate School of Humanities and Sciences, 2-1-1 Ohtsuka, Tokyo, Bunkyo-ku, 112-8610, Japan

    Daisuke Bekki & Moe Masuko

  2. National Institute of Informatics, 2-1-2 Hitotsubashi, Tokyo, Chiyoda-ku, 101-8430, Japan

    Daisuke Bekki

  3. CREST, Japan Science and Technology Agency, 4-1-8 Honcho, Saitama, Kawaguchi, 332-0012, Japan

    Daisuke Bekki

  4. Research Fellow of the Japan Society for the Promotion of Science, Tokyo, Japan

    Moe Masuko

Authors
  1. Daisuke Bekki
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Moe Masuko
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Daisuke Bekki .

Editor information

Editors and Affiliations

  1. Department of English, Aoyama Gakuin University, Tokyo, Japan

    Elin McCready

  2. Department of English, Naruto University of Education, Naruto, Tokushima, Japan

    Katsuhiko Yabushita

  3. Center for the Advancement of Higher Education, Tohoku University, Sendai, Miyagi, Japan

    Kei Yoshimoto

Rights and permissions

Reprints and permissions

Copyright information

© 2014 Springer Science+Business Media Dordrecht

About this chapter

Cite this chapter

Bekki, D., Masuko, M. (2014). Meta-Lambda Calculus and Linguistic Monads. In: McCready, E., Yabushita, K., Yoshimoto, K. (eds) Formal Approaches to Semantics and Pragmatics. Studies in Linguistics and Philosophy, vol 95. Springer, Dordrecht. https://doi.org/10.1007/978-94-017-8813-7_3

Download citation

Publish with us

Policies and ethics

Search

Navigation