Skip to main content
SpringerLink
Log in

Generalized Elimination Inferences, Higher-Level Rules, and the Implications-as-Rules Interpretation of the Sequent Calculus

  • Chapter
  • First Online:
Advances in Natural Deduction

Part of the book series: Trends in Logic ((TREN,volume 39))

Abstract

We investigate the significance of higher-level generalized elimination rules as proposed by the author and compare them with standard-level generalized elimination rules as proposed by Dyckhoff, Tennant, López-Escobar and von Plato. Many of the results established for natural deduction with higher-level rules such as normalization and the subformula principle immediately translate to the standard-level case. The sequent-style interpretation of higher-level natural deduction as proposed by Avron and by the author leads to a system with a weak rule of cut, which enjoys the subformula property. The interpretation of implications-as-rules motivates a different left-introduction schema for implication in the ordinary (standard-level) sequent calculus, which conceptually is more basic than the implication-left schema proposed by Gentzen. Corresponding to the result for the higher-level system, it enjoys the subformula property and cut elimination in a weak form.

This chapter was completed during a research stay at IHPST Paris supported by the Foundation Maison des Sciences de l’Homme, by the ESF research project “Dialogical Foundations of Semantics (DiFoS)” within the ESF-EUROCORES programme “LogICCC—Modelling Intelligent Interaction” (DFG Schr 275/15-1) and the French-German DFG-ANR project “Hypothetical Reasoning—Logical and Semantical Perspectives (HYPOTHESES)” (DFG Schr 275/16-1, 16-2)

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 109.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD 139.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    In [29] this approach was extended to quantifiers, and in [30] to various other applications, including the sequent calculus, certain substructural logics (in particular relevant logic), and Martin-Löf’s logic. In [7, 32] and in later publications it was extended to the realm of clausal-based reasoning in general. For a general description of the programme of proof-theoretic semantics see [38], and for a formal rendering of proof-theoretic harmony see [19, 40]

  2. 2.

    A generalized schema for elimination rules which contains (\({\wedge }\) E\(_\textsc {GEN}\)) as an instance was proposed by Prawitz in [25]. I have made this point clear in all relevant publications. In fact, a fundamental error in Prawitz’s treatment of implication in his elimination schema was one of my motivations to develop the idea of rules of higher levels, another one being von Kutschera’s [11] treatment of logical constants in terms of an iterated sequent arrow in what he very appropriately called Gentzen semantics (Ger. ‘Gentzensemantik’). So I claim authorship for the general schema for elimination rules, but not for the particular idea of generalized conjunction elimination (\({\wedge }\) E\(_\textsc {GEN}\)). I mention this point as I have been frequently acknowledged as the author or (\({\wedge }\) E\(_\textsc {GEN}\)), without reference to its embedding into a higher-level framework. When the higher-level framework is mentioned, it is often not considered relevant, as transcending the means of expression of standard natural deduction. Although it extends natural deduction, the results obtained for the general higher-level case can easily be specialized to the case of generalized standard-level elimination rules for implication. In this sense, a direct normalization and subformula proof for standard-level systems with generalized rules is already contained in [27]. For a discussion of inversion in relation to Lorenzen’s and Prawitz’s semantical approaches see [16, 34, 35].

  3. 3.

    Although stated as a result, the proof was omitted from the English journal publication [28], both for space constraints and because its character is that of an exercise.

  4. 4.

    From the fact that none of these authors mentions the earlier one, we conclude that none of them was aware of the fact that (\(\rightarrow \) E\(_\textsc {SL}\)) had been discussed before. Dyckhoff’s chapter appeared in a volume of a kind often called a ‘grey’ publication (similar to a technical report), which was difficult to notice and to get hold of, at least in pre-Internet times. It mentions (\(\rightarrow \) E\(_\textsc {SL}\)) neither in the title nor in the abstract nor in the display of the inference rules of natural deduction. The only sentence mentioning (\(\rightarrow \) E\(_\textsc {SL}\)) explicitly as a possible primitive rule for implication elimination occurs in the discussion of proof tactics for implication: ‘this makes it clear that a possible form of the rule \(\supset \) _elim might be that from proofs of \(A {\supset }B\), of \(A\), and (assuming \(B\)) of \(C\) one can construct a proof of \(C\). Such a form fits in better with the pattern for elimination rules now increasingly regarded as orthodox, and is clearer than the other possibility for \(\supset \) _elim advocated by Schroeder-Heister and Martin-Löf \([\ldots ]\)’ ([4], p. 55). Before the appearance of von Plato’s papers, Dyckhoff never referred to this publication in connection with the particular form of \(\, \rightarrow \, \) elimination, in order to make his idea visible.

  5. 5.

    The way in which letters \(C\) are schematic, i.e., which propositions may be substituted for them, becomes important, if one investigates extensions of the language considered, i.e., in connection with the problem of uniqueness of connectives (see [3]).

  6. 6.

    López-Escobar [12] proves strong normalization. Other such proofs are given in [10] and [43].

  7. 7.

    In his discussion of generalized left inferences in his higher-level sequent framework, von Kutschera ([11], p. 15) gives an example similar to \(c_2\) (namely the ternary connective with the meaning \((A_1 {\,\rightarrow \,}A_2) {\vee }(A_3 {\,\rightarrow \,}A_2)\)) to show that the higher-level left rules cannot be expressed by lower-level left rules along the lines of the standard implication-left rule (\(\rightarrow \) L) in the sequent calculus (which corresponds to (\(\rightarrow \) E\(_\textsc {SL}\)), see Sect. 6)

  8. 8.

    If we also consider operators definable in terms of others, i.e., if the premisses \(\Delta _i\) of introduction rules (\(c_{}\) I) are allowed to contain operators \(c'\) which have already been given introduction and elimination rules, then \(c_3\) is, of course, trivially definable, with

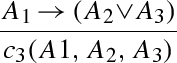
    being its introduction rule. This may be considered a rationale to confine oneself, as in the standard-level approach, to the standard operators. Such an approach fails, of course, to tell anything about the distinguished character of the standard operators as being capable to express all possible operators based on rules of a certain form. This is a point in which the goals of the generalized\(_\textsc {SL}\) and the generalized\(_\textsc {HL}\) approaches fundamentally differ from one another. (In [27–29] operators definable from other operators in the higher-level framework are considered, in addition to those definable without reference to others.)

  9. 9.

    For the symmetry in Gentzen’s sequent calculus and its description in terms of definitional reflection see [2, 39].

  10. 10.

    Following [23], a segment is a succession of formula occurrences of the same form \(C\) such that immediately succeeding occurrences are minor premiss \(C\) and conclusion \(C\) of a generalized\(_\textsc {HL}\) elimination step.

  11. 11.

    What one essentially does here, is carrying out permutative reductions as known from [23]. Their general treatment, without assuming that segments are maximal (and thus start with the conclusion of an introduction inference), but only that they end with an elimination inference, was proposed by Martin-Löf (see [24], p. 253f.) For the higher-level case, these reductions are used in [27].

  12. 12.

    As an assumption formula can be viewed as the conclusion of a first-level assumption rule, the second alternative actually includes the first one.

  13. 13.

    For a detailed proof of normalization and subformula property for higher-level natural deduction see [27].

  14. 14.

    Von Kutschera’s [11] approach using an iteration of the sequent arrow should be mentioned as well, although it needs some reconstruction to fit into our framework.

  15. 15.

    We can here neglect the difference between lists, multisets, and sets, as for simplicity we always assume that the usual structural rules of the intuitionistic sequent calculus (permutation, contraction, and thinning) are available—with the exception of cut, whose availability or non-availability as a primitive or admissible rule will always be explicitly stated.

  16. 16.

    This corresponds to functional completeness in the case of truth functions. In a further generalized setting this way of establishing completeness of systems of constants by translating structural operations into logical ones is used in [44] for many substructural logics.

  17. 17.

    Avron also remarks that the standard (\(\rightarrow \) L) rule is a way of avoiding the multi-ary character of this rule, which cannot be effected by means of (\(\rightarrow \) L)\(^\circ \) alone (if conjunction is not available). Negri and von Plato [17] (p. 184) mention the rule (\(\rightarrow \) L)\(^\circ \) as a sequent calculus rule corresponding to modus ponens, followed by a counterexample to cut analogous to (12), which is based on implication only. This counterexample shows again that for cut elimination in the implicational system the multi-ary form of (\(\rightarrow \) L)\(^\circ \) considered in [1] and the corresponding forms of rule introduction in the antecedent considered in [30] and [7] are really needed.

References

  1. Avron, A. (1990). Gentzenizing Schroeder-Heister’s natural extension of natural deduction. Notre Dame Journal of Formal Logic, 31, 127–135.

    Google Scholar 

  2. de Campos Sanz, W., & Piecha, T. (2009). Inversion by definitional reflection and the admissibility of logical rules. Review of Symbolic Logic, 2, 550–569.

    Google Scholar 

  3. Došen, K., & Schroeder-Heister, P. (1988). Uniqueness, definability and interpolation. Jounal of Symbolic Logic, 53, 554–570.

    Google Scholar 

  4. Dyckhoff, R. (1988). Implementing a simple proof assistant. Workshop on Programming for Logic Teaching (Leeds, 6–8 July 1987): Proceedings 23/1988 (pp. 49–59). Centre for Theoretical Computer Science: University of Leeds.

    Google Scholar 

  5. Garner, R. (2009). On the strength of dependent products in the type theory of Martin-Löf. Annals of Pure and Applied Logic, 160, 1–12.

    Google Scholar 

  6. Gentzen, G. (1934/35). Untersuchungen über das logische Schließen. Mathematische Zeitschrift, 39:176–210, 405–431 (English translation in: The Collected Papers of Gerhard Gentzen (ed. M. E. Szabo), Amsterdam: North Holland (1969), pp. 68–131).

    Google Scholar 

  7. Hallnäs, L., & Schroeder-Heister, P. (1990/91). A proof-theoretic approach to logic programming: I. Clauses as rules. II. Programs as definitions. Journal of Logic and Computation, 1, 261–283, 635–660.

    Google Scholar 

  8. Hallnäs, L. & Schroeder-Heister, P. (2014). A survey of definitional reflection. In T. Piecha & P. Schroeder-Heister(Eds.), Advances in Proof-Theoretic Semantics, Heidelberg: Springer.

    Google Scholar 

  9. Harper, R., Honsell, F., & Plotkin, G. (1987). A framework for defining logics. Journal of the Association for Computing Machinery, 40, 194–204.

    Google Scholar 

  10. Joachimski, F., & Matthes, R. (2003). Short proofs of normalization for the simply-typed \(\lambda \)-calculus, permutative conversions and Gödel’s T. Archive for Mathematical Logic, 42, 59–87.

    Google Scholar 

  11. von Kutschera, F. (1968). Die Vollständigkeit des Operatorensystems \(\{\lnot , \wedge ,\vee ,\supset \}\) für die intuitionistische Aussagenlogik im Rahmen der Gentzensemantik. Archiv für mathematische Logik und Grundlagenforschung, 11, 3–16.

    Google Scholar 

  12. López-Escobar, E. G. K. (1999). Standardizing the N systems of Gentzen. In X. Caicedo & C. H. Montenegro (Eds.), Models, Algebras and Proofs (Lecture Notes in Pure and Applied Mathematics Vol. 203) (pp. 411–434). New York: Marcel Dekker.

    Google Scholar 

  13. Lorenzen, P. (1950). Konstruktive Begründung der Mathematik. Mathematische Zeitschrift, 53, 162–202.

    Google Scholar 

  14. Lorenzen, P. (1955). Einführung in die operative Logik und Mathematik (2nd ed 1969). Berlin: Springer.

    Google Scholar 

  15. Martin-Löf, P. (1984). Intuitionistic Type Theory. Napoli: Bibliopolis.

    Google Scholar 

  16. Moriconi, E., & Tesconi, L. (2008). On inversion principles. History and Philosophy of Logic, 29, 103–113.

    Google Scholar 

  17. Negri, S., & von Plato, J. (2001). Structural Proof Theory. Cambridge: Cambridge University Press.

    Google Scholar 

  18. Olkhovikov, G. K., & Schoeder-Heister, P. (2014). On flattening elimination rules. Review of Symbolic Logic, 7.

    Google Scholar 

  19. Olkhovikov, G. K., & Schoeder-Heister, P. (2014). Proof-theoretic harmony and the levels of rules: General non-flattening results. In E. Moriconi & L. Tesconi (Eds.), Second Pisa Colloquim in Logic, Language and Epistemology. ETS, Pisa.

    Google Scholar 

  20. Paulson, L. C. (1994). Isabelle: A Generic Theorem Prover. Berlin: Springer.

    Google Scholar 

  21. von Plato, J. (2000). A problem of normal form in natural deduction. Mathematical Logic Quarterly, 46, 121–124.

    Google Scholar 

  22. von Plato, J. (2001). Natural deduction with general elimination rules. Archive for Mathematical Logic, 40, 541–567.

    Google Scholar 

  23. Prawitz, D. (1965). Natural Deduction: A Proof-Theoretical Study. Almqvist & Wiksell (Reprinted Mineola NY: Dover Publ., 2006), Stockholm.

    Google Scholar 

  24. Prawitz, D. (1971). Ideas and results in proof theory. In J. E. Fenstad (Ed.), Proceedings of the Second Scandinavian Logic Symposium (Oslo 1970) (pp. 235–308). Amsterdam: North-Holland.

    Google Scholar 

  25. Prawitz, D. (1979). Proofs and the meaning and completeness of the logical constants. In J. Hintikka, I. Niiniluoto & E. Saarinen (Eds.), Essays on Mathematical and Philosophical Logic: Proceedings of the Fourth Scandinavian Logic Symposium and the First Soviet-Finnish Logic Conference, Jyväskylä, Finland, June 29 - July 6, 1976 (pp. 25–40) (revised German translation ‘Beweise und die Bedeutung und Vollständigkeit der logischen Konstanten’, Conceptus, 16. (1982). 31–44). Dordrecht: Kluwer.

    Google Scholar 

  26. Read, S. (2014). General-elimination harmony and higher-level rules. In H. Wansing (Ed.), Dag Prawitz on Proofs and Meaning. Heidelberg: Springer.

    Google Scholar 

  27. Schroeder-Heister, P. (1981). Untersuchungen zur regellogischen Deutung von Aussagenverknüpfungen. Diss: Universität Bonn.

    Google Scholar 

  28. Schroeder-Heister, P. (1984). A natural extension of natural deduction. Journal of Symbolic Logic, 49, 1284–1300.

    Google Scholar 

  29. Schroeder-Heister, P. (1984). Generalized rules for quantifiers and the completeness of the intuitionistic operators \({\wedge , \vee , \rightarrow , \bot , \forall , \exists }\). In M. M. Richter, E. Börger, W. Oberschelp, B. Schinzel & W. Thomas (Eds.) Computation and Proof Theory. Proceedings of the Logic Colloquium held in Aachen, July 18–23, 1983, Part II. (Lecture Notes in Mathematics, Vol. 1104), (pp. 399–426). Berlin: Springer.

    Google Scholar 

  30. Schroeder-Heister, P. (1987). Structural Frameworks with Higher-Level Rules. Habilitations- schrift: Universität Konstanz.

    Google Scholar 

  31. Schroeder-Heister, P. (1991). Structural frameworks, substructural logics, and the role of elimination inferences. In G. Huet & G. Plotkin (Eds.) Logical Frameworks (pp. 385–403). Cambridge: Cambridge University Press.

    Google Scholar 

  32. Schroeder-Heister, P. (1993). Rules of definitional reflection. Proceedings of the 8th Annual IEEE Symposium on Logic in Computer Science (Montreal 1993) (pp. 222–232). Los Alamitos: IEEE Press.

    Google Scholar 

  33. Schroeder-Heister, P. (2004). On the notion of assumption in logical systems. In R. Bluhm & C. Nimtz (Eds.) Selected Papers Contributed to the Sections of GAP5, Fifth International Congress of the Society for Analytical Philosophy, Bielefeld, 22–26 September 2003 (pp. 27–48). mentis (Online publication: http://www.gap5.de/proceedings), Paderborn.

  34. Schroeder-Heister, P. (2007). Generalized definitional reflection and the inversion principle. Logica Universalis, 1, 355–376.

    Google Scholar 

  35. Schroeder-Heister, P. (2008). Lorenzen’s operative justification of intuitionistic logic. In M. van Atten, P. Boldini, M. Bourdeau & G. Heinzmann (Eds.), One Hundred Years of Intuitionism (1907–2007): The Cerisy Conference, (pp. 214–240) [References for whole volume: 391–416]. Birkhäuser, Basel.

    Google Scholar 

  36. Schroeder-Heister, P. (2009). Sequent calculi and bidirectional natural deduction: On the proper basis of proof-theoretic semantics. In M. Peliš (Ed.), The Logica Yearbook 2008. London: College Publications.

    Google Scholar 

  37. Schroeder-Heister, P. (2011). Implications-as-rules vs. implications-as-links: an alternative implication-left schema for the sequent calculus. Journal of Philosophical Logic, 40, 95–101.

    Google Scholar 

  38. Schroeder-Heister, P. (2012). Proof-theoretic semantics. In E.N. Zalta, (Ed.), Stanford Encyclopedia of Philosophy.http://plato.stanford.edu.

  39. Schroeder-Heister, P. (2013). Definitional reflection and Basic Logic. Annals of Pure and Applied Logic (Special issue, Festschrift 60th Birthday Giovanni Sambin), 164, 491–501.

    Google Scholar 

  40. Schroeder-Heister, P. (2014). Harmony in proof-theoretic semantics: A reductive analysis. In H. Wansing (Ed.), Dag Prawitz on Proofs and Meaning, Heidelberg: Springer.

    Google Scholar 

  41. Tennant, N. (1992). Autologic. Edinburgh: Edinburgh University Press.

    Google Scholar 

  42. Tennant, N. (2002). Ultimate normal forms for parallelized natural deductions. Logic Journal of the IGPL, 10, 299–337.

    Google Scholar 

  43. Tesconi, L. (2004). Strong Normalization Theorem for Natural Deduction with General Elimination Rules. Ph. D. thesis: University of Pisa.

    Google Scholar 

  44. Wansing, H. (1993). The Logic of Information Structures. Berlin: Springer (Lecture Notes in Artificial Intelligence, Vol. 681).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Wilhelm-Schickard-Institut für Informatik, Universität Tübingen, Sand 13, 72076, Tübingen, Germany

    Peter Schroeder-Heister

Authors
  1. Peter Schroeder-Heister
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Peter Schroeder-Heister .

Editor information

Editors and Affiliations

  1. Departamento de Filosofia, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil

    Luiz Carlos Pereira

  2. Departamento de Informática, Pontifícia Universidade Católica do Rio de Janeiro, Rio de Janeiro, Brazil

    Edward Hermann Haeusler

  3. School of Computer Science, University of Birmingham, Birmingham, United Kingdom

    Valeria de Paiva

Rights and permissions

Reprints and permissions

Copyright information

© 2014 Springer Science+Business Media Dordrecht

About this chapter

Cite this chapter

Schroeder-Heister, P. (2014). Generalized Elimination Inferences, Higher-Level Rules, and the Implications-as-Rules Interpretation of the Sequent Calculus. In: Pereira, L., Haeusler, E., de Paiva, V. (eds) Advances in Natural Deduction. Trends in Logic, vol 39. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-7548-0_1

Download citation

Publish with us

Policies and ethics

Search

Navigation