Skip to main content
SpringerLink
Log in

Solitons

  • Chapter
Nonlinear Dynamics and Chaotic Phenomena: An Introduction

Part of the book series: Fluid Mechanics and Its Applications ((FMIA,volume 103))

  • 2714 Accesses

Abstract

Studies of nonlinear phenomena of various systems have revealed that certain generic equations can be used to describe the nonlinear evolution of a large class of physical systems. This is due to the fact that the underlying dynamics of many diverse physical systems have a degree of commonality which can be condensed into relatively simple model evolution equations. The similarity of the asymptotic behavior of solutions to these generic equations further suggests the possibility of a unified treatment of nonlinear phenomena and hence an apparent underlying “simplicity” in their description. Some of these solutions exhibit remarkably stable structures called solitons. In this chapter, we will do a discussion centered around the Korteweg-de Vries equation which is a prime example of such nonlinear evolution equations.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 129.00
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Hardcover Book
USD 169.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    There was in fact a fourth person, Mary Tsingou, who also participated in this numerical exploration (Douxois 2008).

  2. 2.

    The Korteweg-de Vries equation was apparently first obtained (Grimshaw 2007), by Boussinesq (1877).

  3. 3.

    The truncations in equations (7.3) and (7.4) signify that the long waves described by equation (7.5) are weakly nonlinear and weakly dispersive.

  4. 4.

    Equation (7.89) turns out to be the limiting member of a three-parameter family of periodic traveling wave solutions of equation (7.2), called cnoidal waves (see Sect. 7.6.6).

  5. 5.

    The amplitude-wave length relationship for a Korteweg-de Vries solitary wave is

    $$ a = \biggl(\frac{1}{\lambda}\biggr)^2\frac{12}{\sigma}. $$
  6. 6.

    Solitary waves were first observed by J. Scott Russell on the Edinburgh-Glasgow canal as a moving “well-defined heap of water” in 1834. Russell also performed laboratory experiments on solitary waves and empirically deduced that the speed u of the solitary wave is given by

    $$ u^2=g (h_0+a) $$

    a being the amplitude of the wave and h 0 being the undisturbed depth of water. However, the great significance of Russell’s discoveries had to wait more than 130 years for proper appreciation.

  7. 7.

    \(\operatorname{cn}(\zeta,s)\), for s away from 1, is qualitatively similar to cosζ. In fact,

    $$ \operatorname{cn}(\zeta, 0)\equiv\cos\zeta. $$
  8. 8.

    It is of interest to note that (7.111) implies, in conjunction with (7.97),

    $$ u=\sigma\alpha-k^2,\quad k^2\equiv\frac{\sigma}{3}(\alpha-\gamma) $$

    which agrees with the dispersion relation given by equation (7.2) for linear waves propagating on the basic state ϕ 0=α.

  9. 9.

    Alternatively, noting further that

    $$ \operatorname{cn}(\zeta,1)=\operatorname{sech}\zeta $$

    equation (7.109) leads to

    $$ \phi(\xi)=\gamma+(\alpha-\gamma)\operatorname{sech}^2 \biggl(\sqrt{\frac{\sigma(\alpha-\gamma)}{12}}\xi\biggr) $$

    as in (7.113)!

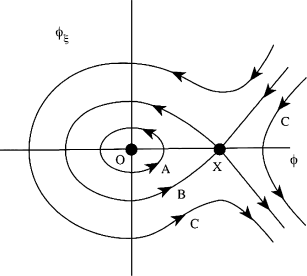
    The phase-plane portrait (see figure above) also shows the existence of periodic solutions corresponding to closed curves about a center. The homoclinic orbit starting and ending at the saddle point x has infinite period and represents the solitary wave!

  10. 10.

    Such a “self truncation” is believed (Hietarinta 1990) to signify integrability of the nonlinear evolution equation.

  11. 11.

    Hirota transformation has some analogy with the well known Cole-Hopf transformation (Cole 1951; Hopf 1950): Consider Burgers equation,

    $$ \phi_t+\phi\phi_x=\nu\phi_{xx}. $$

    Putting,

    $$ \phi=-2\nu(\ln\psi)_x $$

    we obtain

    $$ \psi_t =\nu\psi_{xx} $$

    which is the linear diffusion equation!

  12. 12.

    Putting f 2≡0, leads to F k ≡0, ∀k>1, and substituting (7.125), (7.118) leads to the solitary wave solution (7.88) for ϕ.

  13. 13.

    There is no phase change, by contrast, for two interacting linear waves, even though they emerge unchanged by the interaction as well.

  14. 14.

    Zakharov and Shabat (1972) and Ablowitz et al. (1974) showed that this method can be adapted to solve other nonlinear evolution equations.

  15. 15.

    One may indeed view the bound states as the analytic continuation of the scattering states, defined on the real k-axis, to the upper half of the complex k-plane.

  16. 16.

    Note that,

    $$ (NM-MN)[\varPsi]=-(\phi_t-6\phi\phi_x+\phi_{xxx})\varPsi+3\phi_x M[\varPsi]. $$
  17. 17.

    Goursat problem (Garabedian 1984) has to do with finding the solution of a linear hyperbolic PDE satisfying conditions prescribed on a characteristic curve ξ=const and a monotonically increasing curve ξ=ξ(x).

  18. 18.

    One may also view the inverse-scattering problem, as represented by the GLM equation as a Riemann-Hilbert boundary-value problem in the scattering space (Ablowitz and Clarkson 1991).

  19. 19.

    Here, we have used the identity,

    $$ \varGamma(p)\varGamma(1-p)=\frac{\pi}{\sin p \pi} $$

    or

    $$ \varGamma \biggl(\frac{1}{2}+p \biggr)\varGamma \biggl(\frac{1}{2}-p \biggr)=\frac{\pi}{\cos p \pi}. $$

References

  • M.J. Ablowitz, P.A. Clarkson, Solitons, Nonlinear Evolution Equations and Inverse Scattering (Cambridge University Press, Cambridge, 1991)

    Book  MATH  Google Scholar 

  • M.J. Ablowitz, D.J. Kaup, A.C. Newell, H. Segur, The inverse scattering transform—Fourier analysis for nonlinear problems. Stud. Appl. Math. 53, 249 (1974)

    MATH  MathSciNet  Google Scholar 

  • A.V. Bäcklund, Über Curven und Flachentransformationen. Lund Univ. Arsskr. 10, 1 (1875)

    Google Scholar 

  • G.N. Balanis, The plasma inverse problem. J. Math. Phys. 13, 1001 (1972)

    Article  MathSciNet  Google Scholar 

  • P.L. Bhatnagar, Nonlinear Waves in One-Dimensional Dispersive Systems (Oxford University Press, London, 1979)

    MATH  Google Scholar 

  • G.W. Bluman, J.D. Cole, Similarity Methods for Differential Equations (Springer, Berlin, 1974)

    Book  MATH  Google Scholar 

  • M.J. Boussinesq, Essai sur la theorie des eaux courantes. Mem. Present. Savants Divers. Acad. R. Sci. Inst. France, Ser. 2 23, 1 (1877)

    Google Scholar 

  • J.D. Cole, On a quasilinear parabolic equation occurring in aerodynamics. Q. Appl. Math. 9, 225 (1951)

    MATH  Google Scholar 

  • P. Debye, Vortrage über die Kinetische Theorie der Materie und der Elektrizitat (Teubner, Leipzig, 1914)

    Google Scholar 

  • T. Douxois, Fermi-Pasta-Ulam and a mysterious lady. Phys. Today 61(1), 55 (2008)

    Article  Google Scholar 

  • P.G. Drazin, R.S. Johnson, Solitons: An Introduction (Cambridge University Press, Cambridge, 1989)

    Book  MATH  Google Scholar 

  • L.P. Eisenhart, A Treatise on the Differential Geometry of Curves and Surfaces (Ginn, Needham Heights, 1901), p. 190 (also Dover, 1960)

    Google Scholar 

  • E. Fermi, J. Pasta, S. Ulam, Studies of nonlinear problems. Los Alamos Sci. Lab. Report LA-1940 (1955)

    Google Scholar 

  • P. Garabedian, Partial Differential Equations (Chelsea, New York, 1984)

    Google Scholar 

  • C.S. Gardner, J.M. Greene, M.D. Kruskal, R.M. Miura, Method for solving the Korteweg-deVries equation. Phys. Rev. Lett. 19, 1095 (1967)

    Article  Google Scholar 

  • I.M. Gel’fand, B.M. Levitan, On the determination of a differential equation from its spectral function. Am. Math. Soc. Transl. (2) 1, 253 (1955)

    MATH  MathSciNet  Google Scholar 

  • R. Grimshaw, Introduction, in Solitary Waves in Fluids, ed. by R. Grimshaw (WIT Press, Ashurst, 2007)

    Chapter  Google Scholar 

  • J. Hietarinta, Hirota’s bilinear method and integrability, in Partially Integrable Evolution Equations in Physics, ed. by R. Conte, N. Boccara (Kluwer Academic, Dordrecht, 1990)

    Google Scholar 

  • R. Hirota, Exact solution of the Korteweg-de Vries equation for multiple collision of solitons. Phys. Rev. Lett. 27, 1192 (1971)

    Article  MATH  Google Scholar 

  • E. Hopf, The partial differential equation u t +uu x =μu xx . Commun. Pure Appl. Math. 3, 201 (1950)

    Article  MATH  MathSciNet  Google Scholar 

  • H. Ikezi, R.J. Taylor, D.R. Baker, Formation and interaction of ion-acoustic solitons. Phys. Rev. Lett. 25, 11 (1970)

    Article  Google Scholar 

  • A. Jeffrey, T. Kakutani, Weak nonlinear dispersive waves, a discussion centered around the Korteweg-de Vries equation. SIAM Rev. 14, 582 (1972)

    Article  MATH  MathSciNet  Google Scholar 

  • D.J. Korteweg, G. de Vries, On the change of form of long waves advancing in a rectangular canal and on a new type of long stationary waves. Philos. Mag. (5) 39, 422 (1895)

    Article  MATH  Google Scholar 

  • G.L. Lamb, Jr., Analytical descriptions of ultrashort optical pulse propagating in a resonant medium. Rev. Mod. Phys. 43, 99 (1971)

    Article  MathSciNet  Google Scholar 

  • G.L. Lamb, Jr., Elements of Soliton Theory (Wiley-Interscience, New York, 1980)

    MATH  Google Scholar 

  • P.D. Lax, Integrals of nonlinear equations of evolution and solitary waves. Commun. Pure Appl. Math. 21, 467 (1968)

    Article  MATH  MathSciNet  Google Scholar 

  • V.A. Marchenko, On the reconstruction of the potential energy from phases of scattered waves. Dokl. Akad. Nauk SSSR 104, 695 (1955)

    MATH  MathSciNet  Google Scholar 

  • R.M. Miura, The Korteweg-de Vries equation: a survey of results. SIAM Rev. 18, 412 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  • R.M. Miura, C.S. Gardner, M.D. Kruskal, Korteweg-de Vries equation and generalizations, II. Existence of conservation laws and constants of motion. J. Math. Phys. 9, 1204 (1968)

    Article  MATH  MathSciNet  Google Scholar 

  • B.K. Shivamoggi, Introduction to Nonlinear Fluid-Plasma Waves, Chap. 3 (Kluwer Academic, Dordrecht, 1988)

    Book  MATH  Google Scholar 

  • B.K. Shivamoggi, in Theoretical Fluid Dynamics 2nd edn., Chap. 2 (Wiley-Interscience, New York, 1998).

    Book  MATH  Google Scholar 

  • B.K. Shivamoggi, Perturbation Methods for Differential Equations, Chap. 3 (Birkhäuser, Basel, 2003)

    Book  MATH  Google Scholar 

  • H.D. Wahlquist, F.B. Estabrook, Bäcklund transformation for solutions of the Korteweg-de Vries equation. Phys. Rev. Lett. 31, 1386 (1973)

    Article  MathSciNet  Google Scholar 

  • H. Washimi, T. Taniuti, Propagation of ion-acoustic solitary waves of small amplitude. Phys. Rev. Lett. 17, 996 (1966)

    Article  Google Scholar 

  • N.J. Zabusky, A synergetic approach to problems of nonlinear dispersive wave propagation and interaction, in Symposium on Proceedings of the Nonlinear Partial Differential Equations, ed. by W.F. Ames (Academic Press, San Diego, 1967)

    Google Scholar 

  • N.J. Zabusky, Fermi-Pasta-Ulam, solitons and the fabric of nonlinear and computational science: history, synergetics, and visiometrics. Chaos 15, 015102 (2005)

    Article  MathSciNet  Google Scholar 

  • N.J. Zabusky, M.D. Kruskal, Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys. Rev. Lett. 15, 240 (1965)

    Article  MATH  Google Scholar 

  • V.E. Zakharov, A.B. Shabat, Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. Sov. Phys. JETP 34, 62 (1972)

    MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Dept. Mathematics, University of Central Florida, Orlando, FL, USA

    Bhimsen K. Shivamoggi

Authors
  1. Bhimsen K. Shivamoggi
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

Copyright information

© 2014 Springer Science+Business Media Dordrecht

About this chapter

Cite this chapter

Shivamoggi, B.K. (2014). Solitons. In: Nonlinear Dynamics and Chaotic Phenomena: An Introduction. Fluid Mechanics and Its Applications, vol 103. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-7094-2_7

Download citation

Publish with us

Policies and ethics

Search

Navigation