Abstract
In the first volume we have presented the theory of General Relativity comparing it at all times with the other Gauge Theories that describe non-gravitational interactions. We have also followed the complicated historical development of the ideas and of the concepts underlying both of them. In particular we have traced back the origin of our present understanding of all fundamental interactions as mediated by connections on principal fibre-bundles and emphasized the special status of Gravity within this general scheme. While recalling the historical development we have provided a, hopefully rigorous, exposition of all the mathematical foundations of gravity and gauge theories in a contemporary geometrical approach.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Author information
Authors and Affiliations
Appendices
Appendix A: Spinors and Gamma Matrix Algebra
8.1.1 A.1 Introduction to the Spinor Representations of SO(1,D−1)
The spinor representations of the orthogonal and pseudo-orthogonal groups have different structure in various dimensions. Starting from the representation of the Dirac gamma matrices one begins with a complex representation whose dimension is equal to the dimension of the gammas. A vector in this complex linear space is named a Dirac spinor. Typically Dirac spinors do not form irreducible representations. Depending on the dimensions, one can still impose SO(1,D−1) invariant conditions on the Dirac spinor that separate it into irreducible parts. These constraints can be of two types:
-
(a)
A reality condition which maintains the number of components of the spinor but relates them to their complex conjugates by means of linear relations. This reality condition is constructed with an invariant matrix
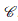 , named the charge conjugation matrix whose properties depend on the dimensions D.
, named the charge conjugation matrix whose properties depend on the dimensions D. -
(b)
A chirality condition constructed with a chirality matrix Γ D+1 that halves the number of components of the spinor. The chirality matrix exists only in even dimensions.
Depending on which conditions can be imposed, besides Dirac spinors, in various dimensions D, one has Majorana spinors, Weyl spinors and, in certain dimensions, also Majorana-Weyl spinors. In this appendix we discuss the properties of gamma matrices and we present the various types of irreducible spinor representations in all relevant dimensions from D=4 to D=11. The upper bound D=11 is dictated by supersymmetry since supergravity, i.e. the supersymmetric extension of Einstein gravity, can be constructed in all dimensions up to D=11, which is maximal in this respect. In the present volume, supergravity is not discussed, but some glances of it will occur in the second volume and for this reason, while discussing the necessary topic of gamma matrix algebra, we present a complete description of the available spinors in the various relevant dimensions.
8.1.2 A.2 The Clifford Algebra
In order to describe spinors one needs the Dirac gamma matrices. These form the Clifford algebra:

where η ab is the invariant metric of SO(1,D−1), that we always choose according to the mostly minus conventions, namely:

To study the general properties of the Clifford algebra (A.2.1) we use a direct construction method.
We begin by fixing the following conventions. Γ 0=Γ 0 corresponding to the time direction is Hermitian:
while the matrices Γ i =−Γ i corresponding to space directions are anti-Hermitian:
In the study of Clifford algebras it is necessary to distinguish the case of even and odd dimensions.
8.1.2.1 A.2.1 Even Dimensions
When D=2ν is an even number the representation of the Clifford algebra (A.2.1) has dimension:
In other words the gamma matrices are 2ν×2ν. The proof of such a statement is easily obtained by iteration. Suppose that we have the gamma matrices γ a corresponding to the case ν′=ν−1, satisfying the Clifford algebra (A.2.1) in D−2 dimensions and that they are 2ν′-dimensional. We can write down the following representation for the gamma matrices in D-dimension by means of the following 2ν×2ν matrices:

which satisfy the correct anticommutation relations and have the correct hermiticity properties specified above. This representation admits the following interpretation in terms of matrix tensor products:
where σ 1,2,3 denote the Pauli matrices:
To complete the proof of our statement we just have to show that for ν=2, corresponding to D=4 we have a 4-dimensional representation of the gamma matrices. This is well established. For instance we have the representation:

In D=2ν one can construct the chirality matrix defined as follows:
where α D is a phase-factor to be fixed in such a way that:
By direct evaluation one can verify that:
The normalization α D is easily derived. We have:
so that imposing (A.2.11) results into the following equation for α D :
which has solution:
With the same token we can show that the chirality matrix is Hermitian:
8.1.2.2 A.2.2 Odd Dimensions
When D=2ν+1 is an odd number, the Clifford algebra (A.2.1) can be represented by 2ν×2ν matrices. It suffices to take the matrices Γ a′ corresponding to the even case D′=D−1 and add to them the matrix Γ D =iΓ D′+1, which is anti-Hermitian and anti-commutes with all the other ones.
8.1.3 A.3 The Charge Conjugation Matrix
Since Γ
a
and their transposed  satisfy the same Clifford algebras it follows that there must be a similarity transformation connecting these two representations of the same algebra on the same carrier space. Such statement relies on Schur’s lemma and it is proved in the following way. We introduce the notation:
satisfy the same Clifford algebras it follows that there must be a similarity transformation connecting these two representations of the same algebra on the same carrier space. Such statement relies on Schur’s lemma and it is proved in the following way. We introduce the notation:
where ∑
P
denotes the sum over the n! permutations of the indices and δ
P
the parity of permutation P, i.e. the number of elementary transpositions of which it is composed. The set of all matrices  constitutes a finite group of 2[D/2]-dimensional matrices. Furthermore the groups generated in this way by Γ
a
, −Γ
a
or
constitutes a finite group of 2[D/2]-dimensional matrices. Furthermore the groups generated in this way by Γ
a
, −Γ
a
or  are isomorphic. Hence by Schur’s lemma two irreducible representations of the same group, with the same dimension and defined over the same vector space, must be equivalent, that is there must be a similarity transformation that connects the two. The matrix realizing such a similarity is called the charge conjugation matrix. Instructed by this discussion we define the charge conjugation matrix by means of the following equations:
are isomorphic. Hence by Schur’s lemma two irreducible representations of the same group, with the same dimension and defined over the same vector space, must be equivalent, that is there must be a similarity transformation that connects the two. The matrix realizing such a similarity is called the charge conjugation matrix. Instructed by this discussion we define the charge conjugation matrix by means of the following equations:

By definition  connects the representation generated by Γ
a
to that generated by
connects the representation generated by Γ
a
to that generated by  . In even dimensions both
. In even dimensions both  and \({{\mathcal{C}}_{+}}\) exist, while in odd dimensions only one of the two is possible. Indeed in odd dimensions Γ
D−1 is proportional to Γ
0
Γ
1…Γ
D−2 so that the \({{\mathcal{C}}_{-}}\) and \({{\mathcal{C}}_{+}}\) of D−1 dimensions yield the same result on Γ
D−1. This decides which
and \({{\mathcal{C}}_{+}}\) exist, while in odd dimensions only one of the two is possible. Indeed in odd dimensions Γ
D−1 is proportional to Γ
0
Γ
1…Γ
D−2 so that the \({{\mathcal{C}}_{-}}\) and \({{\mathcal{C}}_{+}}\) of D−1 dimensions yield the same result on Γ
D−1. This decides which  exists in a given odd dimension.
exists in a given odd dimension.
Another important property of the charge conjugation matrix follows from iterating (A.3.2). Using Schur’s lemma one concludes that \({{\mathcal{C}}_{\pm }}=\alpha \mathcal{C}_{\pm }^{T}\) so that iterating again we obtain α 2=1. In other words \({{\mathcal{C}}_{+}}\) and \({{\mathcal{C}}_{-}}\) are either symmetric or antisymmetric. We do not dwell on the derivation which can be obtained by explicit iterative construction of the gamma matrices in all dimensions and we simply collect below the results for the properties of \({{\mathcal{C}}_{\pm }}\) in the various relevant dimensions (see Table A.1).
8.1.4 A.4 Majorana, Weyl and Majorana-Weyl Spinors
The Dirac conjugate of a spinor ψ is defined by the following operation:
and the charge conjugate of ψ is defined as:
where \(\mathcal{C}\) is the charge conjugation matrix. When we have such an option we can either choose \({{\mathcal{C}}_{+}}\) or \({{\mathcal{C}}_{-}}\). By definition a Majorana spinor λ satisfies the following condition:
Equation (A.4.3) is not always self-consistent. By iterating it a second time we get the consistency condition:
There are two possible solutions to this constraint. Either \({{\mathcal{C}}_{-}}\) is antisymmetric or \({{\mathcal{C}}_{+}}\) is symmetric. Hence, in view of the results displayed above, Majorana spinors exist only in
In D=4,10,11 they are defined using the \({{\mathcal{C}}_{-}}\) charge conjugation matrix while in D=8,9 they are defined using \({{\mathcal{C}}_{+}}\).
Weyl spinors, on the contrary, exist in every even dimension; by definition they are the eigenstates of the Γ D+1 matrix, corresponding to the +1 or −1 eigenvalue. Conventionally the former eigenstates are named left-handed, while the latter are named right-handed spinors:
In some special dimensions we can define Majorana-Weyl spinors which are both eigenstates of Γ D+1 and satisfy the Majorana condition (A.4.3). In order for this to be possible we must have:
which implies:
With some manipulations the above condition becomes:
which can be checked case by case, using the definition of Γ D+1 as product of all the other gamma matrices. In the range 4≤D≤11 the only dimension where (A.4.9) is satisfied is D=10 which is the critical dimensions for superstrings. This is not a pure coincidence.
Summarizing we have:
Spinors in 4≤D≤11 | ||||
|---|---|---|---|---|
D | Dirac | Majorana | Weyl | Majora-Weyl |
4 | Yes | Yes | Yes | No |
5 | Yes | No | No | No |
6 | Yes | No | Yes | No |
7 | Yes | No | No | No |
8 | Yes | Yes | Yes | No |
9 | Yes | Yes | No | No |
10 | Yes | Yes | Yes | Yes |
11 | Yes | Yes | No | No |
8.1.5 A.5 A Particularly Useful Basis for D=4 γ-Matrices
In this section we construct a D=4 gamma matrix basis which is convenient for various purposes. Let us first specify the basis and then discuss its convenient properties.
In terms of the standard matrices (A.2.8) we realize the \(\mathfrak {so}(1,3)\) Clifford algebra:
by setting:
where γ 5 is the chirality matrix and \(\mathcal{C}\) is the charge conjugation matrix. In this basis the generators of the Lorentz algebra \(\mathfrak {so}(1,3)\), namely γ ab are particularly simple and nice 4×4 matrices. Explicitly we get:
Let us mention some relevant formulae that are easily verified in the above basis:
and if we fix the convention:
we obtain:
Appendix B: Mathematica Packages
In this appendix we describe (for pedagogical reasons) the structure of two Mathematica Packages constructed by the author that can be used to calculate geometrical quantities relevant to the problems addressed in the main text and also to draw plots and pictures.
The MATHEMATICA notebook files can be downloaded as supplementary material from the Springer distribution site.
8.1.1 B.1 Periastropack
This is a MATHEMATICA package for the calculation and drawing of orbits of massive particles in a Schwarzschild metric. After letting the computer read the programme, the package is initialized by typing: periastro.
We suggest that you type periastro in a separate NoteBook, different from the NoteBook containing the package. This package solves the numerical differential equation and plots the orbit curve in the xy-plane, comparing it with the Keplerian ellipsis. It is an interactive programme that asks the user to supply the semilatus rectum of the orbit expressed in units of the Schwarzschild emiradius and the eccentricity. Next after showing the Keplerian orbit and the General Relativity orbit after one revolution the programme stops and ask whether the user wants to display the orbit for more revolutions and for how many. It goes back to such a question until the user is satisfied and decides to stop.
8.1.1.1 Programme
Main Programme Periastro
This is the main programme which asks for the inputs of the parameters and then calls the calculation subroutines

Subroutine Perihelkep
This is the routine that plots the Keplerian orbit with the chosen parameters

Subroutine Perihelgr
This is the subroutine for the calculation and drawing of the orbit with the same parameters in the Schwarzschild metric

8.1.1.2 Examples
This section contains some examples of orbits calculated with Periastro.
With a= 60 m and ε= 0.6
\(\mathbf{Periastro}\)
\(\text{===========================}\)
\(\text{We make a comparison between orbits in Newton's Theory}\)
\(\text{and in Schwarzschild geometry}\)
\(\text{---------------------------}\)
\(\text{Input of geometrical parameters}\)
\(\text{===========================}\)
\(\text{PLOT of the ORBIT with the following parameters:}\)
\(\text{Semilatus rectum = }60\ \mathrm{m}\)
\(\text{eccentricity = }0.6\)
\(\text{===========================}\)
\(\text{Keplerian orbit with these parameters}\)

\(\text{===========================}\)
\(\text{The Schwarzschild orbit with the same parameters}\)
\(\text{---------------------------}\)
\(\text{After }1\text{ revolutions}\)

\(\text{After more revolutions, Yes or No?}\)
\(\text{---------------------------}\)
\(\text{After }3\text{ revolutions}\)

\(\text{After more revolutions, Yes or No?}\)
\(\text{---------------------------}\)
\(\text{After }10\text{ revolutions}\)

\(\text{After more revolutions, Yes or No?}\)

\(\text{---------------------------}\)
\(\{\text{Null}\}\)
In this example we see, highly emphasized by the smallness of the orbit and by its large eccentricity the phenomenon of periastron advance.
With a= 10, ε= 0.1
\(\mathbf{Periastro}\)
\(\text{===========================}\)
\(\text{We make a comparison between orbits in Newton's Theory}\)
\(\text{and in Schwarzschild geometry}\)
\(\text{---------------------------}\)
\(\text{Input of geometrical parameters}\)
\(\text{===========================}\)
\(\text{PLOT of the ORBIT with the following parameters:}\)
\(\text{Semilatus rectum = }10 \ \mathrm{m}\)
\(\text{eccentricity = }0.1\)
\(\text{===========================}\)
\(\text{Keplerian orbit with these parameters}\)

\(\text{===========================}\)
\(\text{The Schwarzschild orbit with the same parameters}\)
\(\text{---------------------------}\)
\(\text{After }1\text{ revolutions}\)

\(\text{After more revolutions, Yes or No?}\)
\(\text{---------------------------}\)
\(\text{After }2\text{ revolutions}\)

\(\text{After more revolutions, Yes or No?}\)
\(\text{Finished}\)
\(\text{---------------------------}\)
\(\{\text{Null}\}\)
In this example the test particle, placed at distance of only 10 Schwarzschild radii from the center falls into the singularity in just two revolutions if its eccentricity is different from zero, no matter how it is small.
8.1.2 B.2 Metrigravpack
This is a MATHEMATICA package for the calculation of the Riemann and Ricci tensors of an arbitrary (pseudo) Riemannian metric in arbitrary space-time dimensions using the standard tensor calculus. It is an interactive package that is initialized and then waits fur further inputs by the user.
8.1.2.1 Metric Gravity
In this section we provide a package to calculate Einstein equations for any given metric in arbitrary dimensions and using the metric formalism
Routines: Metrigrav
This routine is devised to calculate the Levi Civita connection, the Riemann curvature and the Einstein Tensor for general manifolds in the metric formalism. The inputs are
-
(1)
the dimension n
-
(2)
the set of coordinates a n vector = \(\mathbf{coordi}\)
-
(3)
the set of differentials, a n vector = \(\mathbf{diffe}\)
-
(4)
the metric given as a quadratic differential ds2=g [[i,j]] \(\text{dx}^{i}\) \(\text{dx}^{j}\).
TO START this programme you type \(\mathbf{mainmetric}\) and then you follow instructions
Mainmetric

Metricresume

Routine Metrigrav

8.1.2.2 Calculation of the Ricci Tensor of the Reissner Nordstrom Metric Using Metrigrav
\(\mathbf{mainmetric}\)
\(\text{OK I calculate your space, Give me the data}\)
\(\text{Give me the dimension of your space}\)
\(\text{Your space has dimension n = }4\)
\(\text{Now I stop and you give me two vectors of dimension }4\)
\(\text{vector coordi = vector of coordinates}\)
\(\text{vector diffe = vector of differentials}\)
\(\text{Next you give me the metric as ds2 = }\)
\(\text{Then to resume calculation you print metricresume}\)
\(\{\text{Null}\}\)
\(\mathbf{coordi}=\left\{ t,r,\theta ,\varphi \right\};\)
\(\mathbf{diffe}=\left\{ dt,dr,d\theta ,d\varphi \right\};\)
\(\mathbf{ds2}=-\left( 1-\frac{A}{r}+\frac{Q}{{{r}^{2}}} \right)*d{{t}^{2}}+{{\left( 1-\frac{A}{r}+\frac{Q}{{{r}^{2}}} \right)}^{-1}}*d{{r}^{2}}+{{r}^{2}}*Sin{{\left[ \theta \right]}^{2}}*d{{\varphi }^{2}}+{{r}^{2}}*d{{\theta }^{2}};\)
\(\mathbf{metricresume}\)
\(\text{I resume the calculation}\)
\(\text{First I extract the metric coefficients from your data}\)
\(\text{Then I calculate the inverse metric}\)
\(\text{Done!}\)
\(\text{and I calculate also the metric determinant}\)
\(\text{Done}\)
\(\text{I perform the calculation of the Christoffel symbols}\)
\(\text{-----------------}\)
\(\text{I finished}\)
\(\text{the Levi Civita connection is given by:}\)
\(\text{$\varGamma $[}11\text{] = }\frac{\text{dr} (-2 Q+A r)}{2 r (Q+r (-A+r))}\)
\(\text{$\varGamma $[}12\text{] = }\frac{\text{dt} (-2 Q+A r)}{2 r (Q+r (-A+r))}\)
\(\text{$\varGamma $[}13\text{] = }0\)
\(\text{$\varGamma $[}14\text{] = }0\)
\(\text{$\varGamma $[}21\text{] = }\frac{\text{dt} (-2 Q+A r) (Q+r (-A+r))}{2 r^{5}}\)
\(\text{$\varGamma $[}22\text{] = }\frac{\text{dr} (2 Q-A r)}{2 Q r-2 A r^{2}+2 r^{3}}\)
\(\text{$\varGamma $[}23\text{] = }\text{d$\theta$} \bigl(A-\frac {Q+r^{2}}{r}\bigr)\)
\(\text{$\varGamma $[}24\text{] =}\,{-}\frac{\text{d$\varphi$} (Q+r (-A+r)) \text{Sin}[\theta]^{2}}{r}\)
\(\text{$\varGamma $[}31\text{] = }0\)
\(\text{$\varGamma $[}32\text{] = }\frac{\text{d$\theta$}}{r}\)
\(\text{$\varGamma $[}33\text{] = }\frac{\text{dr}}{r}\)
\(\text{$\varGamma $[}34\text{] =}\,{-}\text{d$\varphi$} \text {Cos}[\theta] \text{Sin}[\theta]\)
\(\text{$\varGamma $[}41\text{] = }0\)
\(\text{$\varGamma $[}42\text{] = }\frac{\text{d$\varphi$}}{r}\)
\(\text{$\varGamma $[}43\text{] = }\text{d$\varphi$} \text {Cot}[\theta]\)
\(\text{$\varGamma $[}44\text{] = }\frac{\text{dr}}{r}+\text {d$\theta$} \text{Cot}[\theta]\)
\(\text{Task finished}\)
\(\text{The result is encoded in a tensor Gam[a,b,c]}\)
\(\text{-----------------}\)
\(\text{Now I calculate the Riemann tensor}\)
\(\text{I tell you my steps:}\)
\(\text{ a = }1\)
\(\text{ b = }1\)
\(\text{ b = }2\)
\(\text{ b = }3\)
\(\text{ b = }4\)
\(\text{ a = }2\)
\(\text{ b = }1\)
\(\text{ b = }2\)
\(\text{ b = }3\)
\(\text{ b = }4\)
\(\text{ a = }3\)
\(\text{ b = }1\)
\(\text{ b = }2\)
\(\text{ b = }3\)
\(\text{ b = }4\)
\(\text{ a = }4\)
\(\text{ b = }1\)
\(\text{ b = }2\)
\(\text{ b = }3\)
\(\text{ b = }4\)
\(\text{Finished}\)
\(\text{-------------------------}\)
\(\text{Now I evaluate the curvature 2-form of your space}\)
\(\text{I find the following answer}\)
\(\text{R[}11\text{] = }0\)
\(\text{R[}12\text{] = }\frac{(-3 Q+A r) \text{dt}\text {**}\text{dr}}{r^{2} (Q+r (-A+r))}\)
\(\text{R[}13\text{] = }\frac{(2 Q-A r) \text{dt}\text{**}\text {d$\theta$}}{2 r^{2}}\)
\(\text{R[}14\text{] =}\,{-}\frac{(-2 Q+A r) \text{dt}\text {**}\text{d$\varphi$} \text{Sin}[\theta]^{2}}{2 r^{2}}\)
\(\text{R[}21\text{] = }\frac{\left(-3 Q^{2}+Q (4 A-3 r) r+A r^{2} (-A+r)\right) \text{dt}\text{**}\text{dr}}{r^{6}}\)
\(\text{R[}22\text{] = }0\)
\(\text{R[}23\text{] = }\frac{(2 Q-A r) \text{dr}\text{**}\text {d$\theta$}}{2 r^{2}}\)
\(\text{R[}24\text{] =}\,{-}\frac{(-2 Q+A r) \text{dr}\text {**}\text{d$\varphi$} \text{Sin}[\theta]^{2}}{2 r^{2}}\)
\(\text{R[}31\text{] =}\,{-}\frac{(-2 Q+A r) (Q+r (-A+r)) \text {dt}\text{**}\text{d$\theta$}}{2 r^{6}}\)
\(\text{R[}32\text{] = }\frac{(-2 Q+A r) \text{dr}\text {**}\text{d$\theta$}}{2 r^{2} (Q+r (-A+r))}\)
\(\text{R[}33\text{] = }0\)
\(\text{R[}34\text{] = }\frac{(-Q+A r) \text{d$\theta$}\text {**}\text{d$\varphi$} \text{Sin}[\theta]^{2}}{r^{2}}\)
\(\text{R[}41\text{] =}\,{-}\frac{(-2 Q+A r) (Q+r (-A+r)) \text {dt}\text{**}\text{d$\varphi$}}{2 r^{6}}\)
\(\text{R[}42\text{] = }\frac{(-2 Q+A r) \text{dr}\text {**}\text{d$\varphi$}}{2 r^{2} (Q+r (-A+r))}\)
\(\text{R[}43\text{] = }\frac{(Q-A r) \text{d$\theta$}\text {**}\text{d$\varphi$}}{r^{2}}\)
\(\text{R[}44\text{] = }0\)
\(\text{The result is encoded in a tensor RR[i,j]}\)
\(\text{Its components are encoded in a tensor Rie[i,j,a,b]}\)
\(\text{---------------------------}\)
\(\text{Now I calculate the Ricci tensor}\)
\(1 1 \text{ non-zero}\)
\(\text{Ricci[}11\text{] = }\frac{Q (Q+r (-A+r))}{2 r^{6}}\)
\(2 2 \text{ non-zero}\)
\(\text{Ricci[}22\text{] =}{-}\frac{Q}{2 r^{2} (Q+r (-A+r))}\)
\(3 3 \text{ non-zero}\)
\(\text{Ricci[}33\text{] = }\frac{Q}{2 r^{2}}\)
\(4 4 \text{ non-zero}\)
\(\text{Ricci[}44\text{] = }\frac{Q \text{Sin}[\theta]^{2}}{2 r^{2}}\)
\(\text{I have finished the calculation}\)
\(\text{The tensor ricten[[a,b]] giving the Ricci tensor }\)
\(\text{is ready for storing on hard disk}\)
\(\text{----------------------------}\)
\(\{\text{Null}\}\)
\(\mathbf{MatrixForm}\left[ \mathbf{gg} \right]\)
\(\left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} -1-\frac{Q}{r^{2}}+\frac{A}{r} & 0 & 0 & 0 \\ 0 & \frac{1}{1+\frac{Q}{r^{2}}-\frac{A}{r}} & 0 & 0 \\ 0 & 0 & r^{2} & 0 \\ 0 & 0 & 0 & r^{2} \text{Sin}[\theta]^{2} \end{array} \right)\)
\(\mathbf{MatrixForm}\left[ \mathbf{ricten} \right]\)
\(\left( \begin{array}{c@{\quad}c@{\quad}c@{\quad}c} \frac{Q (Q+r (-A+r))}{2 r^{6}} & 0 & 0 & 0 \\ 0 & -\frac{Q}{2 r^{2} (Q+r (-A+r))} & 0 & 0 \\ 0 & 0 & \frac{Q}{2 r^{2}} & 0 \\ 0 & 0 & 0 & \frac{Q \text{Sin}[\theta]^{2}}{2 r^{2}} \end{array} \right)\)
Rights and permissions
Copyright information
© 2013 Springer Science+Business Media Dordrecht
About this chapter
Cite this chapter
Frè, P.G. (2013). Conclusion of Volume 1. In: Gravity, a Geometrical Course. Springer, Dordrecht. https://doi.org/10.1007/978-94-007-5361-7_8
Download citation
DOI: https://doi.org/10.1007/978-94-007-5361-7_8
Publisher Name: Springer, Dordrecht
Print ISBN: 978-94-007-5360-0
Online ISBN: 978-94-007-5361-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)


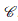 , named the charge conjugation matrix whose properties depend on the dimensions D.
, named the charge conjugation matrix whose properties depend on the dimensions D.