Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

Introduction

It seems obvious that a teacher’s mathematical knowledge is an important ingredient for teaching, and while a teacher needs to be able to do the mathematics required for the curricular level being taught, this may not be sufficient to ensure pupil progress. Indeed, research on effective primary teachers indicates that those who produce the highest numeracy gains in pupils do not necessarily hold advanced qualifications in mathematics (Askew, Brown, Rhodes, Johnson, & William, 1997). We need to know what other factors come into play, and how these interact with each other in the teaching process. Internationally, however, there is no universal agreement on a widely-accepted framework for describing teachers’ mathematical knowledge in teaching (Tirosh & Even, 2007). This is a concern not only for pre-service teacher education and professional development courses, but also for research, since without some common understanding of what subject knowledge means and what it looks like in practice, there can be no coherent approach to designing courses, or answering research questions about the role of teachers’ mathematical knowledge in teaching. None of these issues is politically neutral. International comparisons of pupil performance in the 1990s fuelled widespread anxiety in both the United States and England and Wales about mathematical standards. Teachers were seen to be part of the problem of relatively poor performance and strengthening their subject knowledge as a contribution to the improvement of overall standards. In this chapter, the meaning, importance and limitations of several analytical models of teachers’ mathematical knowledge will be discussed with some reference to their political context, and a synthesis will be proposed. Finally, the implications of using this synthesis in future teacher development programmes will be presented.

Shulman’s Conceptualisation

In the United States in the 1980s, broad agreement on the inadequacy of the traditional curriculum for preparing students for the demands of the 21st century, coupled with disappointing results from international comparisons of mathematical achievement, led to calls for reform in the mathematics curriculum, and its teaching and assessment (Schoen, Fey, Hirsch, & Coxford, 1999). At the same time, but independently from the reform agenda, Shulman (1986, p. 6) identified a blind spot with respect to content knowledge in the teacher effectiveness research for as much attention to be paid to what the teacher is teaching as is paid to generic pedagogic factors such as wait time and time on task: “How do teachers decide what to teach, how to represent it, how to question students about it and how to deal with problems of misunderstanding?” His work with secondary teachers of English, biology, mathematics and social studies allowed him and his colleagues to develop a more coherent theoretical framework of teacher knowledge which has since become widely influential (Grossman, Wilson, & Shulman, 1989; Shulman, 1986, 1987). There was an immediate interest in his ideas, and Shulman’s (1986) new conceptualisation led to a new phase, continuing to the present, of research on teacher knowledge. In these studies, the focus is on teaching itself, and on providing rich descriptions of teachers’ actions while teaching. Ball, Thames, and Phelps (2008) point out that Shulman’s work has been cited in more that 1,200 refereed journal articles in a wide variety of disciplines. Given its importance, a review of the model will be presented, interwoven and supplemented with a discussion of how the ideas have been modified and expanded by others.

Shulman and his colleagues proposed different categories of teacher knowledge that are needed for effective teaching. Although the specific boundaries and the names of the categories varied across publications, one of the most detailed descriptions of their model is given in Shulman (1987) publication. Here Shulman proposed seven different categories of teacher knowledge:

  • general pedagogical knowledge;

  • knowledge of learners’ characteristics;

  • knowledge of educational context;

  • knowledge of educational purposes and values;

  • content knowledge;

  • curriculum knowledge;

  • pedagogical content knowledge.

The first four categories listed above refer to general aspects of teacher knowledge and were not the focus of Shulman’s work (Ball et al., 2008), which focused on the missing-content dimension of teacher knowledge. In his account, however, Shulman (1987) made it clear that an emphasis placed on this was not intended to limit the importance of general categories of teacher knowledge in teaching.

The last three categories – content knowledge, curriculum knowledge and pedagogical content knowledge – describe the content dimensions of teacher knowledge and together make up, what Shulman referred to as, the missing paradigm in research on teaching. These three content dimensions of teacher knowledge are discussed in detail in Shulman (1986) publication. Content knowledge includes knowledge of the subject and its organising structures, and is what Shulman called Subject Matter Knowledge (SMK). SMK refers to “the amount and organization of knowledge per se in the mind of the teacher” (Shulman, 1986, p. 9). Shulman went on to suggest that, “to think properly about content knowledge requires going beyond knowledge of the facts or the concepts of a domain” (p. 9). Thus, understanding subject matter not only includes awareness of its facts, but also goes beyond the facts to include understanding of its structure. SMK consists of what Schwab (1978) named ‘substantive’ and ‘syntactic’ knowledge. Substantive knowledge concerns the organisation of key facts, theories, models and concepts, while syntactic knowledge concerns the processes by which theories and models are generated and established as valid. For example, in mathematics, syntactic knowledge consists of activities such as formulating and testing generalisations and constructing proofs. Ball (1991) echoes Schwab’s concepts of substantive and syntactic knowledge discipline makes a distinction between knowledge of mathematics and knowledge about mathematics.

The second content-related category is curriculum knowledge, that is:

Represented by the full range of programs designed for the teaching of particular subjects and topics at a given level, the variety of instructional materials available in relation to those programs, and the set of characteristics that serve as both the indications and the contraindications for the use of particular curriculum or program materials in particular circumstances (Shulman, 1986, p. 10).

Thus, curriculum knowledge is knowledge of the available instructional materials, such as the curriculum and textbooks (what Shulman calls lateral curriculum knowledge), as well as knowledge of the topics and the ways in which these were addressed during the previous and subsequent years in schools (what Shulman calls vertical curriculum knowledge). The United States does not have a national curriculum, and Shulman’s early work coincided with a period in the US when a variety of reform programs were being funded (Schoen et al., 1999). Shulman’s description of content knowledge conjures up a view of a loose curriculum frame with a degree of choice about materials and approaches, which may not be applicable in different contexts. Contemporary practice in the UK, for instance, is strongly constrained by official guidance and assessment systems; so the teachers’ curriculum knowledge not only includes the materials and resources from which they can draw, but also the frame in which they are working. Thus teachers may not draw on the full range of what is available to them, or even know about what is available to them, because they are limited by the testing regime.

The last and most influential of the three content-related categories is the new concept of Pedagogical Content Knowledge (PCK). PCK is:

That special amalgam of content and pedagogy that is uniquely the province of teachers, their own special form of professional understanding […] It goes beyond knowledge of subject matter per se to the dimension of subject matter knowledge for teaching (Shulman, 1986, p. 9).

It includes the content specific representations, examples and applications that teachers use in order to make subject matter comprehensible to students together with the strategies that teachers use in order to overcome their students’ difficulties. PCK suggests that it is not just knowledge of the subject, or knowledge of pedagogy that is needed in mathematics teaching, but rather a combination of both.

The power of PCK is illustrated by a number of researchers who have assimilated, criticised and reformulated the concept. For example, Meredith (1995) suggests a reformulation of the concept of PCK and claims that a wider framework, extending PCK to incorporate alternative forms of teaching, is needed.

In particular, Meredith (1995, p.176) argues that PCK, as defined by Shulman:

seems to imply one type of pedagogy rooted in particular representations of prior knowledge. Most of the research posits a teacher-directed, didactic model of teaching. PCK does not seem to encompass alternative views of teaching which, for instance, conceive of learners as autonomous agents constructing their own understanding of subject matter.

Meredith’s stance is clearly influenced by the reform agenda mentioned earlier, which included a much greater emphasis on problem solving, in contrast to the predominant teaching method where teachers explain and illustrate procedures, and pupils practice the procedures using examples. Her argument is that PCK, as defined by Shulman, seems to see the teacher’s role as transmitting mathematical knowledge and helping learners to acquire understanding. In addition, Meredith claims that Shulman’s conceptualisation does not acknowledge that teachers develop different forms of PCK depending on the knowledge and beliefs they bring to learning. Shulman’s concept of PCK:

is perfectly adequate if mathematical knowledge is seen as absolute, incontestable, unidimensional and static. On the other hand, teachers who conceive of subject knowledge as multidimensional, dynamic and generated through problem solving may require and develop very different knowledge for teaching (Meredith, 1995, p. 184).

It is debatable, however, whether Shulman’s conceptualisation necessarily entails a view of knowledge as incontestable or of teachers as transmissive. It seems just as important for teachers working in a constructivist way to have a range of alternative ways of representing mathematics and responding to pupils’ ideas and to have a rich knowledge base on which to draw.

Although Shulman’s work was ground-breaking and his ideas continue to influence the majority of research in the field, later researchers in the same tradition argue that it is not sufficiently developed to be operationalised in research on teacher knowledge and teacher education. According to Ball et al. (2008), the distinction between Shulman’s notions of content knowledge and pedagogical content knowledge is often unclear. In addition, the conceptualisation does not acknowledge the interactions between the different knowledge categories (Hashweh, 2005) and can be criticised for presenting what seems to be a static view of teaching knowledge. It ignores the dynamic nature of knowledge, and that teacher knowledge often develops through classroom interactions with the students on the subject matter (Fennema & Franke, 1992).

Fennema and Franke’s Conceptualisation

Fennema and Franke (1992) work is discussed here because it responds to the last criticism and focuses specifically the case of mathematics teaching. Their model builds on and modifies Shulman’s framework by suggesting that the knowledge needed in teaching is interactive and dynamic in nature. They propose a model of teacher knowledge that can be used to describe what teachers need in mathematics teaching. They argue that mathematical knowledge for teaching includes four components: knowledge of the content, knowledge of pedagogy, knowledge of students’ cognition and teachers’ beliefs (Fig. 2.1). Their model centres on teacher knowledge as it occurs in the context of the classroom. Central to their conceptualisation is the claim that knowledge is interactive in nature, and that, in a given context, teachers’ knowledge of content is related to knowledge of pedagogy and students’ cognition and combines with beliefs to create a knowledge set that determines teaching practices and teachers’ behaviour in the classroom. Moreover, they suggest that knowledge is of a dynamic nature and claim that teaching is a process in which teachers can change their existing knowledge and create new knowledge.

Fig. 2.1
figure 2_1_186043_1_En

Teacher knowledge: developing in context (Fennema & Franke, 1992, p. 162)

Full size image

The content of the mathematics component includes:

teachers’ knowledge of the concepts, procedures, and problem-solving processes within the domain in which they teach […] It includes knowledge of the concepts underlying the procedures, the interrelatedness of these concepts, and how these concepts and procedures are used in various types of problem solving (Fennema & Franke, 1992, p. 162).

The parallels between the definition of content of mathematics domain and the definition of SMK as conceptualised by Shulman (1986) are clearly visible. Central to both accounts is the idea that teachers need not just to know the procedures, but also to understand the concepts underlying them. They need to know that something is so, and also why it is so.

The pedagogical knowledge component refers to “teachers’ knowledge of teaching procedures such as effective strategies for planning, classroom routines, behavior management techniques, classroom organisation procedures, and motivational techniques” (Fennema & Franke, 1992, p. 162). From Fennema and Franke’s conceptualisation, it can be said that the pedagogical knowledge component is related to Shulman’s category of general pedagogical knowledge which includes broad principles and strategies of classroom management. Furthermore, in considering teachers’ knowledge of pedagogy, they discuss teachers’ knowledge of representation in a manner similar to Shulman’s conceptualisation, according to which the use of representations is central in teaching.

The learner’s cognition component includes:

knowledge of how students think and learn and, in particular, how this occurs within specific mathematics content […] as well as understanding the processes that students will use and the difficulties and successes that are likely to occur (Fennema & Franke, 1992, p. 162).

In Shulman’s conceptualisation of knowledge, students’ conceptions are considered as part of teachers’ pedagogical knowledge. In Fennema and Franke (1992) model, this kind of knowledge is considered as a category on its own, not as a subcategory of teachers’ pedagogical knowledge. What is common to both accounts is the idea that knowledge of how students think and learn is central to effective mathematics teaching. This idea is consistent with later publications from Shulman’s colleagues (Grossman, 1990). The foremost claim in Grossman’s approach is the recognition that teachers must also know their learners. According to Marks (1990), this includes knowing learners’ cognitive processes, typical patterns of understanding, common errors, things frequently found to be difficult or easy, and interpreting students’ understanding in the midst of a lesson.

Fennema and Franke (1992) see teacher knowledge as both interactive and dynamic in nature. Knowledge is developed in a specific context and often develops through interactions with the subject matter and the students in the classroom. In their model, all aspects of teacher knowledge and beliefs are related to each other, and all must be considered to understand mathematics teaching. They suggest that no one domain of teacher knowledge has a singular role in ‘effective’ mathematics teaching.

Therefore, for Fennema and Franke, the challenge for research in the field of teacher knowledge is to develop methodology that can encompass all of these, with the aim of understanding the interaction between different categories of teacher knowledge, the roles they play in mathematics teaching and how these roles differ as teachers’ knowledge changes when they interact with their students. Adding to this, they claim that the key to understanding this kind of relationship requires researchers to carefully take into account the context in which teachers work, as central to the knowledge and beliefs that are evidenced in mathematics teaching.

The Mathematics Teaching and Learning to Teach Project (MTLT) and the Learning Mathematics for Teaching Project (LMT): A Practice-Based Framework of Teachers’ Mathematical Knowledge for Teaching

The third US model to be described, whilst influenced by critiques of Shulman, falls broadly within his cognitive tradition. Like Fennema and Franke, the team at University of Michigan examines ways in which Shuman’s ideas can be operationalised in mathematics education. For the past 15 years, the work of Mathematics Teaching and Learning to Teach Project (MTLT) and Learning Mathematics for Teaching Project (LMT) have focused both on the teaching of mathematics and on the mathematics used in teaching. The aim was to develop a practice-based theory of content knowledge needed for mathematics teaching. The first project focused on what teachers do while teaching. By teaching was meant:

everything that teachers do to support the instruction of their students […] the interactive work of teaching lessons in classrooms, and all the tasks that arise in the course of that […] Each of these tasks involves knowledge of mathematical ideas, skills of mathematical reasoning […] fluency with examples, and thoughtfulness about the nature of mathematical proficiency (Ball, Hill, & Bass, 2005, p. 17).

The team used qualitative methods to collect and analyse data in order to investigate what teachers do as they teach mathematics and what mathematical knowledge and skills teachers need to hold in order to be able to teach mathematics effectively. Data analysis led to the conceptualisation of a model of mathematical knowledge for teaching as illustrated in Fig. 2.2.

Fig. 2.2
figure 2_2_186043_1_En

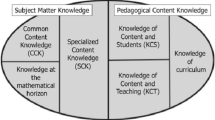
Mathematical knowledge for teaching (Ball, Thames, & Phelps, 2008, p. 403)

Full size image

This model builds on Shulman’s work by clarifying the distinction between SMK and PCK. The team’s work attempts to validate Shulman’s conceptualisation by developing reliable and valid measures of mathematical knowledge for teaching. The model suggests that Shulman’s SMK can be divided into three categories: common content knowledge, specialised content knowledge and horizon knowledge. Common content knowledge refers to mathematical knowledge and skills that are used in any setting, not necessarily that of teaching, and includes an individual’s ability to calculate an answer and to solve mathematical problems correctly. Specialised content knowledge, a central idea in the model proposed, is the knowledge that is used in classroom settings and is needed by teachers in order to teach effectively (Ball et al., 2008). Finally, horizon knowledge includes teachers’ awareness of how the mathematical topics covered in previous years in schools are related to curriculum topics addressed in the subsequent years in schools.

In addition to this, they suggest that PCK, as conceptualised by Shulman, can be divided into Knowledge of Content and Students (KCS), Knowledge of Content and Teaching (KCT) and Knowledge of Content and Curriculum (KCC) (Ball et al., 2008). KCS is ‘knowledge that combines knowledge about students and knowing about mathematics’ (Ball et al., 2008, p. 36). This means that teachers must be able to anticipate students’ difficulties and obstacles, hear and respond appropriately to students’ thinking and choose appropriate examples and representations while teaching. Both in planning and teaching, teachers must show awareness of students’ conceptions and misconceptions about a mathematics topic.

Finally, KCT is ‘knowledge that combines knowledge about mathematics and knowledge about teaching’ (Ball et al., 2008, p. 401). It refers to teachers’ decisions on the sequencing of activities and exercises, their awareness of the possible advantages and disadvantages of representations used while they teach and to their decisions to pause a classroom discussion for more clarifications, or to use a student’s opinion to make a mathematical remark.

The framework presented in Fig. 2.2 supports Shulman (1986) idea that knowledge for teaching includes a specialised knowledge of content which elaborates the constructs of SMK and PCK. For example, the two central dimensions of PCK as defined by Shulman (1986) are included in the constructs of KCS and KCT. These are, firstly, teachers’ awareness of their students’ conceptions and misconceptions and, secondly, the representations and examples that teachers use in order to make subject matter comprehensible to students. Furthermore, this framework develops the concept of SMK in more detail by proposing its sub-domains and developing measures of these sub-domains. For instance, the way horizon knowledge is defined is clearly related to Shulman’s notion of vertical curriculum knowledge.

However, Ball et al.’s (2008) conceptualisation of mathematical knowledge for teaching does not acknowledge the importance of teachers’ beliefs in their teaching. Research has suggested that teachers’ “beliefs about the nature of mathematics may be tied up with subject-matter knowledge in the way in which teachers approach mathematical situations” (Goulding, Rowland, & Barber, 2002, p. 691). If teachers believe that mathematics is principally a subject of rules and routines which have to be remembered, then their own approach to unfamiliar problems will be constrained, and this may impact on their teaching. Beliefs may be particularly salient in the development of syntactic knowledge, where conjecturing, finding evidence and seeking explanations is quite different from finding rules and routines in recognizable contexts.

Furthermore, Ball et al.’s new framework can be criticised for its account of the concept of SCK. This concept is central in the conceptualisation of teachers’ mathematical knowledge and is defined as the mathematical knowledge that is used in classroom settings and needed by teachers in order to teach effectively. The definition of SCK, as it stands, does not clearly distinguish between SCK and PCK. After all, PCK is also uniquely needed by teachers and is used in classroom settings. As Shulman (1987, p. 8) noted, PCK is “a special amalgam of content and pedagogy that is uniquely the province of teachers, their own special form of professional understanding.”

What is valuable in the development of this framework of teacher knowledge is that the Michigan team made some progress in identifying the relationship between teacher knowledge and students’ achievement in mathematics. Hill, Rowan, and Ball (2005) argue that teachers’ mathematical knowledge is related to students’ achievement in mathematics and they provide evidence that teachers with weak knowledge transmit this to their students. Another central contribution of the MTLT and LMT projects was the development of measures of teachers’ mathematical knowledge. In his account, Shulman (1986) hopes that researchers working in the field of teacher knowledge will manage to develop instruments that could be used to test aspects of teacher knowledge. Within the work of these two projects, the research teams managed to develop a series of multiple choice items that can be used to measure mathematical knowledge for teaching. These kinds of items could reasonably be used to inform the content and structure of different courses within teachers’ initial training.

Ball’s work was of interest to both sides of the ‘maths wars’ that followed what had seemed like a broad consensus on the need for major curriculum, teaching and assessment reform in the United States. Into this acrimonious debate, the work of Liping Ma, a Ball’s student at Michigan, brought surprising agreement between the reformers and the traditionalists. Her comparative study of Chinese and US teachers’ knowledge of fundamental mathematics found a knowledge gap between the US and Chinese teachers (who had significantly fewer years of formal mathematics education at school) which mirrored the gap between US and Chinese students found in other studies. She argued that in the US, the lack of attention to mathematical content knowledge in teacher education programmes reinforced low quality school mathematics education and that this was an important impediment to reform. Her conclusions found favour with both the reformers advocating a focus on problem solving and teachers as facilitators of children’s thinking, and the traditionalists with a concern for underlying structure, formal reasoning and deductive proof. (Shulman in Ma, 1999).

The Knowledge Quartet

Also, in a broadly cognitive tradition, but in the different political circumstances of England and Wales, is the theoretical model reported in the findings of the SKIMA (Subject Knowledge in Mathematics) project by members of the Faculty of Education at the University of Cambridge (Rowland, 2005; Rowland, 2007; Rowland, Huckstep, & Thwaites, 2003). This arose out of earlier work on primary pre-service mathematical subject knowledge which was a response to the increased prescription of the initial teacher training curriculum and its assessment by the government, over a decade after the introduction of the National Curriculum in 1989.

The Knowledge Quartet is a theoretical framework which arose from the investigation of the mathematical content knowledge of pre-service elementary school teachers in England and Wales. The project is set within the theoretical framework set out by Shulman (1986) but responds to Fennema and Franke (1992) by categorising situations from classrooms where mathematical knowledge surfaces in teaching. The team’s approach to investigate the relationship between pre-service teachers’ SMK and PCK of mathematics was to observe and videotape mathematics lessons taught by pre-service teachers in a 1-year Postgraduate Certificate of Education course.

The detailed analysis of the lessons observed resulted in the identification of a framework called ‘The Knowledge Quartet’. This framework can be used as a tool for classifying ways in which the pre-service teachers’ SMK and PCK come into play in the classroom. The Knowledge Quartet consists of four dimensions, namely, Foundation, Transformation, Connection and Contingency.

(Foundation) consists of trainees’ knowledge, beliefs and understanding acquired in the academy, in preparation for their role in the classroom. Such knowledge and beliefs inform pedagogical choices and strategies in a fundamental way […] the second category (Transformation) concerns knowledge-in-action as demonstrated both in planning to teach and in the act of teaching itself […] Connection binds together certain choices and decisions that are made for the more or less discrete parts of mathematical content […] contingency concerns classroom events that are almost impossible to plan for (Rowland et al., 2003, pp. 97–98).

Each component of the Knowledge Quartet is composed of a number of codes. The key components of the Foundation category are teachers’ knowledge and understanding of mathematics pedagogy, as well as their beliefs about it. Transformation includes the kind of representation and examples used by teachers, as well as teachers’ explanations and questions asked from students. The third category, Connection, includes the links made between different lessons, between different mathematical ideas and between the different parts of a lesson. It also includes the sequencing of activities for instruction and an awareness of possible difficulties and obstacles that students may have with different mathematical topics and tasks. Finally, the fourth category, Contingency, concerns teachers’ readiness to respond to students’ questions, to respond appropriately to students’ wrong answers and to deviate from their lesson plan. In other words, it concerns teachers’ readiness to react to situations that are almost impossible to plan for.

This framework elaborates the constructs of SMK and PCK as these were defined by Shulman, and takes up Hashweh (2005) suggestion that what is missing from Shulman’s account is the identification of interactions among the different categories of teachers’ knowledge. The Knowledge Quartet can be used in understanding the ways in which SMK and PCK are related and come into play in the classroom. In this framework, all aspects of teachers’ knowledge and beliefs come together as resources from which to draw both in planning and in the act of teaching. The Knowledge Quartet can be seen as a response to Fennema and Franke (1992) call to develop studies that focus on the identification of a framework for thinking about the ways in which different components of teachers’ knowledge are integrated and come into play in the classroom. In addition, the Foundation dimension of the framework can be understood as a response to Meredith (1995) call for a model that acknowledges that pre-service teachers may develop different forms of PCK depending on the knowledge and views they bring to their training.

The Knowledge Quartet is currently used as a framework for lesson observation and for mathematics learning development within the primary PGCE programme at Cambridge University (Rowland, 2007). The framework is also being applied to support teaching development in early career teachers in England (Turner, 2006) and structuring initial teacher education in Ireland (Corcoran, 2007). Finally, the framework was used with the aim of understanding what relationship can be observed between Cypriot pre-service teachers’ mathematical knowledge and their teaching (Petrou, 2009). Petrou (2009) argued that, in general, the Knowledge Quartet was comprehensive in the classification of teaching situations in which participants’ mathematical knowledge surfaces in teaching. Issues related to the interpretation and use of textbooks in mathematics teaching were not addressed by the framework; however, they proved important in analysing the mathematics lessons taught in Cypriot classrooms. This suggested that when adapting the Knowledge Quartet for observing lessons in Cyprus, and indeed, in many other countries, there is a need to take careful account of possible differences between the context in which the framework was originally developed and the context in which it is being applied.

The neglect of textbooks in the English conception of the Knowledge Quartet may be partly because they were less visible than they are in Cyprus. But it may be because the original study was very focused on SMK and PCK and not so much on curriculum knowledge. According to Shulman (1986), curriculum knowledge includes the ‘knowledge of instructional materials’, such as textbooks. So, the enlargement of the Knowledge Quartet to include use of textbooks brings curriculum knowledge within the orbit of the Knowledge Quartet in a way that it was not before. Petrou (2009) argues that the original analysis of the video data in the English study may have been limited by the neglect of curriculum knowledge. Indeed, although texts were less visible, practice in the UK is strongly framed by the National Curriculum and its associated assessment systems. Therefore, since the curriculum is the key to mathematics teaching in the UK, and we imagine this is to be true in many countries, it seems reasonable to argue that ‘curriculum knowledge’ is important in any attempt to understand what teachers need to know in order to teach mathematics effectively.

Synthesis

The models about teacher knowledge described above can be understood as elaborating, and not replacing, Shulman’s (1986) conceptualisation of content-related categories of teacher knowledge, and in particular, the notions of SMK and PCK. The conceptualisations of teacher knowledge proposed are not inconsistent; rather, they build on each other. Even though the researchers have stressed different domains of teacher knowledge, all focus on the importance of seeing the content to be taught as an important part of teaching.

However, the conceptualisations raise questions about whether the distinction between SMK and PCK could and should be made. Aubrey (1997) and McEwan and Bull (1991) agree with McNamara (1991) in arguing that there is no distinction between SMK and PCK, and that for teachers, all knowledge is pedagogic. Similarly, An, Kulm, and Wu (2004, p. 146) define PCK as “the knowledge of effective teaching, which includes three components, knowledge of content, knowledge of curriculum, and knowledge of teaching.”

The advantage of these perspectives is that they acknowledge the importance of teaching and are very appropriate when we are seeking to understand what is going on in the classroom. After all, “teachers use mathematical knowledge not so much for the doing of mathematics but rather for the teaching of mathematics” (Hodgen, 2003, p. 106).

However, considering all mathematical knowledge in teaching as pedagogic may not be helpful in teacher preparation and development programmes. There is an argument for some specific attention to be paid to SMK. For instance, those who have had limited experience of reasoning and proof, may need opportunities to work on this at their own level as learners of mathematics. The important thing here would be that the examples and activities chosen for this work would not be far removed from the school curriculum. For instance, reasoning associated with odd and even numbers and operations upon them, or algebraically generalizing patterns in number squares, could be appropriate for primary pre-service teachers. Secondary teachers may not be called upon to prove the rules for operations on directed numbers in the classroom, but being exposed to this exercise could enlarge their own understanding and help them to see that understanding is a continual process. In geometry, secondary teachers may know the conditions for congruency of the triangles, but may not fully understand why these conditions hold and what can be deduced, once congruency has been established. The unpacking and deepening of SMK can be seen as part of the process of transformation required for robust PCK to be developed.

For this reason, the synthesis proposed here (Fig. 2.3) maintains a distinction between SMK and PCK, but recognizes the interplay between the two categories. We position ourselves with Fennema and Franke (1992) in believing that teacher knowledge can only be understood in the context in which they work. We take the view that the context in which teachers work is the structure that defines the components of knowledge central to mathematics teaching. Included in this ‘context’ are the educational system, the aims of mathematics education, the curriculum and its associated materials (such as textbooks) and the assessment system. Within a particular country, therefore, the curriculum and its associated materials provide the frame within which teachers work. They reflect beliefs about what mathematics is, what students need to know about mathematics, and in what ways mathematics needs to be taught. However, we acknowledge that context is also local. This would include the resources, both material and human, that teachers have in their school or locality, as well as the practices and ethos of the workplace.

Fig. 2.3
figure 2_3_186043_1_En

Synthesis of models on teacher mathematical knowledge

Full size image

In focusing on investigating the nature, role and importance of SMK, PCK and the related categories in the Knowledge Quartet, the earlier models neglect the importance of curriculum knowledge in conceptualising mathematical knowledge for teaching. In Ball et al., (2008, p. 403), Curriculum Knowledge is provisionally placed within pedagogical content knowledge:

We are not yet sure whether this may be a part of our category of knowledge of content and teaching or whether it may run across the several categories or be a category in its own right. We also provisionally include a third category within subject matter knowledge, what we call “horizon knowledge” […] Again we are not sure whether this category is part of subject matter knowledge or whether it may run across the other categories. We hope to explore these ideas theoretically, empirically, and also pragmatically as the ideas are used in teacher education or in the development of curriculum materials for use in professional development.

Ball et al. seem to recognise that there is need in their model to further refine and investigate the concept of curriculum knowledge.

Our model suggests that Curriculum Knowledge as defined by Shulman (1986) is central in understanding what teachers need to know in order to teach mathematics effectively. In addition, the model implies that teachers’ SMK and PCK can determine the ways in which teachers understand, interpret and use the mathematics curriculum and its associated materials. Indeed, research suggests that teachers interpret the curriculum materials, such as textbooks, in different ways and that their interpretation determines the ways they use these in their teaching (Ball & Cohen, 1996; Petrou, 2009). In a study that focuses on investigating how pre-service teachers interpret and use mathematics textbooks, Nicol and Crespo (2006) show that teachers have various approaches to using textbooks, ranging from adherence (the textbook is seen as authority), elaboration (the textbook is seen as the main resource, but teachers elaborate it with other resources), and creation (the teacher examines the textbook with a critical eye for its potential and limitations in deciding what to teach). Clearly, SMK and PCK are factors influencing these three approaches.

Elsewhere, Ball and Feiman-Nemser (1988) show how pre-service teachers’ beliefs and knowledge of mathematics influence the way they use textbooks. They describe how one teacher had problems in understanding the suggestions in the textbook about a lesson on measurement, because of her insufficient knowledge of the content and of how students make sense of measurement. Thus, curriculum materials may provide ways of organising content, activities and tasks that help teachers in their planning and teaching. However, in order to implement a curriculum that was designed to promote students’ deep understanding of mathematics effectively, teachers themselves need the understanding to exploit the potential of texts and other resources.

Implications and Limitations

The synthesis proposed above demonstrates the multidimensional nature of teacher knowledge and the connections between different categories, but like all models, there are inevitably some over-simplifications. We have already pointed out the ambiguous boundary between SMK and PCK, but feel that the two categories are useful organizing devices in describing teacher knowledge for research purposes, and particularly in devising pre-service and professional development programmes. For instance, an appropriate level of mathematical knowledge will be one of the criteria for entry into a course of training. This may simply be a question of providing evidence of achieving a specific examination qualification, but it could also be probed in an interview. We would also argue for the provision of opportunities for all teachers to work on mathematics relevant to the school curriculum, but at their own level. Later chapters in this book will cover those areas of primary teachers’ knowledge, such as fractions, division, and proof, where common weaknesses have been identified. Work on these areas and others, about which less is known, would not only strengthen the resource of SMK from which teachers can draw in teaching, but would also give them opportunities to reflect upon the experience of doing mathematics themselves. Moreover, they may experience different ways of learning mathematics which could impact on their beliefs of how it can be learned.

In many of the projects described earlier, this kind of approach to strengthen SMK has already been adopted. One of the dilemmas here, however, is how the approach is implemented. If implemented through an audit, the dimensions of fear and control may inhibit pre-service teachers and encourage compliance rather than engagement. If the approach is developmental, there is a danger that it receives lower priority than other elements, and is not taken very seriously. Moreover, a developmental approach may be time consuming, expensive and difficult to track as teachers move through their professional careers.

One of the common features of the different models of teacher knowledge discussed here is the largely individualistic assumption which underpins them. Despite the acknowledgement of context, the focus tends to be on the knowledge that an individual teacher brings to a course of teacher education and then into the classroom. This can result in a deficit view of the individual teacher, who at worst needs remediating and at best developing, rather than seeing teacher knowledge as a product of the educational system in which she is located. We cannot assume that the frameworks discussed here are universal. Even if there are some commonalities, there may be great differences in emphasis in various cultural contexts and different priorities for research and development. Switching attention to the system would mean paying more attention to the prior mathematical experiences of teachers and to the resources available to teachers for their own use. In situations where the assessment of subject knowledge is seen as a means of weeding out prospective teachers, more communal ways in which teachers’ mathematical knowledge in teaching could be encouraged, whether in training or professional development. This could include paying more attention to the mathematical knowledge which teachers want help with, as well as the elements deemed important by teacher educators. It could also mean more use of peer teaching and development.

Switching the focus from the individual teacher to the system brings in the third element – curriculum knowledge. The curriculum and its associated materials can act as both a resource and a constraint on the teacher. Critical analysis can expose the intentions of both the policy makers and the writers of curriculum materials, whether these materials are for pupils (e.g. textbooks), or for teachers (e.g. teachers’ guides). These may be quite different from the knowledge that teachers use and reveal through their practice, either because of inadequacies in the teacher’s knowledge base, or because of informed rational choices. We need to know more about how teachers use curriculum materials to improve their teaching, and which curriculum materials are most effective in doing this. For instance, building on the work of Davis and Krajcik (2005) and Stylianides (2007) provides a theoretical framework showing how features of educative curriculum materials may promote teacher learning by enabling them to engage their students effectively in tasks related to proof. These materials may be strengthening teachers’ own knowledge of proof through the development of their teaching.

We would also argue that the Knowledge Quartet is a framework that can be used for developing educative curriculum materials. For instance, in terms of the Transformation dimension, curriculum materials can provide several appropriate representations of different ideas. Also, a discussion of the possible advantages or disadvantages of using a certain representation can support teachers in adapting and using the suggested representation in their teaching. This can help make teachers better prepared not only to explain concepts to their students, but also to understand the ways their students make sense of different ideas in mathematics. However, such guidance cannot help every teacher. Educative curriculum materials, like any innovation, are not a solution in themselves. Their effectiveness might be limited by teacher knowledge and beliefs. Nevertheless, Ball and Cohen (1996) showed that when educative elements were included in the guidance provided to teachers about using textbooks, and when these textbooks were used as an important part of teacher training, this resulted in favourable gains in both teachers’ SMK and PCK.