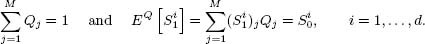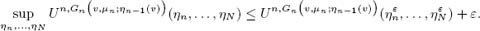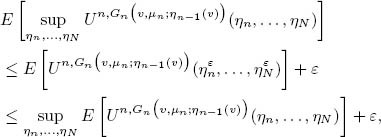Abstract
This chapter concerns portfolio optimization, which is one of the historically first problems in financial mathematics. Indeed, one of the basic problems that a given subject (physical person or institution), possessing a certain amount of wealth, has to deal with is the following: how to invest this wealth in the financial market over a given period of time in order to be able to consume optimally (according to a given criterion) from this portfolio over time and at the end have a residual amount leading to benefit, also this one optimal according to a given criterion. The optimality criterion that we shall consider is the most common one, namely the maximization of expected utility of the various monetary amounts.
This is a preview of subscription content, log in via an institution to check access.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
1Since we are interested in the utility maximization problem, putting u(v) = −∞ for v ∈ ℝ \ I is equivalent to excluding values outside the interval I from being optimal.
- 2.
2Recall that by our assumptions a≤ 0 and 1 + r> 0.
- 3.
3For a full proof see for example Proposition 2.7.2 in [7].
- 4.
For example, in the one-period case, assuming for simplicity r = 0, we havethat \( Q\in {\mathbb{R}}_{+}^M \) is a martingale measure if
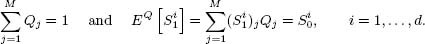
- 5.
5The inequality “≥” is obvious. To show the inverse inequality, fix ε> 0 and consider functions η ε N , …, η ε N such that
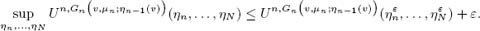
Then, in the mean, we obtain
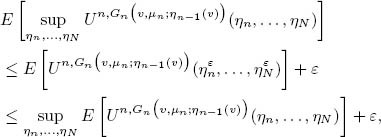
from which the thesis follows, given the arbitrariness of ε.
- 6.
6It holds, furthermore, that C max N (υ) = υ.
- 7.
It holds, furthermore, that C maxN (v) = v.
- 8.
It holds, furthermore, that C maxN (v) = v.
- 9.
If V n–1 = 0 then V n ≤ K for any π n ∈ ℝ
- 10.
M can be computed explicitly as in (2.129).
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2012 Springer-Verlag Italia
About this chapter
Cite this chapter
Pascucci, A., Runggaldier, W.J. (2012). Portfolio optimization. In: Financial Mathematics. Unitext(). Springer, Milano. https://doi.org/10.1007/978-88-470-2538-7_2
Download citation
DOI: https://doi.org/10.1007/978-88-470-2538-7_2
Publisher Name: Springer, Milano
Print ISBN: 978-88-470-2537-0
Online ISBN: 978-88-470-2538-7
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)