Liver Disease Diagnosis Using Quantum-based Binary Neural Network Learning Algorithm

Abstract

In this paper, a liver disease diagnosis is carried out using quantum-based binary neural network learning algorithm (QBNN-L). The proposed method constructively form the neural network architecture, and weights are decided by quantum computing concept. The use of quantum computing improves performance in terms of number of neurons at hidden layer and classification accuracy and precision. Same is compared with various classification algorithms such as logistic, linear logistic regression, multilayer perceptron, support vector machine (SVM). Results are showing improvement in terms of generalization accuracy and precision.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Bad eating habits of people causes many disease such as obesity and metabolic syndrome, diabetes, cancer, and liver disorder. Due to increase in consumption of alcohol world wide specially in developing countries, liver disease such as liver cancer, liver swelling, and liver inflammation are very common. Diagnosis of this disease in early stages can stop several death world wide. In recent years, several new techniques have been developed to identify liver disease. Neural network has also attracted attention of many researchers to diagnosis liver related disease. This technique has given better result than tradition method for diagnosis, but still finding an optimal result using neural network is an open area of research. To find an optimal result using neural network, it depends on several parameters of networks as network architecture, weights, training time, testing time, connections, number of neurons at hidden layer, and number of hidden layers [1]. For optimizing the parameters such as weight and connection, Lu et al. [2] proposed a quantum-based algorithm. This algorithm works on the concept of quantum computing for optimizing connections and weights in MLP-based neural network structure. Designing a neural network architecture using MLP causes much iteration for convergence and also causes under-fitting and over-fitting problem.

There are many ways available through which neural network architecture can be formed constructively during learning [3]. One such algorithm based on binary neural network is proposed by Kim and Park named as ETL algorithm. It classifies data on the basis of hyperplane generation and works for two class problem [4]. Chaudhari et al. proposed mETL which uses geometric concepts of ETL for classification of multiclass data. It starts learning by selecting any random sample as core vertex. Thus, network formed after learning depends on the core selection; therefore, solution is not unique [5]. In this paper, an algorithm is proposed for binary neural network using quantum computing concept. This algorithm constructively formed network architecture by updating network weights using quantum processing concept.

This paper is organized as follows: Sect. 2 describes required preliminaries briefly. Section 3 describes details of proposed methodology. Section 4 is presented with the experimental work which shows the performance of proposed algorithm on BUPA liver dataset; then, it is compared with various machine learning algorithms [6]. Section 5 is presented with the concluding remarks.

2 Preliminaries

Here, we are proposing a liver disease diagnosis system using quantum algorithm using binary neural network learning. Network formed consist of 3 layers: input layer, hidden layer, and output layer. Let $X = (x_{1} ,x_{2} ,x_{3} , \ldots ,x_{n} )$ denote the input samples which are in binary form, where $n$ is the number of input sample. Let $W = (w_{1} ,w_{2} ,w_{3} , \ldots ,w_{n} )$ be a connection weights for a neurons, which are updated by using quantum concept and quantum gates [7]. Quantum gates are described briefly and presented subsequently.

In the proposed learning algorithm, we make use of sigmoid activation function for neuron which is given as follows:

$$ f({\text{net}}) = \frac{1}{{1 + e^{{ - {\text{net}}}} }} $$

(1)

where

$$ {\text{net}} = \sum\limits_{i = 1}^{n} w_{i} \times x_{i} $$

(2)

Quantum concept make uses of quantum bits called as qubits. It uses probability to represent binary information. Qubit represent linear superposition of ‘1’ and ‘0’ bits probabilistically which is represented as follows:

$$ \psi = \alpha |0\rangle + \beta |1\rangle $$

(3)

where $\alpha^{2}$ is the probability of bit in 0 state and $\beta^{2}$ is the probability of bit in 1 state defined as follows:

$$ \alpha^{2} + \beta^{2} = 1;\quad 0 \le \alpha \le 1,\,0 \le \beta \le 1 $$

Qubit represent any superposition of 0’s and 1’s state. For example, two-qubit system would perform the operation on 4 values and a three-qubit system on eight; thus, n qubit will perform operation of $2^{n}$ values. A quantum bit individual contains a string of q quantum bits.

Let us take an example of two quantum bits, which are represented as follows:

$$ \psi = \left\langle {\begin{array}{*{20}c} {1/\sqrt 2 |1/\sqrt 2 } \\ {1/\sqrt 2 |1/\sqrt 2 } \\ \end{array} } \right\rangle $$

(4)

$$ \begin{aligned} \psi & = (1/\sqrt 2 \times 1/\sqrt 2 )\langle 00\rangle + 1/\sqrt 2 \times 1/\sqrt 2 )\langle 01\rangle + 1/\sqrt 2 \times 1/\sqrt 2 )\langle 10\rangle \\ & \quad + 1/\sqrt 2 \times 1/\sqrt 2 )\langle 11\rangle \\ \end{aligned} $$

(5)

These quantum bits used later on for representing the quantum weight are as follows:

$$ Q^{g} = (q_{1}^{g} ,q_{2}^{g} ,q_{3}^{g} , \ldots ,q_{n}^{g} ); $$

(6)

where $q_{i}^{g,i} = [y_{1}^{g,i} ,y_{2}^{g,i} ]$; $0 \le y_{1}^{g,i} \le 1$ and $0 \le y_{2}^{g,i} \le 1$; $i = 1,2,3 \ldots n,$ n is number of input sample; $g = 1,2,3 \ldots m,$ m is number of iterations required for finding an optimal weight.

These quantum bits are updated using quantum gates [6]. This is a concept through which qubits are updated with operations given as follows:

$$ \alpha = [\cos\Delta \theta - \sin\Delta \theta ]\left[ {\frac{\alpha }{{\sqrt {1 - \alpha^{2} } }}} \right] $$

(7)

$$ \alpha = \left\{ {\begin{array}{*{20}l} {\sqrt \epsilon ,} \hfill & {\text{if}} \hfill & {\alpha < \sqrt \epsilon } \hfill \\ \alpha \hfill & {\text{if}} \hfill & {\sqrt \epsilon \le \alpha \le \sqrt {1 - \epsilon } } \hfill \\ {\sqrt {1 - \epsilon } } \hfill & {\text{if}} \hfill & {\alpha > \sqrt {1 - \epsilon } } \hfill \\ \end{array} } \right. $$

(8)

where $\Delta \theta$ is angular displacement to update qubits. $\epsilon$ represent a very small value (approximately approaching to zero) for the purpose of varying the qubits in the range within 0 and 1. It is necessary to apply quantum computing idea in weight updation so that it gives larger subspace for weight value during iteration without making weight zero or one only. Observation process: Classical computers work on bits; therefore, it is necessary to convert quantum bits in terms of classical bits 1 and 0. To generate classical bit from qubits, a random vector $r = [r_{1} ,r_{2} ,r_{3} , \ldots r_{n} ]$ is generated where $r_{i} = (r_{1}^{i} ,r_{2}^{i} )$ and $0 \le r_{1,2}^{i} \le 1$ and following operations are performed.

$$ {\text{if}}(r_{i} \le (\alpha^{2} )),\quad {\text{then}}\,\,s_{b} = 1\,\,{\text{else}}\,\,s_{b} = 0\,\,{\text{where}}\,\,b = 1,2. $$

(9)

Here, let us take vector $S^{g} = [S_{1}^{g} ,S_{2}^{g} ,S_{3}^{g} , \ldots ,S_{n}^{g} ),$ where $S_{i}^{g} = [s_{1} s_{2} ]$ corresponds to qubit vector $Q^{g}$. String $S_{i}$ is of two bit length which corresponds to the quantum weight space. This is then mapped to the final weights in first iteration. Further, the weights for the neuron are selected using Gaussian random generator.

To select weights from binary values here, the Gaussian random generator has been used with mean value $\mu_{i}^{g}$ and variance $\sigma_{i}^{g}$. Therefore, weight vector is now formalized as follows:

$$ W^{g} = (w_{1}^{g} ,w_{2}^{g} ,w_{3}^{g} , \ldots ,w_{n}^{g} ),\quad{\text{where}}\,w_{i}^{g} = N(\mu_{i}^{g} ,\sigma_{i}^{g} ) $$

(10)

3 Proposed Approach

A liver disease’s diagnosis quantum-based algorithm using binary neural network (L-QBNN) is proposed. This approach makes use of quantum concept for constructing neural network. Network structure formed is of three layers: input, hidden, and output layer, which accepts binary form of inputs and generate binary form of outputs. The approach works in two phases, hidden layer learning and output layer learning.

3.1 Hidden Layer

Hidden neurons are added constructively. Initially, we take one neuron at the hidden layer and initialize quantum values by $0.707$ (this is 50 % probability of any bit in 0 or 1 position) for $Q^{1}$. After initialization of quantum bits, vector r is generated with random values. Then, observation process generates vector $S^{1}$ in terms of bits. With the help of this vector, final weight values are $W^{1}$ achieved by Gaussian random generator. These weights are applied as an input to the hidden neuron using Eqs. 1 and  2. In order to check number of sample learned by a neuron for both class, a parameter $\lambda$ is taken, which is compared with output values of hidden neurons. The value of $\lambda$ is taken as 0.6 on the basis of learning of neurons at hidden layer for input samples. This value has been taken on the basis output value of activation function of hidden neuron. This process will continue till all iterations for learning all sample which presented subsequently. Whenever new samples are coming for learning, it is checked with present neurons. If it is not learned with the existing ones, then a new neuron will be added and processed. All process is repeated from initialization of qubits to find out optimal weight for new neuron. After finding weights for hidden neurons, outputs of all hidden neurons are connected to a simple output layer. Thus, output is presented next.

3.2 Output Layer

Since this method handles only two class problem, only one neuron will be required at the output layer. The weights of output layer are in simple qubits form and set to (0.707) for all the connections from hidden layers. The same activation function is used for output neuron as used for hidden layer neuron. If number of neurons at hidden layer is more than two, then quantum weights of output layer will be updated with same approach to get optimized result. Based on the above discussion, QL-BNN in the form of algorithm is presented subsequently.

In this algorithm, input layer is just the number of input nodes corresponding to the number of bits representing a particular sample, where one by one input samples are applied and then following algorithm is used for learning of hidden neurons. In this algorithm, some necessary parameter has been used which is described as follows:

$$ \begin{aligned} & X(j)\quad{\text{where}}\, j = 1,2,3 \ldots ,r;\,{\text{is}}\,{\text{sample}}\,{\text{of}}\,{\text{class}}\,A\,{\text{which}}\,{\text{gives}}\,{\text{output}}\,' 1 '. \\ & {\text{Y}}({\text{k}})\quad{\text{where}}\, {{k = 1}}, 2, 3, \ldots ,{{s}};\,{\text{is}}\,{\text{sample}}\,{\text{of}}\,{\text{class}}\,{\text{B}}\,{\text{which}}\,{\text{gives}}\,{\text{output}}\,' 0 '. \\ \end{aligned} $$

Two values, ${{count}}\,1$ and ${{count}}\,2$, have been taken, and they describe the number of sample of class A and B. Here, $S^{*}$ vector is used which stores best value from $S^{g}$ corresponding to best result or value of sum which is explained in algorithm 1 subsequently.

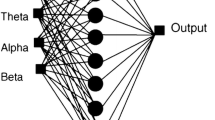
Working of L-QBNN is explained by taking simple example. Let us consider a database of eight instances with 3 input variable (000, 001, 010, 011, 100, 101, 110, 111). Dataset $(000,010,111)$ belongs to class A which generates output 1, and dataset $(100,101,110)$ belongs to class B which generates output 0. Now initialize quantum values $Q^{1} = (0.707|0.707,0.707|0.707,0.707|0.707,0.707|0.707)$. Initialize random vector r, let us say $r = (0.8|0.3,0.69|0.15,0.37|0.77,0.75|0.83)$. By using Eq. 6, observation process gives following result $S = (01,01,10,00)$. Now according to step-5 in Algorithm 1 and Fig. 1 link second from the weight space for first weight and second weight is used. Similarly, link 4 for third weight and link 1 for fourth weight are used. Here, Gaussian random generator is used for generating weight; let us say it gives following weight values for $W^{1} = (0.23, - 0.078,0.25, - 0.36)$. Now, these weight values (using step 7 ${\text{net}}_{A} (1)$ and ${\text{net}}_{B} (1)$) are calculated for given dataset. Also count number of samples which satisfy $f({\text{net}}_{A} (1)) > \lambda$ and $f({\text{net}}_{B} (1)) \le \lambda$.

Fig. 1

Selection of weight

Let us say class A sample $(000,010)$ and class B samples $(100,101)$ satisfy the above stated condition for generated weight values. It shows that out of 6 dataset from both the classes, this neuron learned for 4 samples in first iteration. Now, update qubits by quantum gate and again check value of sum for all iterations for first neuron only. If value of sum in all iterations found more than 4, then weight corresponding to this value will be considered as final weight, else weight corresponding to ${\text{sum}} = 4$ will be the final weight. The value of angular displacement $\Delta \theta$ will be decided on the basis of sum and bit values of s and $s^{*}$ as described in Table 1. After deciding the number of neuron required at hidden layer, only one neuron is required at the output layer.

Table 1 Parameters for qubits updation

4 Experimental Results

In this section, L-QBNN has been tested on BUPA liver dataset. These dataset are collected from UCI repository of machine learning [8].

4.1 Experimental Setup

Experimental setup starts with initialization of quantum bits $Q^{g}$ and random vector r. To update quantum weights, let us take angular value $\Delta \theta = 0.03*\varPi$ and total 100 iterations. To stop quantum weight to converge from 0 and 1, the value of $\varepsilon = 0.05$ is an account. The value of $\lambda$ is taken into account 0.6. The Gaussian random value has been taken from both range positive and negative, and values corresponding to four weight space are N(−0.15, 0.03), N(−0.65, 0.03), N(0.15, 0.03), and N(0.65, 0.03). Experiments have been carried out on Intel core i-5 processor with 4 GB RAM and on Windows 7. All necessary parameters have been described in Table 2. The performance of proposed method has been evaluated on BUPA liver dataset, which is describe next.

Table 2 Parameters used for experimentation

4.1.1 Classification of BUPA Liver Dataset

BUPA liver dataset has a total of 345 instances having 6 features consisting of 42 attributes after converting it in terms of bits. To test the proposed algorithm, the dataset has been divided into two subsets 75 %, i.e., 259 instances are used for training and 25 %, i.e., 86 instances are used for testing. Table 2 illustrates the parameters used in the experimentation.

Table 3 shows the classification and precision result. This algorithm is tested on 10 sets of BUPA liver data. It can be observed that value of classification and precision is best among all available method. On the contrary, the best generalization accuracy is achieved for set-1 which is $74.41\,\%$ with testing time $0.6261$ seconds and the worst generalization accuracy is achieved for set-3 which is $73.15\,\%$ with testing time $0.6280$ s.

Table 3 Experimental results for BUPA liver dataset

4.2 Discussion

As result shown in Table 3, the L-QBNN algorithm produces better results than various machine learning algorithm [8] and they are compared in terms of generalization accuracy and precision.

With all the parameter taken into account and discussed above, Table 4 shows the comparative results with various machine learning algorithm, which are reported in terms of two parameters: generalization accuracy and precision.

Table 4 Comparison of various learning algorithms with QBNN-L on BUPA liver dataset

5 Conclusion

In this paper, liver disease diagnosis using quantum-based binary neural network algorithm is presented. It can solve any two class classification problem by forming three layer network structure. The neural network architecture is formed constructively, and weights are updated by quantum computing concept. This algorithm is tested on BUPA liver dataset and compared with various machine learning algorithm. From the experimental results, it is observed that QL-BNN algorithm is better in terms of generalization accuracy and precision. Since this problem is for two class problem, there is no overhead involved in learning output layer.