Abstract
In this chapter, we explain basics of string theory and how one reaches AdS/CFT. The relation between string theory and gauge theory has been discussed for many years, and AdS/CFT solved the “homework” to some extent.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Such a figure is known as a Chew-Frautschi plot [2].
- 2.
To be precise, this line does not represent a single trajectory but represents degenerate trajectories which are distinguished by the other quantum numbers. Incidentally, the \(\omega \) mesons contain \(s\bar{s}\), but they are similar to the \(\rho \) mesons in the sense that they do not carry quantum numbers such as strangeness, charm, bottom, and top.
- 3.
The parameters \(\mathsf {T}\), \(\alpha '\), and \(l_s\) are related by

- 4.
Classically, such a string oscillation represents a massive particle as one can expect from Eq. (5.2). But it is actually massless because of the quantum correction [the second term of Eq. (5.2)]. This is true only in 26-dimensional spacetime for the bosonic string and in 10-dimensional spacetime for superstrings. This is one reason why higher-dimensional spacetime is necessary in string theory.
- 5.
More precisely, the simplest oscillations of a closed string represents a graviton and two undiscovered scalar particles, the dilaton and the axion. Since left and right-moving modes each have two degrees of freedom, a closed string has four degrees of freedom at this level (in four dimensions). The graviton has only two degrees of freedom, and two scalar fields cover the remaining degrees of freedom.
- 6.
More precisely, the D-branes represent a \(U(N_c)\) gauge theory, but the \(U(1)\) part describes the center of mass motion of the branes and decouple from the \(SU(N_c)\) part.
- 7.
This is not necessarily the case if one compactifies part of brane directions (e.g., Sakai-Sugimoto model [5]). Incidentally, the D1-brane is a string-like object, but it is different from the “fundamental string” we have discussed so far.
- 8.
One can consider string theories with closed string alone, but we will not discuss such theories.
- 9.
Below we often consider only vacuum amplitudes for simplicity, but one can consider scattering amplitudes by adding appropriate external lines. Incidentally, \(g_s\) looks like a free parameter of the theory at this stage, but actually it is not a free parameter (Sect. 5.2.5).
- 10.
If one adds three external lines (factor \(g_s^3\)) to the sphere \(1/g_s^2\), the diagram is proportional to \(g_s\), which is consistent with the interaction vertex in Fig. 5.10b.
- 11.
See Ref. [6] for a textbook of supergravity. The name, supergravity, comes from the fact that the theory has local supersymmetry, but we will not discuss the terms with fermions below.
- 12.
More properly, one calculates string Feynman diagrams as in Sect. 5.2.4 and writes down a field theory action which reproduces these scattering amplitudes.
- 13.
We write the \((p+1)\)-dimensional action instead of a 10-dimensional action because one can consider \((p+1)\)-dimensional gauge theories using D-branes.
- 14.
Recall that the parameter \(\alpha '\) is related to the string length \(l_s\) by \(\alpha '=l_s^2\).
- 15.
See Ref. [7] for a review of effective field theories.
- 16.
The parameters \(N_c\) and \(\lambda \) are dimensionless whereas \(G\) and \(l_s\) are dimensionful, but we make the dimensions to come out right in Sect. 5.3.3.
- 17.
The Poincaré invariance is also called the inhomogeneous Lorentz invariance. \(\textit{ISO}(1,3)=\mathbb {R}^{1,3} \times \textit{SO}(1,3)\).
- 18.
- 19.
The factor \(\varOmega \) does not depend on \((t, {\varvec{x}}_3)\) because of the translational invariance on \((t, {\varvec{x}}_3)\). Incidentally, one can consider the metric of the form
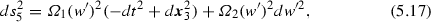
but the metric reduces to Eq. (5.18) by redefining \(w'\).
- 20.
The scaling dimension is also called the conformal weight or the conformal dimension .
- 21.
Here, \(F_{\mu \nu } := F_{\mu \nu }^a t^a\). We normalize the gauge group generators \(t^a\) by \(\text {tr}(t^a t^b) = \frac{1}{2} \delta ^{ab}\).
- 22.
We can set this without loss of generality. We can always bring the translation into this form by redefining the parameter \(L\).
- 23.
- 24.
The overall coefficient for \(\lambda = (L/l_s)^4\) depends on the normalization of gauge group generators \(t^a\). See, e.g., Sect. 13.4 of Ref. [13]. We use \(\text {tr}(t^a t^b) = \frac{1}{2} \delta ^{ab}\).
- 25.
We describe one simple way to include fundamental representations in Sect. 8.2.
- 26.
\({}^\blacklozenge \)To see the relation, we need to discuss the decoupling limit more carefully. Denote the typical scale of the gauge theory as \(l_{\text {obs}}\). One can ignore the string length scale \(l_s\) when

As \(l_{\text {obs}}\), let us take the “W-boson” mass scale. Here, the “W-boson” is the gauge boson which arises by breaking the gauge group \(SU(N_c) \rightarrow SU(N_c-1) \times U(1)\). This corresponds to separating a D-brane from \(N_c\) D-branes. The gauge boson corresponds to an open string, but the open string between the D-brane and \((N_c-1)\) D-branes is stretched, and the open string has a tension. So, the corresponding W-boson becomes massive. The mass is given by

[The tension of the open string is \(O(1/l_s^2)\)]. From Eqs. (5.65) and (5.66), one gets

This is the decoupling limit.
When \(g_s N_c \gg 1\), the \(r \ll l_s\) limit implies \(r \ll L\), which is the near-horizon limit.
References
S. Donnachie, H.G. Dosch, O. Nachtmann, P. Landshoff, Pomeron Physics and QCD (Cambridge University Press, Cambridge, 2002)
G.F. Chew, S.C. Frautschi, Regge trajectories and the principle of maximum strength for strong interactions. Phys. Rev. Lett. 8, 41 (1962)
J. Dai, R.G. Leigh, J. Polchinski, New connections between string theories. Mod. Phys. Lett. A 4, 2073 (1989)
J. Polchinski, Dirichlet Branes and Ramond-Ramond charges. Phys. Rev. Lett. 75, 4724 (1995). arXiv:hep-th/9510017
T. Sakai, S. Sugimoto, Low energy hadron physics in holographic QCD. Prog. Theor. Phys. 113, 843 (2005). arXiv:hep-th/0412141
D.Z. Freedman, A. Van Proeyen, Supergravity (Cambridge University Press, Cambridge, 2012)
J. Polchinski, Effective field theory and the Fermi surface. TASI1992. arXiv:hep-th/9210046
A.M. Polyakov, Quantum geometry of bosonic strings. Phys. Lett. B 103, 207 (1981)
M. Natsuume, Nonlinear sigma model for string solitons. Phys. Rev. D 48, 835 (1993). arXiv:hep-th/9206062
J. Polchinski, Scale and conformal invariance in quantum field theory. Nucl. Phys. B 303, 226 (1988)
S.S. Gubser, I.R. Klebanov, A.M. Polyakov, Gauge theory correlators from noncritical string theory. Phys. Lett. B428, 105 (1998). arXiv:hep-th/9802109
E. Witten, Anti-de Sitter space and holography. Adv. Theor. Math. Phys. 2, 253 (1998). arXiv:hep-th/9802150
E. Kiritsis, String Theory in a Nutshell (Princeton University Press, New York, 2007)
R.M. Wald, General Relativity (The University of Chicago Press, Chicago, 1984)
R. Baier, P. Romatschke, D.T. Son, A.O. Starinets, M.A. Stephanov, Relativistic viscous hydrodynamics, conformal invariance, and holography. JHEP 0804, 100 (2008). arXiv:0712.2451 [hep-th]
G.T. Horowitz, A. Strominger, Black strings and P-branes. Nucl. Phys. B 360, 197 (1991)
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Scale, Conformal, and Weyl Invariance \({}^\blacklozenge \)
In this appendix, we discuss three closely related symmetries, the scale invariance, the conformal invariance, and (local and global) Weyl invariances.
The scale transformation \(x^\mu \rightarrow a x^\mu \) implies \(ds^2 = \eta _{\mu \nu } dx^\mu dx^\nu \rightarrow a^2\eta _{\mu \nu } dx^\mu dx^\nu \). So, it is convenient to consider the scale transformation of the metric \(g_{\mu \nu } \rightarrow a^2 g_{\mu \nu }\), which is called the Weyl transformation.
The local Weyl invariance We start with the local Weyl transformation \(g_{\mu \nu } \rightarrow a(x)^2 g_{\mu \nu }\) which is strongest among the symmetries we discuss here. The Maxwell theory in the curved spacetime
is local Weyl invariant with \(A_\mu \rightarrow A_\mu \).
If a theory is local Weyl invariant under \(\delta g_{\mu \nu } = \varepsilon (x) g_{\mu \nu }\) or \(\delta g^{\mu \nu } = -\varepsilon (x) g^{\mu \nu }\),
In order for this to be true for any \(\varepsilon (x)\), the energy-momentum tensor must be traceless:
When \(g_{\mu \nu }=\eta _{\mu \nu }\), the local Weyl invariance reduces to the conformal invariance.
Note that \(A_\mu \rightarrow a^{-1} A_\mu \) under the scale transformation \(x^\mu \rightarrow a x^\mu \) whereas \(A_\mu \rightarrow A_\mu \) under the local Weyl transformation. Thus, the scaling dimension under the local Weyl transformation in general differs from the scaling dimension under the scale transformation and from the naive mass dimension. As a related issue, for the local Weyl transformation, one has to assign a scaling dimension to the metric since it transforms nontrivially. Then, for a tensor, the scaling dimension depends on index positions (i.e., either lower or upper). See, e.g., App. D of Ref. [14] and Ref. [15], for more details.
The global Weyl invariance The global Weyl invariance \(\delta g^{\mu \nu } = -\varepsilon g^{\mu \nu }\) requires
so the trace does not have to vanish but vanishes up to a total derivative. When \(g_{\mu \nu }=\eta _{\mu \nu }\),
for some \(K^\mu \). The global Weyl invariance reduces to the scale invariance in the flat spacetime.
The conformal invariance The conformal invariance is the flat spacetime limit of the local Weyl invariance \(\eta _{\mu \nu } \rightarrow a(x)^2 \eta _{\mu \nu }\). For a scale-invariant theory, \(T^\mu _{~\mu }\) vanishes up to a total derivative. A theorem states [10] that for a conformal invariant theory,
for some \(L^{\nu \mu }\) and that there exists an “improved” energy-momentum tensor \(\tilde{T}_{\mu \nu }\) which is traceless. (In the flat spacetime, the energy-momentum tensor is not unique. We discuss the related issue in the curved spacetime below.) For many four-dimensional relativistic field theories, there is no nontrivial candidate for \(K^\mu \) which is not a divergence. Then, the scale invariance implies the conformal invariance.
Scalar field example As another example, consider a scalar field:
When \(m=0\), the theory is scale invariant with \(\phi \rightarrow a^{-1}\phi \). The scalar field has scaling dimension 1. But when \(m\ne 0\), the theory is not scale invariant since we do not scale \(m\).
The energy-momentum tensor of the massless scalar field is given by
so \(T_{\mu \nu }\) is not traceless:
where we used the equation of motion \(\partial ^2\phi =0\) in the last equality. Comparing with Eq. (5.46), \(K^\mu = -\partial ^\mu \phi ^2/2\). However, \(K^\mu \) is a divergence, so the “improved” energy-momentum tensor \(\tilde{T}_{\mu \nu }\) exists:
which is traceless using the equation of motion. Then, the massless scalar theory is conformally invariant.
Now, consider the Weyl invariance. In the curved spacetime, a simple extension of the scalar theory (so-called “comma-goes-to-semicolon rule”) is
As one can see easily, the theory is global Weyl invariant with \(\phi \rightarrow a^{-1}\phi \). However, it is not local Weyl invariant. As a result, the energy-momentum tensor is not traceless as in Eq. (5.50).
However, given a flat spacetime action, the curved spacetime extension is not unique. In the flat spacetime, \(T_{\mu \nu }\) is not unique, and this is its curved-spacetime counterpart. There is a local Weyl invariant scalar theory:
where \(\xi =1/6\). The theory is local Weyl invariant with \(\phi \rightarrow a(x)^{-1}\phi \). The energy-momentum tensor is given by
One can show that it is traceless using the equation of motion. In the flat spacetime, Eq. (5.54) reduces to
which is the curved-spacetime counterpart of \(\tilde{T}_{\mu \nu }\) (5.51).
Appendix 2: D-brane and AdS/CFT \({}^\blacklozenge \)

It is not necessary for beginners to understand this appendix completely. It is enough to go back to this section after you get accustomed to AdS/CFT computations.
The D3-brane in Sect. 5.2.2 has two descriptions as
-
gauge theory,
-
black brane in supergravity.
As we see below, these two descriptions give the \(\mathcal{N}=4\) SYM and the AdS\(_5\) spacetime in appropriate limits.
5.1.1 D-brane and Gauge Theory
In order to know more about the gauge theory the D-brane describes, let us look at open string oscillations more carefully.
The open strings on a D-brane are bounded on the D-brane, so the D3-brane represents a four-dimensional gauge theory, but superstring theory actually requires 10-dimensional spacetime for consistency. Then, the open strings on the D-brane still oscillate in the full 10-dimensional spacetime. Thus, the simplest open string oscillations have 8 degrees of freedom instead of 2. What are these degrees of freedom? In other words, what kind of gauge theory the D3-brane represents?
To see this, note that there are two types of string oscillations. First are the oscillations in the brane and the other are the oscillations out of the brane. From the four-dimensional point of view [in terms of \(\textit{SO}(1,3)\) representations], the former represents a gauge field, and the latter represents scalars. The spatial dimension is 9 and the brane dimension is 3, so there are 6 scalar fields. Thus, the gauge theory represented by the D3-brane inevitably comes with scalar fields. In addition, there are fermions due to supersymmetry (which comes from the supersymmetry in superstring but we omit the details.) The Lorentz transformation properties are different, but they all come from similar string oscillations, which means that all these fields transform as the adjoint representation of \(SU(N_c)\). Namely, the theory has no fundamental representation such as quarks.Footnote 25 These properties coincide with the \(\mathcal{N}=4\) SYM.
The D-brane consideration provides us one more important information about the \(\mathcal{N}=4\) SYM. If we have only D3-branes, as in the present case, the directions transverse to the brane are all isotropic. These directions correspond to the scalar fields \(\phi _i\), so the isotropy means that there is a global \(\textit{SO}(6)\) symmetry for \(\phi _i\). Such a global symmetry is known as R-symmetry . Thus, combining with the conformal invariance \(\textit{SO}(2,4)\),

We get the \(\mathcal{N}=4\) SYM from the D-brane, but it is not yet clear if the D-brane is simply described by a gauge theory. This is because string theory is more than a gauge theory.
-
In particular, string theory contains graviton since string theory is the unified theory.
-
The simplest oscillations (harmonics) of an open string corresponds to a gauge theory as we saw before, but the string has higher harmonics which correspond to massive particles.
At this point, it is not clear if these effects can be ignored.
First, let us consider gravity. According to general relativity, any energy- momentum tensor curves spacetime. The D-brane has some energy, so how does the D-brane curve spacetime? Since gravity is described by the Newtonian potential
one can measure the effect of curvature by \(\textit{GM}\). However, this is the case for a point particle in three-dimensional space. We have to use the 10-dimensional Newton’s constant \(G_{10}\) instead of the four-dimensional Newton’s constant \(G_4\). Also, the brane has the spatial extension. So, we have to use the mass density of the brane, \(\mathsf {T}_3\), instead of \(M\). We also have to take into account that the number of the spatial dimensions transverse to the brane is six. Then,
According to string theory, the D-brane mass density is given by
Since \(G_{10} \simeq g_s^2 l_s^8\) from Eq. (5.10),
On the other hand, the effective coupling constant of the gauge theory is the ’t Hooft coupling constant \(\lambda := g_\text {YM}^2 N_c \simeq g_s N_c\). To summarize,
If one takes the limit \(l_s \rightarrow 0\) (decoupling limit), one can leave nontrivial dynamics of the gauge theory and at the same time one can ignore the effect of gravity.
Second, let us consider the massive particles. They have the mass \(M \simeq 1/l_s\). Thus, they also decouple from the theory in the limit \(l_s \rightarrow 0\).
In conclusions, what we get from the D3-brane is
(\(\mathcal{N}=4\) SYM)
+ (supergravity in the 10-dimensional flat spacetime)
5.1.2 D-brane and Curved Spacetime
The D3-brane describes the \(\mathcal{N}=4\) SYM in the flat spacetime. But this conclusion is not valid when \(g_s N_c \gg 1\) because the D-brane starts to curve the spacetime. Going back to the Newtonian potential argument, we essentially took the \(\textit{GM} \rightarrow 0\) limit in order to ignore the effect of gravity. But one cannot ignore gravity near the origin \(r\rightarrow 0\) even in this limit. As a consequence, a curved spacetime appears near the origin \(r^4 \ll g_s N_c l_s^4\) (Fig. 5.15).
In the \(g_s N_c \ll 1\) limit, the curved region is small. Then, one can consider that there exists a source represented by the D-brane in the flat spacetime. This is the case we considered in the above subsection. But a macroscopic curved spacetime appears in the \(g_s N_c \gg 1\) limit.
The supergravity description is appropriate in the \(g_s N_c \gg 1\) limit. The black D3-brane is given by [16]
where \({\varvec{x}}_3=(x,y,z)\) represents the directions of the spatial extension of the brane. The behavior of the factor \(Z\) comes from the Newtonian potential (5.59). We are interested in how the D-brane curves the spacetime near the origin. So, taking the limit \(r \ll L\) ( near-horizon limit ), one gets
The part \(L^2 d\varOmega _5^2\) represents \(S^5\) with radius \(L\). The remaining five-dimensional part is the AdS\(_5\) spacetime. This near-horizon limit corresponds to the decoupling limit from the gauge theory point of view.Footnote 26
Therefore, let us roughly divide the spacetime made by the D3-brane into AdS\(_5 \times S^5\) near the origin and the nearly flat spacetime around:
(supergravity on AdS\(_5 \times S^5\))
+ (supergravity in the 10-dimensional flat spacetime)
As we will see in Chap. 6, the AdS\(_5\) spacetime has the \(\textit{SO}(2,4)\) invariance. In addition, the full geometry (5.64) involves \(S^5\) which has the \(\textit{SO}(6)\) invariance. This is the same symmetry as the \(\mathcal{N}=4\) R-symmetry. Thus,

The gauge theory description fails when \(g_s N_c \gg 1\). On the other hand, the supergravity description fails when \(g_s N_c \ll 1\). This is because the curvature of the metric (5.64) behaves as
When \(g_s N_c \ll 1\), the curvature becomes large. The \(\alpha '\) -corrections become important, which can change the metric (5.64) in general. The metric such as Eq. (5.64) is trustable when \(g_s N_c \gg 1\).
We obtained two systems from the D3-brane, the \(\mathcal{N}=4\) SYM and supergravity on AdS\(_5 \times S^5\). These two theories are complementary to each other. Each theory has a region where analysis is relatively easy (shaded region), but they do not overlap. AdS/CFT claims that two systems are equivalent
5.1.3 Gauge Theory and Curved Spacetime
To summarize our discussion so far, we obtained two systems from the D3-brane, the \(\mathcal{N}=4\) SYM and supergravity on AdS\(_5 \times S^5\). We also obtained a common system which is decoupled from the rest, supergravity in the 10-dimensional flat spacetime, in both cases. Since this part is common, one can forget it. Then, the \(\mathcal{N}=4\) SYM corresponds to supergravity on AdS\(_5 \times S^5\).
These two descriptions of the brane, gauge theory and supergravity, are complementary to each other (Fig. 5.16). The former description is valid when \(g_s \ll 1\) and \(g_s N_c \ll 1\), whereas the latter description is valid when \(g_s \ll 1\) and \(g_s N_c \gg 1\).
However, in principle, both theories exist for all \(g_s\) and \(g_s N_c\). Taking Sect. 5.3 discussion into account, it is natural to imagine that both theories are equivalent for all \(g_s\) and \(g_s N_c\). If this is true, we can make computations using one theory even when the other theory is hard to compute.
We should stress that this is not a logical consequence. We obtained two systems from the D3-brane. But these two systems are two different limits of the brane. In order to justify the above claim, one has to compare results in both theories computed at the same \(g_s\) and \(g_s N_c\). There are many circumstantial evidences when one can rely on supersymmetry, but we will not discuss such evidences in this book. Rather, we go through computations related to actual applications, and we will see that gravity results can indeed be interpreted as physical quantities of gauge theories. We also compare the AdS/CFT results with experiments and with the other theoretical tools such as the lattice gauge theory in order to see that AdS/CFT is likely to be true.
5.1.4 What D-brane Tells Us
The D-brane taught us two things. First, the GKP-Witten relation (5.35) becomes more precise:
The left-hand side is the partition function of the \(\mathcal{N}=4\) SYM, and the right-hand side is the partition function of string theory on AdS\(_5 \times S^5\).
We mainly focused on the conformal invariance. But, in retrospect, we are able to identify the gauge theory because we take the \(\mathcal{N}=4\) R-symmetry into account. One would say that we added \(S^5\) on the gravity side to reflect the R-symmetry on the gauge theory side. Thus, when we try to find a gravity dual, it is in general important to take care of the symmetries both theories have.
Second, from the D-brane, we are able to obtain the AdS/CFT dictionary (5.39). This is possible by combining various expressions we encountered:
Eliminating \(g_s\) from these expressions give
Now, \(S^5\) corresponds to the R-symmetry from the point of view of the \(\mathcal{N}=4\) SYM and is an important part of the theory. But one often compactifies \(S^5\) and consider the resulting five-dimensional gravitational theory. The theory obtained in this way is called gauged supergravity .
The actual procedure of the \(S^5\) compactification is rather complicated, and the full gauged supergravity action is complicated as well. But in our case, we do not have to go through such a computation, and we can infer the action. The five-dimensional part is the AdS\(_5\) spacetime, so the five-dimensional action should be given by (5.34). Since \(S^5\) has radius \(L\), the compactification gives
Thus, the five-dimensional Newton’s constant is given by \(G_5 \simeq G_{10}/L^5\). Then, the AdS/CFT dictionary (5.73) can be rewritten by \(G_5\). If one works out numerical coefficients, the results are

Finite-temperature case The metric (5.62) is the zero-temperature solution of the D3-brane, or the extreme black hole solution, which corresponds to the \(\mathcal{N}=4\) SYM at zero temperature. In order to discuss the finite temperature gauge theory, we use the finite temperature solution of the D3-brane:
The horizon is located at \(r=r_0\). Again take the near-horizon limit \(r \ll L\). In order to remain outside the horizon \(r > r_0\) even in the near-horizon limit, take \(r_0 \ll L\). Then, the resulting geometry is
This is known as the Schwarzschild-AdS \(_5\) black hole (Chap. 7). When \(h=1\), the geometry reduces to the AdS\(_5\) spacetime. Also, the factor similar to \(h\) appeared in the higher-dimensional Schwarzschild black holes.
Rights and permissions
Copyright information
© 2015 Springer Japan
About this chapter
Cite this chapter
Natsuume, M. (2015). The Road to AdS/CFT. In: AdS/CFT Duality User Guide. Lecture Notes in Physics, vol 903. Springer, Tokyo. https://doi.org/10.1007/978-4-431-55441-7_5
Download citation
DOI: https://doi.org/10.1007/978-4-431-55441-7_5
Published:
Publisher Name: Springer, Tokyo
Print ISBN: 978-4-431-55440-0
Online ISBN: 978-4-431-55441-7
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)