Abstract
In the last chapter we discussed the shell structure of nuclei by assuming a simplified mean field such as the Wood–Saxon potential or the harmonic oscillator potential, which appears realistic. However, properly speaking, it is necessary to self-consistently determine the mean field and the whole nucleus as well as the individual states of nucleons inside the nucleus, because the mean field itself is determined based on the interaction between constituent nucleons. In this chapter we describe the basic ingredients of the Hartree–Fock theory, which is a representative of such self-consistent approaches, and of some related microscopic theories. It will not be an overstatement to say that the self-consistent calculations from microscopic points of view are at the center of current theoretical studies of nuclear structure. An important aspect in performing microscopic calculations such as the Hartree–Fock calculations is that the force between the constituent particles, i.e., the nuclear force, is not necessarily well established or involves some features which make the theoretical treatment difficult in contract to the systems which are objects of, e.g., condensed matter physics, where the interaction between the constituent particles is the well-known Coulomb interaction. The studies based on microscopic theories utilizes interdependence of theory and experiments. One analyzes experimental data with theories using the new nuclear force which looks more realistic. One then improves the nuclear force so as to incorporate the results of the analysis, then reconfirms thus obtained new theoretical predictions with experimental data.
This is a preview of subscription content, log in via an institution.
Buying options
Tax calculation will be finalised at checkout
Purchases are for personal use only
Learn about institutional subscriptionsNotes
- 1.
Such a medium made of nucleons which has uniform density and an infinite spatial extension is called nuclear matter.
- 2.
- 3.
Such potentials are often called well-behaved potentials.
- 4.
The study of equation of state using the simple perfect rigid sphere model shows that the saturation property is guaranteed by the repulsive core in the high density region higher than about six times the standard density \(\rho _0\sim 0.14\,\text {fm}^{-3}\) if one assumes the radius of the repulsive core to be 0.4 fm.
- 5.
This term is an effective interaction, which represents the many-body effects and the effect of repulsive core appearing in the G-matrix theory and has been introduced to avoid the collapse of nuclei, and should be distinguished from the genuine three-body force appearing in the discussion of nuclear force based on the meson theory as the force involving three nucleons [1]. The magnitude of the latter has been discussed through detailed calculations of the binding energy and the form factor of light nuclei such as the triton and \({}^3\)He using, e.g., the Faddeev equation.
- 6.
Instead of the Yukawa type, we assumed the Gauss type as a two-body central force to facilitate calculations.
- 7.
Here, we eliminate the center-of-mass motion and formulate only for the relative motion, and treat it as a one-body problem.
- 8.
Alternatively, the nuclear incompressibility is defined also by \(k\equiv -V\frac{\partial }{\partial V}P=\rho \frac{\partial P}{\partial \rho }\). The two nuclear incompressibilities are related as \(K=\frac{9k(\rho _0)}{\rho _0}\) if we denote the equilibrium density, which gives \(P(\rho _0)=0\), by \(\rho _0\).
- 9.
It is, however, not so easy to determine the incompressibility of nuclear matter to a good accuracy from the data of actual nuclei with finite sizes.
- 10.
It is known that the fragmentation reactions observed in medium energy nucleus–nucleus collisions also reflect the hard or soft property of the EOS [8].
- 11.
Nuclear reactions observed in the nucleus-nucleus collisions at medium energies of several tens MeV per nucleon, where the colliding nuclei dissociate into nucleons and fragments with various small mass numbers.
- 12.
The prescription which takes into account the finite range property of the nuclear force through the \(t_1\) and \(t_2\) terms following Skyrme would need to be reconsidered when we use \(\alpha \) smaller than 2/3 in discussing the saturation, since the last term on the right-hand side of Eq. (6.46) is proportional to \(\rho ^{5/3}\).
- 13.
The equation of state at high density is one of the crucial issues in the problems of the neutron stars and the supernova explosions. However, it is not precisely known yet. Concerning neutron stars, it has been reported that the pressure gets lower if one takes into account baryons other than protons and neutrons, that is, hyperons. This is natural, because for a given baryon density the degeneracy pressure must decrease if more different kinds of baryon exist. A problem is that the softening of the equation of state by the presence of hyperons contradicts the experimental observation of massive neutron stars with the mass as large as about two times the solar mass. This problem is often referred to as the hyperon puzzle or the hyperon crisis. Various possibilities such as the recovery of the stiffness of the equation of state at the high density side due to the repulsive effect of a three-body force working universally among all baryons [11] are now under investigation to resolve this puzzle and to establish a theory which is compatible with the data of both neutron stars and hypernuclei [12]. In this connection, we note that the density at deep inside of neutron stars is thought to be significantly higher than the normal nuclear density, although the actual value is not known and varies over a wide range between 4 and 8 times the normal nuclear density depending on the theoretical models.
- 14.
If one considers the nucleus as a Fermi gas, then the level density \(\rho _L\) exponentially increases with the excitation energy E and can be roughly given by \(\rho _L(E)\sim \exp (aE)^{1/2}\) (see [17] for details).
- 15.
Another attractive point of the relativistic treatment is that one can reproduce the saturation property of nuclei within the framework of the mean-field theory. Although it is different from the relativistic mean-field theory which we describe in this section, in the case of the Brueckner–Hartree–Fock calculations using the nuclear force obtained from the experimental data of the nucleon–nucleon scattering, the relativistic treatment can simultaneously reproduce the Fermi momentum and the binding energy per nucleon of the nuclear matter. On the other hand, if one uses non-relativistic theories, there exists a correlation between the Fermi momentum and the binding energy per nucleon, called the Coester line, and one cannot simultaneously reproduce both of them in the way to match with the mass formula irrespective of the nuclear force.
- 16.
The relativistic approach reproduces the experimental data of the polarization phenomena in the proton–nucleus scattering much better than the non-relativistic approach.
- 17.
The \(\pi \) mesons are not introduced, because one tries to establish the theory under the mean-field approximation as will be described later. Recently, the theory which explicitly includes the \(\pi \) mesons is also being developed (see, e.g., [19]).
- 18.
In this section, we use the natural units, where one sets \(\hbar =1,c=1\).
- 19.
\(\mu \) and \(\nu \) denote the four-dimensional time–space components (see Appendix A.10), while a the component in the isospin space.
- 20.
As Eq. (6.74) shows, the surface thickness of nuclei is intimately related to the nuclear incompressibility. The incompressibility K takes a large value of about 500 MeV if the non-linear terms are not introduced, and the surface properties of nuclei are not well reproduced. The value \(K\sim 500\) MeV is too large also in comparison with about 210 MeV, which is suggested from the experimental value of the excitation energy of the breathing mode.
- 21.
Note that the central force is governed by \(V+S\) in contrast to the \(\varvec{\ell }\cdot \mathbf {s}\) force (see Eq. (6.106)).
- 22.
The case of electrons in atoms corresponds to the case when there exists only the V term. Thanks to the S term, the sign of the spin–orbit potential for nucleons inside a nucleus becomes opposite to that for the electrons in atoms [25].
- 23.
Sharma [26] succeeded in explaining the kink phenomenon which the radii of Pb isotopes show when they cross the neutron magic number \(N=126\) by replacing the \(W_0\) term in Eq. (6.25) with \(\mathrm{i}W_0(1 + x_wP_\tau )( \varvec{\sigma }_{1} + \varvec{\sigma }_{2})\cdot \mathbf {k}_L \times \delta (\mathbf {r}_1-\mathbf {r}_2)\mathbf {k}_R\).
- 24.
In neutron stars, it is considered that neutrons in the outer region with low density called crust are in the \({}^1S_0\) superfluid state, the neutrons in more inner region with high density are in the \({}^3P_2\) superfluid state, and protons are in the \({}^1S_0\) superfluid state. Also, these superfluidities are considered to play important roles in the cooling and the phenomena called glitches of pulsars. See [29].
- 25.
Since \(\langle jjm-m|00\rangle =(-)^{j-m}/\sqrt{2j+1}\), \(S_+\) and \(S_-\) are the creation and annihilation operators, respectively, of the pair of nucleons whose total angular momentum couples to 0.
- 26.
For Eq. (6.123) and correspondingly also for Eq. (6.124), we determined the phase in the same way as that in Ref. [30]. In Ref. [17], the phase of Eq. (6.123) is taken to be \((-1)^{J+M}\). Correspondingly, the time-reversal operator is taken to be \(\hat{\mathscr {T}}= \mathrm{i}\sigma _y \hat{K}\).
- 27.
The quasi-spin method is advantageous in the sense that it has no fluctuation of the particle number, although it is difficult to be applied to general cases because of the restriction on the degeneracy of the energy levels.
- 28.
Equation (6.128) corresponds to the monopole pairing correlation approximation described in the previous section. In more advanced treatments the strength of the pairing correlation G depends on the states and is generalized to \(G_{kk'}\). As the result, the gap parameter becomes state dependent \(\varDelta _k\), and the gap equation is generalized to [34]
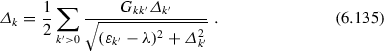
.
- 29.
The masses of nuclei have been taken from [35].
- 30.
There exist also empirical formulae which take into account the isospin dependence [36].
- 31.
References
G.E. Brown, Unified Theory of Nuclear Models and Forces (North-Holland, Amsterdam, 1967)
K. Sugimoto, M. Muraoka, Nuclear Physics, Japanese edn. (Kyouritsu, Tokyo, 1998)
D. Vautherin, D.M. Brink, Phys. Rev. C 5, 626 (1972)
J.P. Blaizot, Phys. Rep. 64, 171 (1980)
M. Beiner, H. Flocard, N. Van Giai, P. Quentin. Nucl. Phys. A 238, 29 (1975)
J. Bartel, P. Quentin, M. Brack, C. Guet, H.-B. Hakansson, Nucl. Phys. A 386, 79 (1982)
E. Chabanat, P. Bonche, P. Haensel, J. Meyer, R. Schaeffer, Nucl. Phys. A 627, 710 (1997); 635, 231 (1998)
A. Ono, H. Horiuchi, Prog. Part. Nucl. Phys. 53, 501 (2004)
H. Ichimura, Statistical Mechanics, Japanese edn. (Shoukabou, 1992)
R. Kubo, H. Ichimura, T. Usui, N. Hashitsume, Statistical Mechanics–An Advanced Course with Problems and Solutions (Elsevier, Amsterdam, 1990)
S. Nishizaki, Y. Yamamoto, T. Takatsuka, Prog. Theor. Phys. 105, 607 (2001); 108, 703 (2002); Y. Yamamoto, T. Furumoto, N. Yasutake, Th. A. Rijken. Phys. Rev. C 90, 045805 (2014)
T. Takatsuka, Genshikaku Kenkyu 57, Suppl. 3, 270 (2013); K. Masuda, T. Hatsuda, T. Takatsuka, Eur. Phys. J. A 52, 65 (2016); I. Vidana. J. Phys. Conf. Ser. 668, 012031 (2016)
P.J. Siemens, A.S. Jensen, Elements of Nuclei: Many-Body Physics with the Strong Interaction (Addison and Wesley, California, 1987)
T. Furuta, A. Ono, Phys. Rev. C 74, 014612 (2006); 79, 014608 (2009)
T.H.R. Skyrme, Philos. Mag. 1, 1043 (1956); Proc. Phys. Soc. (Lond.) A 70, 433 (1957); Nucl. Phys. 9, 615 (1958)
J.P. Jeukenne, A. Lejeune, C. Mahaux, Phys. Rep. 25, 83 (1976); C. Mahaux, P. F. Bortignon, R.A. Broglia, C.H. Dasso. Phys. Rep. 120, 1 (1985)
Aage Bohr, Ben R. Mottelson, Nuclear Structure, vol. I (Benjamin, New York, 1969)
S. Shlomo, J.B. Natowitz, Phys. Lett. B 252, 187 (1990)
H. Toki, S. Sugimoto, K. Ikeda, Prog. Theor. Phys. 108, 903 (2002)
B.D. Serot, J.D. Walecka, Adv. Nucl. Phys. 16, 1 (1986)
P. Ring, Y. K. Gambhir, G. A. Lalazissis, Comp. Phys. Commun. 105, 77 (1997); Y.K. Gambhir, P. Ring, A. Thimet, Ann. Phys. (N.Y.) 198, 132 (1990)
W. Greiner, Relativistic Quantum Mechanics (Springer, Berlin, 2000)
J. Meng, Nucl. Phys. A 635, 3 (1998)
J.D. Bjorken, S.D. Drell, Relativistic Quantum Mechanics (McGraw-Hill, New York, 1964)
H. Kurasawa, Butsuri 49, 628 (1994); J.V. Noble. Nucl. Phys. A 329, 354 (1979)
M.M. Sharma, G. Lalazissis, J. König, P. Ring, Phys. Rev. Lett. 74, 3744 (1995)
T. Tsuneto, Superconductivity and Superfluidity (Iwanami Modern Physics 17, Japanese edition) (Iwanami, Tokyo, 1993)
D.M. Brink, R.A. Broglia, Nuclear Superfluidity-Pairing in Finite Systems (Cambridge University Press, Cambridge, 2005)
R. Tamagaki, High density nuclear matter (Frontiers of Physics 15, Japanese edition) (Kyouritsu, 1986); Prog. Theor. Phys. 44, 905 (1970)
W. Greiner, J.A. Maruhn, Nuclear Models (Springer, Berlin, 1995)
K. Dietrich, H.J. Mang, J.H. Pradal, Phys. Rev. 135, B22 (1964)
H.J. Lipkin, Ann. Phys. (N.Y.) 9, 272 (1960); 12, 452 (1961)
Y. Nogami, Phys. Rev. 134, B313 (1964)
P. Ring, P. Schuck, The Nuclear Many-Body Problem (Springer, Berlin, 1980)
G. Audi, A.H. Wapstra, C. Thibault, Nucl. Phys. A 729, 337 (2003)
D.G. Madland, J.R. Nix, Nucl. Phys. A 476, 1 (1988)
H. Koura, private communication
S.G. Nilsson, O. Prior, Mat. Fys. Medd. Dan. Vid. Selsk. 32, 16 (1961)
S.G. Nilsson, I. Ragnarsson, Shapes and Shells in Nuclear Structure (Cambridge University Press, Cambridge, 1995)
A. Bulgac, Y. Yu, Phys. Rev. Lett. 88, 042504 (2002)
M. Matsuo, Phys. Rev. C 73, 044309 (2006)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Copyright information
© 2017 Springer Japan
About this chapter
Cite this chapter
Takigawa, N., Washiyama, K. (2017). Microscopic Mean-Field Theory (Hartree–Fock Theory). In: Fundamentals of Nuclear Physics. Springer, Tokyo. https://doi.org/10.1007/978-4-431-55378-6_6
Download citation
DOI: https://doi.org/10.1007/978-4-431-55378-6_6
Published:
Publisher Name: Springer, Tokyo
Print ISBN: 978-4-431-55377-9
Online ISBN: 978-4-431-55378-6
eBook Packages: Physics and AstronomyPhysics and Astronomy (R0)