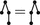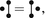Skip to main content
SpringerLink
Log in

Renormalization and Mellin Transforms

  • Chapter
  • First Online:
Computer Algebra in Quantum Field Theory

Part of the book series: Texts & Monographs in Symbolic Computation ((TEXTSMONOGR))

Abstract

We study renormalization in a kinetic scheme (realized by subtraction at fixed external parameters as implemented in the BPHZ and MOM schemes) using the Hopf algebraic framework, first summarizing and recovering known results in this setting. Then we give a direct combinatorial description of renormalized amplitudes in terms of Mellin transform coefficients, featuring the universal property of rooted trees H R . In particular, a special class of automorphisms of H R emerges from the action of changing Mellin transforms on the Hochschild cohomology of perturbation series. Furthermore, we show how the Hopf algebra of polynomials carries a refined renormalization group property, implying its coarser form on the level of correlation functions. Application to scalar quantum field theory reveals the scaling behaviour of individual Feynman graphs.

This is a preview of subscription content, log in via an institution to check access.

Access this chapter

Log in via an institution
Chapter
USD 29.95
Price excludes VAT (USA)
  • Available as PDF
  • Read on any device
  • Instant download
  • Own it forever
eBook
USD 84.99
Price excludes VAT (USA)
  • Available as EPUB and PDF
  • Read on any device
  • Instant download
  • Own it forever
Softcover Book
USD 109.99
Price excludes VAT (USA)
  • Compact, lightweight edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info
Hardcover Book
USD 109.99
Price excludes VAT (USA)
  • Durable hardcover edition
  • Dispatched in 3 to 5 business days
  • Free shipping worldwide - see info

Tax calculation will be finalised at checkout

Purchases are for personal use only

Institutional subscriptions

Notes

  1. 1.

    We consider unordered trees

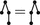
    and forests

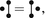
    sometimes called non-planar.

  2. 2.

    By wv we denote the subtree of w rooted at the node v ∈ V (w).

  3. 3.

    Even if the divergence of a Feynman graph does depend on external momenta as happens for higher degrees of divergence, the Hopf algebra is defined such that the counterterms are evaluations on certain external structures, given by distributions in [9]. So in any case, ϕ − maps to scalars.

  4. 4.

    This already implies Ï• to be a morphism of Hopf algebras.

  5. 5.

    This combinatorial relation among tree factorials, noted in [17], thus drops out of \({\varDelta }^{}\varphi = {(}^{}\varphi {\otimes }^{}\varphi )\circ \varDelta\).

  6. 6.

    As x0 =1, for arbitrary p the series \({\left [X(g)\right ]}^{p} \mathop{:}=\sum _{n\in \mathbb{N}_{0}}\binom{p}{n}{\left [X(g) -1\!\!1\right ]}^{n} \in H_{R}[[g]]\) is well defined.

  7. 7.

    A proof of (30) may be found in[11] and [12, 13] study systems of Dyson-Schwinger equations.

  8. 8.

    Counting the number of corresponding ordered trees.

  9. 9.

    For this generality we need decorated rooted trees as commented on in Sect. 6.1

  10. 10.

    We prefer to work in the parametric representation as introduced in [14, Sect. 6-2-3].

  11. 11.

    This simple form circumvents the decomposition into one-scale graphs utilized in [6] and therefore holds in the original renormalization Hopf algebra H.

References

  1. Bergbauer, C., Kreimer, D.: Hopf algebras in renormalization theory: locality and Dyson-Schwinger equations from Hochschild cohomology. IRMA Lect. Math. Theor. Phys. 10, 133–164 (2006)

    MathSciNet  Google Scholar 

  2. Bierenbaum, I., Kreimer, D., Weinzierl, S.: The next-to-ladder approximation for Dyson-Schwinger equations. Phys. Lett. B646, 129–133 (2007). doi:10.1016/j.physletb.2007.01.018

    Article  ADS  Google Scholar 

  3. Bloch, S., Kreimer, D.: Mixed Hodge structures and renormalization in physics. Commun. Number Theory Phys. 2, 637–718 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  4. Broadhurst, D.J., Kreimer, D.: Renormalization automated by Hopf algebra. J. Symb. Comput. 27, 581 (1999). doi:10.1006/jsco.1999.0283

    Article  MathSciNet  MATH  Google Scholar 

  5. Broadhurst, D.J., Kreimer, D.: Exact solutions of Dyson-Schwinger equations for iterated one-loop integrals and propagator-coupling duality. Nucl. Phys. B600, 403–422 (2001). doi:10.1016/S0550-3213(01)00071-2

    Article  ADS  Google Scholar 

  6. Brown, F., Kreimer, D.: Angles, scales and parametric renormalization. Lett. Math. Phys. 103(9), 933–1007 (2013)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  7. Collins, J.C.: Renormalization. Cambridge Monographs on Mathematical Physics. Cambridge University Press, Cambridge/New York (1984)

    Book  MATH  Google Scholar 

  8. Connes, A., Kreimer, D.: Hopf algebras, renormalization and noncommutative geometry. Commun. Math. Phys. 199, 203–242 (1998). doi:10.1007/s002200050499

    Article  MathSciNet  ADS  MATH  Google Scholar 

  9. Connes, A., Kreimer, D.: Renormalization in quantum field theory and the Riemann-Hilbert problem I: the Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 210, 249–273 (2000). doi:10.1007/s002200050779

    Article  MathSciNet  ADS  MATH  Google Scholar 

  10. Connes, A., Kreimer, D.: Renormalization in quantum field theory and the Riemann-Hilbert problem II: the β-function, diffeomorphisms and the renormalization group. Commun. Math. Phys. 216, 215–241 (2001). doi:10.1007/PL00005547

    Article  MathSciNet  ADS  MATH  Google Scholar 

  11. Foissy, L.: Faà di Bruno subalgebras of the Hopf algebra of planar trees from combinatorial Dyson-Schwinger equations. Adv. Math. 218(1), 136–162 (2008). doi:10.1016/j.aim.2007.12.003. http://www.sciencedirect.com/science/article/pii/S0001870807003301

  12. Foissy, L.: Classification of systems of Dyson-Schwinger equations in the Hopf algebra of decorated rooted trees. Adv. Math. 224(5), 2094–2150 (2010). doi:10.1016/j.aim.2010.01.024. http://www.sciencedirect.com/science/article/pii/S0001870810000435

  13. Foissy, L.: General Dyson-Schwinger equations and systems. ArXiv e-prints (2011)

    Google Scholar 

  14. Itzykson, C., Zuber, J.B.: Quantum Field Theory. Dover, New York (2005)

    Google Scholar 

  15. Kontsevich, M., Zagier, D.: Periods. In: Mathematics Unlimited – 2001 and Beyond. Springer, Berlin (2001)

    Google Scholar 

  16. Kreimer, D.: On the Hopf algebra structure of perturbative quantum field theories. Adv. Theor. Math. Phys. 2, 303–334 (1997)

    MathSciNet  Google Scholar 

  17. Kreimer, D.: Chen’s iterated integral represents the operator product expansion. Adv. Theor. Math. Phys. 3, 3 (2000)

    MathSciNet  Google Scholar 

  18. Kreimer, D.: Factorization in quantum field theory: an exercise in hopf algebras and local singularities. In: Cartier, P., Moussa, P., Julia, B., Vanhove, P. (eds.) On Conformal Field Theories, Discrete Groups and Renormalization, Frontiers in Number Theory, Physics, and Geometry, vol. 2, pp. 715–736. Springer, Berlin/Heidelberg (2007). http://dx.doi.org/10.1007/978-3-540-30308-4_14

  19. Kreimer, D.: Étude for linear Dyson-Schwinger equations. In: Albeverio, S., Marcolli, M., Paycha, S., Plazas, J. (eds.) Traces in Number Theory, Geometry and Quantum Fields. Aspects of Mathematics E, vol. 38, pp. 155–160. Vieweg, Wiesbaden (2008). http://preprints.ihes.fr/2006/P/P-06-23.pdf

  20. Kreimer, D., Yeats, K.: An étude in non-linear Dyson-Schwinger equations. Nucl. Phys. Proc. Suppl. 160, 116–121 (2006). doi:10.1016/ j.nuclphysbps.2006.09.036. Proceedings of the 8th DESY workshop on elementary particle theory

    Google Scholar 

  21. Manchon, D.: Hopf Algebras in Renormalisation. pp. 365–427. Elsevier/North-Holland (2008). doi:10.1016/S1570-7954(07)05007-3. http://www.sciencedirect.com/science/article/pii/S1570795407050073

  22. Panzer, E.: Hopf-algebraic renormalization of kreimer’s toy model. Master’s thesis, Humboldt-Universität zu Berlin (2011)

    Google Scholar 

  23. Schnetz, O.: Quantum periods: a census of ϕ 4-transcendentals. Commun. Number Theory Phys. 4, 1–48 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  24. Yeats, K.A.: Rearranging Dyson-Schwinger equations. Mem. Am. Math. Soc. 211(995), 1–82 (2011)

    MathSciNet  Google Scholar 

Download references

Acknowledgements

Alexander von Humboldt Chair in Mathematical Physics, supported by the Alexander von Humboldt Foundation and the BMBF.

Author information

Authors and Affiliations

  1. Departments of Mathematics and Physics, Humboldt University, Unter den Linden 6, 10099, Berlin, Germany

    Dirk Kreimer & Erik Panzer

Authors
  1. Dirk Kreimer
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Erik Panzer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Dirk Kreimer .

Editor information

Editors and Affiliations

  1. RISC, Johannes Kepler University, Linz, Austria

    Carsten Schneider

  2. DESY, Zeuthen, Germany

    Johannes Blümlein

Rights and permissions

Reprints and permissions

Copyright information

© 2013 Springer-Verlag Wien

About this chapter

Cite this chapter

Kreimer, D., Panzer, E. (2013). Renormalization and Mellin Transforms. In: Schneider, C., Blümlein, J. (eds) Computer Algebra in Quantum Field Theory. Texts & Monographs in Symbolic Computation. Springer, Vienna. https://doi.org/10.1007/978-3-7091-1616-6_8

Download citation

  • DOI: https://doi.org/10.1007/978-3-7091-1616-6_8

  • Published:

  • Publisher Name: Springer, Vienna

  • Print ISBN: 978-3-7091-1615-9

  • Online ISBN: 978-3-7091-1616-6

  • eBook Packages: Computer ScienceComputer Science (R0)

Publish with us

Policies and ethics

Search

Navigation