Abstract
We introduce new algebraic and topological semantics for inquisitive logic. The algebraic semantics is based on special Heyting algebras, which we call inquisitive algebras, with propositional valuations ranging over only the \(\lnot \lnot \)-fixpoints of the algebra. We show how inquisitive algebras arise from Boolean algebras: for a given Boolean algebra B, we define its inquisitive extension H(B) and prove that H(B) is the unique inquisitive algebra having B as its algebra of \(\lnot \lnot \)-fixpoints. We also show that inquisitive algebras determine Medvedev’s logic of finite problems. In addition to the algebraic characterization of H(B), we give a topological characterization of H(B) in terms of the recently introduced choice-free duality for Boolean algebras using so-called upper Vietoris spaces (UV-spaces) [2]. In particular, while a Boolean algebra B is realized as the Boolean algebra of compact regular open elements of a UV-space dual to B, we show that H(B) is realized as the algebra of compact open elements of this space. This connection yields a new topological semantics for inquisitive logic.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Change history
23 June 2019
In the original version of the chapter titled “Algebraic and Topological Semantics for Inquisitive Logic via Choice-Free Duality”, the acknowledgement was missing. It has been added.
Notes
- 1.
Here we consider the standard extension of valuations over atomic propositions to arbitrary propositional formulas.
- 2.
Under the intuitionistic semantics, we
 as the intuitionistic disjunction.
as the intuitionistic disjunction. - 3.
Notice that Theorem 4.9 ensures that
 .
. - 4.
Here we are adopting the convention
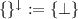 , so that
, so that  .
.
References
Bezhanishvili, G., Holliday, W.H.: Inquisitive intuitionistic logic. Manuscript (2019)
Bezhanishvili, N., Holliday, W.H.: Choice-free Stone duality. J. Symb. Log. (Forthcoming)
Chagrov, A., Zakharyaschev, M.: Modal logic. In: Oxford Logic Guides, vol. 35. The Clarendon Press, New York (1997)
Ciardelli, I.: Inquisitive semantics and intermediate logics. MSc thesis, University of Amsterdam (2009)
Ciardelli, I.: Questions in logic. Ph.D. thesis, Institute for Logic, Language and Computation, University of Amsterdam (2016)
Ciardelli, I., Groenendijk, J., Roelofsen, F.: Inquisitive semantics: a new notion of meaning. Lang. Linguist. Compass 7(9), 459–476 (2013)
Ciardelli, I., Groenendijk, J., Roelofsen, F.: Inquisitive Semantics. Oxford University Press, Oxford (2018)
Frittella, S., Greco, G., Palmigiano, A., Yang, F.: A multi-type calculus for inquisitive logic. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 215–233. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_14
Johnstone, P.T.: Stone spaces. In: Cambridge Studies in Advanced Mathematics, vol. 3. Cambridge University Press, Cambridge (1982)
Medvedev, Y.T.: Interpretation of logical formulas by means of finite problems. Sov. Math. Dokl. 7(4), 857–860 (1966)
Acknowledgment
This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement No 680220).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Examples 1 and 2
Proof of (3)
Given a complete Boolean algebra B, we show that \(\mathrm {Dw}_p(B) = (\mathrm {Dw}_0(B))_{\lnot \lnot }\). First, if we consider a principal downset, we have

So \(\mathrm {Dw}_p(B) \subseteq (\mathrm {Dw}_0(B))_{\lnot \lnot }\). For the other inclusion, it suffices to show that \(\lnot D\) is principal for every downset D. We have

On the other hand, \(\bigvee \lnot D \in \lnot D\), since for every \(e \in D\), we have

It follows that \(\lnot D = \left\{ \bigvee \lnot D\right\} ^{\downarrow }\). Thus, \(\lnot D\) is principal.
Proof of (4)
Given a Boolean algebra B, we show that \(\mathrm {Dw}_p(B) = (\mathrm {Dw}_{fg}(B))_{\lnot \lnot }\). The inclusion \(\mathrm {Dw}_p(B) \subseteq (\mathrm {Dw}_{fg}(B))_{\lnot \lnot }\) is proved as above. For the other inclusion it suffices to show that for any \(b_1,\dots ,b_n \in B\), \(\lnot \{b_1,\dots ,b_n\}^{\downarrow }\) is principal. This follows from the equalities

B Proof of Proposition 4.2
We divide the proof in two steps: proving that every element \(x\in H(B)\) can be written in the form  with \(b_1,\dots ,b_m \in B\); and proving that from this form we can obtain a non-redundant representation.
with \(b_1,\dots ,b_m \in B\); and proving that from this form we can obtain a non-redundant representation.
For the first part: since H(B) is the quotient of the set \(\mathcal {T}\) of terms, we can proceed by induction on \(t\in \mathcal {T}\).
-
If \(x\in B\), then we are done.
-
If \(x = y \wedge z\), then consider two representations
 and
and  . Then
. Then 
-
If
 , then
, then 
-
If \(x = y \rightarrow z\), then

For the second part: let  be an arbitrary representation of x. If \(\forall i,j.\; b_i \not \le b_j\), then we are done. Otherwise, suppose (without loss of generality) that \(b_1 \le b_2\). Then
be an arbitrary representation of x. If \(\forall i,j.\; b_i \not \le b_j\), then we are done. Otherwise, suppose (without loss of generality) that \(b_1 \le b_2\). Then

Repeating this procedure, we obtain a non-redundant representation of x.
C Proof of Theorem 4.6
It only remained to prove that h is injective. Let \(x,y \in H(B)\) and suppose that \(h(x) = h(y)\). Let  and
and  be their non-redundant representations. Then where \(\sqcap ,\sqcup ,\Rightarrow \) are the operations of H, we have
be their non-redundant representations. Then where \(\sqcap ,\sqcup ,\Rightarrow \) are the operations of H, we have
So h is injective and thus an isomorphism, as required.
D Proof of Theorem 4.9
To prove Theorem 4.9, we will use the following lemma.
Lemma D.1
Let \(A = \bigcup _{i\in I} U_i\) and \(B = \bigcup _{j\in J} V_j\) be open sets of a UV-space X, where \(U_i, V_j\) are \(\mathsf {CO}\mathcal {RO}\)-sets. Then \(A \subseteq B\) iff \(\forall i \in I.\; \exists j\in J.\; U_i \subseteq V_j\).
Proof
Firstly, we show that every \(\mathsf {CO}\mathcal {RO}\)-set U is the upset of a singleton: since \(\{U\}^{\uparrow }\) is a filter in \(\mathsf {CO}\mathcal {RO}(X)\), there exists a point x such that \(\{U\}^{\uparrow } = \mathsf {CO}\mathcal {RO}(X)\). It follows that \(U = \bigcap \mathsf {CO}\mathcal {RO}(x) = \{x\}^{\uparrow }\).
We can use this to prove the result. Call \(x_i\) the generator of \(U_i\) for each \(i\in I\).

We are now ready to prove Theorem 4.9.
Proof of Theorem 4.9.
For the first part: consider the map \(f: O(X) \rightarrow \mathrm {Dw}_0(B)\) defined byFootnote 4
To show that f is well defined and order preserving and reflecting, we observe the following equivalences, using Lemma D.1 for the first:
Thus, f is also injective. Notice that surjectivity is trivially satisfied. Hence f is an isomorphism.
For the second part: since elements of \(\mathsf {CO}(X)\) are exactly the sets of the form \(\widehat{a_1} \cup \dots \cup \widehat{a_n}\) for some \(a_1,\dots , a_n\in B\), we obtain that \(f|_{\mathsf {CO}(X)}\) is an isomorphism with range \(\mathrm {Dw}_{fg}(B)\), as required.
E Proof of Proposition 4.10
It is immediate that r is well defined and order preserving. For injectivity, notice that a prime filter \(\mathfrak {p}\) of H(B) is completely determined by the elements of B it contains, since for every non-redundant representation  , we have
, we have

Using this fact, we can also show surjectivity: let F be a filter of B and define \(\mathfrak {p}_F\) as the smallest set including F and respecting (5). Then clearly \(\mathfrak {p}_F\) is an upset and respects the  of prime filters. Moreover, it is closed under meets, since
of prime filters. Moreover, it is closed under meets, since

Since \(r(\mathfrak {p}_F) = F\), we also have surjectivity.
F Proof of Lemma 5.2
To prove Lemma 5.2, we first need to establish some technical results. In the following we denote \(X \setminus A\) by \(\overline{A}\). For a UV space X and \(x,y\in X\), let \(x\sqcap y\) be the greatest lower bound of x and y in the specialization order of X [2, Corollary 5.4].
Lemma F.1
Let \(U \in \mathsf {CO}\mathcal {RO}(X)\) and \(x_1,x_2 \in U\). Then \(x_1 \sqcap x_2 \in U\).
Proof
By Corollary 5.4 of [2], \(U = U \vee U = U \cup \left\{ x\sqcap y \mid x,y \in U \right\} \).
Lemma F.2
Given \(U,V \in \mathsf {CO}\mathcal {RO}(X)\), \(\mathtt {Int}_\le \left( \overline{U} \cup V \right) = \lnot U \vee V\).
Proof
Left-to-right inclusion. Consider an element \(x \in \mathtt {Int}_\le \left( \overline{U} \cup V \right) \). If \(x \in \lnot U \cup V\), then there is nothing to prove; so suppose this is not the case. By Corollary 5.4 of [2], there is a decomposition \(x = x_1 \sqcap x_2\) such that \(x_1 \in \lnot U\) and \(x_2 \in U\).
Since \(x_2\notin \overline{U}\) and \(x_2 \ge x \in \mathtt {Int}_\le \left( \overline{U} \cup V \right) \), it follows that \(x_2 \in V\). So \(x \in \{ y\sqcap z \mid y\in \lnot U, z\in V\} \subseteq \lnot U \vee V\), as desired.
Right-to-left inclusion. Consider \(x \in \lnot U \vee V\) and take an arbitrary \(w \ge x\). We want to show that \(w \in \overline{U} \cup V\).
If \(w \in \lnot U \cup V \subseteq \overline{U} \cup V\), then there is nothing to prove; so suppose this is not the case. By Corollary 5.4 of [2], we can write \(w = w_1 \sqcap w_2\) with \(w_1 \in \lnot U\) and \(w_2 \in V\). In particular, \(w_1\) is a successor of w not in U, and since \(\overline{U}\) is a \(\le \)-downset, it follows that \( w \in \overline{U} \subseteq \overline{U} \cup V\).
Since w was an arbitrary successor of x, it follows \(x\in \mathtt {Int}_\le \left( \overline{U} \cup V \right) \).
Lemma F.3
Given \(U_i, V_j \in \mathsf {CO}\mathcal {RO}(X)\), the following identity holds:
Proof
By Lemma F.2, the identity is equivalent to
Let L and R be the left-hand side and right-hand side, respectively.
Right-to-left inclusion. Consider \(x \in R\). This means that:
So with fixed f as above, given \(y\ge x\), we have:
As y was an arbitrary successor of x, it follows that \(x \in L\).
Left-to-right inclusion. We will show this step by contradiction. Suppose that \(x \notin R\). This means that:
or equivalently
Fix an index k instantiating the first quantifier, and consider for each \(j \in [n]\) an element \(y_j \in \{x\}^{\uparrow } \cap U_k \cap \overline{V}_{j}\). Define \(y = y_1 \sqcap \dots \sqcap y_n\). We have:
-
For every \( j\in [n]\), \(y_j \ge x\), and thus \(y \ge x\).
-
Since \(y_j \in \overline{V}_j\) and \(V_j\) is open, it follows that \(\mathtt {Cl}(\{y_j\}) \subseteq \overline{V}_j\); and consequently \(y \in \overline{V}_j\), since \(y \le y_j\).
-
Since \(y_1, \dots , y_n \in U_k\), we have \(y \in U_k\) (see Lemma F.1).
So it follows that \(y \ge x\) and \(y \in U_k \cap \overline{V_1} \cap \dots \cap \overline{V_n}\). Thus in particular
\(y \notin \left( \bigcap _{i=1}^m \overline{U}_i \right) \cup \left( \bigcup _{j=1}^n V_j \right) \), from which we obtain \(x\notin L\), as desired.
We are now able to prove Lemma 5.2.
Proof
(Proof of Lemma 5.2). By Lemma F.3, \(\mathtt {Int}_\le ( \overline{A} \cup B ) \in \mathsf {CO}(X)\). Since the order topology is finer than the main topology, we have
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Bezhanishvili, N., Grilletti, G., Holliday, W.H. (2019). Algebraic and Topological Semantics for Inquisitive Logic via Choice-Free Duality. In: Iemhoff, R., Moortgat, M., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2019. Lecture Notes in Computer Science(), vol 11541. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-59533-6_3
Download citation
DOI: https://doi.org/10.1007/978-3-662-59533-6_3
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-59532-9
Online ISBN: 978-3-662-59533-6
eBook Packages: Computer ScienceComputer Science (R0)


 as the intuitionistic disjunction.
as the intuitionistic disjunction. .
.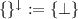 , so that
, so that  .
. and
and  . Then
. Then 
 , then
, then 
