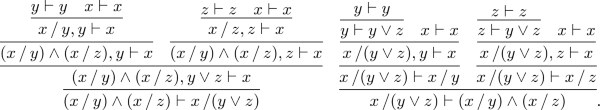Abstract
Language and relational models, or L-models and R-models, are two natural classes of models for the Lambek calculus. Completeness w.r.t. L-models was proved by Pentus and completeness w.r.t. R-models by Andréka and Mikulás. It is well known that adding both additive conjunction and disjunction together yields incompleteness, because of the distributive law. The product-free Lambek calculus enriched with conjunction only, however, is complete w.r.t. L-models (Buszkowski) as well as R-models (Andréka and Mikulás). The situation with disjunction turns out to be the opposite: we prove that the product-free Lambek calculus enriched with disjunction only is incomplete w.r.t. L-models as well as R-models. If the empty premises are allowed, the product-free Lambek calculus enriched with conjunction only is still complete w.r.t. L-models but in which the empty word is allowed. Both versions are decidable (PSPACE-complete in fact). Adding the multiplicative unit to represent explicitly the empty word within the L-model paradigm changes the situation in a completely unexpected way. Namely, we prove undecidability for any L-sound extension of the Lambek calculus with conjunction and with the unit, whenever this extension includes certain L-sound rules for the multiplicative unit, to express the natural algebraic properties of the empty word. Moreover, we obtain undecidability for a small fragment with only one implication, conjunction, and the unit, obeying these natural rules. This proof proceeds by the encoding of two-counter Minsky machines.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The derivations establishing equivalence are as follows:
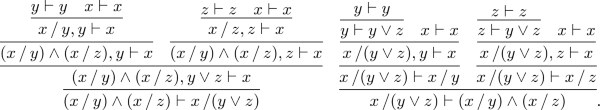
- 2.
Due to Lambek’s restriction, \(\varPhi \) should be non-empty, i.e., \(m > 0\).
References
Abrusci, V.M.: A comparison between Lambek syntactic calculus and intuitionistic linear logic. Zeitschr. math. Logik Grundl. Math. (Math. Logic Q.) 36, 11–15 (1990)
Andréka, H., Mikulás, Sz.: Lambek calculus and its relational semantics: completeness and incompleteness. J. Log. Lang. Inform. 3(1), 1–37 (1994)
Buszkowski, W.: Compatibility of a categorial grammar with an associated category system. Zeitschr. math. Log. Grundl. Math. 28, 229–238 (1982)
Buszkowski, W.: On the complexity of the equational theory of relational action algebras. In: Schmidt, R.A. (ed.) RelMiCS 2006. LNCS, vol. 4136, pp. 106–119. Springer, Heidelberg (2006). https://doi.org/10.1007/11828563_7
Galatos, N., Jipsen, P., Kowalski, T., Ono, H.: Residuated lattices. An algebraic Glimpse at Substructural Logics. Elsevier, Amsterdam (2007)
Girard, J.-Y.: Linear logic. Theor. Comput. Sci. 50(1), 1–101 (1987)
Jipsen, P., Tsinakis, C.: A survey of residuated lattices. In: Martinez, J. (ed.) Ordered Algebraic Structures, pp. 19–56. Kluwer Academic Publishers, Dordrecht (2002)
Jipsen, P.: From semirings to residuated Kleene lattices. Stud. Logica 76(2), 291–303 (2004)
Kanovich, M.: The direct simulation of Minsky machines in linear logic. In: Girard, J.-Y., Lafont, Y., Regnier, L. (eds.) Advances in Linear Logic, London Mathematical Society Lecture Notes, vol. 222, pp. 123–145. Cambridge University Press, Cambridge (1995)
Kanovich, M., Kuznetsov, S., Nigam, V., Scedrov, A.: Subexponentials in non-commutative linear logic. Math. Struct. Comput. Sci. (2018). https://doi.org/10.1017/S0960129518000117. FirstView
Kanovich, M., Kuznetsov, S., Scedrov, A.: The complexity of multiplicative-additive Lambek calculus: 25 years later. In: Iemhoff, R. et al. (eds.) WoLLIC 2019. LNCS, vol. 11541, pp. 356–372, Springer, Heidelberg (2019)
Kuznetsov, S.L.: Trivalent logics arising from L-models for the Lambek calculus with constants. J. Appl. Non-Class. Log. 4(1–2), 132–137 (2014)
Lafont, Y.: The undecidability of second order linear logic without exponentials. J. Symb. Log. 61(2), 541–548 (1996)
Lafont, Y., Scedrov, A.: The undecidability of second order multiplicative linear logic. Inf. Comput. 125(1), 46–51 (1996)
Lambek, J.: The mathematics of sentence structure. Amer. Math. Monthly 65, 154–170 (1958)
Lambek, J.: Deductive systems and categories II: standard constructions and closed categories. In: Hilton, P. (ed.) Category Theory, Homology Theory and Their Applications I. LNM, vol. 86, pp. 76–122. Springer, Berlin (1969)
Moot, R., Retoré, C.: The Logic of Categorial Grammars. A Deductive Account of Natural Language Syntax and Semantics. LNCS, vol. 6850. Springer, Heidelberg (2012)
Okada, M., Terui, K.: The finite model property for various fragments of intuitionistic linear logic. J. Symb. Log. 64(2), 790–802 (1999)
Ono, H., Komori, Y.: Logics without contraction rule. J. Symb. Log. 50(1), 169–201 (1985)
Pentus, M.: The conjoinability relation in Lambek calculus and linear logic. J. Log. Lang. Inform. 3(2), 121–140 (1994)
Pentus, M.: Models for the Lambek calculus. Ann. Pure Appl. Log. 75(1–2), 179–213 (1995)
Wald, M., Dilworth, R.P.: Residuated lattices. Trans. Amer. Math. Soc. 45, 335–354 (1939)
Wurm, C.: Language-theoretic and finite relation models for the (full) Lambek calculus. J. Log. Lang. Inform. 26(2), 179–214 (2017)
Acknowledgments
We would like to thank the anonymous referees for their helpful comments. We also thank the participants of the Logical Problems in Computer Science seminar at the Lomonosov Moscow State University for fruitful discussions and helpful remarks.
Funding
The work of Max Kanovich and Andre Scedrov was supported by the Russian Science Foundation under grant 17-11-01294 and performed at National Research University Higher School of Economics, Moscow, Russia. The work of Stepan Kuznetsov was supported by the Young Russian Mathematics award, by the grant MK-430.2019.1 of the President of Russia, and by the Russian Foundation for Basic Research grant 18-01-00822. Section 2 was contributed by Kuznetsov. Section 3 was contributed by Kanovich and Scedrov. Sections 1 and 4 were contributed jointly and equally by all co-authors.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendix
Appendix
In this Appendix, we give a complete proof of the fact that the sequent from Theorem 1, namely
is not derivable in  .
.
Our argument is based on brute-force proof search; however, some of the sequents proven to be non-derivable get marked (numbered) and then referred to, if they appear in the proof search again. This makes our proof a bit shorter.
Due to cut elimination, we seek only for a cut-free proof. We start with the well-known fact that rules \(\cdot \mathrm {L}\), \(\mathop {/}\mathrm {R}\), \(\mathop {\backslash }\mathrm {R}\), and \(\vee \mathrm {L}\) are invertible: derivability of their conclusion yields derivability of their premise(s). Thus, in our proof search, if such a rule is applicable, we can always suppose that it was applied immediately, as the last (lowermost) rule in the derivation. Moreover, \(\vee \mathrm {L}\) has two premises, and they should be both derivable if so is the goal sequent. Hence, when trying to prove non-derivability of the goal sequent we can choose one of the premises of \(\vee \mathrm {L}\) and prove that it is not derivable.
Now, we are ready to prove that the sequent of Theorem 1 is not derivable in  . First, by invertibility of \(\cdot \mathrm {L}\) we replace all \(\cdot \)’s by commas in the left-hand side of the sequent:
. First, by invertibility of \(\cdot \mathrm {L}\) we replace all \(\cdot \)’s by commas in the left-hand side of the sequent:
Next, we apply invertibility of \(\vee \mathrm {L}\) to \((x \mathop {/}y) \vee x\). The sequent should be derivable with both \(x \mathop {/}y\) and x in this place; we choose \(x \mathop {/}y\):
The lowermost rule in the definition introduces one of the main connectives. There are now 4 of them:
Now we consider all possible cases. The enumeration of cases is as follows: for \(\mathop {/}\) and \(\mathop {\backslash }\) connectives, the case number is of the form n–m, where n is the number of the connective (as shown above) and m is the number of formulae that are sent to \(\varPhi \) by the \(\mathop {/}\mathrm {L}\) or \(\mathop {\backslash }\mathrm {L}\) rule.Footnote 2 For the 4th connective, \(\vee \), we have cases 4a and 4b, for choosing \(x \mathop {/}(y \vee z)\) or x, respectively.
Case 1–1. In this case we have \(x \mathop {/}y \vdash (x \mathop {/}y) \vee (x \mathop {/}z) \vee x\) (fine) and
Invert \(\vee \mathrm {L}\) and choose \(x \mathop {/}y\). Now we have 3 options:
Notice that here \(\varPhi \) in \(\mathop {/}\mathrm {L}\) or \(\mathop {\backslash }\mathrm {L}\) is determined in a unique way.
Subcase 1. We get
as the left premise. This sequent is not derivable (\(\mathop {\backslash }\) cannot be decomposed, since there is nothing to the left of the formula).
Subcase 2. Here we have \(x \mathop {/}y \vdash (x \mathop {/}y) \vee x\) (fine) as the left premise and
as the right one. We show that (33) is not derivable. Inverting \(\vee \mathrm {L}\) and choosing \(x \mathop {/}z\) yields \(x \mathop {/}z \vdash (x \mathop {/}(y \vee z)) \vee x\), and now either \(x \mathop {/}z \vdash x \mathop {/}(y \vee z)\) or \(x \mathop {/}z \vdash x\) should be derivable. The latter is trivially not. For the former, inverting \(\mathop {/}\mathrm {R}\) and \(\vee \mathrm {L}\), choosing y, gives \(x \mathop {/}z, y \vdash x\), which is also not derivable.
Subcase 3a. Here we get
Inverting \(\mathop {/}\mathrm {R}\) and \(\vee \mathrm {L}\), choosing y, gives
Decomposing \(\mathop {/}\) with \(\varPhi = ((x \mathop {/}y) \vee x) \mathop {\backslash }((x \mathop {/}z) \vee x)\) gives the left premise \(((x \mathop {/}y) \vee x) \mathop {\backslash }((x \mathop {/}z) \vee x) \vdash y\), which is already shown to be non-derivable (32). Decomposing \(\mathop {/}\) with \(\varPhi = ((x \mathop {/}y) \vee x) \mathop {\backslash }((x \mathop {/}z) \vee x), y\) gives a non-derivable right premise \(x \mathop {/}y \vdash x\). Finally, decomposing \(\mathop {\backslash }\) gives \((x \mathop {/}z) \vee x, y \vdash x\), which is also not derivable: inverting \(\vee \mathrm {L}\) and choosing x gives \(x, y \vdash x\).
Subcase 3b. In this case we have
Decomposing \(\mathop {/}\) yields (32), which is not derivable. Decomposing \(\mathop {\backslash }\) yields \(((x \mathop {/}z) \vee x \vdash x\), which is shown to be non-derivable by inverting \(\vee \mathrm {L}\) and choosing \(x \mathop {/}z\).
Case 1–2. The right premise now is
which is shown to be non-derivable exactly as (33).
Case 2–1. The left premise here is (32), which is not derivable.
Case 3–1. Here the left premise is fine, and the right one is
Invert \(\vee \mathrm {L}\) and choose \(x \mathop {/}z\):
Decomposing the left \(\mathop {/}\) yields (34), which is not derivable, as the right premise. Decomposing the right \(\mathop {/}\) is impossible, since \(\varPhi \) should be non-empty. Finally, decomposing \(\vee \) on the right yields two subcases.
Subcase a.
Inverting \(\mathop {/}\mathrm {R}\) and \(\vee \mathrm {L}\), choosing y, yields
Decomposing the right \(\mathop {/}\) would yield \(y \vdash z\), which is not derivable. So the only option is decomposing the left \(\mathop {/}\). This gives two possible situations, depending on how many formulae go to \(\varPhi \). If \(\varPhi \) takes one formula, then the right premise of \(\mathop {/}\mathrm {L}\) is
The choice of x in inverting \(\vee \mathrm {L}\) gives \(x, y \vdash x\), which is not derivable. If \(\varPhi \) takes two formulae, then we have the right premise of the form
which is also not derivable, now by choosing \(x \mathop {/}y\).
Subcase b.
Now we can only decompose the left \(\mathop {/}\), which yields
as the right premise. Both choices in inverting \(\vee \mathrm {L}\) fail: neither \(x \mathop {/}y, x \mathop {/}z \vdash x\), nor \(x, x \mathop {/}z \vdash x\) is derivable.
Case 3–2. Here the right premise is (33), which is not derivable.
Case 4a. Here we again invert \(\mathop {/}\mathrm {R}\) and \(\vee \mathrm {L}\), choosing y:
Again, as in the top-level analysis, we consider several cases.
Subcase 1–1. The right premise is of the form
Invert \(\vee \mathrm {L}\) choosing x:
Here decomposition 1–1 yields non-derivable (32); 1–2 yields
which is also not derivable (no decomposition possible). Decomposition 2–1 gives right premise
and choosing x in the inversion of \(\vee \mathrm {L}\) gives non-derivable \(x, x, y \vdash x\). Finally, decomposition 2–2 gives
as the right premise, and choosing x also makes it non-derivable: \(x, y \vdash x\).
Subcase 1–2. This gives a non-derivable right premise (37).
Subcase 1–3. Here the right premise is \((x \mathop {/}y) \vee x \vdash x\), which is invalidated by choosing \(x \mathop {/}y\) in the inversion of \(\vee \mathrm {L}\).
Subcases 2–1 and 2–2 give non-derivable left premises: (32) and (36) respectively.
Subcase 3–1. Here we get
Inverting \(\vee \mathrm {L}\), choosing \(x \mathop {/}z\), yields (35), which is not derivable.
Subcase 3–2. Here the right premise is
which is not derivable (37).
Case 4b. In this case we have
Here we return to the beginning of the proof and consider the same cases 1–1, 1–2, 2–1, 3–1, and 3–2. Each of these cases decomposes \(\mathop {/}\) or \(\mathop {\backslash }\), with the same left premise. The right premises are here are of the form \(\Gamma \vdash x\). We suppose that such a sequent is derivable. Then, by application of \(\vee \mathrm {L}\), we get \(\Gamma \vdash (x \mathop {/}(y \vee z)) \vee x\). Now we are exactly in the situation of one of the cases from 1–1 to 3–2, and can use the argumentation above “as is.”
This finishes our case analysis and thus the proof of Theorem 1.
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Kanovich, M., Kuznetsov, S., Scedrov, A. (2019). L-Models and R-Models for Lambek Calculus Enriched with Additives and the Multiplicative Unit. In: Iemhoff, R., Moortgat, M., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2019. Lecture Notes in Computer Science(), vol 11541. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-59533-6_23
Download citation
DOI: https://doi.org/10.1007/978-3-662-59533-6_23
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-59532-9
Online ISBN: 978-3-662-59533-6
eBook Packages: Computer ScienceComputer Science (R0)