Abstract
We prove an analogue of the McKinsey and Tarski theorem for the recently introduced dense-interior semantics of topological evidence logics. In particular, we show that in this semantics the modal logic \(\mathsf {S4.2}\) is sound and complete for any dense-in-itself metrizable space. As a result \(\mathsf {S4.2}\) is complete with respect to the real line \(\mathbb {R}\), the rational line \(\mathbb {Q}\), the Baire space \(\mathfrak {B}\), the Cantor space \(\mathfrak {C}\), etc. We also show that an extension of this logic with the universal modality is sound and complete for any idempotent dense-in-itself metrizable space, obtaining as a result that this logic is sound and complete with respect to \(\mathbb {Q}\), \(\mathfrak {B}\), \(\mathfrak {C}\), etc.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
Given a topological space \((X,\tau )\) and a set \(Y\subseteq X\), we can define the subspace topology \(\tau |_Y\) on Y as the set
$$\tau |_Y:=\{U\cap Y:U\in \tau \}.$$Note that \((Y,\tau |_Y)\) is trivially a topological space.
- 2.
Given a preordered set \((X,\le )\), the collection of upwards-closed sets defines an Alexandroff topology on X, i.e., a topology closed under infinite intersections. Conversely, given an Alexandroff topological space \((X,\tau )\) the relation \(x\le y\) iff \(x\in U\) implies \(y\in U\), for all \(U\in \tau \), defines a preorder. This correspondence is 1–1 and moreover
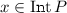 iff \(y\in P\) for all \(y\ge x\). For details, see, e.g., [3].
iff \(y\in P\) for all \(y\ge x\). For details, see, e.g., [3]. - 3.
I.e. a map \(d:X\times X\rightarrow [0,\infty )\) satisfying for all \(x,y,z\in X\): (i.) \(d(x,y)=0\) iff \(x=y\); (ii.) \(d(x,y)=d(y,x)\); (iii.) \(d(x,z)\le d(x,y)+d(y,z)\). A metric d on X induces a topology \(\tau _d\): we say that a set \(U\subseteq X\) is open if, for every \(x\in U\), there exists some \(\varepsilon >0\) such that \(d(x,y)<\varepsilon \) implies \(y\in U\).
- 4.
The original formulation of this theorem talked about dense-in-itself, metrizable, separable spaces. It was shown in [16] that the separability condition can be dropped.
- 5.
\(B P = \lnot d(\lnot P)\), where \(d(P)=\{x: \forall U\in \tau (x\in U \text { implies } \exists y\in P\cap U,y\ne x)\}\).
- 6.
A space is extremally disconnected (e.d.) if the closure of an open set is open, and hereditarily so if all its subspaces are e.d.
- 7.
A set \(U\subseteq X\) is dense whenever
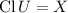 or equivalently whenever \(U\cap V\ne \varnothing \) for all nonempty open set V.
or equivalently whenever \(U\cap V\ne \varnothing \) for all nonempty open set V. - 8.
\(K\phi \equiv \square \phi \wedge [\forall ]\square \Diamond \phi \) and \(B\phi \equiv \lnot K \lnot K\phi \).
- 9.
A map \(f:(X,\tau )\rightarrow (Y,\sigma )\) is continous is \(U\in \sigma \) implies \(f^{-1}[U]\in \tau \) and open if \(U\in \tau \) implies \(f[U]\in \sigma \).
- 10.
A relation \(\le \) is weakly directed whenever \(x\le y, z\) implies that there exists \(t\ge y,z\).
- 11.
A space X is connected if there is no proper subset \(A\subseteq X\) such that both A and \(X{\setminus }A\) are open. \(\mathbb {R}\) is a connected space.
- 12.
I.e. a set \(A\subseteq W\) such that wRa for all \(a\in A\) and all \(w\in W\).
- 13.
\((X,\tau )\oplus (Y,\sigma )\) is the space which has the disjoint union \((X\times \{1\}) \cup (Y\times \{2\})\) as its underlying set and \(\tau \oplus \sigma =\{ (U\times \{1\})\cup (V\times \{2\}):U\in \tau ,V\in \sigma \}\) as its topology.
- 14.
We wish to thank Guram Bezhanishvili for the idea of this construction.
- 15.
Lemma A.1 is a cornerstone of the proof of McKinsey and Tarski’s theorem.
References
Baltag, A., Bezhanishvili, N., Özgün, A., Smets, S.: The topology of belief, belief revision and defeasible knowledge. In: Grossi, D., Roy, O., Huang, H. (eds.) LORI 2013. LNCS, vol. 8196, pp. 27–40. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40948-6_3
Baltag, A., Bezhanishvili, N., Özgün, A., Smets, S.: Justified belief and the topology of evidence. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 83–103. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_6
van Benthem, J., Bezhanishvili, G.: Modal logics of space. In: Aiello, M., Pratt-Hartmann, I., Van Benthem, J. (eds.) Handbook of Spatial Logics, pp. 217–298. Springer, Dordrecht (2007). https://doi.org/10.1007/978-1-4020-5587-4_5
van Benthem, J., Pacuit, E.: Dynamic logics of evidence-based beliefs. Stud. Log. 99(1–3), 61–92 (2011)
Bezhanishvili, G., Bezhanishvili, N., Lucero-Bryan, J., van Mill, J.: A new proof of the McKinsey-Tarski theorem. Stud. Log. 106(6), 1291–1311 (2018)
Blackburn, P., De Rijke, M., Venema, Y.: Modal Logic, vol. 53. Cambridge University Press, Cambridge (2001)
Engelking, R.: General Topology. Sigma Series in Pure Mathematics. Heldermann Verlag, Berlin (1989)
Gettier, E.L.: Is justified true belief knowledge? Analysis 23(6), 121–123 (1963)
Goranko, V., Passy, S.: Using the universal modality: gains and questions. J. Log. Comput. 2(1), 5–30 (1992)
Hewitt, E.: A problem of set-theoretic topology. Duke Math. J. 10(2), 309–333 (1943)
Hintikka, J.: Knowledge and Belief: An Introduction to the Logic of the Two Notions. Contemporary Philosophy. Cornell University Press, Ithaca (1962)
Kelly, K.: The Logic of Reliable Inquiry. Logic and Computation in Philosophy. Oxford University Press, Oxford (1996)
Kremer, P.: Strong completeness of S4 for any dense-in-itself metric space. Rev. Symb. Log. 6(3), 545–570 (2013)
McKinsey, J.C.C., Tarski, A.: The algebra of topology. Ann. Math. 45, 141–191 (1944)
Munkres, J.R.: Topology. Prentice Hall, Upper Saddle River (2000)
Rasiowa, H., Sikorski, R.: The Mathematics of Metamathematics. Institut Mathematyczny, Polskiej Akademii Nauk: Monographie Mathematyczne. PWN-Polish Scientific Publishers, Warszawa (1970)
Shehtman, V.: “Everywhere” and “Here”. J. Appl. Non-Class. Log. 9(2–3), 369–379 (1999)
Stalnaker, R.: On logics of knowledge and belief. Philos. Stud. 128(1), 169–199 (2006)
Steinsvold, C.: Topological models of belief logics. City University of New York (2006)
Acknowledgements
We would like to thank Guram Bezhanishvili for helpful discussions and for suggesting the proof of Theorem 2.8. We are also grateful to the reviewers of WoLLIC 2019 for useful comments, which improved the presentation of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Appendices
A Appendices
1.1 A.1 Proof of Theorem 2.8
Let us take a finite rooted preorder \(\mathfrak {F}= (W,\le )\) and a dense-in-itself metrizable space \((X,\tau )\) and construct a dense-interior onto map \(\bar{f}:(X,\tau )\twoheadrightarrow (W,\le )\).Footnote 14 For this construction, we will use the following two lemmas. Their proofsFootnote 15 can be found respectively in [5, Lemmas 4.13 and 4.22] and [10, Thm. 41].
Lemma A.1
-
(i)
If \(\mathfrak {F}=(W,\le )\) is a finite rooted preorder, and \((G,\tau )\) is a dense-in-itself metrizable space, there exists a continuous, open and surjective map
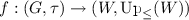 .
. -
(ii)
(Partition Lemma) Let X be a dense-in-itself metrizable space and \(n\ge 1\). Then there is a partition \(\{G,U_1,...,U_n\}\) of X such that G is a dense-in-itself closed subspace of X with dense complement and each \(U_i\) is an open set.
Lemma A.2
Given a dense-in-itself metrizable space X and \(n\ge 1\), X can be partitioned in n dense sets.
Note that \(\mathfrak {F}\) has a final cluster, i.e., a set \(A\subseteq W\) with the property that \(w\le a\) for all \(w\in W\) and all \(a\in A\). Indeed, let \(r\in W\) be the root and let \(x,y\in W\) be any two maximal elements (which exist, on account that \(\mathfrak {F}\) is finite). Since \(r\le x\) and \(r\le y\), by weak directedness, there is a z such that \(x, y\le z\). But by maximality of x and y, we have that \(z\le x\) and \(z\le y\), hence, by transitivity, \(x\le y\) and \(y\le x\): the maximal elements of \(\mathfrak {F}\) form a final cluster. Let this cluster be \(A=\{a_1,...,a_n\}\).
If \(W=A\), then we simply partition X in n dense sets \(\{A_1,...,A_n\}\) as per Lemma A.2 and we take \(\bar{f}\) to map each \(x\in A_i\) to \(a_i\). It is a straightforward check that \(\bar{f}\) is dense-open (the image of a dense open set is W) and dense-continuous (the preimage of a nonempty upset is X). Otherwise, let us call \(B:=W\setminus A\), which is a finite rooted preorder. Let \(\{G,U_1,...,U_n\}\) be a partition of X as given by the Partition Lemma. Since G is a dense-in-itself metrizable space and B is a finite rooted preorder, by Lemma A.1(i), there exists an onto interior map (with respect to the subspace topology of G) \(f: G\twoheadrightarrow B\). We extend this map to \(\bar{f}:X\twoheadrightarrow W\) by mapping each \(x\in U_i\) to \(a_i\).
We now show that \(\bar{f}\) is the desired map. It is surjective by construction. It is dense-open, for given a nonempty dense open set \(U\subseteq X\), we have that \(U\cap G\) is an open set in the subspace topology of G and therefore \(\bar{f}[U\cap G]=f[U\cap G]\) is an upset in B. On the other hand, \(U\setminus G=U\cap (X\setminus G)\) is the intersection of two dense open sets and therefore is dense open, which means it has nonempty intersection with each of the \(U_i\) and hence \(\bar{f}[U\setminus G]=A\). Therefore, \(\bar{f}[U]\) is the union of an upset in B with A, and thus is an upset in W.
To see that \(\bar{f}\) is dense-continuous, take a nonempty upset \(U\subseteq W\), which will be a disjoint union \(U=B'\cup A\), with \(B'\) being an upset in B. Then \(\bar{f}^{-1}[B']=f^{-1}[B']\) is an open set in X and \(\bar{f}^{-1}[A]=U_1\cup ...\cup U_n = X\setminus G\). Therefore, \(\bar{f}^{-1}[U]\) is the union of an open set and a dense open set and thus a dense open set. This concludes the proof.
1.2 A.2 Proof of Theorem 2.13
Let \((W,\le )\) be a finite preorder with a final cluster. We have the following:
Lemma A.3
\((W,\le )\) is a p-morphic image of a finite disjoint union of finite rooted \(\mathsf {S4.2}\) frames, via a dense-open and dense-continuous p-morphism.
Proof
Let \(x_1,...,x_n\) be the minimal elements of W. Now, for \(1\le i \le n\) take \(W'_i={\uparrow }x_i \times \{i \}\). Define an order on \(W'=W'_1\cup ...\cup W'_n\) by: \((x,i)\le (y,j)\) iff \(i=j\) and \(x\le y\). Then \(W'_1,...,W'_n\) are pairwise disjoint finite rooted \(\mathsf {S4.2}\) frames (with \(A\times \{i\}\) as a final cluster) and \((x,i)\mapsto x\) is a p-morphism from \(W'\) onto W. It is easy to see that this mapping is dense-open (for every nonempty open set is dense in W) and dense-continuous (for the preimage of a nonempty W-upset is a \(W'\)-upset which contains all the final clusters, and thus is dense).
We can use Lemma A.3 to construct the map: let \(W'_1,...,W'_n\) be the family of pairwise disjoint finite rooted \(\mathsf {S4.2}\) frames whose union \(W'\) has \((W,\le )\) as a p-morphic image.
Take \(z_1,...,z_{n-1}\in \mathbb {R}{\setminus } \mathbb {Q}\) and consider the intervals \(A_1=(-\infty ,z_1)\), \(A_n=(z_{n-1},\infty )\) and \(A_i=(z_{i-1},z_i)\) for \(1<i<n\). Now, each \(A_i\), as a subspace, is homeomorphic to \(\mathbb {Q}\) (and thus a dense-in-itself metrizable space). From each \((A_i,\tau |_{A_i})\) we can find a dense-open, dense-continuous and surjective map \(f_i\) onto \(W'_i\). Then \(f=f_1\cup ...\cup f_n\) is a dense-interior map onto \(W'\) which, when composed with the p-morphism in Lemma A.3, gives us the desired map.
1.3 A.3 Proof of Theorem 2.15
We show that \(E_0^{\mathbb {Q}}\) is a subbasis for \(\mathbb {Q}\). First, given that \(X\in E^X_0\) and \(f[\mathbb {Q}]=X\), we have that \(\mathbb {Q}\in E^\mathbb {Q}_0\), thus \(\bigcup E^\mathbb {Q}_0 =\mathbb {Q}\).
Now, suppose \(p\in U\in \tau _\mathbb {Q}\). We show that there exist \(e^q_1,...,e^q_n\in E^\mathbb {Q}_0\) such that \(p\in e^q_1\cap ...\cap e^q_n\subseteq U\). Note that \(fp\in f[U]\) which is an open set. Since \(E^X_0\) is a subbasis for \((X,\le )\) this means that there exist \(e^x_1,...,e^x_n\in E^X_0\) with \(fp\in e^x_1\cap ...\cap e^x_n \subseteq f[U]\). Now set
The fact that \(e^q_i\in E^\mathbb {Q}_0\) follows from the fact that \(f[e^q_i]=e^x_i\). Indeed, if \(y\in f[e^q_i]\) then \(y\in ff^{-1}[e^x_i]=e^x_i\) and conversely if \(y\in e^x_i\), then either \(y\in f[U]\) (in which case \(y=fz\) for some \(z\in U\) and thus \(z\in f^{-1} [e^x_i]\) and therefore \(z\notin \{z'\notin U: fz'\in f[U] \}\), which implies \(z\in e^q_i\)) or \(y\notin f[U]\) (in which case \(y=fz\) for some z by surjectivity and \(z\notin \{z'\notin U: fz'\in f[U] \}\), thus \(z\in e^q_i\)). In either case, \(y\in f[e^q_i]\).
Finally, note that \(e^q_1\cap ...\cap e^q_n\subseteq U\). Indeed, for any \(x\in e^q_1\cap ...\cap e^q_n\) we have that \(fx\in e^x_1\cap ...\cap e^x_n\subseteq f[U]\), and thus by the definition of the \(e^q_i\)’s it cannot be the case that \(x\notin U\).
So for \(p\in U\in \tau _\mathbb {Q}\) we have found elements \(e^q_1,...e^q_n\in E^\mathbb {Q}_0\) such that \(p\in e^q_1\cap ...\cap e^q_n\subseteq U\), and therefore \(E_0^\mathbb {Q}\) is a subbasis.
Now set a valuation \(V^\mathbb {Q}(p)=\{x\in \mathbb {Q}: fx\in V(p)\}\) and let us show that, for any formula \(\phi \) in the language and any \(x\in \mathbb {Q}\), we have that \((\mathbb {Q},\tau _\mathbb {Q},E^\mathbb {Q}_0,V^\mathbb {Q}),x\,\models \, \phi \) if and only if \((X,\le ,E^X_0,V),fx\,\models \, \phi \). This is done by an induction on formulas; the only induction step that requires some attention is the one referring to \(\square _0\).
Let \(x\,\models \,\square _0 \psi \). This means that there exists some \(e\in E^\mathbb {Q}_0\) with \(x\in e\) and \(y\,\models \, \psi \) for all \(y\in e\). But then \(fx\in f[e]\in E^X_0\) and by the induction hypothesis we have \(fy\,\models \, \psi \) for all \(fy\in f[e]\) and thus \(fx\,\models \,\square _0\psi \). Conversely, if \(fx\in e'\subseteq \llbracket \psi \rrbracket ^X\) for some \(e'\in E^X_0\), we have that \(x\in f^{-1}[e']\in E^\mathbb {Q}_0\) and \(fy\,\models \, \psi \) for each \(y\in f^{-1}[e']\) and thus, by induction hypothesis, \(y\,\models \,\psi \). Therefore \(x\,\models \, \square _0\psi \).
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Baltag, A., Bezhanishvili, N., Fernández González, S. (2019). The McKinsey-Tarski Theorem for Topological Evidence Logics. In: Iemhoff, R., Moortgat, M., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2019. Lecture Notes in Computer Science(), vol 11541. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-59533-6_11
Download citation
DOI: https://doi.org/10.1007/978-3-662-59533-6_11
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-59532-9
Online ISBN: 978-3-662-59533-6
eBook Packages: Computer ScienceComputer Science (R0)


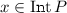 iff
iff 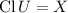 or equivalently whenever
or equivalently whenever 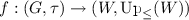 .
.