Im Wasser wird’s bunt: Licht, Brechung und Farben

Zusammenfassung

Der Ausflug in die Welt der Optik beginnt mit einem sehr bunten Kapitel. Vieläugige Fische im Aquarium führen zur Lichtbrechung an Grenzflächen. Diese kann auch auf Partys und bei optischer Datenübertragung eine große Rolle spielen. Es folgt ein genauer Blick auf das gesamte elektromagnetische Spektrum, angefangen bei den Radiowellen bis hin zur Gammastrahlung, mit den unterschiedlichsten Anwendungsgebieten. Und was sind eigentlich Farben? Ist weiß eine Farbe? Schließlich endet das Kapitel mit einer ausführlichen Erklärung des Regenbogens und seiner Entstehung. In den Aufgaben wird unter anderem dem Aussehen von Fettflecken auf den Grund gegangen.

Appendices

Aufgaben

1.1.1 1.1 Fisch im Aquarium

Am Anfang des Kapitels wird ein Fisch im Aquarium von einer Person außerhalb des Aquariums beobachtet. Jetzt drehen wir den Spieß um: Kann der Fisch seinerseits den Beobachter sehen? Wenn ja, wie oft?

1.1.2 1.2 Zwei Grenzflächen

Die Brechungseffekte zwischen Wasser und Luft beim Aquarium lassen sich mit dem Snelliusschen Brechungsgesetz beschreiben, obwohl sich zwischen diesen beiden Medien noch das Glas als drittes Medium befindet.

• a) Erstelle eine Skizze, die diesen Sachverhalt beschreibt.

• b) Leite anhand der Skizze die Formel für Brechung an zwei parallelen Grenzflächen hintereinander her.

• c) Blicke aus dem Fenster.

• d) Überlege dir, warum du Aufgabe (c) machen musstest.

1.1.3 1.3 Prisma

Ein Prisma ist ein keilförmiges Stück Glas, mit dessen Hilfe Licht aufgrund der Dispersion in seine Spektralfarben aufgespaltet wird. Anbei findet ihr eine Skizze zum Strahlengang.

• a) Berechne allgemein eine Formel für den Austrittswinkel $\theta _4$, die nur von $\theta _1$, $\alpha$, $n_1$ und $n_2$ abhängt.

• b) Berechne den Unterschied $\Delta \theta _4$ im Austrittswinkel, wenn statt violettem ($n_{2\mathrm {v}}=1{,}47$) rotes Licht ($n_{2\mathrm {r}}=1{,}45$) im Winkel $\theta _1=30^\circ$ aus Luft ($n_1=1$) auf das Prisma ($\alpha =45^\circ$) trifft.

1.1.4 1.4 Reflexionen

Berechne, wie viel Lichtintensität an einer ebenen Grenzfläche Luft-Glas bei senkrechtem Lichteinfall

• a) reflektiert und

• b) transmittiert wird.

Rechne dabei jeweils für senkrecht und parallel zur Einfallsebene polarisiertes Licht.

1.1.5 1.5 Fettflecken

Lässt man fettige Pommes oder Pizza auf einer weißen Serviette liegen, so saugt sich diese mit Fett ($n_\mathrm {F}=1{,}46\dots 1{,}50$) voll. Die Serviette besteht aus Zellulose ($n_\mathrm {Z}=1{,}47$). Warum erscheint die fettige Serviette in Abb. 1.30 durchsichtig? Begründe deine Erklärung durch Formeln.

Abb. 1.30

Ein Fettfleck auf einer Serviette sorgt dafür, dass Licht durch die Serviette durchscheinen kann. Warum?

Lösungen

1.1.1 1.1 Fisch im Aquarium

Ja, der Fisch kann den Beobachter sehen, und zwar ebenfalls zweimal. Klar wird dies, wenn man berücksichtigt, dass für die Brechung an einer Grenzfläche irrelevant ist, in welche Richtung das Licht unterwegs ist, also aus welchem der beiden Medien das Licht in das andere übergeht. Das heißt, überall dort, wo der Beobachter das Auge des Fischs sieht, sieht der Fisch das Auge des Beobachters, also zweimal. Blickkontakt garantiert.

1.1.2 1.2 Zwei Grenzflächen

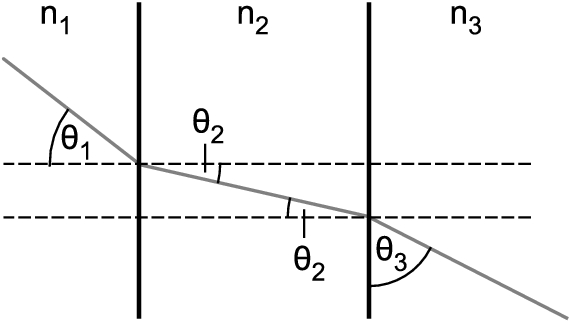
• a) Licht trifft zunächst unter dem Winkel $\theta _1$ auf eine Grenzfläche $n_1-n_2$, wird gebrochen und verlässt diese unter dem Winkel $\theta _2$. Aufgrund der Geometrie der parallelen Grenzflächen, Stichwort Z-Winkel, trifft es anschließend unter dem gleichen Winkel $\theta _2$ auf die Grenzfläche $n_2-n_3$ und verlässt diese unter dem Winkel $\theta _3$.

  

• b) Um die Formel für Brechung an zwei parallelen Grenzflächen zu erhalten, müssen wir den Austrittswinkel $\theta _3$ bzw. $\sin {\theta _3}$ in Abhängigkeit von dem Einfallswinkel $\theta _1$ und den Brechungsindizes der Medien beschreiben. Wir nutzen Formel 1.1 für das Snelliussche Brechungsgesetz und erhalten für den Austrittswinkel $\theta _3$:

  $$ \sin {\theta _3} = \frac{n_2}{n_3} \sin {\theta _2} $$

  Um jetzt noch den Winkel $\theta _2$ aus der Gleichung verschwinden zu lassen, drücken wir ihn wieder mithilfe des Brechungsgesetzes aus:

  $$ \sin {\theta _2} = \frac{n_1}{n_2} \sin {\theta _1} $$

  Das oben für $\sin {\theta _2}$ eingesetzt ergibt

  $$ \sin {\theta _3} = \frac{n_2}{n_3} \frac{n_1}{n_2} \sin {\theta _1} $$

  und schließlich

  $$ \sin {\theta _3} = \frac{n_1}{n_3} \sin {\theta _1}. $$

  Hier hat sich interessanterweise der Brechungsindex $n_2$ rausgekürzt. Das heißt, die Brechung an mehreren (parallelen!) Grenzflächen hängt ausschließlich vom ersten und vom letzten Medium ab.

• c) *aus dem Fenster blick*

• d) Jegliches Licht, das von draußen durch das Fenster in den Raum gelangt, durchlebt ebenfalls den Gang durch zwei Grenzflächen, nämlich Luft-Glas und Glas-Luft. Trotzdem sehen wir die Welt da draußen so, als wäre überhaupt keine Grenzfläche vorhanden. Dies kommt daher, dass hier $n_1 = n_3$ gilt, da sich auf beiden Seiten des Glases Luft befindet. Mithilfe der in (b) hergeleiteten Formel sehen wir, dass sich die Brechungsindizes dadurch rauskürzen und der Austrittswinkel $\theta _3$ gleich dem Einfallswinkel $\theta _1$ entspricht, der Brechungseffekt verschwindet. Die Lichtstrahlen erfahren allerdings einen leichten seitlichen Versatz d. Erstelle dazu eine Skizze und versuche, dessen Abhängigkeit von den Parametern durch Rechnung zu bestimmen.

1.1.3 1.3 Prisma

• a) Gegeben: $\theta _1$, $\alpha$, $n_1$, $n_2$

  Gesucht: $\theta _4$

  Um $\theta _4$ zu bestimmen, nutzen wir das Snelliussche Brechungsgesetz, laut Skizze

  $$ \sin {\theta _4} = \frac{n_2}{n_1} \sin {\theta _3}. $$

  Die einzige Unbekannte ist hier $\theta _3$. Dieses gewinnen wir über die Winkelsumme im Dreieck zu

  $$ \theta _3 = 180^\circ - \beta - \theta _2. $$

  Hier sind $\theta _2$ und $\beta$ noch unbekannt. Ersteres ergibt sich wieder über Snellius:

  $$ \sin {\theta _2} = \frac{n_1}{n_2} \sin {\theta _1} $$

  Das $\beta$ erhalten wir über die Winkelsumme im Viereck zu

  $$ \beta = 360^\circ - 2\cdot 90^\circ -\alpha = 180^\circ -\alpha . $$

  Die beiden rechten Winkel treten hierbei an den Einfallsloten auf.

  Über $\beta$ und $\theta _2$ ergibt sich nun $\theta _3$ zu

  $$ \theta _3 = 180^\circ - 180^\circ +\alpha - \arcsin {\left( \frac{n_1}{n_2} \sin {\theta _1}\right) }=\alpha - \arcsin {\left( \frac{n_1}{n_2} \sin {\theta _1}\right) }. $$

  Das setzen wir nun in die erste Gleichung ein:

  $$ \sin {\theta _4} = \frac{n_2}{n_1} \sin {\left[ \alpha - \arcsin {\left( \frac{n_1}{n_2} \sin {\theta _1}\right) }\right] } $$

  Aufgelöst nach $\theta _4$ also

  $$ \theta _4 = \arcsin {\left[ \frac{n_2}{n_1} \sin {\left[ \alpha - \arcsin {\left( \frac{n_1}{n_2} \sin {\theta _1}\right) }\right] }\right] }. $$

  Obwohl sie etwas sperrig ist, erfüllt diese Gleichung die Bedingung, nur noch von bekannten Variablen abhängig zu sein.

• b) Um den Unterschied $\Delta \theta _4 = \theta _\mathrm {{4v}} - \theta _\mathrm {4{r}}$ zu berechnen, bestimmen wir zunächst die beiden Winkel für Violett und Rot. Einsetzen in die vorher bestimmte Gleichung liefert uns

  $$ \theta _\mathrm {{4v}} = 38{,}60^\circ $$

  und

  $$ \theta _\mathrm {{4r}} = 37{,}51^\circ . $$

  Die Differenz ergibt sich also zu

  $$ \Delta \theta _{4} = 1{,}09^\circ . $$

  Dies beschreibt den Winkel, unter dem wir die Regenbogenfarben zwischen Violett und Rot sehen können, zu sehen in Abb. 1.31.

Abb. 1.31

Ein Prisma spaltet Licht mithilfe der Dispersion in seine Spektralfarben auf

1.1.4 1.4 Reflexionen

Gegeben: $n_\mathrm {L}=1$, $n_\mathrm {G}=1{,}5$, $\theta _\mathrm {E}=90^\circ$

• a) Gesucht: $R_\mathrm {s}$, $R_\mathrm {p}$

  Aus den Fresnelschen Formeln folgt für senkrecht polarisiertes Licht ein Reflexionsgrad von

  $$ R_\mathrm {s}=r_\mathrm {s}^2=\left( \dfrac{n_\mathrm {E}\cos \theta _\mathrm {E}-\sqrt{n_\mathrm {T}^2-n_\mathrm {E}^2\sin ^2\theta _\mathrm {E}}}{n_\mathrm {E}\cos \theta _\mathrm {E}+\sqrt{n_\mathrm {T}^2-n_\mathrm {E}^2\sin ^2\theta _\mathrm {E}}}\right) ^2. $$

  Durch Einsetzen von $\theta _\mathrm {E}=90^\circ$ vereinfacht sich die Gleichung sehr stark:

  $$ R_\mathrm {s}=\left( \dfrac{n_\mathrm {E}-n_\mathrm {T}}{n_\mathrm {E}+n_\mathrm {T}}\right) ^2 $$

  Einsetzen der Brechungsindizes für Glas und Luft liefert uns

  $$ R_\mathrm {s}=0{,}04. $$

  Es werden also $4\,\%$ des einfallenden Lichts an der Grenzfläche reflektiert. Für parallel zur Einfallsebene polarisiertes Licht ergibt sich über

  $$ R_\mathrm {p}=r_\mathrm {p}^2=\left( \dfrac{n_\mathrm {T}\cos \theta _\mathrm {E}-\dfrac{n_\mathrm {E}}{n_\mathrm {T}}\sqrt{n_\mathrm {T}^2-n_\mathrm {E}^2\sin ^2\theta _\mathrm {E}}}{n_\mathrm {T}\cos \theta _\mathrm {E}+\dfrac{n_\mathrm {E}}{n_\mathrm {T}}\sqrt{n_\mathrm {T}^2-n_\mathrm {E}^2\sin ^2\theta _\mathrm {E}}}\right) ^2 $$

  und $\theta _\mathrm {E}=90^\circ$

  $$ R_\mathrm {p}=\left( \dfrac{n_\mathrm {T}-\dfrac{n_\mathrm {E}}{n_\mathrm {T}}n_\mathrm {T}}{n_\mathrm {T}+\dfrac{n_\mathrm {E}}{n_\mathrm {T}}n_\mathrm {T}}\right) ^2=\left( \dfrac{n_\mathrm {T}-n_\mathrm {E}}{n_\mathrm {T}+n_\mathrm {E}}\right) ^2=0{,}04. $$

  Die Polarisationsrichtung spielt für senkrechten Lichteinfall also keine Rolle. Dies ist auch sinnvoll, denn bei senkrechtem Einfall lässt sich keine eindeutige Einfallsebene definieren.

• b) Gesucht: $T_\mathrm {s}$, $T_\mathrm {p}$

  Aus den Fresnelschen Formeln folgt für senkrecht polarisiertes Licht ein Transmissionsgrad von

  $$ T_\mathrm {s}=\dfrac{\sqrt{n_\mathrm {T}^2-n_\mathrm {E}^2\sin ^2\theta _\mathrm {E}}}{n_\mathrm {E}\cos {\theta _\mathrm {E}}} t_\mathrm {s}^2=\dfrac{\sqrt{n_\mathrm {T}^2-n_\mathrm {E}^2\sin ^2\theta _\mathrm {E}}}{n_\mathrm {E}\cos {\theta _\mathrm {E}}}\left( \dfrac{2n_\mathrm {E}\cos \theta _\mathrm {E}}{n_\mathrm {E}\cos \theta _\mathrm {E}+\sqrt{n_\mathrm {T}^2-n_\mathrm {E}^2\sin ^2\theta _\mathrm {E}}}\right) ^2. $$

  Durch Einsetzen von $\theta _\mathrm {E}=90^\circ$ vereinfacht sich die Gleichung wieder sehr stark:

  $$ T_\mathrm {s}=\dfrac{n_\mathrm {T}}{n_\mathrm {E}}\left( \dfrac{2n_\mathrm {E}}{n_\mathrm {E}+n_\mathrm {T}}\right) ^2=\dfrac{4n_\mathrm {E}n_\mathrm {T}}{(n_\mathrm {E}+n_\mathrm {T})^2}=0{,}96 $$

  Analog ergibt sich auch

  $$ T_\mathrm {p}=\dfrac{n_\mathrm {T}}{n_\mathrm {E}}\left( \dfrac{2n_\mathrm {E}}{n_\mathrm {T}+n_\mathrm {E}}\right) ^2=\dfrac{4n_\mathrm {E}n_\mathrm {T}}{(n_\mathrm {T}+n_\mathrm {E})^2}=0{,}96. $$

  Es werden also $96\,\%$ des einfallenden Lichts durch die Grenzfläche transmittiert, unabhängig von der Polarisation des Lichts. Bei sehr vielen Grenzflächen hintereinander, wie zum Beispiel bei der Kamera in Abschn. 3.1.2, reduziert sich die Transmission sehr stark. Um dies zu verhindern, werden Antireflexschichten wie in Abschn. 6.2 auf die Grenzflächen aufgebracht. Addiert man Reflexions- und Transmissionsgrad, so erhält man genau $100\,\%$. Dies gilt für sämtliche Einfallswinkel $\theta _\mathrm {E}$ und lässt sich in Abb. 1.5 auch erkennen.

1.1.5 1.5 Fettflecken

Um diese Frage beantworten zu können, müssen wir uns zunächst überlegen, warum wir durch die Serviette ohne Fett nicht durchsehen können. Dies liegt, ähnlich wie beim Schaum in Abschn. 1.3.2, an den unzähligen Grenzflächen zwischen den Zellulosefasern ($n_\mathrm {Z}=1{,}47$) und der Luft $n=1$. An diesen wird das einfallende Licht vielfach reflektiert und die Serviette erscheint wie der Schaum weiß.

Durch das Einbringen von Fett mit $n_\mathrm {F}=1{,}46\ldots 1{,}50$ in die zuvor von Luft gefüllten Bereiche zwischen den Fasern reduzieren wir den Unterschied in den Brechungsindizes.

Dadurch nimmt gemäß der Fresnelschen Formeln aus Abschn. 1.1.1 der Reflexionsfaktor ab, die Reflexionen werden reduziert. So kann mehr Licht ungehindert durch die Serviette durchscheinen, sie wird transparent, zu sehen in Abb. 1.32.

Abb. 1.32

Durch den Fettfleck nimmt die Reflexion an der Serviette ab und die Transmission zu. Dadurch erscheint sie vor dunklerem Hintergrund dunkler und vor hellerem Hintergrund heller. Genauso ist es mit nasser Kleidung

Aus demselben Grund erscheint übrigens auch nasse Kleidung dunkler (und nasse T-Shirts werden durchsichtig). Das Wasser zwischen den Fasern führt nämlich ebenfalls zu einer Abschwächung der Reflexionen, wodurch weniger einfallendes Licht zurückgeworfen wird und die Helligkeit der Kleidung abnimmt.