Abstract
Taking an algebraic perspective on the basic structures of Rough Concept Analysis as the starting point, in this paper we introduce some varieties of lattices expanded with normal modal operators which can be regarded as the natural rough algebra counterparts of certain subclasses of rough formal contexts, and introduce proper display calculi for the logics associated with these varieties which are sound, complete, conservative and with uniform cut elimination and subformula property. These calculi modularly extend the multi-type calculi for rough algebras to a ‘nondistributive’ (i.e. general lattice-based) setting.
The research of the fourth author is supported by the NWO Vidi grant 016.138.314, the NWO Aspasia grant 015.008.054, and a Delft Technology Fellowship awarded in 2013.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
In [22], sequent calculi for non-distributive versions of the logics associated with varieties of ‘rough algebras’ are introduced, which are sound and complete but without cut elimination.
- 2.
When \(B=\{a\}\) (resp. \(Y=\{x\}\)) we write \(a^{\uparrow \downarrow }\) for \(\{a\}^{\uparrow \downarrow }\) (resp. \(x^{\downarrow \uparrow }\) for \(\{x\}^{\downarrow \uparrow }\)).
- 3.
The assumption that E is I-compatible does not follow from R and S being I-compatible. Let \(\mathbb {G} = (\mathbb {P}, Id_A)\) for any polarity \(\mathbb {P}\) such that not all singleton sets of objects are Galois-stable. Hence \(E = Id_A\) is not I-compatible. However, if \(E = Id_A\), then \(R = S = I\) are I-compatible.
- 4.
Condition H3 implies that \(\blacksquare _I\,: \mathbb {L}\twoheadrightarrow \mathsf {S}_{\mathsf{I}}\) and \(\Box _I\,: \mathsf {L}_{\mathsf{I}} \hookrightarrow \mathbb {L}\) are \(\wedge \)-hemimorphisms and
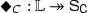 and \(\Diamond _C\,: \mathsf {L_C} \hookrightarrow \mathbb {L}\) are \(\vee \)-hemimorphisms; condition H4 implies that the black connectives are surjective and the white ones are injective.
and \(\Diamond _C\,: \mathsf {L_C} \hookrightarrow \mathbb {L}\) are \(\vee \)-hemimorphisms; condition H4 implies that the black connectives are surjective and the white ones are injective. - 5.
The connectives which appear in a grey cell in the synoptic tables will only be included in the present language at the structural level.
References
Banerjee, M., Chakraborty, M.K.: Rough sets through algebraic logic. Fundamenta Informaticae 28(3, 4), 211–221 (1996)
Conradie, W., Frittella, S., Palmigiano, A., Piazzai, M., Tzimoulis, A., Wijnberg, N.M.: Categories: how I learned to stop worrying and love two sorts. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 145–164. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_10
Conradie, W., Frittella, S., Palmigiano, A., Piazzai, M., Tzimoulis, A., Wijnberg, N.M.: Toward an epistemic-logical theory of categorization. In: Proceedings of the TARK 2017. EPTCS, vol. 251, pp. 167–186 (2017)
Conradie, W., Palmigiano, A.: Algorithmic correspondence and canonicity for non-distributive logics. Annals of Pure and Applied Logic ArXiv:1603.08515
Frittella, S., Greco, G., Kurz, A., Palmigiano, A., Sikimić, V.: Multi-type sequent calculi. In: Indrzejczak, A., et al. (eds.) Proceedings of the Trends in Logic XIII, pp. 81–93 (2014)
Frittella, S., Greco, G., Palmigiano, A., Yang, F.: A multi-type calculus for inquisitive logic. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 215–233. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_14
Greco, G., Ma, M., Palmigiano, A., Tzimoulis, A., Zhao, Z.: Unified correspondence as a proof-theoretic tool. J. Logic Comput. 28(7), 1367–1442 (2018)
Ganter, B., Wille, R.: Formal Concept Analysis: Mathematical Foundations. Springer, Heidelberg (1999). https://doi.org/10.1007/978-3-642-59830-2
Greco, G., Kurz, A., Palmigiano, A.: Dynamic epistemic logic displayed. In: Grossi, D., Roy, O., Huang, H. (eds.) LORI 2013. LNCS, vol. 8196, pp. 135–148. Springer, Heidelberg (2013). https://doi.org/10.1007/978-3-642-40948-6_11
Greco, G., Liang, F., Manoorkar, K., Palmigiano, A.: Proper multi-type display calculi for rough algebras. arXiv preprint 1808.07278
Greco, G., Liang, F., Moshier, M.A., Palmigiano, A.: Multi-type display calculus for semi De Morgan logic. In: Kennedy, J., de Queiroz, R.J.G.B. (eds.) WoLLIC 2017. LNCS, vol. 10388, pp. 199–215. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-55386-2_14
Greco, G., Liang, F., Palmigiano, A., Rivieccio, U.: Bilattice logic properly displayed. Fuzzy Sets Syst. (2018). https://doi.org/10.1016/j.fss.2018.05.007
Greco, G., Palmigiano, A.: Linear logic properly displayed. arXiv preprint: 1611.04184
Greco, G., Palmigiano, A.: Lattice logic properly displayed. In: Kennedy, J., de Queiroz, R.J.G.B. (eds.) WoLLIC 2017. LNCS, vol. 10388, pp. 153–169. Springer, Heidelberg (2017). https://doi.org/10.1007/978-3-662-55386-2_11
Kent, R.E.: Rough concept analysis: a synthesis of rough sets and formal concept analysis. Fundamenta Informaticae 27(2, 3), 169–181 (1996)
Liang, F.: Multi-type algebraic proof theory. Ph.D. thesis, TU Delft (2018)
Ma, M., Chakraborty, M.K., Lin, Z.: Sequent calculi for varieties of topological quasi-Boolean algebras. In: Nguyen, H.S., Ha, Q.-T., Li, T., Przybyła-Kasperek, M. (eds.) IJCRS 2018. LNCS (LNAI), vol. 11103, pp. 309–322. Springer, Cham (2018). https://doi.org/10.1007/978-3-319-99368-3_24
Manoorkar, K., Nazari, S., Palmigiano, A., Tzimoulis, A., Wijnberg, N.M.: Rough concepts (2018, Submitted)
Pawlak, Z.: Rough set theory and its applications to data analysis. Cybern. Syst. 29(7), 661–688 (1998)
Saha, A., Sen, J., Chakraborty, M.K.: Algebraic structures in the vicinity of pre-rough algebra and their logics. Inf. Sci. 282, 296–320 (2014)
Saha, A., Sen, J., Chakraborty, M.K.: Algebraic structures in the vicinity of pre-rough algebra and their logics II. Inf. Sci. 333, 44–60 (2016)
Sen, J., Chakraborty, M.K.: A study of interconnections between rough and 3-valued Łukasiewicz logics. Fundamenta Informaticae 51(3), 311–324 (2002)
Tzimoulis, A.: Algebraic and proof-theoretic foundations of the logics for social behaviour. Ph.D. thesis, TUDelft (2018)
Wansing, H.: Sequent systems for modal logics. In: Gabbay, D.M., Guenthner, F. (eds.) Handbook of Philosophical Logic, vol. 8, pp. 61–145. Springer, Dordrecht (2002). https://doi.org/10.1007/978-94-010-0387-2_2
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Properties
A Properties
Throughout this section, we let \(\mathsf {K}\in \{aKa, aKa5', K\text {-}IA3_{\ell }\}\), and \(\mathsf {HK}\) the class of heterogeneous algebras corresponding to \(\mathsf {K}\). Further, we let \(\text {D.K}\) denote the multi-type calculus for the logic \(\text {H.K}\) canonically associated with \(\mathsf {K}\).
1.1 A.1 Soundness for Perfect \(\mathsf {HK}\) Algebras
The verification of the soundness of the rules of \(\text {D.K} \) w.r.t. the semantics of perfect elements of \(\mathsf {HK}\) (see Definition 9) is analogous to that of many other multi-type calculi (cf. [6, 11,12,13,14, 16, 23]). Here we only discuss the soundness of the rule \(k\text {-}ia3_{\ell }\). By definition, the following quasi-inequality is valid on every K-IA3\(_{\ell }\):
This quasi-inequality equivalently translates into the multi-type language as follows:
By adjunction, the quasi-inequality above can be equivalently rewritten as follows:
which, thanks to a well known property of adjoint maps, simplifies as:
Hence, the quasi-inequality above is equivalent to the following inequality:
The inequality above is analytic inductive (cf. [7, Definition 55]), and hence running ALBA on this inequality produces:

The last quasi-inequality above is the semantic translation of the rule \(k\text {-}ia3_{\ell }\):

which we then proved to be sound on every perfect heterogeneous K-IA3\(_{\ell }\), by the soundness of the ALBA steps. Likewise, the defining condition of K-IA3\(_{\ell }\) translates into the inequality

which, however, is not analytic inductive, and hence it cannot be transformed into an analytic rule via ALBA.
1.2 A.2 Completeness
Let \(A^\tau \vdash B^\tau \) be the translation of any sequent \(A\vdash B\) in the language of \(\text {H.K}\) into the language of \(\text {D.K}\) induced by the correspondence between \(\mathsf {K}\) and \(\mathsf {HK}\) described in Sect. 5.
Proposition 3
For every \(\text {H.K}\)-derivable sequent \(A {\ \vdash \ }B\), the sequent \(A^{\tau } {\ \vdash \ }B^{\tau }\) is derivable in \(\text {D.K}\).
Below we provide the multi-type translations of the single-type sequents corresponding to inequalities (11). All of them are derivable in D.AKA by logical introduction rules, display rules, and the rules \(\,\check{\Box }\, \,\tilde{{\bullet }}\, \) and  .
.

Below we provide the multi-type translations of the single-type sequents corresponding to inequalities (12) and (13), respectively. All of them are derivable in D.AKA by logical introduction rules and display rules.

Below we provide the multi-type translation of the single-type sequents corresponding to inequalities (18). All of them are derivable in D.AKA5’.

Below we provide the multi-type translations of the single-type rules corresponding to quasi-inequality (20), respectively.

Below, we derive (20). Firstly, \(A \wedge \Box _C\, {\bullet _C}\, B {\ \vdash \ }\Diamond _I\, {\bullet _I}\, A \vee B\) is derivable via \(k\text {-}ia3_\ell \) by means of the following derivation \(\mathcal {D}\):

Assuming \(\Diamond _I\, {\bullet _I}\, A {\ \vdash \ }\Diamond _I\, {\bullet _I}\, B\) and \(\Box _C\, {\bullet _C}\, A {\ \vdash \ }\Box _C\, {\bullet _C}\, B\), we derive \(A{\ \vdash \ }B\) via cut as follows:

1.3 A.3 Conservativity
To argue that \(\text {D.K}\) is conservative w.r.t. \(\text {H.K}\), we follow the standard proof strategy discussed in [7, 9]. We need to show that, for all formulas A and B in the language of \(\text {H.K}\), if \(A^\tau \vdash B^\tau \) is a \(\text {D.K}\)-derivable sequent, then \(A \vdash B\) is derivable in \(\text {H.K}\). This claim can be proved using the following facts: (a) The rules of \(\text {D.K}\) are sound w.r.t. perfect members of \(\mathsf {HK}\) (cf. Sect. A.1); (b) \(\text {H.K}\) is complete w.r.t. the class of perfect algebras in \(\mathsf {K}\); (c) A perfect element of \(\mathsf {K}\) is equivalently presented as a perfect member of \(\mathsf {HK}\) so that the semantic consequence relations arising from each type of structures preserve and reflect the translation. Let A, B be as above. If \(A^\tau \vdash B^\tau \) is \(\text {D.K}\)-derivable, then by (a), \(\models _{\mathbb {HK}} A^\tau \vdash B^\tau \). By (c), this implies that \(\models _{\mathsf {K}} A\vdash B\), where \(\models _{\mathsf {K}}\) denotes the semantic consequence relation arising from the perfect members of class \(\mathsf {K}\). By (b), this implies that \(A\vdash B\) is derivable in \(\text {H.K}\), as required.
1.4 A.4 Cut Elimination and Subformula Property
Cut elimination and subformula property for each \(\text {D.K}\) are obtained by verifying the assumptions of [5, Theorem 4.1]. All of them except \(\mathrm {C}'_8\) are readily satisfied by inspecting the rules. Condition \(\mathrm {C}'_8\) requires to check that reduction steps can be performed for every application of cut in which both cut-formulas are principal, which either remove the original cut altogether or replace it by one or more cuts on formulas of strictly lower complexity. In what follows, we only show \(\mathrm {C}'_8\) for some heterogeneous connectives.


The remaining cases are analogous.
Rights and permissions
Copyright information
© 2019 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Greco, G., Jipsen, P., Manoorkar, K., Palmigiano, A., Tzimoulis, A. (2019). Logics for Rough Concept Analysis. In: Khan, M., Manuel, A. (eds) Logic and Its Applications. ICLA 2019. Lecture Notes in Computer Science(), vol 11600. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-58771-3_14
Download citation
DOI: https://doi.org/10.1007/978-3-662-58771-3_14
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-58770-6
Online ISBN: 978-3-662-58771-3
eBook Packages: Computer ScienceComputer Science (R0)


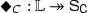 and
and