Anschauliche Vektorgeometrie

Kapitelvorwort

Mit Vektoren wird ein neuer Typ von Zahlobjekten eingeführt, die man addieren, subtrahieren und auf besondere Weise multiplizieren kann. Manche der hier geltenden Rechengesetze sind schon von den reellen Zahlen her bekannt. Sowohl diese Rechenoperationen als auch die Vektoren selbst kann man wieder am besten verstehen, wenn man sie geometrisch veranschaulicht.

Appendices

Aufgaben

17.1

• a) Welche Pfeile gehören zum Vektor $\vec{p}={-2\choose 3}$?

• b) Betrachtet man $\vec{p}$ als Ortsvektor eines Punktes $P$, welcher dieser Pfeile wäre dann geeignet, den Ort von $P$ anzuzeigen?

17.2

Zeichnen Sie mindestens drei verschiedene Pfeile zum Vektor $\vec{p}={-1\choose 5}$, darunter auch den, der die Lage des zugehörigen Punktes $P(-1|5)$ anzeigt.

17.3

Berechnen Sie und veranschaulichen Sie jede Rechnung durch Pfeilkombinationen im Koordinatensystem.

• a) $\displaystyle{1\choose-2}+2\cdot{-3\choose-1}$

• b) $\displaystyle-3\cdot{2\choose 0}-{1\choose 3}$

17.4

Berechnen Sie:

• a) $\displaystyle 2\cdot\left({1\choose 2}-{3\choose 5}\right)+3\cdot{1\choose-2}$

• b) $\displaystyle-\left(\left(\begin{array}[]{c}0\\ -3\\ 2\end{array}\right)+5\cdot\left(\begin{array}[]{c}1\\ 0\\ 4\end{array}\right)\right)+2\cdot\left(\begin{array}[]{c}-3\\ -1\\ 0\end{array}\right)+\left(\begin{array}[]{c}0\\ 0\\ 2\end{array}\right)$

17.5

Ergänzen Sie so, dass die Gleichung stimmt:

• a) $\displaystyle{\Box\choose 3}+{2\choose\Box}={5\choose 4}$

• b) $\displaystyle\Box{2\choose-3}={6\choose-9}$

• c) $\displaystyle\Box\cdot{2\choose 5}+{\Box\choose 5}={9\choose-15}$

17.6

• a) Begründen Sie mittels Vektorrechnung, dass die Punkte $A(2|3)$, $B(0|2)$ und $C(-4|0)$ auf derselben Geraden liegen. Liegt auch der Punkt $D(-6|{-1})$ auf dieser Geraden?

• b) Gegeben seien die Punkte $P(-1|2)$, $Q(-2|{-1})$ und $R(2|{-3})$. Ergänzen Sie diese Punkte so durch einen vierten Punkt $S$, dass ein Parallelogramm entsteht. Begründen Sie Ihre Behauptung mittels Vektorrechnung.

17.7

Gegeben sei ein Viereck mit den Eckpunkten $A(-2|3)$, $B(1|{-4})$, $C(5|2)$ und $D(-3|0)$. Zeigen Sie, dass das aus den Mittelpunkten der Seiten des Vierecks gebildete Viereck ein Parallelogramm ist.

17.8

Nur zwei der drei Geradengleichungen passen zur abgebildeten Geraden. Welche sind dies?

• $\displaystyle g_{1}\colon\vec{x}={2\choose 0}+\lambda{-2\choose 1}$

• $\displaystyle g_{2}\colon\vec{x}={-2\choose 3}+\lambda{2\choose 1}$

• $\displaystyle g_{3}\colon\vec{x}={4\choose-1}+\lambda{4\choose-2}$

Ändern Sie einen Vektor der verbleibenden Gleichung so, dass er ebenfalls zur gezeigten Geraden passt.

17.9

Gegeben seien die Punkte $A(0|0|1)$, $B(2|0|{-1})$ und $C(0|3|4)$. Geben Sie jeweils eine passende Parametergleichung an:

• Die Gerade durch $A$ und $B$

• Die Gerade durch $B$ und $C$

• Die Ebene durch $A$, $B$ und $C$

Geben Sie auch eine Parametergleichung der zu $ABC$ parallelen Ebene durch $D(0|2|3)$ an.

Lösungen zu den Aufgaben

17.1

• a) Es ist $\vec{a}=\vec{e}={-2\choose 3}$.

• b) Der mit $\vec{a}$ bezeichnete Pfeil zeigt zum Punkt mit den Koordinaten $(-2|3)$ und ist damit der gesuchte Ortsvektor. Übrigens bezeichnet $\vec{b}$ den einzigen weiteren Ortsvektor, und zwar zum Punkt mit den Koordinaten $(3|{-2})$.

17.2

Die folgende Grafik zeigt mögliche Pfeile:

17.3

• a) $\displaystyle{1\choose-2}+2\cdot{-3\choose-1}={1\choose-2}+{-6\choose-2}={-5\choose-4}$

  

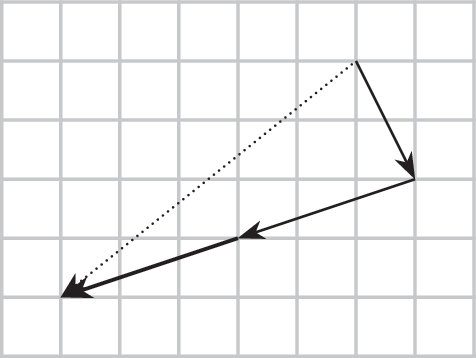
• b) $\displaystyle-3\cdot{2\choose 0}-{1\choose 3}={-6\choose 0}-{1\choose 3}={-7\choose-3}$

  

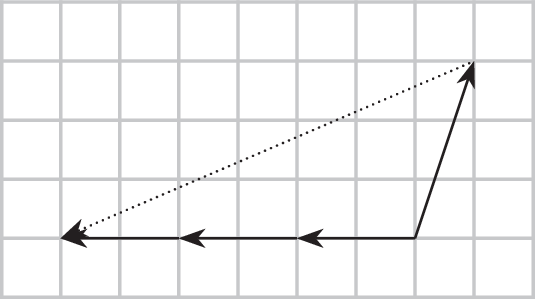
17.4

• a) $\displaystyle 2\cdot\left({1\choose 2}-{3\choose 5}\right)+3\cdot{1\choose-2}=2\cdot{-2\choose-3}+{3\choose-6}={-4\choose-6}+{3\choose-6}={-1\choose-12}$

• b) $\displaystyle-\left(\left(\begin{array}[]{c}0\\ -3\\ 2\end{array}\right)+5\cdot\left(\begin{array}[]{c}1\\ 0\\ 4\end{array}\right)\right)+2\cdot\left(\begin{array}[]{c}-3\\ -1\\ 0\end{array}\right)+\left(\begin{array}[]{c}0\\ 0\\ 2\end{array}\right)=-\left(\left(\begin{array}[]{c}0\\ -3\\ 2\end{array}\right)+\left(\begin{array}[]{c}5\\ 0\\ 20\end{array}\right)\right)+\left(\begin{array}[]{c}-6\\ -2\\ 2\end{array}\right)=\left(\begin{array}[]{c}-11\\ 1\\ -20\end{array}\right)$

17.5

• a) $\displaystyle{3\choose 3}+{2\choose 1}={5\choose 4}$

• b) $\displaystyle 3\cdot{2\choose-3}={6\choose-9}$

• c) $\displaystyle-4\cdot{2\choose 5}+{17\choose 5}={9\choose-15}$

17.6

• a) Es reicht zu zeigen, dass zwei der drei Verbindungsvektoren der drei Punkte parallel sind. Mit $\overrightarrow{AB}={-2\choose-1}$, $\overrightarrow{BC}={-4\choose-2}$ wird deutlich, dass $\overrightarrow{BC}=2\cdot\overrightarrow{AB}$ ist. $A$, $B$ und $C$ liegen also auf einer Geraden. Wegen $\overrightarrow{AD}={-8\choose-4}=4\cdot\overrightarrow{AB}$ liegt auch der Punkt $D$ auf der Geraden.

• b) Behauptung: Der Punkt $S(3|0)$ ist ein solcher Punkt (z. B. durch Ablesen aus einer Zeichnung). Denn man erhält $\overrightarrow{PQ}={-1\choose-3}$, $\overrightarrow{QR}={4\choose-2}$, $\overrightarrow{SR}={-1\choose-3}$ und $\overrightarrow{PS}={4\choose-2}$, woraus folgt, dass $\overrightarrow{PQ}=\overrightarrow{SR}$ (und $\overrightarrow{QR}=\overrightarrow{PS}$) ist. Die gegenüberliegenden Seiten im Viereck $PQRS$ sind also parallel. (Übrigens gibt es neben $S(3|0)$ zwei weitere Punkte, die $ABC$ zu einem Parallelogramm ergänzen. Finden Sie diese und begründen Sie Ihre Behauptung analog.)

17.7

Die Mittelpunkte der Seiten des Vierecks haben die Koordinaten

$$\begin{aligned}\displaystyle&\displaystyle M_{AB}(-0{,}5|{-0{,}5})&\displaystyle&\displaystyle M_{BC}(3|{-1})\\ \displaystyle&\displaystyle M_{CD}(1|1)&\displaystyle&\displaystyle M_{DA}(-2{,}5|1{,}5).\end{aligned}$$

Die Verbindungsvektoren der Mittelpunkte lauten

$$\begin{aligned}\displaystyle\overrightarrow{M_{AB}M_{BC}}&\displaystyle={3{,}5\choose-0{,}5}&\displaystyle\overrightarrow{M_{DA}M_{CD}}&\displaystyle={3{,}5\choose-0{,}5}\\ \displaystyle\overrightarrow{M_{BC}M_{CD}}&\displaystyle={-2\choose 2}&\displaystyle\overrightarrow{M_{AB}M_{DA}}&\displaystyle={-2\choose 2}.\end{aligned}$$

Demzufolge sind die gegenüberliegenden Verbindungsvektoren gleich, d. h., die Mittelpunkte der Seiten des Vierecks bilden ein Parallelogramm.

17.8

$g_{1}$ und $g_{3}$ sind passende Geraden. $g_{2}$ würde dann ebenfalls passen, wenn man z. B. genau eine der beiden Komponenten des Richtungsvektors mit einem negativen Vorzeichen versehen würde.

17.9

Mögliche Parametergleichungen sind

• $\displaystyle g_{AB}\colon\quad\vec{x}=\left(\begin{array}[]{c}2\\ 0\\ -1\end{array}\right)+\lambda\cdot\left(\begin{array}[]{c}-2\\ 0\\ 2\end{array}\right)$

• $\displaystyle g_{BC}\colon\quad\vec{x}=\left(\begin{array}[]{c}2\\ 0\\ -1\end{array}\right)+\lambda\cdot\left(\begin{array}[]{c}-2\\ 3\\ 5\end{array}\right)$

• $\displaystyle E_{ABC}\colon\quad\vec{x}=\left(\begin{array}[]{c}0\\ 0\\ 1\end{array}\right)+\lambda\cdot\left(\begin{array}[]{c}2\\ 0\\ -2\end{array}\right)+\mu\cdot\left(\begin{array}[]{c}0\\ 3\\ 3\end{array}\right)$

  Eine zu $E_{ABC}$ parallele Ebene erhält man schnell, indem man die Richtungsvektoren beibehält und als Stützvektor den Ortsvektor von $D$ verwendet.

• $\displaystyle E_{ABC}\colon\quad\vec{x}=\left(\begin{array}[]{c}0\\ 2\\ 3\end{array}\right)+\lambda\cdot\left(\begin{array}[]{c}2\\ 0\\ -2\end{array}\right)+\mu\cdot\left(\begin{array}[]{c}0\\ 3\\ 3\end{array}\right)$

Ausführliche Lösungen zu den Aufgaben finden Sie im Online-Material.

tiny.cc/to5l1y