Probleme lösen

Kapitelvorwort

Wie bei allen mathematischen Aufgaben wird auch bei mathematischen Problemen aus etwas Gegebenem mithilfe von mathematischen Verarbeitungsschritten etwas Gesuchtes ermittelt. Allerdings sind im Gegensatz zu mathematischen Standardaufgaben beim Problemlösen diese Verarbeitungsschritte nicht von vornherein festgelegt, sondern erfordern oft den Einsatz unterschiedlicher mathematischer Herangehensweisen. Problemstellungen, die im Rahmen des WiMINT-Studiums auftreten, können in unterschiedlichen Formen vorliegen, z. B. als offen formulierter Text, als Grafik, Bild, Tabelle oder Modell.

Der in Ungarn geborene Mathematiker György Pólya (1887–1985) hat in seinem 1967 veröffentlichten Buch „Die Schule des Denkens. Vom Lösen mathematischer Probleme“ die vier Schritte charakterisiert, die notwendig sind, um ein Problem mathematisch zu lösen. Sie machen sich in diesem Kapitel diese vier Schritte bewusst und können am Ende des Kapitels Strategien des Problemlösens anwenden.

Achtung  Probleme mathematisch lösen zu können, gehört zu den allgemeinen mathematischen Kompetenzen. In diesem Kapitel werden in einigen Beispielen und Übungsaufgaben auch Rechentechniken und Lösungsverfahren verwendet, die in den späteren Kapiteln eingehend behandelt werden. Bitte folgen Sie in solchen Fällen den Verweisen im Text.

Appendices

Aufgaben

1.1

Formulieren Sie jeweils mindestens zwei Fragen, um folgende Probleme zu verstehen:

• a) Wie hoch ist eine fünfseitige Pyramide, deren Seitenflächen gleichseitige Dreiecke mit der Seitenlänge 1 m sind?

• b) Gibt es eine Parabel mit dem Scheitel im Ursprung, die den Graphen der Funktion $f$ mit $f(x)=e^{x}$ berührt?

• c) Das Statistische Bundesamt veröffentlichte 2017 folgende Daten über Griechenland:

  Jahr	2007	2010	2013	2016
  BIP$/$Kopf in US-Dollar	28 900	26 973	21 805	17 900
  Arbeitslosenquote in %	8,4	12,73	27,48	23,76

1.2

Beantworten Sie folgende Fragen mithilfe eines mathematischen Modells:

• a) Eine Hohlkugel aus Stahl von $3$ cm Wanddicke hat die Masse $39{,}360$ kg. Die Dichte von Stahl beträgt $7{,}85\,\textnormal{kg}/\textnormal{dm}^{3}$. Wie groß sind der innere und äußere Durchmesser der Hohlkugel? ($\rightarrow$ Abschn. 11.9)

• b) Ist es möglich, einen Balken mit den Maßen $200\,\textnormal{cm}\times 10\,\textnormal{cm}\times 15\,\textnormal{cm}$ durch ein Rohr mit einem Innendurchmesser von 18 cm zu schieben? ($\rightarrow$ Abschn. 11.8)

• c) Fließt durch eine verdünnte Kupfersulfatlösung ein Gleichstrom, so entsteht am negativen Pol metallisches Kupfer. Die abgeschiedene Kupfermenge ist sowohl zur Dauer des Stromflusses als auch zur Stromstärke direkt proportional. Bei einer Stromstärke von $0{,}4$ A werden in 15 Minuten $0{,}12$ g Kupfer abgeschieden. Wie lange dauert es, bis $0{,}2$ g Kupfer bei einer Stromstärke von $0{,}6$ A abgeschieden werden? ($\rightarrow$ Abschn. 5.6)

1.3

Im skizzierten Rechteck sind eine Diagonale und eine Seitenhalbierende eingezeichnet. In welchem Verhältnis teilt deren Schnittpunkt diese beiden Strecken? ($\rightarrow$ Abschn. 11.4)

• a) Wenden Sie bei der Lösung dieser Aufgabe die vier Schritte des Problemlösens an.

• b) Notieren Sie anschließend die Strategien, die zur Lösung geführt haben.

1.4

Bestimmen Sie mit einem elektronischen Hilfsmittel die Lösungen folgender Optimierungsprobleme. ($\rightarrow$ Abschn. 13.7)

• a) Der skizzierte Viertelkreis hat einen Radius von 4 cm. Bestimmen Sie den Punkt $P$, sodass das eingezeichnete Rechteck maximalen Umfang hat.

  

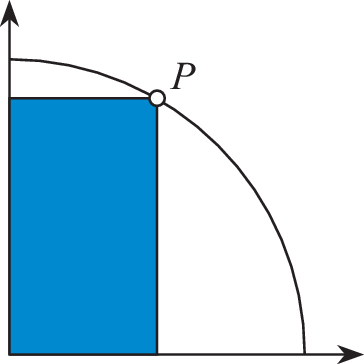
• b) Ein Behälter hat die Form eines Zylinders mit ebenem Boden und aufgesetzter Halbkugel als Deckel. Das Volumen des Behälters einschließlich der Wände soll $5\,\textnormal{m}^{3}$ betragen. Welche Maße hat der Behälter, dessen Oberfläche einschließlich Boden minimal ist?

Lösungen zu den Aufgaben

1.1

• a)

  • Was für eine Grundfläche hat die Pyramide?

  • Welche Eigenschaften haben die Dreiecke, aus denen die Grundfläche zusammengesetzt werden kann?

  • Welche Eigenschaften hat ein Dreieck, das aus der Höhe der Pyramide und einer der Steilkanten gebildet wird?

  • …

• b)

  • Welche Lage hat eine beliebige Ursprungsparabel in Bezug auf das Schaubild von $f$?

  • Wie viele Punkte hat die Normalparabel mit dem Schaubild von $f$ gemeinsam? Wie viele sind es bei einer anderen Ursprungsparabel?

  • Wo müsste ein Berührpunkt der beiden Kurven liegen?

  • Welche Bedingungen gelten für Kurven, die sich berühren?

  • …

• c)

  • Kann man die Entwicklung des BIP$/$Kopf durch eine mathematische Funktion beschreiben?

  • Gibt es eine ähnliche Funktion, mit der man die Entwicklung der Arbeitslosenquote beschreiben kann?

  • Gibt es einen mathematisch begründeten Zusammenhang zwischen der Arbeitslosenquote und dem BIP$/$Kopf?

  • …

1.2

• a) Volumen einer Kugel mit Durchmesser $d$ in cm:

  $$\begin{aligned}\displaystyle V(d)=\frac{1}{6}\pi d^{3}\end{aligned}$$

  Volumen der Hohlkugel:

  $$\displaystyle V=V(d)-V(d-6)=\frac{1}{6}\pi\left(d^{3}-(d-6)^{3}\right)\ [\textnormal{cm}^{3}]$$
  $$\displaystyle{Volumen}=\frac{\textnormal{Masse}}{\textnormal{Dichte}}=\frac{39\,360\,\textnormal{g}}{7{,}85\,\frac{\textnormal{g}}{\textnormal{cm}^{3}}}\approx 5\,014\,\textnormal{cm}^{3}$$
  $$\displaystyle V(d)-V(d-6)=5\,014\quad\Leftrightarrow\quad d\approx 26\leavevmode\nobreak\ (\vee\leavevmode\nobreak\ d\approx-20)$$

  Der äußere Durchmesser ist etwa 26 cm, der innere etwa 20 cm.

• b) Skizze des Sachverhalts:

  

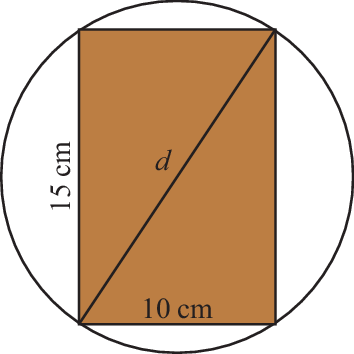
  Diagonale des Balkenquerschnitts $d$:

  $$\begin{aligned}\displaystyle d=\sqrt{\left(10\,\textnormal{cm}\right)^{2}+\left(15\,\textnormal{cm}\right)^{2}}\approx 18{,}03\,\textnormal{cm}\end{aligned}$$

  $d> 18$, also ist der Balken zu groß.

• c) Mit der abgeschiedenen Kupfermenge $M$ in g, der Stromstärke $I$ in A, der Dauer $t$ in h und der Proportionalitätskonstanten $c$ in $\frac{\textnormal{g}}{\textnormal{A\,h}}$ gilt

  $$\begin{aligned}\displaystyle M=c\cdot I\cdot t.\end{aligned}$$

  Damit:

  $$\begin{aligned}\displaystyle&\displaystyle 0{,}12\,\textnormal{g}=c\cdot 0{,}4\,\textnormal{A}\cdot 0{,}25\,\textnormal{h}=0{,}1\,\textnormal{A\,h}\cdot c\\ \displaystyle\Leftrightarrow\quad&\displaystyle c=1{,}2\,\frac{\textnormal{g}}{\textnormal{A\,h}}\end{aligned}$$

  Daraus ergibt sich:

  $$\begin{aligned}\displaystyle t=\frac{M}{c\cdot I}=\frac{0{,}2\,\textnormal{g}}{1{,}2\,\frac{\textnormal{g}}{\textnormal{A\,h}}\cdot 0{,}6\,\textnormal{A}}=\frac{5}{18}\,\textnormal{h}\end{aligned}$$

  Es dauert 16 Minuten und 40 Sekunden.

1.3

1. Schritt::

Gesucht $b:c$ bzw. $d:e$.

2. Schritt::

$b:c=d:e$. Untersuchung von $b:c$ mit dem Strahlensatz.

3. Schritt::

$b:c=a:2a=1:2$.

4. Schritt::

Jede der beiden Strecken wird im Verhältnis $1:2$ geteilt.

Überprüfung z. B. durch Nachmessen an unterschiedlichen Beispielen.

1.4

• a) Bezeichnungen gemäß folgender Skizze:

  

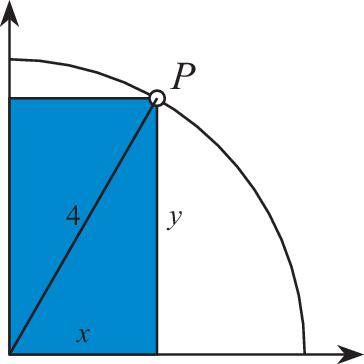
  Damit gilt:

  $$\begin{aligned}\displaystyle&\displaystyle y=\sqrt{16-x^{2}}\\ \displaystyle&\displaystyle U(x)=2x+2\sqrt{16-x^{2}}\quad\textnormal{mit\leavevmode\nobreak\ }x\in[0;4]\\ \displaystyle&\displaystyle U^{\prime}(x)=2-\frac{2x}{\sqrt{16-x^{2}}}\\ \displaystyle&\displaystyle U^{\prime}(x)=0\quad\Leftrightarrow\quad x=2\sqrt{2}\\ \displaystyle&\displaystyle U(0)=U(4)=8\textnormal{ und }U\left(2\sqrt{2}\right)=8\sqrt{2}> 8\end{aligned}$$

  Der Umfang des Rechtecks ist maximal für $P\left(2\sqrt{2}\middle|2\sqrt{2}\right)$.

• b) Skizze des Behälters:

  

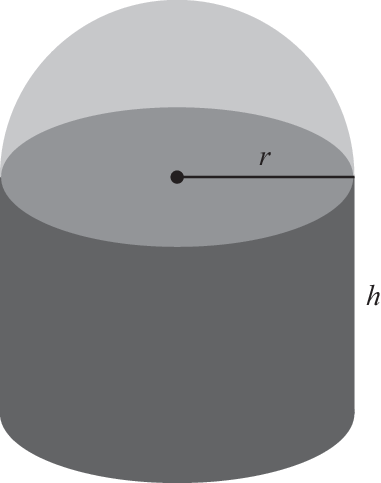
  Volumen des Behälters:

  $$\begin{aligned}\displaystyle 5=\pi r^{2}h+\frac{2}{3}\pi r^{3}\quad\Leftrightarrow\quad h=\frac{5}{\pi r^{2}}-\frac{2}{3}r\end{aligned}$$

  Da $h> 0$, gilt $r<\sqrt[3]{\frac{15}{2\pi}}\approx 1{,}3365$.

  Oberfläche des Behälters:

  $$\begin{aligned}\displaystyle&\displaystyle O=\pi r(3r+2h)\\ \displaystyle&\displaystyle O(r)=\frac{10}{r}+\frac{5}{3}\pi r^{2}\quad\textnormal{mit\leavevmode\nobreak\ }0<r<\sqrt[3]{\frac{15}{2\pi}}\\ \displaystyle&\displaystyle O^{\prime}(r)=-\frac{10}{r^{2}}+\frac{10}{3}\pi r\\ \displaystyle&\displaystyle O^{\prime}(r)=0\quad\Leftrightarrow\quad r=\sqrt[3]{\frac{3}{\pi}}\\ \displaystyle&\displaystyle O\left(\sqrt[3]{\frac{3}{\pi}}\right)=5\sqrt[3]{9\pi}\approx 15{,}23\\ \displaystyle&\displaystyle O(r)\to\infty\textnormal{\leavevmode\nobreak\ f{\"u}r\leavevmode\nobreak\ }r\to 0\quad\textnormal{und}\quad O(r)\to 16{,}835\textnormal{\leavevmode\nobreak\ f{\"u}r\leavevmode\nobreak\ }r\to\sqrt[3]{\frac{15}{2\pi}}\end{aligned}$$

  Minimale Oberfläche für $r=\sqrt[3]{\frac{3}{\pi}}\approx 0{,}985$.

  In diesem Fall ist $h=\frac{5}{\pi r^{2}}-\frac{2}{3}r=\sqrt[3]{\frac{3}{\pi}}=r$.

  Höhe und Radius des optimalen Behälters sind gleich groß, und zwar ungefähr $0{,}985\,\textnormal{m}$.

Ausführliche Lösungen zu den Aufgaben finden Sie im Online-Material.

tiny.cc/to5l1y