Abstract
In this paper, we study doxastic attitudes that emerge on the basis of argumentational reasoning. In order for an agent’s beliefs to be called ‘rational’, they ought to be well-grounded in strong arguments that are constructed by combining her available evidence in a specific way. A study of how these rational and grounded beliefs emerge requires a new logical setting. The language of the logical system in this paper serves this purpose: it is expressive enough to reason about concepts such as factive combined evidence, correctly grounded belief, and infallible knowledge, which are the building blocks on which our notions of argument and grounded belief can be defined. Building further on previous work, we use a topological semantics to represent the structure of an agent’s collection of evidence, and we use input from abstract argumentation theory to single out the relevant sets of evidence to construct the agent’s beliefs. Our paper provides a sound and complete axiom system for the presented logical language, which can describe the given models in full detail, and we show how this setting can be used to explore more intricate epistemic notions.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
- 2.
A topology over a non-empty domain X is a family \(\tau \subseteq 2^X\) containing both X and \(\varnothing \), and is closed under both finite intersections and arbitrary unions. The elements of a topology are called open sets. The topology generated by a given \(\mathcal {Y}\subseteq 2^X\) is the smallest topology \(\tau _{\mathcal {Y}}\) over X such that \(\mathcal {Y}\subseteq \tau _{\mathcal {Y}}\).
- 3.
When no confusion arises, \(\tau _{\mathcal {E}_0}\) will be denoted simply by \(\tau \).
- 4.
In fact, as the first condition implies, it only attacks itself.
- 5.
Attack edges involving the empty set are not drawn.
- 6.
The ‘pullout’ axiom is from [14], where it is used with the operator for evidence \(\mathop {\Box }\).
- 7.
Note that “the agent has argument
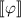 ” is different from “the agent has an argument for
” is different from “the agent has an argument for 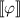 ”. The former is expressed by \(\mathop {{\text {K}}}(\varphi \rightarrow \mathop {\Box }\varphi )\), semantically stating that there is an argument T such that
”. The former is expressed by \(\mathop {{\text {K}}}(\varphi \rightarrow \mathop {\Box }\varphi )\), semantically stating that there is an argument T such that 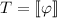 ; the latter corresponds to \(\mathop {\widehat{{\text {K}}}}\mathop {\Box }\varphi \), semantically stating that there is an argument T such that
; the latter corresponds to \(\mathop {\widehat{{\text {K}}}}\mathop {\Box }\varphi \), semantically stating that there is an argument T such that 
- 8.
A similar strategy is used in [16]: show that any consistent set of formulas is satisfiable in a quasi-model, then turn it into a modally-equivalent topological evidence model.
References
Hintikka, J.: Knowledge and Belief. Cornell University Press, Ithaca (1962)
Board, O.: Dynamic interactive epistemology. Games Econ. Behav. 49(1), 49–80 (2004)
Baltag, A., Smets, S.: A qualitative theory of dynamic interactive belief revision. Texts Log. Games 3, 9–58 (2008)
Spohn, W.: Ordinal conditional functions: a dynamic theory of epistemic states. In: Harper, W.L., Skyrms, B. (eds.) Causation in Decision, Belief Change, and Statistics, pp. 105–134. Kluwer, Dordrecht (1988)
van Fraassen, B.C.: Fine-grained opinion, probability, and the logic of full belief. J. Philos. Log. 24(4), 349–377 (1995)
Baltag, A., Smets, S.: Probabilistic dynamic belief revision. In: Johan van Benthem, S.J., Veltman, F. (eds.) A Meeting of the Minds: Proceedings of the Workshop on Logic, Rationality and Interaction, vol. 8 (2007)
Doyle, J.: A truth maintenance system. Artif. Intell. 12(3), 231–272 (1979)
de Kleer, J.: An assumption-based TMS. Artif. Intell. 28(2), 127–162 (1986)
Dung, P.M.: On the acceptability of arguments and its fundamental role in nonmonotonic reasoning, logic programming and n-person games. Artif. Intell. 77, 321–357 (1995)
Grossi, D.: Abstract argument games via modal logic. Synthese 190, 5–29 (2013)
Caminada, M.W.A., Gabbay, D.M.: A logical account of formal argumentation. Stud. Log. 93(2–3), 109 (2009)
Grossi, D., van der Hoek, W.: Justified beliefs by justified arguments. In: Proceedings of the Fourteenth International Conference on Principles of Knowledge Representation and Reasoning, pp. 131–140. AAAI Press (2014)
Artemov, S.N.: The logic of justification. Rev. Symb. Log. 1(4), 477–513 (2008)
van Benthem, J., Pacuit, E.: Dynamic logics of evidence-based beliefs. Stud. Log. 99(1–3), 61–92 (2011)
van Benthem, J., Duque, D.F., Pacuit, E.: Evidence and plausibility in neighborhood structures. Ann. Pure Appl. Log. 165(1), 106–133 (2014)
Baltag, A., Bezhanishvili, N., Özgün, A., Smets, S.: Justified belief and the topology of evidence. In: Väänänen, J., Hirvonen, Å., de Queiroz, R. (eds.) WoLLIC 2016. LNCS, vol. 9803, pp. 83–103. Springer, Heidelberg (2016). https://doi.org/10.1007/978-3-662-52921-8_6
Shi, C., Smets, S., Velázquez-Quesada, F.R.: Argument-based belief in topological structures. In: Lang, J. (ed.) Proceedings Sixteenth Conference on Theoretical Aspects of Rationality and Knowledge, TARK 2017, University of Liverpool, Liverpool, UK, 24–26 June 2017, Volume 251 of Electronic Proceedings in Theoretical Computer Science, pp. 489–503. Open Publishing Association (2017)
van Benthem, J., Fernández-Duque, D., Pacuit, E.: Evidence logic: a new look at neighborhood structures. In: Bolander, T., Braüner, T., Ghilardi, S., Moss, L. (eds.) Proceedings of Advances in Modal Logic, vol. 9, pp. 97–118. King’s College Press (2012)
Özgün, A.: Evidence in epistemic logic: a topological perspective. Ph.D. thesis. Institute for Logic, Language and Computation, Amsterdam, The Netherlands, ILLC Dissertation series DS-2017-07, October 2017
Knaster, B.: Un théorème sur les fonctions d’ensembles. Annales de la Société Polonaise de Mathématiques 6, 133–134 (1928)
Tarski, A.: A lattice-theoretical theorem and its applications. Pac. J. Math. 5(2), 285–309 (1955)
Author information
Authors and Affiliations
Corresponding authors
Editor information
Editors and Affiliations
Completeness for \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)
Completeness for \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)
The proof shows that any \(\mathsf {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-consistent set of \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-formulas is satisfiable. Satisfiability will be proved in an Alexandroff qTA models (see below), which is \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-equivalent to its corresponding TA model.Footnote 8 Here are the details.
Definition 11
(qTA model). A quasi-topological argumentation model (qTA) is a tuple  = \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\) in which \((W, \mathcal {E}_0, \tau , \leftarrowtail , V)\) is a TA model (with \(\tau \) generated by \(\mathcal {E}_0\), as before) and \({\leqslant } \subseteq (W \times W)\) a preorder such that, for every \(E \in \mathcal {E}_0\), if \(u \in E\) and \(u \leqslant v\), then \(v \in E\).
= \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\) in which \((W, \mathcal {E}_0, \tau , \leftarrowtail , V)\) is a TA model (with \(\tau \) generated by \(\mathcal {E}_0\), as before) and \({\leqslant } \subseteq (W \times W)\) a preorder such that, for every \(E \in \mathcal {E}_0\), if \(u \in E\) and \(u \leqslant v\), then \(v \in E\).
Formulas in \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) are interpreted in qTA models just as in TA models. The only difference is \(\mathop {\Box }\), which becomes a normal universal modality for \(\leqslant \). More precisely,  \(w\,\models \,\mathop {\Box }\varphi \) iff for all \(v \in W\), if \(w \leqslant v\) then
\(w\,\models \,\mathop {\Box }\varphi \) iff for all \(v \in W\), if \(w \leqslant v\) then  \(w\,\models \,\mathop {\Box }\varphi \). Now, two topological definitions, a refined qTA model, and the connection.
\(w\,\models \,\mathop {\Box }\varphi \). Now, two topological definitions, a refined qTA model, and the connection.
Definition 12
(Specification preorder). Let \((X,\tau )\) be a topological space. Its specification preorder \({\sqsubseteq _\tau } \subseteq (X \times X) \) is defined, for any \(x, y \in X\), as \(x \sqsubseteq _\tau y\) iff for all \(T \in \tau \), \(x \in T\) implies \(y \in T\).
Definition 13
(Alexandroff space). A topological space \((X, \tau )\) is Alexandroff iff \(\tau \) is closed under arbitrary intersections (i.e., \(\bigcap T \in \tau \) for any \(T \subseteq \tau \)).
Definition 14
(Alexandroff qTA model). A qTA-model  = \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\) is called Alexandroff iff (i) \((W, \tau _{\mathcal {E}_0})\) is Alexandroff, and (ii) \({\leqslant } = {\sqsubseteq _\tau }\).
= \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\) is called Alexandroff iff (i) \((W, \tau _{\mathcal {E}_0})\) is Alexandroff, and (ii) \({\leqslant } = {\sqsubseteq _\tau }\).
Proposition 11
Given an Alexandroff qTA model  = \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\), take \(M= (W, \mathcal {E}_0, \tau , \leftarrowtail , V)\). Then,
= \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\), take \(M= (W, \mathcal {E}_0, \tau , \leftarrowtail , V)\). Then,  for every \(\varphi \in {\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}}\).
for every \(\varphi \in {\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}}\).
Proof
Exactly as that of [19, Proposition 5.6.14] for topological evidence models and \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}}\), as \(\mathop {\mathfrak {T}}\) has the same truth condition in qTA and TA models.
For notation, define \(\varGamma ^\bigcirc = \{\varphi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\mid \bigcirc \varphi \in \varGamma \}\) for \(\varGamma \subseteq \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) and \(\bigcirc \in \{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}\}\). For the proof, let \(\varPhi _0\) be a \(\mathsf {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-consistent set of \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-formulas. A slightly modified version of Lindenbaum Lemma shows that it can be extended to a maximal consistent one. Let \({\text {MCS}}\) be the family of all maximally \(\mathsf {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-consistent sets of \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-formulas; let \(\varPhi \) be an element of \({\text {MCS}}\) extending \(\varPhi _0\).
Definition 15
(Canonical qTA model). The canonical qTA model for \(\varPhi \),  = \((W^\varPhi , \mathcal {E}_0^\varPhi , \leqslant ^\varPhi , \leftarrowtail ^\varPhi , V^\varPhi )\), is defined as follows.
= \((W^\varPhi , \mathcal {E}_0^\varPhi , \leqslant ^\varPhi , \leftarrowtail ^\varPhi , V^\varPhi )\), is defined as follows.
-
\(W^\varPhi := \{ \varGamma \in {\text {MCS}}\mid \varGamma ^{\mathop {{\text {K}}}} = \varPhi ^{\mathop {{\text {K}}}} \}\) and \(V^\varPhi (p) := \{ \varGamma \in W^\varPhi \mid p \in \varGamma \}\).
-
For \(\varGamma , \varDelta \in W^\varPhi \), \( \varGamma \leqslant ^\varPhi \varDelta \quad iff _{ def }\quad \text {for any } \varphi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}},\; \mathop {\Box }\varphi \in \varGamma \text { implies } \varphi \in \varDelta . \)
-
For any \(\varGamma \in W^\varPhi \), define the set \({\leqslant ^{\varPhi }}[\varGamma ] := \{ \varOmega \in W^\varPhi \mid \varGamma \leqslant ^\varPhi \varOmega \}\). Then, let \( \mathcal {E}_0^\varPhi := \{ \bigcup _{\varGamma \in U} {\leqslant ^{\varPhi }}[\varGamma ] \mid U \subseteq W^\varPhi \} \setminus \{\varnothing \}. \)
While \(\leqslant ^\varPhi \) and \(V^{\varPhi }\) are standard (recall: \(\mathop {\Box }\) is a normal universal modality for \(\leqslant \)), each \(E \in \mathcal {E}_0^{\varPhi }\) is a non-empty union of the \(\leqslant ^{\varPhi }\)-upwards closure of the elements of some subset of \(W^{\varPhi }\). The last component, the attack relation \(\leftarrowtail ^{\varPhi }\), is the novel one in this model, and it requires more care. First, define \( \{\!\vert \varphi \vert \!\}_M:= \{ \varGamma \in W^{\varPhi } \mid \varphi \in \varGamma \}. \) Then, by taking \(\tau ^\varPhi \) to be the topology generated by \(\mathcal {E}_0^\varPhi \) define, for any \(T, T' \in \tau ^\varPhi \),
In the rest, and when no confusion arises, the superscript \(\varPhi \) will be omitted.
Note how  is indeed a qTA model (Definition 11). First, it is clear that \(\varnothing \notin \mathcal {E}_0\) and \(W \in \mathcal {E}_0\). Moreover, \(\leqslant \) is indeed a preorder (see its axioms) satisfying the extra condition. Finally, it can be proved that \(\leftarrowtail \) satisfies the three conditions.
is indeed a qTA model (Definition 11). First, it is clear that \(\varnothing \notin \mathcal {E}_0\) and \(W \in \mathcal {E}_0\). Moreover, \(\leqslant \) is indeed a preorder (see its axioms) satisfying the extra condition. Finally, it can be proved that \(\leftarrowtail \) satisfies the three conditions.
Lemma 1
Let  = \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\) be the model of Definition 15. Then,
= \((W, \mathcal {E}_0, \leqslant , \leftarrowtail , V)\) be the model of Definition 15. Then,
-
1.
for every \(T_1, T_2 \in \tau \): \(T_1 \cap T_2 = \varnothing \) if and only if \(T_1 \leftarrowtail T_2\) or \(T_2 \leftarrowtail T_1\);
-
2.
for every \(T, T_1, T'_1 \in \tau \): if \(T_1 \leftarrowtail T\) and \(T'_1 \subseteq T_1\), then \(T'_1 \leftarrowtail T\);
-
3.
for every \(T \in \tau \setminus \{\varnothing \}\): \(\varnothing \leftarrowtail T\) and \(T \not \leftarrowtail \varnothing \).
Thus,  is a qTA model. The next proposition (standard proof) provides existence lemmas for the standard modality \(\mathop {\Box }\) and the global modality \(\mathop {\widehat{{\text {K}}}}\).
is a qTA model. The next proposition (standard proof) provides existence lemmas for the standard modality \(\mathop {\Box }\) and the global modality \(\mathop {\widehat{{\text {K}}}}\).
Proposition 12
For any \(\varphi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) and any \(\varGamma \in W\):
-
\(\mathop {\Diamond }\varphi \in \varGamma \) iff there is \(\varDelta \in W\) s.t. \(\varGamma \leqslant \varDelta \) and \(\varphi \in \varDelta \).
-
\(\mathop {\widehat{{\text {K}}}}\varphi \in \varGamma \) iff there is \(\varDelta \in W\) s.t. \(\varphi \in \varDelta \).
Now, tools to prove a similar result for the operator \(\mathop {\mathfrak {T}}\), whose truth clause relies on  , given by \(\leftarrowtail \). First, some useful properties of the model.
, given by \(\leftarrowtail \). First, some useful properties of the model.
Fact 1
(1) \(\tau = \mathcal {E}_0\cup \{\varnothing \}\). (2)If \(\mathop {\widehat{{\text {K}}}}\mathop {\Box }\varphi \in \varPhi \), then \(\{\!\vert \mathop {\Box }\varphi \vert \!\} \in \tau \). (3) If \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi \in \varPhi \), then \(\{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\} \in \tau \). (4) For any \(T \in \tau \) and any \(\varphi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\): if \(T \subseteq \{\!\vert \varphi \vert \!\}\), then \(T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\).
Here are the first steps towards locating  .
.
Definition 16
(Semi-acceptable and Acceptable). Define \(\mathcal {C}_1\) as
\(\mathcal {C}_1= \{ T \in \tau \mid \text {there exists } \varphi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\text { such that } \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\} \subseteq T \text { and } \mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi \in \varPhi \}\)
-
An open \(T \in \tau \) is semi-acceptable if and only if, for any \(\psi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) with \(T \subseteq \{\!\vert \mathop {\Box }\psi \vert \!\}\), there is \(\xi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) such that \(\{\!\vert \mathop {\mathfrak {T}}\xi \vert \!\} \subseteq \{\!\vert \mathop {\Box }\psi \vert \!\}\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\xi \in \varPhi \).
-
An open \(T \in \tau \) is acceptable if and only if T is semi-acceptable and there is no \(T' \in \tau \) such that \(T \cap T' = \varnothing \) and \(T' \cap T'' \ne \varnothing \) for all \(T'' \in \mathcal {C}_1\).
Define \(\mathcal {C}_2\) as \(\mathcal {C}_2= \{T \in \tau \setminus \mathcal {C}_1\mid T \text { is acceptable} \}\).
Note that no element of \(\mathcal {C}_1\) is attacked by elements of \(\tau \). Moreover,
Fact 2
(i) For any \(T \in \tau \), if \(T \in \mathcal {C}_1\), then T is acceptable. (ii) If \(T \in \tau \) is semi-acceptable, then \(T \cap T' \ne \varnothing \) for all \(T' \in \mathcal {C}_1\).
Lemma 2
Let \(\mathcal {C}= \mathcal {C}_1\cup \mathcal {C}_2\). Then,  .
.
Proof
\(\varvec{(\supseteq })\) The proof of this direction can be fulfilled by checking two cases (i) \(T \in \mathcal {C}_1\) and (ii) \(T \in \mathcal {C}_2\), which is relatively simple, so we turn to the details of the other direction’s proof.
\(\varvec{(\subseteq })\) Take now \(T \in \tau \) such that \(T \notin \mathcal {C}\); it will be shown that  . The case with \(T = \varnothing \) is immediate, as \(\varnothing \leftarrowtail \varnothing \). Thus, suppose \(T \ne \varnothing \).
. The case with \(T = \varnothing \) is immediate, as \(\varnothing \leftarrowtail \varnothing \). Thus, suppose \(T \ne \varnothing \).
From \(T \notin \mathcal {C}\) it follows that \(T \notin \mathcal {C}_1\), so there is no \(\phi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) such that \(\{\!\vert \mathop {\mathfrak {T}}\phi \vert \!\} \subseteq T\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\phi \in \varPhi \); hence, from \(\leftarrowtail \)’s definition, every \(T' \in \tau \) with \(T \cap T' = \varnothing \) is such that \(T \leftarrowtail T'\). It can be proved by using axiom \(\mathop {{\text {K}}}\mathop {\Diamond }\mathop {\Box }\varphi \rightarrow \mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi \) that there is at least one \(T' \in \tau \) with \(T \cap T' = \varnothing \). Thus, the rest of the proof is divided into two cases: either there is \(T' \in \tau \) with \(T \cap T' = \varnothing \) and \(T' \in \mathcal {C}\) (at least one \(T'\) contradicting T is in \(\mathcal {C}\)), or else for any \(T'\in \tau \) with \(T \cap T' = \varnothing \), \(T'\notin \mathcal {C}\) (no \(T'\) contradicting T is in \(\mathcal {C}\)). In the first case, take any \(T' \in \tau \) such that \(T \cap T' = \varnothing \) and \(T' \in \mathcal {C}\). Then, as it has been argued, \(T \leftarrowtail T'\); moreover, as it has been proved,  . Thus,
. Thus,  , as
, as  has to be conflict-free.
has to be conflict-free.
In the second case, it follows that \(C \in \mathcal {C}\) implies \(T \cap C \ne \varnothing \). Now, consider the following two sub-cases: either T is semi-acceptable, or it is not. Next, we prove that in both two cases, \(T\notin d(\mathcal {C})\). The case where T is semi-acceptable is relatively easy, so we focus on the case where T is not semi-acceptable.
If T is not semi-acceptable, there is \(\varphi _T \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) such that \(T \subseteq \{\!\vert \mathop {\Box }\varphi _T \vert \!\}\) and there is no \(\psi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) such that both \(\{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\} \subseteq \{\!\vert \mathop {\Box }\varphi _T \vert \!\}\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\psi \in \varPhi \). In particular, \(\varphi _T\) itself cannot be such \(\psi \), so either \(\{\!\vert \mathop {\mathfrak {T}}\varphi _T \vert \!\} \not \subseteq \{\!\vert \mathop {\Box }\varphi _T \vert \!\}\) or else \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi _T \not \in \varPhi \). But axiom \(\mathop {\mathfrak {T}}\varphi \rightarrow \mathop {\Box }\varphi \) implies \(\{\!\vert \mathop {\mathfrak {T}}\varphi _T \vert \!\}\subseteq \{\!\vert \mathop {\Box }\varphi _T \vert \!\}\), so \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi _T \notin \varPhi \). Now, take any \(C \in \mathcal {C}_1\); let \(\varphi _C \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) be one of the formulas satisfying both \(\{\!\vert \mathop {\mathfrak {T}}\varphi _C \vert \!\} \subseteq C\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi _C \in \varPhi \) (by \(\mathcal {C}\)’s definition, there is at least one). From theorem \(\mathop {\mathfrak {T}}\varphi \rightarrow \mathop {\Box }\mathop {\mathfrak {T}}\varphi \), it follows that \((\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C) \rightarrow (\mathop {\Box }\varphi _T \wedge \mathop {\Box }\mathop {\mathfrak {T}}\varphi _C)\) is a theorem too, and thus so are \((\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C) \rightarrow (\mathop {\Box }\mathop {\Box }\varphi _T \wedge \mathop {\Box }\mathop {\mathfrak {T}}\varphi _C)\) (by axiom \(\mathop {\Box }\varphi \rightarrow \mathop {\Box }\mathop {\Box }\varphi \)) and \((\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C) \rightarrow \mathop {\Box }(\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C)\) (axiom K for \(\mathop {\Box }\)). Hence, by Proposition 12, \(\mathop {{\text {K}}}\big ((\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C) \rightarrow \mathop {\Box }(\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C) \big ) \in \varPhi \).
So far we have \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi _T \notin \varPhi \) and, for every \(C \in \mathcal {C}_1\), not only \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi _C \in \varPhi \) but also \(\mathop {{\text {K}}}\big ((\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C) \rightarrow \mathop {\Box }(\mathop {\Box }\varphi _T \wedge \mathop {\mathfrak {T}}\varphi _C) \big ) \in \varPhi \). The first and theorem \(\mathop {\mathfrak {T}}\varphi \leftrightarrow \mathop {\mathfrak {T}}\mathop {\Box }\varphi \) imply \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\mathop {\Box }\varphi _T \notin \varPhi \); the second and axiom \(\mathop {\mathfrak {T}}\varphi \rightarrow \mathop {\mathfrak {T}}\mathop {\mathfrak {T}}\varphi \) imply \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\mathop {\mathfrak {T}}\varphi _C \in \varPhi \). These two, the third, and axiom \(\big (\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi \wedge \lnot \mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\psi \wedge \mathop {{\text {K}}}((\varphi \wedge \psi ) \rightarrow \mathop {\Box }(\varphi \wedge \psi ))\big ) \rightarrow \mathop {\widehat{{\text {K}}}}\mathop {\Box }(\varphi \wedge \lnot \psi )\) imply \(\mathop {\widehat{{\text {K}}}}\mathop {\Box }(\mathop {\mathfrak {T}}\varphi _C \wedge \lnot \mathop {\Box }\varphi _T) \in \varPhi \). For the final part, take the union of \(\{\!\vert \mathop {\Box }(\mathop {\mathfrak {T}}\varphi _C \wedge \lnot \mathop {\Box }\varphi _T) \vert \!\}\) for all \(C \in \mathcal {C}_1\), i.e.
\(S = \bigcup _{C \in \mathcal {C}_1} \{\!\vert \mathop {\Box }(\mathop {\mathfrak {T}}\varphi _C \wedge \lnot \mathop {\Box }\varphi _T) \vert \!\}\)
The following two facts about S (whose proof we omit here) are key to what we want to prove (\(T \notin d(\mathcal {C})\)): (i) \(S \cap T = \varnothing \). (ii) For any \(C' \in \mathcal {C}\), \(C' \cap S \ne \varnothing \). Since \(S \cap T = \varnothing \) and T is not semi-acceptable (so there is no \(\varphi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) s.t. both \(\{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\} \subseteq T\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi \in \varPhi \)), we have found an open S in \(\tau \) with \(T \leftarrowtail S\), according to the definition of \(\leftarrowtail \). But \(S \cap C \ne \varnothing \) for all \(C \in \mathcal {C}\), so \(S \not \leftarrowtail C\) for all \(C \in \mathcal {C}\): no open in \(\mathcal {C}\) attacks S. Hence, \(T \notin d(\mathcal {C})\).
Therefore, regardless of whether T is semi-acceptable or not, we have \(T \notin d(\mathcal {C})\). Since d is monotonic and  (as it has been shown), it follows that
(as it has been shown), it follows that  , which implies
, which implies  .
.
Thus, in both cases \(T \notin \mathcal {C}\) implies  . This completes the proof.
. This completes the proof.
Proposition 13
(Truth lemma). For any \(\varphi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) and any \(\varGamma \in W\),

Proof
The proof proceeds by induction, with the cases for atomic propositions and Boolean connectives being routine, and those for and \(\mathop {\Box }\) and \(\mathop {{\text {K}}}\) relying on Proposition 12. Here we focus on the case for \(\mathop {\mathfrak {T}}\).
From left to right, suppose \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\). Then, \(\mathop {\mathfrak {T}}\varphi \in \varGamma \) so, by Proposition 12, \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi \in \varPhi \) which, by item 3 of Fact 1, implies \(\{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\} \in \tau \). Now, let \(T = \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\). Then,(i) from \(\{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\} \subseteq T\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\varphi \in \varPhi \), it follows that \(T \in \mathcal {C}_1\) which, by Lemma 2, implies  ; (ii) \(\varGamma \in T\), as \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\); (iii) from axiom \(\mathop {\mathfrak {T}}\varphi \rightarrow \varphi \) it follows that \(T \subseteq \{\!\vert \varphi \vert \!\}\) which, by inductive hypothesis
; (ii) \(\varGamma \in T\), as \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\); (iii) from axiom \(\mathop {\mathfrak {T}}\varphi \rightarrow \varphi \) it follows that \(T \subseteq \{\!\vert \varphi \vert \!\}\) which, by inductive hypothesis  implies
implies  Hence, by \(\mathop {\mathfrak {T}}\)’s truth condition, \(\varGamma \in \llbracket \mathop {\mathfrak {T}}\varphi \rrbracket \).
Hence, by \(\mathop {\mathfrak {T}}\)’s truth condition, \(\varGamma \in \llbracket \mathop {\mathfrak {T}}\varphi \rrbracket \).
From right to left, suppose \(\varGamma \in \llbracket \mathop {\mathfrak {T}}\varphi \rrbracket \). Then, by \(\mathop {\mathfrak {T}}\)’s truth condition, there is  with \(\varGamma \in T\) and
with \(\varGamma \in T\) and  But, from
But, from  ’s definition, \(\varGamma \in T\) implies \({\leqslant }[\varGamma ] \subseteq T\); hence, by \(\mathop {\Box }\)’s truth condition, \(T \subseteq \llbracket \mathop {\Box }\varphi \rrbracket \). The inductive hypothesis implies \(\llbracket \mathop {\Box }\varphi \rrbracket = \{\!\vert \mathop {\Box }\varphi \vert \!\}\), so then we have \(\varGamma \in T\) and \(T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\).
’s definition, \(\varGamma \in T\) implies \({\leqslant }[\varGamma ] \subseteq T\); hence, by \(\mathop {\Box }\)’s truth condition, \(T \subseteq \llbracket \mathop {\Box }\varphi \rrbracket \). The inductive hypothesis implies \(\llbracket \mathop {\Box }\varphi \rrbracket = \{\!\vert \mathop {\Box }\varphi \vert \!\}\), so then we have \(\varGamma \in T\) and \(T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\).
By Lemma 2,  ; thus, \(T \in \mathcal {C}_1\cup \mathcal {C}_2\). Suppose \(T \in \mathcal {C}_1\); then there is \(\psi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) with \(\{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\} \subseteq T\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\psi \in \varPhi \). Thus, \(\{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\} \subseteq T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\), so \(\mathop {{\text {K}}}(\mathop {\mathfrak {T}}\psi \rightarrow \mathop {\Box }\varphi ) \in \varPhi \). Now, take any \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\}\); then, \(\mathop {{\text {K}}}(\mathop {\mathfrak {T}}\psi \rightarrow \mathop {\Box }\varphi ) \in \varDelta \). This, together with theorem \(\mathop {{\text {K}}}(\varphi \rightarrow \psi ) \rightarrow (\mathop {\mathfrak {T}}\varphi \rightarrow \mathop {\mathfrak {T}}\psi )\) (Proposition 4), implies \(\mathop {\mathfrak {T}}\mathop {\mathfrak {T}}\psi \rightarrow \mathop {\mathfrak {T}}\mathop {\Box }\varphi \in \varDelta \). Moreover: \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\}\) implies \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\mathop {\mathfrak {T}}\psi \vert \!\}\), so \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\mathop {\Box }\varphi \vert \!\}\), that is, \(\mathop {\mathfrak {T}}\mathop {\Box }\varphi \in \varDelta \). The latter, together with theorem \(\mathop {\mathfrak {T}}\varphi \leftrightarrow \mathop {\mathfrak {T}}\mathop {\Box }\varphi \) and axiom \(\mathop {\mathfrak {T}}\varphi \rightarrow \mathop {{\text {K}}}(\mathop {\Box }\varphi \rightarrow \mathop {\mathfrak {T}}\varphi )\), imply \(\mathop {{\text {K}}}(\mathop {\Box }\varphi \rightarrow \mathop {\mathfrak {T}}\varphi ) \in \varDelta \), and thus \(\mathop {{\text {K}}}(\mathop {\Box }\varphi \rightarrow \mathop {\mathfrak {T}}\varphi ) \in \varPhi \). Hence, \(\{\!\vert \mathop {\Box }\varphi \vert \!\} \subseteq \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\) and thus, since \(\varGamma \in T\) and \(T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\), we have \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\). Otherwise, \(T \in \mathcal {C}_2\), and hence for any \(\psi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) with \(T \subseteq \{\!\vert \mathop {\Box }\psi \vert \!\}\) there is \(\xi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) with \(\{\!\vert \mathop {\mathfrak {T}}\xi \vert \!\} \subseteq \{\!\vert \mathop {\Box }\psi \vert \!\}\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\xi \in \varPhi \). Thus, since \(\varphi \) is such that \(T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\), there is \(\eta \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) such that \(\{\!\vert \mathop {\mathfrak {T}}\eta \vert \!\} \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\eta \in \varPhi \). From here we can repeat the argument used in the case of \(T \in \mathcal {C}_1\) in order to get \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\) again. Thus, in both cases, \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\), which completes the proof.
; thus, \(T \in \mathcal {C}_1\cup \mathcal {C}_2\). Suppose \(T \in \mathcal {C}_1\); then there is \(\psi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) with \(\{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\} \subseteq T\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\psi \in \varPhi \). Thus, \(\{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\} \subseteq T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\), so \(\mathop {{\text {K}}}(\mathop {\mathfrak {T}}\psi \rightarrow \mathop {\Box }\varphi ) \in \varPhi \). Now, take any \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\}\); then, \(\mathop {{\text {K}}}(\mathop {\mathfrak {T}}\psi \rightarrow \mathop {\Box }\varphi ) \in \varDelta \). This, together with theorem \(\mathop {{\text {K}}}(\varphi \rightarrow \psi ) \rightarrow (\mathop {\mathfrak {T}}\varphi \rightarrow \mathop {\mathfrak {T}}\psi )\) (Proposition 4), implies \(\mathop {\mathfrak {T}}\mathop {\mathfrak {T}}\psi \rightarrow \mathop {\mathfrak {T}}\mathop {\Box }\varphi \in \varDelta \). Moreover: \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\psi \vert \!\}\) implies \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\mathop {\mathfrak {T}}\psi \vert \!\}\), so \(\varDelta \in \{\!\vert \mathop {\mathfrak {T}}\mathop {\Box }\varphi \vert \!\}\), that is, \(\mathop {\mathfrak {T}}\mathop {\Box }\varphi \in \varDelta \). The latter, together with theorem \(\mathop {\mathfrak {T}}\varphi \leftrightarrow \mathop {\mathfrak {T}}\mathop {\Box }\varphi \) and axiom \(\mathop {\mathfrak {T}}\varphi \rightarrow \mathop {{\text {K}}}(\mathop {\Box }\varphi \rightarrow \mathop {\mathfrak {T}}\varphi )\), imply \(\mathop {{\text {K}}}(\mathop {\Box }\varphi \rightarrow \mathop {\mathfrak {T}}\varphi ) \in \varDelta \), and thus \(\mathop {{\text {K}}}(\mathop {\Box }\varphi \rightarrow \mathop {\mathfrak {T}}\varphi ) \in \varPhi \). Hence, \(\{\!\vert \mathop {\Box }\varphi \vert \!\} \subseteq \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\) and thus, since \(\varGamma \in T\) and \(T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\), we have \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\). Otherwise, \(T \in \mathcal {C}_2\), and hence for any \(\psi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) with \(T \subseteq \{\!\vert \mathop {\Box }\psi \vert \!\}\) there is \(\xi \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) with \(\{\!\vert \mathop {\mathfrak {T}}\xi \vert \!\} \subseteq \{\!\vert \mathop {\Box }\psi \vert \!\}\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\xi \in \varPhi \). Thus, since \(\varphi \) is such that \(T \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\), there is \(\eta \in \mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\) such that \(\{\!\vert \mathop {\mathfrak {T}}\eta \vert \!\} \subseteq \{\!\vert \mathop {\Box }\varphi \vert \!\}\) and \(\mathop {\widehat{{\text {K}}}}\mathop {\mathfrak {T}}\eta \in \varPhi \). From here we can repeat the argument used in the case of \(T \in \mathcal {C}_1\) in order to get \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\) again. Thus, in both cases, \(\varGamma \in \{\!\vert \mathop {\mathfrak {T}}\varphi \vert \!\}\), which completes the proof.
Lemma 3
 is Alexandroff.
is Alexandroff.
Proof
Whether  is Alexandroff has nothing to do with \(\leftarrowtail \); thus, we can apply Proposition 5.6.15 in [19], which states that if \(\tau = \{\bigcup _{\varGamma \in U} {\leqslant }[\varGamma ] \mid U \subseteq W\}\) then
is Alexandroff has nothing to do with \(\leftarrowtail \); thus, we can apply Proposition 5.6.15 in [19], which states that if \(\tau = \{\bigcup _{\varGamma \in U} {\leqslant }[\varGamma ] \mid U \subseteq W\}\) then  is Alexandroff. But item 1 of Fact 1 and the definition of \(\mathcal {E}_0\) imply the required condition; then,
is Alexandroff. But item 1 of Fact 1 and the definition of \(\mathcal {E}_0\) imply the required condition; then,  is Alexandroff.
is Alexandroff.
Since  is Alexandroff, Proposition 11 tells us it has a modally equivalent topological argumentation model. Hence, the \(\mathsf {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-consistent set of \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-formulas \(\varPhi _0\) is satisfiable in a topological argumentation model.
is Alexandroff, Proposition 11 tells us it has a modally equivalent topological argumentation model. Hence, the \(\mathsf {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-consistent set of \(\mathcal {L}_{\mathop {\Box }, \mathop {{\text {K}}}, \mathop {\mathfrak {T}}}\)-formulas \(\varPhi _0\) is satisfiable in a topological argumentation model.
Rights and permissions
Copyright information
© 2018 Springer-Verlag GmbH Germany, part of Springer Nature
About this paper
Cite this paper
Shi, C., Smets, S., Velázquez-Quesada, F.R. (2018). Beliefs Based on Evidence and Argumentation. In: Moss, L., de Queiroz, R., Martinez, M. (eds) Logic, Language, Information, and Computation. WoLLIC 2018. Lecture Notes in Computer Science(), vol 10944. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-57669-4_17
Download citation
DOI: https://doi.org/10.1007/978-3-662-57669-4_17
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-57668-7
Online ISBN: 978-3-662-57669-4
eBook Packages: Computer ScienceComputer Science (R0)


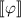 ” is different from “the agent has an argument for
” is different from “the agent has an argument for 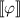 ”. The former is expressed by
”. The former is expressed by 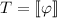 ; the latter corresponds to
; the latter corresponds to 
