Abstract
Strictly positive logics recently attracted attention both in the description logic and in the provability logic communities for their combination of efficiency and sufficient expressivity. The language of Reflection Calculus RC consists of implications between formulas built up from propositional variables and the constant ‘true’ using only conjunction and the diamond modalities which are interpreted in Peano arithmetic as restricted uniform reflection principles.
We extend the language of \(\mathrm {RC}\) by another series of modalities representing the operators associating with a given arithmetical theory T its fragment axiomatized by all theorems of T of arithmetical complexity \(\varPi ^0_n\), for all \(n>0\). We note that such operators, in a precise sense, cannot be represented in the full language of modal logic.
We formulate a formal system extending \(\mathrm {RC}\) that is sound and, as we conjecture, complete under this interpretation. We show that in this system one is able to express iterations of reflection principles up to any ordinal \(<\varepsilon _0\). On the other hand, we provide normal forms for its variable-free fragment. Thereby, the variable-free fragment is shown to be algorithmically decidable and complete w.r.t. its natural arithmetical semantics.
This work is supported by the Russian Science Foundation under grant 16–11–10252.
Access this chapter
Tax calculation will be finalised at checkout
Purchases are for personal use only
Notes
- 1.
The paper [3] is a longer version of the present one containing additional material and more detailed proofs of some results.
- 2.
Over \(\mathrm {EA}+\mathrm {B\varSigma }_1\) one can work with a natural r.e. axiomatization of \(\mathrm {\varPi }_n(S)\).
References
Beklemishev, L.: A note on strictly positive logics and word rewriting systems. Preprint ArXiv:1509.00666 [math.LO] (2015)
Beklemishev, L.D., Onoprienko, A.A.: On some slowly terminating term rewriting systems. Sbornik: Math. 206, 1173–1190 (2015)
Beklemishev, L.D.: Reflection calculus and conservativity spectra. ArXiv:1703.09314 [math.LO], March 2017
Beklemishev, L.D.: Proof-theoretic analysis by iterated reflection. Arch. Math. Logic 42, 515–552 (2003). doi:10.1007/s00153-002-0158-7
Beklemishev, L.D.: Provability algebras and proof-theoretic ordinals, I. Ann. Pure Appl. Logic 128, 103–123 (2004)
Beklemishev, L.D.: Reflection principles and provability algebras in formal arithmetic. Russ. Math. Surv. 60(2), 197–268 (2005). Russian original. Uspekhi Matematicheskikh Nauk 60(2), 3–78 (2005)
Beklemishev, L.D.: The Worm principle. In: Chatzidakis, Z., Koepke, P., Pohlers, W. (eds.) Lecture Notes in Logic 27. Logic Colloquium 2002, pp. 75–95. AK Peters (2006). Preprint: Logic Group Preprint Series 219, Utrecht University, March 2003
Beklemishev, L.D.: Calibrating provability logic: from modal logic to reflection calculus. In: Bolander, T., Braüner, T., Ghilardi, S., Moss, L. (eds.) Advances in Modal Logic, vol. 9, pp. 89–94. College Publications, London (2012)
Beklemishev, L.D.: Positive provability logic for uniform reflection principles. Ann. Pure Appl. Logic 165(1), 82–105 (2014)
Beklemishev, L.D.: On the reduction property for GLP-algebras. Doklady: Math. 95(1), 50–54 (2017)
Beklemishev, L.D., Joosten, J., Vervoort, M.: A finitary treatment of the closed fragment of Japaridze’s provability logic. J. Logic Comput. 15(4), 447–463 (2005)
Boolos, G.: The Logic of Provability. Cambridge University Press, Cambridge (1993)
Dashkov, E.V.: On the positive fragment of the polymodal provability logic GLP. Matematicheskie Zametki 91(3), 331–346 (2012). English translation. Math. Notes 91(3), 318–333 (2012)
de Jongh, D., Japaridze, G.: The Logic of Provability. In: Buss, S.R. (ed.) Handbook of Proof Theory. Studies in Logic and the Foundations of Mathematics, vol. 137, pp. 475–546. Elsevier, Amsterdam (1998)
Feferman, S.: Arithmetization of metamathematics in a general setting. Fundamenta Math. 49, 35–92 (1960)
Goris, E., Joosten, J.J.: A new principle in the interpretability logic of all reasonable arithmetical theories. Logic J. IGPL 19(1), 1–17 (2011)
Ignatiev, K.N.: On strong provability predicates and the associated modal logics. J. Symbolic Logic 58, 249–290 (1993)
Japaridze, G.K.: The modal logical means of investigation of provability. Thesis in Philosophy, in Russian, Moscow (1986)
Joosten, J., Reyes, E.H.: Turing Schmerl logic for graded Turing progressions. ArXiv:1604.08705v1 [math.LO] (2016)
Joosten, J.J.: Turing-Taylor expansions of arithmetical theories. Stud. Log. 104, 1225–1243 (2015). doi:10.1007/s11225-016-9674-z
Kikot, S., Kurucz, A., Tanaka, Y., Wolter, F., Zakharyaschev, M.: On the completeness of EL-equiations: first results. In: 11th International Conference on Advances in Modal Logic, Short Papers (Budapest, 30 August–2 September 2016), pp. 82–87 (2016)
Pakhomov, F.: On the complexity of the closed fragment of Japaridze’s provability logic. Arch. Math. Logic 53(7), 949–967 (2014)
Pakhomov, F.: On elementary theories of ordinal notation systems based on reflection principles. Proc. Steklov Inst. Math. 289, 194–212 (2015)
Shamkanov, D.: Nested sequents for provability logic GLP. Logic J. IGPL 23(5), 789–815 (2015)
Shapirovsky, I.: PSPACE-decidability of Japaridze’s polymodal logic. In: Areces, C., Goldblatt, R. (eds.) Advances in Modal Logic, vol. 7, pp. 289–304. King’s College Publications (2008)
Turing, A.M.: System of logics based on ordinals. Proc. Lond. Math. Soc. 45, 161–228 (1939)
Visser, A.: An overview of interpretability logic. In: Kracht, M., de Rijke, M., Wansing, H., Zakhariaschev, M. (eds.) Advances in Modal Logic, CSLI Lecture Notes, vol. 1, no. 87, pp. 307–359. CSLI Publications, Stanford (1998)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Appendices
A Iterating Monotone Operators on \(\mathfrak {G}_\mathrm {EA}\)
Transfinite iterations of reflection principles play an important role in proof theory starting from the work of A. Turing on recursive progressions [26]. Here we present a general result on defining iterations of monotone semi-idempotent operators in \(\mathfrak {G}_\mathrm {EA}\).
An operator \(R:\mathfrak {G}_\mathrm {EA}\rightarrow \mathfrak {G}_\mathrm {EA}\) is called computable if so is the function \(\ulcorner \sigma \urcorner \mapsto \ulcorner R(\sigma ) \urcorner \). By extension of terminology we also call computable any operator \(R'\) such that \(\forall \sigma \in \mathfrak {G}_\mathrm {EA}\, R'(\sigma )=_\mathrm {EA}R(\sigma )\), for some computable R.
An operator \(R:\mathfrak {G}_\mathrm {EA}\rightarrow \mathfrak {G}_\mathrm {EA}\) is called uniformly definable if there is an elementary formula \(\mathrm {Ax}_R(x,y)\) such that
-
(i)
For each \(\sigma \in \mathfrak {G}_\mathrm {EA}\) one has \(R(\sigma )=_\mathrm {EA}\mathrm {Ax}_R(x,\overline{\ulcorner \sigma \urcorner })\),
-
(ii)
\(\mathrm {EA}\vdash \forall x,y\,(\mathrm {Ax}_R(x,y) \rightarrow x\geqslant y).\)
The operators \(\mathrm {R}_n\) and \(\mathrm {\varPi }_{n+1}\) are uniformly definable in a very special way. For example, the formula \(\mathrm {R}_n(\sigma )\) is obtained by substituting \(\sigma (x)\) for X(x) into a fixed elementary formula containing a single positive occurrence of a predicate variable X. In fact, the following more general proposition holds that we leave here without proof. (Nothing below depends on it.)
Proposition 1
An operator \(R:\mathfrak {G}_\mathrm {EA}\rightarrow \mathfrak {G}_\mathrm {EA}\) is uniformly definable iff R is computable.
Definition 4
A uniformly definable R is called
-
provably monotone if
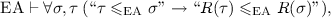
-
reflexively monotone if
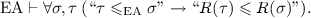
Here, \(\sigma ,\tau \) range over Gödel numbers of elementary formulas in one free variable,  abbreviates \(\Box _\mathrm {EA}\forall x\,(\Box _\sigma (x)\rightarrow \Box _\tau (x))\) and
abbreviates \(\Box _\mathrm {EA}\forall x\,(\Box _\sigma (x)\rightarrow \Box _\tau (x))\) and  stands for \(\forall x\,(\Box _{\mathrm {Ax}_R(\cdot ,\bar{\sigma })}(x)\rightarrow \Box _{\mathrm {Ax}_R(\cdot ,\bar{\tau })}(x)).\) Reflexivity here refers to the fact that
stands for \(\forall x\,(\Box _{\mathrm {Ax}_R(\cdot ,\bar{\sigma })}(x)\rightarrow \Box _{\mathrm {Ax}_R(\cdot ,\bar{\tau })}(x)).\) Reflexivity here refers to the fact that  is the statement of inclusion of theories rather than provable inclusion. Since the formula
is the statement of inclusion of theories rather than provable inclusion. Since the formula  implies its own provability in \(\mathrm {EA}\), reflexively monotone operators are (provably) monotone but not necessarily vice versa.
implies its own provability in \(\mathrm {EA}\), reflexively monotone operators are (provably) monotone but not necessarily vice versa.
It is also easy to see that the operators \(\mathrm {R}_n\) (along with all the usual reflection principles) are reflexively monotone.
An elementary well-ordering is a pair of bounded formulas D(x) and \(x\prec y\) and a constant 0 such that in the standard model the relation \(\prec \) well-orders the domain D and is provably linear in \(\mathrm {EA}\) with the least element 0. Given an elementary well-ordering \((D,\prec ,0)\), we will denote its elements by Greek letters and will identify them with an initial segment of the ordinals.
Let R be an uniformly definable monotone operator. The \(\alpha \) -th iterate of R along \((D,\prec )\) is a map associating with any numeration \(\sigma \) the Gödelian extension of \(\mathrm {EA}\) numerated by an elementary formula \(\rho (\overline{\alpha },x)\) such that provably in \(\mathrm {EA}\):
We notice that the natural Gödel numbering of formulas and terms should satisfy the inequalities \(\ulcorner \rho (\bar{\beta },x) \urcorner \geqslant \ulcorner \bar{\beta } \urcorner \geqslant \beta \). Hence, the quantifier on \(\beta \) in Eq. (3) can be bounded by x. Thus, some elementary formula \(\rho (\alpha ,x)\) satisfying (3) can always be constructed by the fixed point lemma.
The parametrized family of theories numerated by \(\rho (\alpha ,x)\) will be denoted \(R^\alpha (\sigma )\) and the formula \(\rho (\alpha ,x)\) will be more suggestively written as \(x\in R^\alpha (\sigma )\). Then, Eq. (3) can be interpreted as saying that \(R^0(\sigma ) =_\mathrm {EA}\sigma \) and, if \(\alpha \succ 0\),
Lemma 9
Suppose R is uniformly definable.
-
(i)
If \(0\prec \alpha \preceq \beta \) then \(R^\beta (\sigma )\leqslant _\mathrm {EA}R^\alpha (\sigma )\);
-
(ii)
EA

Proof
Obviously, Claim (i) follows from Claim (ii). For the latter we unwind the definition of \(\rho (\alpha ,x)\) and prove within \(\mathrm {EA}\)
This is sufficient to obtain from the same premise \(\forall x\,(\Box _{\rho (\alpha ,\cdot )}(x)\rightarrow \Box _{\rho (\beta ,\cdot )}(x)).\)
Reason within \(\mathrm {EA}\): If \(\rho (\alpha ,x)\) and \(\alpha \ne 0\) then there is a \(\gamma \prec \alpha \) such that \(\mathrm {Ax}_R(x,\ulcorner \rho (\overline{\gamma }, x) \urcorner )\). By the provable transitivity of \(\prec \) from \(\alpha \prec \beta \) we obtain \(\gamma \prec \beta \), hence \(\rho (\beta ,x)\).
Lemma 10
Suppose R is reflexively monotone. If \(\tau \leqslant _\mathrm {EA}\sigma \) then \(R^\alpha (\tau )\leqslant _\mathrm {EA}R^\alpha (\sigma )\) and, moreover, EA 
Proof
We argue by reflexive induction similarly to [4], that is, we prove in \(\mathrm {EA}\) that
and then apply Löb’s theorem in \(\mathrm {EA}\). Assume \(\tau \leqslant _\mathrm {EA}\sigma \).
Reason within \(\mathrm {EA}\): If \(\Box _{R^\alpha (\sigma )}(x)\) then either \(\alpha =0\wedge \Box _\sigma (x)\), or there is a \(\beta \prec \alpha \) such that \(\Box _{R(R^{\overline{\beta }}(\sigma ))}(x)\). In the first case we obtain \(\Box _{\tau }(x)\) by the external assumption \(\tau \leqslant _\mathrm {EA}\sigma \) and are done. In the second case, by the premise and the reflexive monotonicity of R we obtain \(\Box _{R(R^{\overline{\beta }}(\tau ))}(x)\) which yields \(\Box _{R^\alpha (\tau )}(x)\).
Corollary 7
The iteration of R along \((D,\prec )\) is uniquely defined, that is, equation (3) has a unique solution modulo \(=_\mathrm {EA}\).
The following corollary is most naturally stated for elementary well-orderings equipped with an elementary successor function \(\alpha \mapsto \alpha +1\) such that provably in \(\mathrm {EA}\)
Corollary 8
Suppose R is provably monotone and semi-idempotent. Then
-
(i)
\(R^0(\sigma )=_\mathrm {EA}\sigma \),
-
(ii)
\(R^{\alpha +1}(\sigma )=_\mathrm {EA}R(R^\alpha (\sigma ))\),
-
(iii)
\(R^{\lambda }(\sigma )=_\mathrm {EA}\bigcup \{R^\alpha (\sigma ):\alpha <\lambda \}\) if \(\lambda \in \mathrm {Lim}\).
Proof
For Claim (ii), the implication \(R^{\alpha +1}(\sigma )\leqslant _\mathrm {EA}R(R^\alpha (\sigma ))\) is easy, since provably \(\alpha \prec \alpha +1\). For the opposite implication it is sufficient to prove
Then one will be able to conclude (within \(\mathrm {EA}+\mathrm {B\varSigma }_1\)) that \(\forall x\,(\Box _{R^{\alpha +1}(\sigma )}(x) \rightarrow \Box _{R(R^\alpha (\sigma ))}(x))\) and then appeal to the \(\varPi _2^0\)-conservativity of \(\mathrm {B\varSigma }_1\) over \(\mathrm {EA}\).
Reason in \(\mathrm {EA}\): Assume \(x\in R^{\alpha +1}(\sigma )\) then (since \(\alpha +1\ne 0\)) there is a \(\beta \prec \alpha +1\) such that \(x\in R(R^\beta (\sigma ))\). If \(\beta =\alpha \) then \(x\in R(R^\alpha (\sigma ))\) and we are done. Otherwise, \(\beta \prec \alpha \) and we consider two cases.
If \(\beta \succ 0\) then we have \(R^\alpha (\sigma )\leqslant _\mathrm {EA}R^\beta (\sigma )\) by Lemma 9 (ii). By the provable monotonicity of R we obtain \(R(R^\alpha (\sigma ))\leqslant _\mathrm {EA}R(R^\beta (\sigma ))\), whence \(\Box _{R(R^\alpha (\sigma ))}(x)\).
If \(\beta =0\) then \(x\in R(\sigma )\). We have \(R^\alpha (\sigma )\leqslant _\mathrm {EA}R(\sigma )\), since \(\alpha \succ 0\). Hence, \(R(R^\alpha (\sigma ))\leqslant _\mathrm {EA}R(R(\sigma ))\leqslant _\mathrm {EA}R(\sigma )\) by the semi-idempotence of R. So, from \(x\in R(\sigma )\) we infer \(\Box _{R(R^\alpha (\sigma ))}(x)\).
B Expressibility of Iterated Reflection
In this section we confuse the arithmetical and reflection calculus notation. We write \(\Diamond _n\) for \(\mathrm {R}_n\) and \(\nabla _n\) for \(\mathrm {\varPi }_{n+1}\). Our goal is to show that iterated operators \(\Diamond _n^\alpha \), for natural ordinal notations \(\alpha <\varepsilon _0\), are expressible in the language of \({\mathrm {RC}^\nabla }\). We will rely on the so-called reduction property (cf. [5], the present version is somewhat more general and follows from [4, Theorem 2], see also [10]).
We write \(\Diamond _{n,\sigma }(\tau )\) for \(\Diamond _n(\sigma \wedge \tau )\), hence \(\Diamond _{n,\sigma }\) is a monotone semi-idempotent operator, for each \(\sigma \). Let \(\mathrm {EA}^+\) denote the theory \(\mathrm {R}_1(\mathrm {EA})\) which is known to be equivalent to \(\mathrm {EA}+\text {Supexp}\).
Theorem 5
(reduction property). For all \(\sigma \in \mathfrak {G}_\mathrm {EA}\), \(n\in \omega \),
We also remark that the theory \(\Diamond _{n,\sigma }^\omega (1)\) is equivalent to the one axiomatized over \(\mathrm {EA}\) by the set \(\bigcup \{\mathrm {Q}_n^k(\sigma ):k<\omega \}\), where \(\mathrm {Q}_n^0(\sigma ):=\Diamond _n\sigma \) and \(\mathrm {Q}_n^{k+1}(\sigma ):=\Diamond _n(\sigma \wedge \mathrm {Q}_n^k(\sigma ))\) are formulas in one variable expressible in \(\mathrm {RC}\).
Concerning these formulas we note three well-known facts.
Lemma 11
Provably in \(\mathrm {EA}\),
-
1.
\(\forall B\in \mathbb {W}_n\, \forall k\, \mathrm {Q}_n^{k+1}(B)\vdash _\mathrm {RC}\mathrm {Q}_n^{k}(B)\wedge \Diamond _n \mathrm {Q}_n^{k}(B)\);
-
2.
\(\forall B\in \mathbb {W}_n\, \forall k\, \mathrm {Q}_n^{k}(B)<_n \Diamond _{n+1} B\);
-
3.
\(\forall B\in \mathbb {W}_n\, \forall k\, \exists A\in \mathbb {W}_n\, \mathrm {Q}_n^{k}(B)=_\mathrm {RC}A\).
The first two of these claims are proved by an easy induction on k. The third one is a consequence of a more general theorem that any variable-free formula of \(\mathrm {RC}\) is equivalent to a word. An explicit rule for calculating such an A is also well-known and related to the so-called Worm sequence, see [6, Lemma 5.9].
We consider the set of words \((\mathbb {W}_n,<_n)\) modulo equivalence in \(\mathrm {RC}\), together with its natural representation in \(\mathrm {EA}\), as an elementary well-ordering. For each \(A\in \mathbb {W}_n\), let \(o_n(A)\) denote the order type of \(\{B<_n A:B\in \mathbb {W}_n\}\) modulo \(=_\mathrm {RC}\). In a formalized context, the ordinal \(o_n(A)\) is represented by its notation, the word A, however we still write \(o_n(A)\), as it reminds us that A must be viewed as an ordinal.
From the reduction property we obtain the following theorem that was stated in [5] in a somewhat more restricted way.
Theorem 6
For all words \(A\in \mathbb {W}_n\), in \(\overline{\mathfrak {G}}_{\mathrm {EA}^+}\) there holds
Theorem 6 of [5] used extensions of \(\sigma \) rather than extensions of \(\mathrm {EA}^+\) by iterated reflection principles and as a result involved unnecessary restrictions of the complexity of \(\sigma \). However, the idea of the present proof is the same.
Proof
We argue by reflexive induction in \(\mathrm {EA}^+\) and prove that, for all \(\sigma \in \mathfrak {G}_{\mathrm {EA}^+}\) and all \(n<\omega \),

Arguing inside \(\mathrm {EA}^+\), we will omit the quotation marks and read the expressions \(\tau \leqslant \nu \) as \(\forall x\,(\Box _\nu (x)\leftrightarrow \Box _\tau (x))\) and \(\tau =\nu \) as \(\forall x\,(\Box _\tau (x)\leftrightarrow \Box _\nu (x))\).
If \(A\circeq \top \) the claim amounts to \(\nabla _n 1=1\).
If \(A\circeq \Diamond _n B\) then \(o_n(A)=o_n(B)+1\), hence by the reflexive induction hypothesis \(\nabla _n B^*_\sigma =_{\mathrm {EA}^+} \Diamond _{n,\sigma }^{o_n(B)}(1)\). It follows that \(\Diamond _{n,\sigma }(\Diamond _{n,\sigma }^{o_n(B)}(1))= \Diamond _{n,\sigma }\nabla _n B^*_\sigma = \Diamond _{n,\sigma } B^*_\sigma .\) Therefore, we obtain
If \(A\circeq \Diamond _{m+1} B\) with \(m\geqslant n\) then \(\nabla _n A^*_\sigma =\nabla _n\nabla _{m}\Diamond _{m+1,\sigma } B^*_\sigma \). By the reduction property \(\nabla _{m}\Diamond _{m+1,\sigma } B^*_\sigma = \bigcup _{k<\omega } (\mathrm {Q}_m^k(B))^*_\sigma \). Moreover, by Lemma 11 (i), if a sentence is provable in \(\bigcup _{k<\omega } (\mathrm {Q}_m^k(B))^*_\sigma \), it must be provable in \((\mathrm {Q}_m^k(B))^*_\sigma \), for some \(k<\omega \). Hence, we can infer
By Lemma 11(ii) and (iii), each of \(\mathrm {Q}_m^k(B)\) is \(<_n\)-below \(A\circeq \Diamond _{m+1} B\) and is equivalent to a word in \(\mathbb {W}_n\). Hence,
By the reflexive induction hypothesis, for each \(C<_n A\) we have
It follows that

On the other hand, if \(C<_n A\) then \(A^*_\sigma \leqslant \Diamond _{n,\sigma } C^*_\sigma \) and \(\nabla _n A^*_\sigma \leqslant \nabla _n\Diamond _{n,\sigma } C^*_\sigma \leqslant \Diamond _{n,\sigma } C^*_\sigma \). Hence,
Thus, we have proved \(\nabla _n A^*_\sigma = \Diamond _{n,\sigma }^{o_n(A)}(1)\), as required.
For ordinals \(\alpha <\varepsilon _0\), let \(\mathrm {A}^n_\alpha \in \mathbb {W}_n\) denote a canonical notation for \(\alpha \) in the system \((\mathbb {W}_n,<_n)\). Thus, \(o_n(\mathrm {A}^n_\alpha )= \alpha \). We are going to show that the operations \(\Diamond _n^\alpha \) are expressible in \({\mathrm {RC}^\nabla }\) in the following sense.
Theorem 7
For each \(n<\omega \) and \(0<\alpha <\varepsilon _0\) there is an \(\mathrm {RC}\)-formula A(p) such that \(\forall \sigma \in \mathfrak {G}_{\mathrm {EA}^+}\, \Diamond _n^\alpha (\sigma ) =_{\mathrm {EA}^+} \nabla _n A(\sigma )\).
Note that \(A(\sigma )\) denote the interpretation of the formula \(A[p/\top ]\) in \(\overline{\mathfrak {G}}_{\mathrm {EA}^+}\) sending p to \(\sigma \). The theorem follows from the following main lemma.
Lemma 12
For all \(n<\omega \) and \(\alpha <\varepsilon _0\), for all \(\sigma \in \mathfrak {G}_{\mathrm {EA}^+}\),
The proof relies on a few observations.
Lemma 13
Suppose \(\Diamond _n\sigma \leqslant _{\mathrm {EA}^+} \sigma \). Then, for all \(A\in \mathbb {W}_n\),
-
(i)
\(A(\sigma )\leqslant _{\mathrm {EA}^+} \sigma \);
-
(ii)
\(A^*_\sigma =_{\mathrm {EA}^+} A(\sigma )\);
-
(iii)
\(\forall m\geqslant n\,\forall \alpha <\varepsilon _0\, \, \Diamond _{m,\sigma }^\alpha 1=_{\mathrm {EA}^+} \Diamond ^\alpha _m(\sigma )\).
Proof
Claim (i) is proved by induction on the build-up of A. Claim (ii) follows from (i), since \(\Diamond _{m,\sigma }\tau = \Diamond _m(\sigma \wedge \tau ) = \Diamond _m\tau \), if \(\tau \leqslant \sigma \). Claim (iii) is proved by reflexive induction using the same observation as in (i) and (ii).
Proof of Theorem 7. We observe that the formula \(\Diamond _n \sigma \) satisfies the assumption of Lemma 13. Let \(B:=\mathrm {A}^n_\alpha \), then by Theorem 6
However, \(o_n(B)=\alpha \) and the claim follows.
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Beklemishev, L.D. (2017). On the Reflection Calculus with Partial Conservativity Operators. In: Kennedy, J., de Queiroz, R. (eds) Logic, Language, Information, and Computation. WoLLIC 2017. Lecture Notes in Computer Science(), vol 10388. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-55386-2_4
Download citation
DOI: https://doi.org/10.1007/978-3-662-55386-2_4
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-55385-5
Online ISBN: 978-3-662-55386-2
eBook Packages: Computer ScienceComputer Science (R0)