Abstract
Family-based model checking targets the simultaneous verification of multiple system variants, a technique to handle feature-based variability that is intrinsic to software product lines (SPLs). We present an approach for family-based verification based on the feature \(\mu \)-calculus \(\mu L {}_f\), which combines modalities with feature expressions. This logic is interpreted over featured transition systems, a well-accepted model of SPLs, which allows one to reason over the collective behavior of a number of variants (a family of products). Via an embedding into the modal \(\mu \)-calculus with data, underpinned by the general-purpose mCRL2 toolset, off-the-shelf tool support for \(\mu L {}_f\) becomes readily available. We illustrate the feasibility of our approach on an SPL benchmark model and show the runtime improvement that family-based model checking with mCRL2 offers with respect to model checking the benchmark product-by-product.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Many software systems are configurable systems whose variants differ by the features they provide, i.e. the functionality that is relevant for an end-user, and are therefore referred to as software product lines (SPLs) or product families. SPLs challenge existing formal methods and analysis tools by the potentially high number of different products, each giving rise to a large behavioral state space in general. SPLs are popular in the embedded and critical systems domain. Therefore, analysis techniques for proving the correctness of SPL models are widely studied (cf. [1] for a survey).
Because for larger SPL models enumerative product-by-product approaches become unfeasible, dedicated family-based techniques have been developed, exploiting variability in product families in terms of features (cf., e.g., [2,3,4,5,6,7,8]). In this paper, we contribute to the field of family-based model checking. Over the past decades, model checking has seen significant progress [9]. However, state-space explosion remains an issue, amplified for SPL models by the accumulation of possible variants and configurations. To mitigate these problems, family-based model checking was proposed as a means to simultaneously verify multiple variants in a single run (cf. [1]). To make SPL models amenable to family-based reasoning, feature-based variability was introduced in many behavioral models, e.g. based on process calculi [2, 10,11,12] and labeled transition systems (LTSs) [3, 13,14,15].
Arguably the most widely used behavioral SPL models are featured transition systems (FTSs) [13]. An FTS compactly represents multiple behaviors in a single transition system by exploiting transitions guarded by feature expressions. A transition of a given product can be taken if the product fulfills the feature expression associated with the transition. Thus, an FTS incorporates the behavior of all eligible products, while individual behavior can be extracted as LTSs. Properties of such models can be verified with dedicated SPL model checkers [16,17,18] or, to a certain degree, with single system model checkers [7, 12, 14].
As far as we know, none of the existing tools can verify modal \(\mu \)-calculus properties over FTSs in a family-based manner. However, there have been earlier proposals for using the \(\mu \)-calculus to analyze SPLs (cf., e.g., [2, 10, 12, 19, 20]). In [19], for instance, mCRL2 and its toolset [21, 22] were used for product-based model checking. The flexibility of mCRL2’s data language allowed to model and select valid product configurations and to model and check the behavior of individually generated products. While the SPL models of [19] have an FTS-like semantics, to actually perform family-based model checking also the supporting logic must be able to handle the specificity of FTSs, viz. transitions labeled withfeature expressions. In [20], we generalized the approach that led to the feature-oriented variants fLTL [13] and fCTL [14] of LTL and CTL to the modal \(\mu \)-calculus by defining \(\mu L {}_f\), a feature-oriented variant of \(\mu L\) with an FTS semantics obtained by incorporating feature expressions. While \(\mu L {}_f\) paves the way for family-based model checking, so far the logic was without tool support, and it remained unclear whether it could be used effectively to model check FTSs.
Contributions. In this paper, we show how to effectively perform family-based model checking for \(\mu L {}_f\) by exploiting the mCRL2 toolset as-is, i.e. avoiding the implementation of a dedicated SPL-oriented verifier. We first show how to solve the family-based model-checking problem via an embedding of \(\mu L {}_f\) into mCRL2’s modal \(\mu \)-calculus with data. Then we define a partitioning procedure for \(\mu L {}_f\) that allows us to apply our results from [20]. Next, we evaluate our approach by verifying a number of representative properties over an mCRL2 specification of the minepump SPL benchmark model [8, 13, 23,24,25]. We verify typical linear-time and branching-time properties. We also verify properties involving more than one feature modality in a single formula, which is a novelty that allows to check different behavior for different variants at once. Finally, we discuss the improvement in runtime that results from using mCRL2 for family-based model checking as opposed to product-based model checking.
Further Related Work. There is a growing body of research on customizing model-checking techniques for SPLs. Like our FTS-based proposals [19, 20], the CCS-based proposals PL-CCS [2, 10] and DeltaCCS [12] are grounded in the \(\mu \)-calculus. In [26], PL-CCS was proven to be less expressive (in terms of the sets of definable products) than FTSs, while DeltaCCS allows only limited family-based model checking (viz. verifying family-wide invariants for entire SPLs). DeltaCCS does provide efficient incremental model checking, a technique that improves product-based model checking by partially reusing verification results obtained for previously considered products. The state-of-the-art by the end of 2013 is summarized in [1], which also discusses type checking, static analysis, and theorem proving tailored for SPLs, as well as software model checking.
In a broader perspective, also probabilistic model checking was applied to SPLs recently, e.g. on feature-oriented (parametric) Markov chains [27,28,29] or Markov decision processes [30], and via a feature-oriented extension of the input language of the probabilistic model checker Prism [31], making the tool amenable to (family-based) SPL model checking [32]. Most recently, also statistical model checking was applied to SPLs [33, 34], based on a probabilistic extension of the feature-oriented process calculus of [11].
2 A Feature \(\mu \)-Calculus \(\mu L {}_f\) over FTSs
The \(\mu \)-calculus is an extension of modal logic with fixpoint operators whose formulas are interpreted over LTSs (cf. [35]). We fix a set of actions  , ranged over by \(a,b,\ldots \), and a set of variables \({\mathcal {X}}\), ranged over by \(X,Y,\ldots \).
, ranged over by \(a,b,\ldots \), and a set of variables \({\mathcal {X}}\), ranged over by \(X,Y,\ldots \).
Definition 1
The \(\mu \)-calculus \(\mu L\) over  and \({\mathcal {X}}\) is given by
and \({\mathcal {X}}\) is given by

where for \(\mu X . \varphi \) and \(\nu X . \varphi \) all free occurrences of X in \(\varphi \) are in the scope of an even number of negations (to guarantee well-definedness of the fixpoint semantics). \(\square \)
Next to the Boolean constants falsum and verum, \(\mu L\) contains the connectives \(\lnot \), \(\vee \) and \(\wedge \) of propositional logic and the diamond and box operators \(\langle {\,} \rangle \) and \([{\,} ]\) of modal logic. The least and greatest fixpoint operators \(\mu \) and \(\nu \) provide recursion used for ‘finite’ and ‘infinite’ looping, respectively.
Definition 2
An LTS over  is a triple \(L = ( S, {\rightarrow }, s_{{*}})\), with states from S, transition relation
is a triple \(L = ( S, {\rightarrow }, s_{{*}})\), with states from S, transition relation  , and initial state \(s_{{*}}\in S\). \(\square \)
, and initial state \(s_{{*}}\in S\). \(\square \)
Definition 3
Let L be an LTS with set of states S. Let  be the set of state sets with typical element U and
be the set of state sets with typical element U and  the set of state-based environments. The semantics
the set of state-based environments. The semantics  is given by
is given by

where \(\varepsilon [U/X]\), for  , denotes the environment which yields \(\varepsilon (Y)\) for variables Y different from the variable X and the set
, denotes the environment which yields \(\varepsilon (Y)\) for variables Y different from the variable X and the set  for X itself. \(\square \)
for X itself. \(\square \)
As typical for model checking, we only consider closed \(\mu L\)-formulas whose interpretation is independent of the environment. In such case we write \(\mathopen {[\! [}{\varphi } \mathclose {]\! ]}_L\) for the interpretation of \(\varphi \). Given a state s of an LTS L, we set \(s \mathrel {\models _{L}}\varphi \) iff \(s \in \mathopen {[\! [}{\varphi } \mathclose {]\! ]}_L\).
We next fix a finite non-empty set  of features, with \(\textsf {f}\) as typical element. Let \(\mathbb {B}[ {\mathcal {F}}]\) denote the set of Boolean expressions over
of features, with \(\textsf {f}\) as typical element. Let \(\mathbb {B}[ {\mathcal {F}}]\) denote the set of Boolean expressions over  . Elements \(\chi \) and \(\gamma \) of \(\mathbb {B}[ {\mathcal {F}}]\) are referred to as feature expressions. A product is a set of features, and
. Elements \(\chi \) and \(\gamma \) of \(\mathbb {B}[ {\mathcal {F}}]\) are referred to as feature expressions. A product is a set of features, and  szdenotes the set of products, thus
szdenotes the set of products, thus  , with \(p, q, \ldots \) ranging over
, with \(p, q, \ldots \) ranging over  . A subset
. A subset  is referred to as a family of products. A feature expression \(\gamma \), as Boolean expression over
is referred to as a family of products. A feature expression \(\gamma \), as Boolean expression over  , can be interpreted as a set of products \(Q_\gamma \), viz. the products p for which the induced truth assignment (\(\mathbf true \) for \(\textsf {f}\in p\), \(\mathbf false \) for \(\textsf {f}\notin p\)) validates \(\gamma \). Reversely, for each family
, can be interpreted as a set of products \(Q_\gamma \), viz. the products p for which the induced truth assignment (\(\mathbf true \) for \(\textsf {f}\in p\), \(\mathbf false \) for \(\textsf {f}\notin p\)) validates \(\gamma \). Reversely, for each family  we fix a feature expression \(\gamma _{\text {P}}\) to represent it. The constant \(\mathord {\top }\) denotes the feature expression that is always true. We now recall FTSs from [13] as a model for SPLs, using the notation of [20].
we fix a feature expression \(\gamma _{\text {P}}\) to represent it. The constant \(\mathord {\top }\) denotes the feature expression that is always true. We now recall FTSs from [13] as a model for SPLs, using the notation of [20].
Definition 4
An FTS over  and
and  is a triple \(F {=} ( S, \theta , s_{{*}})\), with states from S, transition constraint function
is a triple \(F {=} ( S, \theta , s_{{*}})\), with states from S, transition constraint function  , and initial state \(s_{{*}}\!\in \!S\). \(\square \)
, and initial state \(s_{{*}}\!\in \!S\). \(\square \)
For states \(s, t \in S\), we write  if \(\theta (s,a,t) = \gamma \) and \(\gamma \not \equiv \bot \). The projection of an FTS \(F = ( S ,\, \theta ,\, s_{{*}})\) onto a product
if \(\theta (s,a,t) = \gamma \) and \(\gamma \not \equiv \bot \). The projection of an FTS \(F = ( S ,\, \theta ,\, s_{{*}})\) onto a product  is the LTS \(F|p = ( S ,\, {\rightarrow }_{F|p} ,\, s_{{*}})\) over
is the LTS \(F|p = ( S ,\, {\rightarrow }_{F|p} ,\, s_{{*}})\) over  with
with  iff \(p \in Q_\gamma \) for a transition
iff \(p \in Q_\gamma \) for a transition  of F.
of F.
Example 1
Let P be a product line of (four) coffee machines, with independent features  representing the presence of a coin slot accepting dollars or euros.
representing the presence of a coin slot accepting dollars or euros.

FTS F models its family behavior, with actions to insert coins (\(\textit{ins}\)) and to pour standard (\(\textit{std}\)) or extra large (\(\textit{xxl}\)) coffee. Each coffee machine accepts either dollars or euros. Extra large coffee is exclusively available for two dollars. LTSs \(F| p_1\) and  model the behavior of products
model the behavior of products  and
and  . Note that \(F| p_2\) lacks the transition from \(s_1\) to \(s_2\) that requires feature
. Note that \(F| p_2\) lacks the transition from \(s_1\) to \(s_2\) that requires feature  . \(\square \)
. \(\square \)
In [20], we introduced \(\mu L {}_f\), an extension with features of the \(\mu \)-calculus \(\mu L\), interpreted over FTSs rather than LTSs.
Definition 5
The feature \(\mu \)-calculus \(\mu L {}_f\) over  ,
,  and \({\mathcal {X}}\), is given by
and \({\mathcal {X}}\), is given by

where for  and
and  all free occurrences of X in
all free occurrences of X in  are in the scope of an even number of negations. \(\square \)
are in the scope of an even number of negations. \(\square \)
Also for \(\mu L {}_f\) we mainly consider closed formulas. The logic \(\mu L {}_f\) replaces the binary operators \(\langle {a} \rangle \varphi \) and \([{a} ]\varphi \) of \(\mu L\) by ternary operators  and
and  , respectively, where \(\chi \) is a feature expression.
, respectively, where \(\chi \) is a feature expression.
A Product-Based Semantics. In [20], we gave a semantics  for closed \(\mu L {}_f\)-formulas
for closed \(\mu L {}_f\)-formulas  with subsets of
with subsets of  as denotations. We showed that this product-based semantics can be characterized as follows
as denotations. We showed that this product-based semantics can be characterized as follows

where the projection function  is given by
is given by

Thus, for a formula  and a product
and a product  , a \(\mu L\)-formula
, a \(\mu L\)-formula  is obtained from
is obtained from  , by replacing subformulas \(\langle {a|\chi } \rangle \psi _{f}\) by \(\mathord {\perp }\) and \([{a|\chi } ]\psi _{f}\) by \(\mathord {\top }\), respectively, in case \(p\!\notin \!Q_\chi \), while omitting \(\chi \) otherwise. Formulas of \(\mu L {}_f\) permit reasoning about the behavior of products, as illustrated below.
, by replacing subformulas \(\langle {a|\chi } \rangle \psi _{f}\) by \(\mathord {\perp }\) and \([{a|\chi } ]\psi _{f}\) by \(\mathord {\top }\), respectively, in case \(p\!\notin \!Q_\chi \), while omitting \(\chi \) otherwise. Formulas of \(\mu L {}_f\) permit reasoning about the behavior of products, as illustrated below.
Example 2
Formulas of \(\mu L {}_f\) for Example 1 include the following.
-
(a)
 characterizes the family of products P that can execute \(\textit{ins}\), after which \(\textit{ins}\) cannot be executed by products satisfying
characterizes the family of products P that can execute \(\textit{ins}\), after which \(\textit{ins}\) cannot be executed by products satisfying  , while \(\textit{std}\) can be executed by all products of P.
, while \(\textit{std}\) can be executed by all products of P. -
(b)
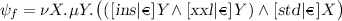 characterizes the (sub)family of products which, when having feature
characterizes the (sub)family of products which, when having feature  , action \(\textit{std}\) occurs infinitely often on all infinite runs over \(\textit{ins}\), \(\textit{xxl}\), and \(\textit{std}\). \(\square \)
, action \(\textit{std}\) occurs infinitely often on all infinite runs over \(\textit{ins}\), \(\textit{xxl}\), and \(\textit{std}\). \(\square \)
In practice, we are often interested in deciding whether a family of products P satisfies a formula  . The semantics of \(\mu L {}_f\), however, does not allow for doing so in a family-based manner as it is product-oriented. For that reason, we introduced in [20] a second semantics \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_F\) for \(\mu L {}_f\) (cf. Definition 6 below) providing a stronger interpretation for the modalities to enable family-based reasoning. We stress that this second, family-based interpretation was designed to specifically support efficient model checking; the product-oriented
. The semantics of \(\mu L {}_f\), however, does not allow for doing so in a family-based manner as it is product-oriented. For that reason, we introduced in [20] a second semantics \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_F\) for \(\mu L {}_f\) (cf. Definition 6 below) providing a stronger interpretation for the modalities to enable family-based reasoning. We stress that this second, family-based interpretation was designed to specifically support efficient model checking; the product-oriented  remains the semantic reference. The correspondence between the two interpretations was studied in detail in [20]. We next summarize the most important results.
remains the semantic reference. The correspondence between the two interpretations was studied in detail in [20]. We next summarize the most important results.
A Family-Based Semantics. In our family-based interpretation, the ternary operator  holds for a family P with respect to an FTS F in a state s, if all products in P satisfy the feature expression \(\chi \) and there is an a-transition, shared among all products in P, that leads to a state where
holds for a family P with respect to an FTS F in a state s, if all products in P satisfy the feature expression \(\chi \) and there is an a-transition, shared among all products in P, that leads to a state where  holds for P (i.e. the products in P can collectively execute a). The
holds for P (i.e. the products in P can collectively execute a). The  modality holds in a state of F for a set of products P, if for each subset \(P'\) of P for which an a-transition is possible,
modality holds in a state of F for a set of products P, if for each subset \(P'\) of P for which an a-transition is possible,  holds for \(P'\) in the target state of that a-transition. While under the product-based interpretation
holds for \(P'\) in the target state of that a-transition. While under the product-based interpretation  of \(\mu L {}_f\), the two modalities in \(\mu L {}_f\) are, like in \(\mu L\), each other’s dual, this is no longer the case under the family-based interpretation \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_F\) below.
of \(\mu L {}_f\), the two modalities in \(\mu L {}_f\) are, like in \(\mu L\), each other’s dual, this is no longer the case under the family-based interpretation \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_F\) below.
Definition 6
Let \(F = ( S, \theta , s_{{*}})\) be an FTS. Let  be the set of state-family pairs with typical element W and \(\textit{sPEnv}\!=\!{\mathcal {X}}\!\rightarrow \!\textit{sPSet}\) the set of state-family environments. The semantics \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_F : \mu L {}_f\rightarrow \textit{sPEnv}\!\rightarrow \!\textit{sPSet}\) is given by
be the set of state-family pairs with typical element W and \(\textit{sPEnv}\!=\!{\mathcal {X}}\!\rightarrow \!\textit{sPSet}\) the set of state-family environments. The semantics \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_F : \mu L {}_f\rightarrow \textit{sPEnv}\!\rightarrow \!\textit{sPSet}\) is given by

where \(\zeta [W/X]\), for \(\zeta \in \textit{sPEnv}\), denotes the environment which yields \(\zeta (Y)\) for variables Y different from X and the set \(W \mathbin {\in } \textit{sPSet}\) for X. \(\square \)
The interpretation of a closed \(\mu L {}_f\) formula  is independent of the environment and we therefore again simply write
is independent of the environment and we therefore again simply write  . Given a state s of an FTS F, and a set of products
. Given a state s of an FTS F, and a set of products  , we write
, we write  iff
iff  .
.
The theorem below summarizes the main results of [20], relating the family-based interpretation of \(\mu L {}_f\) to the LTS semantics of \(\mu L\) (and by extension, \(\mu L {}_f\)’s product-based interpretation).
Theorem 1
Let F be an FTS, and let  be a set of products.
be a set of products.
-
(a)
For each formula
 , state \(s\in S\), and individual product
, state \(s\in S\), and individual product  :
: 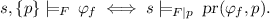
-
(b)
For negation-free formula
 , state \(s \in S\), and product family
, state \(s \in S\), and product family  :
:  \(\square \)
\(\square \)
Note that in general,  does not imply
does not imply  for all products in the family P. In the next section, we discuss how the above results can be exploited for family-based model checking of \(\mu L {}_f\)-formulas.
for all products in the family P. In the next section, we discuss how the above results can be exploited for family-based model checking of \(\mu L {}_f\)-formulas.
3 Family-Based Model Checking with mCRL2
In this section, we show how to obtain a decision procedure for  via a mapping into the first-order \(\mu \)-calculus \(\mu L {}_{\text {FO}}\) and solving the corresponding model-checking problem. Our approach consists of two steps: (i) translation of the \(\mu L {}_f\)-formula at hand; (ii) translation of the FTS describing the family behavior into an LTS with parametrized actions. Since \(\mu L {}_{\text {FO}}\) is a fragment of the logic from [36, 37], we can use off-the-shelf tools such as the mCRL2 toolset [21, 22] to perform family-based model checking of properties expressed in \(\mu L {}_f\). We first review \(\mu L {}_{\text {FO}}\) before we proceed to describe the above translations.
via a mapping into the first-order \(\mu \)-calculus \(\mu L {}_{\text {FO}}\) and solving the corresponding model-checking problem. Our approach consists of two steps: (i) translation of the \(\mu L {}_f\)-formula at hand; (ii) translation of the FTS describing the family behavior into an LTS with parametrized actions. Since \(\mu L {}_{\text {FO}}\) is a fragment of the logic from [36, 37], we can use off-the-shelf tools such as the mCRL2 toolset [21, 22] to perform family-based model checking of properties expressed in \(\mu L {}_f\). We first review \(\mu L {}_{\text {FO}}\) before we proceed to describe the above translations.
3.1 The First-Order \(\mu \)-Calculus \(\mu L {}_{\text {FO}}\)
The first-order \(\mu \)-calculus with data of [36, 37] is given in the context of a data signature \(\Sigma = (S,O)\), with set of sorts S and set of operations O, and of a set of ‘sorted’ actions  . \(\mu L {}_{\text {FO}}\) is essentially a fragment of the logic of [36, 37] in which S is the single sort \(\textsf {FExp} \), with typical elements \(\beta ,\chi ,\gamma \), representing Boolean expressions over features and data variables taken from a set \({\mathcal {V}}\), with typical element v. In toolsets such as mCRL2, \(\textsf {FExp} \) can be formalized as an abstract data type defining BDDs ranging over features (cf. [38]). We fix a set of recursion variables \(\tilde{\mathcal {X}}\). Formulas \(\varphi \in \mu L {}_{\text {FO}}\) are then given by
. \(\mu L {}_{\text {FO}}\) is essentially a fragment of the logic of [36, 37] in which S is the single sort \(\textsf {FExp} \), with typical elements \(\beta ,\chi ,\gamma \), representing Boolean expressions over features and data variables taken from a set \({\mathcal {V}}\), with typical element v. In toolsets such as mCRL2, \(\textsf {FExp} \) can be formalized as an abstract data type defining BDDs ranging over features (cf. [38]). We fix a set of recursion variables \(\tilde{\mathcal {X}}\). Formulas \(\varphi \in \mu L {}_{\text {FO}}\) are then given by

where for \(\mu \tilde{X}(\upsilon _{\tilde{X}} {:}{=} \gamma ) . \varphi \) and \(\nu \tilde{X}(\upsilon _{\tilde{X}} {:}{=} \gamma ). \varphi \) all free occurrences of \(\tilde{X}\) in \(\varphi \) are in the scope of an even number of negations, and each variable \(\tilde{X}\) is bound at most once. To each recursion variable \(\tilde{X}\) a unique data variable \(\upsilon _{\tilde{X}}\) is associated, but we often suppress this association and simply write \(\mu \tilde{X}(\upsilon {:}{=} \gamma ) . \varphi \) and \(\nu \tilde{X}(\upsilon {:}{=} \gamma ). \varphi \) instead. The language construct \(\gamma _1 {\Rightarrow } \gamma _2\) is used to express that the set of products characterized by \(\gamma _1\) is a subset of those characterized by \(\gamma _2\).
We interpret \(\mu L {}_{\text {FO}}\) over LTSs whose actions carry closed feature expressions.
Definition 7
A parametrized LTS over  and
and  is a triple \((S,{\rightarrow }, s_{{*}})\) with states from S, transition relation
is a triple \((S,{\rightarrow }, s_{{*}})\) with states from S, transition relation  where
where  , and initial state \(s_{{*}}\in S\). \(\square \)
, and initial state \(s_{{*}}\in S\). \(\square \)
In the presence of variables ranging over feature expressions, we distinguish two sets of environments, viz. data environments  and recursion variable environments
and recursion variable environments  . The semantics \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_{F O}\) is then of type
. The semantics \(\mathopen {[\! [}{\cdot } \mathclose {]\! ]}_{F O}\) is then of type  . To comprehend our translation of \(\mu L {}_f\) into \(\mu L {}_{\text {FO}}\), we address the semantics for the non-trivial constructs of \(\mu L {}_{\text {FO}}\). The full semantics can be found in [36, 37].
. To comprehend our translation of \(\mu L {}_f\) into \(\mu L {}_{\text {FO}}\), we address the semantics for the non-trivial constructs of \(\mu L {}_{\text {FO}}\). The full semantics can be found in [36, 37].

For existential quantification, the data environment \(\theta [Q/\upsilon ]\) assigns a family of products Q to the data variable \(\upsilon \); the set of states that satisfy \(\exists \upsilon . \varphi \) is then the set of states satisfying \(\varphi \) for any possible assignment to data variable \(\upsilon \).
For the diamond modality, a state s is included in its semantics, if in the parametrized LTS, state s admits a transition with parametrized action \(a(\gamma )\) to a state t such that the set of products \(\theta (\upsilon )\) is exactly the set of products \(Q_\gamma \) associated with the feature expression \(\gamma \) of the transition, while the target state t satisfies \(\varphi \). Note that the set of products \(Q_\gamma \) can be established independently from the environment \(\theta \) since \(\gamma \) is closed, i.e. variable-free.
The least fixpoint construction is more involved compared to the corresponding construct of \(\mu L {}_f\) because of the parametrization. Here the semantics of the least fixpoint is taken for the functional that fixes both the recursion variable \(\tilde{X}\) and the data variable \(\upsilon \), with \(\pi \) and Q, respectively. Next, application to the value of the initializing feature expression \(\gamma \) yields a set of states.
With respect to a parametrized LTS L, we put \(s \mathrel {\models _{L}}\varphi \), for \(s \in S\) and \(\varphi \in \mu L {}_{\text {FO}}\) closed, if \(s \in \mathopen {[\! [}{ \varphi } \mathclose {]\! ]}_{F O}(\xi _0)(\theta _0)\) for some \(\xi _0 \in \textit{XEnv}\) and \(\theta _0 \in \textit{VEnv}\).
3.2 Translating the Family-Based Interpretation of \(\mu L {}_f\) to \(\mu L {}_{\text {FO}}\)
To model check a \(\mu L {}_f\)-formula against an FTS, we effectively verify its corresponding \(\mu L {}_{\text {FO}}\)-formula against the parametrized LTS that is obtained as follows.
Definition 8
Let \(F = ( S ,\, \theta ,\, s_{{*}})\) be an FTS over  and
and  . Take
. Take  . Define the parametrized LTS \(L(F)\) for F by \(L(F)\!=\!( S , {\rightarrow } , s_{{*}})\) where \({\rightarrow }\) is defined by
. Define the parametrized LTS \(L(F)\) for F by \(L(F)\!=\!( S , {\rightarrow } , s_{{*}})\) where \({\rightarrow }\) is defined by  iff \(\theta (s,a,t) = \gamma \) and \(\gamma \not \equiv \mathord {\perp }\). \(\square \)
iff \(\theta (s,a,t) = \gamma \) and \(\gamma \not \equiv \mathord {\perp }\). \(\square \)
Thus, we use the parameter of an action as placeholder for the feature expression that guards a transition, writing  .
.
Next, we define a translation \(\textit{tr} \) that yields for a set of products P, represented by a closed feature expression \(\gamma _{\text {P}}\) of sort \(\textsf {FExp} \), and a \(\mu L {}_f\)-formula  , a \(\mu L {}_{\text {FO}}\)-formula
, a \(\mu L {}_{\text {FO}}\)-formula  . We provide an explanation of this transformation, guided by the family-based semantics of \(\mu L {}_f\), afterwards (cf. Definition 6).
. We provide an explanation of this transformation, guided by the family-based semantics of \(\mu L {}_f\), afterwards (cf. Definition 6).
Definition 9
The translation function \(\textit{tr} : \textsf {FExp} \times \mu L {}_f\rightarrow \mu L {}_{\text {FO}}\) is given by

Logical constants and propositional connectives are translated as expected. The feature expression \(\gamma \) in our translation symbolically represents the set of products that collectively can reach a given state in our parametrized LTS. Note that this expression is ‘updated’ only in our translation of the modal operators and passed on otherwise. For the \(\langle {\cdot |\cdot } \rangle \)-operator, the existence of a feature expression \(\beta \) in Definition 6 with an \(a | \beta \)-transition is captured by the existentially quantified data variable \(\upsilon \): a state s in a parametrized LTS satisfies \(\exists \upsilon . \langle {a(\upsilon )} \rangle ( (\gamma \Rightarrow \upsilon )\) \(\wedge \)  only when a transition from s exists labeled with a parametrized action \(a(\beta )\) such that for \(\upsilon \) matching \(\beta \), also \(\gamma \mathop {\Rightarrow } \upsilon \) and
only when a transition from s exists labeled with a parametrized action \(a(\beta )\) such that for \(\upsilon \) matching \(\beta \), also \(\gamma \mathop {\Rightarrow } \upsilon \) and  hold. Likewise, for the \([{\cdot |\cdot } ]\)-operator, the universal quantification over feature expressions guarding transitions is captured by a universally quantified data variable \(\upsilon \) that is passed as a parameter to the action a. The formula \(( \gamma {\wedge } \chi {\wedge } \upsilon \Rightarrow \! \mathord {\perp })\) expresses that the corresponding product families are disjoint.
hold. Likewise, for the \([{\cdot |\cdot } ]\)-operator, the universal quantification over feature expressions guarding transitions is captured by a universally quantified data variable \(\upsilon \) that is passed as a parameter to the action a. The formula \(( \gamma {\wedge } \chi {\wedge } \upsilon \Rightarrow \! \mathord {\perp })\) expresses that the corresponding product families are disjoint.
We utilize the data variables associated to recursion variables in \(\textit{tr} (\gamma ,X)\) to pass the feature expression \(\gamma \) to the recursion variable \(\tilde{X}\). A similar mechanism applies to the fixpoint constructions. Thus, we assign \(\gamma \) to the data variable \(\upsilon \) associated with \(\tilde{X}\), signified by the bindings \(\mu \tilde{X}(\upsilon {:}{=} \gamma )\) and \(\nu \tilde{X}(\upsilon {:}{=} \gamma )\), and use the data variable in the translation of the remaining subformula, i.e.  .
.
Next, we state the correctness of the translation.
Theorem 2
Let F be an FTS and let  be a set of products. For each \(\mu L {}_f\)-formula
be a set of products. For each \(\mu L {}_f\)-formula  , state \(s\in S\) and product family
, state \(s\in S\) and product family  , it holds that
, it holds that

Proof
(Sketch) The proof relies on the claim that, for state s, product family P, data environment \(\theta \), and feature expression \(\gamma \) such that \(\theta (\gamma ) = P\), we have

for environments \(\zeta \!\in \textit{sPEnv}\), and \(\xi \!\in \!\textit{XEnv}\) such that \({(s,P) \in \zeta (X)}\) iff \({s \in \xi (\tilde{X})(P)}\) for all \(X \in {\mathcal {X}}\). The claim is shown by structural induction, exploiting iteration for the fixpoint constructions. From the claim the theorem follows directly. \(\square \)
As a consequence of the above theorem we can model check a \(\mu L {}_f\)-formula over an FTS by model checking the corresponding \(\mu L {}_{\text {FO}}\)-formula over the corresponding parametrized LTS.

Example 3
From Examples 1 and 2, recall FTS F of family P and \(\mu L {}_f\)-formula \(\psi _{f}\) stating that for products with  , action \(\textit{std}\) occurs infinitely often on all infinite runs over \(\{\textit{ins}, \textit{xxl}, \textit{std}\}\). Take the corresponding parametrized LTS L(F). Clearly, \(\psi _{f}\) holds in state \(s_0\) for all products without both features
, action \(\textit{std}\) occurs infinitely often on all infinite runs over \(\{\textit{ins}, \textit{xxl}, \textit{std}\}\). Take the corresponding parametrized LTS L(F). Clearly, \(\psi _{f}\) holds in state \(s_0\) for all products without both features  and
and  . mCRL2 can verify this, as deciding \(s_0 , P' \mathrel {\models _{F}}\psi _{f}\) for the family
. mCRL2 can verify this, as deciding \(s_0 , P' \mathrel {\models _{F}}\psi _{f}\) for the family  translates to model checking
translates to model checking  , where \(\textit{tr} (\gamma _{\text {P}},\psi _{f})\) is the \(\mu L {}_{\text {FO}}\)-formula
, where \(\textit{tr} (\gamma _{\text {P}},\psi _{f})\) is the \(\mu L {}_{\text {FO}}\)-formula

Note the passing of \(\gamma _{\text {P}}\) via the respective assignments \(\upsilon _x {:}{=} \gamma _{\text {P}}\) and \(\upsilon _y {:}{=} \upsilon _x\). \(\square \)
4 Family-Based Partitioning for \(\mu L {}_f\)
With Theorem 2 in place we are in a position where family-based model-checking a system can be performed using a standard \(\mu \)-calculus model checker. The final issue we face is to find, given a formula  and a family of products P, the subfamily of P whose products satisfy
and a family of products P, the subfamily of P whose products satisfy  , as well as the subfamily whose pro- ducts do not satisfy
, as well as the subfamily whose pro- ducts do not satisfy  . Thus, given a negation-free formula
. Thus, given a negation-free formula  and a family of products P, we are interested in computing a partitioning \((P_{\! \oplus },P_{\! \ominus })\) of P such that
and a family of products P, we are interested in computing a partitioning \((P_{\! \oplus },P_{\! \ominus })\) of P such that

Rather than establishing this product-by-product, we are after a procedure that decides Property (1) in a family-based manner.
The previous section provides a sound decision procedure for  . If the procedure returns true for the family P, we are done: Theorem 1 guarantees that the property holds for all products of P, i.e.
. If the procedure returns true for the family P, we are done: Theorem 1 guarantees that the property holds for all products of P, i.e.  for all \(p \in P\). If, on the other hand, the decision procedure for
for all \(p \in P\). If, on the other hand, the decision procedure for  returns false and P is not a singleton family, we cannot draw a conclusion for any of the products. However, in view of Lemma 1 below, we can run the decision procedure to decide
returns false and P is not a singleton family, we cannot draw a conclusion for any of the products. However, in view of Lemma 1 below, we can run the decision procedure to decide  , where
, where  is the complement of
is the complement of  . Formally, for negation-free \(\mu L {}_f\)-formula
. Formally, for negation-free \(\mu L {}_f\)-formula  , the formula
, the formula  is defined inductively by
is defined inductively by

We have the following result.
Lemma 1
For each negation-free formula  and set of products P, it holds that
and set of products P, it holds that  implies
implies  for all \(p \in P\).
for all \(p \in P\).
Proof
Let  be closed and negation-free, and let P be a family of products. For closed and negation-free \(\psi _{f}\in \mu L {}_f\), state s, and product p,
be closed and negation-free, and let P be a family of products. For closed and negation-free \(\psi _{f}\in \mu L {}_f\), state s, and product p,
a fact readily proven by induction on \(\psi _{f}\). Assume  . Observe, if
. Observe, if  is negation-free then so is
is negation-free then so is  . Hence, by Theorem 1,
. Hence, by Theorem 1,  for every \(p \in P\). By Equivalence (2) we find
for every \(p \in P\). By Equivalence (2) we find  for all \(p \in P\). \(\square \)
for all \(p \in P\). \(\square \)
On the lemma we base the straightforward partition procedure  of Algorithm 1 for computing \((P_{\! \oplus }, P_{\! \ominus })\) for a product family P such that each product in \(P_{\! \oplus }\) satisfies the \(\mu L {}_f\)-formula
of Algorithm 1 for computing \((P_{\! \oplus }, P_{\! \ominus })\) for a product family P such that each product in \(P_{\! \oplus }\) satisfies the \(\mu L {}_f\)-formula  , while each product in \(P_{\! \ominus }\) fails
, while each product in \(P_{\! \ominus }\) fails  .
.

Theorem 3
For closed and negation-free  , procedure
, procedure  terminates and returns a partitioning \((P_{\! \oplus }, P_{\! \ominus })\) of P satisfying Property (1).
terminates and returns a partitioning \((P_{\! \oplus }, P_{\! \ominus })\) of P satisfying Property (1).
Proof
Observe that the algorithm can be called at most \(2^{|P|}\) times as each call is performed on a strictly smaller subset of P. Therefore, the algorithm terminates iff the procedure for deciding  terminates. The correctness of the resulting partitioning \((P_{\! \oplus },P_{\! \ominus })\) follows by a straightforward induction, using Theorem 1 and Lemma 1. \(\square \)
terminates. The correctness of the resulting partitioning \((P_{\! \oplus },P_{\! \ominus })\) follows by a straightforward induction, using Theorem 1 and Lemma 1. \(\square \)
Example 4
Applying the algorithm to the FTS of Example 1 and the formula \(\psi _{f}\) of Example 2, running \(\textsc {fbp}(\mathord {\top },\psi _{f})\), we find \(s_0, \mathord {\top }\mathrel {{{\not \models }}_{F}}\psi _{f}\) and \(s_0, \mathord {\top }\mathrel {{{\not \models }}_{F}}\psi _{f}^{c}\). Splitting the family in sets  and
and  and recursively running
and recursively running  , returns the partition
, returns the partition  , since we have
, since we have  , and subsequently running
, and subsequently running  returns
returns  since
since  . Therefore
. Therefore  . \(\square \)
. \(\square \)
Clearly, repeatedly splitting families into subfamilies may lead to an exponential blow-up, in the worst case ultimately yielding a product-based analysis. Examples can be synthesized achieving this. However, in the SPL setting, an obvious strategy to partition a family P is to split along a feature \(\textsf {f}\), i.e. in the algorithm set \(P_1 = \mathopen {\lbrace \,}p\!\in \!P\mid \textsf {f}\!\in \!p \mathclose {\, \rbrace }\) and \(P_2 = \mathopen {\lbrace \,}p\!\in \!P \mid \textsf {f}\!\notin \!p \mathclose {\, \rbrace }\). In general, the order of subsequent features \(\textsf {f}\) will influence the number of split-ups needed. Fortunately, candidate features for splitting along may be distilled from the structure of the system and from specific domain knowledge. The experiments reported in the next section confirm this. As we will see, with an appropriate decomposition a low number of splittings will do.
5 Case Study
In this section, we report on our experiments to use the mCRL2 toolset to perform product-based and family-based model checking of an SPL model of the minepump from [39], making use of the logics and translations discussed above.
The SPL minepump model was first introduced in [4] as a reformulation of the configurable software system controlling a pump for mine drainage. The purpose of the minepump is to pump water out of a mine shaft, for which a controller operates a pump that may not start nor continue running in the presence of a dangerously high level of methane gas. Therefore, it communicates with a number of sensors measuring the water and methane levels. Here, we consider the model as used in [13] that consists of 7 independent optional features for a total of \(2^7 = 128\) variants. These features concern command types, methane detection, and water levels, abbreviated as Ct, Cp, Ma, Mq, L \(\ell \), Ln, and Lh.
The minepump model of [13] is distributed with the ProVeLines SPL toolset [18] (http://projects.info.unamur.be/fts/provelines/). We first manually translated the fPROMELA model to a parametrized LTS encoded in mCRL2.Footnote 1 For our model checking we considered twelve properties expressed in \(\mu L {}_f\). The first six are \(\mu \)-calculus versions of LTL properties of [13] (four of which are analyzed also in [8]). The others are CTL-like properties. Following the approach described in this paper, the formulas were translated into \(\mu L {}_{\text {FO}}\) and model checked over the mCRL2 model representing a parametrized LTS. The properties, results, and runtimes are summarized in Table 1. All our experiments were run on a standard Macbook Pro using revision 14493 of the mCRL2 toolset.
Family-Based Model Checking. For each of the twelve properties, we provide its intuitive meaning, its specification in \(\mu L {}_f\), and the result of model checking the property (indicating also the number of products for which the result holds). This concerns the first three columns of Table 1.Footnote 2 \({}^,\) Footnote 3 In the remaining columns, we report the runtimes (in seconds) needed to verify the properties with mCRL2, both product-based (one-by-one, abbreviated to ‘one’) and family-based (all-in-one, abbreviated to ‘all’). We report the internal time as measured by the tools. We immediately notice that family-based model checking with mCRL2 compares rather favorably to product-based model checking.
Next we discuss the verification of the properties listed in Table 1. Absence of deadlock turns out to be one of the more involved formulas to check family-wise for the case of the minepump. This is because in search for the truth value of the formula, all reachable states need to be visited. The \(\mu L\)-formula \([{ \texttt {true}^*} ]\langle { \texttt {true}} \rangle \mathord {\top }\), translates to the \(\mu L {}_f\)-formula \([{ \texttt {true}^*| \mathord {\top }} ]\langle { \texttt {true}| \mathord {\top }} \rangle \mathord {\top }\). The main complication arises from the fact that for each non-empty set of products P that can reach a state s in the FTS, the family-based semantics of \(\langle {\texttt {true}| \mathord {\top }} \rangle \mathord {\top }\) requires that there is a transition from s shared among all P. A partitioning of the set of all products that is too coarse leads to a trace indicating a violation of the \(\mu L {}_f\)-formula. Next, the trace can be analyzed with the mCRL2 toolset to identify a suitable decomposition into subfamilies.
For the minepump we identified 12 subfamilies, whose sets of trajectories are pairwise independent (i.e. for any two distinct subfamilies there exists a complete path possible for all products in one family, but not for all products in the other, and vice versa). These are the product sets characterized by the feature expressions \(\textit{Ct} \mathbin {\wedge } \tilde{\textit{Cp}} \mathbin {\wedge } \tilde{\textit{Ma}} \mathbin {\wedge } \tilde{\textit{Mq}} \), where \(\tilde{\textsf {f}} = \textsf {f} , \lnot \textsf {f} \), yielding eight families, and four further families yielded by the product sets given by \(\lnot \textit{Ct} \mathbin {\wedge } \tilde{\textit{Cp}} \mathbin {\wedge } \tilde{\textit{Ma}} \). As we shall see below, the combinations of features mentioned turn up in the analysis of other properties as well, which shows that the analysis of deadlock freedom (property \(\varphi _1\)) is a fruitful investigation.
Since no specific feature setting is involved in performing \(\textit{levelMsg} \) infinitely often (for a stable and acceptable water level), property \(\varphi _{2}\) can be refuted for the complete family of products at once by proving its complement. Also property \(\varphi _{3}\), seemingly more complex, can be refuted via its complement, requiring a decomposition in subfamilies given by the four Boolean combinations of \(\textit{Cp} \) and \(\textit{Ma} \).
The properties discussed so far cover general system aspects: absence of deadlock, future execution of an action, and fairness between subsystems. In contrast, property \(\varphi _{4}\) is specific to the minepump model. The property, modeled as a fluent [40], states that every computation involving \(\textit{pumpStart} \) has, after a while, a finite number of alternations of starting and subsequent stopping the pump (fluent \(\textit{pumpStart} .(\lnot \textit{pumpStop} )^*. \textit{pumpStop} \)), after which it is never again started, and after starting the pump (fluent \(\texttt {true}^*. \textit{pumpStart} \)) it is inevitably switched off. This property does not hold for all eligible products. However, a decomposition into a subfamily of 96 products given by \(\lnot (\textit{Ct} \mathbin {\wedge } \textit{Lh} )\), i.e. products missing \(\textit{Ct} \) or \(\textit{Lh} \), and in two subfamilies \(\textit{Ct} \mathbin {\wedge } \textit{Mq} \mathbin {\wedge } \textit{Lh} \) and \(\textit{Ct} \mathbin {\wedge } \lnot \textit{Mq} \mathbin {\wedge } \textit{Lh} \), of 32 products in total, does the job. The products in the first family satisfy \(\varphi _{4}\), whereas products in the second and third family do not.
More involved system properties are \(\varphi _{5}\) and \(\varphi _{6}\), mixing starting and stopping of the pump with the rising and dropping of the methane level. Property \(\varphi _{5}\) considers the rising of methane after the pump started but did not stop (fluent \(\textit{pumpStart} . (\lnot \textit{pumpStop} )^*. \textit{methaneRise} \)) and, symmetrically, starting the pump after the methane level rose (fluent \(\textit{methaneRise} . (\lnot \textit{methaneLower} )^*\! . \textit{pumpStart} \)). Formula \(\varphi _{6}\) is a refinement of formula \(\varphi _{5}\), restricting it to fair computations. For property \(\varphi _{5}\), family-based model checking is achieved using the same decomposition of the product space, with the same outcome, as for property \(\varphi _{4}\). For property \(\varphi _{6}\), because of the fairness requirement, the number of satisfying products increases from 96 to 112. This can be checked for all 112 products at once. To identify the violating products, we consider \(\varphi _{6}\)’s complement \(\varphi _{6}^{c}\) which is proven to hold for the family \(\textit{Ct} \wedge \lnot \textit{Ma} \wedge \textit{Lh} \) of 16 products as a whole.
An important liveness property for circuit design, the so-called reset property \(AG \, E F \, reset \), is expressible in CTL, but not in LTL (cf., e.g., [41]). For our case study, \(\varphi _{7}\) is such a reset property. It states that from any state the controller can, possibly after a finite number of steps, receive a message. Thus, it can always return to the initial state. The \(\mu L\)-formula \([\texttt {true}^*]\,\langle { \texttt {true}^*. \textit{receiveMsg} } \rangle \mathord {\top }\) can be verified using the same split-up in subfamilies that was used before for absence of deadlock (\(\varphi _1\)). A typical safety property is property \(\varphi _{8}\), expressing that the pump is not started as long as water levels are low. It holds for all products, which can be verified for all product families at once. The third CTL-type property \(\varphi _{9}\) states that when the level of methane rises, it inevitably drops again. It holds for no products. Refuting \(\varphi _{9}\) can also be done for all product families at once.
Finally, we have verified feature-rich \(\mu L {}_f\)-formulas. Properties \(\varphi _{10}\) and \(\varphi _{11}\) focus on the family of products featuring \(\textit{Ct} \) by means of the modalities \([{ \texttt {true}^*\,|\, \textit{Ct} } ]\) and \(\langle { \texttt {true}^*.\,\textit{pumpStart} \,|\, \textit{Ct} } \rangle \). However, by definition of \(\textit{pr} \), for products without feature \(\textit{Ct} \), property \(\varphi _{10}\) translates into \(\mathord {\perp }\) of \(\mu L\). Since a formula \([{ R^*| \chi } ]\varphi \) is to be read as \(\nu X . [{R | \chi } ]X \wedge \varphi \), we have that property \(\varphi _{11}\), for products without \(\textit{Ct} \), coincides with \(\nu X . [{ \texttt {true}| \textit{Ct} } ]\mathbin {\wedge } \mathord {\perp }\). Apparently, comparing \(\varphi _{10}\) and \(\varphi _{11}\), four more products with \(\textit{Ct} \) (viz. those without any \(\textit{Cp} \),  , or
, or  ) fail to meet the stronger \(\varphi _{11}\). Finally, property \(\varphi _{12}\) holds for all products. Note that the first conjunct \([{\, \textit{highLevel} \,|\, \textit{Ct} \wedge \textit{Ma} \wedge \textit{Lh} \,} ]\, \langle {\texttt {true}^*. \, \textit{pumpStart} \,|\, \mathord {\top }} \rangle \, \mathord {\top }\) is trivially true for products without any \(\textit{Ct} \), \(\textit{Ma} \), or \(\textit{Lh} \) due to the box modality, while the second conjunct \([{\, \textit{pumpStart} \,|\, \lnot \textit{Lh} \,} ]\, \mathord {\perp }\) holds trivially for products that include \(\textit{Lh} \). Model checking this property requires a decomposition into two subfamilies, viz. the set of products with the feature \(\textit{Mq} \) and the set of products without.
) fail to meet the stronger \(\varphi _{11}\). Finally, property \(\varphi _{12}\) holds for all products. Note that the first conjunct \([{\, \textit{highLevel} \,|\, \textit{Ct} \wedge \textit{Ma} \wedge \textit{Lh} \,} ]\, \langle {\texttt {true}^*. \, \textit{pumpStart} \,|\, \mathord {\top }} \rangle \, \mathord {\top }\) is trivially true for products without any \(\textit{Ct} \), \(\textit{Ma} \), or \(\textit{Lh} \) due to the box modality, while the second conjunct \([{\, \textit{pumpStart} \,|\, \lnot \textit{Lh} \,} ]\, \mathord {\perp }\) holds trivially for products that include \(\textit{Lh} \). Model checking this property requires a decomposition into two subfamilies, viz. the set of products with the feature \(\textit{Mq} \) and the set of products without.
Family-Based Partitioning. The results from the case study underline thatfamily-based model checking has the potential to outperform product-based model checking. Next, we explore the requirements for a successful implementation of family-based partitioning using off-the-shelf technology.
Figure 1 (left) shows the runtimes (in seconds) associated with the model-checking problems of lines 2 and 4 of Algorithm 1 for deadlock freedom (property \(\varphi _1\)). The total time needed to run this algorithm, given the refinement strategy indicated in Fig. 1, is 27.9 s. Observe that checking all leaves takes 8.4 s.Footnote 4 We see similar figures for other properties we verified.
Execution of Algorithm 1 for deadlock freedom (property \(\varphi _{1}\)) and the initial product family \(\top \), using an optimal partitioning strategy (depicted on the left) vs. using an ‘unproductive’ refinement strategy, splitting \(\textit{Ln} \) and \(\lnot \textit{Ln} \) and following the optimal strategy afterwards (excerpt depicted on the right). The characterized family described at each node is the conjunction of the features along the path from the root to that node. Total computation time for the optimal strategy: 27.9 s; total computation time for the 12 leaves (i.e. all \(\textit{Mq} \), \(\lnot \textit{Mq} \), and \(\lnot \textit{Ct} \) nodes): 8.4 s. Total computation time for partitioning using the ‘unproductive’ strategy: 45.0 s.
We draw two further conclusions from our experiments. First, as expected, refining a family of products with respect to non-relevant features can have a negative effect on runtime. For instance, partitioning with respect to a single non-essential feature \(\textit{Ln} \) at an early stage, cf. Fig. 1 (right), while following an optimal splitting otherwise, increases the runtime to 45 s; i.e. an additional 60%. Second, as illustrated by Fig. 1 (left), even for ‘productive’ refinements, model checking a property for a large family of products can consume a disproportionate amount of time. For instance, the three top nodes together account for almost 8 s, a quarter of the time spent on all model-checking problems combined.
We conclude that the performance of SPL verification using a general-purpose model checker for family-based partitioning crucially depends on the initial partitioning of products and the ‘quality’ of the refinements of families of products in the algorithm. This suggests that one must invest in: (i) determining heuristics for finding a good initial partitioning of a family of products, (ii) extracting information from the failed model-checking problems that facilitates an informed/productive split-up of the family of products in line 5 of Algorithm 1. In particular for the \(\mu \)-calculus, the second challenge may be difficult, since easily-interpretable feedback from its model checkers is generally missing so far.
6 Concluding Remarks and Future Work
We have showed how the feature \(\mu \)-calculus \(\mu L {}_f\) can be embedded in \(\mu L {}_{\text {FO}}\), a logic accepted by toolsets such as mCRL2. Through this embedding, we obtain a family-based model-checking procedure for verifying \(\mu \)-calculus properties of SPLs, and similar systems with variability, using off-the-shelf verifiers. Moreover, as our experiments indicate, the resulting family-based model-checking approach trumps the product-based model-checking approach of [19].
The efficiency of computing a partitioning of a product family from which we can read which products satisfy which formula, strongly depends on the adopted strategy for splitting product families and may constitute a bottleneck in practice. We leave it for future research to find heuristics to guide this splitting. One possibility may be to deduce an effective strategy from the lattice of product families that can be obtained by exploring the FTS model and keeping track of (the largest) product families that are capable of reaching states. This lattice may even allow for determining a proper partitioning a priori. Another potentially promising direction is to split product families using information that is obtained from counterexamples. Indeed, in our product-based and family-based model-checking experiments we used counterexamples to find suitable subfamilies of products by splitting with respect to feature expressions on transitions that led to the violations. We must note, however, that this was largely a manual activity which required a fair share of tool experience. More generally, we note that constructing and interpreting counterexamples for the modal \(\mu \)-calculus is notoriously difficult, as such counterexamples are not necessarily linear.
Finally, we believe that for particular properties specific insight regarding the model under study is required to quickly identify a successful split-up. We liken this to the approach taken in [8], where the theory of Galois connections is used to establish suitable abstractions of the minepump model prior to model checking with \(\texttt {SPIN}\); we quote “Given sufficient knowledge of the system and the property, we can easily tailor an abstraction for analyzing the system more effectively”. It is indeed common in SPL engineering to assume substantial understanding of the SPL under scrutiny, in particular of its commonalities and variability as documented in variability models like feature diagrams.
Notes
- 1.
The mCRL2 code is distributed with the mCRL2 toolset (svn revision 14493).
- 2.
- 3.
Standard \(\mu \)-calculus formulas in \(\mu L\) can be seen as \(\mu L {}_f\)-formulas by adjoining the feature expression \(\mathord {\top }\) to every modality, i.e. replacing each ‘diamond’ modality \(\langle {a} \rangle \) by \(\langle {a | \mathord {\top }} \rangle \) and each ‘box’ modality \([{a } ]\) by \([{a | \mathord {\top }} ]\).
- 4.
The additional overhead of approximately 6 s compared to the 2.07 s we reported in Table 1 is due to the fact that there we could inspect the model once for all possible families, whereas here we must inspect the model once per family.
References
Thüm, T., et al.: A classification and survey of analysis strategies for software product lines. ACM Comput. Surv. 47(1), 1–45 (2014)
Gruler, A., Leucker, M., Scheidemann, K.: Modeling and model checking software product lines. In: Barthe, G., Boer, F.S. (eds.) FMOODS 2008. LNCS, vol. 5051, pp. 113–131. Springer, Heidelberg (2008). doi:10.1007/978-3-540-68863-1_8
Lauenroth, K., Pohl, K., Töhning, S.: Model checking of domain artifacts in product line engineering. In: ASE, pp. 269–280. IEEE (2009)
Classen, A., et al.: Model checking \(\underline{\text{lots}}\) of systems: efficient verification of temporal properties in software product lines. In: ICSE, pp. 335–344. ACM (2010)
Damiani, F., Schaefer, I.: Family-based analysis of type safety for delta-oriented software product lines. In: Margaria, T., Steffen, B. (eds.) ISoLA 2012. LNCS, vol. 7609, pp. 193–207. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34026-0_15
Thüm, T., Schaefer, I., Hentschel, M., Apel, S.: Family-based deductive verification of software product lines. In: GPCE, pp. 11–20. ACM (2012)
ter Beek, M.H., Fantechi, A., Gnesi, S., Mazzanti, F.: Using FMC for family-based analysis of software product lines. In: SPLC, pp. 432–439. ACM (2015)
Dimovski, A.S., Al-Sibahi, A.S., Brabrand, C., Wąsowski, A.: Family-based model checking without a family-based model checker. In: Fischer, B., Geldenhuys, J. (eds.) SPIN 2015. LNCS, vol. 9232, pp. 282–299. Springer, Cham (2015). doi:10.1007/978-3-319-23404-5_18
Clarke, E.M., Emerson, E.A., Sifakis, J.: Model checking: algorithmic verification and debugging. C. ACM 52(11), 74–84 (2009)
Gruler, A., Leucker, M., Scheidemann, K.: Calculating and modeling common parts of software product lines. In: SPLC, pp. 203–212. IEEE (2008)
ter Beek, M.H., Lluch Lafuente, A., Petrocchi, M.: Combining declarative and procedural views in the specification and analysis of product families. In: SPLC, vol. 2, pp. 10–17. ACM (2013)
Lochau, M., Mennicke, S., Baller, H., Ribbeck, L.: Incremental model checking delta-oriented software product lines. J. Log. Algebr. Meth. Program. 85(1), 245–267 (2016)
Classen, A., et al.: Featured transition systems: foundations for verifying variability-intensive systems and their application to LTL model checking. IEEE Trans. Softw. Eng. 39(8), 1069–1089 (2013)
Classen, A., et al.: Formal semantics, modular specification, and symbolic verification of product-line behaviour. Sci. Comput. Program. 80(B), 416–439 (2014)
ter Beek, M.H., Fantechi, A., Gnesi, S., Mazzanti, F.: Modelling and analysing variability in product families: model checking of modal transition systems with variability constraints. J. Log. Algebr. Meth. Program. 85(2), 287–315 (2016)
ter Beek, M.H., Mazzanti, F., Sulova, A.: VMC: a tool for product variability analysis. In: Giannakopoulou, D., Méry, D. (eds.) FM 2012. LNCS, vol. 7436, pp. 450–454. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32759-9_36
Classen, A., et al.: Model checking software product lines with SNIP. Int. J. Softw. Tools Technol. Transf. 14(5), 589–612 (2012)
Cordy, A., et al.: ProVeLines: a product line of verifiers for software product lines. In: SPLC, vol. 2, pp. 141–146. ACM (2013)
ter Beek, M.H., de Vink, E.P.: Using mCRL2 for the analysis of software product lines. In: FormaliSE, pp. 31–37. IEEE (2014)
ter Beek, M.H., de Vink, E.P., Willemse, T.A.C.: Towards a feature mu-calculus targeting SPL verification. In: FMSPLE, EPTCS, vol. 206, pp. 61–75 (2016)
Cranen, S., Groote, J.F., Keiren, J.J.A., Stappers, F.P.M., de Vink, E.P., Wesselink, W., Willemse, T.A.C.: An overview of the mCRL2 toolset and its recent advances. In: Piterman, N., Smolka, S.A. (eds.) TACAS 2013. LNCS, vol. 7795, pp. 199–213. Springer, Heidelberg (2013). doi:10.1007/978-3-642-36742-7_15
Groote, J.F., Mousavi, M.R.: Modeling and Analysis of Communicating Systems. MIT Press, Cambridge (2014)
Kim, C.H.P., et al.: SPLat: lightweight dynamic analysis for reducing combinatorics in testing configurable systems. In: ESEC/FSE, pp. 257–267. ACM (2013)
Bürdek, J., Lochau, M., Bauregger, S., Holzer, A., von Rhein, A., Apel, S., Beyer, D.: Facilitating reuse in multi-goal test-suite generation for software product lines. In: Egyed, A., Schaefer, I. (eds.) FASE 2015. LNCS, vol. 9033, pp. 84–99. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46675-9_6
Lity, S., Morbach, T., Thüm, T., Schaefer, I.: Applying incremental model slicing to product-line regression testing. In: Kapitsaki, G.M., Santana de Almeida, E. (eds.) ICSR 2016. LNCS, vol. 9679, pp. 3–19. Springer, Cham (2016). doi:10.1007/978-3-319-35122-3_1
Beohar, H., Varshosaz, M., Mousavi, M.R.: Basic behavioral models for software product lines: expressiveness and testing pre-orders. Sci. Comput. Program. 123, 42–60 (2016)
Ghezzi, C., Sharifloo, A.: Model-based verification of quantitative non-functional properties for software product lines. Inform. Softw. Technol. 55(3), 508–524 (2013)
Varshosaz, M., Khosravi, R.: Discrete time markov chain families: modeling and verification of probabilistic software product lines. In: SPLC, vol. 2, pp. 34–41. ACM (2013)
Rodrigues, G.N., et al.: Modeling and verification for probabilistic properties in software product lines. In: HASE, pp. 173–180. IEEE (2015)
Dubslaff, C., Baier, C., Klüppelholz, S.: Probabilistic model checking for feature-oriented systems. In: Chiba, S., Tanter, É., Ernst, E., Hirschfeld, R. (eds.) Transactions on Aspect-Oriented Software Development XII. LNCS, vol. 8989, pp. 180–220. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46734-3_5
Kwiatkowska, M., Norman, G., Parker, D.: PRISM 4.0: verification of probabilistic real-time systems. In: Gopalakrishnan, G., Qadeer, S. (eds.) CAV 2011. LNCS, vol. 6806, pp. 585–591. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22110-1_47
Chrszon, P., Dubslaff, C., Klüppelholz, S., Baier, C.: Family-based modeling and analysis for probabilistic systems – featuring ProFeat. In: Stevens, P., Wąsowski, A. (eds.) FASE 2016. LNCS, vol. 9633, pp. 287–304. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49665-7_17
ter Beek, M.H., Legay, A., Lluch Lafuente, A., Vandin, A.: Statistical analysis of probabilistic models of software product lines with quantitative constraints. In: SPLC, pp. 11–15. ACM (2015)
ter Beek, M.H., Legay, A., Lluch Lafuente, A., Vandin, A.: Statistical model checking for product lines. In: Margaria, T., Steffen, B. (eds.) ISoLA 2016. LNCS, vol. 9952, pp. 114–133. Springer, Cham (2016). doi:10.1007/978-3-319-47166-2_8
Bradfield, J.C., Stirling, C.: Modal logics and \(\mu \)-calculi: an introduction. In: Handbook of Process Algebra, Chap. 4, pp. 293–330. Elsevier (2001)
Groote, J.F., Mateescu, R.: Verification of temporal properties of processes in a setting with data. In: Haeberer, A.M. (ed.) AMAST 1999. LNCS, vol. 1548, pp. 74–90. Springer, Heidelberg (1998). doi:10.1007/3-540-49253-4_8
Groote, J.F., Willemse, T.A.C.: Model-checking processes with data. Sci. Comput. Program. 56(3), 251–273 (2005)
Zantema, H., van de Pol, J.C.: A rewriting approach to binary decision diagrams. J. Log. Algebr. Program. 49(1–2), 61–86 (2001)
Kramer, J., Magee, J., Sloman, M., Lister, A.: CONIC: an integrated approach to distributed computer control systems. IEE Proc. E 130(1), 1–10 (1983)
Giannakopoulou, D., Magee, J.: Fluent model checking for event-based systems. In: ESEC/FSE, pp. 257–266. ACM (2003)
Clarke, E.M., Grumberg, O., Peled, D.A.: Model Checking. MIT Press, Cambridge (1999)
Acknowledgements
Maurice ter Beek was supported by the EU FP7 project QUANTICOL (600708). The authors are grateful to Franco Mazzanti for his help with the minepump model. Finally, we thank the anonymous referees for their suggestions, which helped improve the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
ter Beek, M.H., de Vink, E.P., Willemse, T.A.C. (2017). Family-Based Model Checking with mCRL2. In: Huisman, M., Rubin, J. (eds) Fundamental Approaches to Software Engineering. FASE 2017. Lecture Notes in Computer Science(), vol 10202. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54494-5_23
Download citation
DOI: https://doi.org/10.1007/978-3-662-54494-5_23
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54493-8
Online ISBN: 978-3-662-54494-5
eBook Packages: Computer ScienceComputer Science (R0)





 characterizes the family of products P that can execute
characterizes the family of products P that can execute  , while
, while 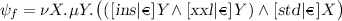 characterizes the (sub)family of products which, when having feature
characterizes the (sub)family of products which, when having feature  , action
, action  , state
, state  :
: 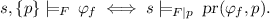
 , state
, state  :
: 

