Abstract
We generalize the recursive path order (RPO) to higher-order terms without \(\lambda \)-abstraction. This new order fully coincides with the standard RPO on first-order terms also in the presence of currying, distinguishing it from previous work. It has many useful properties, including well-foundedness, transitivity, stability under substitution, and the subterm property. It appears promising as the basis of a higher-order superposition calculus.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Most automatic reasoning tools are restricted to first-order formalisms, even though many proof assistants and specification languages are higher-order. Translations bridge the gap, but they usually have a cost. Thus, a recurrent question in our field is, Which first-order methods can be gracefully extended to a higher-order setting? By “gracefully,” we mean that the higher-order extension of the method is as powerful as its first-order counterpart on the first-order portions of the input.
The distinguishing features of higher-order terms are that (1) they support currying, meaning that an n-ary function may be applied to fewer than n arguments, (2) variables can be applied, and (3) \(\lambda \)-abstractions, written  , can be used to specify anonymous functions
, can be used to specify anonymous functions  . Iterated applications are written without parentheses or commas, as in
. Iterated applications are written without parentheses or commas, as in  . Many first-order proof calculi have been extended to higher-order logic, including resolution and tableaux, but so far there exists no sound and complete higher-order version of superposition [29], where completeness is considered with respect to Henkin semantics [4, 18]. Together with CDCL(T) [17], superposition is one of the leading proof calculi for classical first-order logic with equality.
. Many first-order proof calculi have been extended to higher-order logic, including resolution and tableaux, but so far there exists no sound and complete higher-order version of superposition [29], where completeness is considered with respect to Henkin semantics [4, 18]. Together with CDCL(T) [17], superposition is one of the leading proof calculi for classical first-order logic with equality.
To prune the search space, superposition depends on a term order, which is fixed in advance of the proof attempt. For example, from \(\textsf {{p}}(\textsf {{a}})\) and \(\lnot \, \textsf {{p}}( x ) \mathrel \vee \textsf {{p}}(\textsf {{f}} ( x ))\), resolution helplessly derives infinitely many clauses of the form \(\textsf {{p}}(\textsf {{f}} ^{\,i}(\textsf {{a}}))\), whereas for superposition the literal \(\textsf {{p}}(\textsf {{f}} ( x ))\) is maximal in its clause and blocks all inferences. To work with superposition, the order must fulfill many requirements, including compatibility with contexts, stability under substitution, and totality on ground (variable-free) terms. The lexicographic path order (LPO) and the Knuth–Bendix order (KBO) [3] both fulfill the requirements. LPO is a special case of the recursive path order (RPO), which also subsumes the multiset path order [38]. Suitable generalizations of LPO and KBO appear to be crucial ingredients of a future higher-order superposition prover.
A simple technique to support currying and applied variables is to make all symbols nullary and to represent application by a distinguished binary symbol \(\textsf {{@}}.\) Thus, the higher-order term  is translated to \(\textsf {{@}}(\textsf {{f}}, \textsf {{@}}( x , \textsf {{f}}))\), which can be processed by first-order methods. We call this the applicative encoding. As for \(\lambda \)-abstractions, in many settings they can be avoided using \(\lambda \)-lifting [21] or SK combinators [36]. A drawback of the applicative encoding is that argument tuples cannot be compared using different methods for different function symbols. The use of an application symbol also weakens the order in other ways [25, Sect. 2.3.1]. Hybrid schemes have been proposed to strengthen the encoding: If a function \(\textsf {{f}} \) always occurs with at least k arguments, these can be passed directly in an uncurried style—e.g., \(\textsf {{@}}(\textsf {{f}} (\textsf {{a}}, \textsf {{b}}), x ).\) However, this relies on a closed-world assumption—namely, that all terms that will ever be compared arise in the input problem. This is at odds with the need for complete higher-order proof calculi to synthesize arbitrary terms during proof search [4], in which a symbol \(\textsf {{f}} \) may be applied to fewer arguments than anywhere in the problem. A scheme by Hirokawa et al. [19] circumvents this issue but requires additional symbols and rewrite rules.
is translated to \(\textsf {{@}}(\textsf {{f}}, \textsf {{@}}( x , \textsf {{f}}))\), which can be processed by first-order methods. We call this the applicative encoding. As for \(\lambda \)-abstractions, in many settings they can be avoided using \(\lambda \)-lifting [21] or SK combinators [36]. A drawback of the applicative encoding is that argument tuples cannot be compared using different methods for different function symbols. The use of an application symbol also weakens the order in other ways [25, Sect. 2.3.1]. Hybrid schemes have been proposed to strengthen the encoding: If a function \(\textsf {{f}} \) always occurs with at least k arguments, these can be passed directly in an uncurried style—e.g., \(\textsf {{@}}(\textsf {{f}} (\textsf {{a}}, \textsf {{b}}), x ).\) However, this relies on a closed-world assumption—namely, that all terms that will ever be compared arise in the input problem. This is at odds with the need for complete higher-order proof calculi to synthesize arbitrary terms during proof search [4], in which a symbol \(\textsf {{f}} \) may be applied to fewer arguments than anywhere in the problem. A scheme by Hirokawa et al. [19] circumvents this issue but requires additional symbols and rewrite rules.
Versions of RPO tailored for higher-order terms are described in the literature, including Lifantsev and Bachmair’s LPO on \(\lambda \)-free higher-order terms [27], Jouannaud and Rubio’s higher-order RPO (HORPO) [23], Kop and van Raamsdonk’s iterative HORPO [26], the HORPO extension with polynomial interpretation orders by Bofill et al. [12], and the computability path order by Blanqui et al. [10], also a variant of HORPO. All of these combine uncurrying and currying: They distinguish between functional arguments, which are passed directly as a tuple to a function, and applicative arguments, which are optional. Coincidence with the standard RPO on first-order terms is achieved only for uncurried functions. Techniques to automatically curry or uncurry functions have been developed, but they rely on the closed-world assumption. Moreover, the orders all lack totality on ground terms; the HORPO variants also lack the subterm property, and only their (noncomputable) transitive closure is transitive.
We introduce a new “graceful” order \(>_{\textsf {ho}}\) for untyped \(\lambda \)-free higher-order terms (Sect. 3). It generalizes the first-order RPO along two main axes: (1) It relies on a higher-order notion of subterm; (2) it supports terms with applied variables—e.g., \( x \textsf {{b}} >_{\textsf {ho}} x \textsf {{a}} \) if \(\textsf {{b}} \succ \textsf {{a}} \) according to the underlying precedence \(\succ \) on symbols. The order is parameterized by a family of abstractly specified extension operators indexed by function symbols, allowing lexicographic, multiset, and other extension operators. An optimized variant, \(>_{\textsf {oh}}\), coincides with \(>_{\textsf {ho}}\) under a reasonable assumption on the extension operator. For comparison, we also present the first-order RPO \(>_{\textsf {fo}}\) and its composition \(>_{\textsf {ap}}\) with the applicative encoding, both recast to our abstract framework.
The \(\lambda \)-free fragment is useful in its own right and constitutes a stepping stone towards full higher order. Our new order operates exclusively on curried functions while coinciding with the standard RPO on first-order terms. This was considered impossible by Lifantsev and Bachmair [27]:
Pairs, or more generally tuples, allow one to compare the arguments of different functions with greater flexibility. For instance, the arguments of one function may be compared lexicographically, whereas in other cases comparison may be based on the multisets of arguments. ... But since function symbols are much more decoupled from their arguments in a higher-order setting than in a first-order setting, the information needed for different argument-comparison methods would be lost if one, say, just curried all functions.
The order \(>_{\textsf {ho}}\) enjoys many useful properties (Sect. 4). One property that is missing is compatibility with a specific type of higher-order context: If \(s ' >_{\textsf {ho}}s \), it is still possible that  . For example, if \(\textsf {{g}} \succ \textsf {{f}} \succ \textsf {{b}} \succ \textsf {{a}} \), then \(\textsf {{f}} (\textsf {{g}} \textsf {{a}}) >_{\textsf {ho}}\textsf {{g}} \) by the subterm property, but \(\textsf {{f}} (\textsf {{g}} \textsf {{a}})\textsf {{b}} <_{\textsf {ho}}\textsf {{g}} \textsf {{b}} \) by coincidence with the first-order RPO [35]. Nonetheless, we expect the order to be usable for \(\lambda \)-free higher-order superposition, at the cost of some complications [13]. The proofs of the properties were carried out in a proof assistant, Isabelle/HOL [31], and are publicly available [7]. Informal proofs are included in this paper and in a technical report [8].
. For example, if \(\textsf {{g}} \succ \textsf {{f}} \succ \textsf {{b}} \succ \textsf {{a}} \), then \(\textsf {{f}} (\textsf {{g}} \textsf {{a}}) >_{\textsf {ho}}\textsf {{g}} \) by the subterm property, but \(\textsf {{f}} (\textsf {{g}} \textsf {{a}})\textsf {{b}} <_{\textsf {ho}}\textsf {{g}} \textsf {{b}} \) by coincidence with the first-order RPO [35]. Nonetheless, we expect the order to be usable for \(\lambda \)-free higher-order superposition, at the cost of some complications [13]. The proofs of the properties were carried out in a proof assistant, Isabelle/HOL [31], and are publicly available [7]. Informal proofs are included in this paper and in a technical report [8].
Beyond superposition, the order can also be employed to prove termination of higher-order term rewriting systems. Because it treats all functions as curried, it differs from the other higher-order RPOs on many examples (Sect. 5), thereby enriching the portfolio of methods available to termination provers.
Conventions. We fix a set  of variables with typical elements \( x , y .\) A higher-order signature consists of a nonempty set \(\mathrm {\Sigma }\) of (function) symbols \(\textsf {{a}}, \textsf {{b}}, \textsf {{f}}, \textsf {{g}}, \textsf {{h}}, \ldots {}\). Untyped \(\lambda \)-free higher-order (\(\mathrm {\Sigma } \)-)terms
of variables with typical elements \( x , y .\) A higher-order signature consists of a nonempty set \(\mathrm {\Sigma }\) of (function) symbols \(\textsf {{a}}, \textsf {{b}}, \textsf {{f}}, \textsf {{g}}, \textsf {{h}}, \ldots {}\). Untyped \(\lambda \)-free higher-order (\(\mathrm {\Sigma } \)-)terms  (
( ) are defined inductively by the grammar
) are defined inductively by the grammar  . These are isomorphic to applicative terms [24].
. These are isomorphic to applicative terms [24].
A term of the form tu is called an application. Non-application terms  are called heads. Terms can be decomposed in a unique way as a head applied to zero or more arguments: \(\zeta s _1\,\ldots \,s _m.\) This view corresponds to the first-order, uncurried syntax \(\zeta (s _1,\ldots ,s _m)\), except that \(\zeta \) may always be a variable.
are called heads. Terms can be decomposed in a unique way as a head applied to zero or more arguments: \(\zeta s _1\,\ldots \,s _m.\) This view corresponds to the first-order, uncurried syntax \(\zeta (s _1,\ldots ,s _m)\), except that \(\zeta \) may always be a variable.
The size \(\left| s \right| \) of a term is the number of grammar rule applications needed to construct it. The set of variables occurring in \(s \) is written  . The set of subterms of a term \(s \) always contains \(s \); for applications \(t u \), it also includes all the subterms of t and u.
. The set of subterms of a term \(s \) always contains \(s \); for applications \(t u \), it also includes all the subterms of t and u.
A first-order signature \(\mathrm {\Sigma } \) extends a higher-order signature by associating an arity with each symbol belonging to \(\mathrm {\Sigma }.\) A first-order term is a term in which variables are unapplied and symbols are applied to the number of arguments specified by their arity. For consistency, we will use a curried syntax for first-order terms.
2 Extension Orders
Orders such as RPO depend on extension operators to recurse through tuples of arguments. The literature is mostly concerned with the lexicographic and multiset orders [3, 38]. We favor an abstract treatment that formulates requirements on the extension operators. Beyond its generality, this approach emphasizes the complications arising from the higher-order setting.
Let \(A^* = \bigcup _{i =0}^\infty A^i \) be the set of tuples (or finite lists) of arbitrary length whose components are drawn from a set A. We write its elements as \((a _1,\ldots ,a _m)\), where \(m \ge 0\), or simply \(\bar{a}.\) The empty tuple is written \(().\) Singleton tuples are identified with elements of A. The number of components of a tuple \(\bar{a}\) is written \(\left| \smash {\bar{a}}\right| \). Given an \(m \)-tuple \(\bar{a}\) and an \(n \)-tuple \(\bar{b}\), we denote by \(\bar{a}\cdot \bar{b}\) the \((m +n)\)-tuple consisting of the concatenation of \(\bar{a}\) and \(\bar{b}.\)
Given a function \(h : A \rightarrow A\), we let \(h(\bar{a})\) stand for the componentwise application of h to \(\bar{a}.\) Abusing notation, we sometimes use a tuple where a set or multiset is expected, ignoring the extraneous structure. Moreover, since all our functions are curried, we write \(\zeta \bar{s}\) for a curried application \(\zeta s _1\,\ldots \,s _m \), without risk of ambiguity.
Given a relation >, we write < for its inverse (i.e.,  ) and \(\ge \) for its reflexive closure (i.e.,
) and \(\ge \) for its reflexive closure (i.e.,  ). A (strict) partial order is a relation that is irreflexive (i.e.,
). A (strict) partial order is a relation that is irreflexive (i.e.,  ) and transitive (i.e.,
) and transitive (i.e.,  ). A (strict) total order is a partial order that satisfies totality (i.e.,
). A (strict) total order is a partial order that satisfies totality (i.e.,  ). A relation > is well founded if and only if there exists no infinite chain of the form \(a _0> a _1 > \cdots .\)
). A relation > is well founded if and only if there exists no infinite chain of the form \(a _0> a _1 > \cdots .\)
Let  be a family of relations indexed by a relation
be a family of relations indexed by a relation  . For example, \({\mathrel {{>}\!\!{{>}}}}\) could be the lexicographic or multiset extension of \({>}\). The following properties are essential for all the orders defined later, whether first- or higher-order:
. For example, \({\mathrel {{>}\!\!{{>}}}}\) could be the lexicographic or multiset extension of \({>}\). The following properties are essential for all the orders defined later, whether first- or higher-order:
-
X1.
Monotonicity: \(\bar{b} \mathrel {{\mathrel {{>}\!\!{{>}}}}_1} \bar{a}\) implies \(\bar{b} \mathrel {{\mathrel {{>}\!\!{{>}}}}_2} \bar{a}\) if \(b \mathrel {{>}_1} a \) implies \(b \mathrel {{>}_2} a \) for all \(a,\,b \);
-
X2.
Preservation of stability:
\(\bar{b} \mathrel {{>}\!\!{{>}}}\bar{a}\) implies \(h(\bar{b}) \mathrel {{>}\!\!{{>}}}h(\bar{a})\) if \(b > a \) implies \(h(b) > h(a)\) for all \(a,\,b \);
-
X3.
Preservation of transitivity: \(\mathrel {{>}\!\!{{>}}}\) is transitive if > is transitive;
-
X4.
Preservation of irreflexivity: \(\mathrel {{>}\!\!{{>}}}\) is irreflexive if > is irreflexive and transitive;
-
X5.
Preservation of well-foundedness: \(\mathrel {{>}\!\!{{>}}}\) is well founded if > is well founded;
-
X6.
Compatibility with tuple contexts: \(b > a \) implies \(\bar{c}\cdot b \cdot \bar{d} \mathrel {{>}\!\!{{>}}}\bar{c}\cdot a \cdot \bar{d}.\)
Because the relation > will depend on \({\mathrel {{>}\!\!{{>}}}}\) for its definition, we cannot assume outright that it is a partial order, a fine point that is sometimes overlooked [38, Sect. 6.4.2].
The remaining properties of \(\mathrel {{>}\!\!{{>}}}\) will be required only by some of the orders or for some optional properties of >:
-
X7.
Preservation of totality: \(\mathrel {{>}\!\!{{>}}}\) is total if > is total;
-
X8.
Compatibility with prepending: \(\bar{b} \mathrel {{>}\!\!{{>}}}\bar{a}\) implies \(a \cdot \bar{b} \mathrel {{>}\!\!{{>}}}a \cdot \bar{a}\);
-
X9.
Compatibility with appending: \(\bar{b} \mathrel {{>}\!\!{{>}}}\bar{a}\) implies
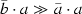 ;
; -
X10.
Minimality of empty tuple:

We now define the extension operators and study their properties. All of them are also defined for tuples of different lengths.
Definition 1
The lexicographic extension \(\mathrel {{>}\!\!{{{>}^\textsf {lex}}}}\) of the relation > is defined recursively by \(()\not \mathrel {{>}\!\!{{{>}^\textsf {lex}}}}\bar{a}\), \(b \cdot \bar{b} \mathrel {{>}\!\!{{{>}^\textsf {lex}}}}()\), and  .
.
The reverse, or right-to-left, lexicographic extension is defined analogously. Both operators lack the essential property X5. In addition, the left-to-right version lacks X9, and the right-to-left version lacks X8. The other properties are straightforward to prove.
Definition 2
The length-lexicographic extension \(\mathrel {{>}\!\!{{{>}^\textsf {llex}}}}\) of the relation > is defined by  .
.
The length-lexicographic extension and its right-to-left counterpart satisfy all of the properties listed above. We can also apply arbitrary permutations on same-length tuples before comparing them lexicographically; however, the resulting operators generally fail to satisfy properties X8 and X9.
Definition 3
The multiset extension \(\mathrel {{>}\!\!{{{>}^\textsf {ms}}}}\) of the relation > is defined by  , where X, Y range over multisets, the tuples \(\bar{a}, \bar{b}\) are implicitly converted to multisets, and \(\uplus \) denotes multiset sum (the sum of the multiplicity functions).
, where X, Y range over multisets, the tuples \(\bar{a}, \bar{b}\) are implicitly converted to multisets, and \(\uplus \) denotes multiset sum (the sum of the multiplicity functions).
The multiset extension, due to Dershowitz and Manna [16], satisfies all properties except X7. Huet and Oppen [20] give an alternative formulation that is equivalent for partial orders > but exhibits subtle differences if > is an arbitrary relation. In particular, the Huet–Oppen order does not satisfy property X3.
Finally, we consider the componentwise extension of relations to pairs of tuples of the same length. For partial orders >, this order underapproximates any extension that satisfies properties X3 and X6. It also satisfies all properties except X7.
Definition 4
The componentwise extension \(\mathrel {{>}\!\!{{{>}^\textsf {cw}}}}\) of the relation > is defined so that \((b _1,\ldots ,b _n) \mathrel {{>}\!\!{{{>}^\textsf {cw}}}}(a _1,\ldots ,a _m)\) if and only if \(m = n \), \(b _1 \ge a _1\), \(\cdots \), \(b _m \ge a _m \), and \(b _i > a _i \) for some \(i \in \{1,\cdots ,m \}\).
3 Term Orders
This section presents four orders: the standard first-order RPO (Sect. 3.1), the applicative RPO (Sect. 3.2), our new \(\lambda \)-free higher-order RPO (Sect. 3.3), and an optimized variant of our new RPO (Sect. 3.4).
3.1 The Standard First-Order RPO
The following definition is close to Zantema’s formulation [38, Definition 6.4.4] but adapted to our setting. With three rules instead of four, it is more concise than Baader and Nipkow’s formulation of LPO [3, Definition 5.4.12] and lends itself better to a higher-order generalization.
Definition 5
Let \(\succ \) be a well-founded total order on \(\mathrm {\Sigma } \), and let  be a family of relations indexed by
be a family of relations indexed by  and by \(\textsf {{f}} \in \mathrm {\Sigma } \) and satisfying properties X1–X6. The induced recursive path order \(>_{\textsf {fo}}\) on first-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {fo}}s \) if any of the following conditions is met, where \(t = \textsf {{g}} \bar{t}\):
and by \(\textsf {{f}} \in \mathrm {\Sigma } \) and satisfying properties X1–X6. The induced recursive path order \(>_{\textsf {fo}}\) on first-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {fo}}s \) if any of the following conditions is met, where \(t = \textsf {{g}} \bar{t}\):
-
F1.
\(t ' \ge _{\textsf {fo}}s \) for some term \(t ' \in \bar{t}\);
-
F2.
\(s = \textsf {{f}} \bar{s}\), \(\textsf {{g}} \succ \textsf {{f}} \), and
 ;
; -
F3.
\(s = \textsf {{f}} \bar{s}\), \(\textsf {{f}} = \textsf {{g}} \), \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {fo}}^\textsf {{f}}}}} \bar{s}\), and
 .
.
The auxiliary predicate  is true if and only if \(t >_{\textsf {fo}}s '\) for all terms \(s ' \in \bar{s}.\) The inductive definition is legitimate by the monotonicity of \({\mathrel {{>}\!\!{{>}}}}^\textsf {{f}} \) (property X1).
is true if and only if \(t >_{\textsf {fo}}s '\) for all terms \(s ' \in \bar{s}.\) The inductive definition is legitimate by the monotonicity of \({\mathrel {{>}\!\!{{>}}}}^\textsf {{f}} \) (property X1).
RPO is a compromise between two design goals. On the one hand, rules F2 and F3, which form the core of the order, attempt to perform a comparison of two terms by first looking at their heads, proceeding recursively to break ties. On the other hand, rule F1 ensures that terms are larger than their proper subterms and, transitively, larger than terms smaller than these. The  predicate prevents the application of F2 and F3 when F1 is applicable in the other direction, ensuring irreflexivity.
predicate prevents the application of F2 and F3 when F1 is applicable in the other direction, ensuring irreflexivity.
The more recent literature defines RPO somewhat differently: Precision is improved by replacing recursive calls to \(\ge _{\textsf {fo}}\) with a nonstrict quasiorder  and by exploiting a generalized multiset extension [14, 33]. These extensions are useful but require substantial duplication in the definitions and the proofs, without yielding much new insight into orders for higher-order terms.
and by exploiting a generalized multiset extension [14, 33]. These extensions are useful but require substantial duplication in the definitions and the proofs, without yielding much new insight into orders for higher-order terms.
3.2 The Applicative RPO
Applicative orders are built by encoding applications using a binary symbol \(\textsf {{@}}\) and by employing a first-order term order. For RPO, the precedence \(\succ \) must be extended to consider \(\textsf {{@}}.\) A natural choice is to make \(\textsf {{@}}\) the least element of \(\succ \). Because \(\textsf {{@}}\) is the only symbol that may be applied, \(\mathrel {{>}\!\!{{>}}}^\textsf {{@}}\) is the only member of the \(\mathrel {{>}\!\!{{>}}}\) family that is relevant. This means that it is impossible to use the lexicographic extension for some functions and the multiset extension for others.
Definition 6
Let \(\mathrm {\Sigma } \) be a higher-order signature, and let \(\mathrm {\Sigma } ' = \mathrm {\Sigma } \mathrel \uplus \{\textsf {{@}}\}\) be a first-order signature in which all symbols belonging to \(\mathrm {\Sigma } \) are assigned arity 0 and \(\textsf {{@}}\) is assigned arity 2. The applicative encoding  is defined recursively by the equations \(\llbracket \zeta \rrbracket = \zeta \) and \(\llbracket s t \rrbracket = \textsf {{@}}\llbracket s \rrbracket \llbracket t \rrbracket \).
is defined recursively by the equations \(\llbracket \zeta \rrbracket = \zeta \) and \(\llbracket s t \rrbracket = \textsf {{@}}\llbracket s \rrbracket \llbracket t \rrbracket \).
Assuming that \(\textsf {{@}}\) has the lowest precedence, the composition of the first-order RPO with the encoding \(\llbracket {i}\rrbracket \) can be formulated directly as follows.
Definition 7
Let \(\succ \) be a well-founded total order on \(\mathrm {\Sigma } \), and let  be a family of relations indexed by
be a family of relations indexed by  and satisfying properties X1–X6. The induced applicative recursive path order \(>_{\textsf {ap}}\) on higher-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {ap}}s \) if any of the following conditions is met:
and satisfying properties X1–X6. The induced applicative recursive path order \(>_{\textsf {ap}}\) on higher-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {ap}}s \) if any of the following conditions is met:
-
A1.
\(t = t _1t _2\) and either \(t _1 \ge _{\textsf {ap}}s \) or \(t _2 \ge _{\textsf {ap}}s \) (or both);
-
A2.
\(t = \textsf {{g}} \succ \textsf {{f}} = s \);
-
A3.
\(t = \textsf {{g}} \), \(s = s _1s _2\), and
 ;
; -
A4.
\(t = t _1t _2\), \(s = s _1s _2\), \((t _1, t _2) \mathrel {{>}\!\!{{>_{\textsf {ap}}}}} (s _1, s _2)\), and
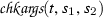 .
.
The predicate  is true if and only if \(t >_{\textsf {ap}}s _1\) and \(t >_{\textsf {ap}}s _2.\)
is true if and only if \(t >_{\textsf {ap}}s _1\) and \(t >_{\textsf {ap}}s _2.\)
3.3 A Graceful Higher-Order RPO
Our new “graceful” higher-order RPO is much closer to the first-order RPO than the applicative RPO. It reintroduces the symbol-indexed family of extension operators and consists of three rules H1–H3 corresponding to F1–F3.
The order relies on a mapping  from variables to nonempty sets of possible ground heads that may arise when instantiating the variables. This mapping is extended to symbols \(\textsf {{f}} \) by taking
from variables to nonempty sets of possible ground heads that may arise when instantiating the variables. This mapping is extended to symbols \(\textsf {{f}} \) by taking  . A substitution
. A substitution  is said to respect the
is said to respect the  mapping if for all variables
mapping if for all variables  , we have
, we have  whenever
whenever  . This mapping allows us to restrict instantiations, typically based on a typing discipline, and thereby increase the applicability of rules H2 and especially H3. Precedences \(\succ \) are extended to variables by taking
. This mapping allows us to restrict instantiations, typically based on a typing discipline, and thereby increase the applicability of rules H2 and especially H3. Precedences \(\succ \) are extended to variables by taking  .
.
Definition 8
Let \(\succ \) be a well-founded total order on \(\mathrm {\Sigma } \), let  be a family of relations indexed by
be a family of relations indexed by  and by \(\textsf {{f}} \in \mathrm {\Sigma } \) and satisfying properties X1–X6 and X8, and let
and by \(\textsf {{f}} \in \mathrm {\Sigma } \) and satisfying properties X1–X6 and X8, and let  . The induced graceful recursive path order \(>_{\textsf {ho}}\) on higher-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {ho}}s \) if any of the following conditions is met, where \(s = \zeta \bar{s}\) and \(t = \xi \bar{t}\):
. The induced graceful recursive path order \(>_{\textsf {ho}}\) on higher-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {ho}}s \) if any of the following conditions is met, where \(s = \zeta \bar{s}\) and \(t = \xi \bar{t}\):
-
H1.
\(t = t _1t _2\) and either \(t _1 \ge _{\textsf {ho}}s \) or \(t _2 \ge _{\textsf {ho}}s \) (or both);
-
H2.
\(\xi \succ \zeta \),
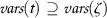 , and
, and  ;
; -
H3.
\(\xi = \zeta \), \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\) for all symbols
 , and
, and  .
.
The predicate  is true if and only if term \(s \) is a head or an application of the form \(s _1s _2\) with \(t >_{\textsf {ho}}s _1\) and \(t >_{\textsf {ho}}s _2.\)
is true if and only if term \(s \) is a head or an application of the form \(s _1s _2\) with \(t >_{\textsf {ho}}s _1\) and \(t >_{\textsf {ho}}s _2.\)
There are two main novelties compared with \({>_{\textsf {fo}}}\). First, rule H1 and the  predicate traverse subterms in a genuinely higher-order fashion. Second, rules H2 and H3 can compare terms with variable heads.
predicate traverse subterms in a genuinely higher-order fashion. Second, rules H2 and H3 can compare terms with variable heads.
Property X8, compatibility with prepending, is necessary to ensure stability under substitution: If \( x \textsf {{b}} >_{\textsf {ho}} x \textsf {{a}} \), we want \(\textsf {{f}} \bar{s}\textsf {{b}} >_{\textsf {ho}}\textsf {{f}} \bar{s}\textsf {{a}} \) to hold as well.
Example 9
It is instructive to contrast our new order with the applicative order by studying a few small examples. Let \(\textsf {{h}} \succ \textsf {{g}} \succ \textsf {{f}} \succ \textsf {{b}} \succ \textsf {{a}} \), let \(\mathrel {{>}\!\!{{>}}}\) be the length-lexicographic extension (which degenerates to the plain lexicographic extension for \(>_{\textsf {ap}}\)), and let  for all variables \( x .\) Sect. 1 already presented a case where \(>_{\textsf {ho}}\) and \(>_{\textsf {ap}}\) disagree: \(\textsf {{g}} \textsf {{b}} >_{\textsf {ho}}\textsf {{f}} (\textsf {{g}} \textsf {{a}})\textsf {{b}} \) but \(\textsf {{g}} \textsf {{b}} <_{\textsf {ap}}\textsf {{f}} (\textsf {{g}} \textsf {{a}})\textsf {{b}}.\) Other disagreements include
for all variables \( x .\) Sect. 1 already presented a case where \(>_{\textsf {ho}}\) and \(>_{\textsf {ap}}\) disagree: \(\textsf {{g}} \textsf {{b}} >_{\textsf {ho}}\textsf {{f}} (\textsf {{g}} \textsf {{a}})\textsf {{b}} \) but \(\textsf {{g}} \textsf {{b}} <_{\textsf {ap}}\textsf {{f}} (\textsf {{g}} \textsf {{a}})\textsf {{b}}.\) Other disagreements include
and \(\textsf {{g}} \textsf {{g}} \textsf {{g}} (\textsf {{f}} (\textsf {{g}} (\textsf {{g}} \textsf {{g}} \textsf {{g}}))) >_{\textsf {ho}}\textsf {{g}} (\textsf {{g}} \textsf {{g}} \textsf {{g}})(\textsf {{g}} \textsf {{g}} \textsf {{g}}).\) For all of these, the core rules H2 and H3 are given room for maneuver, whereas \(>_{\textsf {ap}}\) must consider subterms using A1. In the presence of variables, some terms are comparable only with \(>_{\textsf {ho}}\) or only with \(>_{\textsf {ap}}\):
To apply rule A4 on the first example, we would need \((\textsf {{g}}, x ) \mathrel {{>}\!\!{{>_{\textsf {ap}}^\textsf {lex}}}} (\textsf {{f}} x , x )\), but the term \(\textsf {{g}} \) cannot be larger than \(\textsf {{f}} x \) since it does not contain \( x .\) The last two examples reveal that the applicative order tends to be stronger when either side is a variable applied to some arguments—at least when  is not restricting the variable instantiations.
is not restricting the variable instantiations.
3.4 An Optimized Variant of the Graceful Higher-Order RPO
The higher-order term \(\textsf {{f}} \textsf {{a}} \textsf {{b}} \) has four proper subterms: \(\textsf {{a}} \), \(\textsf {{b}} \), \(\textsf {{f}} \), and \(\textsf {{f}} \textsf {{a}}.\) In contrast, the corresponding first-order term, traditionally written \(\textsf {{f}} (\textsf {{a}},\textsf {{b}})\), has only the arguments \(\textsf {{a}} \) and \(\textsf {{b}} \) as proper subterms. In general, a term of size k has up to \(k - 1\) distinct proper subterms in a higher-order sense but only half as many in a first-order sense. By adding a reasonable requirement on the extension operator, we can avoid this factor-of-2 penalty when computing the order.
Definition 10
Let \(\succ \) be a well-founded total order on \(\mathrm {\Sigma } \), let  be a family of relations indexed by
be a family of relations indexed by  and by \(\textsf {{f}} \in \mathrm {\Sigma } \) and satisfying properties X1–X6, X8, and X10, and let
and by \(\textsf {{f}} \in \mathrm {\Sigma } \) and satisfying properties X1–X6, X8, and X10, and let  . The induced optimized graceful recursive path order \(>_{\textsf {oh}}\) on higher-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {oh}}s \) if any of the following conditions is met, where \(s = \zeta \bar{s}\) and \(t = \xi \bar{t}\):
. The induced optimized graceful recursive path order \(>_{\textsf {oh}}\) on higher-order \(\mathrm {\Sigma } \)-terms is defined inductively so that \(t >_{\textsf {oh}}s \) if any of the following conditions is met, where \(s = \zeta \bar{s}\) and \(t = \xi \bar{t}\):
-
O1.
\(t ' \ge _{\textsf {oh}}s \) for some term \(t ' \in \bar{t}\);
-
O2.
\(\xi \succ \zeta \),
 , and
, and  ;
; -
O3.
\(\xi = \zeta \), \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {oh}}^\textsf {{f}}}}} \bar{s}\) for all symbols
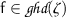 , and
, and  .
.
The predicate  is true if and only if \(t >_{\textsf {oh}}s '\) for all terms \(s ' \in \bar{s}\).
is true if and only if \(t >_{\textsf {oh}}s '\) for all terms \(s ' \in \bar{s}\).
The optimized \(>_{\textsf {oh}}\) depends on the same parameters as \(>_{\textsf {ho}}\) except that it additionally requires minimality of the empty tuple (property X10). In conjunction with compatibility with prepending (X8), this property ensures that  As a result, \(\textsf {{f}} \bar{s}s \) is greater than its subterm \(\textsf {{f}} \bar{s}\), relieving rule O1 from having to consider such subterms.
As a result, \(\textsf {{f}} \bar{s}s \) is greater than its subterm \(\textsf {{f}} \bar{s}\), relieving rule O1 from having to consider such subterms.
Syntactically, the definition of \(>_{\textsf {oh}}\) generalizes that of the first-order \({>_{\textsf {fo}}}\). Semantically, the restriction of \(>_{\textsf {oh}}\) to first-order terms coincides with \({>_{\textsf {fo}}}\). The requirements X8 and X10 on \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) can be made without loss of generality in a first-order setting.
The quantification over  in rule O3 can be inefficient in an implementation, when different symbols in
in rule O3 can be inefficient in an implementation, when different symbols in  disagree on which \(\mathrel {{>}\!\!{{>}}}\) to use. We could generalize the definition of \(>_{\textsf {oh}}\) further to allow underapproximation, but some care would be needed to ensure transitivity. A simple alternative is to enrich all sets
disagree on which \(\mathrel {{>}\!\!{{>}}}\) to use. We could generalize the definition of \(>_{\textsf {oh}}\) further to allow underapproximation, but some care would be needed to ensure transitivity. A simple alternative is to enrich all sets  that disagree on \(\mathrel {{>}\!\!{{>}}}\) with a distinguished symbol for which the componentwise extension is used. Since this extension operator is more restrictive than any other ones, whenever it is present in a set
that disagree on \(\mathrel {{>}\!\!{{>}}}\) with a distinguished symbol for which the componentwise extension is used. Since this extension operator is more restrictive than any other ones, whenever it is present in a set  there is no need to compute the other ones.
there is no need to compute the other ones.
4 Properties
We now state and prove the main properties of our RPO. We focus on the general variant \(>_{\textsf {ho}}\) and show that it is equivalent to the optimized variant \(>_{\textsf {oh}}\) (assuming property X10). Many of the proofs are adapted from Baader and Nipkow [3] and Zantema [38].
Lemma 11
If \(t >_{\textsf {ho}}s \), then  .
.
As a consequence of Lemma 11, the condition  of rule H2 could be written equivalently (but less efficiently) as
of rule H2 could be written equivalently (but less efficiently) as  .
.
Theorem 12
(Transitivity). If \(u >_{\textsf {ho}}t \) and \(t >_{\textsf {ho}}s \), then \(u >_{\textsf {ho}}s.\)
Proof
By well-founded induction on the multiset \(\{\left| s \right| , \left| t \right| , \left| u \right| \}\) with respect to the multiset extension of > on \(\mathbb {N}\).
If \(u >_{\textsf {ho}}t \) was derived by rule H1, we have \(u = u _1u _2\) and \(u _k \ge _{\textsf {ho}}t \) for some \(k.\) Since \(t >_{\textsf {ho}}s \) by hypothesis, \(u _k >_{\textsf {ho}}s \) follows either immediately (if \(u _k = t \)) or by the induction hypothesis (if \(u _k >_{\textsf {ho}}t \)). We get \(u >_{\textsf {ho}}s \) by rule H1.
Otherwise, \(u >_{\textsf {ho}}t \) was derived by rule H2 or H3. The  condition ensures that \(u \) is greater than any immediate subterms of \(t.\) We proceed by case analysis on the rule that derived \(t >_{\textsf {ho}}s.\)
condition ensures that \(u \) is greater than any immediate subterms of \(t.\) We proceed by case analysis on the rule that derived \(t >_{\textsf {ho}}s.\)
If \(t >_{\textsf {ho}}s \) was derived by H1, we have \(t = t _1t _2\) and \(t _{\!j} \ge _{\textsf {ho}}s \) for some \(j.\) We already noted that \(u >_{\textsf {ho}}t _{\!j}\) thanks to  . In conjunction with \(t _{\!j} \ge _{\textsf {ho}}s \), we derive \(u >_{\textsf {ho}}s \) either immediately or by the induction hypothesis.
. In conjunction with \(t _{\!j} \ge _{\textsf {ho}}s \), we derive \(u >_{\textsf {ho}}s \) either immediately or by the induction hypothesis.
Otherwise, \(t >_{\textsf {ho}}s \) was derived by rule H2 or H3. The  condition ensures that \(t \) is greater than any immediate subterms of \(s.\) We derive \(u >_{\textsf {ho}}s \) by applying H2 or H3. We first prove
condition ensures that \(t \) is greater than any immediate subterms of \(s.\) We derive \(u >_{\textsf {ho}}s \) by applying H2 or H3. We first prove  . The only nontrivial case is \(s = s _1s _2.\) Using \(u >_{\textsf {ho}}t \), we get \(u >_{\textsf {ho}}s _1\) and \(u >_{\textsf {ho}}s _2\) by the induction hypothesis.
. The only nontrivial case is \(s = s _1s _2.\) Using \(u >_{\textsf {ho}}t \), we get \(u >_{\textsf {ho}}s _1\) and \(u >_{\textsf {ho}}s _2\) by the induction hypothesis.
If both \(u >_{\textsf {ho}}t \) and \(t >_{\textsf {ho}}s \) were derived by rule H3, we apply H3 to derive \(u >_{\textsf {ho}}s.\) This relies on the preservation by \(\mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}}\) of transitivity (property X3) on the set consisting of the argument tuples of \(s, t, u.\) Transitivity of \(>_{\textsf {ho}}\) on these tuples follows from the induction hypothesis. Finally, if either \(u >_{\textsf {ho}}t \) or \(t >_{\textsf {ho}}s \) was derived by rule H2, we apply H2, relying on the transitivity of \(\succ \) and on Lemma 11. \(\square \)
Theorem 13
(Irreflexivity). \(s \not >_{\textsf {ho}}s.\)
Proof
By strong induction on \(\left| s \right| \). We assume \(s >_{\textsf {ho}}s \) and show that this leads to a contradiction. If \(s >_{\textsf {ho}}s \) was derived by rule H1, we have \(s = s _1s _2\) with \(s _i \ge _{\textsf {ho}}s \) for some \(i.\) Since a term cannot be equal to one of its proper subterms, the comparison is strict. Moreover, we have \(s >_{\textsf {ho}}s _i \) by rule H1. Transitivity yields \(s _i >_{\textsf {ho}}s _i \), contradicting the induction hypothesis. If \(s >_{\textsf {ho}}s \) was derived by rule H2, the contradiction follows immediately from the irreflexivity of \(\succ \). Otherwise, \(s >_{\textsf {ho}}s \) was derived by rule H3. Let \(s = \zeta \bar{s}.\) We have \(\bar{s} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\) for all  . Since \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) preserves irreflexivity for transitive relations (property X4) and \(>_{\textsf {ho}}\) is transitive (Theorem 12), there must exist a term \(s ' \in \bar{s}\) such that \(s ' >_{\textsf {ho}}s '.\) However, this contradicts the induction hypothesis. \(\square \)
. Since \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) preserves irreflexivity for transitive relations (property X4) and \(>_{\textsf {ho}}\) is transitive (Theorem 12), there must exist a term \(s ' \in \bar{s}\) such that \(s ' >_{\textsf {ho}}s '.\) However, this contradicts the induction hypothesis. \(\square \)
By Theorems 12 and 13, \(>_{\textsf {ho}}\) is a partial order. In the remaining proofs, we will often leave applications of these theorems (and of antisymmetry) implicit.
Theorem 14
(Subterm Property). If \(s \) is a proper subterm of \(t \), then \(t >_{\textsf {ho}}s.\)
Proof
By structural induction on \(t \), exploiting rule H1 and transitivity of \({>_{\textsf {ho}}}\). \(\square \)
The first-order RPO satisfies compatibility with \(\mathrm {\Sigma } \)-operations. A slightly more general property holds for \(>_{\textsf {ho}}\):
Theorem 15
(Compatibility with Functions). If \(t ' >_{\textsf {ho}}t \), then \(s t '\bar{u} >_{\textsf {ho}}s t \bar{u}.\)
Proof
By induction on the length of \(\bar{u}.\) The base case, \(\bar{u} = ()\), follows from rule H3, compatibility of \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) with tuple contexts (property X6), and the subterm property (Theorem 14). The step case, \(\bar{u} = \bar{u}'\cdot u \), also follows from rule H3 and compatibility of \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) with contexts. The  condition follows from the induction hypothesis and the subterm property. \(\square \)
condition follows from the induction hypothesis and the subterm property. \(\square \)
A related property, compatibility with arguments, is useful to rewrite subterms such as \(\textsf {{f}} \textsf {{a}} \) in \(\textsf {{f}} \textsf {{a}} \textsf {{b}} \) using a rewrite rule \(\textsf {{f}} x \rightarrow t _ x .\) Unfortunately, \(>_{\textsf {ho}}\) does not enjoy this property: \(s ' >_{\textsf {ho}}s \) does not imply \(s 't >_{\textsf {ho}}s t.\) Two counterexamples follow:
-
1.
Given \(\textsf {{g}} \succ \textsf {{f}} \), we have \(\textsf {{f}} \textsf {{g}} >_{\textsf {ho}}\textsf {{g}} \) by rule H1, but \(\textsf {{f}} \textsf {{g}} \textsf {{f}} <_{\textsf {ho}}\textsf {{g}} \textsf {{f}} \) by rule H2.
-
2.
Let \(\textsf {{f}} \succ \textsf {{b}} \succ \textsf {{a}} \), and let \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) be the lexicographic extension. Then \(\textsf {{f}} \textsf {{a}} >_{\textsf {ho}}\textsf {{f}} \) by rule H3, but \(\textsf {{f}} \textsf {{a}} \textsf {{b}} <_{\textsf {ho}}\textsf {{f}} \textsf {{b}} \) also by rule H3.
The second counterexample and similar ones involving rule H3 can be excluded by requiring that \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) is compatible with appending (property X9), which holds for the length-lexicographic and multiset extensions. But there is no way to rule out the first counterexample without losing coincidence with the first-order RPO.
Theorem 16
(Compatibility with Arguments). Assume that \(\mathrel {{>}\!\!{{>}}}^{\textsf {{f}}}\) is compatible with appending (property X9) for every symbol \(\textsf {{f}} \in \mathrm {\Sigma }.\) If \(s ' >_{\textsf {ho}}s \) is derivable by rule H2 or H3, then \(s 't >_{\textsf {ho}}s t.\)
Proof
If \(s ' >_{\textsf {ho}}s \) is derivable by rule H2, we apply H2 to derive \(s 't >_{\textsf {ho}}s t.\) To show  , we must show that \(s 't >_{\textsf {ho}}s \) and \(s 't >_{\textsf {ho}}t.\) Both are consequences of the subterm property (Theorem 14), together with \(s ' >_{\textsf {ho}}s.\)
, we must show that \(s 't >_{\textsf {ho}}s \) and \(s 't >_{\textsf {ho}}t.\) Both are consequences of the subterm property (Theorem 14), together with \(s ' >_{\textsf {ho}}s.\)
If \(s ' >_{\textsf {ho}}s \) is derivable by rule H3, we apply H3 to derive \(s 't >_{\textsf {ho}}s t.\) The condition on the variables of the head of \(s 't \) can be shown by exploiting the condition on the variables of the head of \(s '.\) The  condition is shown as above. The condition on the argument tuples follows by property X9. \(\square \)
condition is shown as above. The condition on the argument tuples follows by property X9. \(\square \)
Theorem 17
(Stability under Substitution). If \(t >_{\textsf {ho}}s \), then \(t \sigma >_{\textsf {ho}}s \sigma \) for any substitution \(\sigma \) that respects the mapping  .
.
Proof
By well-founded induction on the multiset \(\{\left| s \right| , \left| t \right| \}\) with respect to the multiset extension of > on \(\mathbb {N}\).
If \(t >_{\textsf {ho}}s \) was derived by rule H1, we have \(t = t _1t _2\) and \(t _{\!j} \ge _{\textsf {ho}}s \) for some \(j.\) By the induction hypothesis, \(t _{\!j}\sigma \ge _{\textsf {ho}}s \sigma .\) Hence, \(t \sigma >_{\textsf {ho}}s \sigma \) by rule H1.
If \(t >_{\textsf {ho}}s \) was derived by rule H2, we have \(s = \zeta \bar{s}\), \(t = \xi \bar{t}\), \(\xi \succ \zeta \), and  . We derive \(t \sigma >_{\textsf {ho}}s \sigma \) by applying H2. Since \(\sigma \) respects
. We derive \(t \sigma >_{\textsf {ho}}s \sigma \) by applying H2. Since \(\sigma \) respects  , we have \(\xi \sigma \succ \zeta \sigma .\) From \(t >_{\textsf {ho}}s \), we have
, we have \(\xi \sigma \succ \zeta \sigma .\) From \(t >_{\textsf {ho}}s \), we have  by Lemma 11 and hence
by Lemma 11 and hence  . To show
. To show  , the nontrivial cases are \(s = x \) and is \(s = s _1s _2.\) If \(s = x \), then \(s \) must be a subterm of \(t \) by Lemma 11, and therefore \(s \sigma \) is a subterm of \(t \sigma .\) Thus, we have \(t \sigma >_{\textsf {ho}}s \sigma \) by the subterm property (Theorem 14), from which it is easy to derive
, the nontrivial cases are \(s = x \) and is \(s = s _1s _2.\) If \(s = x \), then \(s \) must be a subterm of \(t \) by Lemma 11, and therefore \(s \sigma \) is a subterm of \(t \sigma .\) Thus, we have \(t \sigma >_{\textsf {ho}}s \sigma \) by the subterm property (Theorem 14), from which it is easy to derive  , as desired. If \(s = s _1s _2\), we get \(t >_{\textsf {ho}}s _1\) and \(t >_{\textsf {ho}}s _2\) from
, as desired. If \(s = s _1s _2\), we get \(t >_{\textsf {ho}}s _1\) and \(t >_{\textsf {ho}}s _2\) from  . By the induction hypothesis, \(t \sigma >_{\textsf {ho}}s _1\sigma \) and \(t >_{\textsf {ho}}s _2\sigma \), as desired.
. By the induction hypothesis, \(t \sigma >_{\textsf {ho}}s _1\sigma \) and \(t >_{\textsf {ho}}s _2\sigma \), as desired.
If \(t >_{\textsf {ho}}s \) was derived by rule H3, we have \(s = \zeta \bar{s}\), \(t = \zeta \bar{t}\),  , and
, and  . We derive \(t \sigma >_{\textsf {ho}}s \sigma \) by applying H3. Clearly, \(s \sigma \) and \(t \sigma \) have the same head. The
. We derive \(t \sigma >_{\textsf {ho}}s \sigma \) by applying H3. Clearly, \(s \sigma \) and \(t \sigma \) have the same head. The  condition is proved as for rule H2 above. Finally, we must show that \(\bar{t}\sigma \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\sigma \) for all
condition is proved as for rule H2 above. Finally, we must show that \(\bar{t}\sigma \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\sigma \) for all  , where \(\zeta \sigma = \zeta '\bar{u}\) for some \(\bar{u}.\) Since \(\sigma \) respects
, where \(\zeta \sigma = \zeta '\bar{u}\) for some \(\bar{u}.\) Since \(\sigma \) respects  , we have
, we have  ; hence, \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\) for all
; hence, \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\) for all  . By the induction hypothesis, \(t ' >_{\textsf {ho}}s '\) implies \(t '\sigma >_{\textsf {ho}}s '\sigma \) for all \(s ', t ' \in \bar{s} \mathrel \cup \bar{t}.\) By preservation of stability (property X2), we have \(\bar{t}\sigma \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\sigma .\) By compatibility with prepending (property X8), we get \(\bar{u} \cdot \bar{t}\sigma \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{u} \cdot \bar{s}\sigma \), as required to apply H3. \(\square \)
. By the induction hypothesis, \(t ' >_{\textsf {ho}}s '\) implies \(t '\sigma >_{\textsf {ho}}s '\sigma \) for all \(s ', t ' \in \bar{s} \mathrel \cup \bar{t}.\) By preservation of stability (property X2), we have \(\bar{t}\sigma \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\sigma .\) By compatibility with prepending (property X8), we get \(\bar{u} \cdot \bar{t}\sigma \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{u} \cdot \bar{s}\sigma \), as required to apply H3. \(\square \)
Theorem 18
(Well-foundedness). There exists no infinite descending chain \(s _0>_{\textsf {ho}}s _1 >_{\textsf {ho}}\cdots .\)
Proof
We assume that there exists a chain \(s _0>_{\textsf {ho}}s _1 >_{\textsf {ho}}\cdots \) and show that this leads to a contradiction. If the chain contains nonground terms, we can instantiate all variables by arbitrary terms respecting  and exploit stability under substitution (Theorem 17). Thus, we may assume without loss of generality that the terms \(s _0\), \(s _1\), ... are ground.
and exploit stability under substitution (Theorem 17). Thus, we may assume without loss of generality that the terms \(s _0\), \(s _1\), ... are ground.
We call a ground term bad if it belongs to an infinite descending \(>_{\textsf {ho}}\)-chain. Without loss of generality, we assume that \(s _0\) has minimal size among all bad terms and that \(s _{i +1}\) has minimal size among all bad terms \(t \) such that \(s _i >_{\textsf {ho}}t.\)
For each index \(i \), the term \(s _{i}\) must be of the form \(\textsf {{f}} u _1\,\ldots \,u _n \) for some symbol \(\textsf {{f}} \) and ground terms \(u _1,\cdots ,u _n.\) Let \(U_i = \emptyset \) if \(n = 0\); otherwise, let \(U_i = \{u _1,\cdots {,}\>u _n {,}\; \textsf {{f}} u _1\cdots u _{n-1}\}\). Now let \(U = \bigcup _{i =0}^\infty U_i.\) All terms belonging to U are good: A term from \(U_0\)’s badness would contradict the minimality of \(s _0\); and if a term \(u \in U_{i +1}\) were bad, we would have \(s _{i +1} >_{\textsf {ho}}u \) by rule H1 and \(s _{i} >_{\textsf {ho}}u \) by transitivity, contradicting the minimality of \(s _{i +1}\).
Next, we show that the only rules that can be used to derive \(s _i >_{\textsf {ho}}s _{i +1}\) are H2 and H3. Suppose H1 were used. Then there would exist a good term \(u \in U_i \) such that \(u \ge _{\textsf {ho}}s _{i +1} >_{\textsf {ho}}s _{i +2}\). This would imply the existence of an infinite chain \(u>_{\textsf {ho}}s _{i +2}>_{\textsf {ho}}s _{i +3} >_{\textsf {ho}}\cdots \), contradicting the goodness of u.
Because \(\succ \) is well founded and H3 preserves the head symbol, rule H2 can be applied only a finite number of times in the chain. Hence, there must exist an index \(k \) such that \(s _i >_{\textsf {ho}}s _{i +1}\) is derived using H3 for all \(i \ge k.\) Consequently, all terms \(s _i \) for \(i \ge k \) share the same head symbol \(\textsf {{f}}.\)
Let \(s _i = \textsf {{f}} \bar{u}_i \) for all \(i \ge k.\) Since H3 is used consistently from index \(k \), we have an infinite \(\mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}}\)-chain: \(\bar{u}_k \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{u}_{k +1} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{u}_{k +2} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \cdots \). But since U contains only good terms and comprises all terms occurring in some argument tuple \(\bar{u}_i \), \(>_{\textsf {ho}}\) is well founded on U. By preservation of well-foundedness (property X5), \(\mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}}\) is well founded. This contradicts the existence of the above \(\mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}}\)-chain. \(\square \)
Theorem 19
(Ground Totality). Assume \(\mathrel {{>}\!\!{{>}}}^{\textsf {{f}}}\) preserves totality (property X7) for every symbol \(\textsf {{f}} \in \mathrm {\Sigma } \), and let \(s, t \) be ground terms. Then either \(t \ge _{\textsf {ho}}s \) or \(t <_{\textsf {ho}}s.\)
Proof
By strong induction on \(\left| s \right| + \left| t \right| \). If not  , then \(t \not >_{\textsf {ho}}s _1\) and \(t \not >_{\textsf {ho}}s _2\) for \(s = s _1s _2.\) By the induction hypothesis, \(s _1 \ge _{\textsf {ho}}t \) and \(s _2 \ge _{\textsf {ho}}t.\) Thus, \(s >_{\textsf {ho}}t \) by rule H1. Analogously, if not
, then \(t \not >_{\textsf {ho}}s _1\) and \(t \not >_{\textsf {ho}}s _2\) for \(s = s _1s _2.\) By the induction hypothesis, \(s _1 \ge _{\textsf {ho}}t \) and \(s _2 \ge _{\textsf {ho}}t.\) Thus, \(s >_{\textsf {ho}}t \) by rule H1. Analogously, if not  , then \(t >_{\textsf {ho}}s.\) Hence, we may assume
, then \(t >_{\textsf {ho}}s.\) Hence, we may assume  and
and  . Let \(s = \textsf {{f}} \bar{s}\) and \(t = \textsf {{g}} \bar{t}.\) If \(\textsf {{g}} \succ \textsf {{f}} \) or \(\textsf {{g}} \prec \textsf {{f}} \), we have \(t >_{\textsf {ho}}s \) or \(s >_{\textsf {ho}}t \) by rule H2. Otherwise, \(\textsf {{f}} = \textsf {{g}}.\) By preservation of totality (property X7), we have either \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\), \(\bar{t} \mathrel {{<}\!\!{{<_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\), or \(\bar{s} = \bar{t}.\) In the first two cases, we have \(t >_{\textsf {ho}}s \) or \(t <_{\textsf {ho}}s \) by rule H3. In the third case, we have \(s = t.\) \(\square \)
. Let \(s = \textsf {{f}} \bar{s}\) and \(t = \textsf {{g}} \bar{t}.\) If \(\textsf {{g}} \succ \textsf {{f}} \) or \(\textsf {{g}} \prec \textsf {{f}} \), we have \(t >_{\textsf {ho}}s \) or \(s >_{\textsf {ho}}t \) by rule H2. Otherwise, \(\textsf {{f}} = \textsf {{g}}.\) By preservation of totality (property X7), we have either \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\), \(\bar{t} \mathrel {{<}\!\!{{<_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\), or \(\bar{s} = \bar{t}.\) In the first two cases, we have \(t >_{\textsf {ho}}s \) or \(t <_{\textsf {ho}}s \) by rule H3. In the third case, we have \(s = t.\) \(\square \)
Having now established the main properties of \(>_{\textsf {ho}}\), we turn to the correspondence between \(>_{\textsf {ho}}\), its optimized variant \(>_{\textsf {oh}}\), and the first-order RPO \({>_{\textsf {fo}}}\).
Lemma 20
(1) If \(u >_{\textsf {oh}}t \) and \(t >_{\textsf {oh}}s \), then \(u >_{\textsf {oh}}s \). (2) \(s t >_{\textsf {oh}}s \).
Theorem 21
(Coincidence with Optimized Variant). Let \(>_{\textsf {ho}}\) and \(>_{\textsf {oh}}\) be orders induced by the same precedence \(\succ \) and extension operator family \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) (which must satisfy property X10 by the definition of \(>_{\textsf {oh}}\)). Then \(t >_{\textsf {ho}}s \) if and only if \(t >_{\textsf {oh}}s.\)
Proof
By strong induction on \(\left| s \right| + \left| t \right| \). The interesting implication is  .
.
If \(t >_{\textsf {ho}}s \) was derived by rule H1, we have \(t = t _1t _2\) and \(t _{\!j} \ge _{\textsf {ho}}s \) for some \(j.\) Hence \(t _{\!j} \ge _{\textsf {oh}}s \) by the induction hypothesis, and \(t >_{\textsf {oh}}t _{\!j}\) by Lemma 20(2) or rule O1. We get \(t >_{\textsf {oh}}s \) either immediately or by Lemma 20(1).
If \(t >_{\textsf {ho}}s \) was derived by rule H2, we derive \(t >_{\textsf {oh}}s \) by applying O2. We must show that  implies
implies  . We have \(s = s _1s _2\) with \(t >_{\textsf {ho}}s _1\) and \(t >_{\textsf {ho}}s _2.\) Let \(s = \zeta \bar{s}s _2.\) We must show that \(t >_{\textsf {oh}}s '\) for all \(s ' \in \bar{s} \mathrel \cup \{s _2\}\). If \(s ' = s _2\), we have \(t >_{\textsf {ho}}s _2\) immediately. Otherwise, from \(t >_{\textsf {ho}}s _1\), we have \(t >_{\textsf {ho}}s '\) by the subterm property (Theorem 14). In both cases, we get
. We have \(s = s _1s _2\) with \(t >_{\textsf {ho}}s _1\) and \(t >_{\textsf {ho}}s _2.\) Let \(s = \zeta \bar{s}s _2.\) We must show that \(t >_{\textsf {oh}}s '\) for all \(s ' \in \bar{s} \mathrel \cup \{s _2\}\). If \(s ' = s _2\), we have \(t >_{\textsf {ho}}s _2\) immediately. Otherwise, from \(t >_{\textsf {ho}}s _1\), we have \(t >_{\textsf {ho}}s '\) by the subterm property (Theorem 14). In both cases, we get  by the induction hypothesis.
by the induction hypothesis.
If \(t >_{\textsf {ho}}s \) was derived by rule H3, we derive \(t >_{\textsf {oh}}s \) by applying O3. The  condition is proved as in the H2 case. From \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\), we derive \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {oh}}^\textsf {{f}}}}} \bar{s}\) by the induction hypothesis and monotonicity of \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) (property X1). \(\square \)
condition is proved as in the H2 case. From \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {ho}}^\textsf {{f}}}}} \bar{s}\), we derive \(\bar{t} \mathrel {{>}\!\!{{>_{\textsf {oh}}^\textsf {{f}}}}} \bar{s}\) by the induction hypothesis and monotonicity of \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) (property X1). \(\square \)
Corollary 22
(Coincidence with First-Order RPO). Let \(>_{\textsf {ho}}\) and \(>_{\textsf {fo}}\) be orders induced by the same precedence \(\succ \) and extension operator family \(\mathrel {{>}\!\!{{>}}}^\textsf {{f}} \) satisfying minimality of the empty tuple (property X10). Then \(>_{\textsf {ho}}\) and \(>_{\textsf {fo}}\) coincide on first-order terms.
5 Examples
Although our motivation was to design a term order suitable for higher-order superposition, we can use \(>_{\textsf {ho}}\) (and \(>_{\textsf {oh}}\)) to show the termination of \(\lambda \)-free higher-order term rewriting systems or, equivalently, applicative term rewriting systems [24]. We present a selection of examples of how this can be done, illustrating the strengths and weaknesses of the order in this context. Many of the examples are taken from the literature. Since \(>_{\textsf {ho}}\) coincides with the standard RPO on first-order terms, we consider only examples featuring higher-order constructs.
To establish termination of a term rewriting system, a standard approach is to show that all of its rewrite rules \(t \rightarrow s \) can be oriented as \(t > s \) by a single reduction order: a well-founded partial order that is compatible with contexts and stable under substitutions. Regrettably, \(>_{\textsf {ho}}\) is not a reduction order since it lacks compatibility with arguments. But the conditional Theorem 16 is often sufficient in practice. Assuming that the extension operator is compatible with appending (property X9), we may apply H2 and H3 to orient rewrite rules. Moreover, we may even use H1 for rewrite rules that operate on non-function terms; supplying an argument to a non-function would violate typing. To identify non-functions and to restrict instantiations, we assume that terms respect the typing discipline of the simply typed \(\lambda \)-calculus. Together, property X9 and the restriction on the application of H1 achieve the same effect as \(\eta \)-saturation [19].
For simplicity, the examples are all monolithic, but a modern termination prover would use the dependency pair framework [2] to break down a large term rewriting system into smaller components that can be analyzed separately. Unless mentioned otherwise, the RPO instances considered employ the length-lexicographic extension operator. We consistently use italics for variables and sans serif for symbols
Example 23
Consider the following term rewriting system:
Rule 1 captures a set-theoretic property: \(\{{ f}( n )\} \mathrel \cup { f}[ A ] = f[\{ n \} \mathrel \cup A ]\). We can prove termination using \(>_{\textsf {ho}}\): By letting \(\textsf {{insert}}\succ \textsf {{image}}\) and \(\textsf {{square}}\succ \textsf {{times}}\), both rules can be oriented by H2. In contrast, rule 2 is beyond the reach of the applicative order \(>_{\textsf {ap}}\) for the same reason that \(\textsf {{g}} x \not >_{\textsf {ap}}\textsf {{f}} x x \) in Example 9. The system is also beyond the scope of the uncurrying approach of Hirokawa et al. [19] because of the variable application \({ f} n \).
Example 24
The following system specifies a map function on an ML-style option type equipped with two constructors, \(\textsf {{None}}\) and \(\textsf {{Some}}\):
To establish termination, it would appear that it suffices to apply H2 to orient both rules, using a precedence such that \(\textsf {{omap}}\succ \textsf {{None}}, \textsf {{Some}}.\) However, a closer inspection reveals that the  condition blocks the application of H2 to orient rule 2: We would need \(\textsf {{omap}}{ f}(\textsf {{Some}} n ) >_{\textsf {ho}}{ f} n \), which cannot be established without further assumptions. With a typing discipline that distinguishes between options and other data, \({ f}\) cannot be instantiated by a term having \(\textsf {{omap}}\) as its head. Thus, we can safely restrict
condition blocks the application of H2 to orient rule 2: We would need \(\textsf {{omap}}{ f}(\textsf {{Some}} n ) >_{\textsf {ho}}{ f} n \), which cannot be established without further assumptions. With a typing discipline that distinguishes between options and other data, \({ f}\) cannot be instantiated by a term having \(\textsf {{omap}}\) as its head. Thus, we can safely restrict  to \(\mathrm {\Sigma }- \{\textsf {{omap}}\}\) and assign the highest precedence to \(\textsf {{omap}}.\) We then have \(\textsf {{omap}}{ f}(\textsf {{Some}} n ) >_{\textsf {ho}}{ f} n \) by H2, as required to orient rule 2.
to \(\mathrm {\Sigma }- \{\textsf {{omap}}\}\) and assign the highest precedence to \(\textsf {{omap}}.\) We then have \(\textsf {{omap}}{ f}(\textsf {{Some}} n ) >_{\textsf {ho}}{ f} n \) by H2, as required to orient rule 2.
The above example suggests a general strategy for coping with variables that occur unapplied on the left-hand side of a rewrite rule and applied on the right-hand side.
Example 25
The next system is taken from Lysne and Piris [28, Example 5], with an additional rule adapted from Lifantsev and Bachmair [27, Example 6]:
The \(\textsf {{iter}}{}\) function is a general iterator on lists of numbers. Reasoning about the types, we can safely take  . By letting \(\textsf {{sum}}\succ \textsf {{iter}}\) and ensuring that \(\textsf {{iter}}\) is greater than any other symbol, rule 1 can be oriented by H1, rule 2 can be oriented by H3, and rules 3 and 4 can be oriented by H2. The application of H1 is legitimate if numbers are distinguished from functions.
. By letting \(\textsf {{sum}}\succ \textsf {{iter}}\) and ensuring that \(\textsf {{iter}}\) is greater than any other symbol, rule 1 can be oriented by H1, rule 2 can be oriented by H3, and rules 3 and 4 can be oriented by H2. The application of H1 is legitimate if numbers are distinguished from functions.
Example 26
The following rules are taken from Jouannaud and Rubio [22, Sect. 4.2]:
The \(\textsf {{fmap}}\) function applies each function from a list to a value \( x \) and returns the list of results. The typing discipline allows us to take  . By making \(\textsf {{fmap}}\) greater than any other symbol, both rules can be oriented by H2.
. By making \(\textsf {{fmap}}\) greater than any other symbol, both rules can be oriented by H2.
Example 27
The next system is from Toyama [35, Example 4]:
The typing discipline allows us to take  . Given \(\textsf {{filter}}\succ \textsf {{f}} \) for all \(\textsf {{f}} \in \mathrm {\Sigma } \), rules 1 and 2 can be oriented by H1, and rules 3 and 4 can be oriented by H2. The application of H1 is legitimate if lists are distinguished from functions.
. Given \(\textsf {{filter}}\succ \textsf {{f}} \) for all \(\textsf {{f}} \in \mathrm {\Sigma } \), rules 1 and 2 can be oriented by H1, and rules 3 and 4 can be oriented by H2. The application of H1 is legitimate if lists are distinguished from functions.
Example 28
Sternagel and Thiemann [32, Example 1] compare different approaches to uncurrying on the following system:

The \(\textsf {{minus}}{}\) function implements subtraction on Peano numbers, whereas \(\textsf {{map}}{}\) applies a function elementwise to a finite list. We establish termination by employing \(>_{\textsf {ho}}\) with a precedence such that \(\textsf {{minus}}\succ \textsf {{K}}, \textsf {{0}}\) and \(\textsf {{map}}\succ \textsf {{Cons}}.\) Rules 2, 5, and 6 are oriented by H1; rules 1, 3, and 7 are oriented by H2; and rule 4 is oriented by H3. The application of H1 is legitimate if numbers and lists are distinguished from functions.
Example 29
Lifantsev and Bachmair [27, Example 8] define a higher-order function that applies its first argument twice to its second argument: \(\textsf {{twice}}{ f} x \,\rightarrow \,{ f}({ f} x ).\) This rewrite rule is problematic in our framework, because we cannot rely on the typing discipline to prevent the instantiation of \({ f}\) by a term with \(\textsf {{twice}}\) as its head. Indeed, \(\textsf {{twice}}(\textsf {{twice}}\textsf {{S}})\) is a natural way to specify the function \( x \mapsto \textsf {{S}}(\textsf {{S}}(\textsf {{S}}(\textsf {{S}} x ))).\)
Example 30
Toyama’s recursor specification [35, Example 6] exhibits the same limitation in a more general context:
Example 31
Let  , and consider the system
, and consider the system
These rules can be used to simplify nested \(\textsf {{prod}}\) terms; for example: \(\textsf {{prod}}(\textsf {{prod}}\textsf {{a}} \textsf {{b}}) \mathrel {\smash {\mathop {\rightarrow }\limits ^{\scriptscriptstyle 4 {\,}}}} \textsf {{prod}}\textsf {{b}} (\textsf {{prod}}\textsf {{a}}) \mathrel {\smash {\mathop {\rightarrow }\limits ^{\scriptscriptstyle 4 {\,}}}} \textsf {{prod}}\textsf {{b}} \textsf {{a}} \textsf {{prod}}\mathrel {\smash {\mathop {\rightarrow }\limits ^{\scriptscriptstyle 3 {\,}}}} \textsf {{prod}}\textsf {{b}} \textsf {{a}}.\) The \(>_{\textsf {ho}}\) order can be employed by taking \(\mathrel {{>}\!\!{{>}}}^\textsf {{prod}}\) to be the multiset extension and by relying on typing to orient rule 1 with H1. The applicative order \(>_{\textsf {ap}}\) fails because a combination of lexicographic and multiset extensions is needed to orient rules 2 and 4. The uncurrying approach of Hirokawa et al. [19] also fails because of the applied variables on the left-hand side of rule 4.
Carsten Fuhs, a developer of the AProVE termination prover, generously offered to apply his tool to our examples, expressed as untyped applicative term rewriting systems. Using AProVE’s web interface with a 60 s time limit, he could establish the termination of Examples 23, 24, 28, 29, and 31. The tool timed out for Examples 25–27 and 30. For Example 31, the tool found a complex proof involving several applications of linear polynomial interpretations, dependency pairs, and \(2\times 2\) matrix interpretations (to cope with rule 4). Although our focus is on superposition, it would be interesting to implement the new RPO in a tool such as AProVE and to conduct a more systematic evaluation on standard higher-order termination benchmarks against higher-order termination provers such as THOR [12] and WANDA [25].
6 Discussion
Rewriting of \(\lambda \)-free higher-order terms has been amply studied in the literature, under various names such as applicative term rewriting [24] and simply typed term rewriting [37]. Translations from higher-order to first-order term rewriting systems were designed by Aoto and Yamada [1], Toyama [35], Hirokawa et al. [19], and others. Toyama also studied S-expressions, a formalism that regards \(((\textsf {{f}} \textsf {{a}})\textsf {{b}})\) and \((\textsf {{f}} \textsf {{a}} \textsf {{b}})\) as distinct. For higher-order terms with \(\lambda \)-abstraction, various frameworks have been proposed, including Nipkow’s higher-order rewrite systems [30], Blanqui’s inductive data type systems [9], and Kop’s algebraic functional systems with metavariables [25]. Kop’s thesis [25, Chapter 3] includes a comprehensive overview.
When designing our RPO \(>_{\textsf {ho}}\), we aimed at full coincidence with the first-order case. Our goal is to gradually transform first-order automatic provers into higher-order provers. By carefully generalizing the proof calculi and data structures, we aim at designing provers that behave like first-order provers on first-order problems, perform mostly like first-order provers on higher-order problems that are mostly first-order, and scale up to arbitrary higher-order problems.
The simplicity of \(>_{\textsf {ho}}\) fails to do justice to the labor of exploring the design space. Methodologically, the use of a proof assistant [31] equipped with a model finder [6] and automatic theorem provers [5] was invaluable for designing the orders, proving their properties, and carrying out various experiments. As one example among many, at a late stage in the design process, we generalized the rules H2 and O2 to allow variable heads. Thanks to the tool support, which keeps track of what must be changed, it took us less than one hour to adapt the main proofs and convince ourselves that the new approach worked, and a few more hours to complete the proofs. Performing such changes on paper is a less reliable, and less satisfying, enterprise. Another role of the formal proofs is to serve as companions to the informal proofs, clarifying finer points. Term rewriting lends itself well to formalization in proof assistants, perhaps because it requires little sophisticated mathematics beyond well-founded induction and recursion. The CoLoR library by Blanqui and Koprowski [11], in Coq, the CiME3 toolkit by Contejean et al. [15], also in Coq, and the IsaFoR library by Thiemann and Sternagel [34], in Isabelle/HOL, have already explored this territory, providing formalized metatheory but also certified termination and confluence checkers.
The \(>_{\textsf {ho}}\) order is in some ways less flexible than the hybrid curried–uncurried approaches, where the currying is one more parameter that can be adjusted. In exchange, it raises the level of abstraction, by providing a uniform view of higher-order terms, and it works in the open-world setting of higher-order proof search. For example, consider the proof obligation \(\exists g .\;\forall x {,}\> y .\; g x y = \textsf {{f}} y x \) and the SK combinator definitions \(\forall x {,}\> y .\;\textsf {{K}} x y = x \) and \(\forall x {,}\> y {,}\> z .\;\textsf {{S}} x y z = x z ( y z ).\) A prover will need to synthesize the witness \(\textsf {{S}}(\textsf {{K}}(\textsf {{S}}\textsf {{f}}))\textsf {{K}}\), representing \(\lambda x \> y .\;\textsf {{f}} y x ,\) for the existential variable \( g .\) A hybrid approach such as HORPO might infer arity 2 for \(\textsf {{f}} \) based on the problem, but then the witness, in which \(\textsf {{f}} \) appears unapplied, cannot be expressed.
An open question is whether it is possible to design an order that largely coincides with the first-order RPO while enjoying compatibility with arbitrary contexts. This could presumably be achieved by weakening rule H1 and strengthening the  condition of H2 and H3 accordingly; so far, our attempts have resulted only in a rediscovery of the applicative RPO.
condition of H2 and H3 accordingly; so far, our attempts have resulted only in a rediscovery of the applicative RPO.
For superposition, richer type systems would be desirable. These could be incorporated either by simply ignoring the types, by encoding them in the terms, or by generalizing the order. Support for \(\lambda \)-abstraction would be useful but challenging. Any well-founded order enjoying the subterm property would need to distinguish \(\beta \)-equivalent terms, to exclude the cycle \(\textsf {{a}} =_\beta (\lambda x .\; \textsf {{a}})(\textsf {{f}} \textsf {{a}})> \textsf {{f}} \textsf {{a}} > \textsf {{a}}.\) We could aim at compatibility with \(\beta \)-reduction, but even this property might be irrelevant for higher-order superposition. It might even be preferable to avoid \(\lambda \)-abstractions altogether, by relying on SK combinators or by adding new symbols and their definitions during proof search.
References
Aoto, T., Yamada, T.: Termination of simply typed term rewriting by translation and labelling. In: Nieuwenhuis, R. (ed.) RTA 2003. LNCS, vol. 2706, pp. 380–394. Springer, Heidelberg (2003). doi:10.1007/3-540-44881-0_27
Arts, T., Giesl, J.: Termination of term rewriting using dependency pairs. Theor. Comput. Sci. 236(1–2), 133–178 (2000)
Baader, F., Nipkow, T.: Term Rewriting and All That. Cambridge University Press, Cambridge (1998)
Benzmüller, C., Miller, D.: Automation of higher-order logic. In: Siekmann, J.H. (ed.) Computational Logic, Handbook of the History of Logic, vol. 9, pp. 215–254. Elsevier (2014)
Blanchette, J.C., Kaliszyk, C., Paulson, L.C., Urban, J.: Hammering towards QED. J. Formalized Reasoning 9(1), 101–148 (2016)
Blanchette, J.C., Nipkow, T.: Nitpick: A counterexample generator for higher-order logic based on a relational model finder. In: Kaufmann, M., Paulson, L.C. (eds.) ITP 2010. LNCS, vol. 6172, pp. 131–146. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14052-5_11
Blanchette, J.C., Waldmann, U., Wand, D.: Formalization of recursive path orders for lambda-free higher-order terms. Archive of Formal Proofs, formal proof development (2016). https://isa-afp.org/entries/Lambda_Free_RPOs.shtml
Blanchette, J.C., Waldmann, U., Wand, D.: A lambda-free higher-order recursive path order. Technical report (2016). http://people.mpi-inf.mpg.de/jblanche/lambda_free_rpo_rep.pdf
Blanqui, F.: Termination and confluence of higher-order rewrite systems. In: Bachmair, L. (ed.) RTA 2000. LNCS, vol. 1833, pp. 47–61. Springer, Heidelberg (2000). doi:10.1007/10721975_4
Blanqui, F., Jouannaud, J., Rubio, A.: The computability path ordering. Log. Meth. Comput. Sci. 11(4) (2015)
Blanqui, F., Koprowski, A.: CoLoR: A Coq library on well-founded rewrite relations and its application to the automated verification of termination certificates. Math. Struct. Comput. Sci. 21(4), 827–859 (2011)
Bofill, M., Borralleras, C., Rodríguez-Carbonell, E., Rubio, A.: The recursive path and polynomial ordering for first-order and higher-order terms. J. Log. Comput. 23(1), 263–305 (2013)
Bofill, M., Rubio, A.: Paramodulation with non-monotonic orderings and simplification. J. Autom. Reasoning 50(1), 51–98 (2013)
Codish, M., Giesl, J., Schneider-Kamp, P., Thiemann, R.: SAT solving for termination proofs with recursive path orders and dependency pairs. J. Autom. Reasoning 49(1), 53–93 (2012)
Contejean, É., Courtieu, P., Forest, J., Pons, O., Urbain, X.: Automated certified proofs with CiME3. In: Schmidt-Schauß, M. (ed.) Rewriting Techniques and Applications (RTA 2011). Leibniz International Proceedings in Informatics (LIPIcs), vol. 10, pp. 21–30. Schloss Dagstuhl-Leibniz-Zentrum für Informatik (2011)
Dershowitz, N., Manna, Z.: Proving termination with multiset orderings. Commun. ACM 22(8), 465–476 (1979)
Ganzinger, H., Hagen, G., Nieuwenhuis, R., Oliveras, A., Tinelli, C.: DPLL(T): Fast decision procedures. In: Alur, R., Peled, D.A. (eds.) CAV 2004. LNCS, vol. 3114, pp. 175–188. Springer, Heidelberg (2004). doi:10.1007/978-3-540-27813-9_14
Henkin, L.: Completeness in the theory of types. J. Symb. Log. 15(2), 81–91 (1950)
Hirokawa, N., Middeldorp, A., Zankl, H.: Uncurrying for termination and complexity. J. Autom. Reasoning 50(3), 279–315 (2013)
Huet, G., Oppen, D.C.: Equations and rewrite rules: A survey. In: Book, R.V. (ed.) Formal Language Theory: Perspectives and Open Problems, pp. 349–405. Academic Press (1980)
Hughes, R.J.M.: Super-combinators: A new implementation method for applicative languages. In: ACM Symposium on LISP and Functional Programming (LFP 1982), pp. 1–10. ACM Press (1982)
Jouannaud, J.-P., Rubio, A.: A recursive path ordering for higher-order terms in \(\eta \)-long \(\beta \)-normal form. In: Ganzinger, H. (ed.) RTA 1996. LNCS, vol. 1103, pp. 108–122. Springer, Heidelberg (1996). doi:10.1007/3-540-61464-8_46
Jouannaud, J., Rubio, A.: Polymorphic higher-order recursive path orderings. J. ACM 54(1), 2:1–2:48 (2007)
Kennaway, R., Klop, J.W., Sleep, M.R., de Vries, F.: Comparing curried and uncurried rewriting. J. Symb. Comput. 21(1), 15–39 (1996)
Kop, C.: Higher Order Termination. Ph.D. thesis, Vrije Universiteit Amsterdam (2012)
Kop, C., Raamsdonk, F.: A higher-order iterative path ordering. In: Cervesato, I., Veith, H., Voronkov, A. (eds.) LPAR 2008. LNCS (LNAI), vol. 5330, pp. 697–711. Springer, Heidelberg (2008). doi:10.1007/978-3-540-89439-1_48
Lifantsev, M., Bachmair, L.: An LPO-based termination ordering for higher-order terms without \(\lambda \)-abstraction. In: Grundy, J., Newey, M. (eds.) TPHOLs 1998. LNCS, vol. 1479, pp. 277–293. Springer, Heidelberg (1998). doi:10.1007/BFb0055142
Lysne, O., Piris, J.: A termination ordering for higher order rewrite systems. In: Hsiang, J. (ed.) RTA 1995. LNCS, vol. 914, pp. 26–40. Springer, Heidelberg (1995). doi:10.1007/3-540-59200-8_45
Nieuwenhuis, R., Rubio, A.: Paramodulation-based theorem proving. In: Robinson, J.A., Voronkov, A. (eds.) Handbook of Automated Reasoning, vol. I, pp. 371–443. Elsevier and MIT Press (2001)
Nipkow, T.: Higher-order critical pairs. In: Logic in Computer Science (LICS 1991), pp. 342–349. IEEE Computer Society (1991)
Nipkow, T., Paulson, L.C., Wenzel, M.: Isabelle/HOL: A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002)
Sternagel, C., Thiemann, R.: Generalized and formalized uncurrying. In: Tinelli, C., Sofronie-Stokkermans, V. (eds.) FroCoS 2011. LNCS (LNAI), vol. 6989, pp. 243–258. Springer, Heidelberg (2011). doi:10.1007/978-3-642-24364-6_17
Thiemann, R., Allais, G., Nagele, J.: On the formalization of termination techniques based on multiset orderings. In: Tiwari, A. (ed.) Rewriting Techniques and Applications (RTA 2012). LIPIcs, vol. 15, pp. 339–354. Schloss Dagstuhl–Leibniz-Zentrum für Informatik (2012)
Thiemann, R., Sternagel, C.: Certification of termination proofs using CeTA. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 452–468. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_31
Toyama, Y.: Termination of S-expression rewriting systems: lexicographic path ordering for higher-order terms. In: Oostrom, V. (ed.) RTA 2004. LNCS, vol. 3091, pp. 40–54. Springer, Heidelberg (2004). doi:10.1007/978-3-540-25979-4_3
Turner, D.A.: A new implementation technique for applicative languages. Softw.: Pract. Experience 9(1), 31–49 (1979)
Yamada, T.: Confluence and termination of simply typed term rewriting systems. In: Middeldorp, A. (ed.) RTA 2001. LNCS, vol. 2051, pp. 338–352. Springer, Heidelberg (2001). doi:10.1007/3-540-45127-7_25
Zantema, H.: Termination. In: Bezem, M., Klop, J.W., de Vrijer, R. (eds.) Term Rewriting Systems. Cambridge Tracts in Theoretical Computer Science, vol. 55, pp. 181–259. Cambridge University Press (2003)
Acknowledgment
We are grateful to Stephan Merz, Tobias Nipkow, and Christoph Weidenbach for making this research possible; to Heiko Becker and Dmitriy Traytel for proving some theorems on the lexicographic and multiset extensions in Isabelle/HOL; to Carsten Fuhs for his invaluable feedback and his experiments; to Alexander Steen for pointing us to related work; and to Simon Cruanes, Mark Summerfield, Dmitriy Traytel, and the anonymous reviewers for suggesting textual improvements.
Blanchette has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 713999, Matryoshka). Wand is supported by the Deutsche Forschungsgemeinschaft (DFG) grant Hardening the Hammer (NI 491/14-1).
Author information
Authors and Affiliations
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Blanchette, J.C., Waldmann, U., Wand, D. (2017). A Lambda-Free Higher-Order Recursive Path Order. In: Esparza, J., Murawski, A. (eds) Foundations of Software Science and Computation Structures. FoSSaCS 2017. Lecture Notes in Computer Science(), vol 10203. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54458-7_27
Download citation
DOI: https://doi.org/10.1007/978-3-662-54458-7_27
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54457-0
Online ISBN: 978-3-662-54458-7
eBook Packages: Computer ScienceComputer Science (R0)


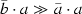 ;
;
 ;
; .
. ;
;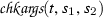 .
.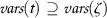 , and
, and  ;
; , and
, and  .
. , and
, and  ;
;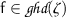 , and
, and  .
.