Abstract
Some interesting communication protocols can be precisely described only by context-free session types, an extension of conventional session types with a general form of sequential composition. The complex metatheory of context-free session types, however, hinders the definition of corresponding checking and inference algorithms. In this work we address and solve these problems introducing a new type system for context-free session types of which we provide two OCaml embeddings.
L. Padovani—Partly supported by European project HyVar (grant agreement H2020-644298).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Session types [9, 10, 12] are an established formalism for the enforcement of communication protocols through static analysis. Recently, Thiemann and Vasconcelos [25] have proposed context-free session types to enhance the expressiveness of conventional session types. Protocols that benefit from such enhancement include the serialization of tree-like data structures and XML documents [25], interactions with non-uniform objects such as stacks and reentrant locks [6, 19], and recursive protocols for trust management [24]. Thiemann and Vasconcelos [25] study the metatheory of context-free session types, leaving the definition of a type checking algorithm for future work. In this paper we point out additional issues that specifically afflict context-free session type inference and we describe a practical solution to its implementation.

Let us consider the OCaml code on the right to illustrate the problem concretely. The code models a stack, a non-uniform object [19, 22] offering different interfaces through a session endpoint u depending on its internal state. An empty stack (lines 2–7) accepts either a \(\mathtt {Push}\) or an \(\mathtt {End}\) operation. In the first case, the stack  s the element x to be pushed and moves into the non-empty state with the recursive application some x u. In the second case, it just returns the endpoint u. A non-empty stack (lines 8–13) with y on top accepts either a \(\mathtt {Push}\) operation, as in the empty case, or a \(\mathtt {Pop}\) operation, in which case it
s the element x to be pushed and moves into the non-empty state with the recursive application some x u. In the second case, it just returns the endpoint u. A non-empty stack (lines 8–13) with y on top accepts either a \(\mathtt {Push}\) operation, as in the empty case, or a \(\mathtt {Pop}\) operation, in which case it  s y back to the client. When an application some x u terminates, meaning that x has been popped, the stack returns to its previous state, whatever it was (lines 6 and 12). Note that, according to established conventions [8], all session primitives including
s y back to the client. When an application some x u terminates, meaning that x has been popped, the stack returns to its previous state, whatever it was (lines 6 and 12). Note that, according to established conventions [8], all session primitives including  return the endpoint u possibly paired with the received message (
return the endpoint u possibly paired with the received message ( ) or injected through a tag that represents an operation (
) or injected through a tag that represents an operation ( ). Using the FuSe implementation of binary sessions [21], OCaml infers for stack the type \(S_{\mathtt {reg}}\rightarrow \upbeta \) where \(S_{\mathtt {reg}}\) is the (equi-recursive) session type that satisfies the equation
). Using the FuSe implementation of binary sessions [21], OCaml infers for stack the type \(S_{\mathtt {reg}}\rightarrow \upbeta \) where \(S_{\mathtt {reg}}\) is the (equi-recursive) session type that satisfies the equation
according to which the client can only push elements of type \(\upalpha \). To understand the reason why the \(\mathtt {End}\) and \(\mathtt {Pop}\) operations are not allowed by \(S_{\mathtt {reg}}\), we have to consider that conventional session types can only describe protocols whose set of (finite) traces is regular, whereas the set of (finite) traces that describe legal interactions with stack is isomorphic to the language of balanced parentheses, a typical example of context-free language that is not regular. The session type \(S_{\mathtt {reg}}\) above corresponds to the best \(\omega \)-regular and safe approximation of this context-free language that OCaml manages to infer from the code of stack. When OCaml figures that the session type cannot precisely track whether the stack is empty or not, it computes the “intersection” of the interfaces of these two states, which results in \(S_{\mathtt {reg}}\) (along with warnings informing that lines 7 and 13 are dead code).
Driven by similar considerations, Thiemann and Vasconcelos [25] propose context-free session types as a more expressive protocol description language. The key idea is to enforce the order of interactions in a protocol using a general form of sequential composition \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\) instead of the usual prefix operator. For example, the context-free session types \(S_{\mathtt {none}}\) and \(S_{\mathtt {some}}\) that satisfy the equations
provide accurate descriptions of the legal interactions with stack: all finite, maximal traces described by \(S_{\mathtt {none}}\) have each \(\mathtt {Push}\) eventually followed by a matching \(\mathtt {Pop}\). The “empty” protocol \({\varvec{1}}\) marks the end of a legal interaction. Using Thiemann and Vasconcelos’ type system, it is then possible to work out a typing derivation showing that stack has type \(S_{\mathtt {none}}\texttt {;} A\rightarrow A\), where \(A\) is a session type variable that can be instantiated with any session type.
In the present work we address the problem of inferring a type as precise as \(S_{\mathtt {none}}\texttt {;} A\rightarrow A\) from the code of a function like stack. There are two major obstacles that make the type system in [25] unfit as the basis for a type inference algorithm: (1) a structural rule that rearranges session types according to the monoidal and distributive laws of sequential composition and (2) the need to support polymorphic recursion which, as explained in [25], ultimately arises as a consequence of (1). Type inference in presence of polymorphic recursion is known to be undecidable in general [13], a problem which often requires programmers to explicitly annotate polymorphic-recursive functions with their type. In addition, the liberal handling of sequential compositions means that functions like stack admit very different types (such as \(S_{\mathtt {reg}}\rightarrow \upbeta \) and \(S_{\mathtt {none}}\texttt {;} A\rightarrow A\)) which do not appear to be instances of a unique, more general type scheme. It is therefore unclear which notion of principal type should guide the type inference algorithm.
These observations lead us to reconsider the way sequential compositions are handled by the type system. More specifically, we propose to eliminate sequential compositions through an explicit, higher-order combinator  called resumption that is akin to functional application but has the following signature:
called resumption that is akin to functional application but has the following signature:

Suppose \(f : T\rightarrow {\varvec{1}}\) is a function that, applied to a session endpoint of type \(T\), carries out the communication over the endpoint and returns the depleted endpoint, of type \({\varvec{1}}\). Using  we can supply to f an endpoint \(u\) of type \(T\texttt {;} S\) knowing that f will take care of the prefix \(T\) of \(T\texttt {;} S\) leaving us with an endpoint of type \(S\). In other words,
we can supply to f an endpoint \(u\) of type \(T\texttt {;} S\) knowing that f will take care of the prefix \(T\) of \(T\texttt {;} S\) leaving us with an endpoint of type \(S\). In other words,  allows us to modularize the enforcement of a sequential protocol \(T\texttt {;} S\) by partitioning the program into a part – the function f – that carries out the prefix \(T\) of the protocol and another part – the evaluation context in which
allows us to modularize the enforcement of a sequential protocol \(T\texttt {;} S\) by partitioning the program into a part – the function f – that carries out the prefix \(T\) of the protocol and another part – the evaluation context in which  occurs – that carries out the continuation \(S\).
occurs – that carries out the continuation \(S\).
This informal presentation of  uncovers a potential flaw of our approach. The type \(T\rightarrow {\varvec{1}}\) describes a function that takes an endpoint of type \(T\) and returns an endpoint of type \({\varvec{1}}\), but does not guarantee that the returned endpoint is the same endpoint supplied to the function. Only in this case the endpoint can be safely resumed. What we need is a type-level mechanism to reason about the identity of endpoints. Similar requirements have already arisen in different contexts, to identify regions [2, 30] and to associate resources with capabilities [1, 26, 28]. Reframing the techniques used in these works to our setting, the idea is to refine endpoint types to a form
uncovers a potential flaw of our approach. The type \(T\rightarrow {\varvec{1}}\) describes a function that takes an endpoint of type \(T\) and returns an endpoint of type \({\varvec{1}}\), but does not guarantee that the returned endpoint is the same endpoint supplied to the function. Only in this case the endpoint can be safely resumed. What we need is a type-level mechanism to reason about the identity of endpoints. Similar requirements have already arisen in different contexts, to identify regions [2, 30] and to associate resources with capabilities [1, 26, 28]. Reframing the techniques used in these works to our setting, the idea is to refine endpoint types to a form  where \(\uprho \) is a variable that represents the abstract identity of the endpoint at the type level. The signature of
where \(\uprho \) is a variable that represents the abstract identity of the endpoint at the type level. The signature of  becomes
becomes

where the fact that the same \(\uprho \) decorates both \({[T]}_{\uprho }\) and \({[{\varvec{1}}]}_{\uprho }\) means that  can only be used on functions that accept and return the same endpoint. In turn, the fact that the same \(\uprho \) decorates both \({[T\texttt {;} S]}_{\uprho }\) and \({[S]}_{\uprho }\) guarantees that
can only be used on functions that accept and return the same endpoint. In turn, the fact that the same \(\uprho \) decorates both \({[T\texttt {;} S]}_{\uprho }\) and \({[S]}_{\uprho }\) guarantees that  evaluates to the same endpoint \(u\) that was supplied to f, but with type \(S\).
evaluates to the same endpoint \(u\) that was supplied to f, but with type \(S\).
Going back to stack, how should we patch its code so that the (inferred) session type of the endpoint accepted by stack is \(S_{\mathtt {none}}\) instead of \(S_{\mathtt {reg}}\)? We are guided by an easy rule of thumb: place resumptions in the code anywhere a \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\) is expected in the corresponding point of the protocol. In this specific case, looking at the protocols (1.2), we turn the recursive applications (some x u) on lines 6 and 12 to  . Thus, using the type system we present in this paper, we obtain a typing derivation proving that the revised stack has type \({[S_{\mathtt {none}}]}_{\uprho }\rightarrow {[{\varvec{1}}]}_{\uprho }\). Most importantly, the type system makes no use of structural rules or polymorphic recursion and there is no ambiguity as to which protocol stack is supposed to carry out, for occurrences of \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\) in a protocol are tied to the occurrences of
. Thus, using the type system we present in this paper, we obtain a typing derivation proving that the revised stack has type \({[S_{\mathtt {none}}]}_{\uprho }\rightarrow {[{\varvec{1}}]}_{\uprho }\). Most importantly, the type system makes no use of structural rules or polymorphic recursion and there is no ambiguity as to which protocol stack is supposed to carry out, for occurrences of \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\) in a protocol are tied to the occurrences of  in code that complies with such protocol.
in code that complies with such protocol.
As we will see, these properties make our type system easy to embed in any host programming language supporting parametric polymorphism and (optionally) existential types. This way, we can benefit from an off-the-shelf solution to context-free session type checking and inference instead of developing specific checking/inference algorithms. In the remainder of the paper:
-
We formalize a core functional programming language called
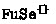 featuring threads, session-based communication primitives and a distinctive low-level construct for resuming session endpoints (Sect. 2). The semantics of resumption combinators (including
featuring threads, session-based communication primitives and a distinctive low-level construct for resuming session endpoints (Sect. 2). The semantics of resumption combinators (including  ) will be explained using this construct.
) will be explained using this construct. -
We equip
 with an original sub-structural type system that features context-free session types and abstract endpoint identities (Sect. 3). We prove fundamental properties of well-typed programs emphasizing the implications of these properties in presence of resumptions.
with an original sub-structural type system that features context-free session types and abstract endpoint identities (Sect. 3). We prove fundamental properties of well-typed programs emphasizing the implications of these properties in presence of resumptions. -
We detail two implementations of
 primitives as OCaml modules which embed
primitives as OCaml modules which embed  type discipline into OCaml’s type system (Sect. 4). The two modules solve the problems of context-free session type checking [25] and inference, striking different balances between static safety and portability.
type discipline into OCaml’s type system (Sect. 4). The two modules solve the problems of context-free session type checking [25] and inference, striking different balances between static safety and portability.
We defer a more technical discussion of related work to the end of the paper (Sect. 5). Proofs and additional technical material can be found in the associated technical report [20]. All the code in shaded background can be type checked, compiled and run using OCaml and both implementations of  [21].
[21].
2 A Calculus of Functions, Sessions and Resumptions
The syntax of  is given in Table 1 and is based on infinite sets of variables, identity variables, and of session channels. We use an involution \(\overline{\,\cdot \,}\) that turns an identity variable or channel into the (distinct) corresponding identity co-variable or co-channel. Each session channel a has two endpoints, one denoted by the channel a itself, the other by the corresponding co-channel \(\overline{a}\). We say that a is the peer endpoint of \(\overline{a}\) and vice versa. Given an endpoint \(\varepsilon \), we write \(\overline{\varepsilon }\) for its peer. A name is either an endpoint or a variable. An identity is either an endpoint or an identity (co-)variable. We write \(\overline{\iota }\) for the co-identity of \(\iota \), which is defined in such a way that \(\overline{\overline{\uprho }} = \uprho \).
is given in Table 1 and is based on infinite sets of variables, identity variables, and of session channels. We use an involution \(\overline{\,\cdot \,}\) that turns an identity variable or channel into the (distinct) corresponding identity co-variable or co-channel. Each session channel a has two endpoints, one denoted by the channel a itself, the other by the corresponding co-channel \(\overline{a}\). We say that a is the peer endpoint of \(\overline{a}\) and vice versa. Given an endpoint \(\varepsilon \), we write \(\overline{\varepsilon }\) for its peer. A name is either an endpoint or a variable. An identity is either an endpoint or an identity (co-)variable. We write \(\overline{\iota }\) for the co-identity of \(\iota \), which is defined in such a way that \(\overline{\overline{\uprho }} = \uprho \).
 : syntax (\(\ddagger \) marks the runtime syntax not used in source programs).
: syntax (\(\ddagger \) marks the runtime syntax not used in source programs).The syntax of expressions is mostly standard and comprises constants, variables, abstractions, applications, and two forms for splitting pairs and matching tagged values. Constants, ranged over by  , comprise the unitary value \(\texttt {(}\!\!\texttt {)}\), the pair constructor
, comprise the unitary value \(\texttt {(}\!\!\texttt {)}\), the pair constructor  , an arbitrary set of tags \(\mathtt {C}\) for tagged unions, the fixpoint operator
, an arbitrary set of tags \(\mathtt {C}\) for tagged unions, the fixpoint operator  , a primitive
, a primitive  for creating new threads, and a standard set of session primitives [8] whose semantics will be detailed shortly. To improve readability, we write \(\texttt {(}\!e_1\texttt {,}e_2\!\texttt {)}\) in place of the saturated application
for creating new threads, and a standard set of session primitives [8] whose semantics will be detailed shortly. To improve readability, we write \(\texttt {(}\!e_1\texttt {,}e_2\!\texttt {)}\) in place of the saturated application  . In addition, the calculus provides abstraction, application, packing and unpacking of identities. These respectively correspond to introduction and elimination constructs for universal and existential types, which are limited to identities in the formal development of
. In addition, the calculus provides abstraction, application, packing and unpacking of identities. These respectively correspond to introduction and elimination constructs for universal and existential types, which are limited to identities in the formal development of  . The distinguishing feature of
. The distinguishing feature of  is the resumption construct
is the resumption construct  indicating that \(e\) uses the endpoint \(u\) for completing some prefix of a sequentially composed protocol. As we will see in Example 1, resumptions are key to define operators such as
indicating that \(e\) uses the endpoint \(u\) for completing some prefix of a sequentially composed protocol. As we will see in Example 1, resumptions are key to define operators such as  introduced in Sect. 1. Values are fairly standard except for two details that are easy to overlook. First,
introduced in Sect. 1. Values are fairly standard except for two details that are easy to overlook. First,  is a value and reduces only when applied to a further argument. This approach, already used by Tov [26], simplifies the operational semantics (and the formal proofs) sparing us the need to \(\eta \)-expand
is a value and reduces only when applied to a further argument. This approach, already used by Tov [26], simplifies the operational semantics (and the formal proofs) sparing us the need to \(\eta \)-expand  each time it is unfolded [31]. Second, the body of an identity abstraction \(\mathrm {\Lambda }\uprho .v\) is a value and not an arbitrary expression. This restriction, inspired by [26, 28], simplifies the type system without affecting expressiveness since the body of an identity abstraction is usually another (identity or value) abstraction. In this respect, the fact that
each time it is unfolded [31]. Second, the body of an identity abstraction \(\mathrm {\Lambda }\uprho .v\) is a value and not an arbitrary expression. This restriction, inspired by [26, 28], simplifies the type system without affecting expressiveness since the body of an identity abstraction is usually another (identity or value) abstraction. In this respect, the fact that  is a value allows us to write identity-monomorphic, recursive functions of the form
is a value allows us to write identity-monomorphic, recursive functions of the form  which are both common and useful in practice. Processes are parallel compositions of threads possibly connected by sessions. Note that the restriction (\({\varvec{\nu }a}\))P binds the two endpoints a and \(\bar{a}\) in P. The definition of free and bound names for both expressions and processes is the obvious one. We identify terms modulo alpha-renaming of bound names.
which are both common and useful in practice. Processes are parallel compositions of threads possibly connected by sessions. Note that the restriction (\({\varvec{\nu }a}\))P binds the two endpoints a and \(\bar{a}\) in P. The definition of free and bound names for both expressions and processes is the obvious one. We identify terms modulo alpha-renaming of bound names.
 : operational semantics.
: operational semantics.Table 2 defines the (call-by-value) operational semantics of  , where we write \(e\{v/x\}\) and \(e\{\iota /\uprho \}\) for the (capture-avoiding) substitutions of values and identities in place of variables and identity variables, respectively. Evaluation contexts are essentially standard, with the obvious addition of
, where we write \(e\{v/x\}\) and \(e\{\iota /\uprho \}\) for the (capture-avoiding) substitutions of values and identities in place of variables and identity variables, respectively. Evaluation contexts are essentially standard, with the obvious addition of  :
:

Reduction of expressions is mostly conventional. The reduction rule [R7] erases the resumption  around a pair \(\texttt {(}\!v\texttt {,}\varepsilon \!\texttt {)}\), provided that the endpoint in the right component of the pair matches the annotation of the resumption. The type system for
around a pair \(\texttt {(}\!v\texttt {,}\varepsilon \!\texttt {)}\), provided that the endpoint in the right component of the pair matches the annotation of the resumption. The type system for  that we are going to define enforces this condition statically. However, the rule also suggests an implementation of resumptions based on a simple runtime check:
that we are going to define enforces this condition statically. However, the rule also suggests an implementation of resumptions based on a simple runtime check:  reduces to \(\texttt {(}\!v\texttt {,}\varepsilon \!\texttt {)}\) if \(\varepsilon \) and \(\varepsilon '\) are the same endpoint and fails (e.g. raising an exception) otherwise. This alternative semantics may be useful if the type system of the host language is not expressive enough to enforce the typing discipline described in Sect. 3. We will consider this alternative semantics for one of the two implementations of
reduces to \(\texttt {(}\!v\texttt {,}\varepsilon \!\texttt {)}\) if \(\varepsilon \) and \(\varepsilon '\) are the same endpoint and fails (e.g. raising an exception) otherwise. This alternative semantics may be useful if the type system of the host language is not expressive enough to enforce the typing discipline described in Sect. 3. We will consider this alternative semantics for one of the two implementations of  (Sect. 4.2).
(Sect. 4.2).
Reduction of processes is essentially the same appearing in [8, 25]. Rule [R8] describes the spawning of a new thread, whose body is the application of  ’s arguments. We have chosen this semantics of
’s arguments. We have chosen this semantics of  so that it matches OCaml’s. Rule [R9] models session initiation, whereby
so that it matches OCaml’s. Rule [R9] models session initiation, whereby  reduces a pair with the two endpoints of the newly created session. Compared to [8], we have one primitive that returns both endpoints of a new session instead of a pair of primitives that synchronize over shared/public channels. This choice is mostly a matter of simplicity: session initiation based on shared/public channels can be programmed on top of this mechanism. Also, the pair returned by
reduces a pair with the two endpoints of the newly created session. Compared to [8], we have one primitive that returns both endpoints of a new session instead of a pair of primitives that synchronize over shared/public channels. This choice is mostly a matter of simplicity: session initiation based on shared/public channels can be programmed on top of this mechanism. Also, the pair returned by  is packed to account for the fact that the caller of
is packed to account for the fact that the caller of  does not know the identities of the endpoints therein. Note that, in the residual process, the leftmost occurrence of a represents an identity, hence it does not count as an actual usage of the endpoint a. Rules [R10] and [R11] model the exchange of messages. The first one moves the message from the sender to the receiver, pairing the message with the continuation endpoint on the receiver side. The second one applies the first argument of
does not know the identities of the endpoints therein. Note that, in the residual process, the leftmost occurrence of a represents an identity, hence it does not count as an actual usage of the endpoint a. Rules [R10] and [R11] model the exchange of messages. The first one moves the message from the sender to the receiver, pairing the message with the continuation endpoint on the receiver side. The second one applies the first argument of  to the receiver’s continuation endpoint. Typically, the first argument of
to the receiver’s continuation endpoint. Typically, the first argument of  will be a tag \(\mathtt {C}\) which is effectively the message being exchanged in this case. We adopt this slightly unusual semantics of
will be a tag \(\mathtt {C}\) which is effectively the message being exchanged in this case. We adopt this slightly unusual semantics of  because it models accurately the implementation and, at the same time, it calls for specific features of the type system concerning the type-level identification of endpoints. Rule [R12] lifts reductions from expressions to processes and rules [R13–R15] close reductions under parallel compositions, restrictions, and structural congruence, which is basically the same of the \(\pi \)-calculus and is therefore omitted.
because it models accurately the implementation and, at the same time, it calls for specific features of the type system concerning the type-level identification of endpoints. Rule [R12] lifts reductions from expressions to processes and rules [R13–R15] close reductions under parallel compositions, restrictions, and structural congruence, which is basically the same of the \(\pi \)-calculus and is therefore omitted.
3 Type System
In this section we define the typing discipline for  . To keep the formal development as simple as possible, we work with a minimal type system and limit polymorphism to identity variables. These limitations do not have interesting effects on resumptions and will be lifted in the actual implementation.
. To keep the formal development as simple as possible, we work with a minimal type system and limit polymorphism to identity variables. These limitations do not have interesting effects on resumptions and will be lifted in the actual implementation.
The (finite) syntax of kinds, types, and session types is given below:

Instead of introducing concrete syntax for recursive (session) types, we let \(t\), \(s\) and \(T\), \(S\) range over the possibly infinite, regular trees generated by the above constructors for types and session types, respectively. We introduce recursive (session) types as solutions of finite systems of (session) type equations, such as (1.1). The shape of the equation, with the metavariable \(S_{\mathtt {reg}}\) occurring unguarded on the lhs and guarded by at least one constructor on the rhs, guarantees that the equation has exactly one solution [3]. Type equality corresponds to regular tree equality.
The kinds \(\mathsf {U}\) and \(\mathsf {L}\) are used to classify types as unlimited and linear, respectively. Types of kind \(\mathsf {U}\) denote values that can be used any number of times. Types of kind \(\mathsf {L}\) denote values that must be used exactly once. We have to introduce a few more notions before seeing how kinds are assigned to types.
Types include a number of base types (such as  and possibly others used in the examples), products \(t \times s\), and tagged unions
and possibly others used in the examples), products \(t \times s\), and tagged unions  . The function type \(t\rightarrow ^{\smash {\kappa }} s\) has a kind annotation \(\kappa \) indicating whether the function can be applied any number of times (\(\kappa = \mathsf {U}\)) or must be applied exactly once (\(\kappa = \mathsf {L}\)). This latter constraint typically arises when the function contains linear values in its closure. We omit the annotation \(\kappa \) when it is \(\mathsf {U}\). An endpoint type \({[T]}_{\iota }\) consists of a session type \(T\), describing the protocol according to which the endpoint must be used, and an identity \(\iota \) of the endpoint. Finally, we have existential and universal quantifiers \(\exists \uprho .t\) and \(\forall \uprho .t\) over identity variables. These are the only binders in types. We write \(\mathsf {fid}(t)\) for the set of identities occurring free in \(t\) and we identify (session) types modulo renaming of bound identities.
. The function type \(t\rightarrow ^{\smash {\kappa }} s\) has a kind annotation \(\kappa \) indicating whether the function can be applied any number of times (\(\kappa = \mathsf {U}\)) or must be applied exactly once (\(\kappa = \mathsf {L}\)). This latter constraint typically arises when the function contains linear values in its closure. We omit the annotation \(\kappa \) when it is \(\mathsf {U}\). An endpoint type \({[T]}_{\iota }\) consists of a session type \(T\), describing the protocol according to which the endpoint must be used, and an identity \(\iota \) of the endpoint. Finally, we have existential and universal quantifiers \(\exists \uprho .t\) and \(\forall \uprho .t\) over identity variables. These are the only binders in types. We write \(\mathsf {fid}(t)\) for the set of identities occurring free in \(t\) and we identify (session) types modulo renaming of bound identities.
A session type describes the sequence of actions to be peformed on an endpoint. The basic actions \({\texttt {?}}{t}\) and \({\texttt {!}}{t}\) respectively denote the input and the output of a message of type \(t\). As in [25] and unlike most presentations of session types, these forms do not specify a continuation, which can be attached using sequential composition. External choices  and internal choices
and internal choices  describe protocols that can proceed according to different continuations \(T_i\) each associated with a tag \(\mathtt {C}_i\). When the choice is internal, the process using the endpoint selects the continuation. When the choice is external, the process accepts the selection performed on the peer endpoint. Therefore, an external choice corresponds to an input (of a tag \(\mathtt {C}_i\)) and an internal choice to an output. Sequential composition \(T\texttt {;} S\) combines two sub-protocols \(T\) and \(S\) into a protocol where all the actions in \(T\) are supposed to be performed before any action in \(S\). We have two terminal protocols: \({\varvec{0}}\) indicates that no further action is to be performed on the endpoint; \({\varvec{1}}\) indicates that the endpoint is meant to be resumed. As we will see, this distinction affects also the kinding of endpoint types: an endpoint whose protocol is \({\varvec{0}}\) can be discarded for it serves no purpose; an endpoint whose protocol is \({\varvec{1}}\) must be resumed exactly once.
describe protocols that can proceed according to different continuations \(T_i\) each associated with a tag \(\mathtt {C}_i\). When the choice is internal, the process using the endpoint selects the continuation. When the choice is external, the process accepts the selection performed on the peer endpoint. Therefore, an external choice corresponds to an input (of a tag \(\mathtt {C}_i\)) and an internal choice to an output. Sequential composition \(T\texttt {;} S\) combines two sub-protocols \(T\) and \(S\) into a protocol where all the actions in \(T\) are supposed to be performed before any action in \(S\). We have two terminal protocols: \({\varvec{0}}\) indicates that no further action is to be performed on the endpoint; \({\varvec{1}}\) indicates that the endpoint is meant to be resumed. As we will see, this distinction affects also the kinding of endpoint types: an endpoint whose protocol is \({\varvec{0}}\) can be discarded for it serves no purpose; an endpoint whose protocol is \({\varvec{1}}\) must be resumed exactly once.
We proceed defining a labeled transition system that formalizes the (observable) actions allowed by a protocol. This notion is instrumental in defining protocol equivalence which, in turn, is key in various parts of the type system.
Definition 1
(protocol LTS). Let \(\mathsf {done}(\cdot )\) be the least predicate on protocols inductively defined by the following axiom and rule:

Let \(\mathop {\longrightarrow }\limits ^{\smash {\mu }}\) be the least family of relations on protocols inductively defined by the following axioms and rules, where \(\mu \) ranges over labels  :
:

Protocol equivalence is defined in terms of a bisimulation relation:
Definition 2
(equivalent protocols). We write \(\sim \) for the largest binary relation on protocols such that \(T\sim S\) implies:
-
\(\mathsf {done}(T)\) if and only if \(\mathsf {done}(S)\);
-
\(T\mathop {\longrightarrow }\limits ^{\smash {\mu }}T'\) implies \(S\mathop {\longrightarrow }\limits ^{\smash {\mu }}S'\) and \(T' \sim S'\);
-
\(S\mathop {\longrightarrow }\limits ^{\smash {\mu }}S'\) implies \(T\mathop {\longrightarrow }\limits ^{\smash {\mu }}T'\) and \(T' \sim S'\).
We say that \(T\) and \(S\) are equivalent if \(T\sim S\) holds.
Note that \({\varvec{0}}\) is equivalent to all non-resumable session types that cannot make any progress. For example, \(T_1 = T_1\texttt {;} S\) and \(T_2 = {\varvec{1}}\texttt {;} T_2\) are all equivalent to \({\varvec{0}}\).
Proposition 1
(properties of \(\sim \)). The following properties hold:
-
1.
(equivalence) \(\sim \) is reflexive and transitive;
-
2.
(associativity) \(T\texttt {;} (S\texttt {;} R) \sim (T\texttt {;} S)\texttt {;} R\);
-
3.
(unit) \({\varvec{1}}\texttt {;} T\sim T\texttt {;} {\varvec{1}}\sim T\).
-
4.
(congruence) \(T\sim T'\) and \(S\sim S'\) imply \(T\texttt {;} S\sim T'\texttt {;} S'\).
The congruence property of \(\sim \) is particularly important in our setting since we use sequential composition as a modular construct for structuring programs. We do not identify equivalent session types and assume that sequential composition associates to the right: \(T\texttt {;} S\texttt {;} R\) means \(T\texttt {;} (S\texttt {;} R)\). Although equivalence is decidable, this fact has little importance in our setting compared to [25] since \(\sim \) is never used in the typing rules concerning user syntax.
We are now ready to classify types according to their kind. We resort to a coinductive definition to cope with possibly infinite types.
Definition 3
(kinding). Let \({}\,{:}{:}{}\,{}\) be the largest relation between types and kinds such that \({t}\,{:}{:}{}\,{\kappa }\) implies either \(\kappa = \mathsf {L}\) or
-
 or \(t= t_1 \rightarrow ^{\smash {}}t_2\) or \(t= {[T]}_{\iota }\) and \(T\sim {\varvec{0}}\), or
or \(t= t_1 \rightarrow ^{\smash {}}t_2\) or \(t= {[T]}_{\iota }\) and \(T\sim {\varvec{0}}\), or -
\(t= \exists \uprho .s\) or \(t= \forall \uprho .s\) and \({s}\,{:}{:}{}\,{\kappa }\), or
-
\(t= t_1 \times t_2\) and \({t_i}\,{:}{:}{}\,{\kappa }\) for every \(i=1,2\), or
-
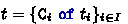 and \({t_i}\,{:}{:}{}\,{\kappa }\) for every \(i\in I\).
and \({t_i}\,{:}{:}{}\,{\kappa }\) for every \(i\in I\).
We say that \(t\) is unlimited if \({t}\,{:}{:}{}\,{\mathsf {U}}\) and that \(t\) is linear if its only kind is \(\mathsf {L}\), namely if \({t}\,{:}{:}{}\,{\kappa }\) implies \(\kappa = \mathsf {L}\). Endpoint types with a non-terminated session type and function types with kind annotation \(\mathsf {L}\) are linear since they denote values that must be used exactly once. Base types and function types with kind annotation \(\mathsf {U}\) are unlimited since they denote values that can be used (or discarded) without restrictions. Note that the kind of a function type \(t\rightarrow ^{\smash {\kappa }} s\) solely depends on \(\kappa \), but not on the kind of \(t\) or \(s\). For example,  is unlimited even if
is unlimited even if  is not. Endpoint types \({[T]}_{\iota }\) are unlimited if \(T\sim {\varvec{0}}\): non-resumable endpoints on which no further actions can be performed can be discarded. On the contrary, \({[{\varvec{1}}]}_{\iota }\) is linear, since it denotes an endpoint that must be resumed once. The kind of existential and universal types, products and tagged unions is determined by that of the component types. For example, the type
is not. Endpoint types \({[T]}_{\iota }\) are unlimited if \(T\sim {\varvec{0}}\): non-resumable endpoints on which no further actions can be performed can be discarded. On the contrary, \({[{\varvec{1}}]}_{\iota }\) is linear, since it denotes an endpoint that must be resumed once. The kind of existential and universal types, products and tagged unions is determined by that of the component types. For example, the type  of integer lists is unlimited, whereas the type
of integer lists is unlimited, whereas the type  is linear. Finally, note that Definition 3 accounts for a form of subkinding: \({t}\,{:}{:}{}\,{\mathsf {U}}\) implies \({t}\,{:}{:}{}\,{\mathsf {L}}\). This is motivated by the observation that it is safe to use a value of an unlimited type exactly once.
is linear. Finally, note that Definition 3 accounts for a form of subkinding: \({t}\,{:}{:}{}\,{\mathsf {U}}\) implies \({t}\,{:}{:}{}\,{\mathsf {L}}\). This is motivated by the observation that it is safe to use a value of an unlimited type exactly once.
As usual, the session types associated with peer endpoints must be dual to each other to guarantee communication safety. Duality expresses the fact that every input action performed on an endpoint is matched by a corresponding output performed on its peer and is defined thus:
Definition 4
(session type duality). Session type duality is the function \(\overline{\,\cdot \,}\) coinductively defined by the following equations:

It is easy to verify that duality is an involution, that is \(\overline{\overline{T}} = T\).
The type system makes use of two environments: identity environments \(\Updelta \) are sets of identities written \(\iota _1, \dots , \iota _n\), representing the endpoints statically known to a program fragment; type environments \(\Upgamma \) are finite maps from names to types written \(u_1 : t_1, \dots , u_n : t_n\) associating a type with every (free) name occurring in an expression. We write \(\Updelta , \Updelta '\) for \(\Updelta \cup \Updelta '\) when \(\Updelta \cap \Updelta ' = \emptyset \). We write \(\Upgamma (u)\) for the type associated with \(u\) in \(\Upgamma \), \(\mathsf {dom}(\Upgamma )\) for the domain of \(\Upgamma \), and \(\Upgamma _1,\Upgamma _2\) for the union of \(\Upgamma _1\) and \(\Upgamma _2\) when \(\mathsf {dom}(\Upgamma _1) \cap \mathsf {dom}(\Upgamma _2) = \emptyset \). We extend kinding to type environments in the obvious way, writing \({\Upgamma }\,{:}{:}{}\,{\kappa }\) if \({\Upgamma (u)}\,{:}{:}{}\,{\kappa }\) for all \(u\in \mathsf {dom}(\Upgamma )\). We also need a more flexible way of combining type environments that allows names with unlimited types to be used any number of times.
Definition 5
(environment combination [15]). We write \(+\) for the partial operation on type environments such that:

Note that \(\Upgamma + \Upgamma '\) is undefined if \(\Upgamma \) and \(\Upgamma '\) contain associations for the same name with different or linear types. When \({\Upgamma }\,{:}{:}{}\,{\mathsf {U}}\), we have that \(\Upgamma + \Upgamma \) is always defined and equal to \(\Upgamma \) itself.
 constants.
constants.The type schemes of  constants are given in Table 3 as associations
constants are given in Table 3 as associations  . Note that, in general, each constant has infinitely many types. Although most associations are as expected, it is worth commenting on a few details. First, observe that the kind annotation \(\kappa \) in the types of
. Note that, in general, each constant has infinitely many types. Although most associations are as expected, it is worth commenting on a few details. First, observe that the kind annotation \(\kappa \) in the types of  and
and  coincides with the kind of the first argument of these constants. In particular, when \(t\) is linear and
coincides with the kind of the first argument of these constants. In particular, when \(t\) is linear and  is supplied one argument \(v\) of type \(t\), the resulting partial application is also linear. Second, in accordance with their operational semantics (Table 2) all the primitives for session communications (
is supplied one argument \(v\) of type \(t\), the resulting partial application is also linear. Second, in accordance with their operational semantics (Table 2) all the primitives for session communications ( , and
, and  ) return the very same endpoint they take as input as indicated by the identity \(\iota \) that annotates the endpoint types in both the domain and range of these constants. Finally, in an application
) return the very same endpoint they take as input as indicated by the identity \(\iota \) that annotates the endpoint types in both the domain and range of these constants. Finally, in an application  the function \(v\) is meant to be applied to the peer of \(\varepsilon \). This constraint is indicated by the use of the co-identity \(\overline{\iota }\) and is key for the soundness of the type system. Note also that the codomain of \(v\) matches the return type of
the function \(v\) is meant to be applied to the peer of \(\varepsilon \). This constraint is indicated by the use of the co-identity \(\overline{\iota }\) and is key for the soundness of the type system. Note also that the codomain of \(v\) matches the return type of  , following the fact that \(v\) is applied to the peer of \(\varepsilon \) after the communication has occurred (Table 2). Finally,
, following the fact that \(v\) is applied to the peer of \(\varepsilon \) after the communication has occurred (Table 2). Finally,  returns a packaged pair of endpoints with dual session types. The package must be opened before the endpoints can be used for communication.
returns a packaged pair of endpoints with dual session types. The package must be opened before the endpoints can be used for communication.
 : static semantics.
: static semantics.The typing rules for  are given in Table 4 and derive judgments
are given in Table 4 and derive judgments  for expressions and \({\Updelta }; {\Upgamma } \vdash {P}\) for processes. When present, side conditions are written to the right of the rule to which they apply. A judgment is well formed if all the identities occurring free in \(\Upgamma \) and \(t\) are included in \(\Updelta \). From now on we make the implicit assumption that all judgments are well formed.
for expressions and \({\Updelta }; {\Upgamma } \vdash {P}\) for processes. When present, side conditions are written to the right of the rule to which they apply. A judgment is well formed if all the identities occurring free in \(\Upgamma \) and \(t\) are included in \(\Updelta \). From now on we make the implicit assumption that all judgments are well formed.
We now discuss the most important aspects of the typing rules. In [t-const], the implict well-formedness constraint on typing judgments restricts the set of types that we can give to a constant to those whose free identities occur in \(\Updelta \). In [t-const] and [t-name], the unused part of the type environment must be unlimited, to make sure that no linear name is left unused. The elimination rules for products and tagged unions are standard. Note the use of \(+\) for combining type environments so that the same linear resource is not used multiple times in different parts of an expression. Rules [t-fun] and [t-app] deal with function types. In [t-fun], the kind annotation on the arrow must be consistent with the kind of the environment in which the function is typed. If any name in the environment has a linear type, then the function must be linear itself to avoid repeated use of such name. By contrast, the kind annotation plays no role in [t-app]. Abstraction and application of identities are standard. The side condition in [t-id-app] makes sure that the supplied identity is in scope. This condition is not necessarily captured by the well formedness of judgments in case \(\uprho \) does not occur in \(t\). Packing and unpacking are also standard. The identity variable \(\uprho \) introduced in [t-unpack] is different from any other identity known to \(e_2\). This prevents \(e_2\) from using \(\uprho \) in any context where a specific identity is required. Also, well formedness of judgments requires \(\mathsf {fid}(s) \subseteq \Updelta \), meaning that \(\uprho \) is not allowed to escape its scope. The most interesting and distinguishing typing rule of  is [t-resume]. Let us discuss the rule clockwise, starting from
is [t-resume]. Let us discuss the rule clockwise, starting from  and recalling that the purpose of this expression is to resume \(u\) once the evaluation of \(e\) is completed. The rule requires \(u\) to have a type of the form \({[T\texttt {;} S]}_{\iota }\), which specifies the identity \(\iota \) of the endpoint and the protocols \(T\) and \(S\) to be completed in this order. Within \(e\) the type of \(u\) is changed to \({[T]}_{\iota }\) and the evaluation of \(e\) must yield a pair whose first component, of type \(t\), is the result of the computation and whose second component, of type \({[{\varvec{1}}]}_{\iota }\), witnesses the fact that the prefix protocol \(T\) has been entirely carried out on \(u\). Once the evaluation of \(e\) is completed, the type of the endpoint in the pair is reset to the suffix \(S\). The same identity \(\iota \) relates all the occurrences of the endpoint both in the type environments and in the expressions. Note that the annotation \(u\) in
and recalling that the purpose of this expression is to resume \(u\) once the evaluation of \(e\) is completed. The rule requires \(u\) to have a type of the form \({[T\texttt {;} S]}_{\iota }\), which specifies the identity \(\iota \) of the endpoint and the protocols \(T\) and \(S\) to be completed in this order. Within \(e\) the type of \(u\) is changed to \({[T]}_{\iota }\) and the evaluation of \(e\) must yield a pair whose first component, of type \(t\), is the result of the computation and whose second component, of type \({[{\varvec{1}}]}_{\iota }\), witnesses the fact that the prefix protocol \(T\) has been entirely carried out on \(u\). Once the evaluation of \(e\) is completed, the type of the endpoint in the pair is reset to the suffix \(S\). The same identity \(\iota \) relates all the occurrences of the endpoint both in the type environments and in the expressions. Note that the annotation \(u\) in  does not count as a proper “use” of \(u\). Its purpose is solely to identify the endpoint being resumed.
does not count as a proper “use” of \(u\). Its purpose is solely to identify the endpoint being resumed.
The typing rules for processes are mostly unremarkable. In [t-session] the two peers of a session are introduced both in the type environment and in the identity environment. The protocols \(T\) and \(S\) of peer endpoints are required to be dual to each other modulo protocol equivalence. The use of \(\sim \) accounts for the possibility that sequential compositions may be arranged differently in the threads using the two peers. For instance, one thread might be using an endpoint with protocol \(T\), and its peer could have type \({\varvec{1}}\texttt {;} \overline{T}\) in a thread that has not resumed it yet. Still, \(T\sim \overline{{\varvec{1}}\texttt {;} \overline{T}} = {\varvec{1}}\texttt {;} T\).
We state a few basic properties of the typing discipline focusing on those more closely related to resumptions. To begin with, we characterize the type environments in which expressions and processes without free variables reduce.
Definition 6
We say that \(\Upgamma \) is ground if \(\mathsf {dom}(\Upgamma )\) contains endpoints only; that it is well formed if \(\varepsilon \in \mathsf {dom}(\Upgamma )\) implies \(\Upgamma (\varepsilon ) = {[T]}_{\varepsilon }\); that it is balanced if \(\varepsilon , \overline{\varepsilon }\in \mathsf {dom}(\Upgamma )\) implies \(\Upgamma (\varepsilon ) = {[T]}_{\varepsilon }\) and \(\Upgamma (\overline{\varepsilon }) = {[S]}_{\overline{\varepsilon }}\) and \(T\sim \overline{S}\).
Note that in a well-formed environment the type associated with endpoint \(\varepsilon \) is annotated with the correct identity of \(\varepsilon \), that is \(\varepsilon \) itself.
As usual for session type systems, we must take into account the possibility that the type associated with session endpoints changes over time. Normally this only happens when processes use endpoints for communications. In our case, however, also expressions may change endpoint types because of resumptions. In order to track these changes, we introduce two relations that characterize the evolution of type environments alongside expressions and processes. The first relation is the obvious extension of equivalence \(\sim \) to type environments:
Definition 7
(equivalent type environments). Let  and
and  . We write \(\Upgamma \sim \Upgamma '\) if \(T_i \sim S_i\) for every \(i\in I\).
. We write \(\Upgamma \sim \Upgamma '\) if \(T_i \sim S_i\) for every \(i\in I\).
The second relation includes \(\sim \) and mimics communications at the type level:
Definition 8
Let \(\leadsto \) be the least relation between type environments such that:

Concerning subject reduction for expressions, we have:
Theorem 1
(SR for expressions). Let  where \(\Upgamma \) is ground and well formed. If \(e\rightarrow e'\), then
where \(\Upgamma \) is ground and well formed. If \(e\rightarrow e'\), then  for some \(\Upgamma '\) such that \(\Upgamma \sim \Upgamma '\).
for some \(\Upgamma '\) such that \(\Upgamma \sim \Upgamma '\).
Theorem 1 guarantees that resumptions in well-typed programs do not change arbitrarily the session types of endpoints. The only permitted changes are those allowed by session type equivalence. Concerning progress, we have:
Theorem 2
(progress for expressions). If \(\Upgamma \) is ground and well formed and  and
and  , then either \(e\) is a value or \(e= \mathcal {E}[K~v]\) for some \(\mathcal {E}\), \(v\), \(w\), and
, then either \(e\) is a value or \(e= \mathcal {E}[K~v]\) for some \(\mathcal {E}\), \(v\), \(w\), and  .
.
That is, an irreducible expression that is not a value is a term that is meant to reduce at the level of processes. Note that a resumption  is not a value and is meant to reduce at the level of expressions via [R7]. Hence, Theorem 2 guarantees that in a well-typed program all such resumptions are such that \(\varepsilon = \varepsilon '\). An alternative reading for this observation is that each endpoint is guaranteed to have a unique identity in every well-typed program.
is not a value and is meant to reduce at the level of expressions via [R7]. Hence, Theorem 2 guarantees that in a well-typed program all such resumptions are such that \(\varepsilon = \varepsilon '\). An alternative reading for this observation is that each endpoint is guaranteed to have a unique identity in every well-typed program.
Theorem 3
(SR for processes). Let \({\Updelta }; {\Upgamma } \vdash {P}\) where \(\Upgamma \) is ground, well formed and balanced. If \(P\rightarrow Q\), then \({\Updelta }; {\Upgamma '} \vdash {Q}\) for some \(\Upgamma '\) such that \(\Upgamma \leadsto ^* \Upgamma '\).
Apart from being a fundamental sanity check for the type system, Theorem 3 states that the communications occurring in processes are precisely those permitted by the session types in the type environments. Therefore, Theorem 3 gives us a guarantee of protocol fidelity. A particular instance of protocol fidelity concerns sequential composition: a well-typed process using an endpoint with type \(T\texttt {;} S\) is guaranteed to perform the actions described by \(T\) first, and then those described by \(S\). Other standard properties including communication safety and (partial) progress for processes can also be proved [21].
Example 1
(resumption combinators). In prospect of devising a library implementation of  , the resumption expression
, the resumption expression  is challenging to deal with, for its typing rule involves an non-trivial manipulation of the type environment whereby the type of \(u\) changes as \(u\) flows into and out of the expression. In practice, it is convenient to encapsulate
is challenging to deal with, for its typing rule involves an non-trivial manipulation of the type environment whereby the type of \(u\) changes as \(u\) flows into and out of the expression. In practice, it is convenient to encapsulate  expressions in two combinators that can be easily implemented as higher-order functions (Sects. 4.2 and 4.3):
expressions in two combinators that can be easily implemented as higher-order functions (Sects. 4.2 and 4.3):

The combinator  is a general version of
is a general version of  that applies to functions returning an actual result in addition to the endpoint to be resumed. We derive
that applies to functions returning an actual result in addition to the endpoint to be resumed. We derive

for every \(T\), \(\iota \), \(t\) and \(S\) such that  . A similar derivation allows us to derive
. A similar derivation allows us to derive

In the implementation we will give  and
and  their most general type by leveraging OCaml’s support for parametric polymorphism. Other combinators for resuming two or more endpoints can be defined similarly. For example,
their most general type by leveraging OCaml’s support for parametric polymorphism. Other combinators for resuming two or more endpoints can be defined similarly. For example,

is analogous to  , but resumes two endpoints at once. \(\blacksquare \)
, but resumes two endpoints at once. \(\blacksquare \)
Example 2
(alternative communication API). It could be argued that the communication primitives  and
and  are not really “primitive” because their types make use of both I/O actions and sequential composition. Alternatively, we could equip
are not really “primitive” because their types make use of both I/O actions and sequential composition. Alternatively, we could equip  with two primitives
with two primitives  and
and  having the same operational semantics as
having the same operational semantics as  and
and  but the following types:
but the following types:

Starting from  and
and  and
and  could then be derived with the help of
could then be derived with the help of  and
and  , used below in infix notation:
, used below in infix notation:

We find a communication API based on  and
and  appealing for its cleaner correspondence between primitives and session type constructors. In particular, with this API the resumption combinators account for all occurrences of \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\) in protocols. In the formal model of
appealing for its cleaner correspondence between primitives and session type constructors. In particular, with this API the resumption combinators account for all occurrences of \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\) in protocols. In the formal model of  , we have decided to stick to the conventional typing of
, we have decided to stick to the conventional typing of  and
and  for continuity with other presentations of similar calculi [8, 25, 29]. \(\blacksquare \)
for continuity with other presentations of similar calculi [8, 25, 29]. \(\blacksquare \)
Example 3
This example illustrates the sort of havoc that could be caused if two endpoints had the same identity. As a particular instance, we see the importance of distinguishing the identity of peer endpoints. The derivation

can be used to type check a function that, applied to two endpoints \(x\) and \(y\) whose types are \({[{\varvec{1}}\texttt {;} T]}_{\iota }\) and \({[{\varvec{1}}\texttt {;} S]}_{\iota }\) respectively, returns a pair containing the same two endpoints, but with their types changed to \({[S]}_{\iota }\) and \({[T]}_{\iota }\). If there existed two endpoints \(\varepsilon _1\) and \(\varepsilon _2\) with the same identity \(\iota \) from two different sessions, the function could be used to exchange their protocols, almost certainly causing communication errors in the rest of the computation. If \(\varepsilon _1\) and \(\varepsilon _2\) were the peers of the same session, then communication safety would still be guaranteed by the condition \(T\sim \overline{S}\), but protocol fidelity would be violated nonetheless. \(\blacksquare \)
4 Context-Free Session Types in OCaml
In this section we detail two different implementations of  communication and resumption primitives as OCaml functions. We start defining a few basic data structures and a convenient OCaml representation of session types (Sect. 4.1) before describing the actual implementations. The first one (Sect. 4.2) is easily portable to any programming language supporting parametric polymorphism, but relies on lightweight runtime checks to verify when an endpoint can be safely resumed. The second implementation (Sect. 4.3) closely follows the typing discipline of
communication and resumption primitives as OCaml functions. We start defining a few basic data structures and a convenient OCaml representation of session types (Sect. 4.1) before describing the actual implementations. The first one (Sect. 4.2) is easily portable to any programming language supporting parametric polymorphism, but relies on lightweight runtime checks to verify when an endpoint can be safely resumed. The second implementation (Sect. 4.3) closely follows the typing discipline of  presented in Sect. 3, but relies on more advanced features (existential types) of the host language. The particular implementation we describe is based on OCaml’s first-class modules [7, 32]. We conclude the section revisiting and extending the running example of [25] (Sect. 4.4).
presented in Sect. 3, but relies on more advanced features (existential types) of the host language. The particular implementation we describe is based on OCaml’s first-class modules [7, 32]. We conclude the section revisiting and extending the running example of [25] (Sect. 4.4).
4.1 Basic Setup
To begin with, we define a simple module Channel that implements unsafe communication channels. In turn, Channel is based on OCaml’s Event module, which implements communication primitives in the style of Concurrent ML [23].

An unsafe channel is just an Event.channel for exchanging messages of type unit. The  type parameter is just a placeholder, for communication primitives perform unsafe casts (with Obj.magic) on every exchanged message. Note that Event.send and Event.receive only create synchronization events, and communication only happens when these events are passed to Event.sync. Using Event channels is convenient but not mandatory: the rest of our implementation is essentially independent of the underlying communication framework.
type parameter is just a placeholder, for communication primitives perform unsafe casts (with Obj.magic) on every exchanged message. Note that Event.send and Event.receive only create synchronization events, and communication only happens when these events are passed to Event.sync. Using Event channels is convenient but not mandatory: the rest of our implementation is essentially independent of the underlying communication framework.
The second ingredient of our library is an implementation of atomic boolean flags. Since OCaml’s type system is not substructural we are unable to distinguish between linear and unlimited types and, in particular, we are unable to prevent multiple endpoint usages solely using the type system. Following ideas of Tov and Pucella [27] and Hu and Yoshida [11] and the design of FuSe [21], the idea is to associate each endpoint with a boolean flag indicating whether the endpoint can be safely used or not. The flag is initially set to  , indicating that the endpoint can be used, and is tested by every operation that uses the endpoint. If the flag is still
, indicating that the endpoint can be used, and is tested by every operation that uses the endpoint. If the flag is still  , then the endpoint can be used and the flag is reset to
, then the endpoint can be used and the flag is reset to  . If the flag is
. If the flag is  , then the endpoint has already been used in the past and the operation aborts raising an exception. Atomicity is needed to make sure that the flag is tested and updated in a consistent way in case multiple threads try to use the same endpoint simultaneously.
, then the endpoint has already been used in the past and the operation aborts raising an exception. Atomicity is needed to make sure that the flag is tested and updated in a consistent way in case multiple threads try to use the same endpoint simultaneously.

We represent an atomic boolean flag as a Mutex.t, that is a lock in OCaml’s standard library. The value of the flag is the state of the mutex: when the mutex is unlocked, the flag is  . Using the flag means attempting to acquire the lock with the non-blocking function Mutex.try_lock. As for Event channels, the mutex is a choice of convenience more than necessity. Alternative realizations, possibly based on lightweight compare-and-swap operations, can be considered.
. Using the flag means attempting to acquire the lock with the non-blocking function Mutex.try_lock. As for Event channels, the mutex is a choice of convenience more than necessity. Alternative realizations, possibly based on lightweight compare-and-swap operations, can be considered.
We conclude the setup phase by defining a bunch of OCaml singleton types in correspondence with the session type constructors:

The type parameter  is the type of the exchanged message in msg and a polymorphic variant type representing the available choices in tag. The type parameteres
is the type of the exchanged message in msg and a polymorphic variant type representing the available choices in tag. The type parameteres  and
and  in seq stand for the prefix and suffix protocols of a sequential composition \(\upalpha \texttt {;} \upbeta \). The data constructors of these types are never used and are given only because OCaml is more liberal in the construction of recursive types when these are concrete rather than abstract. Hereafter, we use \(\uptau _1\), \(\uptau _2\), \(\dots \) to range over OCaml types and \(\upalpha \), \(\upbeta \), \(\dots \), \(\upvarphi \) to range over OCaml type variables. Considering that OCaml supports equi-recursive types, we ignore once again the concrete syntax for expressing infinite session types and work with infinite trees instead. OCaml uses the notation
in seq stand for the prefix and suffix protocols of a sequential composition \(\upalpha \texttt {;} \upbeta \). The data constructors of these types are never used and are given only because OCaml is more liberal in the construction of recursive types when these are concrete rather than abstract. Hereafter, we use \(\uptau _1\), \(\uptau _2\), \(\dots \) to range over OCaml types and \(\upalpha \), \(\upbeta \), \(\dots \), \(\upvarphi \) to range over OCaml type variables. Considering that OCaml supports equi-recursive types, we ignore once again the concrete syntax for expressing infinite session types and work with infinite trees instead. OCaml uses the notation  for denoting a type \(\uptau \) in which occurrences of \(\upalpha \) stand for the type as a whole.
for denoting a type \(\uptau \) in which occurrences of \(\upalpha \) stand for the type as a whole.
4.2 A Dynamically Checked, Portable Implementation
The first implementation of the library that we present ignores identities in types and verifies the soundness of resumptions by means of a runtime check. In this case, an endpoint type \({[T]}_{\iota }\) is encoded as the OCaml type \(\texttt {(}\!\uptau _1\texttt {,}\uptau _2\!\texttt {)}~\mathtt {t}\) where \(\uptau _1\) and \(\uptau _2\) are roughly determined as follows:
-
when \(T\) is a self-dual session type constructor (either \({\varvec{0}}\), \({\varvec{1}}\), or \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\)), then both \(\uptau _1\) and \(\uptau _2\) are the corresponding OCaml type (\({{\mathbf {\mathtt{{0, 1}}}}}\), or seq, respectively);
-
when \(T\) is an input (either \({\texttt {?}}{t}\) or
 ), then \(\uptau _1\) is the encoding the received message/choice and \(\uptau _2\) is \({{\mathbf {\mathtt{{0}}}}}\); dually when \(T\) is an output.
), then \(\uptau _1\) is the encoding the received message/choice and \(\uptau _2\) is \({{\mathbf {\mathtt{{0}}}}}\); dually when \(T\) is an output.
More precisely, types and session types are encoded thus:
Definition 9
(encoding of types and session types). Let  and
and  be the encoding functions coinductively defined by the following equations:
be the encoding functions coinductively defined by the following equations:

where  is extended homomorphically to all the remaining type constructors erasing kind annotations on arrows and existential and universal quantifiers.
is extended homomorphically to all the remaining type constructors erasing kind annotations on arrows and existential and universal quantifiers.
Note that identities \(\iota \) in endpoint types are simply erased; we will revise this choice in the second implementation (Sect. 4.3). The encoding is semantically grounded through the relationship between sessions and linear channels [4, 5, 14, 21] and is extended here to sequential composition for the first time. The distinguishing feature of this encoding is that is makes it easy to express session type duality constraints solely in terms of type equality:
Theorem 4
If  , then
, then  .
.
That is, we pass from a session type to its dual by flipping the type parameters of the t type. This also works for unknown or partially known session types: the dual of \(\texttt {(}\!\upalpha \texttt {,}\upbeta \!\texttt {)}~\mathtt {t}\) is \(\texttt {(}\!\upbeta \texttt {,}\upalpha \!\texttt {)}~\mathtt {t}\).
We can now look at the concrete representation of the type \(\texttt {(}\!\upalpha \texttt {,}\upbeta \!\texttt {)}~\mathtt {t}\):

An endpoint is a record with three fields, a reference chan to the unsafe channel used for the actual communications, an integer number  representing the endpoint’s polarity, and an atomic boolean flag once indicating whether the endpoint can be safely used or not. Of course, this representation is hidden from the user of the library and any direct access to these fields occurs via one of the public functions that we are going to discuss.
representing the endpoint’s polarity, and an atomic boolean flag once indicating whether the endpoint can be safely used or not. Of course, this representation is hidden from the user of the library and any direct access to these fields occurs via one of the public functions that we are going to discuss.
The  primitives for session communication are implemented by corresponding OCaml functions with the following signatures, which are directly related to the type schemes in Table 3 through the encoding in Definition 9:
primitives for session communication are implemented by corresponding OCaml functions with the following signatures, which are directly related to the type schemes in Table 3 through the encoding in Definition 9:

We take advantage of parametric polymorphism to give these functions their most general types. We implement the alternative communication API with the primitives  and
and  because their type signatures are simpler. From these functions,
because their type signatures are simpler. From these functions,  and
and  can be easily derived as shown in Example 2. We also omit
can be easily derived as shown in Example 2. We also omit  which is just a particular instance of
which is just a particular instance of  (Example 1). The types for
(Example 1). The types for  and
and  are slightly more general than those in Table 3, but the tossing of tags between choices and unions cannot be expressed as accurately in OCaml without fixing the set of tags. The given typing is still sound though.
are slightly more general than those in Table 3, but the tossing of tags between choices and unions cannot be expressed as accurately in OCaml without fixing the set of tags. The given typing is still sound though.
Since this version of the library ignores endpoint identities, the endpoints returned by  are already unpackaged. The implementation of
are already unpackaged. The implementation of  is
is

and consists of the creation of a new unsafe channel ch and two records referring to it with opposite polarities and each with its own validity flag.
The communication primitives are defined in terms of corresponding operations on the underlying unsafe channel and make use of an auxiliary function

that returns a copy of u with once overwritten by a fresh flag. We have:

The flag associated with the endpoint u is used before communication takes place and refreshed just before the endpoint is returned to the user. It is not possible to refresh the flag by just releasing the lock in it, for any existing alias to the endpoint must be permanently marked as invalid [21].
We complete the module with the implementation of  , shown below:
, shown below:

The endpoint u is passed to scope, which evaluates to a pair made of the result res of the computation and the endpoint v to be resumed. The cast Obj.magic u is necessary to turn the type of u from \(T\texttt {;} S\) to \(T\), as required by scope. The second line in the body of  checks that the endpoint v resulting from the evaluation of scope is indeed the same endpoint u that was fed in it. Note the key role of the polarity in checking that u and v are the same endpoint and the use of the physical equality operator ==, which compares only the references to the involved unsafe channels. An exception is raised if v is not the same endpoint as u. Otherwise, the result of the computation and v are returned. The cast Obj.magic v effectively resumes the endpoint turning its type from \({\varvec{1}}\) to \(S\). The two casts roughly delimit the region of code that we would write within
checks that the endpoint v resulting from the evaluation of scope is indeed the same endpoint u that was fed in it. Note the key role of the polarity in checking that u and v are the same endpoint and the use of the physical equality operator ==, which compares only the references to the involved unsafe channels. An exception is raised if v is not the same endpoint as u. Otherwise, the result of the computation and v are returned. The cast Obj.magic v effectively resumes the endpoint turning its type from \({\varvec{1}}\) to \(S\). The two casts roughly delimit the region of code that we would write within  in the formal model.
in the formal model.
4.3 A Statically Checked Implementation
The second implementation we present reflects more accurately the typing information in endpoint types, which includes the identity of endpoints. In this case, we represent an endpoint type \({[T]}_{\uprho }\) as an OCaml type \(\texttt {(}\!\uptau _1\texttt {,}\uptau _2\texttt {,}\uprho \texttt {,}\overline{\uprho }\!\texttt {)}~\mathtt {t}\) where \(\uptau _1\) and \(\uptau _2\) are determined from \(T\) in a similar way as before. In addition, the phantom type parameter \(\uprho \) is the (abstract) identity of the endpoint and \(\overline{\uprho }\) that of its peer (we represent identity variables as OCaml type variables and assume that \(\overline{\uprho }\) is another OCaml type variable distinct from \(\uprho \)). More formally, the revised encoding of (session) types into OCaml types is given below:
Definition 10
(revised encoding of types and session types). Let  and
and  be the encoding functions coinductively defined by the following equations:
be the encoding functions coinductively defined by the following equations:

where \(\langle \langle \cdot \rangle \rangle \) is extended homomorphically to all the remaining type constructors erasing kind annotations on arrows and existential and universal quantifiers.
In Definition 10, \(\iota \) is always an identity (co-)variable for we apply the encoding to user types in which these variables are never instantiated. Once again, the relation between the encoding of a session type and that of its dual can be expressed in terms of type equality:
Theorem 5
If  , then
, then  .
.
The concrete representation of  is the same that we have given in Sect. 4.2. As an optimization, the pol field of that representation could be omitted since there it is only necessary to verify an endpoint equality condition which is statically guaranteed by the implementation we are discussing now.
is the same that we have given in Sect. 4.2. As an optimization, the pol field of that representation could be omitted since there it is only necessary to verify an endpoint equality condition which is statically guaranteed by the implementation we are discussing now.
The easiest way of representing an existential type in OCaml is by means of its built-in module system [17]. In our case, we have to make sure that  returns a packaged pair of peer endpoints, each with its own identity. The OCaml representation of this type can be given by the following module signature
returns a packaged pair of peer endpoints, each with its own identity. The OCaml representation of this type can be given by the following module signature

which contains two abstract type declarations i and j, corresponding to the identities of the two endpoints, and a function unpack to retrieve the endpoints once the module with this signature has been opened. Concerning the implementation of Package, there are two technical issues we have to address, both related to the fact that there cannot be two different endpoints with the same identity. First, we have to make sure that each session has its own implementation of the Package module signature. To this aim, we take advantage of OCaml’s support for first-class modules [7, 32], allowing us to write a function ( in the specific case) that returns a module implementation. The second issue is that we cannot store the two endpoints directly in the module, for the types of the endpoints contain type variables (\(\upalpha \) and \(\upbeta \) in the above signature) which are not allowed to occur free in a module. For this reason, we delay the actual creation of the endpoints at the time unpack is applied. This means, however, that the same implementation of Package could in principle be unpacked several times, instantiating different sessions whose endpoints would share the same identities. To make sure that unpack is applied at most once for each implementation of Package we resort once again to an atomic boolean flag.
in the specific case) that returns a module implementation. The second issue is that we cannot store the two endpoints directly in the module, for the types of the endpoints contain type variables (\(\upalpha \) and \(\upbeta \) in the above signature) which are not allowed to occur free in a module. For this reason, we delay the actual creation of the endpoints at the time unpack is applied. This means, however, that the same implementation of Package could in principle be unpacked several times, instantiating different sessions whose endpoints would share the same identities. To make sure that unpack is applied at most once for each implementation of Package we resort once again to an atomic boolean flag.
The signatures of the functions implementing the communication primitives are essentially the same that we have already seen in Sect. 4.2, except for the presence of identity variables  and
and  and the type of
and the type of  , which now returns a packaged pair of endpoints:
, which now returns a packaged pair of endpoints:

Note in particular the type of  , where we refer to both an endpoint and its peer by flipping the type parameters corresponding to session types (
, where we refer to both an endpoint and its peer by flipping the type parameters corresponding to session types ( and
and  ) and those corresponding to identity variables (
) and those corresponding to identity variables ( and
and  ) as well.
) as well.
The implementation of  is shown below, in which Previous.create refers to the version of
is shown below, in which Previous.create refers to the version of  detailed in Sect. 4.2:
detailed in Sect. 4.2:

The implementation of the I/O primitives is the same as in Sect. 4.2 and need not be repeated here. The resumption combinator shrinks to a simple cast

since the equality condition on endpoints that is necessary for its soundness is now statically guaranteed by the type system. The cast is necessary because  coerces its first argument to a function with a different type. With this implementation of
coerces its first argument to a function with a different type. With this implementation of  , a session is typically created thus
, a session is typically created thus

where client and server are suitable functions that use the two endpoints of the session without making any assumption on their identities. Otherwise, the abstract types A.i and A.j would escape their scope, resulting in a type error.
4.4 Extended Example: Trees over Sessions
In this section we revisit and expand an example taken from [25] to show how context-free session types help improving the precision of (inferred) protocols and the robustness of code. We start from the declaration

defining an algebraic representation of binary trees, and we consider the following function, which sends a binary tree over a session endpoint. Note that, for the sake of readability, in this section we assume that OCaml polymorphic variant tags are curried as in the formal model and write for example  instead of its \(\eta \)-expansion
instead of its \(\eta \)-expansion  .
.

The auxiliary function send_tree_aux serializes a (sub)tree t on the endpoint u, whereas send_tree invokes send_tree_aux once and finally sends a sentinel label  that signals the end of the stream of messages. FuSe infers for send_tree the type \(\upalpha ~\mathtt {tree}\rightarrow T_{\mathtt {reg}}\rightarrow A\) where \(T_{\mathtt {reg}}\) is the session type
that signals the end of the stream of messages. FuSe infers for send_tree the type \(\upalpha ~\mathtt {tree}\rightarrow T_{\mathtt {reg}}\rightarrow A\) where \(T_{\mathtt {reg}}\) is the session type

and \(A\) is a session type variable (the code in send_tree does not specify in any way how u will be used when send_tree returns). Without the sentinel  , the protocol \(T_{\mathtt {reg}}\) inferred by OCaml would never terminate (like \(S_{\mathtt {reg}}\) in (1.1)) making it hardly useful. Even with the sentinel, though, \(T_{\mathtt {reg}}\) is very imprecise. For example, it allows the labels
, the protocol \(T_{\mathtt {reg}}\) inferred by OCaml would never terminate (like \(S_{\mathtt {reg}}\) in (1.1)) making it hardly useful. Even with the sentinel, though, \(T_{\mathtt {reg}}\) is very imprecise. For example, it allows the labels  ,
,  , and
, and  to be selected in this order, even though send_tree never generates such a sequence.Footnote 1
to be selected in this order, even though send_tree never generates such a sequence.Footnote 1
To illustrate the sort of issues that this lack of precision may cause, it helps to look at a consumer process that receives a tree sent with send_tree:

This function consists of a main body (lines 2–9) responsible for building up a (sub)tree received from u, the bootstrap of the reception phase (line 10), and a final reception that awaits for the sentinel (lines 11–13). For receive_tree, OCaml infers the type \(\overline{T_{\mathtt {reg}}} \rightarrow \upalpha ~\mathtt {tree} \times \overline{A}\). The fact that send_tree and receive_tree use endpoints with dual session types should be enough to reassure us that the two functions communicate safely within the same session. Unfortunately, our confidence is spoiled by two suspicious catch-all cases (lines 9 and 13) without which receive_tree would be ill typed. In particular, omitting line 9 would result in a non-exhaustive pattern matching (lines 3–8) because label  can in principle be received along with
can in principle be received along with  and
and  . A similar issue would arise omitting line 13. Omitting both lines 9 and 13 would also be a problem. In search of a typing derivation for receive_tree, OCaml would try to compute the intersection of the labels handled by the two pattern matching constructs, only to find out that such intersection is empty.
. A similar issue would arise omitting line 13. Omitting both lines 9 and 13 would also be a problem. In search of a typing derivation for receive_tree, OCaml would try to compute the intersection of the labels handled by the two pattern matching constructs, only to find out that such intersection is empty.
We clean up and simplify send_tree and receive_tree using resumptions:

In send_tree we use the simple resumption  since the function only returns the endpoint u. In receive_tree we use
since the function only returns the endpoint u. In receive_tree we use  since the function returns the received tree in addition to the continuation endpoint. Note that we no longer need an explicit sentinel message
since the function returns the received tree in addition to the continuation endpoint. Note that we no longer need an explicit sentinel message  that marks the end of the message stream because the protocol now specifies exactly the number of messages needed to serialize a tree. For the same reason, the catch-all cases in receive_tree are no longer necessary. For these functions, OCaml respectively infers the types \(\upalpha ~\mathtt {tree}\rightarrow {[T_{\mathtt {cf}}]}_{\uprho }\rightarrow {[{\varvec{1}}]}_{\uprho }\) and \({[\overline{T_{\mathtt {cf}}}]}_{\uprho }\rightarrow \upalpha ~\mathtt {tree} \times {[{\varvec{1}}]}_{\uprho }\) where \(T_{\mathtt {cf}}\) is the session type such that
that marks the end of the message stream because the protocol now specifies exactly the number of messages needed to serialize a tree. For the same reason, the catch-all cases in receive_tree are no longer necessary. For these functions, OCaml respectively infers the types \(\upalpha ~\mathtt {tree}\rightarrow {[T_{\mathtt {cf}}]}_{\uprho }\rightarrow {[{\varvec{1}}]}_{\uprho }\) and \({[\overline{T_{\mathtt {cf}}}]}_{\uprho }\rightarrow \upalpha ~\mathtt {tree} \times {[{\varvec{1}}]}_{\uprho }\) where \(T_{\mathtt {cf}}\) is the session type such that

The leftmost occurrence of \(\underline{\,\,\,}\texttt {;} \underline{\,\,\,}\) in \({\texttt {!}}{\upalpha }\texttt {;} T_{\mathtt {cf}}\texttt {;} T_{\mathtt {cf}}\) is due to the communication primitive (either  or
or  ) and the rightmost one to the resumption.
) and the rightmost one to the resumption.
Note that the only difference between the revised send_tree and the homonymous function presented in [25] is the occurrence of  . All the other examples in [25] can be patched similarly by resuming endpoints at the appropriate places.
. All the other examples in [25] can be patched similarly by resuming endpoints at the appropriate places.
5 Related Work
The work most closely related to ours is [25] in which Thiemann and Vasconcelos introduce context-free session types, develop their metatheory, and prove that session type equivalence is decidable. In [25], the only typing rules that can eliminate sequential compositions are those concerning  and
and  . This choice calls for a type system with (1) a structural rule that rearranges sequential compositions in session types and (2) support for polymorphic recursion. As a consequence, context-free session type checking, left as an open problem in [25], appears to rely crucially on type annotations provided by the programmer. In contrast, our approach relies on the use of resumptions inserted in the code. As we have seen in Sect. 4, this approach makes it easy to embed the resulting typing discipline in a host programming language and to take advantage of its type inference engine. Overall, we think that our approach strikes a good balance between expressiveness and flexibility: resumptions are unobtrusive and typically sparse, their location is easy to spot in the code, and they give the programmer complete control over the occurrences of sequential compositions in session types, resolving the ambiguities that arise with context-free session type inference (Sects. 1 and 4.4).
. This choice calls for a type system with (1) a structural rule that rearranges sequential compositions in session types and (2) support for polymorphic recursion. As a consequence, context-free session type checking, left as an open problem in [25], appears to rely crucially on type annotations provided by the programmer. In contrast, our approach relies on the use of resumptions inserted in the code. As we have seen in Sect. 4, this approach makes it easy to embed the resulting typing discipline in a host programming language and to take advantage of its type inference engine. Overall, we think that our approach strikes a good balance between expressiveness and flexibility: resumptions are unobtrusive and typically sparse, their location is easy to spot in the code, and they give the programmer complete control over the occurrences of sequential compositions in session types, resolving the ambiguities that arise with context-free session type inference (Sects. 1 and 4.4).
A potential limitation of our approach compared to [25] is that we require processes operating on peer endpoints of a session to mirror each other as far as the placement of resumptions is concerned. For example, a process using an endpoint with type  may interact with another process that uses an endpoint with type
may interact with another process that uses an endpoint with type  , but not with a process using an endpoint with type
, but not with a process using an endpoint with type  even though
even though  . Both processes must resume the endpoints they use after the exchange of the first message. Understanding the practical impact of this limitation requires an extensive analysis of code that deals with context-free protocols. We have not pursued such investigation, but we can make two observations nonetheless. First, resumptions are often used in combination with recursion and interacting recursive processes already tend to mirror each other by their own recursive nature. We can see this by comparing send_tree and receive_tree (Sect. 4.4) and also by looking at the examples in [25]. Second, it is easy to provide explicit coercions corresponding to laws of \(\sim \). Such coercions, whose soundness is already accounted for by Theorem 1, can be used to rearrange sequential compositions in session types. For example, a coercion \((A\texttt {;} {\varvec{1}})\texttt {;} B\rightarrow A\texttt {;} B\) composed with a function
. Both processes must resume the endpoints they use after the exchange of the first message. Understanding the practical impact of this limitation requires an extensive analysis of code that deals with context-free protocols. We have not pursued such investigation, but we can make two observations nonetheless. First, resumptions are often used in combination with recursion and interacting recursive processes already tend to mirror each other by their own recursive nature. We can see this by comparing send_tree and receive_tree (Sect. 4.4) and also by looking at the examples in [25]. Second, it is easy to provide explicit coercions corresponding to laws of \(\sim \). Such coercions, whose soundness is already accounted for by Theorem 1, can be used to rearrange sequential compositions in session types. For example, a coercion \((A\texttt {;} {\varvec{1}})\texttt {;} B\rightarrow A\texttt {;} B\) composed with a function  would turn it into a function
would turn it into a function  . The use of coercions augments the direct involvement of the programmer, but is a low-cost solution to broaden the cases already addressed by plain resumptions.
. The use of coercions augments the direct involvement of the programmer, but is a low-cost solution to broaden the cases already addressed by plain resumptions.
FuSe [21] is an OCaml implementation of binary sessions that combines static protocol enforcement with runtime checks for endpoint linearity [11, 27] and resumption safety (Sect. 4.2). Support for sequential composition of session types based on resumptions was originally introduced in FuSe to describe iterative protocols, showing that a class of unbounded protocols could be described without resorting to (equi-)recursive types. The work of Thiemann and Vasconcelos [25] prompted us to formalize resumptions and to study their implications to the precision of protocol descriptions. This led to the discovery of a bug in early versions of FuSe where peer endpoints were given the same identity (cf. the discussion at the end of Example 3) and then to the development of a fully static typing discipline to enforce resumption safety (Sects. 3 and 4.3).
The use of type variables abstracting over the identity of endpoints has been inspired by works on regions and linear types [2, 30], by \(\mathrm {L}^3\) [1], a language with locations supporting strong updates, and Alms [26, 28], an experimental general-purpose programming language with affine types. In these works, abstract identities are used to associate an object with the region it belongs to [2, 30], or to link the (non-linear) reference to a mutable object with the (linear or affine) capability for accessing it. Interestingly, in these works separating the reference from the capability (hence the use of abstract identities) is not really a necessity, but rather a technique that results in increased flexibility: the reference can be aliased without restrictions to create cyclic graphs [1] or to support “dirty” operations on shared data structures [28]. In our case, endpoint identities are crucial for checking the safety of resumptions. As one of the anonymous reviewers pointed out, the technique of using type variables abstracting over regions can be traced back to the implementation of stateful computations in Haskell [16], which was further elaborated and proven safe in [18].
Notes
- 1.
The claim made in [25] that send_tree_aux is ill typed is incorrect. There exist typing derivations for send_tree_aux proving that it has type \(\upalpha ~\mathtt {tree}\rightarrow T\rightarrow T\) for every \(T\) that satisfies the equation
 .
.
References
Ahmed, A., Fluet, M., Morrisett, G.: L\({}^{{3}}\): a linear language with locations. Fundam. Informaticae 77(4), 397–449 (2007)
Charguéraud, A., Pottier, F.: Functional translation of a calculus of capabilities. In: Proceedings of ICFP 2008, pp. 213–224. ACM (2008)
Courcelle, B.: Fundamental properties of infinite trees. Theor. Comput. Sci. 25, 95–169 (1983)
Dardha, O., Giachino, E., Sangiorgi, D.: Session types revisited. In: Proceedings of PPDP 2012, pp. 139–150. ACM (2012)
Demangeon, R., Honda, K.: Full abstraction in a subtyped pi-calculus with linear types. In: Katoen, J.-P., König, B. (eds.) CONCUR 2011. LNCS, vol. 6901, pp. 280–296. Springer, Heidelberg (2011). doi:10.1007/978-3-642-23217-6_19
Florijn, G.: Object protocols as functional parsers. In: Tokoro, M., Pareschi, R. (eds.) ECOOP 1995. LNCS, vol. 952, pp. 351–373. Springer, Heidelberg (1995). doi:10.1007/3-540-49538-X_17
Frisch, A., Garrigue, J.: First-class modules and composable signatures in Objective Caml 3.12. In: ACM SIGPLAN Workshop on ML (2010)
Gay, S.J., Vasconcelos, V.T.: Linear type theory for asynchronous session types. J. Funct. Program. 20(1), 19–50 (2010)
Honda, K.: Types for dyadic interaction. In: Best, E. (ed.) CONCUR 1993. LNCS, vol. 715, pp. 509–523. Springer, Heidelberg (1993). doi:10.1007/3-540-57208-2_35
Honda, K., Vasconcelos, V.T., Kubo, M.: Language primitives and type discipline for structured communication-based programming. In: Hankin, C. (ed.) ESOP 1998. LNCS, vol. 1381, pp. 122–138. Springer, Heidelberg (1998). doi:10.1007/BFb0053567
Hu, R., Yoshida, N.: Hybrid session verification through endpoint API generation. In: Stevens, P., Wąsowski, A. (eds.) FASE 2016. LNCS, vol. 9633, pp. 401–418. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49665-7_24
Hüttel, H., Lanese, I., Vasconcelos, V.T., Caires, L., Carbone, M., Deniélou, P.-M., Mostrous, D., Padovani, L., Ravara, A., Tuosto, E., Vieira, H.T., Zavattaro, G.: Foundations of session types and behavioural contracts. ACM Comput. Surv. 49(1), 3 (2016)
Kfoury, A.J., Tiuryn, J., Urzyczyn, P.: Type reconstruction in the presence of polymorphic recursion. ACM Trans. Program. Lang. Syst. 15(2), 290–311 (1993)
Kobayashi, N.: Type systems for concurrent programs. In: Aichernig, B.K., Maibaum, T. (eds.) Formal Methods at the Crossroads. From Panacea to Foundational Support. LNCS, vol. 2757, pp. 439–453. Springer, Heidelberg (2003). doi:10.1007/978-3-540-40007-3_26. http://www.kb.ecei.tohoku.ac.jp/koba/papers/tutorial-type-extended.pdf
Kobayashi, N., Pierce, B.C., Turner, D.N.: Linearity and the pi-calculus. ACM Trans. Program. Lang. Syst. 21(5), 914–947 (1999)
Launchbury, J., Jones, S.L.P.: State in Haskell. Lisp Symbolic Comput. 8(4), 293–341 (1995)
Mitchell, J.C., Plotkin, G.D.: Abstract types have existential type. ACM Trans. Program. Lang. Syst. 10(3), 470–502 (1988)
Moggi, E., Sabry, A.: Monadic encapsulation of effects: a revised approach (extended version). J. Funct. Program. 11(6), 591–627 (2001)
Nierstrasz, O.: Regular types for active objects. In: Proceedings of OOPSLA 1993, pp. 1–15. ACM (1993)
Padovani, L.: Context-free session type inference. Technical report, Università di Torino (2016). https://hal.archives-ouvertes.fr/hal-01385258/document. Accessed 04 Jan 2017
Padovani, L.: A simple library implementation of binary sessions. J. Funct. Program. 27 (2017). https://doi.org/10.1017/S0956796816000289
Ravara, A., Vasconcelos, V.T.: Typing non-uniform concurrent objects. In: Palamidessi, C. (ed.) CONCUR 2000. LNCS, vol. 1877, pp. 474–489. Springer, Heidelberg (2000). doi:10.1007/3-540-44618-4_34
Reppy, J.H.: Concurrent Programming in ML. Cambridge University Press, Cambridge (1999)
Südholt, M.: A model of components with non-regular protocols. In: Gschwind, T., Aßmann, U., Nierstrasz, O. (eds.) SC 2005. LNCS, vol. 3628, pp. 99–113. Springer, Heidelberg (2005). doi:10.1007/11550679_8
Thiemann, P., Vasconcelos, V.T.: Context-free session types. In: Proceedings of ICFP 2016, pp. 462–475. ACM (2016)
Tov, J.A.: Practical programming with substructural types. Ph.D. thesis, Northeastern University (2012)
Tov, J.A., Pucella, R.: Stateful contracts for affine types. In: Gordon, A.D. (ed.) ESOP 2010. LNCS, vol. 6012, pp. 550–569. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11957-6_29
Tov, J.A., Pucella, R.: Practical affine types. In: Proceedings of POPL 2011, pp. 447–458. ACM (2011)
Wadler, P.: Propositions as sessions. J. Funct. Program. 24(2–3), 384–418 (2014)
Walker, D., Watkins, K.: On regions and linear types. In: Proceedings of ICFP 2001, pp. 181–192. ACM (2001)
Wright, A.K., Felleisen, M.: A syntactic approach to type soundness. Inf. Comput. 115(1), 38–94 (1994)
Yallop, J., Kiselyov, O.: First-class modules: hidden power and tantalizing promises. In: ACM SIGPLAN Workshop on ML (2010)
Acknowledgments
The author is grateful to the anonymous ESOP reviewers for their detailed and valuable feedback and to Hernán Melgratti for reading and commenting on an early draft of the paper.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Padovani, L. (2017). Context-Free Session Type Inference. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_30
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_30
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)


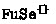 featuring threads, session-based communication primitives and a distinctive low-level construct for resuming session endpoints (Sect.
featuring threads, session-based communication primitives and a distinctive low-level construct for resuming session endpoints (Sect.  ) will be explained using this construct.
) will be explained using this construct. with an original sub-structural type system that features context-free session types and abstract endpoint identities (Sect.
with an original sub-structural type system that features context-free session types and abstract endpoint identities (Sect.  primitives as
primitives as  type discipline into
type discipline into  or
or 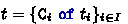 and
and  ), then
), then 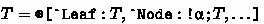 .
.