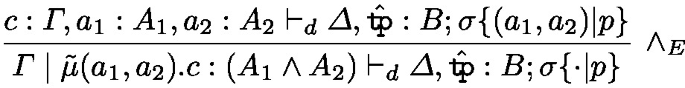A Classical Sequent Calculus with Dependent Types

Abstract

Dependent types are a key feature of type systems, typically used in the context of both richly-typed programming languages and proof assistants. Control operators, which are connected with classical logic along the proof-as-program correspondence, are known to misbehave in the presence of dependent types, unless dependencies are restricted to values. We place ourselves in the context of the sequent calculus which has the ability to smoothly provide control under the form of the $\mu$ operator dual to the common $\mathtt {let}$ operator, as well as to smoothly support abstract machine and continuation-passing style interpretations.

We start from the call-by-value version of the $\lambda \mu \tilde{\mu }$ language and design a minimal language with a value restriction and a type system that includes a list of explicit dependencies and maintains type safety. We then show how to relax the value restriction and introduce delimited continuations to directly prove the consistency by means of a continuation-passing-style translation. Finally, we relate our calculus to a similar system by Lepigre [19], and present a methodology to transfer properties from this system to our own.

1 Introduction

1.1 Control Operators and Dependent Types

Originally created to deepen the connection between programming and logic, dependent types are now a key feature of numerous functional programing languages. On the programming side, they allow for the expression of very precise specifications, while on the logical side, they permit definitions of proof terms for axioms like the full axiom of choice. This is the case in Coq or Agda, two of the most actively developed proof assistants, which both provide dependent types. However, both of them rely on a constructive type theory (Coquand and Huet’s calculus of constructions for Coq [6], and Martin-Löf’s type theory [20] for Agda), and lack classical logic.

In 1990, Griffin discovered [12] that the control operator call/cc (short for call with current continuation) of the Scheme programming language could be typed by Peirce’s $((A\!\rightarrow \! B)\!\rightarrow \! A)\!\rightarrow \! A)$, thus extending the formulæ-as-types interpretation [17]. As Peirce’s law is known to imply, in an intuitionistic framework, all the other forms of classical reasoning (excluded middle, reductio ad absurdum, double negation elimination, etc.), this discovery opened the way for a direct computational interpretation of classical proofs, using control operators and their ability to backtrack. Several calculi were born from this idea, such as Parigot’s $\lambda \mu$-calculus [22], Barbanera and Berardi’s symmetric $\lambda$-calculus [3], Krivine’s $\lambda _c$-calculus [18] or Curien and Herbelin’s $\bar{\lambda }\mu \tilde{\mu }$-calculus [7].

Nevertheless, dependent types are known to misbehave in the presence of control operators, causing a degeneracy of the domain of discourse [14]. Some restrictions on the dependent types are thus necessary to make them compatible with classical logic. Although dependent types and classical logic have been deeply studied separately, the question to know how to design a system compatible with both features does not have yet a general and definitive answer. Recent works from Herbelin [15] and Lepigre [19] proposed some restrictions on the dependent types to tackle the issue in the case of a proof system in natural deduction, while Blot [5] designed a hybrid realizability model where dependent types are restricted to an intuitionistic fragment. Other works by Ahman et al. [1] or Vákár [23] also studied the interplay of dependent types and different computational effects (e.g. divergence, I/O, local references, exceptions).

1.2 Call-By-Value and Value Restriction

In languages enjoying the Church-Rosser property (like the $\lambda$-calculus or Coq), the order of evaluation is irrelevant, and any reduction path will ultimately lead to the same value. In particular, the call-by-name and call-by-value evaluation strategies will always give the same result. However, this is no longer the case in presence of side-effects. Indeed, consider the simple case of a function applied to a term producing some side-effects (for instance increasing a reference). In call-by-name, the computation of the argument is delayed to the time of its effective use, while in call-by-value the argument is reduced to a value before performing the application. If, for instance, the function never uses its argument, the call-by-name evaluation will not generate any side-effect, and if it uses it twice, the side-effect will occurs twice (and the reference will have its value increased by two). On the contrary, in both cases the call-by-value evaluation generates the side-effect exactly once (and the reference has its value increased by one).

In this paper, we present a language following the call-by-value reduction strategy, which is as much a design choice as a goal in itself. Indeed, when considering a language with control operators (or other kind of side-effects), soundness often turns out to be subtle to preserve in call-by-value. The first issues in call-by-value in the presence of side-effects were related to references [25] and polymorphism [13]. In both cases, a simple and elegant solution (but way too restrictive in practice [11, 19]) to solve the inconsistencies consists in a restriction to values for the problematic cases, restoring then a sound type system. Recently, Lepigre presented a proof system providing dependent types and a control operator [19], whose consistency is preserved by means of a semantical value restriction defined for terms that behave as values up to observational equivalence. In the present work, we will rather use a syntactic restriction to a fragment of proofs that allows slightly more than values. This restriction is inspired by the negative-elimination-free fragment of Herbelin’s dPA$\omega$ system [15].

1.3 A Sequent Calculus Presentation

The main achievement of this paper is to give a sequent calculus presentation of a call-by-value language with a control operator and dependent types, and to justify its soundness through a continuation-passing style translation. Our calculus is an extension of the $\lambda \mu \tilde{\mu }$-calculus [7] to dependent types. Amongst other motivations, such a calculus is close to an abstract machine, which makes it particularly suitable to define CPS translations or to be an intermediate language for compilation [8]. In particular, the system we develop might be a first step to allow the adaption of the well-understood continuation-passing style translations for ML in order to design a typed compilation of a system with dependent types such as Coq.

However, in addition to the simultaneous presence of control and dependent types, the sequent calculus presentation itself is responsible for another difficulty. As we will see in Sect. 2.5, the usual call-by-value strategy of the $\lambda \mu \tilde{\mu }$-calculus causes subject reduction to fail. The problem can be understood as a desynchronization of the type system with the reduction. It can be solved by the addition of an explicit list of dependencies in the type derivations.

1.4 Delimited Continuations and CPS Translation

Yet, we will show that the compensation within the typing derivations does not completely fix the problem, and in particular that we are unable to derive a continuation-passing style translation. We present a way to solve this issue by introducing delimited continuations, which are used to force the purity needed for dependent types in an otherwise impure language. It also justifies the relaxation of the value restriction and leads to the definition of the negative-elimination-free fragment (Sect. 3). Finally, it permits the design in Sect. 4 of a continuation-passing style translation that preserves dependent types and allows for proving the soundness of our system.

1.5 Contributions of the Paper

Our main contributions in this paper are:

• we soundly combine dependent types and control operators by mean of a syntactic restriction to the negative-elimination-free fragment;

• we give a sequent calculus presentation and solve the type-soundness issues it raises in two different ways;

• our second solution uses delimited continuations to ensure consistency with dependent types and provides us with a CPS translation (carrying dependent types) to a calculus without control operator;

• we relate our system to Lepigre’s calculus, which offers an additional way of proving the consistency of our system.

For economy of space, most of our statements only comes with sketches of their proofs, full proofs are given in the appendices of a longer version available at:

https://hal.inria.fr/hal-01375977.

2 A Minimal Classical Language

2.1 A Brief Recap on the $\lambda \mu \tilde{\mu }$-Calculus

We recall here the spirit of the $\lambda \mu \tilde{\mu }$-calculus, for further details and references please refer to the original article [7]. The syntax and reduction rules (parameterized over a sets of proofs $\mathcal{V}$ and a set of contexts $\mathcal{E}$) are given by:

where ${{\tilde{\mu }}}a.c$ can be read as a context $\mathbf {let}~{a}=[~]\;\mathbf {in}~c$. A command can be understood as a state of an abstract machine, representing the evaluation of a proof (the program) against a context (the stack). The $\mu$ operator comes from Parigot’s $\lambda \mu$-calculus [22], $\mu \alpha$ binds an evaluation context to a context variable $\alpha$ in the same way ${{\tilde{\mu }}}a$ binds a proof to some proof variable a.

The $\lambda \mu \tilde{\mu }$-calculus can be seen as a proof-as-program correspondence between sequent calculus and abstract machines. Right introduction rules correspond to typing rules for proofs, while left introduction are seen as typing rules for evaluation contexts. For example, the left introduction rule of implication can be seen as a typing rule for pushing an element q on a stack e leading to the new stack $q\cdot e$:

Note that this presentation of sequent calculus involves three kinds of judgments one with a focus on the right for programs, one with a focus on the left for contexts and one with no focus for states, as reflected on the Cut typing rule:

As for the reduction rules, we can see that there is a critical pair if ${\mathcal V}$ and ${\mathcal E}$ are not restricted:

The difference between call-by-name and call-by-value can be characterized by how this critical pair is solved, by defining $\mathcal{V}$ and $\mathcal{E}$ such that the two rules do not overlap. The call-by-name evaluation strategy amounts to the case where $\mathcal{V}\triangleq$ Proofs and $\mathcal{E}\triangleq$ Co-values, while call-by-value corresponds to $\mathcal{V}\triangleq$ Values and $\mathcal{E}\triangleq$ Contexts. Both strategies can also been characterized through different CPS translations [7, Sect. 8].

2.2 The Language

As shown by Herbelin [14], it is possible to derive inconsistencies from a minimal classical language with dependent types. Intuitively, the incoherence comes from the fact that if p is a classical proof of the form

$$\texttt {call/cc}_k\,(0,\mathsf {throw}\, k \, (1,\mathsf {refl})):\varSigma x.x=1,$$

the seek of a witness by a term $\mathsf {wit}\,p$ is likely to reduce to 0, while the reduction of $\mathsf {prf}\,p$ would have backtracked before giving 1 as a witness and the corresponding certificate. The easiest and usual approach to prevent this is to impose a restriction to values for proofs appearing inside dependent types and operators. In this section we will focus on this solution in the similar minimal framework, and show how it permits to keep the proof system coherent. We shall see further in Sect. 3 how to relax this constraint.

We give here a stratified presentation of dependent types, by syntactically distinguishing terms—that represent mathematical objects—from proof terms–that represent mathematical proofs¹. We place ourselves in the framework of the $\lambda \mu \tilde{\mu }$-calculus to which we add:

• a category of terms which contain an encoding² of the natural numbers,

• proof terms (t, p) to inhabit the strong existential $\exists x^{\mathbb {N}} A$ together with the corresponding projections $\mathsf {wit}\,$ and $\mathsf {prf}\,$,

• a proof term $\mathsf {refl}$ for the equality of terms and a proof term $\mathsf {subst}$ for the convertibility of types over equal terms.

For simplicity reasons, we will only consider terms of type $\mathbb {N}$ throughout this paper. We address the question of extending the domain of terms in Sect. 6.2.

The syntax of the corresponding system, that we call dL, is given by:

The formulas are defined by:

$$ A,B \quad {::}{=} \quad \top \mid \bot \mid t = u \mid \forall x^{\mathbb {N}}.A \mid \exists x^{\mathbb {N}}.A \mid \varPi _{a:A}{B}. $$

Note that we included a dependent product $\varPi _{a:A}{B}$ at the level of proof terms, but that in the case where $a\notin FV(B)$ this amounts to the usual implication $A\rightarrow B$.

2.3 Reduction Rules

As explained in the introduction of this section, a backtracking proof might give place to different witnesses and proofs according to the context of reduction, leading to incoherences [14]. On the contrary, the call-by-value evaluation strategy forces a proof to reduce first to a value (thus furnishing a witness) and to share this value amongst all the commands. In particular, this maintains the value restriction along reduction, since only values are substituted.

The reduction rules, defined below (where $t\rightarrow t'$ denotes the reduction of terms and $c\,\rightsquigarrow \, c'$ the reduction of commands), follow the call-by-value evaluation principle:

In particular one can see that whenever the command is of the shape $\langle {C[p]} {\Vert } {e} \rangle$ where C[p] is a proof built on top of p which is not a value, it reduces to $\langle {p} {\Vert } {{{\tilde{\mu }}}a. \langle {C[a]} {\Vert } {e} \rangle } \rangle$, opening the construction to evaluate p³.

Additionally, we denote by $A\equiv B$ the transitive-symmetric closure of the relation $A\vartriangleright B$, defined as a congruence over term reduction (i.e. if $t\rightarrow t'$ then $A[t]~\vartriangleright ~ A[t']$) and by the rules:

2.4 Typing Rules

As we previously explained, in this section we will limit ourselves to the simple case where dependent types are restricted to values, to make them compatible with classical logic. But even with this restriction, defining the type system in the most naive way leads to a system in which subject reduction will fail. Having a look at the $\beta$-reduction rule gives us an insight of what happens. Let us consider a proof $\lambda a.p:\varPi _{a:A}{B}$ and a context $q\cdot e:\varPi _{a:A}{B}$ (with q a value). A typing derivation of the corresponding command is of the form:

while the command will reduce as follows:

On the right side, we see that p, whose type is B[a], is now cut with e which type is B[q]. Consequently we are not able to derive a typing judgment for this command any more.

The intuition is that in the full command, a has been linked to q at a previous level of the typing judgment. However, the command is still safe, since the head-reduction imposes that the command $\langle {p} {\Vert } {e} \rangle$ will not be executed until the substitution of a by q⁴ and by then the problem would have been solved. Somehow, this phenomenon can be seen as a desynchronization of the typing process with respect to the computation. The synchronization can be re-established by making explicit a dependencies list in the typing rules, allowing this typing derivation:

Fig. 1.

Typing rules

Formally, we denote by $\mathcal {D}$ the set of proofs we authorize in dependent types, and define it for the moment as the set of values:

$$\mathcal {D}\triangleq V.$$

We define a dependencies list $\sigma$ as a list binding pairs of proof terms⁵:

$$\sigma \,{::}{=}\, \varepsilon \mid \sigma \{p|q\},$$

and we define $A_\sigma$ as the set of types that can be obtained from A by replacing none or all occurrences of p by q for each binding $\{p|q\}$ in $\sigma$ such that $q\in \mathcal {D}$:

$$ A_\varepsilon \triangleq \{A\}\qquad \quad A_{\sigma \{p|q\}} \triangleq {\left\{ \begin{array}{ll} A_\sigma \cup (A[q/p])_{\sigma } &{} \text {if } q\in \mathcal {D}\\ A_\sigma &{} \text {otherwise}. \end{array}\right. } $$

Furthermore, we introduce the notation $\varGamma \mid e:A\vdash \varDelta ;\sigma \{\cdot |\dag \}$ to avoid the definition of a second type of sequent $\varGamma \mid e:A\vdash \varDelta ;\sigma$ to type contexts when dropping the (open) binding $\{\cdot |p\}$. Alternatively, one can think of $\dag$ as any proof term not in $\mathcal {D}$, which is the same with respect to the dependencies list. The resulting set of typing rules is given in Fig. 1, where we assume that every variable bound in the typing context is bound only once (proofs and contexts are considered up to $\alpha$-conversion).

Note that we work with two-sided sequents here to stay as close as possible to the original presentation of the $\lambda \mu \tilde{\mu }$-calculus [7]. In particular it means that a type in $\varDelta$ might depend on a variable previously introduced in $\varGamma$ and reciprocally, so that the split into two contexts makes us lose track of the order of introduction of the hypothesis. In the sequel, to be able to properly define a typed CPS translation, we consider that we can unify both contexts into a single one that is coherent with respect to the order in which the hypothesis have been introduced. We denote by $\varGamma \cup \varDelta$ this context, where the assumptions of $\varGamma$ remain unchanged, while the former assumptions $(\alpha :A)$ in $\varDelta$ are denoted by $(\alpha :A^{\bot \!\!\!\bot })$.

2.5 Subject Reduction

We start by proving a few technical lemmas we will use to prove the subject reduction property. First, we prove that typing derivations allow weakening on the dependencies list. For this purpose, we introduce the notation $\sigma \Rrightarrow \sigma '$ to denote that whenever a judgment is derivable with $\sigma$ as dependencies list, then it is derivable using $\sigma '$:

$$\sigma \Rrightarrow \sigma ' \,\,\triangleq \,\, \forall c\, \forall \varGamma \, \forall \varDelta ( c:(\varGamma \vdash \varDelta ;\sigma ) \Rightarrow c:(\varGamma \vdash \varDelta ;\sigma ')).$$

This clearly implies that the same property holds when typing contexts, i.e. if $\sigma \Rrightarrow \sigma '$ then $\sigma$ can be replaced by $\sigma '$ in any derivation for typing a context.

Lemma 1

(Dependencies weakening). For any dependencies list $\sigma$ we have:

$$1.~\forall V (\sigma \{V|V\}\Rrightarrow \sigma ) \qquad \qquad \qquad 2.~\forall \sigma '(\sigma \Rrightarrow \sigma \sigma ').$$

Proof

The first statement is obvious. The proof of the second is straightforward from the fact that for any p and q, by definition $A_\sigma \subset A_{\sigma \{a|q\}}$.    $\square$

As a corollary, we get that $\dag$ can indeed be replaced by any proof term when typing a context.

Corollary 2

If $\sigma \Rrightarrow \sigma '$, then for any $p,e,\varGamma ,\varDelta$:

$$\varGamma \mid e:A\vdash \varDelta ;\sigma \{\cdot |\dag \} \,\,\Rightarrow \,\, \varGamma \mid e:A\vdash \varDelta ;\sigma '\{\cdot |p\}.$$

We can now prove the safety of reduction, using the previous lemmas for rules performing a substitution and the dependencies lists to resolve local inconsistencies for dependent types.

Theorem 3

(Subject reduction). If $c,c'$ are two commands of dL such that $c : (\varGamma \vdash \varDelta )$ and $c\,\rightsquigarrow \,c'$, then $c' : (\varGamma \vdash \varDelta )$.

Proof

The proof is done by induction on the typing rules, assuming that for each typing proof, the conv rules are always pushed down and right as much as possible. To save some space, we sometimes omit the dependencies list when empty, noting $c:\varGamma \vdash \varDelta$ instead of $c:\varGamma \vdash \varDelta ;\varepsilon$, and denote the conv-rules by

where the hypothesis $A\equiv B$ is implicit. We only give the key case of $\beta$-reduction.

Case :

A typing proof for the command on the left is of the form:

If $q\notin \mathcal {D}$, we define $B'_q\triangleq B'$ which is the only type in $B'_{\{a|q\}}$. Otherwise, we define $B'_q\triangleq B'[q/a]$ which is a type in $B'_{\{a|q\}}$. In both cases, we can build the following derivation:

using Corollary 2 to weaken the dependencies in $\varPi _e$.    $\square$

2.6 Soundness

We sketch here a proof of the soundness of dL with a value restriction. A more interesting proof through a continuation-passing translation is presented in Sect. 4. We first show that typed commands of dL normalize by translation to the simply-typed $\lambda \mu \tilde{\mu }$-calculus with pairs (i.e. extended with proofs of the form $(p_1,p_2)$ and contexts of the form ${\tilde{\mu }}(a_1,a_2).c$). The translation essentially consists of erasing the dependencies in types, turning the dependent products into arrows and the dependent sum into a pair. The erasure procedure is defined by:

and the translation for proofs, terms, contexts and commands is defined by:

where $\pi _i(p)\triangleq \mu \alpha .\langle {p} {\Vert } {{\tilde{\mu }}(a_1,a_2).\langle {a_1} {\Vert } {\alpha } \rangle } \rangle$. We define $\bar{n}$ as any encoding of the natural numbers with its type $\mathbb {N}^*$, the encoding being irrelevant here.

We can extend the erasure procedure to contexts, and show that it is adequate with respect to the translation of proofs.

Proposition 4

If $c:\varGamma \vdash \varDelta ;\sigma$, then $c^*:\varGamma ^*\vdash \varDelta ^*$. The same holds for proofs and contexts.

We can then deduce the normalization of dL from the normalization of the $\lambda \mu \tilde{\mu }$-calculus, by showing that the translation preserves the normalization in the sense that if c does not normalize, neither does $c^*$.

Proposition 5

If $c:(\varGamma \vdash \varDelta ;\varepsilon )$, then c normalizes.

Using the normalization, we can finally prove the soundness of the system.

Theorem 6

(Soundness). For any $p \in {\text {dL}}$, we have $\nvdash p : \bot$.

Proof

(Sketch) Proof by contradiction, assuming that there is a proof p such that $\vdash p:\bot$, we can form the well-typed command $\langle {p} {\Vert } {\star } \rangle :(\vdash \star :\bot )$ where $\star$ is any fresh $\alpha$-variable, and use the normalization to reduce to a command $\langle {V} {\Vert } {\star } \rangle$. By subject reduction, V would be a value of type $\bot$, which is absurd.    $\square$

2.7 Toward a Continuation-Passing Style Translation

The difficulty we encountered while defining our system mostly came from the simultaneous presence of a control operator and dependent types. Removing one of these two ingredients leaves us with a sound system in both cases: without the part necessary for dependent types, our calculus amounts to the usual $\lambda \mu \tilde{\mu }$-calculus. Without control operator, we would obtain an intuitionistic dependent type theory that would be easy to prove sound.

To demonstrate the correctness of our system, we might be tempted to define a translation to a subsystem without dependent types or control operator. We will discuss later in Sect. 5 a solution to handle the dependencies. We will focus here on the possibility of removing the classical part from dL, that is to define a translation that gets rid of the control operator. The use of continuation-passing style translations to address this issue is very common, and it was already studied for the simply-typed $\lambda \mu \tilde{\mu }$-calculus [7]. However, as it is defined to this point, dL is not suitable for the design of a CPS translation.

Indeed, in order to fix the problem of desynchronization of typing with respect to the execution, we have added an explicit dependencies list to the type system of dL. Interestingly, if this solved the problem inside the type system, the very same phenomenon happens when trying to define a cps-translation carrying the type dependencies.

Let us consider the same case of a command $\langle {q} {\Vert } {{{\tilde{\mu }}}a.\langle {p} {\Vert } {e} \rangle } \rangle$ with p : B[a] and e : B[q]. Its translation is very likely to look like:

$$[\![q ]\!]\,[\![{{\tilde{\mu }}}a.\langle {p} {\Vert } {e} \rangle ]\!]\, = [\![q ]\!]\, (\lambda a.([\![p ]\!])[\![e ]\!]),$$

where $[\![p ]\!]$ has type $(B[a]\rightarrow \bot )\rightarrow \bot$ and $[\![e ]\!]$ type $B[q]\rightarrow \bot$, hence the sub-term $[\![p ]\!]\,[\![e ]\!]$ will be ill-typed. Therefore the fix at the level of typing rules is not satisfactory, and we need to tackle the problem already within the reduction rules.

We follow the idea that the correctness is guaranteed by the head-reduction strategy, preventing $\langle {p} {\Vert } {e} \rangle$ from reducing before the substitution of a was made. We would like to ensure the same thing happens in the target language (that will also be equipped with a head-reduction strategy), namely that $[\![p ]\!]$ cannot be applied to $[\![e ]\!]$ before $[\![q ]\!]$ has furnished a value to substitute for a. This would correspond informally to the term⁶:

$$([\![q ]\!] (\lambda a.[\![p ]\!])) [\![e ]\!].$$

The first observation is that if q was a classical proof throwing the current continuation away instead of a value (for instance $\mu \alpha .c$ where $\alpha \notin FV(c)$), this would lead to an incorrect term $[\![c ]\!]\,[\![e ]\!]$. We thus need to restrict at least to proof terms that could not throw the current continuation.

The second observation is that such a term suggests the use of delimited continuations⁷ to temporarily encapsulate the evaluation of q when reducing such a command:

$$\langle {\lambda a.p} {\Vert } {q\cdot e} \rangle \rightsquigarrow \langle {\mu {\hat{{{\texttt {t}\!\texttt {p}}}}}.\langle {q} {\Vert } {{{\tilde{\mu }}}a.\langle {p} {\Vert } {{\hat{{{\texttt {t}\!\texttt {p}}}}}} \rangle } \rangle } {\Vert } {e} \rangle .$$

This command is safe under the guarantee that q will not throw away the continuation ${{\tilde{\mu }}}a.\langle {p} {\Vert } {{\hat{{{\texttt {t}\!\texttt {p}}}}}} \rangle$. This will also allow us to restrict the use of the dependencies list to the derivation of judgments involving a delimited continuation, and to fully absorb the potential inconsistency in the type of ${\hat{{{\texttt {t}\!\texttt {p}}}}}$.

In Sect. 3, we will extend the language according to this intuition, and see how to design a continuation-passing style translation in Sect. 4.

3 Extension of the system

3.1 Limits of the Value Restriction

In the previous section, we strictly restricted the use of dependent types to proof terms that are values. In particular, even though a proof-term might be computationally equivalent to some value (say $\mu \alpha .\langle {V} {\Vert } {\alpha } \rangle$ and V for instance), we cannot use it to eliminate a dependent product, which is unsatisfying. We shall then relax this restriction to allow more proof terms within dependent types.

We can follow several intuitions. First, we saw in the previous section that we could actually allow any proof terms as long as its CPS translation uses its continuation and uses it only once. We do not have such a translation yet, but syntactically, these are the proof terms that can be expressed (up to $\alpha$-conversion) in the $\lambda \mu \tilde{\mu }$-calculus with only one continuation variable $\star$ (see Fig. 2), and which do not contain application⁸. Interestingly, this corresponds exactly to the so-called negative-elimination-free (nef) proofs of Herbelin [15]. To interpret the axiom of dependent choice, he designed a classical proof system with dependent types in natural deduction, in which the dependent types allow the use of nef proofs.

Second, Lepigre defined in a recent work [19] a classical proof system with dependent types, where the dependencies are restricted to values. However, the type system allows derivations of judgments up to an observational equivalence, and thus any proof computationally equivalent to a value can be used. In particular, any proof in the nef fragment is observationally equivalent to a value, hence is compatible with the dependencies of Lepigre’s calculus.

From now on, we consider $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ the system dL of Sect. 2 extended with delimited continuations, and define the fragment of negative-elimination-free proof terms (nef). The syntax of both categories is given by Fig. 2, the proofs in the nef fragment are considered up to $\alpha$-conversion for the context variables⁹. The reduction rules, given below, are slightly different from the rules in Sect. 2:

where:

$$ V_t \, {::}{=} \, x \mid n \qquad \qquad V_p \,{::}{=}\, a \mid \lambda a . p \mid \lambda x . p \mid (V_t,V_p)\mid \mathsf {refl}. $$

In the case $\langle {\lambda a.p} {\Vert } {q\cdot e} \rangle$ with $q\in \textsc {nef}$ (resp. $\langle {\mathsf {prf}\,p} {\Vert } {e} \rangle$), a delimited continuation is now produced during the reduction of the proof term q (resp. p) that is involved in dependencies. As terms can now contain proofs which are not values, we enforce the call-by-value reduction by asking proof values to only contain term values. We elude the problem of reducing terms, by defining meta-rules for them¹⁰. We add standard rules for delimited continuations [2, 16], expressing the fact that when a proof $\mu {\hat{{{\texttt {t}\!\texttt {p}}}}}.c$ is in active position, the current context is temporarily frozen until c is fully reduced.

Fig. 2.

$\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$: extension of dL with delimited continuations

3.2 Delimiting the Scope of Dependencies

For the typing rules, we can extend the set $\mathcal {D}$ to be the nef fragment:

$$\mathcal {D}\triangleq \textsc {nef}$$

and we now distinguish two modes. The regular mode corresponds to a derivation without dependency issues whose typing rules are the same as in Fig. 1 without the dependencies list (we do not recall them to save some space); plus the new rule of introduction of a delimited continuation ${\hat{{{\texttt {t}\!\texttt {p}}}}}_I$. The dependent mode is used to type commands and contexts involving ${\hat{{{\texttt {t}\!\texttt {p}}}}}$, and we use the sign $\vdash _d$ to denote the sequents. There are three rules: one to type ${\hat{{{\texttt {t}\!\texttt {p}}}}}$, which is the only one where we use the dependencies to unify dependencies; one to type context of the form ${\tilde{\mu }}a.c$ (the rule is the same as the former rule for ${\tilde{\mu }}a.c$ in Sect. 2); and a last one to type commands $\langle {p} {\Vert } {e} \rangle$, where we observe that the premise for p is typed in regular mode.

Additionally, we need to extend the congruence to make it compatible with the reduction of nef proof terms (that can now appear in types), thus we add the rules:

Due to the presence of nef proof terms (which contain a delimited form of control) within types and dependencies lists, we need the following technical lemma to prove subject reduction.

Lemma 7

For any context $\varGamma ,\varDelta$, any type A and any $e,\mu \!\star \!.c$:

$$\langle {\mu \!\star \!.c} {\Vert } {e} \rangle :\varGamma \vdash _d \varDelta ,{\hat{{{\texttt {t}\!\texttt {p}}}}}:B;\varepsilon \quad \Rightarrow \quad c[e/\star ]:\varGamma \vdash _d \varDelta ;\varepsilon .$$

Proof

By definition of the nef proof terms, ${\mu \!\star \!.c}$ is of the general form ${\mu \!\star \!.c = \mu \!\star \!.\langle {p_1} {\Vert } {{\tilde{\mu }}a_1.\langle {p_2} {\Vert } {{\tilde{\mu }}a_2. \langle {\ldots } {\Vert } {{\tilde{\mu }}a_n.\langle {p_n} {\Vert } {\star } \rangle } \rangle } \rangle } \rangle }$. In the case $n=2$, proving the lemma essantially amounts to showing that for any variable a and any $\sigma$:

$$\{a|\mu \!\star \!.c\}\sigma \Rrightarrow \{a_1|p_1\}\{a|p_2\}\sigma .$$

   $\square$

We can now prove subject reduction for $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$.

Theorem 8

(Subject reduction). If $c,c'$ are two commands of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ such that $c : (\varGamma \vdash \varDelta )$ and $c\,\rightsquigarrow \,c'$, then $c' : (\varGamma \vdash \varDelta )$.

Proof

Actually, the proof is slightly easier than for Theorem 3, because most of the rules do not involve dependencies. We only present one case here, other key cases are proved in the appendix.

Case with $q\in \textsc {nef}$:

A typing derivation for the command on the left is of the form:

We can thus build the following derivation for the command on the right:

   $\square$

We invite the reader to check that interestingly, we could have already taken $\mathcal {D}\triangleq \textsc {nef}$ in dL and still be able to prove the subject reduction. This shows that the relaxation to the nef fragment is valid even without delimited continuations.

4 A Continuation-Passing Style Translation

We shall now see how to define a continuation-passing style translation from $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ to an intuitionistic type theory, and use this translation to prove the soundness of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$. Continuation-passing style translations are indeed very useful to embed languages with control operators into purely functional ones [7, 12]. From a logical point of view, they generally amount to negative translations that allow to embed classical logic into intuitionistic logic [9]. Yet, we know that removing the control operator (i.e. classical logic) of our language leaves us with a sound intuitionistic type theory. We will now see how to design a CPS translation for our language which will allow us to prove its soundness.

4.1 Target Language

We choose the target language an intuitionistic theory in natural deduction that has exactly the same elements as $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ but the control operator: the language makes the difference between terms (of type $\mathbb {N}$) and proofs, it also includes dependent sums and products for type referring to term as well as a dependent product at the level of proofs. As it is common for CPS translations, the evaluation follows a head-reduction strategy. The syntax of the language and its reduction rules are given by Fig. 3.

Fig. 3.

Target language

The type system, presented in Fig. 3, is defined as expected, with the addition of a second-order quantification that we will use in the sequel to refine the type of translations of terms and nef proofs. As for $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ the type system has a conversion rule, where the relation $A\equiv B$ is the symmetric-transitive closure of $A\triangleright B$, defined once again as the congruence over the reduction $\longrightarrow$ and by the rules:

4.2 Translation of the Terms

We can now define the translation of terms, proofs, contexts and commands. The translation for delimited continuation follows the intuition we presented in Sect. 2.7, and the definition for stacks $t\cdot e$ and $q\cdot e$ (with q nef) inline the reduction producing a command with a delimited continuation. All the other rules are natural, except for the translation of pairs (t, p) in the nef case:

$$[\![(t,p) ]\!]_p \triangleq \lambda k.([\![t ]\!]_t\,(\lambda ur.r\,(\lambda q.k\,(u,q))))[\![p ]\!]_p$$

The natural definition is the one given in the non nef case, but as we observe in the proof of Lemma 11, this definition is incompatible with the expected type for the translation of nef proofs. This somehow strange definition corresponds to the intuition that we reduce $[\![t ]\!]_t$ within a delimited continuation, in order to guarantee that we will not reduce $[\![p ]\!]_p$ before $[\![t ]\!]_t$ has returned a value to substitute for u. Indeed, the type of $[\![p ]\!]_p$ depends on t, while the continuation $(\lambda q.k\,(u,q))$ depends on u, but both become compatible once u is substituted by the value return by $[\![t ]\!]_t$. The complete translation is given in Fig. 4.

Fig. 4.

Continuation-passing style translation

Before defining the translation of types, we first state a lemma expressing the fact that the translations of terms and nef proof terms use the continuation they are given once and only once. In particular, it makes them compatible with delimited continuations and a parametric return type. This will allow us to refine the type of their translation.

Lemma 9

The translation satisfies the following properties:

• 1. For any term t in $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$, there exists a term $t^+$ such that for any k we have $[\![t ]\!]_t\,k =_\beta k\,t^+$.

• 2. For any nef proof term p, there exists a proof $p^+$ such that for any k we have $[\![p ]\!]_p\,k =_\beta k\,p^+$.

Proof

Straightforward mutual induction on the translation, adding similar induction hypothesis for nef contexts and commands. The terms $t^+$ and proofs $p^+$ are given in Fig. 5. We detail the case (t, p) with $p\in \textsc {nef}$ to give an insight of the proof.

   $\square$

Fig. 5.

Linearity of the translation for nef proofs

Moreover, we easily verify by induction on the reduction rules for $\rightsquigarrow$ that the translation preserves the reduction:

Proposition 10

(Preservation of reduction). Let $c,c'$ be two commands of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$. If $c\,\rightsquigarrow \, c'$, then $[\![c ]\!]_c =_\beta [\![c' ]\!]_c$

We could actually prove a finer result to show that any reduction step in $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ is responsible for at least one step of reduction through the translation, and use the preservation of typing (Proposition 12) together with the normalization of the target language to prove the normalization of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ for typed proof terms.

Claim 1

If $c:\varGamma \vdash \varDelta$, then c normalizes.

4.3 Translation of Types

We can now define the translation of types, in order to show further that the translation $[\![p ]\!]_p$ of a proof p of type A is of type $[\![A ]\!]^*$, where $[\![A ]\!]^*$ is the double-negation of a type $[\![A ]\!]^+$ that depends on the structure of A. Thanks to the restriction of dependent types to nef proof terms, we can interpret a dependency in p (resp. t) in $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ by a dependency in $p^+$ (resp. $t^+$) in the target language. Lemma 9 indeed guarantees that the translation of a nef proof p will eventually return $p^+$ to the continuation it is applied to. The translation is defined by:

Observe that types depending on a term of type T are translated to types depending on a term of the same type T, because terms can only be of type $\mathbb {N}$. As we shall discuss in Sect. 6.2, this will no longer be the case when extending the domain of terms. We naturally extend the translation for types to the translation of contexts, where we consider unified contexts of the form $\varGamma \cup \varDelta$:

As explained informally in Sect. 2.7 and stated by Lemma 9, the translation of a nef proof term p of type A uses its continuation linearly. In particular, this allows us to refine its type to make it parametric in the return type of the continuation. From a logical point of view, it amounts to replace the double-negation $(A\rightarrow \bot )\rightarrow \bot$ by Friedman’s translation [10]: $\forall R.(A\rightarrow R)\rightarrow R$. Moreover, we can even make the return type of the continuation dependent on its argument $\varPi _{a:A}{\rightarrow }R(a)$, so that the type of $[\![p ]\!]_p$ will correspond to the elimination rule:

$$\forall R.(\varPi _{a:A}{\rightarrow }R(a))\rightarrow R(p^+).$$

This refinement will make the translation of nef proofs compatible with the translation of delimited continuations.

Lemma 11

The following holds:

• 1. $\varGamma \vdash t:\mathbb {N}\mid \varDelta ~\Rightarrow ~ [\![\varGamma \cup \varDelta ]\!]\vdash [\![t ]\!]_t: \forall X(\forall x^{T^+} X(x) \rightarrow X(t^+))$.

• 2. $\forall p\in \textsc {nef}, (\varGamma \vdash p:A\mid \varDelta ~\Rightarrow ~ [\![\varGamma \cup \varDelta ]\!]\vdash [\![p ]\!]_p:\forall X.(\varPi _{a:[\![A ]\!]^+}{X(a)} \rightarrow X(p^+)))$.

• 3. $\forall c\in \textsc {nef}, (c:\varGamma \vdash \varDelta ,\star :B ~\Rightarrow ~ [\![\varGamma \cup \varDelta ]\!],\star :\varPi _{b:B^+}{X(b)}\vdash [\![c ]\!]_c: X(c^+))$.

Proof

The proof is done by mutual induction on the typing rule of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ for terms and nef proofs. We only give one case here to give an insight of the proof.

Case (t, p): in $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ the typing rule for (t, p) is the following:

Hence we obtain by induction, using the same notation $\varGamma '$ for $[\![\varGamma \cup \varDelta ]\!]$:

$$ \begin{array}{ll} \varGamma ' \vdash [\![t ]\!]_t:\forall X.(\forall x^{T^+}X(x) \rightarrow X(t^+))\\ \varGamma ' \vdash [\![p ]\!]_p:\forall Y.(\varPi _{a:A(t^+)}{Y(a)} \rightarrow Y(p^+))\\ \end{array} $$

and we want to show that for any Z:

$$\varGamma '\vdash [\![(t,p) ]\!]_p:\varPi _{a:\exists x^{T^+}A}{Z(a)} \rightarrow Z(t^+,p^+).$$

By definition, we have:

$$[\![(t,p) ]\!]_p=\lambda k.([\![t ]\!]_t\,(\lambda ur.r\,(\lambda q.k\,(u,q))))[\![p ]\!]_p,$$

so we need to prove that:

$$\varGamma _k\vdash ([\![t ]\!]_t\,(\lambda ur.r\,(\lambda q.k\,(u,q))))[\![p ]\!]_p:Z(t^+,p^+)$$

where $\varGamma _k=\varGamma ',k:\varPi _{a:\exists x^{T^+}A}{Z(a)}$. We let the reader check that such a type is derivable by using $X(x)\triangleq P(x)\rightarrow Z(x,a)$ in the type of $[\![t ]\!]_p$ where $P(t^+)$ is the type of $[\![p ]\!]_p$, and using $Y(a)\triangleq Z(t^+,a)$ in the type of $[\![p ]\!]_p$. The crucial point is to see that the bounded variable r is abstracted with type P(x) in the derivation, which would not have been possible in the definition of $[\![(t,p) ]\!]_p$ with $p\notin \textsc {nef}$.    $\square$

Using the previous Lemma, we can now prove that the CPS translation is well-typed in the general case.

Proposition 12

(Preservation of typing). The translation is well-typed, i.e. the following holds:

• 1. if $\varGamma \vdash p:A\mid \varDelta$ then $[\![\varGamma \cup \varDelta ]\!]\vdash [\![p ]\!]_p:[\![A ]\!]^*$,

• 2. if $\varGamma \mid e:A\vdash \varDelta$ then $[\![\varGamma \cup \varDelta ]\!]\vdash [\![e ]\!]_e:[\![A ]\!]^+\rightarrow \bot$,

• 3. if $c:\varGamma \vdash \varDelta$ then $[\![\varGamma \cup \varDelta ]\!]\vdash [\![c ]\!]_c: \bot$.

Proof

The proof is done by induction on the typing rules of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$. It is clear that for the nef cases, Lemma 11 implies the result by taking $X(a) = \bot$. The rest of the cases are straightforward, except for the delimited continuations that we detail hereafter. We consider a command $\langle {\mu {\hat{{{\texttt {t}\!\texttt {p}}}}}.\langle {q} {\Vert } {{\tilde{\mu }}a.\langle {p} {\Vert } {{\hat{{{\texttt {t}\!\texttt {p}}}}}} \rangle } \rangle } {\Vert } {e} \rangle$ produced by the reduction of the command $\langle {\lambda a.p} {\Vert } {q\cdot e} \rangle$ with $q\in \textsc {nef}$. Both commands are translated by a proof reducing to $([\![q ]\!]_p\,(\lambda a.[\![p ]\!]_p))\,[\![e ]\!]_e$. The corresponding typing derivation in $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ is of the form:

By induction hypothesis for e and p we obtain:

where $\varGamma '=[\![\varGamma \cup \varDelta ]\!]$. Applying Lemma 11 for $q\in \textsc {nef}$ we can derive:

We can thus derive that:

$$\varGamma '\vdash [\![q ]\!]_p\,(\lambda a.[\![p ]\!]_p):[\![B[q^+] ]\!]^*,$$

and finally conclude that:

$$\varGamma '\vdash ([\![q ]\!]_p\,(\lambda a.[\![p ]\!]_p))\,[\![e ]\!]_e:\bot .$$

   $\square$

We can finally deduce the correctness of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ through the translation, since a closed proof term of type $\bot$ would be translated in a closed proof of ${(\bot \rightarrow \bot )\rightarrow \bot }$. The correctness of the target language guarantees that such proof cannot exist.

Theorem 13

(Soundness). For any $p\in \text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$, we have: $\nvdash p : \bot$.

5 Embedding in Lepigre’s Calculus

In a recent paper [19], Lepigre presented a classical system allowing the use of dependent types with a semantic value restriction. In practice, the type system of his calculus does not contain a dependent product $\varPi _{a:A}{B}$ strictly speaking, but it contains a predicate $a\in A$ allowing the decomposition of the dependent product into

$$\forall a((a\in A) \rightarrow B)$$

as it is usual in Krivine’s classical realizability [18]. In his system, the relativization $a\in A$ is restricted to values, so that we can only type $V:V\in A$, but the typing judgments are defined up to observational equivalence, so that if t is observationally equivalent to V, one can derive the judgment $t:V\in A$.

Interestingly, as highlighted through the CPS translation by Lemma 9, any nef proof p : A is observationally equivalent to some value $p^+$, so that we could derive $p:(p\in A)$ from $p^+:(p^+\in A)$. The nef fragment is thus compatible with the semantical value restriction. The converse is obviously false, observational equivalence allowing us to type realizers that would otherwise be untyped¹¹.

We sketch here an embedding of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ into Lepigre’s calculus, and explain how to transfer normalization and correctness properties along this translation. Actually, his language is more expressive than ours, since it contains records and pattern-matching (we will only use pairs, i.e. records with two fields), but it is not stratified: no distinction is made between a language of terms and a language of proofs. We only recall here the syntax for the fragment of Lepigre’s calculus we use, for the reduction rules and the type system the reader should refer to [19]:

Even though records are only defined for values, we can define pairs and projections as syntactic sugar:

We first define the translation for types (extended for typing contexts) where the predicate $\mathsf {Nat}(x)$ is defined as usual in second-order logic:

$$\mathsf {Nat}(x) \triangleq \forall X(X(0)\rightarrow \forall y(X(y) \rightarrow X(S(y))) \rightarrow X(x))$$

and $[\![t ]\!]_t$ is the translation of the term t given in Fig. 6:

Note that the equality is mapped to Leibniz equality, and that the definitions of ${\bot }^*$ and ${\top }^*$ are completely ad hoc, in order to make the conversion rule admissible through the translation.

Fig. 6.

Translation of proof terms to Lepigre’s calculus

The translation for terms, proofs, contexts and commands of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$, given in Fig. 6 is almost straightforward. We only want to draw the reader’s attention on a few points:

• the equality being translated as Leibniz equality, $\mathsf {refl}$ is translated as the identity $\lambda a.a$, which also matches with $\top ^*$,

• the strong existential is encoded as a pair, hence $\mathsf {wit}\,$ (resp. $\mathsf {prf}\,$) is mapped to the projection $\pi _1$ (resp. $\pi _2$).

In [19], the coherence of the system is justified by a realizability model, and the type system does not allow us to type stacks. Thus we cannot formally prove that the translation preserves the typing, unless we extend the type system in which case this would imply the adequacy. We might also directly prove the adequacy of the realizability model (through the translation) with respect to the typing rules of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$. We detail a proof of adequacy using the former method in the appendix.

Proposition 14

(Adequacy). If $\varGamma \vdash p:A\mid \varDelta$ and $\sigma$ is a substitution realizing ${(\varGamma \cup \varDelta )}^*$, then $[\![p ]\!]_p\sigma \in [\![{A}^* ]\!]_\sigma ^{\bot \bot }$.

This immediately implies the soundness of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$, since a closed proof p of type $\bot$ would be translated as a realizer of $\top \rightarrow \bot$, so that $[\![p ]\!]_p\,\lambda x.x$ would be a realizer of $\bot$, which is impossible. Furthermore, the translation clearly preserves normalization (that is that for any c, if c does not normalize then neither does $[\![c ]\!]_c$), and thus the normalization of $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ is a consequence of adequacy.

It is worth noting that without delimited continuations, we would not have been able to define an adequate translation, since we would have encountered the same problem as for the CPS translation (see Sect. 2.7).

6 Further Extensions

As we explained in the preamble of Sect. 2, we defined dL and $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ as minimal languages containing all the potential sources of inconsistency we wanted to mix: a control operator, dependent types, and a sequent calculus presentation. It had the benefit to focus our attention on the difficulties inherent to the issue, but on the other hand, the language we obtain is far from being as expressive as other usual proof systems. We claimed our system to be extensible, thus we shall now discuss this matter.

6.1 Adding Expressiveness

From the point of view of the proof language (that is of the tools we have to build proofs), $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ only enjoys the presence of a dependent sum and a dependent product over terms, as well as a dependent product at the level of proofs (which subsume the non-dependent implication). If this is obviously enough to encode the usual constructors for pairs $(p_1,p_2)$ (of type $A_1\wedge A_2)$, injections $\iota _i(p)$ (of type $A_1 \vee A_2$), etc., it seems reasonable to wonder whether such constructors can be directly defined in the language of proofs. Actually this is a case, and we claim that is possible to define the constructors for proofs (for instance $(p_1,p_2)$) together with their destructors in the contexts (in that case ${\tilde{\mu }}(a_1,a_2).c$), with the appropriate typing rules. In practice, it is enough to:

• extend the definitions of the nef fragment according to the chosen extension,

• extend the call-by-value reduction system, opening if needed the constructors to reduce it to a value,

• in the dependent typing mode, make some pattern-matching within the dependencies list for the destructors. For instance, for the case of the pairs, the corresponding rule would be:

  

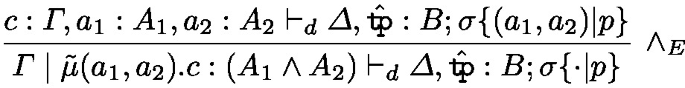
The soundness of such extensions can be justified either by extending the CPS translation, or by defining a translation to Lepigre’s calculus (which already allows records and pattern-matching over general constructors) and proving the adequacy of the translation with respect to the realizability model.

6.2 Extending the Domain of Terms

Throughout the article, we only worked with terms of a unique type $\mathbb {N}$, hence it is natural to wonder whether it is possible to extend the domain of terms in $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$, for instance with terms in the simply-typed $\lambda$-calculus. A good way to understand the situation is to observe what happens through the CPS translation. We see that a term of type $T=\mathbb {N}$ is translated into a proof of type $\lnot \lnot T^+=\lnot \lnot \mathbb {N}$, from which we can extract a term of type $\mathbb {N}$. However, if T was for instance the function type $\mathbb {N}\rightarrow \mathbb {N}$, we would only be able to extract a proof of type $T^+=\mathbb {N}\rightarrow \lnot \lnot \mathbb {N}$. In particular, such a proof would be of the form $\lambda x.p$, where p might backtrack to a former position, for instance before it was extracted, and furnish another proof. This accounts for a well-know phenomenon in classical logic, where witness extraction is limited to formulas in the $\varSigma _0^1$-fragment [21]. It also corresponds to the type we obtain for the image of a dependent product $\varPi _{a:A}{B}$, that is translated to a type $\lnot \lnot \varPi _{a:A^+}{B^*}$ where the dependence is in a proof of type $A^+$. This phenomenon is not surprising and was already observed for other CPS translations for type theories with dependent types [4].

In other words, there is no hope to define a correct translation of $(t_f,p):\exists f^{\mathbb {N}\rightarrow \mathbb {N}} A$ that would allow the extraction of a strong pair $([\![t_f ]\!],[\![p ]\!]):\exists f^{\mathbb {N}\rightarrow \mathbb {N}} A^*$. More precisely, the proof $[\![t_f ]\!]$ is no longer a witness in the usual sense, but a realizer of $f\in \mathbb {N}\rightarrow \mathbb {N}$ in the sense of Krivine classical realizability.

This does not mean that we cannot extend the domain of terms in $\text {dL}_{{\hat{{{\texttt {t}\!\texttt {p}}}}}}$ (in particular, it should affect neither the subject reduction nor the soundness), but it rather means that the stratification between terms and proofs is to be lost through a CPS translation. However, it should still be possible to express the fact that the image of a function through the CPS is a realizer corresponding to this function, by cleverly adapting the predicate $f\in \mathbb {N}\rightarrow \mathbb {N}$ to make it stick to the intuition of a realizer.

6.3 A Fully Sequent-Style Dependent Calculus

While the aim of this paper was to design a sequent-style calculus embedding dependent types, we only present the $\varPi$-type in sequent-style. Indeed, we wanted to ensure ourselves in a first time that we were able of having the key ingredients of dependent types in our language, even presented in a natural deduction spirit. Rather than having left-rules, we presented the existential type and the equality type with the following elimination rules:

However, it is now easy to have both rules in a sequent calculus fashion, for instance we could rather have contexts of the shape ${\tilde{\mu }}(x,a).c$ (to be dual to proofs (t, p)) and (dual to $\mathsf {refl}$). We could then define the following typing rules (where we extend the dependencies list to terms, to compensate the conversion from A[t] to A[u] in the former ($\mathsf {subst}\,\!\,\!$)-rule):

and define $\mathsf {prf}\,p$ and $\mathsf {subst}\,p\,q$ as syntactic sugar:

For any $p\in \textsc {nef}$ and any variables $a,\alpha$, $A(\mathsf {wit}\,p)$ is in $A(\mathsf {wit}\,(x,a))_{\{(x,a)|p\}}$ which allows us to derive (using this in the $(\texttt {cut})$-rule) the admissibility of the former $(\mathsf {prf}\,\!)$-rule (we let the reader check the case of the ($\mathsf {subst}\,\!\,\!$)-rule):

As for the reduction rules, we can define the following (call-by-value) reductions:

and check that they advantageously simulate the previous rules (the expansion rules become useless):