Abstract
The proof assistant Isabelle/HOL is based on an extension of Higher-Order Logic (HOL) with ad hoc overloading of constants. It turns out that the interaction between the standard HOL type definitions and the Isabelle-specific ad hoc overloading is problematic for the logical consistency. In previous work, we have argued that standard HOL semantics is no longer appropriate for capturing this interaction, and have proved consistency using a nonstandard semantics. The use of an exotic semantics makes that proof hard to digest by the community. In this paper, we prove consistency by proof-theoretic means—following the healthy intuition of definitions as abbreviations, realized in HOLC, a logic that augments HOL with comprehension types. We hope that our new proof settles the Isabelle/HOL consistency problem once and for all. In addition, HOLC offers a framework for justifying the consistency of new deduction schemas that address practical user needs.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
1 Introduction
Isabelle/HOL [35, 36] is a popular proof assistant, with hundreds of users world-wide in both academia and industry. It is being used in major verification projects, such as the seL4 operating system kernel [24]. In addition, Isabelle/HOL is a framework for certified programming: functional programming (including lazy (co)programming [9]) is supported natively and imperative programming is supported via a monadic extension [10]. Programs can be written and verified in Isabelle/HOL, and efficient code for them (in Haskell, Standard ML, OCaml and Scala) can be produced using a code generator [19]. This certified programming methodology has yielded a wide range of verified software systems, from a Java compiler [32] to an LTL model checker [14] to a conference management system [23]. The formal guarantees of all such systems, as well as those considered by some formal certification agencies [21], are based on one major assumption: the correctness/consistency of Isabelle/HOL’s inference engine.
Keeping the underlying logic simple, hence manifestly consistent, along with reducing all the user developments to the logic kernel, has been a major tenet of the LCF/HOL approach to formal verification, originating from Robin Milner and Mike Gordon [17]. Yet, Isabelle/HOL, one of the most successful incarnations of this approach, takes some liberties beyond the well-understood higher-order logic kernel. Namely, its definitional mechanism allows delayed ad hoc overloading of constant definitions—in turn, this enables Haskell-style type classes [46] on top of HOL [37].
In standard HOL, a polymorphic constant should either be only declared (and forever left uninterpreted), or fully defined at its most general type.Footnote 1 By contrast, Isabelle/HOL allows first declaring a constant, and at later times overloading it by defining some of its instances, as in the following example:Footnote 2

Recursive overloading is also supported, as in:

In between the declaration and the instance definitions, arbitrary commands may occur, including type definitions (“typedef”) and (co)datatype definitions (which are derived from typedef [7, 45]). For example, the following definition introduces a type of polynomials over an arbitrary domain \(\alpha \), where \(\forall _\infty \) is the “for all but finitely many” quantifier:

When 0 is defined for concrete types, such as \({\mathsf {real}}\) and \(\alpha \;{\mathsf {list}}\), the library theorems about arbitrary-domain polynomials are enabled for polynomials over these concrete types.Footnote 3
To avoid inconsistency, this overloading mechanism is regulated by syntactic checks for orthogonality and termination. Examples like the above should be allowed, whereas examples like the following encoding of Russell’s paradox [29, Sect. 1] should be forbidden:

The above would lead to a proof of false taking advantage of the circularity \(T \rightsquigarrow c_{\mathsf {bool}}\rightsquigarrow T\) in the dependency relation introduced by the definitions: one first defines the type T to contain precisely one element just in case \(c_{\mathsf {bool}}\) is \(\mathsf {{True}}\), and then defines \(c_{\mathsf {bool}}\) to be \(\mathsf {{True}}\) just in case T contains more than one element.
Because Isabelle/HOL has a large user base and is heavily relied upon, it is important that the consistency of its logic be established with a high degree of clarity and a high degree of rigor. In 2014, we started an investigation into the foundations of this logic, which has revealed a few consistency problems (including the above “paradox”). These issues have generated quite a lot of discussion in the Isabelle community, during which some philosophical disagreements and misunderstandings among the users and the developers have surfaced [1]. The technical issues have been addressed [27, 29] and are no longer exhibited in Isabelle2016.Footnote 4
In addition to taking care of these issues, one of course needs some guarantees that similar issues are not still present in the logic. To address this, in previous work [29] we have proved that the logic is now consistent, employing a semantic argument in terms of a nonstandard semantics for HOL. Our original proof was somewhat sketchy and lacking in rigor—full (pen-and-paper) proofs are now included in an extended report [28]. Of course, a machine-checked proof, perhaps building on a recent formalization of HOL [15, 25], would make further valuable progress on the rigor aspect.
In this paper, we hope to improve on the clarity aspect and provide deeper insight into why Isabelle/HOL’s logic is consistent. As mentioned, Isabelle/HOL is richer than HOL not in the rules of deduction, but in the definitional mechanism. A natural reluctance that comes to mind concerning our semantic proof of consistency is best expressed by Isabelle’s creator’s initial reaction to our proof idea [40]:
It’s a bit puzzling, not to say worrying, to want a set-theoretic semantics for plain definitions. The point of definitions (and the origin of the idea that they preserve consistency) is that they are abbreviations.
This paper’s first contribution is a new proof of consistency for Isabelle/HOL’s logic, easy to digest by the large community of “syntacticists” who (quite legitimately) wish to regard definitions as a form of abbreviations. The problem is that type definitions cannot simply be unfolded (and inlined)—a type definition is an axiom that postulates a new type and an embedding-projection pair between the new type and the original type (from where the new type is carved out by a nonempty predicate). But the syntactic intuition persists: what if we were allowed to unfold type definitions? As it turns out, this can be achieved in a gentle extension of HOL featuring comprehension types. This extended logic, called HOL with Comprehension (HOLC), is a syntacticist’s paradise, allowing for a consistency proof along their intuition. This proof is systematically developed in Sect. 3. First, HOLC is introduced (Sect. 3.1) and shown consistent by a standard argument (Sect. 3.2). Then, a translation is defined from well-formed Isabelle/HOL definitions to HOLC, which is proved sound, i.e., deduction-preserving (Sect. 3.3). The key to establishing soundness is the use of a modified deduction system for HOL where type instantiation is restricted—this tames the inherent lack of uniformity brought about by ad hoc overloading. Finally, soundness of the translation together with consistency of HOLC ensures consistency of Isabelle/HOL.
As a second contribution, we use HOLC to justify some recently proposed extensions of Isabelle/HOL—namely, two new deduction schemas [30]. One enables local type definitions inside proof contexts; the other allows replacing undefined instances of overloaded constants with universally quantified variables. As we argue in [30], both extensions are useful for simplifying proof development by enabling the transition from light type-based theorems to heavier but more flexible set-based theorems. However, proving that these extensions do not introduce inconsistency is surprisingly difficult. In particular, our previously defined (consistency-justifying) semantics [29] has a blind spot on the second extension— it is only from the viewpoint of HOLC that the consistency of both extensions is manifest (Sect. 4).
More details on our constructions and proofs can be found in a technical report made available online [31].
2 The Isabelle/HOL Logic Recalled
The logic of Isabelle/HOL consists of:
-
HOL, that is, classical higher-order logic with rank 1 polymorphism, Hilbert choice and the Infinity axiom (recalled in Sect. 2.1)
-
A definitional mechanism for introducing new types and constants in an overloaded fashion (recalled in Sect. 2.2)
2.1 HOL Syntax and Deduction
The syntax and deduction system we present here are minor variations of the standard ones for HOL (as in, e.g., [3, 18, 20]). What we call HOL axioms correspond to the theory INIT from [3].
Syntax. Throughout this section, we fix the following:
-
an infinite set \(\mathsf {{TVar}}\), of type variables, ranged by \(\alpha ,\beta \)
-
an infinite set \(\mathsf {VarN}\), of (term) variable names, ranged by x, y, z
-
a set K of symbols, ranged by k, called type constructors, containing three special symbols: \({\mathsf {bool}}\), \({\mathsf {ind}}\) and \(\rightarrow \) (aimed at representing the type of booleans, an infinite type and the function type constructor, respectively)
We fix a function \({{\textsf {arOf}}}: K \rightarrow \mathbb {N}\) giving arities to type constructors, such that \({{\textsf {arOf}}}({\mathsf {bool}}) = {{\textsf {arOf}}}({\mathsf {ind}}) = 0\) and \({{\textsf {arOf}}}(\rightarrow ) = 2\). Types, ranged by \(\sigma ,\tau \), are defined as follows:

Thus, a type is either a type variable or an n-ary type constructor k postfix-applied to a number of types corresponding to its arity. If \(n=1\), instead of \((\sigma )\,k\) we write \(\sigma \,k\). We write \(\mathsf {{Type}}\) for the set of types.
Finally, we fix the following:
-
a set \({{\textsf {Const}}}\), ranged over by c, of symbols called constants, containing five special symbols: \(\longrightarrow \), \(=\), \({{\varepsilon }}\), \({{\mathsf {zero}}}\) and \({{\mathsf {suc}}}\) (aimed at representing logical implication, equality, Hilbert choice of some element from a type, zero and successor, respectively)
-
a function \({{\mathsf {tpOf}}}: {{\textsf {Const}}}\rightarrow \mathsf {{Type}}\) associating a type to every constant, such that:
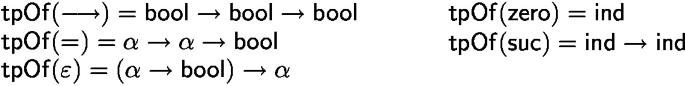
\({{\textsf {TV}}}(\sigma )\) is the set of variables of a type \(\sigma \). Given a function \(\rho : \mathsf {{TVar}}\rightarrow \mathsf {{Type}}\), its support is the set of type variables where \(\rho \) is not the identity: \({\mathsf {supp}}(\rho ) = \{\alpha \mid \rho (\alpha ) \ne \alpha \}\). A type substitution is a function \(\rho : \mathsf {{TVar}}\rightarrow \mathsf {{Type}}\) with finite support. We let \({\textsf {TSubst}}\) denote the set of type substitutions. Each \(\rho \in {\textsf {TSubst}}\) extends to a function \(\overline{\rho } : \mathsf {{Type}}\rightarrow \mathsf {{Type}}\) by defining \(\overline{\rho }(\alpha ) = \rho (\alpha )\) and \(\overline{\rho } ((\sigma _1,\ldots ,\sigma _n)\,k) = (\overline{\rho }(\sigma _1),\ldots ,\overline{\rho }(\sigma _n))\,k\). We write \(\sigma [\tau /\alpha ]\) for \(\overline{\rho }(\sigma )\), where \(\rho \) is the type substitution that sends \(\alpha \) to \(\tau \) and each \(\beta \not = \alpha \) to \(\beta \). Thus, \(\sigma [\tau /\alpha ]\) is obtained from \(\sigma \) by substituting \(\tau \) for all occurrences of \(\alpha \).
We say that \(\sigma \) is an instance of \(\tau \) via a substitution of \(\rho \in {\textsf {TSubst}}\), written \(\sigma \le _\rho \tau \), if \(\overline{\rho }(\tau ) = \sigma \). We say that \(\sigma \) is an instance of \(\tau \), written \(\sigma \le \tau \), if there exists \(\rho \in {\textsf {TSubst}}\) such that \(\sigma \le _\rho \tau \). Two types \(\sigma _1\) and \(\sigma _2\) are called orthogonal, written \(\sigma _1 \#\sigma _2\), if they have no common instance; i.e., for all \(\tau \) it holds that \(\tau \not \le \sigma _1\) or \(\tau \not \le \sigma _2\).
A (typed) variable is a pair of a variable name x and a type \(\sigma \), written \(x_\sigma \). Let \(\mathsf {{Var}}\) denote the set of all variables. A constant instance is a pair of a constant and a type, written \(c_\sigma \), such that \(\sigma \le {{\mathsf {tpOf}}}(c)\). We let \({{\textsf {CInst}}}\) denote the set of constant instances. We extend the notions of being an instance (\(\le \)) and being orthogonal (\(\#\)) from types to constant instances:

The tuple \((K,{{\textsf {arOf}}},{{\textsf {Const}}},{{\mathsf {tpOf}}})\), which will be fixed in what follows, is called a signature. This signature’s terms, ranged over by s, t, are defined by the grammar:
Thus, a term is either a typed variable, or a constant instance, or an application, or an abstraction. As usual, we identify terms modulo alpha-equivalence. Typing is defined as a binary relation between terms and types, written \(t : \sigma \), inductively as follows:

A term is a well-typed term if there exists a (necessarily unique) type \(\tau \) such that \(t : \tau \). We write \({{\mathsf {tpOf}}}(t)\) for this unique \(\tau \). We let \({{\textsf {Term}}}_w\) be the set of well-typed terms. We can apply a type substitution \(\rho \) to a term t, written \(\overline{\rho }(t)\), by applying \(\overline{\rho }\) to the types of all variables and constant instances occurring in t. \({{\textsf {FV}}}(t)\) is the set of t’s free variables. The term t is called closed if it has no free variables: \({{\textsf {FV}}}(t) = \emptyset \). We write \(t[s/x_\sigma ]\) for the term obtained from t by capture-free substituting s for all free occurrences of \(x_\sigma \).
A formula is a term of type \({\mathsf {bool}}\). The formula connectives and quantifiers are defined in a standard way, starting from the implication and equality primitives. When writing terms, we sometimes omit the types of variables if they can be inferred.
Deduction. A theory is a set of closed formulas. The HOL axioms, forming a set denoted by \(\mathsf {Ax}\), are the standard ones, containing axioms for equality, infinity, choice, and excluded middle. (The technical report [31] gives more details.) A context \(\varGamma \) is a finite set of formulas. The notation \(\alpha \notin \varGamma \) (or \(x_\sigma \notin \varGamma \)) means that the variable \(\alpha \) (or \(x_\sigma \)) is not free in any of the formulas in \(\varGamma \). We define deduction as a ternary relation \(\vdash \) between theories D, contexts \(\varGamma \) and formulas \(\varphi \), written \(D;\varGamma \vdash \varphi \).




A theory D is called consistent if \(D;\emptyset \not \vdash {\mathsf {{False}}}\).
Built-Ins and Non-built-Ins. A built-in type is any type of the form \({\mathsf {bool}}\), \({\mathsf {ind}}\), or \(\sigma \rightarrow \tau \) for \(\sigma ,\tau \in \mathsf {{Type}}\). We let \(\mathsf {{Type}}^\bullet \) denote the set of types that are not built-in. Note that a non-built-in type can have a built-in type as a subexpression, and vice versa; e.g., if \({\mathsf {list}}\) is a type constructor, then \({\mathsf {bool}}\,{\mathsf {list}}\) and \((\alpha \rightarrow \beta )\,{\mathsf {list}}\) are non-built-in types, whereas \(\alpha \rightarrow \beta \;{\mathsf {list}}\) is a built-in type.
Given a type \(\sigma \), we define \({{\mathsf {types}}}^{\bullet }(\sigma )\), the set of non-built-in types of \(\sigma \), as follows:
Thus, \({{\mathsf {types}}}^{\bullet }(\sigma )\) is the smallest set of non-built-in types that can produce \(\sigma \) by repeated application of the built-in type constructors. E.g., if the type constructors \({\mathsf {real}}\) (nullary) and \({\mathsf {list}}\) (unary) are in the signature and if \(\sigma \) is \(({\mathsf {bool}}\rightarrow \alpha \;{\mathsf {list}}) \rightarrow {\mathsf {real}}\rightarrow ({\mathsf {bool}}\rightarrow {\mathsf {ind}})\;{\mathsf {list}}\), then \({{\mathsf {types}}}^{\bullet }(\sigma )\) has three elements: \(\alpha \;{\mathsf {list}}\), \({\mathsf {real}}\) and \(({\mathsf {bool}}\rightarrow {\mathsf {ind}})\;{\mathsf {list}}\).
A built-in constant is a constant of the form \(\longrightarrow \), \(=\), \({{\varepsilon }}\), \({{\mathsf {zero}}}\) or \({{\mathsf {suc}}}\). We let \({{\textsf {CInst}}}^\bullet \) be the set of constant instances that are not instances of built-in constants.
As a general notation rule, the superscript \(\bullet \) indicates non-built-in items, where an item can be either a type or a constant instance.
Given a term t, we let \({{\mathsf {consts}}}^{\bullet }(t) \subseteq {{\textsf {CInst}}}^\bullet \) be the set of all non-built-in constant instances occurring in t and \({{\mathsf {types}}}^{\bullet }(t) \subseteq \mathsf {{Type}}^\bullet \) be the set of all non-built-in types that compose the types of non-built-in constants and (free or bound) variables occurring in t. Note that the \({{\mathsf {types}}}^{\bullet }\) operator is overloaded for types and terms.
2.2 The Isabelle/HOL Definitional Mechanisms
Constant(-Instance) Definitions. Given \(c_\sigma \in {{\textsf {CInst}}}^\bullet \) and a closed term \(t : \sigma \), we let \(c_\sigma \equiv t\) denote the formula \(c_\sigma =t\). We call \(c_\sigma \equiv t\) a constant-instance definition provided \({{\textsf {TV}}}(t) \subseteq {{\textsf {TV}}}(c_\sigma )\) (i.e., \({{\textsf {TV}}}(t) \subseteq {{\textsf {TV}}}(\sigma )\)).
Type Definitions. Given the types \(\tau \in \mathsf {{Type}}^\bullet \) and \(\sigma \in \mathsf {{Type}}\) and the closed term t whose type is \(\sigma \rightarrow {\mathsf {bool}}\), we let \(\tau \equiv t\) denote the formula
where \((\tau \approx t)^{{ abs }}_{{ rep }}\) is the formula \((\forall x_\tau .\;t\,({ rep }\;x)) \,\wedge \, (\forall x_\tau .\;{ abs }\,({ rep }\;x) = x) \,\wedge \, (\forall y_\sigma .\;t\;y \longrightarrow { rep }\,({ abs }\;y) = y)\). We call \(\tau \equiv t\) a type definition, provided \(\tau \) has the form \((\alpha _1,\ldots ,\alpha _n)\,k\) such that \(\alpha _i\) are all distinct type variables and \({{\textsf {TV}}}(t) \subseteq \{\alpha _1,\ldots ,\alpha _n\}\). (Hence, we have \({{\textsf {TV}}}(t) \subseteq {{\textsf {TV}}}(\tau )\), which also implies \({{\textsf {TV}}}(\sigma ) \subseteq {{\textsf {TV}}}(\tau )\).)
Thus, \(\tau \equiv t\) means: provided t represents a nonempty subset of \(\sigma \), the new type \(\tau \) is isomorphic to this subset via \({ abs }\) and \({ rep }\). Note that this is a conditional type definition, which distinguishes Isabelle/HOL from other HOL-based provers where an unconditional version is postulated (but only after the user proves nonemptiness). We shall see that this conditional approach, known among the Isabelle developers as the Makarius Wenzel trick, is useful in the overall scheme of proving consistency.
However, as far as user interaction is concerned, Isabelle/HOL proceeds like the other HOL provers, in particular, it requires nonemptiness proofs. When the user issues a command to define \(\tau \) via \(t: \sigma \rightarrow {\mathsf {bool}}\), the system asks the user to prove \(\exists x_\sigma .\; t\;x\), after which the new type \(\tau \) and the morphisms \({ abs }\) and \({ rep }\) are produced and \((\tau \approx t)^{{ abs }}_{{ rep }}\) is proved by applying Modus Ponens.
An Isabelle/HOL development proceeds by declaring types and constants, issuing constant-instance and type definitions, and proving theorems about them via HOL deduction.Footnote 5 Therefore, at any point in the development, there is a finite set D of registered constant-instance and type definitions (over a HOL signature \(\varSigma \))—we call such a set a definitional theory. We are interested in proving the consistency of definitional theories, under the syntactic well-formedness restrictions imposed by the system.
Well-Formed Definitional Theories. Given any binary relation R on \(\mathsf {{Type}}^\bullet \cup {{\textsf {CInst}}}^\bullet \), we write \(R^\downarrow \) for its (type-)substitutive closure, defined as follows: \(p \,R^\downarrow \, q\) iff there exist \(p',q'\) and a type substitution \(\rho \) such that \(p = \overline{\rho }(p')\), \(q = \overline{\rho }(q')\) and \(p' \,R\, q'\). We say that a relation R is terminating if there exists no sequence \((p_i)_{i \in \mathbb {N}}\) such that \(p_i\,R\,p_{i+1}\) for all i. We shall write \(R^+\) and \(R^*\) for the transitive and the reflexive-transitive closure of R.
Let us fix a definitional theory D. We say D is orthogonal if the following hold for any two distinct definitions \({ def }_{\!1},{ def }_{\!2} \in D\):
-
either one of them is a type definition and the other is a constant-instance definition
-
or both are type definitions with orthogonal left-hand sides, i.e., \({ def }_{\!1}\) has the form \(\tau _1 \equiv \ldots \), \({ def }_{\!2}\) has the form \(\tau _2 \equiv \ldots \), and \(\tau _1 \#\tau _2\).
-
or both are constant-instance definitions with orthogonal left-hand sides, i.e., \({ def }_{\!1}\) has the form \(c_{\tau _1} \equiv \ldots \), \({ def }_{\!2}\) has the form \(d_{\tau _2} \equiv \ldots \), and \(c_{\tau _1}\! \#d_{\tau _2}\).
We define the binary relation \(\rightsquigarrow \) on \(\mathsf {{Type}}^\bullet \cup {{\textsf {CInst}}}^\bullet \) by setting \(u \rightsquigarrow v\) iff one of the following holds:
-
1.
there exists in D a definition of the form \(u \equiv t\) such that \(v \in {{\mathsf {consts}}}^{\bullet }(t) \,\cup \, {{\mathsf {types}}}^{\bullet }(t)\).
-
2.
\(u \in {{\textsf {CInst}}}^\bullet \) such that u has the form \(c_{{{\mathsf {tpOf}}}(c)}\), and \(v \in {{\mathsf {types}}}^{\bullet }({{\mathsf {tpOf}}}(c))\).
We call \(\rightsquigarrow \) the dependency relation associated to D: it shows how the types and constant instances depend on each other through definitions in D. The fact that built-in items do not participate at this relation (as shown by the bullets which restrict to non-built-in items) is justified by the built-in items having a pre-determined interpretation, which prevents them from both “depending” and “being depended upon” [29].
We call the definitional theory D well-formed if it is orthogonal and the substitutive closure of its dependency relation, \(\rightsquigarrow ^\downarrow \), is terminating. Orthogonality prevents inconsistency arising from overlapping left-hand sides of definitions: defining \(c_{\alpha \times {\mathsf {ind}}\rightarrow {\mathsf {bool}}}\) to be \(\lambda x_{\alpha \times {\mathsf {ind}}}.{\mathsf {{False}}}\) and \(c_{{\mathsf {ind}}\times \alpha \rightarrow {\mathsf {bool}}}\) to be \(\lambda x_{{\mathsf {ind}}\times \alpha }.\mathsf {{True}}\) yields \(\lambda x_{{\mathsf {ind}}\times {\mathsf {ind}}}.{\mathsf {{False}}}= c_{{\mathsf {ind}}\times {\mathsf {ind}}\rightarrow {\mathsf {bool}}} \) \(=\lambda x_{{\mathsf {ind}}\times {\mathsf {ind}}}.\mathsf {{True}}\) and hence \({\mathsf {{False}}}= \mathsf {{True}}\). Termination prevents inconsistency arising from circularity, as in the encoding of Russel’s paradox in the introduction.
In previous work [29], we proved that these prevention measures are sufficient:
Theorem 1
If D is well-formed, then D is consistent.
Let us briefly recall the difficulties arising in proving the consistency theorem. A main problem problem rests in the fact that (recursive) overloading does not interact well with set-theoretic semantics. This makes it difficult to give a meaning to the overloaded definitions, in spite of the fact that their syntactic dependency terminates.
Example 2

Here, c and k are mutually dependent. Hence, since c is overloaded, both c and k behave differently depending on the types they are instantiated with or applied to. Here are some examples. Because \(c_{{\mathsf {bool}}\rightarrow {\mathsf {bool}}}\) is (vacuously) true, \(({\mathsf {bool}},{\mathsf {bool}})\,k\) contains four elements (corresponding to all elements of \({\mathsf {bool}}\,\times \,{\mathsf {bool}}\)). On the other hand, because \(c_{{\mathsf {nat}}\rightarrow {\mathsf {bool}}}\) is (vacuously) false, \((\alpha ,{\mathsf {nat}})\,k\) and \(({\mathsf {nat}},\alpha )\,k\) each contain one single element (corresponding to (d, d)). Moreover, \(({\mathsf {bool}},({\mathsf {bool}},{\mathsf {nat}})\,k)\,k\) contains two elements, for the following reason: both \(c_{{\mathsf {bool}}\rightarrow {\mathsf {bool}}}\) and \(c_{({\mathsf {bool}},{\mathsf {nat}})\,k\rightarrow {\mathsf {bool}}}\) are true, the latter since \(c_{{\mathsf {bool}}\rightarrow {\mathsf {bool}}}\) is true and \(c_{{\mathsf {nat}}\rightarrow {\mathsf {bool}}}\) is false (as required in the definition of \(c_{(\alpha ,\beta )\,k\rightarrow {\mathsf {bool}}}\)); so \(({\mathsf {bool}},({\mathsf {bool}},{\mathsf {nat}})\,k)\,k\) has as many elements as its host type, \({\mathsf {bool}}\times ({\mathsf {bool}},{\mathsf {nat}})\,k\); and \(({\mathsf {bool}},{\mathsf {nat}})\,k\) has only one element (corresponding to (d, d)). Finally, \(({\mathsf {bool}},({\mathsf {nat}},{\mathsf {bool}})\,k)\,k\) contains only one element, because \(c_{({\mathsf {nat}},{\mathsf {bool}})\,k\rightarrow {\mathsf {bool}}}\) is false (by the definitions of \(c_{(\alpha ,\beta )\,k\rightarrow {\mathsf {bool}}}\) and \(c_{{\mathsf {nat}}\rightarrow {\mathsf {bool}}}\)).
In the standard HOL semantics [41], a type constructor such as k is interpreted compositionally, as an operator [k] on sets (from a suitable universe) obtained from k’s type definition—here, as a binary operator taking the sets A and B to the set \(\{(a,b) \in A \times B \mid [c]_{A}(a) \,\wedge \, [c]_{B}\,(b) \,\vee \, (a,b) = ([d]_A,[d]_B)\}\), where \(([c]_A)_{A}\) and \(([d]_A)_A\) would be the interpretations of c and d as families of sets, with each \([c]_A\) a predicate on A and each \([d]_A\) an element of A. But defining [k] in one go for any sets A and B is impossible here, since the needed instances of [c] are not yet known, and in fact are mutually dependent with [k]. This means that, when defining [k] and [c], the inputs A and B would need to be analyzed in an ad hoc fashion, for the (syntactic!) occurrences of [k] itself. The orthogonality and termination of such semantic definitions would be problematic (and, as far as we see, could only be worked out by a heavy machinery that would constrain semantics to behave like syntax—adding syntactic annotations to the interpreting sets). Using John Reynolds’s famous wording [42], we conclude that ad hoc polymorphism is not set-theoretic.Footnote 6
In [29], we proposed a workaround based on acknowledging that ad hoc overloading regards different instances of the same non-built-in polymorphic type as completely unrelated types. Instead of interpreting type constructors as operators on sets, we interpret each non-built-in ground type and constant instance separately, in the order prescribed by the terminating dependency relation. Here, for example, \(c_{{\mathsf {bool}}\rightarrow {\mathsf {bool}}}\) and \(c_{{\mathsf {nat}}\rightarrow {\mathsf {bool}}}\) are interpreted before \(({\mathsf {bool}},{\mathsf {nat}})\,k\), which is interpreted before \(c_{({\mathsf {bool}},{\mathsf {nat}})\,k \rightarrow {\mathsf {bool}}}\), which is interpreted before \((({\mathsf {bool}},{\mathsf {nat}})\,k,{\mathsf {bool}})\,k\), etc. (But note that termination does not necessarily come from structural descent on types: definitions such as \(e_{{\mathsf {nat}}} \equiv {{\textsf {head}}}(e_{{\mathsf {nat}}\;{\mathsf {list}}})\) are also acceptable.) Finally, polymorphic formulas are interpreted as the infinite conjunction of the interpretation of all their ground instances: for example, \(c_{\alpha \rightarrow {\mathsf {bool}}}\,d_\alpha \) is true iff \(c_{\sigma \rightarrow {\mathsf {bool}}}\,d_\sigma \) is true for all ground types \(\sigma \). This way, we were able to construct a ground model for the definitional theory. And after showing that the deduction rules for (polymorphic) HOL are sound for ground models, we inferred consistency. Thus, our solution was based on a mixture of syntax and semantics: interpret type variables by universally quantifying over all ground instances, and interpret non-built-in ground types disregarding their structure.
Such a hybrid approach, involving a nonstandard semantics, may seem excessive. There is a more common-sense alternative for accommodating the observation that standard semantics cannot be married with ad hoc overloading: view overloaded definitions as mere textual abbreviations. The “semantics” of an overloaded constant will then be the result of unfolding the definitions—but, as we have seen, types must also be involved in this process. This is the alternative taken by our new proof.
3 New Proof of Consistency
The HOL logical infrastructure allows unfolding constant definitions, but not type definitions. To amend this limitation, we take an approach common in mathematics. The reals were introduced by closing the rationals under Cauchy convergence, the complex numbers were introduced by closing the reals under roots of polynomials. Similarly, we introduce a logic, HOL with Comprehension (HOLC), by closing HOL under type comprehension—that is, adding to HOL comprehension types to express subsets of the form \(\{ x : \sigma \mid t\;x \}\) (Sect. 3.1). While there is some tension between these subsets being possibly empty and the HOLC types having to be nonempty due to the Hilbert choice operator, this is resolved thanks to the HOLC comprehension axioms being conditioned by nonemptiness. With this proviso, HOLC admits standard set-theoretical models, making it manifestly consistent (Sect. 3.2). In turn, Isabelle/HOL-style overloaded constants and types can be normalized in HOLC by unfolding their definitions (Sect. 3.3). The normalization process provides an intuition and a justification for the syntactic checks involving non-built-in types and constants. Finally, consistency of Isabelle/HOL is inferable from consistency of HOLC.
3.1 HOL with Comprehension (HOLC)
Syntax. Just like for HOL, we fix the sets \(\mathsf {{TVar}}\) (of type variables) and \(\mathsf {VarN}\) (of term variable names), as well as the following:
-
a set K of type constructors including the built-in ones \({\mathsf {bool}},{\mathsf {ind}},\rightarrow \).
-
a function \({{\textsf {arOf}}}: K \rightarrow \mathbb {N}\) assigning an arity to each type constructor.
-
a set \({{\textsf {Const}}}\) of constants, including the built-in ones \(\longrightarrow \), \(=\), \({{\varepsilon }}\), \({{\mathsf {zero}}}\) and \({{\mathsf {suc}}}\).
The HOLC types and terms, which we call ctypes and cterms, are defined as follows:

Above, we highlight the only difference from the HOL types and terms: the comprehension types, whose presence makes the ctypes and cterms mutually recursive. Indeed,  contains the term t, whereas a typed variable \(x_\sigma \) and a constant instance \(c_\sigma \) contain the type \(\sigma \). We think of a comprehension type
contains the term t, whereas a typed variable \(x_\sigma \) and a constant instance \(c_\sigma \) contain the type \(\sigma \). We think of a comprehension type  with \(t : \sigma \rightarrow {\mathsf {bool}}\) as representing a set of elements which in standard mathematical notation would be written \(\{x : \sigma \mid t\;x\}\), that is, the set of all elements of \(\sigma \) satisfying t. \(\mathsf {{Var}}\) denotes the set of (typed) variables, \(x_\sigma \). \(\mathsf {{CType}}\) and \({{\textsf {CTerm}}}\) denotes the sets of ctypes and cterms.
with \(t : \sigma \rightarrow {\mathsf {bool}}\) as representing a set of elements which in standard mathematical notation would be written \(\{x : \sigma \mid t\;x\}\), that is, the set of all elements of \(\sigma \) satisfying t. \(\mathsf {{Var}}\) denotes the set of (typed) variables, \(x_\sigma \). \(\mathsf {{CType}}\) and \({{\textsf {CTerm}}}\) denotes the sets of ctypes and cterms.
We also fix a function \({{\mathsf {tpOf}}}: {{\textsf {Const}}}\rightarrow \mathsf {{CType}}\), assigning ctypes to constants. Similarly to the case of HOL, we call the tuple \((K,{{\textsf {arOf}}},{{\textsf {Const}}},{{\mathsf {tpOf}}})\), which shall be fixed in what follows, a HOLC signature. Since ctypes contain cterms, we define typing mutually inductively together with the notion of a ctype being well-formed (i.e., only containing well-typed terms):


We let \(\mathsf {{CType}}_w\) and \({{\textsf {CTerm}}}_w\) be the sets of well-formed ctypes and well-typed cterms. Also, we let \(\mathsf {{Var}}_w\) be the set of variables \(x_\sigma \) that are well-typed as cterms, i.e., have their ctype \(\sigma \) well-formed.
The notions of type substitution, a type or a constant instance being an instance of (\(\le \)) or being orthogonal with (\(\#\)) another type or constant instance, are defined similarly to those for HOL. Note that a type  is unrelated to another type
is unrelated to another type  even when the extent of the predicate \(t'\) includes that of t. This is because HOLC, like HOL (and unlike, e.g., PVS [39]), has no subtyping—instead, traveling between smaller and larger types is achieved via embedding-projection pairs.
even when the extent of the predicate \(t'\) includes that of t. This is because HOLC, like HOL (and unlike, e.g., PVS [39]), has no subtyping—instead, traveling between smaller and larger types is achieved via embedding-projection pairs.
Since in HOLC types may contain terms, we naturally lift term concepts to types. Thus, the free (cterm) variables of a ctype \(\sigma \), written \({{\textsf {FV}}}(\sigma \)), are all the free variables occurring in the cterms contained in \(\sigma \). A type is called closed if it has no free variables.
A Note on Declaration Circularity. In HOLC we allow \({{\mathsf {tpOf}}}\) to produce declaration cycles—for example, the type of a constant may contain instances of that constant, as in  . However, the typing system will ensure that no such cyclic entity will be well-typed. For example, to type an instance \(c_\sigma \), we need to apply the rule (Const), requiring that
. However, the typing system will ensure that no such cyclic entity will be well-typed. For example, to type an instance \(c_\sigma \), we need to apply the rule (Const), requiring that  be well-formed. For the latter, we need the rule (W\(_3\)), requiring that \(c_{\mathsf {bool}}\) be well-typed. Finally, to type \(c_{\mathsf {bool}}\), we again need the rule (Const), requiring that
be well-formed. For the latter, we need the rule (W\(_3\)), requiring that \(c_{\mathsf {bool}}\) be well-typed. Finally, to type \(c_{\mathsf {bool}}\), we again need the rule (Const), requiring that  be well-formed. So \(c_\sigma \) can never be typed. It may seem strange to allow constant declarations whose instances cannot be typed (hence cannot belong to well-typed terms and well-formed types)—however, this is harmless, since HOLC deduction only deals with well-typed and well-formed items. Moreover, all the constants translated from HOL will be shown to be well-typed.
be well-formed. So \(c_\sigma \) can never be typed. It may seem strange to allow constant declarations whose instances cannot be typed (hence cannot belong to well-typed terms and well-formed types)—however, this is harmless, since HOLC deduction only deals with well-typed and well-formed items. Moreover, all the constants translated from HOL will be shown to be well-typed.
Deduction. The notion of formulas and all the related notions are defined similarly to HOL, so that HOL formulas are particular cases of HOLC formulas. In addition to the axioms of HOL (the set \(\mathsf {Ax}\)), HOLC shall include the following type comprehension axiom  :
:

This axiom is nothing but a generalization of the HOL type definition \(\tau \equiv t\), taking advantage of the fact that in HOLC we have a way to write the expression defining \(\tau \) as the type  . Note that \(\alpha \) is a type variable standing for an arbitrary type, previously denoted by \(\sigma \). Thus, HOLC allows us to express what in HOL used to be a schema (i.e., an infinite set of formulas, one for each type \(\sigma \)) by a single axiom.
. Note that \(\alpha \) is a type variable standing for an arbitrary type, previously denoted by \(\sigma \). Thus, HOLC allows us to express what in HOL used to be a schema (i.e., an infinite set of formulas, one for each type \(\sigma \)) by a single axiom.
HOLC’s deduction \(\Vdash \) is defined by the same rules as HOL’s deduction \(\vdash \), but applied to ctypes and cterms instead of types and terms and using the additional axiom  . Another difference from HOL is that HOLC deduction does not factor in a theory D—this is because we do not include any definitional principles in HOLC.
. Another difference from HOL is that HOLC deduction does not factor in a theory D—this is because we do not include any definitional principles in HOLC.




3.2 Consistency of HOLC
In a nutshell, HOLC is consistent for a similar reason that HOL (without definitions) is consistent: the types have a straightforward set-theoretic interpretation and the deduction rules are manifestly sound w.r.t. this interpretation. Similar logics, employing mutual dependency between types and terms, have been shown to be consistent for the foundations of Coq [6] and PVS [39].
Compared to these logics, the only twist of HOLC is that all types have to be nonempty. Indeed, HOLC inherits from HOL the polymorphic Hilbert choice operator, \({{\varepsilon }}: (\alpha \rightarrow {\mathsf {bool}}) \rightarrow \alpha \), which immediately forces all types to be inhabited, e.g., by \({{\varepsilon }}\;(\lambda x_\sigma .\;\mathsf {{True}})\).
From a technical point of view, this nonemptiness requirement is easy to satisfy. The only types that are threatened by emptiness are the comprehension types  . We will interpret them according to their expected semantics, namely, as the subset of \(\sigma \) for which t holds, only if this subset turns out to be nonempty; otherwise we will interpret them as a fixed singleton set \(\{*\}\). This is consistent with the HOLC comprehension axiom,
. We will interpret them according to their expected semantics, namely, as the subset of \(\sigma \) for which t holds, only if this subset turns out to be nonempty; otherwise we will interpret them as a fixed singleton set \(\{*\}\). This is consistent with the HOLC comprehension axiom,  , which only requires that
, which only requires that  have the expected semantics if \(\exists x_\alpha .\,t\,x\) holds. Notice how the Makarius Wenzel trick of introducing type definitions as conditional statements in Isabelle/HOL (recalled on page 7), which has inspired a similar condition for
have the expected semantics if \(\exists x_\alpha .\,t\,x\) holds. Notice how the Makarius Wenzel trick of introducing type definitions as conditional statements in Isabelle/HOL (recalled on page 7), which has inspired a similar condition for  , turns out to be very useful in our journey. Of all the HOL-based provers, this “trick” is only used by Isabelle/HOL, as if anticipating the need for a more involved argument for consistency.
, turns out to be very useful in our journey. Of all the HOL-based provers, this “trick” is only used by Isabelle/HOL, as if anticipating the need for a more involved argument for consistency.
A Full-Frame Model for HOLC. We fix a Grothendieck universe \(\mathcal {V}\) and let \(\mathcal {U}= \mathcal {V}\setminus \{\emptyset \}\) (since all types will have nonempty interpretations). We fix the following items in \(\mathcal {U}\) and operators on \(\mathcal {U}\):
-
a two-element set \(\mathbb {B}= \{ \mathsf {{false}}, \mathsf {{true}}\} \in \mathcal {U}\)
-
a singleton set \(\{*\} \in \mathcal {U}\)
-
for each \(k \in K\), a function \(\fbox {k} : \mathcal {U}^{{{\textsf {arOf}}}(k)} \rightarrow \mathcal {U}\)
-
a global choice function, \({{\mathsf {choice}}}\), that assigns to each nonempty set \(A \in \mathcal {U}\) an element \({{\mathsf {choice}}}(A) \in A\).
We wish to interpret well-formed ctypes and well-typed cterms, u, as items [u] in \(\mathcal {U}\). Since ctypes and cterms are mutually dependent, not only the interpretations, but also their domains need to be defined recursively. Namely, we define the following notions together, by structural recursion on \(u \in \mathsf {{CType}}_w \,\cup \, {{\textsf {CTerm}}}_w\):
-
the set \({{\textsf {Compat}}}(u)\), of compatible valuation functions \(\xi : {{\textsf {TV}}}(u) \,\cup \, {{\textsf {FV}}}(u) \rightarrow \mathcal {U}\)
-
the interpretation \([u] : {{\textsf {Compat}}}(u) \rightarrow \mathcal {U}\)
For each u, assuming [v] has been defined for all structurally smaller \(v \in \mathsf {{CType}}_w \,\cup \, {{\textsf {CTerm}}}_w\), we take \({{\textsf {Compat}}}(u)\) to consist of all functions \(\xi : {{\textsf {TV}}}(u) \,\cup \, {{\textsf {FV}}}(u) \rightarrow \mathcal {U}\) such that  for all \(x_\sigma \in {{\textsf {FV}}}(u)\). (Here,
for all \(x_\sigma \in {{\textsf {FV}}}(u)\). (Here,  denotes the restriction of \(\xi \) to the indicated set, which is clearly included in \(\xi \)’s domain, since \({{\textsf {TV}}}(\sigma ) \subseteq {{\textsf {TV}}}(u)\) and \({{\textsf {FV}}}(\sigma ) \subseteq {{\textsf {FV}}}(u)\).)
denotes the restriction of \(\xi \) to the indicated set, which is clearly included in \(\xi \)’s domain, since \({{\textsf {TV}}}(\sigma ) \subseteq {{\textsf {TV}}}(u)\) and \({{\textsf {FV}}}(\sigma ) \subseteq {{\textsf {FV}}}(u)\).)
In turn, [u] is defined as shown below. First, the equations for type interpretations:






The Eq. (7) shows how we interpret comprehension types with no inhabitants (e.g.,  )—we chose the singleton set \(\{*\}\) (in fact, any nonempty set would do the job). As previously discussed, this conforms to the
)—we chose the singleton set \(\{*\}\) (in fact, any nonempty set would do the job). As previously discussed, this conforms to the  axiom, which only prescribes the meaning of inhabited comprehension types.
axiom, which only prescribes the meaning of inhabited comprehension types.
Next, the equations for term interpretations:








Since the logic has no definitions, we are free to choose any interpretation for non-built-in constant instances—as seen in (12), we do this using the global choice operator \({{\mathsf {choice}}}\). In (15), we use \(\Lambda \) for meta-level lambda-abstraction.
We say that a formula \(\varphi \) is true under the valuation \(\xi \in {{\textsf {Compat}}}(\varphi )\) if \([\varphi ](\xi ) = \mathsf {{true}}\). We say that \(\varphi \) is (unconditionally) true if it is true under all \(\xi \in {{\textsf {Compat}}}(\varphi )\). Given a context \(\varGamma \) and a formula \(\varphi \), we write \(\varGamma \models \varphi \) to mean that \(\bigwedge \varGamma \longrightarrow \varphi \) is true, where \(\bigwedge \varGamma \) is the conjunction of all formulas in \(\varGamma \).
Theorem 3
HOLC is consistent, in that \(\emptyset \not \Vdash {\mathsf {{False}}}\).
Proof
It is routine to verify that HOLC’s deduction is sound w.r.t. to its semantics: for every HOLC deduction rule of the form

it holds that \(\varGamma \models \varphi \) if \(\varGamma _i \models \varphi _i\) for all \(i\le n\). Then \(\emptyset \not \Vdash {\mathsf {{False}}}\) follows from \(\emptyset \not \models {\mathsf {{False}}}\). \(\square \)
3.3 Translation of Isabelle/HOL to HOLC
We fix a HOL signature \(\varSigma = (K,{{\textsf {arOf}}},{{\textsf {Const}}},{{\mathsf {tpOf}}})\) and an Isabelle/HOL well-formed definitional theory D over \(\varSigma \). We will produce a translation of the types and well-typed terms of \(\varSigma \) into well-formed ctypes and well-typed cterms of the HOLC signature \(\varSigma _D = (K,{{\textsf {arOf}}},{{\textsf {Const}}},{{\mathsf {tpOf}}}_D)\) (having the same type constructors and constants as \(\varSigma \)). The typing function \({{\mathsf {tpOf}}}_D : {{\textsf {Const}}}\rightarrow \mathsf {{CType}}\) will be defined later. For \(\varSigma _D\), we use all the notations from Sect. 3.1—we write \(\mathsf {{CType}}\) and \({{\textsf {CTerm}}}\) for the sets of cterms and ctypes, etc.
The translation will consist of two homonymous “normal form” functions  and
and  . However, since we have not yet defined \({{\mathsf {tpOf}}}_D\), the sets \(\mathsf {{CType}}_w\) and \({{\textsf {CTerm}}}_w\) (of well-formed ctypes and well-typed cterms) are not yet defined either. To bootstrap the definitions, we first define
. However, since we have not yet defined \({{\mathsf {tpOf}}}_D\), the sets \(\mathsf {{CType}}_w\) and \({{\textsf {CTerm}}}_w\) (of well-formed ctypes and well-typed cterms) are not yet defined either. To bootstrap the definitions, we first define  and
and  , then define \({{\mathsf {tpOf}}}_D\), and finally show that the images of the
, then define \({{\mathsf {tpOf}}}_D\), and finally show that the images of the  functions are included in \(\mathsf {{CType}}_w\) and \({{\textsf {CTerm}}}_w\).
functions are included in \(\mathsf {{CType}}_w\) and \({{\textsf {CTerm}}}_w\).
The  functions are defined mutually recursively by two kinds of equations. First, there are equations for recursive descent in the structure of terms and types:
functions are defined mutually recursively by two kinds of equations. First, there are equations for recursive descent in the structure of terms and types:

Second, there are equations for unfolding the definitions in D. But before listing these, we need some notation. Given \(u,v \in \mathsf {{Type}}\cup {{\textsf {Term}}}_w\), we write \(u \equiv ^{\downarrow }v\) to mean that there exists a definition \(u' \equiv v'\) in D and a type substitution \(\rho \) such that \(u = \rho (u')\) and \(v = \rho (v')\). This notation is intuitively consistent (although slightly abusively so) with the notation for the substitutive closure of a relation, where we would pretend that \({\equiv }\) is a relation on \(\mathsf {{Type}}\cup {{\textsf {Term}}}_w\), with \(u' \equiv v'\) meaning \((u' \equiv v') \in D\). By Orthogonality, we have that, for all \(u \in \mathsf {{Type}}^\bullet \cup {{\textsf {CInst}}}^\bullet \), there exists at most one \(v \in \mathsf {{Type}}\cup {{\textsf {Term}}}_w\) such that \(u \equiv ^{\downarrow }v\). Here are the equations for unfolding:


Thus, the functions  first traverse the terms and types “vertically,” delving into the built-in structure (function types, \(\lambda \)-abstractions, applications, etc.). When a non-built-in item is being reached that is matched by a definition in D,
first traverse the terms and types “vertically,” delving into the built-in structure (function types, \(\lambda \)-abstractions, applications, etc.). When a non-built-in item is being reached that is matched by a definition in D,  proceed “horizontally” by unfolding this definition. Since the right-hand side of the definition can be any term,
proceed “horizontally” by unfolding this definition. Since the right-hand side of the definition can be any term,  switch again to vertical mode. Hence,
switch again to vertical mode. Hence,  repeatedly unfold the definitions when a definitional match in a subexpression is found, following a topmost-first strategy (with the exception that proper subexpressions of non-built-in types are not investigated). For example, if a constant \(c_\sigma \) is matched by a definition, as in \(c_\sigma \equiv ^{\downarrow }t\), then \(c_\sigma \) is eagerly unfolded to t, as opposed to unfolding the items occurring in \(\sigma \). This seems to be a reasonable strategy, given that after unfolding \(c_\sigma \) the possibility to process \(\sigma \) is not lost: since \(t : \sigma \), we have that \(\sigma \) occurs in t.
repeatedly unfold the definitions when a definitional match in a subexpression is found, following a topmost-first strategy (with the exception that proper subexpressions of non-built-in types are not investigated). For example, if a constant \(c_\sigma \) is matched by a definition, as in \(c_\sigma \equiv ^{\downarrow }t\), then \(c_\sigma \) is eagerly unfolded to t, as opposed to unfolding the items occurring in \(\sigma \). This seems to be a reasonable strategy, given that after unfolding \(c_\sigma \) the possibility to process \(\sigma \) is not lost: since \(t : \sigma \), we have that \(\sigma \) occurs in t.
Example 4

Let us show the results of applying  on some of the constant instances and types in the above example.
on some of the constant instances and types in the above example.

The evaluation of  on \({\mathsf {bool}}\;k^n\) terminates in a number of steps depending on n, and the result contains n levels of comprehension-type nesting.
on \({\mathsf {bool}}\;k^n\) terminates in a number of steps depending on n, and the result contains n levels of comprehension-type nesting.
The first fact that we need to show is that  is well-defined, i.e., its recursive calls terminate. For this, we take the relation
is well-defined, i.e., its recursive calls terminate. For this, we take the relation  to be
to be  , where \({\equiv ^{\downarrow }}\) was defined above and
, where \({\equiv ^{\downarrow }}\) was defined above and  simply contains the structural recursive calls of
simply contains the structural recursive calls of  :
:

It is immediate to see that  captures the recursive calls of
captures the recursive calls of  : the structural calls via
: the structural calls via  and the unfolding calls via \({\equiv ^{\downarrow }}\). So the well-definedness of
and the unfolding calls via \({\equiv ^{\downarrow }}\). So the well-definedness of  is reduced to the termination of
is reduced to the termination of  .
.
Lemma 5
The relation  is terminating (hence the functions
is terminating (hence the functions  are well-defined).
are well-defined).
Proof
We shall use the following crucial fact, which follows by induction using the definitions of  and \(\rightsquigarrow ^{\downarrow }\): If \(u, v \in \mathsf {{Type}}^\bullet \cup {{\textsf {CInst}}}^\bullet \) and
and \(\rightsquigarrow ^{\downarrow }\): If \(u, v \in \mathsf {{Type}}^\bullet \cup {{\textsf {CInst}}}^\bullet \) and  . (*)
. (*)
Let us assume, for a contradiction, that  does not terminate. Then there exists an infinite sequence \((w_i)_{i \in \mathbb {N}}\) such that
does not terminate. Then there exists an infinite sequence \((w_i)_{i \in \mathbb {N}}\) such that  for all i. Since
for all i. Since  is defined as
is defined as  and
and  clearly terminates, there must exist an infinite subsequence \((w_{i_j})_{j \in \mathbb {N}}\) such that
clearly terminates, there must exist an infinite subsequence \((w_{i_j})_{j \in \mathbb {N}}\) such that  for all j. Since from the definition of \(\equiv \) we have \(w_{i_j} \in \mathsf {{Type}}^\bullet \cup {{\textsf {CInst}}}^\bullet \), we obtain from (*) that \(w_{i_j} \rightsquigarrow ^{\downarrow }w_{i_{j+1}}\) for all j. This contradicts the termination of \(\rightsquigarrow ^{\downarrow }\). \(\square \)
for all j. Since from the definition of \(\equiv \) we have \(w_{i_j} \in \mathsf {{Type}}^\bullet \cup {{\textsf {CInst}}}^\bullet \), we obtain from (*) that \(w_{i_j} \rightsquigarrow ^{\downarrow }w_{i_{j+1}}\) for all j. This contradicts the termination of \(\rightsquigarrow ^{\downarrow }\). \(\square \)
With  in place, we can define the missing piece of the target HOLC signature: we take \({{\mathsf {tpOf}}}_D\) to be the normalized version of \({{\mathsf {tpOf}}}\), i.e.
in place, we can define the missing piece of the target HOLC signature: we take \({{\mathsf {tpOf}}}_D\) to be the normalized version of \({{\mathsf {tpOf}}}\), i.e.  .
.
Lemma 6
 preserves typing, in the following sense:
preserves typing, in the following sense:
-
 is well-formed in HOLC.
is well-formed in HOLC. -
If \(t : \tau \), then
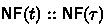 .
.
Our main theorem about the translation will be its soundness:
Theorem 7
If \(D;\emptyset \vdash \varphi \) in HOL, then  in HOLC.
in HOLC.
Let us focus on proving this theorem. If we define  as
as  , the proof that \(D;\varGamma \vdash \varphi \) implies
, the proof that \(D;\varGamma \vdash \varphi \) implies  should proceed by induction on the definition of \(D;\varGamma \vdash \varphi \). Due to the similarity of \(\vdash \) and \(\Vdash \), most of the cases go smoothly.
should proceed by induction on the definition of \(D;\varGamma \vdash \varphi \). Due to the similarity of \(\vdash \) and \(\Vdash \), most of the cases go smoothly.
For the HOL rule \(\textsc {(Beta)}\), we need to prove  , that is,
, that is,  . Hence, in order to conclude the proof for this case using the HOLC rule \(\textsc {(Beta)}\), we need that
. Hence, in order to conclude the proof for this case using the HOLC rule \(\textsc {(Beta)}\), we need that  commutes with term substitution—this is not hard to show, since substituting terms for variables does not influence the matching of definitions, i.e., the behavior of
commutes with term substitution—this is not hard to show, since substituting terms for variables does not influence the matching of definitions, i.e., the behavior of  :
:
Lemma 8

However, our proof (of Theorem 7) gets stuck when handling the \({\textsc {(T}\hbox {-}\textsc {Inst)}}\) case. It is worth looking at this difficulty, since it is revealing about the nature of our encoding. We assume that in HOL we inferred \(D;\varGamma \vdash \varphi [\sigma /\alpha ]\) from \(D;\varGamma \vdash \varphi \), where \(\alpha \notin \varGamma \). By the induction hypothesis, we have  . Hence, by applying \({\textsc {(T}\hbox {-}\textsc {Inst)}}\) in HOLC, we obtain
. Hence, by applying \({\textsc {(T}\hbox {-}\textsc {Inst)}}\) in HOLC, we obtain  . Therefore, to prove the desired fact, we would need that the
. Therefore, to prove the desired fact, we would need that the  functions commute with type substitutions in formulas, and therefore also in arbitrary terms (which may be contained in formulas):
functions commute with type substitutions in formulas, and therefore also in arbitrary terms (which may be contained in formulas):

But this is not true, as seen, e.g., when \({{\mathsf {tpOf}}}(c) = \alpha \) and \(c_{\mathsf {bool}}\equiv \mathsf {{True}}\) is in D:

The problem resides at the very essence of overloading: a constant c is declared at a type \(\sigma \) (\(\alpha \) in the above example) and defined at a less general type \(\tau \) (\({\mathsf {bool}}\) in the example). Our translation reflects this: it leaves \(c_\sigma \) as it is, whereas it compiles away \(c_\tau \) by unfolding its definition. So then how can such a translation be sound? Essentially, it is sound because in HOL nothing interesting can be deduced about the undefined \(c_\sigma \) that may affect what is being deduced about \(c_\tau \)—hence it is OK to decouple the two when moving to HOLC.
To capture this notion, of an undefined \(c_\sigma \) not affecting a defined instance \(c_\tau \) in HOL, we introduce a variant of HOL deduction that restricts type instantiation—in particular, it will not allow arbitrary statements about \(c_\sigma \) to be instantiated to statements about \(c_\tau \). Concretely, we define \(\vdash '\) by modifying \(\vdash \) as follows. We remove \({\textsc {(T}\hbox {-}\textsc {Inst)}}\) and strengthen \(\textsc {(Fact)}\) to a rule that combines the use of axioms with type instantiation:

(where \(\rho \) is a type substitution). Note the difference between \({\textsc {(Fact}\hbox {-}\textsc {T}\hbox {-}\textsc {Inst)}}\) and the combination of \(\textsc {(Fact)}\) and \({\textsc {(T}\hbox {-}\textsc {Inst)}}\): in the former, only axioms and elements of D are allowed to be type-instantiated, whereas in the latter instantiation can occur at any moment in the proof. It is immediate to see that \(\vdash \) is at least as powerful as \(\vdash '\), since \({\textsc {(Fact}\hbox {-}\textsc {T}\hbox {-}\textsc {Inst)}}\) can be simulated by \(\textsc {(Fact)}\) and \({\textsc {(T}\hbox {-}\textsc {Inst)}}\). Conversely, it is routine to show that \(\vdash '\) is closed under type substitution, and a fortiori under \({\textsc {(T}\hbox {-}\textsc {Inst)}}\); and \({\textsc {(Fact}\hbox {-}\textsc {T}\hbox {-}\textsc {Inst)}}\) is stronger than \(\textsc {(Fact)}\).
Using \(\vdash '\) instead of \(\vdash \), we can prove Theorem 7. All the cases that were easy with \(\vdash \) are also easy with \(\vdash '\). In addition, for the case \({\textsc {(Fact}\hbox {-}\textsc {T}\hbox {-}\textsc {Inst)}}\) where one infers \(D;\varGamma \vdash \rho (\varphi )\) with \(\varphi \in \mathsf {Ax}\), we need a less general lemma than commutation of  in an arbitrary term. Namely, noticing that the HOL axioms do not contain non-built-in constants or types, we need the following lemma, which can be proved by routine induction over t:
in an arbitrary term. Namely, noticing that the HOL axioms do not contain non-built-in constants or types, we need the following lemma, which can be proved by routine induction over t:
Lemma 9
 .
.
Now, assume \({\textsc {(Fact}\hbox {-}\textsc {T}\hbox {-}\textsc {Inst)}}\) is being used to derive \(D;\varGamma \vdash ' \overline{\rho }(\varphi )\) for \(\varphi \in \mathsf {Ax}\). We need to prove  , that is,
, that is,  . But this follows from n applications of the (T-Inst) rule (in HOLC), where n is the size of
. But this follows from n applications of the (T-Inst) rule (in HOLC), where n is the size of  ’s support (as any finite-support simultaneous substitution can be reduced to a sequence of unary substitutions).
’s support (as any finite-support simultaneous substitution can be reduced to a sequence of unary substitutions).
It remains to handle the case when \({\textsc {(Fact}\hbox {-}\textsc {T}\hbox {-}\textsc {Inst)}}\) is being used to derive \(D;\varGamma \vdash ' \overline{\rho }(\varphi )\) for \(\varphi \in D\). Here, Lemma 9 does not apply, since of course the definitions in D contain non-built-in items. However, we can take advantage of the particular shape of the definitions. The formula \(\varphi \) necessarily has the form \(u \equiv t\). By Orthogonality, it follows that \(\overline{\rho }(t)\) is the unique term such that \(\overline{\rho }(u) \equiv ^{\downarrow }\overline{\rho }(t)\). We have two cases:
-
If u is a constant instance \(c_\sigma \), then by the definition of
 we have
we have  . But then
. But then  , that is,
, that is,  , follows from \(\textsc {(Fact)}\) applied with the reflexivity axiom.
, follows from \(\textsc {(Fact)}\) applied with the reflexivity axiom. -
If u is a type \(\sigma \) and \(t : \tau \rightarrow {\mathsf {bool}}\), then \(\overline{\rho }(\varphi )\) is \(\overline{\rho }(\sigma ) \equiv ^{\downarrow }\overline{\rho (t)}\). In other words, \(\overline{\rho }(\varphi )\) has the format of a HOL type definition, just like \(\varphi \). Hence,
 is seen to be an instance of
is seen to be an instance of  , namely,
, namely, 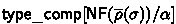 together with
together with  substituted for the first quantifier. Hence
substituted for the first quantifier. Hence  follows from \(\textsc {(Fact)}\) applied with
follows from \(\textsc {(Fact)}\) applied with  , followed by \(\forall \)-instantiation (the latter being the standardly derived rule for \(\forall \)).
, followed by \(\forall \)-instantiation (the latter being the standardly derived rule for \(\forall \)).
In summary, our HOLC translation of overloading emulates overloading itself in that it treats the defined constant instances \(c_\tau \) as being disconnected from their “mother” instances \(c_{{{\mathsf {tpOf}}}(c)}\). The translation is sound thanks to the fact that the considered theory has no axioms about these constants besides the overloaded definitions. This sound translation immediately allows us to reach our overall goal:
Proof of Theorem 1
(Consistency of Isabelle/HOL). By contradiction. Let \(D;\emptyset \vdash {\mathsf {{False}}}\). Then by Theorem 7, we obtain  and since
and since  , we derive contradiction with Theorem 3. \(\square \)
, we derive contradiction with Theorem 3. \(\square \)
4 Application: Logical Extensions
We introduced HOLC as an auxiliary for proving the consistency of Isabelle/HOL’s logic. However, a natural question that arises is whether HOLC would be itself a practically useful extension. We cannot answer this question yet, beyond noting that it would be a significant implementation effort due to the need to reorganize types as mutually dependent with terms. Over the years, some other proposals to go beyond HOL arose. For example, an interesting early proposal by Melham to extend the terms with explicit type quantifiers [34] was never implemented. Homeier’s HOL\(_\omega \) [22], an implemented and currently maintained extension of HOL with first-class type constructors, is another example.
A strong argument for using HOL in theorem proving is that it constitutes a sweet spot between expressiveness and simplicity. The expressiveness part of the claim is debatable—and has been challenged, as shown by the above examples, as well as by Isabelle/HOL itself which extends HOL in a nontrivial way. In our recent work we joined the debate club and advocated a new sweet spot for HOL (and for Isabelle/HOL, respectively) [30] by introducing local type definitions and an unoverloading rule expressing parametricity. HOLC plays a special role in this proposal because we use it to prove the extensions’ consistency.
In the following, we first introduce and motivate the extensions (Sect. 4.1), and then discuss how we applied HOLC to justify their consistency and why our previous ground semantic [29] is not suitable for this job (Sect. 4.2).
4.1 Two Extensions for Traveling from Types to Sets
We start with a theorem stating that all compact sets are closed in T2 spaces (a topological space), whose definition uses an overloaded constant  :
:

Since we quantify over spaces defined on \(\alpha \) here, the theorem is not applicable to spaces defined on a proper subset A of \(\alpha \). Let us recall that types and sets are different syntactic categories in HOL. Defining a new ad hoc type isomorphic to A is undesirable or not even allowed since A can be an open term. Thus a more flexible theorem quantifying over all nonempty carriers A and unary predicates \( open \) forming a T2 space is needed:

As the proof automation works better with types, ideally one should only prove type-based theorems such as (26) and automatically obtain set-based theorems such as (27). Unfortunately, this is not possible in HOL, which is frustrating given that (26) and (27) are semantically equivalent (in the standard interpretation of HOL types).
To address the discrepancy and achieve the automatic translation, we extended the logic of Isabelle/HOL by two new rules: Local Typedef (LT) and Unoverloading (UO).

where \((\beta \approx A)^{{ abs }}_{{ rep }}\) means that \(\beta \) is isomorphic to A via morphisms \({ abs }\) and \({ rep }\); basically the core of the formula (1) from Sect. 2.2, where for notation convenience we identify the set A with its characteristic predicate \(\lambda x.\,x \in A\). The rule allows us to assume the existence of a type isomorphic to a nonempty set A (which syntactically is a possibly open term) inside of a proof.
To formulate (UO), let us recall that \(\rightsquigarrow ^{\downarrow }\) is the substitutive closure of the constant–type dependency relation \(\rightsquigarrow \) from Sect. 2.2 on page 8 and let us define \(\varDelta _c\) to be the set of all types for which the constant c was overloaded. The notation \(\sigma \not \le S\) means that \(\sigma \) is not an instance of any type in S. We write \(\rightsquigarrow ^{\downarrow +}\) for the transitive closure of \(\rightsquigarrow ^{\downarrow }\).

Thus, (UO) tells us that if a constant c was not overloaded for \(\sigma \) (or a more general type), the meaning of the constant instance \(c_\sigma \) is unrestricted, i.e., it behaves as a free term variable of the same type. That is to say, the truth of a theorem \(\varphi \) containing \(c_\sigma \) cannot depend on the definition of \(c_\tau \) for some \(\tau < \sigma \). In summary, (UO) imposes a certain notion of parametricity, which is willing to cohabitate with ad hoc overloading.
We use the two rules in the translation as follows: the (UO) rule allows us to compile out the overloaded constants from (26) (by a dictionary construction) and thus obtain

Then we fix a nonempty set A, locally “define” a type \(\beta \) isomorphic to A by (LT) and obtain (27) from the \(\beta \)-instance of (28) along the isomorphism between \(\beta \) and A.
The extensions have already been picked up by Isabelle/HOL power users for translating between different representations of matrices [12, 13], for implementing a certified and efficient algorithm for factorization [11], and for tightly integrating invariants in proof rules for a probabilistic programming language [33].
4.2 Consistency of the Extensions
We will fist show that HOL + (LT) is consistent by showing (LT) to be admissible in HOLC (as a straightforward consequence of  ).
).
Theorem 10
The inference system consisting of the deduction rules of Isabelle/HOL and the (LT) rule is consistent (in that it cannot prove \({\mathsf {{False}}}\)).
Proof sketch. It is enough if we show that for every step

in a HOL proof, we can construct a step in a HOLC proof of  given
given


The side-condition of the (LT) (freshness of \(\beta \)) transfers into HOLC: if \(\beta \) is fresh for some \(u \in \mathsf {{Type}}\cup {{\textsf {Term}}}\), it must also be fresh for  . This follows from the fact that unfolding a (type or constant) definition \(u \equiv t\) cannot introduce new type variables since we require \({{\textsf {TV}}}(t) \subseteq {{\textsf {TV}}}(u)\). Thus we obtain
. This follows from the fact that unfolding a (type or constant) definition \(u \equiv t\) cannot introduce new type variables since we require \({{\textsf {TV}}}(t) \subseteq {{\textsf {TV}}}(u)\). Thus we obtain

an instance of (30) where we substituted the witness  for \(\beta \). As a last step, we discharge the antecedent of (31) by using
for \(\beta \). As a last step, we discharge the antecedent of (31) by using  (with the help of (29)) and obtain the desired
(with the help of (29)) and obtain the desired  . \(\square \)
. \(\square \)
We were also able to prove Theorem 10 by using our previous ground semantics, as discussed in Kunčar’s thesis [26, Sect. 7.2]. The proof is more technically elaborate and the main idea is to prove that the following principle holds in the semantic world of HOL:

Working in HOLC gives us the advantage to get closer to (\(\star \)) in the following sense: for every nonempty set \(A : \sigma \,{\mathsf {set}}\), not only we can postulate that there always exists a type isomorphic to A, but we can even directly express such a type in HOLC as the comprehension  . That is basically what the axiom
. That is basically what the axiom  tells us. Thus, informally speaking, the property (\(\star \)) is more first-class in HOLC than in HOL.
tells us. Thus, informally speaking, the property (\(\star \)) is more first-class in HOLC than in HOL.
In contrast to (LT), we could not use the ground semantics for the consistency of (UO) and this is where HOLC shows its power.
Theorem 11
The inference system consisting of the deduction rules of Isabelle/HOL, the (LT) rule and the (UO) rule is consistent.
Proof sketch. We will first argue that HOLC + (UO) (without its side-conditions, since they do not make sense in HOLC) is still a consistent logic. This means, from \(\varphi [c_\sigma /x_\sigma ]\) we can derive \(\forall x_\sigma .\;\varphi \) in HOLC + (UO). W.l.o.g. let us assume that the interpretation of type constructors in the semantics of HOLC from Sect. 3.2 is nonoverlapping. Since HOLC does not contain any definitions, we interpret \(c_\sigma \) arbitrarily (as long as the value belongs to the interpretation of \(\sigma \)) in the model construction for HOLC. That is to say, the proof of consistency does not rely on the actual value of \(c_\sigma \)’s interpretation, hence we can replace \(c_\sigma \) by a term variable \(x_\sigma \). Therefore the formula \(\varphi \) must be fulfilled for every evaluation of \(x_\sigma \).
The second step is to show that  is a sound embedding of Isabelle/HOL + (LT) + (UO) into HOLC + (UO). Since we have shown that the translation of (LT) is admissible in HOLC, we only need to focus on (UO). The first side condition of (UO) guarantees that unfolding by
is a sound embedding of Isabelle/HOL + (LT) + (UO) into HOLC + (UO). Since we have shown that the translation of (LT) is admissible in HOLC, we only need to focus on (UO). The first side condition of (UO) guarantees that unfolding by  does not introduce any new \(c_\sigma \) and the second one guarantees that
does not introduce any new \(c_\sigma \) and the second one guarantees that  does not unfold any \(c_\sigma \). Therefore the substitution \([c_\sigma /x_\sigma ]\) commutes with
does not unfold any \(c_\sigma \). Therefore the substitution \([c_\sigma /x_\sigma ]\) commutes with  , i.e.,
, i.e.,  . \(\square \)
. \(\square \)
The reason we could not use the ground semantics to prove Theorem 11 is because the semantics is too coarse to align with the meaning of (UO): that the truth of a theorem \(\varphi \) stating a property of \(c_\sigma \) cannot depend on the fact that a proper instance of \(c_\sigma \), say, \(c_\tau \) for \(\tau < \sigma \), was already overloaded, say, by a definition \(c_\tau \equiv t\). In semantic terms, this means that the interpretation of \(c_\sigma \) cannot depend on the interpretation of \(c_\tau \). Recall that in the ground semantics we considered a polymorphic HOL formula \(\varphi \) to be true just in case all its ground type instances are true. (See also the discussion on page 9.) This definition of truth cannot validate (UO). To see this, let us assume that \(\varphi \) is polymorphic only in \(\alpha \) and \(\tau \) is ground. We want to assume the truth of \(\varphi [\sigma /\alpha ][c_\sigma /x_\sigma ]\) and infer the truth of  . In particular, since
. In particular, since  is a ground instance of the latter, we would need to infer that
is a ground instance of the latter, we would need to infer that  is true, and in particular that \(\varphi [\tau /\alpha ][c_\tau /x_\tau ]\) is true. But this is impossible, since the interpretation of \(c_\tau \) in \(\varphi [\tau /\alpha ][c_\tau /x_\tau ]\) is fixed and dictated by the definitional theorem \(c_\tau \equiv t\).
is true, and in particular that \(\varphi [\tau /\alpha ][c_\tau /x_\tau ]\) is true. But this is impossible, since the interpretation of \(c_\tau \) in \(\varphi [\tau /\alpha ][c_\tau /x_\tau ]\) is fixed and dictated by the definitional theorem \(c_\tau \equiv t\).
5 Conclusions and Related Work
It took the Isabelle/HOL community almost twenty years to reach a definitional mechanism that is consistent by construction, w.r.t. both types and constants.Footnote 7 This paper, which presents a clean syntactic argument for consistency, is a culmination of previous efforts by Wenzel [48], Obua [38], ourselves [27, 29], and many other Isabelle designers and developers.
The key ingredients of our proof are a type-instantiation restricted version of HOL deduction and HOLC, an extension of HOL with comprehension types. HOLC is similar to a restriction of Coq’s Calculus of Inductive Constructions (CiC) [8], where: (a) proof irrelevance and excluded middle axioms are enabled; (b) polymorphism is restricted to rank 1; (c) the formation of (truly) dependent product types is suppressed. However, unlike CiC, HOLC stays faithful to the HOL tradition of avoiding empty types. HOLC also bears some similarities to HOL with predicate subtyping [43] as featured by PVS [44]. Yet, HOLC does not have real subtyping: from \(t : \sigma \rightarrow {\mathsf {bool}}\) and  we cannot infer
we cannot infer  . Instead, HOLC retains HOL’s separation between a type defined by comprehension and the original type: the former is not included, but merely embedded in the latter. Comprehension types are also known in the programming language literature as refinement types [16].
. Instead, HOLC retains HOL’s separation between a type defined by comprehension and the original type: the former is not included, but merely embedded in the latter. Comprehension types are also known in the programming language literature as refinement types [16].
Wiedijk defines stateless HOL [49], a version of HOL where types and terms carry definitions in their syntax. Kumar et al. [25] define a translation from standard (stateful) HOL with definitions to stateless HOL, on the way of proving the consistency of both. Their translation is similar to our HOL to HOLC translation, in that it internalizes HOL definitions as part of “stateless” formulas in a richer logic.
Although a crucial property, consistency is nevertheless rather weak. One should legitimately expect definitions to enjoy a much stronger property: that they can be compiled away without affecting provability not in a richer logic (like HOLC), but in HOL itself. Wenzel calls this property “meta-safety” and proves it for Isabelle/HOL constant definitions [48]. In particular, meta-safety yields proof-theoretic conservativity, itself stronger than consistency: if a formula that contains no defined item is deducible from a definitional theory, then it is deducible in the core (definition-free) logic. Meta-safety and conservativity for arbitrary definitional theories (factoring in not only constant, but also type definitions) are important meta-theoretic problems, which seem to be open not only for Isabelle/HOL, but also for standard HOL [2]. We leave them as future work.
Notes
- 1.
There are other specification schemes supported by some HOL provers, allowing for more abstract (under)specification of constants—but these schemes are known to be captured or over-approximated by the standard (equational) definition scheme [5].
- 2.
To improve readability, in the examples we use a simplified Isabelle syntax. To run these examples in Isabelle, one must enclose in overloading blocks the overloaded definitions of constants and add the overloaded attribute to type definitions that depend on overloaded constants; in addition, one must provide nonemptiness proofs for type definitions [47, Sect. 11(3,7)]. Note also that Isabelle uses \(\Rightarrow \) instead of \(\rightarrow \) for function types and : : instead of : for typing.
- 3.
Isabelle/HOL implements a type-class infrastructure allowing fine control over such instantiations. In this case, \(\alpha \) is assumed to be of type class \({{\mathsf {zero}}}\); then \({\mathsf {real}}\), \(\alpha \;{\mathsf {list}}\) etc. are registered as members of \({{\mathsf {zero}}}\) as soon as 0 is defined for them. Polymorphic properties can also be associated to type classes, and need to be verified upon instantiation. Type classes do not require any logical extension, but are representable as predicates inside the logic—[48, Sect. 5] explains the mechanism in detail.
- 4.
The philosophical dispute about foundations is far from having come to an end [4], and unfortunately tends to obscure what should be a well-defined mathematical problem: the consistency of the Isabelle/HOL logical system (which is of course not the same as the overall reliability of the Isabelle/HOL implementation).
- 5.
Isabelle/HOL is a complex software system, allowing interaction at multiple levels, including by the insertion of ML code. What we care about here is of course an abstract notion of an Isabelle/HOL development—employing the logical mechanisms alone.
- 6.
Reynolds’s result of course refers to (higher-rank) parametric polymorphism.
- 7.
Isabelle is by no means the only prover with longstanding foundational issues [29, Sect. 1].
References
Isabelle Foundation & Certification (2015). https://lists.cam.ac.uk/pipermail/cl-isabelle-users/2015-September/thread.html
Conservativity of HOL constant and type definitions (2016). https://sourceforge.net/p/hol/mailman/message/35448054/
The HOL system logic (2016). https://sourceforge.net/projects/hol/files/hol/kananaskis-10/kananaskis-10-logic.pdf
Type definitions in Isabelle; article “A Consistent Foundation for Isabelle/HOL” by Kunčar/Popescu (2016). https://lists.cam.ac.uk/pipermail/cl-isabelle-users/2016-August/thread.html
Arthan, R.: On definitions of constants and types in HOL. J. Autom. Reason. 56(3), 205–219 (2016)
Barras, B.: Sets in Coq, Coq in sets. J. Formal. Reason. 3(1), 29–48 (2010)
Berghofer, S., Wenzel, M.: Inductive datatypes in HOL – lessons learned in formal-logic engineering. In: Bertot, Y., Dowek, G., Théry, L., Hirschowitz, A., Paulin, C. (eds.) TPHOLs 1999. LNCS, vol. 1690, pp. 19–36. Springer, Heidelberg (1999). doi:10.1007/3-540-48256-3_3
Bertot, Y., Casteran, P.: Interactive Theorem Proving and Program Development. Coq’Art: The Calculus of Inductive Constructions. Springer, Heidelberg (2004)
Blanchette, J.C., Popescu, A., Traytel, D.: Foundational extensible corecursion. In: ICFP 2015. ACM (2015)
Bulwahn, L., Krauss, A., Haftmann, F., Erkök, L., Matthews, J.: Imperative functional programming with Isabelle/HOL. In: Mohamed, O.A., Muñoz, C., Tahar, S. (eds.) TPHOLs 2008. LNCS, vol. 5170, pp. 134–149. Springer, Heidelberg (2008). doi:10.1007/978-3-540-71067-7_14
Divasón, J., Joosten, S., Thiemann, R., Yamada, A.: A formalization of the Berlekamp-Zassenhaus factorization algorithm. In: CPP, pp. 17–29 (2017)
Divasón, J., Kunčar, O., Thiemann, R., Yamada, A.: Certifying exact complexity bounds for matrix interpretations. In: LCC (2016)
Divasón, J., Kunčar, O., Thiemann, R., Yamada, A.: Perron-Frobenius theorem for spectral radius analysis. Archive of Formal Proofs (2016). https://www.isa-afp.org/entries/Perron_Frobenius.shtml
Esparza, J., Lammich, P., Neumann, R., Nipkow, T., Schimpf, A., Smaus, J.-G.: A fully verified executable LTL model checker. In: Sharygina, N., Veith, H. (eds.) CAV 2013. LNCS, vol. 8044, pp. 463–478. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39799-8_31
Fallenstein, B., Kumar, R.: Proof-producing reflection for HOL - with an application to model polymorphism. In: ITP, pp. 170–186 (2015)
Freeman, T., Pfenning, F.: Refinement types for ML. In: PLDI, pp. 268–277 (1991)
Geuvers, H.: Proof assistants: history, ideas and future. Sadhana 34(1), 3–25 (2009)
Gordon, M.J.C., Melham, T.F. (eds.): Introduction to HOL: A Theorem Proving Environment for Higher Order Logic. Cambridge University Press, Cambridge (1993)
Haftmann, F., Nipkow, T.: Code generation via higher-order rewrite systems. In: Blume, M., Kobayashi, N., Vidal, G. (eds.) FLOPS 2010. LNCS, vol. 6009, pp. 103–117. Springer, Heidelberg (2010). doi:10.1007/978-3-642-12251-4_9
Harrison, J.: HOL Light: an overview. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 60–66. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_4
Holger Blasum, O.H., Tverdyshev, S.: Euro-mils: secure European virtualisation for trustworthy applications in critical domains - formal methods used. www.euromils.eu/downloads/Deliverables/Y2/2015-EM-UsedFormalMethods-WhitePaper-October2015.pdf
Homeier, P.V.: The HOL-Omega logic. In: Berghofer, S., Nipkow, T., Urban, C., Wenzel, M. (eds.) TPHOLs 2009. LNCS, vol. 5674, pp. 244–259. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03359-9_18
Kanav, S., Lammich, P., Popescu, A.: A conference management system with verified document confidentiality. In: Biere, A., Bloem, R. (eds.) CAV 2014. LNCS, vol. 8559, pp. 167–183. Springer, Heidelberg (2014). doi:10.1007/978-3-319-08867-9_11
Klein, G., Andronick, J., Elphinstone, K., Heiser, G., Cock, D., Derrin, P., Elkaduwe, D., Engelhardt, K., Kolanski, R., Norrish, M., Sewell, T., Tuch, H., Winwood, S.: seL4: formal verification of an operating-system kernel. Commun. ACM 53(6), 107–115 (2010)
Kumar, R., Arthan, R., Myreen, M.O., Owens, S.: HOL with definitions: semantics, soundness, and a verified implementation. In: Klein, G., Gamboa, R. (eds.) ITP 2014. LNCS, vol. 8558, pp. 308–324. Springer, Heidelberg (2014). doi:10.1007/978-3-319-08970-6_20
Kunčar, O.: Types, abstraction and parametric polymorphism in higher-order logic. Ph.D. thesis, Fakultät für Informatik, Technische Universität München (2016). http://www21.in.tum.de/~kuncar/documents/kuncar-phdthesis.pdf
Kunčar, O.: Correctness of Isabelle’s cyclicity checker: implementability of overloading in proof assistants. In: CPP, pp. 85–94 (2015)
Kunčar, O., Popescu, A.: A Consistent Foundation for Isabelle/HOL - Extended Version. http://www21.in.tum.de/~kuncar/kuncar-popescu-isacons2016.pdf
Kunčar, O., Popescu, A.: A consistent foundation for Isabelle/HOL. In: Urban, C., Zhang, X. (eds.) ITP 2015. LNCS, vol. 9236, pp. 234–252. Springer, Heidelberg (2015). doi:10.1007/978-3-319-22102-1_16
Kunčar, O., Popescu, A.: From types to sets by local type definitions in higher-order logic. In: Blanchette, J.C., Merz, S. (eds.) ITP 2016. LNCS, vol. 9807, pp. 200–218. Springer, Heidelberg (2016). doi:10.1007/978-3-319-43144-4_13
Kunčar, O., Popescu, A.: Comprehending Isabelle/HOL’s consistency. Technical report (2017). http://andreipopescu.uk/pdf/compr_IsabelleHOL_cons_TR.pdf
Lochbihler, A.: Verifying a compiler for Java threads. In: Gordon, A.D. (ed.) ESOP 2010. LNCS, vol. 6012, pp. 427–447. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11957-6_23
Lochbihler, A.: Probabilistic functions and cryptographic oracles in higher order logic. In: Thiemann, P. (ed.) ESOP 2016. LNCS, vol. 9632, pp. 503–531. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49498-1_20
Melham, T.F.: The HOL logic extended with quantification over type variables. In: TPHOLs, pp. 3–17 (1992)
Nipkow, T., Paulson, L., Wenzel, M.: Isabelle/HOL - A Proof Assistant for Higher-Order Logic. LNCS, vol. 2283. Springer, Heidelberg (2002)
Nipkow, T., Klein, G.: Concrete Semantics - With Isabelle/HOL. Springer, Heidelberg (2014)
Nipkow, T., Snelting, G.: Type classes and overloading resolution via order-sorted unification. In: Hughes, J. (ed.) FPCA 1991. LNCS, vol. 523, pp. 1–14. Springer, Heidelberg (1991). doi:10.1007/3540543961_1
Obua, S.: Checking conservativity of overloaded definitions in higher-order logic. In: Pfenning, F. (ed.) RTA 2006. LNCS, vol. 4098, pp. 212–226. Springer, Heidelberg (2006). doi:10.1007/11805618_16
Owre, S., Shankar, N.: The formal semantics of PVS, SRI Technical report, March 1999. http://www.csl.sri.com/papers/csl-97-2/
Paulson, L.: Personal communication (2014)
Pitts, A.: The HOL logic. In: Introduction to HOL: A Theorem Proving Environment for Higher Order Logic, pp. 191–232 (1993). Gordon and Melham [18]
Reynolds, J.C.: Polymorphism is not set-theoretic. In: Kahn, G., MacQueen, D.B., Plotkin, G. (eds.) SDT 1984. LNCS, vol. 173, pp. 145–156. Springer, Heidelberg (1984). doi:10.1007/3-540-13346-1_7
Rushby, J.M., Owre, S., Shankar, N.: Subtypes for specifications: predicate subtyping in PVS. IEEE Trans. Softw. Eng. 24(9), 709–720 (1998)
Shankar, N., Owre, S., Rushby, J.M.: PVS Tutorial. Computer Science Laboratory, SRI International, Menlo Park (1993)
Traytel, D., Popescu, A., Blanchette, J.C.: Foundational, compositional (co)datatypes for higher-order logic: category theory applied to theorem proving. In: LICS, pp. 596–605 (2012)
Wadler, P., Blott, S.: How to make ad-hoc polymorphism less ad-hoc. In: POPL (1989)
Wenzel, M.: The Isabelle/Isar reference manual (2016). http://isabelle.in.tum.de/doc/isar-ref.pdf
Wenzel, M.: Type classes and overloading in higher-order logic. In: Gunter, E.L., Felty, A. (eds.) TPHOLs 1997. LNCS, vol. 1275, pp. 307–322. Springer, Heidelberg (1997). doi:10.1007/BFb0028402
Wiedijk, F.: Stateless HOL. In: TYPES, pp. 47–61 (2009)
Acknowledgments
We thank Tobias Nipkow, Larry Paulson, Makarius Wenzel, and the members of the Isabelle mailing list for inspiring and occasionally intriguing opinions and suggestions concerning the foundations of Isabelle/HOL. We also thank the reviewers for suggestions on how to improve the presentation and for indicating related work. Kunčar is supported by the German Research Foundation (DFG) grant “Security Type Systems and Deduction” (Ni 491/13-3) in the priority program “RS\(^3\) – Reliably Secure Software Systems” (SPP 1496). Popescu is supported by the UK Engineering and Physical Sciences Research Council (EPSRC) starting grant “VOWS – Verification of Web-based Systems” (EP/N019547/1).
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Kunčar, O., Popescu, A. (2017). Comprehending Isabelle/HOL’s Consistency. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_27
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_27
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)





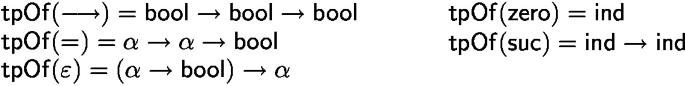
 is well-formed in HOLC.
is well-formed in HOLC.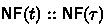 .
. we have
we have  . But then
. But then 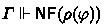 , that is,
, that is,  , follows from
, follows from  is seen to be an instance of
is seen to be an instance of  , namely,
, namely, 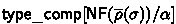 together with
together with  substituted for the first quantifier. Hence
substituted for the first quantifier. Hence 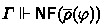 follows from
follows from  , followed by
, followed by 