Abstract
We present a general methodology for adding support for higher-order abstract syntax definitions and first-class contexts to an existing ML-like language. As a consequence, low-level infrastructure that deals with representing variables and contexts can be factored out. This avoids errors in manipulating low-level operations, eases the task of prototyping program transformations and can have a major impact on the effort and cost of implementing such systems.
We allow programmers to define syntax in a variant of the logical framework LF and to write programs that analyze these syntax trees via pattern matching as part of their favorite ML-like language. The syntax definitions and patterns on syntax trees are then eliminated via a translation using a deep embedding of LF that is defined in ML. We take advantage of GADTs which are frequently supported in ML-like languages to ensure our translation preserves types. The resulting programs can be type checked reusing the ML type checker, and compiled reusing its first-order pattern matching compilation. We have implemented this idea in a prototype written for and in OCaml and demonstrated its effectiveness by implementing a wide range of examples such as type checkers, evaluators, and compilation phases such as CPS translation and closure conversion.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
Writing programs that manipulate other programs is a common activity for a computer scientist, either when implementing interpreters, writing compilers, or analyzing phases for static analysis. This is so common that we have programming languages that specialize in writing these kinds of programs. In particular, ML-like languages are well-suited for this task thanks to recursive data types and pattern matching. However, when we define syntax trees for realistic input languages, there are more things on our wish list: we would like support for representing and manipulating variables and tracking their scope; we want to compare terms up-to \(\alpha \)-equivalence (i.e. the renaming of bound variables); we would like to avoid implementing capture avoiding substitutions, which is tedious and error-prone. ML languages typically offer no high-level abstractions or support for manipulating variables and the associated operations on abstract syntax trees.
Over the past decade, there have been several proposals to add support for defining and manipulating syntax trees into existing programming environments. For example: FreshML [22], the related system Romeo [23], and C\(\alpha \)ml [20] use Nominal Logic [18] as a basis and the Hobbits library for Haskell [25] uses a name based formalism. In this paper, we show how to extend an existing (functional) programming language to define abstract syntax trees with variable binders based on higher-order abstract syntax (HOAS) (sometimes also called \(\lambda \)-trees [11]). Specifically, we allow programmers to define object languages in the simply-typed \(\lambda \)-calculus where programmers use the intentional function space of the simply typed \(\lambda \)-calculus to define binders (as opposed to the extensional function space of ML). Hence, HOAS representations inherit \(\alpha \)-renaming from the simply-typed \(\lambda \)-calculus and we can model object-level substitution for HOAS trees using \(\beta \)-reduction in the underlying simply-typed \(\lambda \)-calculus. We further allow programmers to express whether a given sub-tree in the HOAS tree is closed by using the necessity modality of S4 [6]. This additional expressiveness is convenient to describe that sub-trees in our abstract syntax tree are closed.
Our work follows the pioneering work of HOAS representations in the logical framework LF [9]. On the one hand we restrict it to the simply-typed setting to integrate it smoothly into existing simply-typed functional programming languages such as OCaml, and on the other hand we extend its expressiveness by allowing programmers to distinguish between closed and open parts of their syntax trees. As we analyze HOAS trees, we go under binders and our sub-trees may not remain closed. To model the scope of binders in sub-trees we pair a HOAS tree together with its surrounding context of variables following ideas from Beluga [12, 15]. In addition, we allow programmers to pattern match on such contextual objects, i.e. an HOAS tree together with its surrounding context.
Our contribution is two-fold: First, we present a general methodology for adding support for HOAS tree definitions and first-class contexts to an existing (simply-typed) programming language. In particular, programmers can define simply-typed HOAS definitions in the syntactic framework (SF) based on modal S4 following [6, 12]. In addition, programmers can manipulate and pattern match on well-scoped HOAS trees by embedding HOAS objects together with their surrounding context into the programming language using contextual types [15]. The result is a programming language that can express computations over open HOAS objects. We describe our technique abstractly and generically using a language that we call \(\text {Core-ML}\). In particular, we show how \(\text {Core-ML}\) with first-class support for HOAS definitions and contexts can be translated in into a language \(\text {Core-ML}^{\text {gadt}}\) that supports Generalized Abstract Data Types (GADTs) using a deep (first-order) embedding of SF and first-class contexts (see Fig. 1 for an overview). We further show that our translation preserves types.
Second, we show how this methodology can be realized in OCaml by describing our prototype BabybelFootnote 1. In our implementation of Babybel we take advantage of the sophisticated type system, in particular GADTs, that OCaml provides to ensure our translation is type-preserving. By translating HOAS objects together with their context to a first-order representation in OCaml with GADTs we can also reuse OCaml’s first-order pattern matching compilation allowing for a straightforward compilation. Programmers can also exploit OCaml’s impure features such as exceptions or references when implementing programs that manipulate HOAS syntax trees. We have used Babybel to implement a type-checker, an evaluator, closure conversion (shown in Sect. 2.3 together with a variable counting example and a syntax desugaring examples), and a continuation passing style translation. These examples demonstrate that our approach allows programmers to write programs that operate over abstract syntax trees in a manner that is safe and effective.
Finally, we would like to stress that our translation which eliminates the language extensions and permits programmers to define, analyze and manipulate HOAS trees is not specific to OCaml or even to simple types in our implementation. The same approach could be implemented in Haskell, and with some care (to be really useful it would need an equational theory for substitutions) this technique can be extended to a dependently typed language.
2 Main Ideas
In this section, we show some examples that illustrate the use of Babybel, our proof of concept implementation where we embed the syntactic framework SF inside OCaml. To smoothly integrate SF into OCaml, Babybel defines a PPX filter (a mechanism for small syntax extensions for OCaml). In particular, we use attributes and quoted strings to implement our syntax extension.
2.1 Example: Removing Syntactic Sugar
In this example, we describe the compact and elegant implementation of a compiler phase that de-sugars programs functional programs with let-expressions by translating them into function applications. We first specify the syntax of a simple functional language that we will transform. To do this we embed the syntax specification using this tag:

Inside the  block we will embed our SF specifications.
block we will embed our SF specifications.
Our source language is defined using the type tm. It consists of constants (written as cst), pairs (written as pair), functions (built using lam), applications (built using app), and let-expressions.

Our definition of the source language exploits HOAS using the function space of our syntactic framework SF to represent binders in our object language. For example, the constructor lam takes as an argument a term of type  . Similarly, the definition of let-expressions models variable binding by falling back to the function space of our meta-language, in our case the syntactic framework SF. As a consequence, there is no constructor for variables in our syntactic definition and moreover we can reuse the substitution operation from the syntactic framework SF to model substitution in our object language. This avoids building up our own infrastructure for variables bindings.
. Similarly, the definition of let-expressions models variable binding by falling back to the function space of our meta-language, in our case the syntactic framework SF. As a consequence, there is no constructor for variables in our syntactic definition and moreover we can reuse the substitution operation from the syntactic framework SF to model substitution in our object language. This avoids building up our own infrastructure for variables bindings.
We now show how to simplify programs written in our source language by replacing uses of letpair in terms with projections, and uses of letv by \(\beta \) reduction. Note how we use higher-order abstract syntax to represent let-expressions and abstractions.

To implement this simplification phase we implement an OCaml program rewrite: it analyzes the structure of our terms, calls itself on the sub-terms, and eliminates the use of the let-expressions into simpler constructs. As we traverse terms, our sub-terms may not remain closed. For simplicity, we use the same language as source and target for our transformation. We therefore specify the type of the function rewrite using contextual types pairing the type tm together with a context  in which the term is meaningful inside the tag
in which the term is meaningful inside the tag  .
.

The type can be read: for all contexts  , given a tm object in the context
, given a tm object in the context  , we return a tm object in the same context. In general, contextual types associate a context and a type in the syntactic framework SF. For example if we want to specify a term in the empty context we would write
, we return a tm object in the same context. In general, contextual types associate a context and a type in the syntactic framework SF. For example if we want to specify a term in the empty context we would write  or for a term that depends on some context with at least one variable and potentially more we would write
or for a term that depends on some context with at least one variable and potentially more we would write  .
.
We now implement the function rewrite by pattern matching on the structure of a contextual term. In Babybel, contextual terms are written inside boxes ( ) and contextual patterns inside (
) and contextual patterns inside ( ).
).

Note that we are pattern matching on potentially open terms. Although we do not write the context  explicitly, in general patterns may mention their context (i.e.:
explicitly, in general patterns may mention their context (i.e.:  Footnote 2. As a guiding principle, we may omit writing contexts, if they do not mention variables explicitly and are irrelevant at run-time. Inside patterns or terms, we specify incomplete terms using quoted variables (e.g.: ’m). Quoted variables are an ’unboxing’ of a computational expression inside the syntactic framework SF. The quote signals that we are mentioning the computational variable inside SF.
Footnote 2. As a guiding principle, we may omit writing contexts, if they do not mention variables explicitly and are irrelevant at run-time. Inside patterns or terms, we specify incomplete terms using quoted variables (e.g.: ’m). Quoted variables are an ’unboxing’ of a computational expression inside the syntactic framework SF. The quote signals that we are mentioning the computational variable inside SF.
The interesting cases are the let-expressions. For them, we perform the rewriting according to the two rules given earlier. The syntax of the substitutions puts in square brackets the terms that will be substituted for the variables. We consider contexts and substitutions ordered, this allows for efficient implementations and more lightweight syntax (e.g.: substitutions omit the name of the variables because contexts are ordered). Importantly, the substitution is an operation that is eagerly applied during run-time and not part of the representation. Consequently, the representation of the terms remains normal and substitutions cannot be written in patterns. We come back to this design decision later.
To translate contextual SF objects and contexts, Babybel takes advantage of OCaml’s advanced type system. In particular, we use Generalized Abstract Data Types [4, 26] to index types with the contexts in which they are valid. Type indices, in particular contexts, are then erased at run-time.
2.2 Finding the Path to a Variable
In this example, we compute the path to a specific variable in an abstract syntax tree describing a lambda-term. This will show how to specify particular context shapes, how to pattern match on variables, how to manage our contexts, and how the Babybel extensions interact seamlessly with OCaml’s impure features. For this example, we concentrate on the fragment of terms that consists only of abstractions and application which we repeat here.

To find the first occurrence of a particular variable in the HOAS tree, we use backtracking that we implement using the user-defined OCaml exception Not_found. To model the path to a particular variable occurrence in the HOAS tree, we define an OCaml data type step that describes the individual steps we take and finally model a path as a list of individual steps.

The main function path_aux takes as input a term that lives in a context with at least one variable and returns a path to the occurrence of the top-most variable or an empty list, if the variable is not used. Its type is:

We again quantify over all contexts  and require that the input term is meaningful in a context with at least one variable. This specification simply excludes closed terms since there would be no top-most variable. Note also how we mix in the type annotation to this function both contextual types and OCaml data types.
and require that the input term is meaningful in a context with at least one variable. This specification simply excludes closed terms since there would be no top-most variable. Note also how we mix in the type annotation to this function both contextual types and OCaml data types.

All patterns in this example make the context explicit, as we pattern match on the context to identify whether the variable we encounter refers to the top-most variable declaration in the context. The underscore simply indicates that there might be more variables in the context. The first case, matches against the bound variable x. The second case has a special pattern with the sharp symbol, the pattern #y matches against any variable in the context _, x. Because of the first pattern if it had been x it would have matched the first case. Therefore, it simply raises the exception to backtrack to the last choice we had.
The case for lambda expressions is interesting because the recursive call happens in an extended context. Furthermore, in order to keep the variable we are searching for on top, we need to swap the two top-most variables. For that purpose, we apply the  substitution. In this substitution the underscore stands for the identity on the rest of the context, or more precisely, the appropriate shift in our internal representation that relies on de Bruijn encoding. Once elaborated, this substitution becomes
substitution. In this substitution the underscore stands for the identity on the rest of the context, or more precisely, the appropriate shift in our internal representation that relies on de Bruijn encoding. Once elaborated, this substitution becomes  where the shift by two arises, because we are swapping variables as opposed to instantiating them.
where the shift by two arises, because we are swapping variables as opposed to instantiating them.
The final case is for applications. We first look on the left side and if that raises an exception we catch it and search again on the right. We again use quoted variables (e.g.: ’m) to bind and refer to ML variables in patterns and terms of the syntactic framework and more generally be able to describe incomplete terms.

The get_path function has the same type as the path_aux function. It simply handles the exception and returns an empty path in case that variable x is not found in the term.
2.3 Closure Conversion
In the final example, we describe the implementation of a naive algorithm for closure conversion for untyped \(\lambda \)-terms following [3]. We take advantage of the syntactic framework SF to represent source terms (using the type family tm) and closure-converted terms (using the type family ctm). In particular, we use SF’s closed modality box to ensure that all functions in the target language are closed. This is impossible when we simply use LF as the specification framework for syntax as in [3]. We omit here the definition of lambda-terms, our source language, that was given in the previous section and concentrate on the target language ctm.

Applications in the target language are defined using the constructor capp and simply take two target terms to form an application. Functions (constructor clam), however, take a btm object wrapped in \(\mathtt {\{\}}\) braces. This means that the object inside the braces is closed. The curly braces denote the internal closed modality of the syntactic framework. As the original functions may depend on variables in the environment, we need closures where we pair a function with a substitution that points to the appropriate environment. We define our own substitutions explicitly, because they are part of the target language and the built-in substitution is an operation on terms that is eagerly computed away. Inside the body of the function, we need to bind all the variables from the environment that the body uses such that later we can instantiate them applying the substitution. This is achieved by defining multiple bindings using constructors bind and embed inside the term.
When writing a function that translates between representations, their open terms depend on contexts that store assumptions of different representations and it is often the case that one needs to relate these contexts. In our example here we define a context relation that keeps the input and output contexts in sync using a GADT data type rel in OCaml where we model contexts as types. The relation statically checks correspondence between contexts, but it is also available at run-time (i.e. after type-erasure).

The function lookup searches for related variables in the context relation. If we have a source context  and a target context
and a target context  , then we consider two variable cases: In the first case, we use matching to check that we are indeed looking for the top-most variable x and we simply return the corresponding target variable. If we encounter a variable from the context, written as ##v, then we recurse in the smaller context stripping off the variable declaration x. Note that ##v denotes a variable from the context _, that is not x, while #v describes a variable from the context _, x, i.e. it could be also x. The recursive call returns the corresponding variable v1 in the target context that does not include the variable declaration x. We hence need to weaken v1 to ensure it is meaningful in the original context. We therefore associate ’v1 with the identity substitution for the appropriate context, namely:
, then we consider two variable cases: In the first case, we use matching to check that we are indeed looking for the top-most variable x and we simply return the corresponding target variable. If we encounter a variable from the context, written as ##v, then we recurse in the smaller context stripping off the variable declaration x. Note that ##v denotes a variable from the context _, that is not x, while #v describes a variable from the context _, x, i.e. it could be also x. The recursive call returns the corresponding variable v1 in the target context that does not include the variable declaration x. We hence need to weaken v1 to ensure it is meaningful in the original context. We therefore associate ’v1 with the identity substitution for the appropriate context, namely:  . In this case, it will be elaborated into a one variable shift in the internal de Bruijn representation that is used in our implementation. The last case returns an exception whenever we are trying to look up in the context something that is not a variable.
. In this case, it will be elaborated into a one variable shift in the internal de Bruijn representation that is used in our implementation. The last case returns an exception whenever we are trying to look up in the context something that is not a variable.
As we cannot express at the moment in the type annotation that the input to the lookup function is indeed only a variable from the context \(\gamma \) and not an arbitrary term, we added another fall-through case for when the context is empty. In this case the input term cannot be a variable, as it would be out of scope.
Finally, we implement the function conv which takes an untyped source term in a context  and a relation of source and target variables, described by
and a relation of source and target variables, described by  and returns the corresponding target term in the target context
and returns the corresponding target term in the target context  .
.

The core of the translation is defined in functions conv, envr, and close. The main function is conv. It is implemented by recursion on the source term. There are three cases: (i) source variables simply get translated by looking them up in the context relation, (ii) applications just get recursively translated each term in the application, and (iii) lambda expressions are translated recursively by converting the body of the expression in the extended context (notice the recursive call with Both r) and then turning the lambda expression into a closure.
In the first step we generate the closed body by the function close that adds the multiple binders (constructors bind and embed) and generates the closed term. Note that the return type [btm] of close guarantees that the final result is indeed a closed term, because we omit the context. For clarity, we could have written  .
.
Finally, the function envr computes the substitution (represented by the type sub) for the closure.
The implementation of closure conversion shows how to enforce closed terms in the specification, and how to make contexts and their relationships explicit at run-time using OCaml’s GADTs. We believe it also illustrates well how HOAS trees can be smoothly manipulated and integrated into OCaml programs that may use effects.
3 \(\text {Core-ML}\): A Functional Language with Pattern Matching and Data Types
We now introduce \(\text {Core-ML}\), a functional language based on ML with pattern matching and data types. In Sect. 5 we will extend this language to also support contextual types and terms in our syntactic framework SF.
We keep the language design of \(\text {Core-ML}\) minimal in the interest of clarity. However, our prototype implementation which we describe in Sect. 9 supports interaction with all of OCaml’s features such as exceptions, references and GADTs.

In \(\text {Core-ML}\), we declare data-types by adding type formers (D) and type constructors (\(C\)) to the signature (\(\varXi \)). Constructors must be fully-applied. In addition all functions are named and recursive. The language supports pattern matching with nested patterns where patterns consist of just variables and fully applied constructors. We assume that all patterns are linear (i.e. each variable occurs at most once) and that they are covering.
The bi-directional typing rules for \(\text {Core-ML}\) have access to a signature \(\varXi \) and are standard (see Fig. 2). For lack of space, we omit the operational semantics which is standard. We also will not address the details of pattern matching compilation but merely state that it is possible to implement it in an efficient manner using decision trees [1].
4 A Syntactic Framework
In this section we describe the Syntactic Framework (SF) based on S4 [6]. Our framework characterizes only normal forms. All computation is delegated to the ML layer, that will perform pattern matching and substitutions on terms.
4.1 The Definition of SF
The Syntactic Framework (SF) is a simply typed \(\lambda \)-calculus based on S4 where the type system forces all variables to be of base type, and all constants declared in a signature \(\varSigma \) to be fully applied. This simplifies substitution, as variables of base type cannot be applied to other terms, and in consequence, there is no need for hereditary substitution in the specification language. Finally, the syntactic framework supports the box type to describe closed terms [13]. It can also be viewed as a restricted version of the contextual modality in [12] which could be an interesting extension to our work.
Having closed objects enforced at the specification level is not strictly necessary. However, being able to state that some objects are closed in the specification has two distinct advantages: first, the user can specify some objects as closed so their contexts are always empty. This removes the need for some unnecessary substitutions. Second, it allows us to encode more fine-grained invariants and is hence an important specification tool (i.e. when implementing closure conversion in Sect. 2.3).

Figure 3 shows the typing rules for the syntactic framework. Note that constructors always are fully applied (as per rule t-con), and that all variables are of base type as enforced by rules t-var and t-lam.
4.2 Contextual Types
We use contextual types to embed possibly open SF objects in \(\text {Core-ML}\) and ensure that they are well-scoped. Contextual types pair the type A of an SF object together with its surrounding context \(\varPsi \) in which it makes sense. This follows the design of Beluga [3, 15].

Contextual objects, written as \([\hat{\varPsi } \vdash M]\) pair the term M with the variable name context \(\hat{\varPsi }\) to allow for \(\alpha \)-renaming of variables occurring in M. Note how the \(\hat{\varPsi }\) context just corresponds to the context with the typing assumptions erased.
When we embed contextual objects in a programming language we want to refer to variables and expressions from the ambient language, in order to support incomplete terms. Following [12, 15], we extend our syntactic framework SF with two ideas: first, we have incomplete terms with meta-variables to describe holes in terms. As in Beluga, there are two different kinds: quoted variables \(\texttt {'u}\) represent a hole in the term that may be filled by an arbitrary term. In contrast, parameter variables \(\texttt {v}\) represent a hole in a term that may be filled only with some bound variable from the context. Concretely, a parameter variable may be \(\texttt {\#x}\) and describe any concrete variable from a context \(\varPsi \). We may also want to restrict what bound variables a parameter variable describes. For example, if we have two sharp signs (i.e. \(\texttt {\#\#x}\)) the top-most variable declaration is excluded. Intuitively, the number of sharp signs, after the first, in front of x correspond to a weakening (or in de Bruijn lingo the number of shifts). Second, substitution operations allow us to move terms from one context to another.
We hence extend the syntactic framework SF with quoted variables, parameter variables and closures, written as \(M[\sigma ]_{\varPsi }^{\varPhi }\). We annotate the substitution with its domain and range to simplify the typing rule, however our prototype omits these typing annotations and lets type inference infer them.

In addition, we extend the context \(\varGamma \) of the ambient language \(\text {Core-ML}\) to keep track of assumptions that have a contextual type.
Finally, we extend the typing rules of the syntactic framework SF to include quoted variables, parameter variables, closures, and substitutions. We keep all the previous typing rules for SF from Sect. 4 where we thread through the ambient \(\varGamma \), but the rules remain unchanged otherwise.

The rules for quoted variables (t-qvar) and parameter variables (t-pvar) might seem very restrictive as we can only use a meta-variable of type \(\varPsi \vdash \mathbf a \) in the same context \(\varPsi \). As a consequence meta-variables often occur as a closure paired with a substitution (i.e.: \(\texttt {'u}\,[\sigma ]_{\varPsi }^{\varPhi }\)). This leads to the following admissible rule:

The substitution operation is straightforward to define and we omit it here. The next step is to define the embedding of this framework in a programming language that will provide the computational power to analyze and manipulate contextual objects.
5 \(\text {Core-ML}\) with Contextual Types
To embed contextual SF objects into \(\text {Core-ML}\), we extend the syntax of \(\text {Core-ML}\) as follows:

In particular, we allow programmers to directly pattern match on the syntactic structures they define in SF using the case-expression \(\texttt {cmatch}\, e\,\texttt {with}\ \overrightarrow{c}\).
5.1 SF Objects as SF Patterns
The grammar of SF patterns follows the grammar of SF objects.

However, there is an important restriction: closures are not allowed in SF patterns. Intuitively this means that all quoted variables are associated with the identity substitution and hence depend on the entire context in which they occur. Parameter variables may be associated with weakening substitutions. This allows us to easily infer the type of quoted variables and parameter variables as we type check a pattern. This is described by the judgment

We omit these rules as they follow closely the typing rules for SF terms that are given in the previous section. We only show here the interesting rules for parameter patterns. They illustrate the built-in weakening.

Further, the matching algorithm for SF patterns degenerates to simple first-order matching [17] and can be defined straightforwardly. Because of space constraints, we only describe the successful matching operation. However, it is worth considering the matching rules for parameter patterns. As matching will only consider well-typed terms, we know that in the rules  and
and  the variable x is well-typed in the context \(\hat{\varPsi }\).
the variable x is well-typed in the context \(\hat{\varPsi }\).

Finally, it has another important consequence: closures only appear in the branches of case-expressions. As \(\text {Core-ML}\) has a call-by-value semantics, we know the instantiations of quoted variables and parameter variables when they appear in the body of a case-expression and all closures can be eliminated by applying the substitution eagerly.
5.2 Typing Rules for \(\text {Core-ML}\) with Contextual Types
We now add the following typing rules for contextual objects and pattern matching to the typing rules of \(\text {Core-ML}\):

The typing rule for contextual objects (rule t-ctx-obj) simply invokes the typing judgment for contextual objects. Notice, that we need the context \(\varGamma \) when checking contextual objects, as they may contain quoted variables from \(\varGamma \).
Extending the operational semantics to handle contextual SF objects is also straightforward.
6 \(\text {Core-ML}\) with GADTs
So far we reviewed how to support contextual types and contextual objects in a standard functional programming language. This allows us to define syntactic structures with binders and manipulate them with the guarantee that variables will not escape their scopes. This brings some of the benefits of the Beluga system to mainstream languages focusing on writing programs instead of proofs. A naive implementation of this language extension requires augmenting the type checker and operational semantics of the host language. This is a rather significant task – especially if it includes implementing a compiler for the extended language. In this section, we describe how to embed \(\text {Core-ML}\) with contextual types in a functional language with GADTs, called \(\text {Core-ML}^{\text {gadt}}\), based on \(\lambda _{2,G\mu }\) by Xi et al. [26]. The choice of this target language is motivated by the fact that it is close to what realistic typed languages already offer (e.g.: OCaml and Haskell) and it directly lends itself to an implementation.

\(\text {Core-ML}^{\text {gadt}}\) contains polymorphism and GADTs, which makes it a good ersatz OCaml that is still small and easy to reason about. GADTs are particularly convenient, since they allow us to track invariants about our objects in a similar fashion to dependent types. Compared to \(\text {Core-ML}\), \(\text {Core-ML}^{\text {gadt}}\) ’s signatures now store type constants and constructors that are parametrized by other types. We show the typing judgments for the language in Fig. 4.
The operational semantics is fundamentally the same as the semantics for \(\text {Core-ML}\), after all, type information is irrelevant at run-time (i.e. \(\text {Core-ML}^{\text {gadt}}\) has strong type separation). The interested reader can find the operational semantics in [26].
7 Deep Embedding of SF into \(\text {Core-ML}^{\text {gadt}}\)
We now show how to translate objects and types defined in the syntactic framework SF into \(\text {Core-ML}^{\text {gadt}}\) using a deep embedding. We take advantage of the advanced features of \(\text {Core-ML}^{\text {gadt}}\) ’s type system to fully type-check the result. Our representation of SF objects and types is inspired by [2] but uses GADTs instead of full dependent types. We add the idea of typed context shifts, that represent weakening, to be able to completely erase types at run-time.
To ensure SF terms are well-scoped and well-typed, we define SF types in \(\text {Core-ML}^{\text {gadt}}\) and index their representations by their type and context. The following types are only used as indices for GADTs. Because of that, they do not have any term constructors.

We define three type families, one for each of SF’s type constructors. It is important to note the number of type parameters they require. Base types take one parameter: a type from the signature. Function types simply have a source and target type. Finally, boxes contain just one type.
Terms are also indexed by the contexts in which they are valid. To this effect, we define two types to statically represent contexts. Analogously to the representation of types, these two types are only used statically and there will be no instances at run-time. The type nil represents an empty context and thus has no parameters. The constructor cons has two parameters, the first one is the rest of the context and the second one is the type of the top-most variable.

We show the encoding of well-typed SF objects and types in Fig. 5. Every declaration is parametrized with the type of constructors that the user defined inside of the  blocks.
blocks.
The specification takes the form of the type \(\texttt {con} \mathrel {:}(*, *) \rightarrow *\), where \(\texttt {con}\) is the name of a constructor indexed by the type of its parameters and the base type they produce.
Variables and terms are indexed by two types, the first parameter is always their context and the second is their type. The type var represents variables with two constructors: Top represents the variable that was introduced last in the context and if Top corresponds to the de Bruijn index 0 then the constructor Pop represents the successor of the variable that it takes as parameter. It is interesting to consider the parameters of these constructors. Top is simply indexed by its context and type (variables \(\gamma \) and \(\alpha \) respectively). On the other hand, Pop requires three type parameter: the first \(\gamma \) represents a context, \(\alpha \) the resulting type of the variable, and \(\beta \) the type of the extension of the context. These parameter make it so that if we apply the constructor Pop to a variable of type \(\alpha \) in context \(\gamma \), we obtain a variable of type \(\alpha \) in the context \(\gamma \) extended with type \(\beta \).
As mentioned, terms described by the type family tm are indexed by their context and their type. It is interesting to check in some detail how the indices of the term constructors follow the typing rules from Fig. 3. The constructor for lambda terms (Lam), extends the context \(\gamma \) with base type \(\alpha \) and then it produces a term in \(\gamma \) of function type from the base type \(\alpha \) to the type of the body \(\tau \). The constructor for boxes simply forces its body to be closed by using the context type nil. The constructor Var simply embeds variables as terms. Finally the C constructor has two parameters, one is the name of the constructor from the user’s definitions that constrains the type of the second parameter, the other is the term of the appropriated type.
The definition of substitution is a modified presentation of the substitution for well-scoped de Bruijn indices, as for example presented in [2]. We define two types, sub and shift indexed by two contexts, the domain and the range of the substitutions. Substitutions are either a shift (constructor Shift) or the combination of a term for the top-most variable and the rest of the substitution (constructor Dot).
Our implementation differs from Benton et al. [2] in the representation of renamings. Benton et.al define substitutions and renamings, the latter as a way of representing shifts. However to compute a shift, they need the context that they use to index the data-types. Hence, contexts are not erasable during run-time. As we do want contexts to be erasable at run-time, we cannot use renamings. Instead, we replace renamings with typed shifts (defined in type shift), that encode how many variables we are shifting over. This is encoded in the indices of shifts.
Finally, we omit the function implementing the substitution as it is standard We will simply mention that we implement a function apply_sub of type:
\(\forall {\gamma ,\delta ,\tau }\mathrel {.}{\texttt {tm}[\gamma ,\tau ] \rightarrow \texttt {sub}[\gamma ,\delta ] \rightarrow \texttt {tm}[\delta ,\tau ]}\) that applies a substitution moving a term from context \(\gamma \) to context \(\delta \).
8 From \(\text {Core-ML}\) with Contextual Types to \(\text {Core-ML}^{\text {gadt}}\)
In this section, we translate \(\text {Core-ML}\) with contextual types into \(\text {Core-ML}^{\text {gadt}}\). Because our embedding of the syntactic framework SF in \(\text {Core-ML}^{\text {gadt}}\) is intrinsically typed, there is no need to extend the type-checker to accommodate contextual objects. Further, recall that we restricted quoted variables and parameter variables such that the matching operation remains first order. In addition, as our deep embedding uses a representation with canonical names (namely de Bruijn indices), we are able to translate pattern matching into \(\text {Core-ML}^{\text {gadt}}\) ’s pattern matching; thus there is no need to extend the operational semantics of the language.
The translation we describe in this section provides the footprint of an implementation to directly generate OCaml code, as \(\text {Core-ML}^{\text {gadt}}\) is essentially a subset of OCaml. It therefore shows how to extend a functional programming language such as OCaml with the syntactic framework with minimal impact on OCaml’s compiler.
We begin by translating SF types and contexts into \(\text {Core-ML}^{\text {gadt}}\) types. These types are used to index terms in the implementation of SF:

The translation of SF terms is directed by their contextual type \(\varPsi \vdash A\), because it needs the context to perform the translation of names to de Bruijn indices and the types to appropriately index the terms.

There are three kinds of variables in the syntactic framework SF: bound variables, quoted variables and parameter variables. Each kind requires a different translation strategy. Bound variables are translated into de Bruijn indices where the numbers are encoded using the constructors Top and Pop. Quoted variables are simply translated into the \(\text {Core-ML}^{\text {gadt}}\) variables they quote. And finally the parameter variables are translated into a Var constructor to indicate that the resulting expression is an SF variable, and the shifts (indicated by extra ’#’) are translated to applications of the constructor Pop.
Notice how substitutions are not part of the representation. They are translated to the eager application of apply_sub, an OCaml function that performs the substitution. Before we call appy_sub we translate the substitution. This amounts to generating the right shift for empty substitutions and otherwise recursively translating the terms and the substitution.
Translating variables requires computing the de Bruijn index with the appropriate type annotations.
We also need to translate SF patterns into \(\text {Core-ML}^{\text {gadt}}\) expressions with the right structure. The special cases are:
-
Variables are translated to de Bruijn indexes.
-
Quoted variables simply translate to \(\text {Core-ML}^{\text {gadt}}\) variables.
-
Parameter variables translate to a pattern that matches only variables by specifying the Var constructor.
The translation of patterns follows the same line as the translation of terms, however, we do not use the indices of type variables in \(\text {Core-ML}^{\text {gadt}}\) patterns. This is indicated by writing an underscore.

Our main translation of \(\text {Core-ML}\) to \(\text {Core-ML}^{\text {gadt}}\) uses the following main operations:

The translation of \(\text {Core-ML}\) expressions into \(\text {Core-ML}^{\text {gadt}}\) directly follows the structure of programs in \(\text {Core-ML}\) and is type directed to fill in the required types for the \(\text {Core-ML}^{\text {gadt}}\) representation. The translation is as follows:

Translating branches and patterns:

Finally, we define the translation of branches for \(\texttt {cmatch}\, i\,\texttt {with}\ \overrightarrow{c}\). Note how we use the context generated from the pattern to translate the body of the branch.

Finally we show that the translation from \(\text {Core-ML}\) with contextual types into \(\text {Core-ML}^{\text {gadt}}\) preserves types.
Theorem 1
(Main).
-
1.
If \(\varGamma \vdash e\mathrel {\Leftarrow }\tau \) then \(\cdot ;\ulcorner \varGamma \urcorner \vdash \ulcorner e \urcorner _{\varGamma \vdash \tau } \mathrel {:}\ulcorner \tau \urcorner \).
-
2.
If \(\varGamma \vdash i \mathrel {\Rightarrow }\tau \) then \(\cdot ;\ulcorner \varGamma \urcorner \vdash \ulcorner i \urcorner _{\varGamma \vdash \tau } \mathrel {:}\ulcorner \tau \urcorner \).
Our result relies on several lemmas that deal with the other judgments and context lookups:
Lemma 1
(Ambient Context). If \(\varGamma (\texttt {u}) = [\varPsi \vdash \mathbf a ]\) then \( \ulcorner \varGamma \urcorner (u) = \texttt {tm}[ \ulcorner \varPsi \urcorner , \mathbf a ]\).
Lemma 2
(Terms).
-
1.
If \(\varGamma ;\varPsi \vdash M \mathrel {:}A\) then \(\cdot ;\ulcorner \varGamma \urcorner \vdash \ulcorner M \urcorner _{\varPsi \vdash A} \mathrel {:}\ulcorner \varPsi \vdash A \urcorner \).
-
2.
If \(\varGamma ; \varPsi \vdash \sigma \mathrel {:}\varPhi \) then \(\cdot ; \ulcorner \varGamma \urcorner \vdash \ulcorner \sigma \urcorner _ {\varPsi \vdash \varPhi } : \ulcorner \varPsi \vdash \varPhi \urcorner \)
Lemma 3
(Pat.). If \(\vdash pat\mathrel {:}\tau \mathrel {\downarrow }\varGamma \) then \(\cdot \vdash \ulcorner pat \urcorner _{\varPsi \vdash A}^\varGamma \mathrel {:}\ulcorner \tau \urcorner \mathrel {\downarrow }{\varGamma }\).
Lemma 4
(Ctx. Pat.). If \(\varPsi \vdash R\mathrel {:}A\mathrel {\downarrow } \varGamma \) then \(\cdot \vdash \ulcorner R \urcorner _{\varPsi \vdash A}^\varGamma \mathrel {:}\ulcorner \varPsi \vdash A \urcorner \mathrel {\downarrow }{\varGamma }\).
Given our set-up, the proofs are straightforward by induction on the typing derivation.
9 A Proof of Concept Implementation
In this section, we describe the implementationFootnote 3 of Babybel which uses the ideas from previous sections. One major difference is that Babybel translates OCaml programs that use syntax extensions for contextual SF types and terms and translates them into pure OCaml with GADTs. In fact, even our input OCaml programs may use GADTs to for example describe context relations on SF contexts (see also our examples from Sect. 2).
The presence of GADTs in our source language also means that we can specify precise types for functions where we can quantify over contexts. Let’s revisit some of the types of the programs that we wrote earlier in Sect. 2:
-
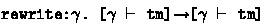 : In this type we implicitly quantify over all contexts g and then we take a potentially open term and return another term in the same context. These constraints imposed in the types are due to being able to index types with types thanks to GADTs.
: In this type we implicitly quantify over all contexts g and then we take a potentially open term and return another term in the same context. These constraints imposed in the types are due to being able to index types with types thanks to GADTs. -
 : In this case we quantify over all contexts, but the input of the function is some term in a non-empty context.
: In this case we quantify over all contexts, but the input of the function is some term in a non-empty context. -
 : This final example shows that we can also use the contexts to index regular OCaml GADTs. In this function we are translating between terms in different representations. To be able to translate between these different context representations, it is necessary to establish a relation between these contexts. So we need to define a special OCaml type (i.e.:rel) that relates variable to variable in each contexts.
: This final example shows that we can also use the contexts to index regular OCaml GADTs. In this function we are translating between terms in different representations. To be able to translate between these different context representations, it is necessary to establish a relation between these contexts. So we need to define a special OCaml type (i.e.:rel) that relates variable to variable in each contexts.
By embedding the SF in OCaml using contextual types, we can combine and use the impure features of OCaml. Our example, in Sect. 2.2 takes advantage of them in our implementation of backtracking with exceptions. Additionally, performing I/O or using references works seamlessly in the prototype.
The presence of GADTs in our target language also makes the actual implementation of Babybel simpler than the theoretical description, as we take advantage of OCaml’s built-in type reconstruction. In addition to GADTs, our implementation depends on several OCaml extensions. We use Attributes from Sect. 7.18 of the reference manual [10] and strings to embed the specification of our signature. We use quoted strings from Sect. 7.20 to implement the boxes for terms ( ) and patterns (
) and patterns ( ). All these appear as annotations in the internal Abstract Syntax Tree in the compiler implementation. To perform the translation (based on Sect. 8) we define a PPX rewriter as discussed in Sect. 23.1 of the OCaml manual. In our rewriter, we implement a parser for the framework SF and translate all the annotations using our embedding.
). All these appear as annotations in the internal Abstract Syntax Tree in the compiler implementation. To perform the translation (based on Sect. 8) we define a PPX rewriter as discussed in Sect. 23.1 of the OCaml manual. In our rewriter, we implement a parser for the framework SF and translate all the annotations using our embedding.
10 Related Work
Babybel and the syntactic framework SF are derived from ideas that originated in proof checkers based on the logical framework LF such as the Twelf system [14]. In the same category are the proof and programming languages Delphin [19] and Beluga [16] that offer a computational language on top of the LF. In many ways, the work that we present in this paper and forms the foundation of Babybel are a distillation of Beluga’s ideas applied to a mainstream programming language. As a consequence, we have shown that we can get some of the benefits from Beluga at a much lower cost, since we do not have to build a stand-alone system or extend the compiler of an existing language to support contexts, contextual types and objects.
Our approach of embedding an LF specification language into a host language is in spirit related to the systems Abella [8] and Hybrid [7] that use a two-level approach. In these systems we embed the specification language (typically hereditary harrop formulas) in first-order logic (or a variant of it). While our approach is similar in spirit, we focus on embedding SF specifications into a programming language instead of embedding it into a proof theory. Moreover, our embedding is type preserving by construction.
There are also many approaches and tools that specifically add support for writing programs that manipulate syntax with binders – even if they do not necessarily use HOAS. FreshML [22] and C\(\alpha \)ml [20] extend OCaml’s data types with the ideas of names and binders from nominal logic [18]. In these system, name generation is an effect, and if the user is not careful variables may extrude their scopes. Purity can be enforced by adding a proof system with a decision procedure that statically guarantees that no variable escapes its scope [21]. This adds some complexity to the system. We feel that Babybel ’s contextual types offer a simpler formalism to deal with bound variables. On the other hand, Babybel ’s approach does not try to model variables that do not have lexical scope, like top-level definitions. Another related language is Romeo [23] that uses ideas from Pure FreshML to represent binders. Where our system statically catches variables escaping their scope, the Romeo system either throws a run time exception or uses an SMT solver to prove the absence of scoping issues. The Hobbits system for Haskell [25] is implemented in a similar way to ours, using quasi-quoting but they use a different formalism based on the concepts of names and freshness. Last but not least, approaches based on parametric HOAS (PHOAS) [5] also model binding in the object language by re-using the function space of the meta-language. In particular, Washburn and Weirich [24] propose a library that uses catamorphisms to compute over a parametric HOAS representation. This is a powerful approach but requires a different way of implementing recursive functions. A fundamental difference between this line of work and ours, is that in PHOAS functions are extensional, i.e. they are black box functions, while our approach introduces a distinction between an intensional and extensional function space. The intensional function space from SF allows us to model binding and supports pattern matching. The extentional function space allows us to write recursive functions.
11 Conclusion and Future Work
In this work, we describe the syntactic framework SF (a simply typed variant of the logical framework LF with the necessity modality from S4) and explain the embedding of SF into a functional programming language using contextual types. This gives programmers the ability to write programs that manipulate abstract syntax trees with binders while knowing at type checking time that no variables extrude their scope. We also show how to translate the extended language back into a first order representation. For this, we use de Bruijn indices and GADTs to implement the SF in \(\text {Core-ML}^{\text {gadt}}\). Important characteristics of the embedding are that it preserves the phase separation, making types (and thus contexts) erasable at run-time. This allows pattern matching to remain first-order and thus it is possible to compile with the traditional algorithms.
Finally, we describe Babybel an implementation of these ideas that embeds SF in OCaml using contextual types. The embedding is flexible enough that we can take advantage of the more powerful type system in OCaml to make the extension more powerful. We use GADTs in our examples to express more powerful invariants (e.g. that the translation preserves the context).
In the future, we plan to implement our approach also in other languages. In particular, it would be natural to implement our approach in Haskell. We do not expect that the the type system extensions to GHC pose any challenging issues. Finally, it would be interesting to extend our approach to type systems with dependent types (e.g. Coq or Agda) where we can reason about the programs we write. This extension would require extending SF with theorems about substitutions (e.g. proving that applying an identity substitution does not change a term).
Notes
- 1.
available at www.github.com/fferreira/babybel/.
- 2.
The underscore means that there might be a context but we do not bind any variable for it because contexts are not available at run-time.
- 3.
Available at www.github.com/fferreira/babybel/.
References
Augustsson, L.: Compiling pattern matching. In: Jouannaud, J.-P. (ed.) FPCA 1985. LNCS, vol. 201, pp. 368–381. Springer, Heidelberg (1985). doi:10.1007/3-540-15975-4_48
Benton, N., Hur, C.K., Kennedy, A.J., McBride, C.: Strongly typed term representations in Coq. J. Autom. Reasoning 49(2), 141–159 (2012)
Cave, A., Pientka, B.: Programming with binders and indexed data-types. In: 39th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL 2012), pp. 413–424. ACM Press (2012)
Cheney, J., Hinze, R.: First-class phantom types. Technical Report CUCIS TR2003-1901, Cornell University (2003)
Chlipala, A.J.: Parametric higher-order abstract syntax for mechanized semantics. In: Hook, J., Thiemann, P. (eds.) 13th ACM SIGPLAN International Conference on Functional Programming (ICFP 2008), pp. 143–156. ACM (2008)
Davies, R., Pfenning, F.: A modal analysis of staged computation. J. ACM 48(3), 555–604 (2001)
Felty, A., Momigliano, A.: Hybrid: a definitional two-level approach to reasoning with higher-order abstract syntax. J. Autom. Reasoning 48(1), 43–105 (2012)
Gacek, A., Miller, D., Nadathur, G.: A two-level logic approach to reasoning about computations. J. Autom. Reasoning 49(2), 241–273 (2012)
Harper, R., Honsell, F., Plotkin, G.: A framework for defining logics. J. ACM 40(1), 143–184 (1993)
Leroy, X., Doligez, D., Frisch, A., Garrigue, J., Rémy, D., Vouillon, J.: The OCaml System Release 4.03 - Documentation and user’s manual. Institut National de Recherche en Informatique et en Automatique (2016)
Miller, D., Palmidessi, C.: Foundational aspects of syntax. ACM Comput. Surv. 31(3es), 11 (1999)
Nanevski, A., Pfenning, F., Pientka, B.: Contextual modal type theory. ACM Trans. Comput. Logic 9(3), 1–49 (2008)
Pfenning, F., Davies, R.: A judgmental reconstruction of modal logic. Math. Struct. Comput. Sci. 11(4), 511–540 (2001)
Pfenning, F., Schürmann, C.: System description: twelf – a meta-logical framework for deductive systems. In: Ganzinger, H. (ed.) CADE 1999. LNCS (LNAI), vol. 1632, pp. 202–206. Springer, Heidelberg (1999). doi:10.1007/3-540-48660-7_14
Pientka, B.: A type-theoretic foundation for programming with higher-order abstract syntax and first-class substitutions. In: 35th Annual ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL 2008), pp. 371–382. ACM Press (2008)
Pientka, B., Cave, A.: Inductive Beluga: programming proofs (system description). In: Felty, A.P., Middeldorp, A. (eds.) CADE 2015. LNCS (LNAI), vol. 9195, pp. 272–281. Springer, Cham (2015). doi:10.1007/978-3-319-21401-6_18
Pientka, B., Pfenning, F.: Optimizing higher-order pattern unification. In: Baader, F. (ed.) CADE 2003. LNCS (LNAI), vol. 2741, pp. 473–487. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45085-6_40
Pitts, A.: Nominal logic, a first order theory of names and binding. Inf. Comput. 186(2), 165–193 (2003)
Poswolsky, A., Schürmann, C.: System description: Delphin–a functional programming language for deductive systems. In: International Workshop on Logical Frameworks and Meta-Languages: Theory and Practice (LFMTP 2008). Electronic Notes in Theoretical Computer Science (ENTCS), vol. 228, pp. 135–141. Elsevier (2009)
Pottier, F.: An overview of C\(\alpha \)ml. In: proceedings of the ACM-SIGPLAN Workshop on ML (ML 2005). Electronic Notes in Theoretical Computer Science, vol. 148(2), pp. 27–52 (2006)
Pottier, F.: Static name control for FreshML. In: 22nd IEEE Symposium on Logic in Computer Science (LICS 2007), pp. 356–365. IEEE Computer Society, July 2007
Shinwell, M.R., Pitts, A.M., Gabbay, M.J.: FreshML: programming with binders made simple. In: 8th International Conference on Functional Programming (ICFP 2003), pp. 263–274. ACM Press (2003)
Stansifer, P., Wand, M.: Romeo: a system for more flexible binding-safe programming. In: Proceedings of the 19th ACM SIGPLAN International Conference on Functional Programming, ICFP 2014, pp. 53–65 (2014)
Washburn, G., Weirich, S.: Boxes go bananas: encoding higher-order abstract syntax with parametric polymorphism. J. Funct. Program. 18(01), 87–140 (2008)
Westbrook, E., Frisby, N., Brauner, P.: Hobbits for Haskell: a library for higher-order encodings in functional programming languages. In: 4th ACM Symposium on Haskell (Haskell 2011), pp. 35–46. ACM (2011)
Xi, H., Chen, C., Chen, G.: Guarded recursive datatype constructors. In: 30th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages (POPL 2003), pp. 224–235. ACM Press (2003)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Ferreira, F., Pientka, B. (2017). Programs Using Syntax with First-Class Binders. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_19
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_19
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)










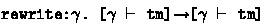 : In this type we implicitly quantify over all contexts
: In this type we implicitly quantify over all contexts  : In this case we quantify over all contexts, but the input of the function is some term in a non-empty context.
: In this case we quantify over all contexts, but the input of the function is some term in a non-empty context. : This final example shows that we can also use the contexts to index regular OCaml GADTs. In this function we are translating between terms in different representations. To be able to translate between these different context representations, it is necessary to establish a relation between these contexts. So we need to define a special OCaml type (i.e.:
: This final example shows that we can also use the contexts to index regular OCaml GADTs. In this function we are translating between terms in different representations. To be able to translate between these different context representations, it is necessary to establish a relation between these contexts. So we need to define a special OCaml type (i.e.: