Abstract
The combination of intersection types, a merge operator and parametric polymorphism enables important applications for programming. However, such combination makes it hard to achieve the desirable property of a coherent semantics: all valid reductions for the same expression should have the same value. Recent work proposed disjoint intersections types as a means to ensure coherence in a simply typed setting. However, the addition of parametric polymorphism was not studied. This paper presents  : a calculus with disjoint intersection types, a variant of parametric polymorphism and a merge operator.
: a calculus with disjoint intersection types, a variant of parametric polymorphism and a merge operator.  is both type-safe and coherent. The key difficult occurs in an intersection type, it is not statically known whether the instantiated type will be disjoint to other components of the intersection. To address this problem we propose disjoint polymorphism: a constrained form of parametric polymorphism, which allows disjointness constraints for type variables. With disjoint polymorphism the calculus remains very flexible in terms of programs that can be written, while retaining coherence.
is both type-safe and coherent. The key difficult occurs in an intersection type, it is not statically known whether the instantiated type will be disjoint to other components of the intersection. To address this problem we propose disjoint polymorphism: a constrained form of parametric polymorphism, which allows disjointness constraints for type variables. With disjoint polymorphism the calculus remains very flexible in terms of programs that can be written, while retaining coherence.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
Intersection types [20, 43] are a popular language feature for modern languages, such as Microsoft’s TypeScript [4], Redhat’s Ceylon [1], Facebook’s Flow [3] and Scala [37]. In those languages a typical use of intersection types, which has been known for a long time [19], is to model the subtyping aspects of OO-style multiple inheritance. For example, the following Scala declaration:

says that the class A implements both B and C. The fact that A implements two interfaces/traits is captured by an intersection type between B and C (denoted in Scala by B with C). Unlike a language like Java, where implements (which plays a similar role to with) would be a mere keyword, in Scala intersection types are first class. For example, it is possible to define functions such as:

taking an argument with an intersection type B with C.
The existence of first-class intersections has led to the discovery of other interesting applications of intersection types. For example, TypeScript’s documentation motivates intersection typesFootnote 1 as follows:
You will mostly see intersection types used for mixins and other concepts that don’t fit in the classic object-oriented mold. (There are a lot of these in JavaScript!)
Two points are worth emphasizing. Firstly, intersection types are being used to model concepts that are not like the classical (class-based) object-oriented programming. Indeed, being a prototype-based language, JavaScript has a much more dynamic notion of object composition compared to class-based languages: objects are composed at run-time, and their types are not necessarily statically known. Secondly, the use of intersection types in TypeScript is inspired by common programming patterns in the (dynamically typed) JavaScript. This hints that intersection types are useful to capture certain programming patterns that are out-of-reach for more conventional type systems without intersection types.
Central to TypeScript’s use of intersection types for modelling such a dynamic form of mixins is the function:

The name extend is given as an analogy to the extends keyword commonly used in OO languages like Java. The function takes two objects (first and second) and produces an object with the intersection of the types of the original objects. The implementation of extend relies on low-level (and type-unsafe) features of JavaScript. When a method is invoked on the new object resulting from the application of extend, the new object tries to use the first object to answer the method call and, if the method invocation fails, it then uses the second object to answer the method call.
The extend function is essentially an encoding of the merge operator. The merge operator is used on some calculi [17, 24, 38, 47, 48] as an introduction form for intersection types. Similar encodings to those in TypeScript have been proposed for Scala to enable applications where the merge operator also plays a fundamental role [39, 46]. Unfortunately, the merge operator is not directly supported by TypeScript, Scala, Ceylon or Flow. There are two possible reasons for such lack of support. One reason is simply that the merge operator is not well-known: many calculi with intersection types in the literature do not have explicit introduction forms for intersection types. The other reason is that, while powerful, the merge operator is known to introduce (in)coherence problems [24, 47]. If care is not taken, certain programs using the merge operator do not have a unique semantics, which significantly complicates reasoning about programs.
Solutions to the problem of coherence in the presence of a merge operator exist for simply typed calculi [17, 38, 47, 48], but no prior work addresses polymorphism. Most recently, we proposed using disjoint intersection types [38] to guarantee coherence in  : a simply typed calculus with intersection types and a merge operator. The key idea is to allow only disjoint types in intersections. If two types are disjoint then there is no ambiguity in selecting a value of the appropriate type from an intersection, guaranteeing coherence.
: a simply typed calculus with intersection types and a merge operator. The key idea is to allow only disjoint types in intersections. If two types are disjoint then there is no ambiguity in selecting a value of the appropriate type from an intersection, guaranteeing coherence.
Combining parametric polymorphism with disjoint intersection types, while retaining enough flexibility for practical applications, is non-trivial. The key issue is that when a type variable occurs in an intersection type it is not statically known whether the instantiated types will be disjoint to other components of the intersection. A naive way to add polymorphism is to forbid type variables in intersections, since they may be instantiated with a type which is not disjoint to other types in an intersection. Unfortunately this is too conservative and prevents many useful programs, including the extend function, which uses an intersection of two type variables T and U.
This paper presents  : a core calculus with disjoint intersection types, a variant of parametric polymorphism and a merge operator. The key innovation in the calculus is disjoint polymorphism: a constrained form of parametric polymorphism, which allows programmers to specify disjointness constraints for type variables. With disjoint polymorphism the calculus remains very flexible in terms of programs that can be written with intersection types, while retaining coherence. In
: a core calculus with disjoint intersection types, a variant of parametric polymorphism and a merge operator. The key innovation in the calculus is disjoint polymorphism: a constrained form of parametric polymorphism, which allows programmers to specify disjointness constraints for type variables. With disjoint polymorphism the calculus remains very flexible in terms of programs that can be written with intersection types, while retaining coherence. In  the extend function is implemented as follows:
the extend function is implemented as follows:

From the typing point of view, the difference between extend in TypeScript and  is that the type variable U now has a disjointness constraint. The notation U * T means that the type variable U can be instantiated to any types that is disjoint to the type T. Unlike TypeScript, the definition of extend is trivial, type-safe and guarantees coherence by using the built-in merge operator (,,).
is that the type variable U now has a disjointness constraint. The notation U * T means that the type variable U can be instantiated to any types that is disjoint to the type T. Unlike TypeScript, the definition of extend is trivial, type-safe and guarantees coherence by using the built-in merge operator (,,).
The applicability of  is illustrated with examples using extend ported from TypeScript, and various operations on polymorphic extensible records [29, 31, 34]. The operations on polymorphic extensible records show that
is illustrated with examples using extend ported from TypeScript, and various operations on polymorphic extensible records [29, 31, 34]. The operations on polymorphic extensible records show that  can encode various operations of row types [52]. However, in contrast to various existing proposals for row types and extensible records,
can encode various operations of row types [52]. However, in contrast to various existing proposals for row types and extensible records,  supports general intersections and not just record operations.
supports general intersections and not just record operations.
 and the proofs of coherence and type-safety are formalized in the Coq theorem prover [2]. The proofs are complete except for a minor (and trivially true) variable renaming lemma used to prove the soundness between two subtyping relations used in the formalization. The problem arizes from the combination of the locally nameless representation of binding [7] and existential quantification, which prevents a Coq proof for that lemma.
and the proofs of coherence and type-safety are formalized in the Coq theorem prover [2]. The proofs are complete except for a minor (and trivially true) variable renaming lemma used to prove the soundness between two subtyping relations used in the formalization. The problem arizes from the combination of the locally nameless representation of binding [7] and existential quantification, which prevents a Coq proof for that lemma.
In summary, the contributions of this paper are:
-
Disjoint Polymorphism: A novel form of universal quantification where type variables can have disjointness constraints. Disjoint polymorphism enables a flexible combination of intersection types, the merge operator and parametric polymorphism.
-
Coq Formalization of
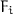 and Proof of Coherence: An elaboration semantics of System
and Proof of Coherence: An elaboration semantics of System 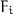 into System F is given. Type-soundness and coherence are proved in Coq. The proofs for these properties and all other lemmata found in this paper are available at: https://github.com/jalpuim/disjoint-polymorphism.
into System F is given. Type-soundness and coherence are proved in Coq. The proofs for these properties and all other lemmata found in this paper are available at: https://github.com/jalpuim/disjoint-polymorphism. -
Applications: We show how
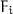 provides basic support for dynamic mixins and various operations on polymorphic extensible records.
provides basic support for dynamic mixins and various operations on polymorphic extensible records.
2 Overview
This section introduces  and its support for intersection types, parametric polymorphism and the merge operator. It then discusses the issue of coherence and shows how the notion of disjoint intersection types and disjoint quantification achieves a coherent semantics. This section uses some syntactic sugar, as well as standard programming language features, to illustrate the various concepts in
and its support for intersection types, parametric polymorphism and the merge operator. It then discusses the issue of coherence and shows how the notion of disjoint intersection types and disjoint quantification achieves a coherent semantics. This section uses some syntactic sugar, as well as standard programming language features, to illustrate the various concepts in  . Although the minimal core language that we formalize in Sect. 4 does not present all such features and syntactic sugar, these are trivial to add.
. Although the minimal core language that we formalize in Sect. 4 does not present all such features and syntactic sugar, these are trivial to add.
2.1 Intersection Types and the Merge Operator
Intersection Types. The intersection of type  and
and  (denoted by A & B in
(denoted by A & B in  ) contains exactly those values which can be used as both values of type
) contains exactly those values which can be used as both values of type  and of type
and of type  . For instance, consider the following program in
. For instance, consider the following program in  :
:

If a value x has type Int & Bool then x can be used anywhere where either a value of type Int or a value of type Bool is expected. This means that, in the program above the functions succ and not – simple functions on integers and booleans, respectively – both accept x as an argument.
Merge Operator. The previous program deliberately omitted the introduction of values of an intersection type. There are many variants of intersection types in the literature. Our work follows a particular formulation, where intersection types are introduced by a merge operator [17, 24, 38, 47, 48]. As Dunfield [24] has argued a merge operator adds considerable expressiveness to a calculus. The merge operator allows two values to be merged in a single intersection type. For example, an implementation of x in  is 1,,True. Following Dunfield’s notation the merge of
is 1,,True. Following Dunfield’s notation the merge of  and
and  is denoted by
is denoted by  .
.
2.2 Coherence and Disjointness
Coherence is a desirable property for a semantics. A semantics is coherent if any valid program has exactly one meaning [47] (that is, the semantics is not ambiguous). Unfortunately the implicit nature of elimination for intersection types built with a merge operator can lead to incoherence. This is due to intersections with overlapping types, as in  . The result of the program ((1,,2) : Int) can be either 1 or 2, depending on the implementation of the language.
. The result of the program ((1,,2) : Int) can be either 1 or 2, depending on the implementation of the language.
Disjoint Intersection Types. One option to restore coherence is to reject programs which may have multiple meanings. The  calculus [38] – a simply-typed calculus with intersection types and a merge operator – solves this problem by using the concept of disjoint intersections. The incoherence problem with the expression
calculus [38] – a simply-typed calculus with intersection types and a merge operator – solves this problem by using the concept of disjoint intersections. The incoherence problem with the expression  happens because there are two overlapping integers in the merge. Generally speaking, if both terms can be assigned some type
happens because there are two overlapping integers in the merge. Generally speaking, if both terms can be assigned some type  then both of them can be chosen as the meaning of the merge, which in its turn leads to multiple meanings of a term. Thus a natural option is to forbid such overlapping values of the same type in a merge. In
then both of them can be chosen as the meaning of the merge, which in its turn leads to multiple meanings of a term. Thus a natural option is to forbid such overlapping values of the same type in a merge. In  intersections such as Int&Int are forbidden, since the types in the intersection overlap (i.e. they are not disjoint). However an intersection such as Char&Int is ok because the set of characters and integers are disjoint to each other.
intersections such as Int&Int are forbidden, since the types in the intersection overlap (i.e. they are not disjoint). However an intersection such as Char&Int is ok because the set of characters and integers are disjoint to each other.
2.3 Parametric Polymorphism
Unfortunately, combining parametric polymorphism with disjoint intersection types is non-trivial. Consider the following program (uppercase Latin letters denote type variables):

The merge3 function takes an argument x of some type (A) and merges x with 3. Thus the return type of the program is A & Int. merge3 is unproblematic for many possible instantiations of A. However, if merge3 instantiates A with a type that overlaps (i.e. is not disjoint) with Int, then incoherence may happen. For example:

can evaluate to both 2 or 3.
Forbidding Type Variables in Intersections. A naive way to ensure that only programs with disjoint types are accepted is simply to forbid type variables in intersections. That is, an intersection type such as Char&Int would be accepted, but an intersection such as A & Int (where A is some type variable) would be rejected. The reasoning behind this design is that type variables can be instantiated to any types, including those already in the intersection. Thus forbidding type variables in the intersection will prevent invalid intersections arising from instantiations with overlapping types. Such design does guarantee coherence and would prevent merge3 from type-checking. Unfortunately the big drawback is that the design is too conservative and many other (useful) programs would be rejected. In particular, the extend function from Sect. 1 would also be rejected.
Other Approaches. Another option to mitigate the issues of incoherence, without the use of disjoint intersection types, is to allow for a biased choice: multiple values of the same type may exist in an intersection, but an implementation gives preference to one of them. The encodings of merge operators in TypeScript and Scala [39, 46] use such an approach. A first problem with this approach, which has already been pointed out by Dunfield [24], is that the choice of the corresponding value is tied up to a particular choice in the implementation. In other words incoherence still exists at the semantic level, but the implementation makes it predictable which overlapping value will be chosen. From the theoretical point-of-view it would be much better to have a clear, coherent semantics, which is independent from concrete implementations. Another problem is that the interaction between biased choice and polymorphism can lead to counter-intuitive programs, since instantiation of type-variables affects the type-directed lookup of a value in an intersection.
2.4 Disjoint Polymorphism
To avoid being overly conservative, while still retaining coherence in the presence of parametric polymorphism and intersection types,  uses disjoint polymorphism. Inspired by bounded quantification [14], where a type variable is constrained by a type bound, disjoint polymorphism allows type variables to be constrained so that they are disjoint to some given types.
uses disjoint polymorphism. Inspired by bounded quantification [14], where a type variable is constrained by a type bound, disjoint polymorphism allows type variables to be constrained so that they are disjoint to some given types.
With disjoint quantification a variant of the program  , which is accepted by
, which is accepted by  , is written as:
, is written as:

In this variant the type A can be instantiated to any types disjoint to Int. Such restriction is expressed by the notation A * Int, where the left-side of * denotes the type variable being declared (A), and the right-side denotes the disjointness constraint (Int). For example,

is accepted. However, instantiating A with Int fails to type-check.
Multiple Constraints. Disjoint quantification allows multiple constraints. For example, the following variant of merge3 has an additional boolean in the merge:

Here the type variable A needs to be disjoint to both Int and Bool. In  such constraint is specified using an intersection type Int & Bool. In general, multiple constraints are specified with an intersection of all required constraints.
such constraint is specified using an intersection type Int & Bool. In general, multiple constraints are specified with an intersection of all required constraints.
Type Variable Constraints. Disjoint quantification also allows type variables to be disjoint to previously defined type variables. For example, the following program is accepted by  :
:

The program has two type variables A and B. A is unconstrained and can be instantiated with any type. However, the type variable B can only be instantiated with types that are disjoint to A. The constraint on B ensures that the intersection type A & B is disjoint for all valid instantiations of  and
and  . In other words, only coherent uses of fst will be accepted. For example, the following use of fst:
. In other words, only coherent uses of fst will be accepted. For example, the following use of fst:

is accepted since Int and Char are disjoint, thus satisfying the constraint on the second type parameter of fst. Furthermore, problematic uses of fst, such as:

are rejected because Int is not disjoint with Int, thus failing to satisfy the disjointness constraint on the second type parameter of fst.
Empty Constraint. The type variable  in the fst function has no constraint. In
in the fst function has no constraint. In  this actually means that
this actually means that  should be associated with the empty constraint, which raises the question: which type should be used to represent such empty constraint? Or, in other words, which type is disjoint to every other type? It is obvious that this type should be one of the bounds of the subtyping lattice: either
should be associated with the empty constraint, which raises the question: which type should be used to represent such empty constraint? Or, in other words, which type is disjoint to every other type? It is obvious that this type should be one of the bounds of the subtyping lattice: either  or
or  . The essential intuition here is that the more specific a type in the subtyping relation is, the less types exist that are disjoint to it. For example,
. The essential intuition here is that the more specific a type in the subtyping relation is, the less types exist that are disjoint to it. For example,  is disjoint to all types except the n-ary intersections that contain
is disjoint to all types except the n-ary intersections that contain  , and
, and  ; while
; while  is disjoint to all types that do not contain \(\texttt {Int}\) or
is disjoint to all types that do not contain \(\texttt {Int}\) or  , and
, and  . This reasoning that
. This reasoning that  should be treated as the empty constraint. Indeed, in
should be treated as the empty constraint. Indeed, in  , a single type variable
, a single type variable  is only syntactic sugar for
is only syntactic sugar for  .
.
3 Applications
 is illustrated with two applications. The first application shows how to mimic some of TypeScript’s examples of dynamic mixins in
is illustrated with two applications. The first application shows how to mimic some of TypeScript’s examples of dynamic mixins in  . The second application shows how
. The second application shows how  enables a powerful form of polymorphic extensible records.
enables a powerful form of polymorphic extensible records.
3.1 Dynamic Mixins
TypeScript is a language that adds static type checking to JavaScript. Amongst numerous static typing constructs, TypeScript supports a form of intersection types, without a merge operator. However, it is possible to define a function extend that mimics the merge operator:

In this example, taken from TypeScript’s documentationFootnote 2, an extend function is defined for mixin composition. Two classes Person and ConsoleLogger are also defined. Two instances of those classes are then composed in a variable jim with the type of the intersection of both using extend. It is type-safe to access both the properties from Person and ConsoleLogger in the object jim.
TypeScript’s implementation of extend relies on a biased choice. The function starts by creating a variable result with the type of the intersection. It then iterates through first’s properties and copies them to result. Next, it iterates through second’s properties but it only copies the properties that result does not possess yet (i.e. the ones present in first). This means that the implementation is left-biased, as the properties of left type of the intersection are chosen in favor of the ones in the right. However, in TypeScript this may be a cause of severe problems since that, at the time of writing, intersections at type-level are right-biased! For example, the following code is well-typed:

There are a few problems here. Firstly both Dog and Person contain a name field, and the use of extend will favour the name field in the first object. This could be surprising for someone unfamiliar with the semantics of extend and, more importantly, it could easily allow unintended name clashes to go undetected. Secondly, note how fool.male is statically bound to a variable of type boolean but, at run-time, it will contain a value of type String! Thus the example shows some run-time type errors can still occur when using extend.
Other problematic issues regarding the semantics of intersection types can include the order of the types in an intersection, or even intersections including repeated types. This motivates the need to define a clear meaning for the practical application of intersection types.
Dynamic Mixins in  . In
. In  , the merge operator is built-in. Thus extend is simply defined as follows:
, the merge operator is built-in. Thus extend is simply defined as follows:

The disjointness constraint on U ensures that no conflicts (such as duplicated fields of the same type) exists when merging the two objects. In practice this approach is quite similar to trait-based OO approaches [50]. If conflicts exist when two objects are composed, then they have to be resolved manually (by dropping fields from some object, for example). Moreover if no existing implementation can be directly reused, a new one must be provided via record extension, analogously to standard method overriding in OO languages.
For the previous TypeScript examples, assuming a straightforward translation from objects to (polymorphic) records, then the composition of person and consoleLogger is well-typed in  :
:

However, the intersection Dog & Person is not accepted. This is due to both types sharing a field with the same name (name) and the same type ( ). Note that the name clash between male fields (which have different types) does not impose any problem in this example:
). Note that the name clash between male fields (which have different types) does not impose any problem in this example:  allows and keeps duplicated fields whose types are disjoint. This feature of
allows and keeps duplicated fields whose types are disjoint. This feature of  is further illustrated next.
is further illustrated next.
3.2 Extensible Records
 can encode polymorphic extensible records. Describing and implementing records within programming languages is certainly not novel and has been extensively studied in the past, including systems with row types [52, 53]; predicates [28,29,30]; flags [45]; conditional constraints [42]; cases [10]; amongst others. However, while most systems have non-trivial built-in constructs to model various aspects of records,
can encode polymorphic extensible records. Describing and implementing records within programming languages is certainly not novel and has been extensively studied in the past, including systems with row types [52, 53]; predicates [28,29,30]; flags [45]; conditional constraints [42]; cases [10]; amongst others. However, while most systems have non-trivial built-in constructs to model various aspects of records,  specializes the more general notion of intersection types to encode complex records.
specializes the more general notion of intersection types to encode complex records.
Records and Record Operations in  . Systems with records usually rely on 3 basic operations: selection, restriction and extension/concatenation. Selection and concatenation (via the merge operator) are built-in in the semantics of
. Systems with records usually rely on 3 basic operations: selection, restriction and extension/concatenation. Selection and concatenation (via the merge operator) are built-in in the semantics of  . Merges in
. Merges in  can be viewed as a generalization of record concatenation. In
can be viewed as a generalization of record concatenation. In  , following well-known encodings of multi-field records in systems with intersection types and a merge operator [47, 48], there are only three rather simple constructs for records: (1) single field record types; (2) single field records; (3) field accessors. Multi-field records in
, following well-known encodings of multi-field records in systems with intersection types and a merge operator [47, 48], there are only three rather simple constructs for records: (1) single field record types; (2) single field records; (3) field accessors. Multi-field records in  are encoded with intersections and merges of single field records. An example is already illustrated in Sect. 3.1. The record type Person is the intersection of two single field record types. The record person "Jim" true is built with a merge of two single field records. Finally, jim.name and jim.log illustrates the use of field accessors. Note how, through the use of subtyping, accessors will accept any intersection type that contains the single record with the corresponding field. This resembles systems with record subtyping [15, 41].
are encoded with intersections and merges of single field records. An example is already illustrated in Sect. 3.1. The record type Person is the intersection of two single field record types. The record person "Jim" true is built with a merge of two single field records. Finally, jim.name and jim.log illustrates the use of field accessors. Note how, through the use of subtyping, accessors will accept any intersection type that contains the single record with the corresponding field. This resembles systems with record subtyping [15, 41].
Restriction via Subtyping. In contrast to most record systems, restriction is not directly embedded in  . Instead,
. Instead,  uses subtyping for restriction:
uses subtyping for restriction:

The function remove drops the field age from the record x.
Polymorphic Extensible Records. Records in  can have polymorphic fields, and disjointness enables encoding various operations expressible in systems with polymorphic records. For example, the following variant of remove
can have polymorphic fields, and disjointness enables encoding various operations expressible in systems with polymorphic records. For example, the following variant of remove

takes a value x which contains a record of type l : A, as well as some extra information of type B. The disjointness constraint on B ensures that values of type B do not contain a record with type l : A. This example shows that one can use disjoint quantification to express negative field information, which is very close to the system described by Harper and Pierce [29]. Note, however, that  requires explicitly stating the type of field in the constraint, whereas systems with a lacks (field) predicate only require the name of the field. The generality of disjoint intersection types, which allows one to encode record types, is exactly what forces us to add this extra type in the constraint. However, there is a slight gain with
requires explicitly stating the type of field in the constraint, whereas systems with a lacks (field) predicate only require the name of the field. The generality of disjoint intersection types, which allows one to encode record types, is exactly what forces us to add this extra type in the constraint. However, there is a slight gain with  ’s approach:
’s approach:  allows B to contain fields with label
allows B to contain fields with label  , as long as the field types are disjoint to
, as long as the field types are disjoint to  . Such fine-grained constraint is not possible to express only with a lacks predicate.
. Such fine-grained constraint is not possible to express only with a lacks predicate.
Expressibility. As noted by Leijen [34], systems can typically be categorized into two distinct groups in what concerns extension: strict and free. The former does not allow field overriding when extending a record (i.e. one can only extend a record with a field that is not present in it); while the latter does account for field overriding. Our system can be seen as hybrid of these two kinds of systems.
With lightweight extensible records [31] – a system with strict extension – an example of a function that uses record types is the following:

The type signature says that any record  , containing fields
, containing fields  and
and  and some more information
and some more information  (which lacks both fields
(which lacks both fields  and
and  ), can be accepted returning an integer. Note how the bounded polymorphism is essential to ensure that
), can be accepted returning an integer. Note how the bounded polymorphism is essential to ensure that  does not contain
does not contain  nor
nor  .
.
On the other hand, in Leijen’s [34] system with free extension the more general program would be accepted:

In this case, if  contains either field
contains either field  or field
or field  , they would be shadowed by the labels present in the type signature. In other words, in a record with multiple
, they would be shadowed by the labels present in the type signature. In other words, in a record with multiple  fields, the most recent (i.e. left-most) is used in any function which accesses
fields, the most recent (i.e. left-most) is used in any function which accesses  .
.
In  the following program can written instead:
the following program can written instead:

Since  accepts duplicated fields as long as the types of the overlapping fields are disjoint, more inputs are accepted by this function than in the first system. However, since Leijen’s system accepts duplicated fields even when types are overlapping,
accepts duplicated fields as long as the types of the overlapping fields are disjoint, more inputs are accepted by this function than in the first system. However, since Leijen’s system accepts duplicated fields even when types are overlapping,  accepts less types than
accepts less types than  . Another major difference between
. Another major difference between  and the two other mentioned systems, is the ability to combine records with arbitrary types. Our system does not account for well-formedness of record types as the other two systems do (i.e. using a special row kind), since our encoding of records piggybacks on the more general notion of disjoint intersection types.
and the two other mentioned systems, is the ability to combine records with arbitrary types. Our system does not account for well-formedness of record types as the other two systems do (i.e. using a special row kind), since our encoding of records piggybacks on the more general notion of disjoint intersection types.
4 The 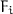 Calculus
Calculus
This section presents the syntax, subtyping, and typing of  : a calculus with intersection types, parametric polymorphism, records and a merge operator. This calculus is an extension of the
: a calculus with intersection types, parametric polymorphism, records and a merge operator. This calculus is an extension of the  calculus [38], which is itself inspired by Dunfield’s calculus [24].
calculus [38], which is itself inspired by Dunfield’s calculus [24].  extends
extends  with (disjoint) polymorphism.
with (disjoint) polymorphism.
4.1 Syntax
The syntax of  (with the differences to
(with the differences to  highlighted in gray) is:
highlighted in gray) is:

Types. Metavariables  ,
,  range over types. Types include all constructs in
range over types. Types include all constructs in  : a top type
: a top type  ; the type of integers
; the type of integers  ; function types
; function types  ; and intersection types
; and intersection types  . The main novelty are two standard constructs of System
. The main novelty are two standard constructs of System  used to support polymorphism: type variables
used to support polymorphism: type variables  and disjoint (universal) quantification
and disjoint (universal) quantification  . Unlike traditional universal quantification, the disjoint quantification includes a disjointness constraint associated to a type variable
. Unlike traditional universal quantification, the disjoint quantification includes a disjointness constraint associated to a type variable  . Finally,
. Finally,  also includes singleton record types, which consist of a label
also includes singleton record types, which consist of a label  and an associated type
and an associated type  . We will use
. We will use  to denote the capture-avoiding substitution of
to denote the capture-avoiding substitution of  for
for  inside
inside  and
and  for sets of free type variables.
for sets of free type variables.
Terms. Metavariables  range over terms. Terms include all constructs in
range over terms. Terms include all constructs in  : a canonical top value
: a canonical top value  ; integer literals
; integer literals  ; variables
; variables  , lambda abstractions (
, lambda abstractions ( ); applications (
); applications ( ); and the merge of terms
); and the merge of terms  and
and  denoted as
denoted as  . Terms are extended with two standard constructs in System
. Terms are extended with two standard constructs in System  : abstraction of type variables over terms
: abstraction of type variables over terms  ; and application of terms to types
; and application of terms to types  . The former also includes an extra disjointness constraint tied to the type variable
. The former also includes an extra disjointness constraint tied to the type variable  , due to disjoint quantification. Singleton records consists of a label
, due to disjoint quantification. Singleton records consists of a label  and an associated term
and an associated term  . Finally, the accessor for a label
. Finally, the accessor for a label  in term
in term  is denoted as
is denoted as  .
.
Contexts. Typing contexts  track bound type variables
track bound type variables  with disjointness constraints
with disjointness constraints  ; and variables
; and variables  with their type
with their type  . We will use
. We will use  to denote the capture-avoiding substitution of
to denote the capture-avoiding substitution of  for
for  in the co-domain of
in the co-domain of  where the domain is a type variable (i.e. all disjointness constraints). Throughout this paper, we will assume that all contexts are well-formed. Importantly, besides usual well-formedness conditions, in well-formed contexts type variables must not appear free within its own disjointness constraint.
where the domain is a type variable (i.e. all disjointness constraints). Throughout this paper, we will assume that all contexts are well-formed. Importantly, besides usual well-formedness conditions, in well-formed contexts type variables must not appear free within its own disjointness constraint.
Syntactic Sugar. In  we may quantify a type variable and omit its constraint. This means that its constraint is
we may quantify a type variable and omit its constraint. This means that its constraint is  . For example, the function type
. For example, the function type  is syntactic sugar for
is syntactic sugar for  . This is discussed in more detail in Sect. 6.
. This is discussed in more detail in Sect. 6.
4.2 Subtyping
The subtyping rules of the form  are shown in Fig. 1. At the moment, the reader is advised to ignore the gray-shaded parts, which will be explained later. Some rules are ported from
are shown in Fig. 1. At the moment, the reader is advised to ignore the gray-shaded parts, which will be explained later. Some rules are ported from  :
:  ,
,  ,
,  ,
,  ,
,  and
and  .
.
Polymorphism and Records. The subtyping rules introduced by  refer to polymorphic constructs and records.
refer to polymorphic constructs and records.  defines subtyping as a reflexive relation on type variables. In S\(\forall \) a universal quantifier (\(\forall \)) is covariant in its body, and contravariant in its disjointness constraints. The
defines subtyping as a reflexive relation on type variables. In S\(\forall \) a universal quantifier (\(\forall \)) is covariant in its body, and contravariant in its disjointness constraints. The  rule says that records are covariant within their fields’ types. The subtyping relation uses an auxiliary unary ordinary relation, which identifies types that are not intersections. The
rule says that records are covariant within their fields’ types. The subtyping relation uses an auxiliary unary ordinary relation, which identifies types that are not intersections. The  conditions on two of the intersection rules are necessary to produce unique coercions [38]. The
conditions on two of the intersection rules are necessary to produce unique coercions [38]. The  relation needs to be extended with respect to
relation needs to be extended with respect to  . As shown at the top of Fig. 1, the new types it contains are type variables, universal quantifiers and record types.
. As shown at the top of Fig. 1, the new types it contains are type variables, universal quantifiers and record types.
Properties of Subtyping. The subtyping relation is reflexive and transitive.
Lemma 1
(Subtyping reflexivity). For any type  ,
,  .
.
Proof
By structural induction on  .\(\Box \)
.\(\Box \)
Lemma 2
(Subtyping transitivity). If  and
and  , then
, then  .
.
Proof
By double induction on both derivations.\(\Box \)
4.3 Typing
Well-Formedness. The well-formedness rules are shown in the top part of Fig. 2. The new rules over  are
are  and
and  . Their definition is quite straightforward, but note that the constraint in the latter must be well-formed.
. Their definition is quite straightforward, but note that the constraint in the latter must be well-formed.
Typing Rules. Our typing rules are formulated as a bi-directional type-system. Just as in  , this ensures the type-system is not only syntax-directed, but also that there is no type ambiguity: that is, inferred types are unique. The typing rules are shown in the bottom part of Fig. 2. Again, the reader is advised to ignore the gray-shaded parts, as these will be explained later. The typing judgements are of the form:
, this ensures the type-system is not only syntax-directed, but also that there is no type ambiguity: that is, inferred types are unique. The typing rules are shown in the bottom part of Fig. 2. Again, the reader is advised to ignore the gray-shaded parts, as these will be explained later. The typing judgements are of the form:  and
and  . They read: “in the typing context
. They read: “in the typing context  , the term
, the term  can be checked or inferred to type
can be checked or inferred to type  , respectively. The rules ported from
, respectively. The rules ported from  are the check rules for
are the check rules for 
 , integers
, integers  , variables
, variables  , application
, application  , merge operator
, merge operator  , annotations
, annotations  ; and infer rules for lambda abstractions
; and infer rules for lambda abstractions  , and the subsumption rule
, and the subsumption rule  .
.
Disjoint Quantification. The new rules, inspired by System  , are the infer rules for type application
, are the infer rules for type application  , and for type abstraction
, and for type abstraction  . Type abstraction is introduced by the big lambda
. Type abstraction is introduced by the big lambda  , eliminated by the usual type application
, eliminated by the usual type application 
 . The disjointness constraint is added to the context in
. The disjointness constraint is added to the context in  . During a type application, the type system makes sure that the type argument satisfies the disjointness constraint. Type application performs an extra check ensuring that the type to be instantiated is compatible (i.e. disjoint) with the constraint associated with the abstracted variable. This is important, as it will retain the desired coherence of our type-system; and it will be further explained in Sect. 5. For ease of discussion, also in
. During a type application, the type system makes sure that the type argument satisfies the disjointness constraint. Type application performs an extra check ensuring that the type to be instantiated is compatible (i.e. disjoint) with the constraint associated with the abstracted variable. This is important, as it will retain the desired coherence of our type-system; and it will be further explained in Sect. 5. For ease of discussion, also in  , we require the type variable introduced by the quantifier to be fresh. For programs with type variable shadowing, this requirement can be met straightforwardly by variable renaming.
, we require the type variable introduced by the quantifier to be fresh. For programs with type variable shadowing, this requirement can be met straightforwardly by variable renaming.
Records. Finally,  and
and  deal with record types. The former infers a type for a record with label
deal with record types. The former infers a type for a record with label  if it can infer a type for the inner expression; the latter says if one can infer a record type
if it can infer a type for the inner expression; the latter says if one can infer a record type  from an expression
from an expression  , then it is safe to access the field
, then it is safe to access the field  , and inferring type
, and inferring type  .
.
5 Disjointness
Section 4 presented a type system with disjoint intersection types and disjoint quantification. In order to prove both type-safety and coherence (in Sect. 6), it is necessary to first introduce a notion of disjointness, considering polymorphism and disjointness quantification. This section presents an algorithmic set of rules for determining whether two types are disjoint. After, it will show a few important properties regarding substitution, which will turn out to be crucial to ensure both type-safety and coherence. Finally, it will discuss the bounds of disjoint quantification and what implications they have on  .
.
5.1 Algorithmic Rules for Disjointness
The rules for the disjointness judgement are shown in Fig. 3, which consists of two judgements.
Main Judgement. The judgement  says two types
says two types  and
and  are disjoint in a context
are disjoint in a context  . The rules are inspired in the disjointness algorithm described by
. The rules are inspired in the disjointness algorithm described by  .
.  and
and  say that any type is disjoint to
say that any type is disjoint to  . This is a major difference to
. This is a major difference to  , where the notion of disjointness explicitly forbids the presence of
, where the notion of disjointness explicitly forbids the presence of  types in intersections. We will further discuss this difference in Sect. 6.
types in intersections. We will further discuss this difference in Sect. 6.
Type variables are dealt with two rules:  is the base rule; and
is the base rule; and  is its twin symmetrical rule. Both rules state that a type variable is disjoint to some type
is its twin symmetrical rule. Both rules state that a type variable is disjoint to some type  , if
, if  contains any subtype of the corresponding disjointness constraint. This rule is a specialization of the more general lemma:
contains any subtype of the corresponding disjointness constraint. This rule is a specialization of the more general lemma:
Lemma 3
(Covariance of disjointness). If  and
and  , then
, then  .
.
Proof
By double induction, first on the disjointness derivation and then on the subtyping derivation. The first induction case for  does not need the second induction as it is a straightforward application of subtyping transitivity.\(\Box \)
does not need the second induction as it is a straightforward application of subtyping transitivity.\(\Box \)
The lemma states that if a type  is disjoint to
is disjoint to  under
under  , then it is also disjoint to any supertype of
, then it is also disjoint to any supertype of  . Note how these two variable rules would allow one to prove
. Note how these two variable rules would allow one to prove  , for any variable
, for any variable  . However, under the assumption that contexts are well-formed, such derivation is not possible as
. However, under the assumption that contexts are well-formed, such derivation is not possible as  cannot occur free in
cannot occur free in  .
.
The rule for disjoint quantification  is the most interesting. To illustrate this rule, consider the following two types:
is the most interesting. To illustrate this rule, consider the following two types:

When are these two types disjoint? In the first type  cannot be instantiated with
cannot be instantiated with  and in the second case
and in the second case  cannot be instantiated with
cannot be instantiated with  . Therefore for both bodies to be disjoint,
. Therefore for both bodies to be disjoint,  cannot be instantiated with either
cannot be instantiated with either  or
or  . The rule for disjoint quantification adds a constraint composed of the intersection of both constraints into
. The rule for disjoint quantification adds a constraint composed of the intersection of both constraints into  and checks for disjointness in the bodies under that environment. The reader might notice how this intersection does not necessarily need to be well-formed, in the sense that the types that compose it might not be disjoint. This is not problematic because the intersections present as constraints in the environment do not contribute directly to the (coherent) coercions generated by the type-system. In other words, intersections play two different roles in
and checks for disjointness in the bodies under that environment. The reader might notice how this intersection does not necessarily need to be well-formed, in the sense that the types that compose it might not be disjoint. This is not problematic because the intersections present as constraints in the environment do not contribute directly to the (coherent) coercions generated by the type-system. In other words, intersections play two different roles in  , as:
, as:
-
1.
Types: restricted (i.e. disjoint) intersections are required to ensure coherence.
-
2.
Constraints: arbitrary intersections are sufficient to serve as constraints under polymorphic instantiation.
The rules  and
and  define disjointness between two single label records. If the labels coincide, then the records are disjoint whenever their fields’ types are also disjoint; otherwise they are always disjoint. Finally, the remaining rules are identical to the original rules.
define disjointness between two single label records. If the labels coincide, then the records are disjoint whenever their fields’ types are also disjoint; otherwise they are always disjoint. Finally, the remaining rules are identical to the original rules.
Axioms. Axiom rules take care of two types with different language constructs. These rules capture the set of rules is that  holds for all two types of different constructs unless any of them is an intersection type, a type variable, or
holds for all two types of different constructs unless any of them is an intersection type, a type variable, or  . Note that disjointness with type variables is already captured by
. Note that disjointness with type variables is already captured by  and
and  , and disjointness with the
, and disjointness with the  type is captured by
type is captured by  and
and  .
.
5.2 Well-Formed Types
In  it is important to show that the type-system only produces well-formed types. This is crucial to ensure coherence, as shown in Sect. 6. However, in the presence of both polymorphism and disjoint intersection types, extra effort is needed to show that all types in
it is important to show that the type-system only produces well-formed types. This is crucial to ensure coherence, as shown in Sect. 6. However, in the presence of both polymorphism and disjoint intersection types, extra effort is needed to show that all types in  are well-formed. To achieve this, not only we need to show that a weaker version of the general substitution lemma holds, but also that disjointness between two types is preserved after substitution. To motivate the former (i.e. why general substitution does not hold in
are well-formed. To achieve this, not only we need to show that a weaker version of the general substitution lemma holds, but also that disjointness between two types is preserved after substitution. To motivate the former (i.e. why general substitution does not hold in  ), consider the type
), consider the type  . The type variable
. The type variable  cannot be substituted by any type: substituting with
cannot be substituted by any type: substituting with  will lead to the ill-formed type
will lead to the ill-formed type  . To motivate the latter, consider the judgement
. To motivate the latter, consider the judgement  . After the substitution of
. After the substitution of  for
for  on the two types, the sentence
on the two types, the sentence  is no longer true, since
is no longer true, since  is clearly not disjoint with itself. Generally speaking, a careless substitution can violate the constraints in the context. However, if appropriate disjointness pre-conditions are met, then disjointness can be preserved. More formally, the following lemma holds:
is clearly not disjoint with itself. Generally speaking, a careless substitution can violate the constraints in the context. However, if appropriate disjointness pre-conditions are met, then disjointness can be preserved. More formally, the following lemma holds:
Lemma 4
(Disjointness is stable under substitution). If  and
and  and
and  and well-formed context
and well-formed context  , then
, then  .
.
Proof
By induction on the disjointness derivation of  and
and  . Special attention is needed for the variable case, where it is necessary to prove stability of substitution for the subtyping relation. It is also needed to show that, if
. Special attention is needed for the variable case, where it is necessary to prove stability of substitution for the subtyping relation. It is also needed to show that, if  and
and  do not contain any variable
do not contain any variable  , then it is safe to make a substitution in the co-domain of the environment.\(\Box \)
, then it is safe to make a substitution in the co-domain of the environment.\(\Box \)
We can now prove a weaker version of the general substitution lemma:
Lemma 5
(Types are stable under substitution). If  and
and  and
and  and
and  and well-formed context
and well-formed context  , then
, then  .
.
Proof
By induction on the well-formedness derivation of  . The intersection case requires the use of Lemma 4. Also, the variable case required proving that if
. The intersection case requires the use of Lemma 4. Also, the variable case required proving that if  does not occur free in
does not occur free in  , and it is safe to substitute it in the co-domain of
, and it is safe to substitute it in the co-domain of  , then it is safe to perform the substitution.\(\Box \)
, then it is safe to perform the substitution.\(\Box \)
Now we can finally show that all types produced by the type-system are well-formed and, more specifically, justify that the disjointness premise on  is sufficient for that purpose. More formally, we have that:
is sufficient for that purpose. More formally, we have that:
Lemma 6
(Well-formed typing). We have that:
-
If
 .
. -
If
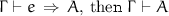 .
.
Proof
By induction on the derivation and applying Lemma 5 in the case of  .\(\Box \)
.\(\Box \)
Even though the meta-theory is consistent, we can still ask: what are the bounds of disjoint quantification? In other words, which type(s) can be used to allow unrestricted instantiation, and which one(s) will completely restrict instantiation? As the reader might expect, the answer is tightly related to subtyping.
5.3 Bounds of Disjoint Quantification
Substitution raises the question of what range of types can be instantiated for a given variable  , under a given context
, under a given context  . To answer this question, we ask the reader to recall the rule
. To answer this question, we ask the reader to recall the rule  , copied below:
, copied below:

Given that the cardinality of  ’s types is infinite, for the sake of this example we will restrict the type universe to a finite number of primitive types (i.e.
’s types is infinite, for the sake of this example we will restrict the type universe to a finite number of primitive types (i.e.  ), disjoint intersections of these types,
), disjoint intersections of these types,  and
and  . Now we may ask: how many suitable types are there to instantiate
. Now we may ask: how many suitable types are there to instantiate  with, depending on
with, depending on  ? The rule above tells us that the more super-types
? The rule above tells us that the more super-types  has, the more types
has, the more types  has to be disjoint with. In other words, the choices for instantiating
has to be disjoint with. In other words, the choices for instantiating  are inversely proportional to the number of super-types of
are inversely proportional to the number of super-types of  . It is easy to see that the number of super-types of
. It is easy to see that the number of super-types of  is directly proportional to the number of intersections in
is directly proportional to the number of intersections in  . For example, taking
. For example, taking  as
as  leads
leads  to be either
to be either  or
or  ; whereas
; whereas  as
as  leaves
leaves  as either
as either  ,
,  or
or  . Thus, the choices of
. Thus, the choices of  are inversely proportional to the number of intersections in
are inversely proportional to the number of intersections in  . Following the same logic, choosing
. Following the same logic, choosing  (i.e. the 0-ary intersection) as constraint leaves
(i.e. the 0-ary intersection) as constraint leaves  with the most options for instantiation; whereas
with the most options for instantiation; whereas  (i.e. the infinite intersection) will deliver the least options. Consequently, we may conclude that
(i.e. the infinite intersection) will deliver the least options. Consequently, we may conclude that  is the empty constraint: a variable associated to it can be instantiated to any well-formed type. It is a subtle but very important property, since
is the empty constraint: a variable associated to it can be instantiated to any well-formed type. It is a subtle but very important property, since  is a generalization of System
is a generalization of System  . Any type variable quantified in System
. Any type variable quantified in System  , can be quantified equivalently in
, can be quantified equivalently in  by assigning it a
by assigning it a  disjointness constraint (as seen in Sect. 2.4).
disjointness constraint (as seen in Sect. 2.4).
6 Semantics, Coherence and Type-Safety
This section discusses the elaboration semantics of  and proves type-safety and coherence. It will first show how the semantics is described by an elaboration to System
and proves type-safety and coherence. It will first show how the semantics is described by an elaboration to System  . Then, it will discuss the necessary extensions to retain coherence, namely in the coercions of top-like types; coercive subtyping, and bidirectional type-system’s elaboration.
. Then, it will discuss the necessary extensions to retain coherence, namely in the coercions of top-like types; coercive subtyping, and bidirectional type-system’s elaboration.
6.1 Target Language
The dynamic semantics of the call-by-value  is defined by means of a type-directed translation to an extension of System
is defined by means of a type-directed translation to an extension of System  with pairs. The syntax and typing of our target language is unsurprising:
with pairs. The syntax and typing of our target language is unsurprising:

The highlighted part shows its difference with the standard System  . The interested reader can find the formalization of the full target language syntax and typing rules in our Coq development.
. The interested reader can find the formalization of the full target language syntax and typing rules in our Coq development.
Type and Context Translation. Figure 4 defines the type translation function  from
from  types
types  to target language types
to target language types  . The notation \(|\cdot |\) is also overloaded for context translation from
. The notation \(|\cdot |\) is also overloaded for context translation from  contexts
contexts  to target language contexts
to target language contexts  .
.
6.2 Coercive Subtyping and Coherence
Coercive Subtyping. The judgement  present in Fig. 1, extends the subtyping relation with a coercion on the right hand side of
present in Fig. 1, extends the subtyping relation with a coercion on the right hand side of  . A coercion
. A coercion  is just a term in the target language and is ensured to have type
is just a term in the target language and is ensured to have type  (by Lemma 7). For example,
(by Lemma 7). For example,  , generates a target coercion function with type:
, generates a target coercion function with type:  .
.
Rules  ,
,  ,
,  ,
, ,
,  ,
,  , and
, and  are taken directly from
are taken directly from  . In rule
. In rule  , the coercion is simply the identity function. Rule
, the coercion is simply the identity function. Rule  elaborates disjoint quantification, reusing only the coercion of subtyping between the bodies of both types. Rule
elaborates disjoint quantification, reusing only the coercion of subtyping between the bodies of both types. Rule  elaborates records by simply reusing the coercion generated between the inner types. Finally, all rules produce type-correct coercions:
elaborates records by simply reusing the coercion generated between the inner types. Finally, all rules produce type-correct coercions:
Lemma 7
(Subtyping rules produce type-correct coercions). If  , then
, then  .
.
Proof
By a straightforward induction on the derivation.\(\Box \)
Unique Coercions. In order to prove the type-system coherent, the subtyping relation also needs to be shown coherent. In  the following lemma holds:
the following lemma holds:
Lemma 8
(Unique subtype contributor). If  , where
, where  and
and  are well-formed types, and
are well-formed types, and  is not top-like, then it is not possible that the following holds at the same time:
is not top-like, then it is not possible that the following holds at the same time:
-
1.

-
2.

Proof
By double induction: the first on the disjointness derivation (which follows from  being well-formed); the second on type
being well-formed); the second on type  . The variable cases
. The variable cases  and
and  needed to show that, for any two well-formed and disjoint types
needed to show that, for any two well-formed and disjoint types  and
and  , and
, and  is not toplike, then
is not toplike, then  cannot be a subtype of
cannot be a subtype of  .\(\Box \)
.\(\Box \)
Using this lemma, we can show that the coercion of a subtyping relation  is uniquely determined. This fact is captured by the following lemma:
is uniquely determined. This fact is captured by the following lemma:
Lemma 9
(Unique coercion). If  , where
, where  and
and  are well-formed types, then
are well-formed types, then  .
.
Proof
By induction on the first derivation and case analysis on the second.\(\Box \)
6.3 Top-Like Types and Their Coercions
Lemma 8, which is fundamental in the proof of coherence of subtyping, holds under the condition that  is not a top-like type. Top-like types in
is not a top-like type. Top-like types in  include
include  as well as other syntactically different types that behave as
as well as other syntactically different types that behave as  (such as
(such as  ). It is easy to see that the unique subtyping contributor lemma is invalidated if no restriction on top-like types exists. Since every type is a subtype of
). It is easy to see that the unique subtyping contributor lemma is invalidated if no restriction on top-like types exists. Since every type is a subtype of  then, without the restriction, the lemma would never hold.
then, without the restriction, the lemma would never hold.
Rules.  ’s definition of top-like types extends that from
’s definition of top-like types extends that from  . The rules that compose this unary relation, denoted as
. The rules that compose this unary relation, denoted as  , are presented at the top of Fig. 5. The new rules are
, are presented at the top of Fig. 5. The new rules are  and
and  . Both rules say that their constructs are top-like whenever their enclosing expressions are also top-like.
. Both rules say that their constructs are top-like whenever their enclosing expressions are also top-like.
Coercions for Top-Like Types. Coercions for top-like types require special treatment for retaining coherence. Although Lemma 8 does not hold for top-like types, we can still ensure that that any coercions for top-like types are unique, even if multiple derivations exist. The meta-function  , shown at the bottom of Fig. 5, defines coercions for top-like types. With respect to
, shown at the bottom of Fig. 5, defines coercions for top-like types. With respect to  the record and \(\forall \) cases are now defined, and there is also a change in the & case (covering types such as
the record and \(\forall \) cases are now defined, and there is also a change in the & case (covering types such as  ). With this definition, although two derivations exist for type
). With this definition, although two derivations exist for type  , they both generate the coercion
, they both generate the coercion  .
.
Allowing Overlapping Top-Like Types in Intersections. In 
 is a well-formed disjoint intersection type. This may look odd at first, since all other types cannot appear more than once in an intersection. Indeed, in
is a well-formed disjoint intersection type. This may look odd at first, since all other types cannot appear more than once in an intersection. Indeed, in  ,
,  is not well-formed. However,
is not well-formed. However,  -types are special in that they have a unique canonical top value, which is translated to the unit value () in the target language. In other words a merge of two
-types are special in that they have a unique canonical top value, which is translated to the unit value () in the target language. In other words a merge of two  -types will always return the same value regardless of which component of the merge is chosen. This is different from merges of non
-types will always return the same value regardless of which component of the merge is chosen. This is different from merges of non  -types, which do not have this property. Thus, one may say that
-types, which do not have this property. Thus, one may say that  -types are coherent with every other type. This property makes
-types are coherent with every other type. This property makes  -types perfect candidates for the empty constraint, but such can only be achieved by allowing
-types perfect candidates for the empty constraint, but such can only be achieved by allowing  in intersections. This explains the more liberal treatment of top types
in intersections. This explains the more liberal treatment of top types  when compared to
when compared to  .
.
6.4 Elaboration of the Type-System and Coherence
In order to prove the coherence result, we refer to the bidirectional type-system introduced in Sect. 4. The bidirectional type-system is elaborating, producing a term in the target language while performing the typing derivation.
Key Idea of the Translation. This translation turns merges into usual pairs, similar to Dunfield’s elaboration approach [24]. It also translates the form of disjoint quantification and disjoint type application into regular (polymorphic) quantification and type application. For example,  in
in  will be translated into System
will be translated into System  ’s
’s  .
.
The Translation Judgement. The translation judgement  extends the typing judgement with an elaborated term on the right hand side of
extends the typing judgement with an elaborated term on the right hand side of  . The translation ensures that
. The translation ensures that  has type
has type  . The two rules for type abstraction
. The two rules for type abstraction  and type application
and type application  generate the expected corresponding coercions in System F. The coercions generated for
generate the expected corresponding coercions in System F. The coercions generated for  and
and  simply erase the labels and translate the corresponding underlying term. All the remaining rules are ported from
simply erase the labels and translate the corresponding underlying term. All the remaining rules are ported from  .
.
Type-Safety. The type-directed translation is type-safe. This property is captured by the following two theorems.
Theorem 1
(Type preservation). We have that:
-
If
 , then
, then 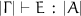 .
. -
If
 , then
, then 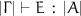 .
.
Proof
By structural induction on the term and the respective inference rule.\(\Box \)
Theorem 2
(Type safety). If  is a well-typed
is a well-typed  term, then
term, then  evaluates to some System
evaluates to some System  value
value  .
.
Proof
Since we define the dynamic semantics of  in terms of the composition of the type-directed translation and the dynamic semantics of System
in terms of the composition of the type-directed translation and the dynamic semantics of System  , type safety follows immediately.\(\Box \)
, type safety follows immediately.\(\Box \)
Uniqueness of Type-Inference. An important property of the bidirectional type-checking is that, given an expression  , if it is possible to infer a type for it, then
, if it is possible to infer a type for it, then  has a unique type.
has a unique type.
Theorem 3
(Uniqueness of type-inference). If  and
and  , then
, then  .
.
Proof
By structural induction on the term and the respective inference rule.\(\Box \)
Coherency of Elaboration. Combining the previous results, we are finally able to show the central theorem:
Theorem 4
(Unique elaboration). We have that:
-
If
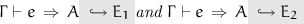 , then
, then  .
. -
If
 , then
, then  .
.
(“\(\equiv \)” means syntactical equality, up to  -equality.)
-equality.)
Proof
By induction on the first derivation. The most important case is the subsumption rule:

We need to show that  is unique (by Lemma 9), and thus to show that
is unique (by Lemma 9), and thus to show that  is well-formed (by Lemma 6). Note that this is the place where stability of substitutions (used by Lemma 6) plays a crucial role in guaranteeing coherence. We also need to show that
is well-formed (by Lemma 6). Note that this is the place where stability of substitutions (used by Lemma 6) plays a crucial role in guaranteeing coherence. We also need to show that  is unique (by Theorem 3). Uniqueness of
is unique (by Theorem 3). Uniqueness of  is needed to apply the induction hypothesis.\(\Box \)
is needed to apply the induction hypothesis.\(\Box \)
7 Related Work
Intersection Types, Polymorphism and the Merge Operator. To our knowledge no previous work presents a coherent calculus which includes parametric polymorphism, intersection types and a merge operator. Only Pierce’s  [40] supports intersection types, polymorphism and, as an extension, the merge operator (called
[40] supports intersection types, polymorphism and, as an extension, the merge operator (called  in
in  ). However, with such extension,
). However, with such extension,  is incoherent. Various simply typed systems with intersections types and a merge operator have been studied in the past. The merge operator was first introduced by Reynold’s in the Forsythe [48] language. The merge operator in Forsythe is coherent [47], but it has various restrictions to ensure coherence. For example Forsythe merges cannot contain more than one function. Many of those restrictions are lifted in
is incoherent. Various simply typed systems with intersections types and a merge operator have been studied in the past. The merge operator was first introduced by Reynold’s in the Forsythe [48] language. The merge operator in Forsythe is coherent [47], but it has various restrictions to ensure coherence. For example Forsythe merges cannot contain more than one function. Many of those restrictions are lifted in  . Castagna et al. [17] studied a coherent calculus with a special merge operator that works on functions only. The goal was to model function overloading. Unlike Reynold’s operator, multiple functions are allowed in merges, but non-functional types are forbidden. More recently, Dunfield [24] formalised a system with intersection types and a merge operator with a type-directed translation to the simply-typed lambda calculus with pairs. Although Dunfield’s calculus is incoherent, it was the inspiration for the
. Castagna et al. [17] studied a coherent calculus with a special merge operator that works on functions only. The goal was to model function overloading. Unlike Reynold’s operator, multiple functions are allowed in merges, but non-functional types are forbidden. More recently, Dunfield [24] formalised a system with intersection types and a merge operator with a type-directed translation to the simply-typed lambda calculus with pairs. Although Dunfield’s calculus is incoherent, it was the inspiration for the  calculus [38], which
calculus [38], which  extends.
extends.
 solves the coherence problem for a calculus similar to Dunfield’s, by requiring that intersection types can only be composed of disjoint types.
solves the coherence problem for a calculus similar to Dunfield’s, by requiring that intersection types can only be composed of disjoint types.  uses a specification for disjointness, which says that two types are disjoint if they do not share a common supertype.
uses a specification for disjointness, which says that two types are disjoint if they do not share a common supertype.  does not use such specification as its adaptation to polymorphic types would require using unification, making the specification arguably more complex than the algorithmic rules (and defeating the purpose of having a specification).
does not use such specification as its adaptation to polymorphic types would require using unification, making the specification arguably more complex than the algorithmic rules (and defeating the purpose of having a specification).  ’s notion of disjointness is based on
’s notion of disjointness is based on  ’s more general notion of disjointness concerning
’s more general notion of disjointness concerning  types, called
types, called  -disjointness.
-disjointness.  -disjointness states that two types
-disjointness states that two types  and
and  are disjoint if two conditions are satisfied:
are disjoint if two conditions are satisfied:
-
1.

-
2.

A significant difference between the  and
and  , is that
, is that  -disjointness does not allow
-disjointness does not allow  in intersections, while
in intersections, while  allows this. In other words, condition (1) is not imposed by
allows this. In other words, condition (1) is not imposed by  . As a consequence, the set of well-formed top-like types is a superset of
. As a consequence, the set of well-formed top-like types is a superset of  ’s. This is covered in greater detail in Sect. 6.3.
’s. This is covered in greater detail in Sect. 6.3.
Intersection Types and Polymorphism, Without the Merge Operator. Recently, Castagna et al. [18] studied a coherent calculus that has polymorphism and set-theoretic type connectives (such as intersections, unions, and negations). Their calculus is based on a semantic subtyping relation due to their interpretation of intersection types. The difference to  , is that their intersections are used between function types, allowing overloading (i.e. branching) of types. For example, they can express a function whose domain is defined on any type, but executes different code depending on that type:
, is that their intersections are used between function types, allowing overloading (i.e. branching) of types. For example, they can express a function whose domain is defined on any type, but executes different code depending on that type:

In our system we cannot express some of these intersections, namely the ones that do not have disjoint co-domains. However,  accepts other kinds of intersections which are not possible to express in their calculus. For example merges with type
accepts other kinds of intersections which are not possible to express in their calculus. For example merges with type  are accepted in
are accepted in  . Similarly to Castagna et al. previous work [17], their work is focused on combining intersections with functions (but without a merge operator), whereas
. Similarly to Castagna et al. previous work [17], their work is focused on combining intersections with functions (but without a merge operator), whereas  is concerned with merges between arbitrary types. Nevertheless, both systems need to express negative information about type variables. That is, which types a given variable cannot be instantiated to. In their calculus, difference takes this role (i.e.
is concerned with merges between arbitrary types. Nevertheless, both systems need to express negative information about type variables. That is, which types a given variable cannot be instantiated to. In their calculus, difference takes this role (i.e.  ); whereas in
); whereas in  , one can express it using disjoint quantification (i.e.
, one can express it using disjoint quantification (i.e.  ).
).
Going in the direction of higher kinds, Compagnoni and Pierce [19] added intersection types to System  and used a new calculus,
and used a new calculus,  , to model multiple inheritance. In their system, types include the construct of intersection of types of the same kind
, to model multiple inheritance. In their system, types include the construct of intersection of types of the same kind  . Davies and Pfenning [22] studied the interactions between intersection types and effects in call-by-value languages. They proposed a “value restriction” for intersection types, similar to value restriction on parametric polymorphism. None of these calculi has a merge operator.
. Davies and Pfenning [22] studied the interactions between intersection types and effects in call-by-value languages. They proposed a “value restriction” for intersection types, similar to value restriction on parametric polymorphism. None of these calculi has a merge operator.
Recently, some form of intersection types has been adopted in object-oriented languages such as Scala [37], TypeScript [4], Flow [3], Ceylon [1], and Grace [9]. There is also a foundational calculus for Scala that incorporates intersection types [49]. The most significant difference between  and those languages/calculi is that they have no explicit introduction construct like our merge operator. The lack of a native merge operator leads to several ad-hoc solutions for defining a merge operator in those languages, as discussed in Sects. 1 and 3.1.
and those languages/calculi is that they have no explicit introduction construct like our merge operator. The lack of a native merge operator leads to several ad-hoc solutions for defining a merge operator in those languages, as discussed in Sects. 1 and 3.1.
Extensible Records. The encoding of multi-field records using intersection types and the merge operator first appeared in Forsythe [48]. Castagna et al. [17] propose an alternative encoding for records. Similarly to  ’s treatment of elaborating records is Cardelli’s work [13] on translating a calculus with extensible records (
’s treatment of elaborating records is Cardelli’s work [13] on translating a calculus with extensible records ( ) to a simpler calculus without records primitives (
) to a simpler calculus without records primitives ( ). However, he does not encode multi-field records as intersections/merges hence his translation is more heavyweight. Crary [21] used intersection types and existential types to address the problem arising from interpreting method dispatch as self-application, but he did not use intersection types to encode multi-field records.
). However, he does not encode multi-field records as intersections/merges hence his translation is more heavyweight. Crary [21] used intersection types and existential types to address the problem arising from interpreting method dispatch as self-application, but he did not use intersection types to encode multi-field records.
Wand [52] started the work on extensible records and proposed row types [53] for records, together with a concatenation operator, which is used in many calculi with extensible records [29, 35, 42, 44, 51, 53]. Cardelli and Mitchell [15] defined three primitive operations on records that are also standard in type-systems with record types: selection, restriction, and extension. Several calculi are based on these three primitive operators (especially extension) [10, 28, 31, 33, 34, 45]. The merge operator in  generalizes the concatenation operator for records, as its components may contain any types (and not just records). Systems with concatenation typically use a set of constraints/filters (such as
generalizes the concatenation operator for records, as its components may contain any types (and not just records). Systems with concatenation typically use a set of constraints/filters (such as  and
and  ) which are useful to combine several, possibly polymorphic, records [34]. In
) which are useful to combine several, possibly polymorphic, records [34]. In  , constraints on labels are encoded using disjoint quantification and intersections. Although systems with records can model structurally typed OO languages, it is harder to encode nominal objects. One advantage of the generality of intersections and merges is that it is easier to have nominal objects. Unlike systems with records, which have been extensively studied, there is much less work on intersection type systems with a merge operator. An interesting avenue for future work is to see whether some known compilation and type-inference techniques for extensible records can be adapted to disjoint intersections and merges.
, constraints on labels are encoded using disjoint quantification and intersections. Although systems with records can model structurally typed OO languages, it is harder to encode nominal objects. One advantage of the generality of intersections and merges is that it is easier to have nominal objects. Unlike systems with records, which have been extensively studied, there is much less work on intersection type systems with a merge operator. An interesting avenue for future work is to see whether some known compilation and type-inference techniques for extensible records can be adapted to disjoint intersections and merges.
Traits and Mixins. Traits [23, 26, 36] and mixins [5, 6, 8, 11, 25, 27] have become very popular in object-oriented languages. They enable restricted forms of multiple inheritance. One of the main differences between traits and mixins are the way in which ambiguity of names is dealt with. Traits reject programs which compose classes with conflicting method implementations, whereas mixins assume a resolution strategy, which is usually language dependent. Our example demonstrated in Sect. 3 suggests that disjointness in  enables a model with a philosophy similar to traits: merging multiple values of overlapping types is forbidden. However while our simple encodings of objects work for very dynamic forms of prototype inheritance, the work on type systems for mixins/traits usually builds on more conventional class-based OO models.
enables a model with a philosophy similar to traits: merging multiple values of overlapping types is forbidden. However while our simple encodings of objects work for very dynamic forms of prototype inheritance, the work on type systems for mixins/traits usually builds on more conventional class-based OO models.
Constrained Types. The notion of disjoint quantification is inspired on bounded polymorphism [12, 16]. Such form of polymorphism typically uses types as subtyping bounds, whereas disjoint quantification uses types as disjoint (i.e. coherent) bounds. Another line of work are qualified types [32], which uses predicates on types to express constraints. However, qualified types are only applicable to the class of Hindley-Milner languages and such predicates are only defined over monotypes.  falls outside this class of languages, plus its constraints can be expressed using any arbitrary type (and not just monotypes).
falls outside this class of languages, plus its constraints can be expressed using any arbitrary type (and not just monotypes).
8 Conclusion and Future Work
This paper described  : a System
: a System  -based language that combines intersection types, parametric polymorphism and a merge operator. The language is proved to be type-safe and coherent. To ensure coherence the type system accepts only disjoint intersections. To provide flexibility in the presence of parametric polymorphism, universal quantification is extended with disjointness constraints. We believe that disjoint intersection types and disjoint quantification are intuitive, and at the same time flexible enough to enable practical applications.
-based language that combines intersection types, parametric polymorphism and a merge operator. The language is proved to be type-safe and coherent. To ensure coherence the type system accepts only disjoint intersections. To provide flexibility in the presence of parametric polymorphism, universal quantification is extended with disjointness constraints. We believe that disjoint intersection types and disjoint quantification are intuitive, and at the same time flexible enough to enable practical applications.
For the future, we intend to create a prototype-based statically typed source language based on  . We are also interested in extending our work to systems with union types and a
. We are also interested in extending our work to systems with union types and a  type. Union types are also widely used in languages such as Ceylon or Flow, but preserving coherence in the presence of union types is challenging. The naive addition of
type. Union types are also widely used in languages such as Ceylon or Flow, but preserving coherence in the presence of union types is challenging. The naive addition of  seems to be problematic. The proofs for
seems to be problematic. The proofs for  rely on the invariant that a type variable
rely on the invariant that a type variable  can never be disjoint to another type that contains
can never be disjoint to another type that contains  . The addition of
. The addition of  breaks this invariant, allowing us to derive, for example,
breaks this invariant, allowing us to derive, for example,  . Finally, we could study a similar system with implicit polymorphism. Such system would require some changes in the subtyping and disjointness relations. For instance, subtyping should allow
. Finally, we could study a similar system with implicit polymorphism. Such system would require some changes in the subtyping and disjointness relations. For instance, subtyping should allow  . Consequently, the disjointness relation would have to be modified, since valid statements in
. Consequently, the disjointness relation would have to be modified, since valid statements in  such as
such as  would no longer hold under the more powerful subtyping relation.
would no longer hold under the more powerful subtyping relation.
Notes
- 1.
- 2.
We have added the field male to the class Person.
References
Ceylon. https://ceylon-lang.org/
The Coq Proof Assistant. https://coq.inria.fr/
Flow. https://flowtype.org/
TypeScript. https://www.typescriptlang.org/
Ancona, D., Lagorio, G., Zucca, E.: Jam-designing a Java extension with mixins. ACM Trans. Program. Lang. Syst. 25(5), 641–712 (2003)
Ancona, D., Zucca, E.: An algebraic approach to mixins and modularity. In: Hanus, M., Rodríguez-Artalejo, M. (eds.) ALP 1996. LNCS, vol. 1139, pp. 179–193. Springer, Heidelberg (1996). doi:10.1007/3-540-61735-3_12
Aydemir, B.E., Charguéraud, A., Pierce, B.C., Pollack, R., Weirich, S.: Engineering formal metatheory. In: POPL 2008 (2008)
Bettini, L., Bono, V., Likavec, S.: A core calculus of higher-order mixins and classes. In: SAC 2004 (2004)
Black, A.P., Bruce, K.B., Homer, M., Noble, J.: Grace: the absence of (inessential) difficulty. In: Onward! 2012 (2012)
Blume, M., Acar, U.A., Chae, W.: Extensible programming with first-class cases. In: ICFP 2006 (2006)
Bracha, G., Cook, W.: Mixin-based inheritance. In: OOPSLA/ECOOP 1990 (1990)
Canning, P., Cook, W., Hill, W., Olthoff, W., Mitchell, J.C.: F-bounded polymorphism for object-oriented programming. In: FPCA 1989 (1989)
Cardelli, L.: Extensible records in a pure calculus of subtyping. In: Theoretical Aspects of Object-oriented Programming. MIT Press, Cambridge (1994)
Cardelli, L., Martini, S., Mitchell, J.C., Scedrov, A.: An extension of system F with subtyping. Inf. Comput. 109(1–2), 4–56 (1994)
Cardelli, L., Mitchell, J.C.: Operations on records. In: Main, M., Melton, A., Mislove, M., Schmidt, D. (eds.) MFPS 1989. LNCS, vol. 442, pp. 22–52. Springer, Heidelberg (1990). doi:10.1007/BFb0040253
Cardelli, L., Wegner, P.: On understanding types, data abstraction, and polymorphism. ACM Comput. Surv. 17(4), 471–522 (1985)
Castagna, G., Ghelli, G., Longo, G.: A calculus for overloaded functions with subtyping. Inf. Comput. 117(1), 115–135 (1995)
Castagna, G., Nguyen, K., Xu, Z., Im, H., Lenglet, S., Padovani, L.: Polymorphic functions with set-theoretic types: part 1: syntax, semantics, and evaluation. In: POPL 2014 (2014)
Compagnoni, A.B., Pierce, B.C.: Higher-order intersection types and multiple inheritance. Math. Struct. Comput. Sci. 6(5), 469–501 (1996)
Coppo, M., Dezani-Ciancaglini, M., Venneri, B.: Functional characters of solvable terms. Math. Logic Q. 27(2–6), 45–58 (1981)
Crary, K.: Simple, efficient object encoding using intersection types. Technical report, CMU-CS-99-100, Cornell University (1998)
Davies, R., Pfenning, F.: Intersection types and computational effects. In: ICFP 2000 (2000)
Ducasse, S., Nierstrasz, O., Schärli, N., Wuyts, R., Black, A.P.: Traits: a mechanism for fine-grained reuse. ACM Trans. Program. Lang. Syst. 28(2), 331–388 (2006)
Dunfield, J.: Elaborating intersection and union types. In: ICFP 2012 (2012)
Findler, R.B., Flatt, M.: Modular object-oriented programming with units and mixins. In: ICFP 1998 (1998)
Fisher, K.: A typed calculus of traits. In: FOOL 2011 (2004)
Flatt, M., Krishnamurthi, S., Felleisen, M.: Classes and mixins. In: POPL 1998 (1998)
Gaster, B.R., Jones, M.P.: A polymorphic type system for extensible records and variants. Technical report, NOTTCS-TR-96-3, University of Nottingham (1996)
Harper, R., Pierce, B.: A record calculus based on symmetric concatenation. In: POPL 1991 (1991)
Harper, R.W., Pierce, B.C.: Extensible records without subsumption. Technical report, CMU-C5-90-102 (1990)
Jones, M., Jones, S.P.: Lightweight extensible records for Haskell. Technical report, UU-CS-1999-28, Haskell Workshop (1999)
Jones, M.P.: Qualified Types: Theory and Practice. Cambridge University Press, Cambridge (1994)
Leijen, D.: First-class labels for extensible rows. Technical report, UU-CS-2004-051, Utrecht University (2004)
Leijen, D.: Extensible records with scoped labels. In: Trends in Functional Programming (2005)
Makholm, H., Wells, J.B.: Type inference, principal typings, and let-polymorphism for first-class mixin modules. In: ICFP 2005 (2005)
Odersky, M., Zenger, M.: Scalable component abstractions. In: OOPSLA 2005 (2005)
Odersky, M., et al.: An overview of the Scala programming language. Technical report, IC/2004/64, EPFL Lausanne, Switzerland (2004)
Oliveira, B.C.S., Shi, Z., Alpuim, J.: Disjoint intersection types. In: ICFP 2016 (2016)
Oliveira, B.C.S., Storm, T., Loh, A., Cook, W.R.: Feature-oriented programming with object algebras. In: Castagna, G. (ed.) ECOOP 2013. LNCS, vol. 7920, pp. 27–51. Springer, Heidelberg (2013). doi:10.1007/978-3-642-39038-8_2
Pierce, B.C.: Programming with intersection types and bounded polymorphism. Ph.D. thesis, Carnegie Mellon University (1991)
Pierce, B.C., Turner, D.N.: Simple type-theoretic foundations for object-oriented programming. J. Funct. Program. 4(2), 207–247 (1994)
Pottier, F.: A constraint-based presentation and generalization of rows. In: LICS 2003 (2003)
Pottinger, G.: A type assignment for the strongly normalizable \(\lambda \)-terms. In: To H. B. Curry: Essays on Combinatory Logic, Lambda Calculus and Formalism (1980)
Rémy, D.: Typing record concatenation for free. In: POPL 1992 (1992)
Rémy, D.: Type inference for records in natural extension of ML. In: Theoretical Aspects of Object-Oriented Programming. MIT Press, Cambridge (1994)
Rendel, T., Brachthäuser, J.I., Ostermann, K.: From object algebras to attribute grammars. In: OOPSLA 2014 (2014)
Reynolds, J.C.: The coherence of languages with intersection types. In: Ito, T., Meyer, A.R. (eds.) TACS 1991. LNCS, vol. 526, pp. 675–700. Springer, Heidelberg (1991). doi:10.1007/3-540-54415-1_70
Reynolds, J.C.: Design of the programming language Forsythe. In: Algol-like languages, Birkhäuser Boston (1997)
Rompf, T., Amin, N.: Type soundness for dependent object types. In: OOPSLA 2016 (2016)
Schärli, N., Ducasse, S., Nierstrasz, O., Black, A.P.: Traits: composable units of behaviour. In: Cardelli, L. (ed.) ECOOP 2003. LNCS, vol. 2743, pp. 248–274. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45070-2_12
Sulzmann, M.: Designing record systems. Technical report, YALEU/DCS/RR-1128, Yale University (1997)
Wand, M.: Complete type inference for simple objects. In: LICS 1987 (1987)
Wand, M.: Type inference for record concatenation and multiple inheritance. In: LICS 1989 (1989)
Acknowledgments
We would like to thank the ESOP reviewers for their helpful comments. This work has been sponsored by the Hong Kong Research Grant Council Early Career Scheme project number 27200514.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 Springer-Verlag GmbH Germany
About this paper
Cite this paper
Alpuim, J., Oliveira, B.C.d.S., Shi, Z. (2017). Disjoint Polymorphism. In: Yang, H. (eds) Programming Languages and Systems. ESOP 2017. Lecture Notes in Computer Science(), vol 10201. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54434-1_1
Download citation
DOI: https://doi.org/10.1007/978-3-662-54434-1_1
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54433-4
Online ISBN: 978-3-662-54434-1
eBook Packages: Computer ScienceComputer Science (R0)


 and Proof of Coherence: An elaboration semantics of System
and Proof of Coherence: An elaboration semantics of System  into System F is given. Type-soundness and coherence are proved in Coq. The proofs for these properties and all other lemmata found in this paper are available at:
into System F is given. Type-soundness and coherence are proved in Coq. The proofs for these properties and all other lemmata found in this paper are available at:  provides basic support for dynamic mixins and various operations on polymorphic extensible records.
provides basic support for dynamic mixins and various operations on polymorphic extensible records. Calculus
Calculus
 .
.
 .
.
 .
.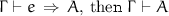 .
.



 , then
, then 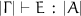 .
. , then
, then 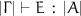 .
.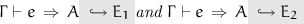 , then
, then  .
. , then
, then  .
.

