Constant Round Adaptively Secure Protocols in the Tamper-Proof Hardware Model

Abstract

Achieving constant-round adaptively secure protocols (where all parties can be corrupted) in the plain model is a notoriously hard problem. Very recently, three works published in TCC 2015 (Dachman-Soled et al., Garg and Polychroniadou, Canetti et al.), solved the problem in the Common Reference String (CRS) model. In this work, we present a constant-round adaptive UC-secure computation protocol for all well-formed functionalities in the tamper-proof hardware model using stateless tokens from only one-way functions. In contrast, all prior works in the CRS model require very strong assumptions, in particular, the existence of indistinguishability obfuscation.

As a corollary to our techniques, we present the first adaptively secure protocols in the Random Oracle Model (ROM) with round complexity proportional to the depth of circuit implementing the functionality. Our protocols are secure in the Global Random Oracle Model introduced recently by Canetti, Jain and Scafuro in CCS 2014 that provides strong compositional guarantees. More precisely, we obtain an adaptively secure UC-commitment scheme in the global ROM assuming only one-way functions. In comparison, the protocol of Canetti, Jain and Scafuro achieves only static security and relies on the specific assumption of Discrete Diffie-Hellman assumption (DDH).

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Background. Secure multi-party computation enables a set of parties to mutually run a protocol that computes some function f on their private inputs, while guaranteeing maximal privacy of the inputs. It is by now well known how to securely compute any efficient functionality [3, 5, 30, 47, 56] in various models and under the stringent simulation-based definitions. However, these results were originally investigated in the stand-alone setting, where a single instance of the protocol is run in isolation. A stronger notion is that of concurrent security, which guarantees security even when many different protocol executions are carried out concurrently. The strongest (as well as most realistic) model of concurrent security is universally-composable (UC) security [5] which guarantees security even when an unbounded number of different protocol executions are run concurrently in an arbitrary uncontrolled environment. Unfortunately, UC-security cannot be achieved for general functions, unless trusted setup is assumed [9, 12, 42]. Previous works overcome this barrier either by using some trusted setup infrastructure [1, 7, 9, 14, 15, 39, 41], or by relaxing the definition of security [2, 13, 27, 37, 52, 54].

Typical protocols, including results mentioned above only consider benign models of static corruption in which the adversary is required to pick which parties it corrupts before the execution (which may include many concurrent protocol sessions) begins. In practice, this is a highly restrictive model. A more realistic model known as the adaptive corruption model, introduced by Canetti et al., considers an adversary that can hijack a host any time during the course of the computation [8]. This models “hacking” attacks where an external attacker breaks into parties’ machines in the midst of a protocol execution and it captures additional threats. In general, security against static corruptions does not guarantee security against adaptive corruptions [6]. Furthermore, adaptive security has been a notoriously difficult notion to achieve.

Adaptive Security Requires Stronger (General) Computational Assumptions. Lindell and Zarosim showed that there exists no black-box construction of an adaptively secure oblivious transfer (OT) protocol from enhanced trapdoor-permutations [45]. In practice, the constructions we know, actually require much stronger assumptions. The smallest general assumption to construct adaptively secure OT in the plain model is trapdoor simulatable public-key encryption [17]. In the UC-setting, the work of [20, 55] showed how to achieve adaptive UC-security in various models (including trusted setups and relaxed security notions) assuming the existence of simulatable public-key encryption [21]. In the Common Reference String model (CRS) model,¹ the construction was improved to rely on the weaker assumption of trapdoor simulatable public-key encryption [36]. In the tamper-proof model, where the parties are assumed to have the capability of creating “tamper-proof hardware tokens”, the work of Goyal et al. [33] shows how to realize unconditional (and hence, adaptive) UC-security in the tamper-proof model assuming stateful tokens. Yet, when we consider the weaker and more realistic model of stateless tokens, there is no known construction of adaptively secure protocols.

Adaptive Security Requires Higher Round Complexity. At present, we have no constant-round adaptively secure protocols for general functionalities in the plain model, where all parties can be corrupted. If we further restrict the constructions to rely on black-box simulation techniques, the work of Garg and Sahai [29] shows that a linear number of rounds are required (in the multi-party setting). A notable exception here, is the work of [22, 38] who provide constant-round adaptively secure protocols under a restricted class of adversaries that is allowed to corrupt at most $n-1$ parties among n parties. [38] also presents constant-round adaptively secure protocols secure against arbitrary corruptions assuming the stronger model of erasures. However, in standard models, where all parties can be corrupted the round-complexity of the best protocol is proportional to the depth of the circuit computing the function [6, 14, 38]. In fact, even in the UC-setting, the round complexity suffers the depth of circuit barrier [14, 20, 55]. Only very recently, and under very strong assumptions, namely existence of (subexponentially-hard) indistinguishability obfuscation (iO) of circuits, the works of [10, 19, 28] provided the first constant-round adaptively secure protocols in the CRS model.²

As such, the best known adaptively secure protocols require very strong assumptions and often higher round complexity. Given the state of affairs, in this work, we are motivated by the following natural question concerning adaptive security:

• Can we construct adaptive UC-secure constant-round protocols under standard polynomial-time assumptions from minimal setup?

As mentioned before, concurrent security cannot be achieved without assuming some form of trusted setup [9, 12, 42]. However, in many scenarios, it is impossible to agree on a trusted entity. Specifically, protocols in the literature that rely on a trusted setup are rendered completely insecure if the setup is compromised. In the absence of setup, concurrently secure protocols have to rely on relaxed notions of security. The most popular notion in this line of work is security with super-polynomial simulators (SPS) [2, 41, 52, 54] which is a relaxation of the traditional simulation-based notion, that allows the simulator to run in super-polynomial time. All these constructions require super-polynomial security of the underlying cryptographic primitives. Breakthrough work by Canetti, Lin and Pass showed how to obtain SPS security from standard polynomial time assumptions [13]. In the adaptive setting, the works of [2, 20, 55] show how to obtain adaptive UC-secure protocols with SPS under super-polynomial time assumptions. More recently, the work of [37] shows how to obtain a $O(n^{\epsilon })$ (for any constant $0<\epsilon <1$) round adaptive UC-secure protocol with SPS under standard polynomial time assumptions.

Motivated by designing practical protocols in the concurrent setting, another approach taken by Canetti et al. [11] considers the Random Oracle Model of Bellare and Rogaway [4]. In order to provide strong compositional guarantees, they introduce the Global Random Oracle Model and show how to obtain UC-secure protocols in the static setting. Their construction is based on the Decisional Diffie-Hellman assumption (DDH). In this line of work, we are interested in addressing the following questions that remain open:

Can we construct UC-secure protocols in the Global Random Oracle Model from minimal general assumptions?, and

Can we construct adaptive UC-secure protocols in the Global Random Oracle Model?

Our Results. We answer all our questions in the affirmative. Furthermore, all our results will be presented in the stronger global-UC (GUC) setting of [7] that provide strong(-er) compositional guarantees. We will rely on the recent work [34] who model tokens for the GUC-setting. In order to incorporate adaptive corruptions we will have to determine the precise capabilities of the adversary when it can also corrupt the creator of the token post-execution and know the actual code embedded in the token. This is discussed in the next section and we argue that the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-functionality introduced in the work [34] will be sufficient to capture the adversary’s capabilities.

Our first result shows how to construct constant-round adaptive GUC-secure protocols in the tamper-proof hardware model assuming only stateless tokens and the existence of one-way functions. More precisely, we obtain the following theorem.

Theorem 1

(Informal). Assuming the existence of one-way functions, there exists a constant-round GUC-secure protocol for the commitment functionality in the presence of adaptive, malicious adversaries in the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-hybrid.

Next, we extend the ideas in this protocol to obtain an adaptive GUC-secure protocol for the oblivious-transfer functionality from one-way functions.

Theorem 2

(Informal). Assuming the existence of one-way functions, there exists a constant-round GUC-secure protocol for the oblivious-transfer functionality in the presence of adaptive, malicious adversaries in the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-hybrid.

Combining this protocol with the adaptive UC-secure protocol in the OT-hybrid of Ishai et al. [38], we can obtain as a corollary an adaptive GUC-secure protocol in the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-hybrid assuming only one-way functions. However, this protocol will require O(d) rounds where d is the depth of the circuit computing the function. Our main contribution in this work is to reduce the round complexity and show how to realize any well-formed functionality in O(1)-rounds independent of the complexity of the function. Below, we state this main theorem.

Theorem 3

(Informal). Assuming the existence of one-way functions, there exists a constant-round GUC-secure two-party protocol to realize any well-formed functionality in the presence of malicious adaptive adversaries in the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-hybrid.

As noted in [34], the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-functionality closely follows the approach taken by Canetti et al. [11] where they capture the global non-programmable random oracle using the $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$-functionality described in [35]. In this work we show that a variant of our GUC-commitment protocol directly yields a GUC-commitment scheme in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$-hybrid. More precisely, we obtain the following theorem.

Theorem 4

(Informal). Assuming the existence of one-way functions, there exists a constant-round GUC-secure protocol for the commitment functionality in the presence of adaptive, malicious adversaries in the global, non-programmable random oracle model, i.e. $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$-hybrid.

This commitment scheme can be combined with the protocol of [17], to obtain a malicious adaptive GUC-oblivious transfer protocol assuming the existence of UC-secure semi-honest adaptive oblivious-transfer protocol. This oblivious-transfer can be further combined with the work of [38] to realize any functionality in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$-hybrid with adaptive security. More formally, we obtain the following corollary.

Corollary 1

Assuming the existence of semi-honest UC-secure adaptive oblivious-transfer protocol, there exists a malicious adaptive $O(d_\mathcal{F})$-round GUC-secure protocol to securely realize any (well-formed) functionality in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$-hybrid where $d_\mathcal{F}$ is the depth of the circuit that implements $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$.

If we instead combine the commitment scheme with the protocol of Hazay and Venkitasubramaniam [36], we obtain a GUC-secure protocol in the static setting assuming stand-alone semi-honest oblivious-transfer.

Corollary 2

Assuming the existence of semi-honest oblivious-transfer protocol, there exists a constant-round static and malicious GUC-secure protocol to securely realize any (well-formed) functionality in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$-hybrid.

We remark that the round complexity of our adaptively secure protocol in Corollary 1 is proportional to the depth of the circuit implementing the functionality, while the protocol in Corollary 2 in the static setting requires only constant number of rounds. These corollaries improve the result of [11] in two ways. First, we show that under the minimal assumption of one-way functions, we can get a GUC-commitment that is adaptively secure. In contrast, the result of [11], obtains a GUC-commitment secure in the static setting assuming DDH. Second, we obtain static and adaptive GUC-secure computation of general functionalities under minimal assumptions, namely, semi-honest OT in the static setting and GUC-secure semi-honest adaptive OT in the adaptive setting.

Related Work. The work of Goldreich and Ostrovsky [31] first considered the use of hardware tokens in the context of software obfuscation via Oblivious RAMs. A decade later, Katz in [40] demonstrated the feasibility of achieving UC-secure protocols for arbitrary functionalities assuming tamper-proof tokens under static corruptions. In his formulation, the parties can create a token that computes arbitrary functionalities such that any adversary that is given access to the token can only observe the input/output behavior of the token. In the UC framework, Katz described an ideal functionality $\mathcal{F}_{{\scriptscriptstyle \mathrm {WRAP}}}$ that captures this model. Note that tokens can either be stateful or stateless, depending on whether the tokens are allowed to maintain some state between invocations (where stateless tokens are easier to implement). Following [40], Goldwasser et al. [32] investigated the use of one-time programs, that allow a semi-honest sender to create simple stateful tokens where a potentially malicious receiver executes them exactly once (or a bounded number of times). Their work considered concrete applications such as zero-knowledge proofs and focused on minimizing the number of required tokens.

The construction of [40] relied on stateful tokens based on the DDH assumption, and was later improved by Lin et al. [41] to rely on the minimal assumption of one-way functions. Goyal et al. [33] resolved the power of stateful tokens and showed how to obtain unconditionally secure protocols using stateful tokens. The work of Chandran et al. [16] was the first to achieve UC-security using only stateless tokens. Choi et al. [18] gave the first constant-round UC-secure protocols using stateless tokens assuming collision-resistant hash-functions. The works of [46, 50] consider a GUC-like formulation of the tokens for the two-party setting where the parties have fixed roles. The focus in [46, 50] was to obtain a formulation that accommodates reusability of a single token for several independent protocols in the UC-setting for the specific two-party case. In contrast to the work of [34, 46, 50] does not explicitly model or discuss adversarial transferability of the tokens. Finally, the work of Hazay et al. [34] resolved the question of identifying the minimal assumptions to construct UC-secure protocols under static corruptions with stateless tokens, namely, they show how to realize constant-round two-party and multi-party UC-secure protocols assuming only the existence of one-way functions. Besides these works, there have been several works in the tamper-proof token model [16, 18, 20, 24,25,26, 33, 41, 48] addressing various efficiency parameters. In the adaptive setting, the works of [20, 55] and [33] construct adaptive UC-secure protocols in the tamper-proof model using stateful tokens with round-complexity proportional to the depth of the circuit. While the works of [20, 55] rely on simulatable public-key encryption schemes, Goyal et al. in [33] provide unconditionally secure protocols (which in particular imply adaptive UC-security). As such, none of the previous works have addressed the feasibility of adaptive security using stateless tokens, and our work is the first to address this question.

2 Modelling Tamper Proof Model with Adaptive Corruptions

We begin with a brief overview of the tamper-proof hardware model and point out some subtleties that arise when considering adaptive adversaries.

In recent work [34], it was shown that the standard (and most popular) formalization of the tamper proof hardware tokens (namely the $\mathcal{F}_{\scriptscriptstyle \mathrm {WRAP}}$-functionality due to Katz [40],) does not fully capture the power of the adversary in a concurrent setting. In particular, the formulation in [40] does not capture a man-in-the-middle attack where an adversary can transfer the tokens received from one session to another. In [34], a new formulation of tamper-proof hardware in the Global Universal Composable (GUC) framework was introduced that addressed these shortcomings. A side effect of this formulation is that this functionality denies the ability of the simulator to “program” the token.³ In the same work [34], they provide constant-round constructions of two party and multi-party secure protocols in the GUC-setting tolerating static adversaries. Our approach is to extend this framework to incorporate adaptive adversaries. First, we explain a subtlety that arises when considering adaptive adversaries. Consider a protocol where one party $P_1$ creates a token $\mathcal{T}$ and sends it to party $P_2$. Suppose an adversary corrupts $P_2$ at the beginning of the protocol and $P_1$ at the end of the execution. This adversary can gain access to the token received by $P_2$ during the protocol and the code of the program P installed in the token at the end of the execution after corrupting $P_1$. In such a scenario, one needs to determine the extent to which an adversary can verify that program P was installed in token $\mathcal{T}$. There are two possible ways to model this:  

First Model: :

In this model, if the receiver of a token is corrupted the adversary has input/output access to the token. If in addition the adversary corrupts the creator of the token, it will obtain the code of the program, i.e. a circuit layout, and it will be able to completely verify that the token precisely contains this circuit.

Second Model: :

In this model, if the receiver of a token is corrupted the adversary has input/output access to the token. If in addition the adversary corrupts the creator of the token, it will obtain the code of the program (by concluding it from the randomness provided by the simulator), however, it will continue to have only input/output access to the physical token. In essence, it will be able to verify the “functionality” on a arbitrary (but bounded) number of points of the function.

It is clear that the first model is stronger as it guarantees that the functionality of the token is exactly the code provided by the creator. In the second model, the adversary will only be able to verify in a polynomial number of points of the function. We argue that the second model is realistic as it is reasonable to assume that the integrity of a physical token remains intact even for an adversary with some auxiliary digital information, such as the code or circuit embedded in the token. In essence, we require that a tamper-proof token remain “tamper-proof” always and restrict the adversary to only input/output access.

All our results will be in the second model with the exception of our adaptive GUC-commitment which will be secure even in the first model. As mentioned before we will rely on the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-functionality to capture tokens. In order to incorporate the second model, we can use the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-functionality without modification. If the creator is corrupted, the creator simply provides the token to the adversary together with the creator’s secret input and randomness, which induce the program code as would have embedded by the honest creator. The $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-functionality will continue to provide only input/output access to the functionality in the token throughout the lifetime of the execution. We remark however that if one wanted to capture the first model, the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-functionality would have to be modified so that when the creator of a token is corrupted, the functionality directly provides the code embedded in the token to the adversary. As we will be considering only the second model, we do not formalize the first model in this work.

3 Our Techniques

We begin with our approach for our main theorem where we construct a constant-round adaptively secure protocol in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid.

Constant-Round Secure Computation. Recently, the works of [10, 19, 28] show how to get constant-round malicious adaptive UC-secure protocols in the CRS model assuming indistinguishability obfuscation. A first attempt here would be to replace the obfuscated programs with tokens. Several problems arise with this intuition:

• The main advantage of the CRS model with obfuscation is that it can provide publicly available (concealed) code that is correct by simply placing an obfuscated code in the CRS. In contrast with tokens, one of the parties need to generate the tokens and it could be malicious.

• Second and more importantly in the case of adaptive corruption, the creator of the token can be corrupted at which point the code embedded in the token needs to be revealed. In contrast, in the CRS model, no adversary can get the random coins used to generate the CRS model.

We instead pursue a different approach. Let us begin with the following simple (yet, incorrect) approach. On a high-level the idea is to use tokens to enable evaluation of the garbled circuit in Yao’s garbling technique [56]. That basic intuition here is that we view the garbling technique as system of labels where evaluation can be performed by “multiplexer” tokens (MPLX) where for each gate given labels corresponding to the inputs, the MPLX picks the corresponding output label for a gate. This basic idea can be made to work in the static setting to construct a secure computation protocol. However, in the adaptive setting things get problematic. The simulator in the garbling technique relies on a “fake” garbled circuit where only the “active keys” are correctly embedded in the garbled tables for the evaluator.⁴ In the adaptive setting, if the garbled circuit evaluator is corrupted at the beginning and the generator is corrupted at the end of the execution the simulator needs to reveal the fake garbling as a real garbling. This is not possible in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$ modelling of the tokens as the simulator is not allowed to “program” the token after creation.⁵

Instead, we solve this problem differently. We will not alter the honest generator’s strategy. We modify the simulation strategy as follows:

• We embed a key K to a symmetric encryption scheme in each gate token.

• The token will be hardwired with three labels, $\ell _{\omega _1},\ell _{\omega _2}$ and $\ell _{\omega _3}$ which will be the active labels for this gate and a random string r.

• On input $\ell _1,\ell _2$, the token will behave as follows: If $\ell _1=\ell _{\omega _1}$ and $\ell _2 = \ell _{\omega _2}$ it will output $\ell _{\omega _3}$. This corresponds to what the evaluator can obtain prior to corrupting the generator.

• If either $\ell _1$ or $\ell _2$ is different from the hardwired labels, it attempts to do the following. It decrypts the label that is different using the key K to obtain a string z that it reads as (x, y). The token then evaluates the circuit assuming the generator’s input is x and the evaluator’s input is y to obtain the actual values in the wires $\omega _1$ and $\omega _2$ that are the inputs to this gate, say $b_1$ and $b_2$. With this information, the token internally assigns the bit $b_1$ to label $\ell _{\omega _1}$ and $b_2$ to label $\ell _{\omega _2}$ and $G(b_1,b_2)$ to $\ell _{\omega _3}$ where $G \in \{\text{ AND },\text{ XOR }\}$ is the gate function. Next, it outputs based on the following strategy:

  • 1. If $\ell _1 = \ell _{\omega _1}$ and $\ell _2 \ne \ell _{\omega _2}$ output $\ell _{\omega _3}$ if $G(b_1,1-b_2) = G(b_1,b_2)$, and output ${\mathsf {Enc}}(K,(x,y);r)$ otherwise.

  • 2. If $\ell _1 \ne \ell _{\omega _1}$ and $\ell _2 = \ell _{\omega _2}$ output $\ell _{\omega _3}$ if $G(1-b_1,b_2) = G(b_1,b_2)$, and output ${\mathsf {Enc}}(K,(x,y);r)$ otherwise.

  • 3. If $\ell _1 \ne \ell _{\omega _1}$ and $\ell _2 \ne \ell _{\omega _2}$ output $\ell _{\omega _3}$ if $G(1-b_1,1-b_2) = G(b_1,b_2)$, and output ${\mathsf {Enc}}(K,(x,y);r)$ otherwise.

  In essence, this strategy figures out what bits the active labels should be associated with, and outputs the labels correctly. Furthermore, the information required to figure out the association is passed along. While this high-level idea allows to “equivocate” the circuit, we need the encryption to satisfy some additional properties such as non-malleability and evasiveness. Note that the above strategy does provide a fake code to be embedded in the token, but once the sender is corrupted post-execution the simulator reveals an honest looking code to the adversary which does not include any information about the fake code e.g., the secret key K.

We formally described our protocol and argue correctness in Sect. 6. Then we show how to adopt the cut-and-choose compilation of Lindell and Pinkas [43] in conjunction with our adaptive GUC-commitment protocol and adaptive GUC-OT protocol that we explain next to obtain a protocol that is secure against malicious adaptive adversaries in Sect. 6.1.

Commitments. Recall that an adaptive GUC-commitment is a commitment scheme between a sender and a receiver that can be (straight-line) equivocated and also allows both parties to be corrupted at the end of the execution. Moreover, as we rely on the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-functionality to model tokens we need a simulator that is only allowed to observe queries to the tokens made by the adversary but not program them.

Our starting point is the static GUC-commitment scheme from  [34] which in turn rely on the work of [33]. Roughly speaking, in order to extract the sender’s input, the receiver chooses a function F from a pseudorandom function family that maps $\{0,1\}^m$ to $\{0,1\}^n$ bits where $m \gg n$, and incorporates it into a token which is transferred to the sender. Next, the sender commits to its input message b by first querying the PRF token on a random string $u \in \{0,1\}^m$ to obtain v. Then, it sends $\mathsf{com}_b = (\mathsf {Ext}(u;r)\,\oplus \,b,r,v)$ where $\mathsf {Ext}(\cdot ,\cdot )$ is a (strong) randomness extractor. Now, since the PRF is highly compressing, it holds with high probability that conditioned on v, u has high min-entropy and therefore $\mathsf {Ext}(u;r)\,\oplus \,b,r$ statistically hides b. Furthermore, since the simulator monitors the queries made by the sender to the PRF token, by observing which query yielded the response v and with the knowledge of this query u it extracts the message b. The commitment is statistically binding since it is computationally infeasible for an adversarial receiver to obtain two values $u,u'$ that map to v. This commitment scheme allows for extraction but not equivocation. To make this protocol equivocal, [34] use the Pass-Wee look-ahead commitment scheme [53] that allows for transforming an extractable commitment to one that also admits equivocation.

If we consider the same protocol under adaptive corruption, we need a simulator that will be able to equivocate. Unfortunately, the previous protocol fails to be secure when the receiver is corrupted first and the sender is corrupted post-execution. This is because, in the Pass-Wee scheme, several commitments are made using the extractable commitment scheme and only a subset of them are revealed during the commitment and decommitment phase. If additionally, the sender is corrupted at the end of the execution, the simulator will have to open the remaining commitments. The simulator will not be able to do this since they will not contain messages generated according to the honest sender’s strategy and given a commitment to some message b, $\mathsf{com}_b = (\mathsf {Ext}(u;r)\,\oplus \,b,r,v)$, the simulator cannot equivocate the message since the value v binds u. This is because given a PRF it is infeasible for a simulator to find $u \ne u'$ such that ${\mathsf {PRF}}(u) = {\mathsf {PRF}}(u')$ (even if the key of the PRF is revealed).

As such this approach does not help us with adaptive corruption. We instead follow a different approach, starting from the work of [36]. More precisely, in this work, the authors show how to construct an adaptive UC-commitment scheme in the CRS model starting from a public-key encryption scheme which additionally has the property that ciphertexts can be obliviously generated and any valid ciphertext can be later revealed as obliviously generated. The high-level idea is that such an encryption scheme provides a mechanism to construct a straight-line extractable commitment scheme which additionally has an oblivious generation property (i.e., analogous to the property for ciphertexts just specified above). Then given such a primitive, it is shown how to compile it into a commitment scheme that is adaptively secure. We will first directly construct a primitive that has this extractability property in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid and then use their compilation to get a full-fledged adaptive GUC-commitment.

To obtain an extractable commitment with oblivious generation, our first attempt is to modify the static extractable commitment from [34] as follows: Instead of sending $\mathsf{com}_b = (\mathsf {Ext}(u;r)\,\oplus \,b,r,v)$ as the message, suppose that the sender sent $(\mathsf {Ext}(u;r)\,\oplus \,b,r,\mathsf {Com}(v))$ where $\mathsf {Com}$ is any non-interactive commitment scheme with pseudorandom commitments.⁶ This commitment scheme has an oblivious generation property where the sender can simply send a random string. However, it loses its extractability property as the simulator will no longer be able to identify the right “u” query that leads to v, as it only sees $\mathsf {Com}(v)$ rather than v.

To regain extractability, we use unique unforgeable signatures. More precisely, the receiver generates a $(\mathsf {sk},\mathsf {vk})$-pair of a signature scheme and sends $\mathsf {vk}$ to the sender. The sender commits to its query u using the scheme $\mathsf {Com}$ and obtains a signature $\sigma$ on the commitment from the receiver. Then we modify the PRF token, to reply with ${\mathsf {PRF}}(u)$ only if it can provide $(c,d,\sigma )$ such that c is a commitment to u with decommitment information d and $\sigma$ is a valid signature of c using $\mathsf {sk}$. We also modify the decommitment phase, were in addition to u, we require the sender to provide a decommitment of u to c. This will allow to regain extractability as this protocol will force the sender to use only the commitment that it used to obtain a signature from the receiver to obtain a response from the PRF token. More precisely, let c be the message that the sender sends in the first step to receive a signature $\sigma$ from the receiver. Then, the simulator will monitor the queries made by the sender to the PRF token and wait until the sender makes a valid query of the form $(c,d,\sigma )$ and use d (i.e., a decommitment of c to u) to extract u.

The binding property of this scheme will follow from the binding property of the $\mathsf {Com}$ scheme and the unforgeability of the signature scheme. Given this extractable commitment scheme with oblivious generation property we compile using the protocol of [36] to obtain a full-fledged adaptive GUC-commitment. We describe and prove correctness of our extractable commitment scheme in Sect. 4.1 and full-fledged GUC-commitment in the full version [35].

Oblivious Transfer. Our oblivious transfer protocol will closely follow the static GUC-secure OT protocol in [34]. On a high-level, the idea here is that the receiver commits to its input bit b and the sender sends a token that contains $s_0,s_1$ and reveals $s_b$ only if the receiver provides a valid decommitment to b. We refer to such a token as an OT-type token. This basic protocol is vulnerable to input-dependent attacks and we rely on standard mechanisms to design a combiner to address this. In particular, following an approach analogous to [34], we will adapt the combiner of [51]. While our protocol structure remains the same as [34], certain subtleties arise that we list below and briefly mention how we address them.

• The protocol in [34] involves the sender sending several OT-type tokens and along with it commitments to all the entries in these tokens via a GUC-commitment. Furthermore, the OT-type tokens in addition to revealing one of the entries in the token given the receiver’s bit b, also reveals a decommitment of that entry for the GUC-commitment scheme. A main issue that arises here is that we require a token to reveal a decommitment of a GUC-commitment scheme and this is infeasible if the GUC-commitments were made in a $\mathcal{F}_{\scriptscriptstyle \mathrm {COM}}$-hybrid since there is no notion of a decommitment besides a message communicated from $\mathcal{F}_{\scriptscriptstyle \mathrm {COM}}$. Previous works in this area [14] rely on a Commit-and-Prove functionality to address this issue. We instead construct an OT protocol directly in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid instead of constructing it in the $(\mathcal{F}_{\scriptscriptstyle \mathrm {COM}},\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}})$-hybrid. More precisely, we first describe an (adaptively secure) commitment scheme $\varPi _{\scriptscriptstyle \mathrm {COM}}$ in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid that comes with an $\mathsf {NP}$-relation for verifying decommitments and is straight-line extractable and equivocable. We then use this as a sub-protocol in our OT-protocol. The formal properties and realization of our commitment scheme, as well as our OT protocol and its security proof can be found in the full version [35].

• Since we need to deal with adaptive corruptions, in the case of a malicious receiver where the adversary also corrupts the sender post-execution we have the following subtle issue. Here the simulator can extract the receiver’s input b and obtain $s_b$ from the $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ functionality. However, the simulator needs to provide the OT-type tokens in the protocol without having complete knowledge of the sender’s real inputs. This is because in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid the simulator is not allowed to program the tokens and needs to provide an actual code to the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid whenever the adversary expects to receive a token. Furthermore, when the sender is corrupted at the end of the execution and the simulator learns the real inputs of the sender, it needs to provide the code incorporated in the tokens (that looks like something the honest sender strategy generated). We handle this issue by providing a strategy for the simulator to provide a fake code to be embedded in the token but later reveal an honest looking code to the adversary. Indistinguishability of the real and ideal world will then follow by establishing that it would be computationally infeasible for the adversary to find the query that distinguishes the alleged code revealed by the simulator and the actual code embedded in the token.

Note that a reader can first read our two-party protocol in Sect. 6 since the OT (Sect. 5) and commitment (Sect. 4) protocols are treated in a black box way.

4 Adaptive GUC-Commitments from OWF Using Tokens

In this section we construct adaptively secure GUC-commitment schemes using tokens. In the heart of our construction lies the observation that the adaptive UC-commitment scheme from [36] can be realized using extractable commitment schemes with some additional feature. Loosely speaking, extractable commitment scheme is a weaker primitive than UC-commitment in the sense that it does not require equivocality. Namely, the simulator is not required to commit to one message and then later convince the receiver that it committed to a different value. In the following section we consider extractable commitment schemes with oblivious generation, for which the committer can obliviously generate a commitment without knowing the committed message. This property is analogue to public key encryption scheme with oblivious sampling of ciphertexts (where the plaintext is not known), and allows to use this primitive as a building block in our adaptively secure GUC-commitments. Moreover, any commitment made to a message can later be revealed as a commitment that was obliviously generated. In Sect. 4.1 we define our new notion of security for extractable commitment schemes with oblivious generation of commitments and present our extractable commitment scheme. In [35] we discuss how to realize UC-commitment schemes based on the construction from [36] and our new notion of extractable commitments with oblivious generation.

4.1 Extractable Commitments with Oblivious Generation

We begin with our definition of extractable commitment schemes. A commitment scheme is a protocol between a sender $\mathrm{S}$ with input a message m and a receiver $\mathrm{R}$. The protocol is marked by two distinct phases: a commitment phase and a decommitment phase. We will consider our definition in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid, i.e. both the sender and the receiver will have access to the ideal $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-functionality. Since, this protocol will eventually be incorporated into a protocol in the GUC-setting, the parties will have as common input a session identifier $\mathsf {sid}$. All the commitment schemes presented in this work will have a non-interactive decommitment phase that can be verified via a $\mathsf {NP}$-relation $\mathcal{R}_{\mathsf {decom}}$ with the statement being the transcript of the commitment phase. This relation will be referred to as the decommitment relation. While our definitions can be generalized, for simplicity of exposition, we will restrict our definition to such protocols in this work. We call this property stand-alone verifiability and define it formally below.

Definition 1

We say that a commitment scheme $\langle \mathrm{S},\mathrm{R} \rangle$ in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid is stand-alone verifiable with $\mathsf {NP}$-relation $\mathcal{R}$ if in the decommitment phase the sender sends a single decommitment message (m, d) and the receiver outputs 1 if and only if $\mathcal{R}(\tau ,(m, d))=1$ where $\tau$ is the transcript of the interaction between $\mathrm{S}$ and $\mathrm{R}$ in the commitment phase (excluding the communication between the parties and the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-functionality).

Definition 2

A commitment scheme $(\langle \mathrm{S},\mathrm{R} \rangle ,\mathcal{R}_{\mathsf {decom}})$ with stand-alone verifiability is said to be an extractable with oblivious generation if the following properties hold.  

Straightline Extractability: :

For every malicious sender $\mathrm{S}^*$, there exists a strategy $\mathsf {Ext}$ that, after the completion of commitment phase in an interaction between $\mathrm{S}^*$ and the honest receiver $\mathrm{R}$ with common input $(1^\kappa ,\mathsf {sid})$ in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid can do the following: On input the transcript of the commitment phase $\tau$ and the queries made by $\mathrm{S}^*$ to all tokens it receives via $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$ for the current session $\mathsf {sid}$ can output m such that, the probability that $\mathrm{S}^*$ outputs $(m',d')$ with $m'\ne m$ and $\mathcal{R}_{\mathsf {decom}}(\tau ,(m',d')) = 1$ is negligible.

Oblivious Generation: :

There is a $\mathsf {PPT}$ algorithm $\widehat{\mathrm{S}}$ and polynomial-time computable function $\mathsf {Adapt}$ such that for any message m and any malicious receiver $\mathrm{R}^*$, it can produce random coins for $\widehat{\mathrm{S}}$ which “explains” a (possibly partial) transcript generated in an interaction using $\langle \mathrm{S},\mathrm{R} \rangle$ with $\mathrm{R}^*$ where $\mathrm{S}$’s input is m. More formally, for every $\mathsf {PPT}$ machine $\mathrm{R}^*$, it holds that, the following ensembles are computationally indistinguishable.

• $\{(\tau ,v) \leftarrow \mathsf {sta}_{\langle \widehat{\mathrm{S}},\mathrm{R} \rangle }^{\mathrm{R}^*}(1^\kappa ,\mathsf {sid},r,m,z): (v,r)\}$

• $\{(\tau ,v) \leftarrow \mathsf {sta}_{\langle \mathrm{S},\mathrm{R} \rangle }^{\mathrm{R}^*}(1^\kappa ,\mathsf {sid},r',z): (v,\mathsf {Adapt}(\tau ))\}$

where ${\kappa \in \mathbb {N},m \in \{0,1\}^\kappa ,r\in \{0,1\}^{p(n)},r'\in \{0,1\}^{q(n)},z\in \{0,1\}^*}$ and where $\mathsf {sta}_{\langle \mathrm{S},\mathrm{R} \rangle }^{\mathrm{R}^*}(1^\kappa ,\mathsf {sid},r,m,z)$ and $\mathsf {sta}_{\langle \widehat{\mathrm{S}},\mathrm{R} \rangle }^{\mathrm{R}^*}(1^\kappa ,\mathsf {sid},r',z)$ denote the random variables describing the (possibly partial) transcript of the interaction and output of $\mathrm{R}^*(z)$ upon interacting with the sender $\mathrm{S}$ on input m randomness r and $\widehat{\mathrm{S}}$ on randomness $r'$, respectively.

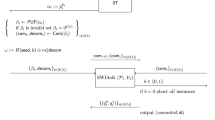
Next, we construct a commitment scheme that satisfies these properties. We present our protocol in Fig. 1. Informally speaking, our construction follows by having the sender commit using a PRF token, where extraction is carried out by monitoring the sender’s queries to this token. In order to force the sender to use the token only once, the receiver signs on a commitment of the PRF query, where the token verifies the validity of both the decommitment and the signature. A similar approach was pursued in the work of [18] where digital signatures, which require an additional property of unique signatures, are employed. Recall first that a signature scheme $(\mathsf {GenSig},\mathsf {Sig},\mathsf {Ver})$ is said to be unique if for every verification key $\mathsf {vk}$ and every message m, there exists only one signature $\sigma$ for which ${\mathsf {Ver}}_\mathsf {vk}(m,\sigma )=1$. Such signature schemes can be constructed based on specific number theoretic assumptions [23]. In [34] a different approach was taken using one-time signatures based on statistically binding commitment schemes that can be based on one-way functions. Their scheme ensures uniqueness in the sense of [18]. We follow their approach in this paper as well.

Fig. 1.

Extractable commitments with oblivious generation.

Lemma 1

Assume the exitance of one-way functions. Then protocol presented in Fig. 1 is an extractable commitment scheme with oblivious generation in the global $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid in the presence of adaptive malicious adversaries.

Proof

We prove that the protocol satisfies both straight-line extractability and the oblivious generation property:  

Straightline Extractability: :

We need to define the $\mathsf {Ext}$ algorithm. Recall that $\mathsf {Ext}$ receives the transcript $\tau$ and the queries that $\mathrm{S}^*$ makes to the token it receives from $\mathrm{R}$, namely the PRF token. This can be obtained from the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$ functionality by issuing the query $(\mathsf {retreive},\mathsf {sid},\mathsf {mid})$. In the list of queries, $\mathsf {Ext}$ finds a tuple $(c,u,\sigma ,r)$ where c is the first message sent by the sender and $\sigma$ is the signature the receiver returned. Then, it checks if the randomness r correctly decommits c to u. If no valid query is made or the decommitment is incorrect, the extracted value is set to $\bot$. Otherwise, it retrieves the message by computing $m = m' + \mathsf {H}(u)$ where $(m',c')$ is the second message sent by the sender in the commit phase. If there are multiple valid queries then it sets the extracted value to $\bot$.

Correctness of extraction follows from the unforgeability of the signature scheme and the statistically-binding property of the commitment scheme $\mathsf {Com}$. More formally, we show that the probability that $\mathsf {Ext}$ fails to retrieve the correct message is negligible. First, we claim that the sender will be able to run the PRF token only on one input, namely $(c,u,\sigma ,r)$ for which $\sigma$ is a valid signature for c and c is a valid commitment to u that was computed using randomness r. This is because for any other valid query, the sender is able to produce a valid signature for message other than c or produce two decommitments of c to $\mathsf {Com}$. Now, since $\mathsf {Ext}$ receives all queries from the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$, given any adversarial sender $\mathrm{S}^*$ that is able to give a valid query $(c',u',\sigma ',r')$ where $c' \ne c$ or $u' \ne u$, we can construct an adversary that respectively breaks the unforgeability of the signature scheme or the binding property of $\mathsf {Com}$.

Oblivious Generation: :

The oblivious sender algorithm $\widehat{\mathrm{S}}$ simply sends random strings of appropriate length in the first and second messages. Namely, in the first message it picks a random string of length C and in the second message it sends $|m|+C$ where $|m|=1$ is the length of the message and C is the length of the commitment message using $\mathsf {Com}$. Given a partial transcript, the $\mathsf {Adapt}$ algorithm simply reconstructs the random tape of $\mathrm{S}$ by observing the messages sent in the transcript by the honest sender $\mathrm{S}$ and placing that message in the random tape.

The indistinguishability property of the randomness output by the $\mathsf {Adapt}$ algorithm follows essentially from the pseudorandomness of the Naor’s commitment scheme $\mathsf {Com}$ [49] and the statistically hiding property of $\mathsf {H}(u)$ given v for any length compressing PRF. More formally, we consider a sequence of hybrids executions, starting from an execution of a commitment to a message m and obtaining an oblivious generated commitment.

• $\mathbf{Hybrid}$ $\mathrm {\mathrm {H}_{1}}$: The output of this hybrid is the view of $\mathrm{R}^*$ when it is interacting with a simulator that follows the honest sender’s strategy $\mathrm{S}$ with input m.

• $\mathbf{Hybrid}$ $\mathrm {\mathrm {H}_{2}}$: In this hybrid, the simulator follows the honest strategy with the exception that in the fourth message instead of committing to v, it sends a random string. The indistinguishability of Hybrids $\mathrm {\mathrm {H}_{1}}$ and $\mathrm {\mathrm {H}_{2}}$ follows from the pseudorandomness of the commitment made using $\mathsf {Com}$.

• $\mathbf{Hybrid}$ $\mathrm {\mathrm {H}_{3}}$: In this hybrid, the simulator follows the strategy as in $\mathrm {\mathrm {H}_{2}}$ with the exception that instead of sending $\mathsf {H}(u)+m$ as part of the fourth message, it sends a random bit. Indistinguishability follows from the hiding property of the $\mathsf {Com}$ scheme. More formally, consider any adversary $\mathrm{R}^*$ such that the outputs of Hybrid $\mathrm {\mathrm {H}_{2}}$ and $\mathrm {\mathrm {H}_{3}}$ can be distinguished. Using $\mathrm{R}^*$ we construct an adversary $\mathcal{A}$, that on input a commitment c made using $\mathsf {Com}$, can extract the committed value by internally emulating $\mathrm {\mathrm {H}_{2}}$ (or $\mathrm {\mathrm {H}_{3}}$), by feeding c as part of the first message and then using the Goldreich-Levin theorem to extract u. In this reduction, $\mathcal{A}$ cannot obtain the value $v = {\mathsf {PRF}}(u)$ since it cannot produce a decommitment of c. Yet, since in hybrid $\mathrm {\mathrm {H}_{2}}$ we already replaced the commitment to v in the fourth message to a random string, $\mathcal{A}$ can still complete the execution without knowing the value v. This adversary $\mathcal{A}$ violates the hiding property of $\mathsf {Com}$.

• $\mathbf{Hybrid}$ $\mathrm {\mathrm {H}_{4}}$: In this hybrid, the simulator follows the strategy $\widehat{S}$. Observe that this strategy is the same strategy as in $\mathrm {\mathrm {H}_{3}}$ with the exception that instead of sending a commitment to randomly sampled u in the second message, it sends a random string. The indistinguishability of Hybrids $\mathrm {\mathrm {H}_{3}}$ and $\mathrm {\mathrm {H}_{4}}$ follows from the pseudorandomness of the commitment made using $\mathsf {Com}$.

We further address here an adaptive corruption of the sender as we use our protocol as a sub-protocol in order to construct a GUC commitment scheme that maintains adaptive security. In case of such corruption the adversary demands the sender’s actual randomness or the randomness according to oblivious generation. The only case we will need to address in our proof is explaining a valid commitment as an obliviously generated one, for which our $\mathsf {Adapt}$ algorithm takes care even on partial transcripts.

4.2 Obtaining GUC-Commitments in the gRO Model

An implication of the above extractable commitment scheme is that we can further realize $\mathcal{F}_{\scriptscriptstyle \mathrm {COM}}$ in the global random oracle model [11]. Specifically, our commitment, shown in the full version [35], calls an extractable commitment which is implemented, in turn, using PRF tokens (for which the simulator exploits in order to extract the committed message). A similar construction can be shown using a global random oracle that is used instead of the PRF tokens. Namely, instead of using signature schemes and pseudorandom commitment schemes in order to enforce a single usage of the PRF token, the sender directly calls the random oracle on some random value u, obtaining the value v, and then masking the committed message by sending $(u+m,v)$. Consequently, we obtain the first GUC-commitment construction in the global random oracle model from OWF with adaptive security. In contrast, the scheme in [11] only achieves security against static corruptions and relies on concrete number theoretic assumptions. We remark here that while the construction of an extractable commitment scheme with oblivious generation is easy to construct in the gRO model following our construction from the previous section, obtaining this corollary relies on the compilation of such a commitment to a full-fledged adaptively secure commitment that we present in the full version [35].

More formally, we claim the following.

Corollary 3

Assume the existence of one-way functions. Then the protocol specified above is an extractable commitment scheme with oblivious generation in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$-hybrid in the presence of adaptive malicious adversaries.

Intuitively, this scheme is extractable since the simulator can monitor the sender’s queries to the random oracle. That is, the simulator obtains from $\mathcal{F}_{\scriptscriptstyle \mathrm {gRO}}$ the query list made by the adversary and search a pair (u, v) that is consistent with the commitment $(m',v)$. If so, it outputs the message $m=m'+u$. Else, it sets the extracted message to $\bot$. Finally, oblivious sampling holds trivially as well due to the fact that the random oracle behaves like a truly random function and given an honestly generated commitment $(u+m,v)$ the message is indistinguishable from a truly random string and therefore can be revealed as something that is obliviously generated.

In [17], they show how to obtain adaptive UC-secure computation of arbitrary functionalities assuming UC-secure adaptive semi-honest oblivious-transfer in the $\mathcal{F}_{\mathsf {Com}}$-hybrid (See Theorem 1). Combining this result with Corollary 3, we obtain the following corollary.

Corollary 4

Assume the existence of UC-secure adaptive semi-honest oblivious transfer. Then for any well-formed functionlaity $\mathcal{F}$, there exists a $O(d_\mathcal{F})$-round protocol that securely realizes $\mathcal{F}$ in the GUC-setting in the presence of adaptive malicious adversaries, where $d_\mathcal{F}$ is the depth of the circuit that implements $\mathcal{F}$.

In [36], they provide a compiler that takes any extractable commitment scheme (even without oblivious generation) and constructs a UC-secure protocols for general functionalities in the static setting assuming semi-honest (static) oblivious transfer. Combining this result with Corollary 3, we obtain the following result:

Corollary 5

Assume the existence of (static) semi-honest oblivious-transfer. Then for any well-formed functionality $\mathcal{F}$, there exists a O(1)-round protocol that securely realizes $\mathcal{F}$ in the GUC-setting in the presence of malicious adversaries.

This result improves the result of Canetti, Jain and Sahai that relies on the specific DDH assumption for their construction.

5 Adaptive OT from OWF Using Tokens

In this section we present our GUC OT protocol. On a high-level, our protocol is identical to the OT protocol from [34] with the exception that the parties apply the adaptive commitment scheme from Sect. 4. In contrast, [34] relies on a UC-commitment scheme in the token model that is secure only against static corruptions. Namely, we describe our protocol $\varPi _{\scriptscriptstyle \mathrm {OT}}$ in the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$-hybrid model with sender $\mathrm{S}$ and receiver $\mathrm{R}$ using the following building blocks: let (1) $\mathsf {Com}$ be a non-interactive perfectly binding commitment scheme, (2) let $\mathcal{SS}=(\mathsf {Share}, \mathsf {Recon})$ be a $(\kappa + 1)$-out-of-$2\kappa$ Shamir secret-sharing scheme over $\mathbb {Z}_p$, together with a linear map $\phi : \mathbb {Z}_p^{2\kappa } \rightarrow \mathbb {Z}^{\kappa -1}_p$ such that $\phi (v) = 0$ iff v is a valid sharing of some secret, (3) $F,F'$ be two families of pseudorandom functions that map $\{0,1\}^{5\kappa }\rightarrow \{0,1\}^{\kappa }$ and $\{0,1\}^{\kappa }\rightarrow \{0,1\}^{p(\kappa )}$, respectively (4) $\mathsf {H}$ denote a hardcore bit function and (5) $\mathsf {Ext}: \{0, 1\}^{5\kappa }\times \{0, 1\}^d \rightarrow \{0, 1\}$ denote a randomness extractor where the source has length $5\kappa$ and the seed has length d. Our protocol is presented in Fig. 2 and involves using our GUC-commitment scheme.

Theorem 5

Assume the existence of one-way functions. Then protocol $\varPi _{\scriptscriptstyle \mathrm {OT}}$ presented in Fig. 2 GUC realizes $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ in the $\mathcal{F}_{{\scriptscriptstyle \mathrm {gWRAP}}}$-hybrid model in the presence of adaptive malicious adversaries.

Fig. 2.

GUC OT with tokens.

Proof Overview. On a high-level, our proof follows analogously to the proof in [34] (which in turn relies on the simulation strategy of [51]). Crucially, we need to address the issue of adaptive corruptions in our proof of both parties. In case of a receiver corruption we need to be able to generate a view for the receiver corresponding to its input and output. As part of the protocol, the receiver commits to its input before receiving the tokens and uses the decommitment as input to the tokens. We further note that the simulation strategy in [34] for a corrupted sender relies on following the honest receiver’s strategy and extracting the sender’s input by monitoring the sender’s queries to the tokens. While this strategy is appropriate to handle static corruptions, it requires handling new subtleties in case of adaptive corruption. Specifically, it is still possible to rely on the honest receiver’s strategy, however, upon post corrupting the receiver the simulator must be able to produce random coins for the receiver that demonstrates consistency with its real input. To achieve this, we make the receiver commit its input using a GUC-commitment scheme secure against adaptive corruptions. Such a scheme is described in our previous section. This enables us to equivocate the receiver’s input. Next, in case of sender corruption we again need to be able to equivocate the sender’s OT inputs. In fact, we need to be able to equivocate $s_{1-b}$ among $(s_0,s_1)$ of the sender’s inputs where b is the receiver’s input. In the protocol, the sender commits to the secret-sharing of two random strings $x_0$ and $x_1$ and masks the real inputs with them. The tokens allow the receiver to extract the shares of $x_b$ and obtain $s_b$. The main argument in [34] is that the receiver will not be able to receive sufficiently many shares of $x_{1-b}$ and hence $s_{1-b}$ remains hidden. In our protocol we first rely on an adaptive GUC-commitment, and thus able to equivocate the sender’s commitments. However, the tokens reveal the values stored in the commitments (by producing the decommitments) and these values need to be changed corresponding to $x_{1-b}$ for equivocation.

In more details, for sender corruption, our simulation proceeds analogously to the simulation from [51] where the simulator generates the view of the malicious sender by following the honest receiver’s strategy to simulate messages and then extracting all the values committed to by the sender. In [51] they rely on extractable commitments and extract the sender’s inputs via rewinding, we here directly extract its inputs by monitoring the queries made by the malicious sender to the tokens embedded within our GUC-commitment protocol $\varPi _{\scriptscriptstyle \mathrm {COM}}$. The proof of correctness follows analogously. More explicitly, the share consistency check ensures that for any particular column that the receiver obtains, if the sum of the values agree on the same bit, then the receiver extracts the correct share of $[x_b]$ with high probability. Note that it suffices for the receiver to obtain $\kappa +1$ good columns for its input b to extract enough shares to reconstruct $x_b$ since the shares can be checked for validity. Namely, the receiver chooses $\kappa /2$ indices $T_b$ and sets its input for these OT executions as b. For the rest of the OT executions, the receiver sets its input as $1-b$. Denote this set of indices by $T_{1-b}$. Then, upon receiving the sender’s response to its challenge and the OT responses, the receiver first performs the shares consistency check. If this check passes, it performs the shares validity check for all columns, both with indices in $T_{1-b}$ and for the indices in a random subset of size $\kappa /2$ within $T_b$. If one of these checks do not pass, the receiver aborts. If both checks pass, it holds with high probability that the decommitment information for $b=0$ and $b=1$ are correct in all but $s \in \omega (\log n)$ indices. Therefore, the receiver will extract $[x_b]$ successfully both when its input $b=0$ and $b=1$. Furthermore, it is ensured that if the two checks performed by the receiver pass, then a simulator can extract both $x_0$ and $x_1$ correctly by simply extracting the sender’s input to the OT protocol and following the receiver’s strategy to extract.

Fig. 3.

Output phase for $\varPi _{\scriptscriptstyle \mathrm {OT}}$.

On the other hand, when the receiver is corrupted, our simulation proceeds analogous to the simulation in [51] where the simulator generates the view of the malicious receiver by first extracting the receiver’s input b and then obtaining $s_b$ from the ideal functionality. It then completes the execution by following the honest sender’s code with $(s_0,s_1)$, where $s_{1-b}$ is set to random. Moreover, while in [51] the authors rely on a special type of interactive commitment that allows the extraction of the receiver’s input via rewinding, we instead extract this input directly by monitoring the queries made by the malicious receiver to the tokens embedded within protocol $\varPi _{\scriptscriptstyle \mathrm {COM}}$. The proof of correctness follows analogously. Informally, the idea is to show that the receiver can learn $\kappa +1$ or more shares for either $x_0$ or $x_1$ but not both. In other words there exists a bit b for which a corrupted receiver can learn at most $\kappa$ shares relative to $s_{1-b}$. Thus, by replacing $s_{1-b}$ with a random string, it follows from the secret-sharing property that obtaining at most $\kappa$ shares keeps $s_{1-b}$ information theoretically hidden. The proof can be found in the full version [35] (Fig. 3).

6 Adaptively Secure Two-Party Computation

In this section we demonstrate the feasibility of constant-round adaptively secure two-party computation in the token model. Loosely speaking, the idea is to associate a token with each gabled gate where the gabled table is embedded within the token, where the token mimics the circuit’s evaluator in the sense that it returns the output label that corresponds to the pair of the input labels of this gate entered by the receiver (if such a key exists). This allows to implement each garbled gate in a form of OT rather than providing a set of four ciphertexts. We further make use of notions such as active/inactive labels as defined in [44], where active labels are the labels that observed by the receiver while evaluating the garbled circuit, while inactive labels are the labels that remain hidden during the evaluation.

In more detail, the basic tokens that we will use in our protocol will intuitively implement the functionality of a garbled gate in Yao’s construction. Given a function f, let $\mathrm {C}$ be the boolean circuit (with the conventions made in [44]) such that for every $x,y \in \{0,1\}^n$, $\mathrm {C}(x,y) = f(x,y)$ where $f: \{0,1\}^n \times \{0,1\}^n \rightarrow \{0,1\}^n$. The sender will follow typical garbled circuit constructions and first create labels for each wire in the circuit. Next, instead of garbling a gate by using the labels as keys to an encryption scheme, we will incorporate in a token the functionality that on input, labels of the incoming wires, will output the corresponding label of the output wire. In essence, the token behaves as 1-out-of-4 OT token. More precisely, for every wire identified by index $\omega$ in the circuit, we pick two random strings $\mathsf {lab}_{\omega }^0,\mathsf {lab}_{\omega }^1 \in \{0,1\}^\kappa$. Then corresponding to gate ${\mathsf {Gate}}_{\mathsf {c}}$, the sender $\mathrm{S}$ creates a token that on input $(\ell _1,\ell _2)$ finds $\alpha$ and $\beta$ such that $\ell _1 = \mathsf {lab}_{\omega _1}^{\alpha }$ and $\ell _1 = \mathsf {lab}_{\omega _2}^{\beta }$ and outputs $\mathsf {lab}_{\omega _3}^{{\mathsf {Gate}}_{\mathsf {c}}(\alpha ,\beta )}$ where $\omega _1,\omega _2$ are the incoming wire identifiers, $\omega _3$ is the identifier of the output wire to gate ${\mathsf {c}}$ and ${\mathsf {Gate}}_{\mathsf {c}}\in \{\text{ AND, } \text{ XOR }\}$ is the corresponding boolean function of the gate c.

Fig. 4.

Adaptively secure 2PC in the presence of malicious receivers

Furthermore, assume that the oblivious transfer protocol that realizes $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ is simulatable in the presence of malicious receivers and semi-honest senders, then the combined protocol is secure with these security guarantees. We note that the main challenge in achieving security for protocols that are based on garbled circuits, is proving the case where the sender is corrupted after the garbled circuit has been sent, whereas the receiver is statically corrupted. This is due to the fact that the corrupted receiver observes active labels that are determined by an arbitrary input for the sender. Then, upon corrupting the sender, the simulator must provide randomness that is consistent with the sender’s real input which is a difficult task. Our idea follows by having the simulator define a different set of tokens in the simulation that are embedded with the active labels and a symmetric key K, where the inactive labels are determined on the fly using key K upon corrupting the sender and obtaining its input x. The complete proof follows.

Theorem 6

Let f be a well-formed functionality. Then, protocol $\varPi$ from Fig. 4 GUC realizes f in the presence of malicious receivers and semi-honest senders in the $\{\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}},\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}\}$-hybrid.

Proof

Let $\mathcal{A}$ be a malicious $\mathsf {PPT}$ real adversary attacking protocol $\varPi$ from Fig. 4 in the $\{\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}},\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}\}$-hybrid model. We construct an ideal adversary $\mathcal{S}$ with access to $\mathcal{F}_f$ which simulates a real execution of $\varPi$ with $\mathcal{A}$ such that no environment $\mathcal{Z}$ can distinguish the ideal process with $\mathcal{S}$ and $\mathcal{F}_f$ from a hybrid execution of $\varPi$ with $\mathcal{A}$. $\mathcal{S}$ starts by invoking a copy of $\mathcal{A}$ and running a simulated interaction of $\mathcal{A}$ with environment $\mathcal{Z}$, emulating the honest party. We describe the actions of $\mathcal{S}$ for every corruption case.

Simulating the Communication with $\mathcal{Z}$ : Every message that $\mathcal{S}$ receives from $\mathcal{Z}$ is internally fed to $\mathcal{A}$ and every output written by $\mathcal{A}$ is relayed back to $\mathcal{Z}$.

The hardest adaptive corruption case to argue here is if the receiver is corrupted at the begining of the execution and the sender is corrupted at the end.

Simulating Static Corruption of the Receiver and Adaptive Corruption of the Sender Post-execution. We begin by describing our simulation:

• 1. Upon corrupting $\mathrm{R}$ the simulator $\mathcal{S}$ generates first the codes to be emulated in the tokens. Towards this it first samples a single label for each wire $\omega$, i.e. $\mathsf {\widetilde{lab}}_\omega \leftarrow \{0,1\}^\kappa$. For each gate ${\mathsf {c}}$, it sends $(\mathsf {Create}, \mathsf {sid}, \mathrm{S}, \mathrm{R}, \mathsf {mid}_{\mathsf {c}}, M_{\mathsf {c}})$ to $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$ for all ${\mathsf {Gate}}_{\mathsf {c}}\in \mathrm {C}$ where the code $M_{\mathsf {c}}$ is defined as follows: Let $\mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^1},\mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^2},\mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^3}$, a secret key K for a non-malleable symmetric encryption $\varPi _{\scriptscriptstyle \mathrm {ENC}}=(\mathsf {Gen}, \mathsf {Enc}, \mathsf {Dec})$ with pseudorandom ciphertext, and randomness r be hardwired in the token where $\omega _{\mathsf {c}}^1,\omega _{\mathsf {c}}^2$ are the input wire identifiers and $\omega _{\mathsf {c}}^3$ is the output wire identifier.⁷ Upon receiving the input $(\ell _1,\ell _2)$, $M_{\mathsf {c}}$ proceeds in one of the following four cases:  

  Case 1: Both labels are active key labels. :

  If $\ell _1=\mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^1}$ and $\ell _2=\mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^2}$ of this gate then output $\mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^3}$.

  Case 2: One of them is active and the other is not. :

  If $\ell _1\ne \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^1}^\alpha$ and $\ell _2= \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^2}^\beta$ then perform the following actions:

  (a):

  Compute $\tau _{\mathsf {c}}={\mathsf {Dec}}_K(\ell _1)$. Check if $\tau _{\mathsf {c}}$ is of the form $(x,y,\omega _{\mathsf {c}}^1)$ where $x,y\in \{0,1\}^n$, and abort if it is not of that form.

  (b):

  Next determine inputs $\alpha ,\beta$ and output $\gamma$ to gate ${\mathsf {c}}$ assuming $\mathrm{S}$’s input is x and $\mathrm{R}$’s input is y by running $\mathrm {C}(x,y)$.

  (c):

  Set $\mathsf {lab}_{\omega _{\mathsf {c}}^1}^\alpha = \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^1}$ and $\mathsf {lab}_{\omega _{\mathsf {c}}^2}^\beta = \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^1}$ and $\mathsf {lab}_{\omega _{\mathsf {c}}^3}^\gamma = \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^3}$. Let $\mathsf {lab}_{\omega _{\mathsf {c}}^3}^{1-\gamma } = {\mathsf {Enc}}_K(x,y,\omega _{\mathsf {c}}^3;r)$ where r is the randomness hardwired in the token.

  (d):

  Output $\mathsf {lab}_{\omega _{\mathsf {c}}^3}^{{\mathsf {Gate}}_{\mathsf {c}}(1-\alpha ,\beta )}$.

  If $\ell _1 = \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^1}^\alpha$ and $\ell _2\ne \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^2}^\beta$, we first compute $\tau _{\mathsf {c}}={\mathsf {Dec}}_K(\ell _2)$ and checking if $\tau _{\mathsf {c}}$ is of the form $(x,y,\omega _{\mathsf {c}}^2)$. Next, we perform the same steps (c) and (d) as above to determine $\alpha , \beta$ and $\gamma$ and make label associations. Finally, instead of the last step (e), we output $\mathsf {lab}_{\omega _{\mathsf {c}}^3}^{{\mathsf {Gate}}_{\mathsf {c}}(\alpha ,1-\beta )}$.

  Case 3: Neither of them is active. :

  If $\ell _1 \ne \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^1}^\alpha$ and $\ell _2\ne \mathsf {\widetilde{lab}}_{\omega _{\mathsf {c}}^2}^\beta$, we first compute $\tau _{\mathsf {c}}={\mathsf {Dec}}_K(\ell _1)$ and $\widetilde{\tau _{\mathsf {c}}}={\mathsf {Dec}}_K(\ell _2)$. Next we check if $\tau _{\mathsf {c}}$ is of the form $(x,y,\omega _{\mathsf {c}}^1)$ and $\widetilde{\tau _{\mathsf {c}}}$ is of the form $(x,y,\omega _{\mathsf {c}}^2)$ for the same x and y. If so, we perform the same steps (c) and (d) as above to determine $\alpha , \beta$ and $\gamma$ and make label associations. Finally, instead of the last step (e), we output $\mathsf {lab}_{\omega _{\mathsf {c}}^3}^{{\mathsf {Gate}}_{\mathsf {c}}(1-\alpha ,1-\beta )}$. Else, if the plaintexts are of incorrect format the token aborts.

  Making the Size of Tokens Proportional to the Width of the Evaluated Circuit. We consider a levelled circuit with fan-in two. A levelled circuit is a circuit in which the incoming edges to the gates of depth i comes only from the gates of depth $i-1$ or from the inputs. That said, edges only exist between adjacent levels of the circuit. Furthermore, the width of a levelled circuit is the maximum size of any level. We define the evaluated circuit as a sequence of circuits $\mathrm {C}=\mathrm {C}_1||...||\mathrm {C}_d$ where $\mathrm {C}_i$ denotes the circuit in level i for $i\in [d]$. The high-level idea is to evaluate the circuit level by level where each level will receive the labels of the previous level and will output the output labels for the next level. In particular, each token will run $\mathrm {C}_d(x_d,y_d)$ instead of $\mathrm {C}(x,y)$ where $x_d$ denotes the input of $\mathrm{S}$ in level d and $y_d$ denotes the input of $\mathrm{R}$ in level d. In addition, the underlying encryption scheme will encrypt plaintexts of the form $(x_d,y_d,\cdot )$. Therefore, each token performs a computation proportional to the width of the circuit rather than the entire circuit.

• 2. $\mathcal{S}$ emulates the OT executions by playing the role of $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ and extracting the receiver’s inputs $y=y_1,\ldots ,y_n$ to these executions. The simulator sends y to the trusted party computing f, receiving back f(x, y). $\mathcal{S}$ completes the $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ executions by sending the receiver the active labels that it picked for the receiver’s input wires.

• 3. When the sender is corrupted post execution, it receives the sender’s real input x. In this case the simulator needs to explain the sender’s view, i.e. it needs to explain the sender’s input to the OT queries and the code for $M_c$ supplied to the $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$. Towards this, the sender first generates labels for the inactive label for all gates. For any input wire $\omega$, the inactive label is set as ${\mathsf {Enc}}_K(x,y,\omega )$ where the randomness is chosen uniformly and for any intermediate wire it is set to ${\mathsf {Enc}}_K(x,y,\omega ;r)$ where r is the randomness hardwired in the gate for which $\omega$ is the output wire. It supplies all the labels to the adversary.

• 4. $\mathcal{S}$ outputs whatever $\mathcal{A}$ does.

Note that the receiver’s view is composed of the set of input labels it obtains from the OT executions and the tokens evaluations. Indistinguishability of real and simulated cases, assuming that the receiver cannot invoke any of the tokens on an inactive label, boils down to the ability of generating a fresh valid ciphertext that encrypts the parties’ inputs and the corresponding identifiers under the key K that is hardwired inside the tokens. Intuitively, this event occurs with negligible probability due to the evasiveness property of the encryption scheme. More formally, we prove indistinguishability of the real and simulated executions via the following sequence of hybrid games.

$\mathbf{Hybrid}_1$: The hybrid is the real execution as defined in Protocol $\varPi$ in Fig. 4.

$\mathbf{Hybrid}_2$: In this hybrid game we consider a simulator $\mathcal{S}_2$ that knows the sender’s real input and generates the tokens just like honest sender. This game produces an identical distribution as the real execution.

$\mathbf{Hybrid}_3$: In this game simulator $\mathcal{S}_3$ generates all active labels uniformly at random, but the inactive labels are generated using random encryptions of $z_{\mathsf {c}}= (x,y,\mathsf {id}_{\mathsf {c}})$. To prove that this game is indistinguishable from the previous hybrid game, we consider a sequence of sub-hybrids $\mathbf{Hybrid}_2^i$ for $i\in [m]$ the total number of inactive labels. Specifically, in $\mathbf{Hybrid}_2^i$ the first i inactive labels are encryptions of $(x,y,\omega _j)$ whereas the rest of the inactive labels are picked uniformly as random. Note that $\mathbf{Hybrid}_2^0$ is identically distributed to hybrid $\mathbf{Hybrid}_2$, whereas $\mathbf{Hybrid}_2^m$ is identically distributed to hybrid $\mathbf{Hybrid}_3$. The indistinguishability of $\mathbf{Hybrid}_2^{i-1}$ and $\mathbf{Hybrid}_2^{i}$ directly follows from the pseudorandomness of the ciphertexts. More formally, assume by contradiction the existence of an adversary $\mathcal{A}$, a distinguisher D and a polynomial $q(\cdot )$ such that $\big |\Pr [D(\mathbf{Hybrid}_2)=1]-\Pr [D(\mathbf{Hybrid}_3)=1]\big |\ge 1/q(\kappa )$ for infinitely many $\kappa$’s, where D obtains the malicious receiver’s view in the corresponding hybrid execution. Then we claim that there exists an index $i\in [m]$ such that

$$ \big |\Pr [D(\mathbf{Hybrid}_2^{i-1})=1]-\Pr [D(\mathbf{Hybrid}_2^{i})=1]\big |\ge 1/(q(\kappa )\cdot m). $$

We define an adversary $\mathcal{A}_{\scriptscriptstyle \mathrm {ENC}}$ that breaks the pseudorandom property of the underlying symmetric encryption scheme as follows. Upon receiving access to the encryption oracle, $\mathcal{A}_{\scriptscriptstyle \mathrm {ENC}}$ uses its oracle to generate the first $i-1$ inactive labels as required in the simulation. For the rest of the inactive labels, namely those with indices in $\{(i+1),\ldots ,m\}$ the adversary picks random strings. Finally, for the $i^{th}$ inactive label, the adversary provides the message $(x,y,\omega _i)$ to the challenger. The challenger either returns a uniform random string or an encryption of $(x,y,\omega _i)$. The adversary feeds whatever the challenger provides in the pseudorandomness security game internally, as the label for the $i^{th}$ inactive label. It follows from our construction that depending on the challenger’s message, the view of the receiver is distributed according to $\mathbf{Hybrid}_2^{i-1}$ or $\mathbf{Hybrid}_2^{i}$ and thus, this adversary breaks the pseudorandomness property of the ciphertexts. In addition, we would like to claim that the adversary, who corrupts the sender after the generation of the garble circuit and the tokens, cannot produce a ciphertext for a valid input which will allow it to query the token on ${\mathsf {Enc}}_K(g_1(x),g_2(y),\cdot )$ where $g_1,g_2$ are arbitrary functions that produce related plaintexts. As such an attack will allow the adversary to learn some additional information about the receiver’s input breaking its privacy or learning a new, in addition to an output he may already learns. We claim that the probability of this event to occur is negligible due to the non-malleability of the encryptions scheme. Specifically, the simulator may monitor the adversary’s queries to the token and observe if such an event occurs.

$\mathbf{Hybrid}_4$: In this game simulator $\mathcal{S}_4$ generates all the tokens as in the simulation. To prove that this game is indistinguishable from the previous hybrid game, we will rely on the evasiveness of the underlying encryption scheme. First, we observe that the distribution of the labels provided by the real simulator before and after the sender is corrupted are identically distributed in both hybrids. This is because the active labels are uniformly generated in both hybrids and the inactive labels are encryptions of $(x,y,\omega _i)$ for the different wires in the circuit. Next, we observe that the only way an adversary can distinguish $\mathbf{Hybrid}_4$ from $\mathbf{Hybrid}_3$ is if it feeds any of the tokens a fresh valid ciphertext of a message that is different from all the labels provided by the simulator after the sender is corrupted. By the evasiveness of the underlying encryption scheme the probability that an adversary can generate such ciphertexts is negligible. Therefore, the view of the adversary in $\mathbf{Hybrid}_3$ and $\mathbf{Hybrid}_4$ is statistically close.

$\mathbf{Hybrid}_5$: The last hybrid game is the simulation which is identical to hybrid $\mathbf{Hybrid}_4$.

Simulating Static Corruption of the Sender. We begin by describing our simulation:

• 1. Upon corrupting $\mathrm{S}$ the simulator receives the adversary’s input x and proceeds as follows.

• 2. $\mathcal{S}$ first communicates with the functionality $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$, that upon receiving the messages for creating the tokens $\{(\mathsf {Create}, \mathsf {sid}, \mathrm{R}, \mathrm{S}, \mathsf {mid}_{\mathsf {c}}, M_{\mathsf {c}})\}_{{\mathsf {Gate}}_{\mathsf {c}}\in \mathrm {C}}$ from $\mathcal{A}$ stores the codes of these tokens.

• 3. $\mathcal{S}$ obtains the inputs labels from $\mathcal{A}$ and then plays the role of $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$, receiving from the adversary n pairs of input labels.

• 4. $\mathcal{S}$ outputs whatever $\mathcal{A}$ does.

Security for this case is proven in a straightforward manner as the adversary does not receive any message from the receiver in the hybrid model.

 

-:

In case no party is corrupted yet, the simulator generates the active labels for the entire set of wires and simulates the message from the sender to the receiver that includes the sender’s input labels and the decoding information.

Simulating the Adaptive Corruption of the Receiver After Corrupting the Sender.

• Upon corrupting the sender, the simulator receives the adversary’s input x and proceeds as follows.

  • 1. $\mathcal{S}$ emulates the tokens transfer phase as the honest sender would do. Namely, $\mathcal{S}$ creates the tokens honestly and provides the corrupted sender with the randomness that is used to generate the garbled gates.

  • 2. Next, $\mathcal{S}$ provides the sender’s queries made to $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ where the input to the $i^{th}$ OT query is the pair of the random labels $((\mathsf {lab}^0_{n+1},\mathsf {lab}^1_{n+1}),\ldots ,(\mathsf {lab}^0_{2n},\mathsf {lab}^1_{2n}))$ that correspond to the receiver’s input labels. $\mathcal{S}$ further explains the message that includes the sender’s input labels and the decoding information.

• Upon corrupting the receiver second, the simulator receives the adversary’s input y and output f(x, y)) and proceeds as follows.

  • 1. In this case the simulator needs to explain the receiver’s internal state condition on the sender’s view. This implies that the simulator needs only to explain the OT queries and the messages to $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ and $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$. Specifically, the description of the garbled circuit is already determined upon corrupting the sender, whereas the sender’s active input labels are already fixed in the protocol communication. The receiver’s OT queries/responses can be explained accordingly to $y_1,\ldots ,y_n$ and the active input labels of the receiver, respectively. Note that the simulator knows the active input labels of the receiver as it generated the garbled circuit.

  • 2. Finally, the communication with $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$ can be explained by mimicking the flow of the garbled circuit evaluation as determined by the simulator. Simulation here follows honestly as the simulator generated the tokens honestly.

  • 3. $\mathcal{S}$ outputs whatever $\mathcal{A}$ does.

  Indistinguishability for this case follows directly as the parties observe the same messages as in the real execution. Specifically, the simulator generates the tokens honestly and the receiver obtains the correct input labels in the OT and thus, the correct labels for the entire evaluation.

6.1 Adaptively Secure Malicious Two-Party Computation

We recall that the protocol presented in Fig. 4 obtains security in the presence of malicious receiver and semi-honest sender. In the following, we briefly discuss how to transform this protocol into fully secure in the presence of malicious senders as well by adopting the protocol from [43]. Loosely speaking the main tool for achieving correctness of garbling is by applying the cut-and-choose technique, where the sender generates s garbled circuits and the receiver asks to open half of them at random. One immediate issue that emerges when considering tokens, is what does it mean to open a garbled circuit that is implemented using tokens and how can the token’s functionality be verified for correctness. Our approach considers asking the sender to commit to any pair of labels through the garbling (that is, the labels associated with each wire). Then, upon receiving an opening request for a garbled circuit, the sender further decommit these commitments for which the receiver can invoke the token on each pair of labels and verify whether the correct output label has been obtained.

We give a high-level description of our protocol based on the [43] protocol with the modifications required for embedding the tokens.

• Auxiliary Input: A boolean circuit $\mathrm {C}$ such that for every $x,y \in \{0,1\}^n$, $\mathrm {C}(x,y) = f(x,y)$ where $f: \{0,1\}^n \times \{0,1\}^n \rightarrow \{0,1\}^n$ and a statistical parameter s.

• Inputs: $\mathrm{S}$ holds $x \in \{0,1\}^n$ and $\mathrm{R}$ holds $y \in \{0,1\}^n$. Let $x = x_1,\ldots ,x_n$ and $y= y_1,\ldots ,y_n$.

• The protocol:

  • 0. Circuit Construction. The parties decide on a circuit computing f. They then change the circuit by replacing each input wire of $\mathrm{R}$ by a gate whose input consists of s new input wires of $\mathrm{R}$ and whose output is the exclusive-or of these wires (such an s-bit exclusive-or gate can be implemented using $s-1$ two-bit exclusive-or gates).

  • 1. Tokens and Commitments Constructions. Next, the sender constructs s independent copies of a garbled circuit of $\mathrm {C}$, where for each such garbled circuit it creates a set of tokens as in Protocol $\varPi$ from Fig. 4. More precisely, for every intermediate wire identified by index $\omega$ in the circuit, let the two random strings $\mathsf {lab}_{\omega }^0,\mathsf {lab}_{\omega }^1 \in \{0,1\}^\kappa$ denote the labels associated with this wire. Then corresponding to gate ${\mathsf {Gate}}_{\mathsf {c}}$, $\mathrm{S}$ creates a token ${\mathsf {TK}}^{{\mathsf {Gate}}_{\mathsf {c}}}_\mathrm{S}$ by sending $(\mathsf {Create}, \mathsf {sid}, \mathrm{R}, \mathrm{S}, \mathsf {mid}_{\mathsf {c}}, M_{\mathsf {c}})$ to $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$, where $M_{\mathsf {c}}$ is the functionality that on input $\ell _1,\ell _2$ proceeds as follows:

    • If $\ell _1 = \mathsf {lab}_{\omega _1}^{\alpha }$ and $\ell _2 = \mathsf {lab}_{\omega _2}^{\beta }$ output $\mathsf {lab}_{\omega _3}^{{\mathsf {Gate}}_{\mathsf {c}}(\alpha ,\beta )}$.

    Where $\omega _1,\omega _2$ are the incoming wire identifiers, $\omega _3$ is the identifier of the output wire to gate ${\mathsf {Gate}}_{\mathsf {c}}$ and ${\mathsf {Gate}}_{\mathsf {c}}\in \{\text{ AND,XOR }\}$ is the corresponding boolean function of this gate.

    $\mathrm{S}$ commits to the garbled values of the wires corresponding to $\mathrm{R}$’s input to each circuit by running n instances of $\varPi _{\scriptscriptstyle \mathrm {COM}}$. Moreover, $\mathrm{S}$ executes additional $s\times n$ instances of $\varPi _{\scriptscriptstyle \mathrm {COM}}$ for the garbled values corresponding to the input wires of the circuits. These commitments-sets are constructed in a special way in order to enable consistency checks (here we follow the same method of [43]). Finally, $\mathrm{S}$ commits to the labels associated with each internal wire in each garbled circuit (we note that these commitments instances are not part of the [43] protocol and are required to verify the tokens’ functionality).

  • 2. Oblivious Transfers. For every $i\in [n]$, the parties call the $\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}$ functionality in which $\mathrm{R}$ receives the garbled values for the wires that correspond to its input bit (in every circuit). This phase is carried out exactly as in [43].

  • 3. Send Tokens and Commitments. $\mathrm{S}$ sends $\mathrm{R}$ all the commitments of Step 1 and forwards the tokens generated in that step to $\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}}$.

  • 4. Coin Tossing. $\mathrm{S}$ and $\mathrm{R}$ run a coin-tossing protocol in order to choose a random string that defines which commitments and garbled circuits will be opened.

  • 5. Decommitment Phase for Check Circuits. $\mathrm{S}$ opens the garbled circuits and committed input values that were chosen in the previous step. $\mathrm{R}$ verifies the correctness of the opened circuits and runs consistency checks based on the decommitted input values and internal wires while verifying the tokens functionality.

    More specifically, the check phase is computed as in [43] with the following additional phase. Upon opening some garbling and obtaining the labels that are associated with all wires, the receiver first verifies that the output label of each garbled gate is consistent with the corresponding committed label from Step 1. Next, the receiver invokes each token on each possible pair of input labels and verifies that the output label is consistent with the committed wires. Meaning, the receiver checks that the token indeed implements a lookup table of size four and that the entries of the table correspond to a valid garbled gate.

  • 6. Send Input Labels. $\mathrm{S}$ sends $\mathrm{R}$ the garbled values corresponding to $\mathrm{S}$’s input wires in the unopened circuits as well as the decoding information.

  • 7. Circuits Evaluations. Assuming that all of the checks pass, $\mathrm{R}$ evaluates the unopened circuits and takes the majority value as its output. Namely, upon receiving the labels $\mathsf {lab}_{1,j}^{x_1},\ldots ,\mathsf {lab}_{n,j}^{x_n}$ and $\mathsf {lab}_{n+1,j}^{y_1},\ldots ,\mathsf {lab}_{2n,j}^{y_n}$ for the $j^{th}$ unopened circuit, $\mathrm{R}$ evaluates the circuit, obtaining the output f(x, y) as follows.

    • (a) For every gate ${\mathsf {Gate}}_{\mathsf {c}}\in \mathrm {C}$, let $\omega _{\mathsf {c}}^1,\omega _{\mathsf {c}}^2$ (resp., $\omega _{\mathsf {c}}^3$) denote the input (resp., output) wires of gate ${\mathsf {Gate}}_{\mathsf {c}}$, then $\mathrm{R}$ sends $(\mathsf {Run}, \mathsf {sid}, \mathrm{S}, \mathsf {mid}_{\mathsf {c}}, (\mathsf {lab}_{\omega _{\mathsf {c}}^1,j}^\alpha , \mathsf {lab}_{\omega _{\mathsf {c}}^2,j}^\beta ))$ and obtains $\mathsf {lab}_{\omega _{\mathsf {c}}^3,j}^{{\mathsf {Gate}}_{\mathsf {c}}(\alpha ,\beta )}$.

    • (b) $\mathrm{R}$ runs the algorithm $z\leftarrow \mathsf {De}(d,{\tilde{z}})$ and outputs z, where ${\tilde{z}}$ is the encoding of the output wires.

Theorem 7

Let f be a well-formed functionality. Then, the above two-party protocol GUC realizes f in the presence of malicious adversaries in the $\{\mathcal{F}_{\scriptscriptstyle \mathrm {gWRAP}},\mathcal{F}_{\scriptscriptstyle \mathrm {OT}}\}$-hybrid.

The proof for a corrupted receiver remains almost identical to the proof of Theorem 6 and the proof from [43], where input extraction is carried out via the OT executions and the original simulation for a single set of tokens is repeated s times with the exception that the simulator prepares s/2 valid garbled circuits and then biases the coin tossing outcome so that the valid garbled circuits are the check circuits.

The main difference is with respect to the security proof of the sender. Loosely speaking, we apply the same standard cut-and-choose analysis from [43], where a corrupted sender cannot cheat in the garbling constructions and the input labels it provides for the evaluations. Yet, when using tokens the prime challenge is to ensure that the tokens’ functionality is correct. We recall that in our protocol the tokens functionality is a lookup table of four rows that corresponds to the garbling of some gate. Then, by enforcing the sender to commit to all wire labels, the receiver can be convinced that the tokens were generated correctly with very high probability. Namely, with all but negligible probability, the tokens’ functionality (for the evaluation circuits) are consistent with the committed labels. We stress that this does not imply that the token cannot be maliciously designed, encoded with some internal state, yet the cut-and-choose argument ensures that with high probability the tokens are encoded with a valid lookup table for their corresponding gates.