Abstract
A public key encryption scheme is said to be n-circular secure if no PPT adversary can distinguish between encryptions of an n length key cycle and n encryptions of zero.
One interesting question is whether circular security comes for free from IND-CPA security. Recent works have addressed this question, showing that for all integers n, there exists an IND-CPA scheme that is not n-circular secure. However, this leaves open the possibility that for every IND-CPA cryptosystem, there exists a cycle length l, dependent on the cryptosystem (and the security parameter) such that the scheme is l-circular secure. If this is true, then this would directly lead to many applications, in particular, it would give us a fully homomorphic encryption scheme via Gentry’s bootstrapping.
In this work, we show that is not true. Assuming indistinguishability obfuscation and leveled homomorphic encryption, we construct an IND-CPA scheme such that for all cycle lengths l, the scheme is not l-circular secure.
B. Waters—Supported by NSF CNS-1228599 and CNS-1414082, DARPA SafeWare, Microsoft Faculty Fellowship, and Packard Foundation Fellowship.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
- Circular Security
- Indistinguishability Obfuscation
- Leveled Homomorphic Encryption (LHE)
- Fully Homomorphic Encryption (FHE)
- Public Key
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Key dependent message security [9] extends the basic notion of semantic security [22] by allowing the adversary to query for encryptions of function evaluations on the hidden secret key. One of the most prominent examples of key dependent message security is that of circular security, which addresses the following question: “What can the adversary learn when given an encryption of the secret key, or more generally, an encryption of a key cycle?”. An n length key cycle consists of n ciphertexts, where the \(i^{th}\) ciphertext is an encryption of the \((i+1)^{th}\) secret key using the \(i^{th}\) public key.Footnote 1 The notion of circular security is captured formally via a security game in which the adversary must distinguish between an n length key cycle and n encryptions of zero (under the n different public keys). An encryption scheme is said to be n-circular secure if no polynomial time adversary can perform this task with non-negligible advantage.
The problem of circular security has received a considerable amount of attention recently because it is a natural question giving rise to different applications [2, 14, 26]. Most notably, it gives us a path to achieve fully homomorphic encryption from leveled homomorphic encryption via Gentry’s bootstrapping approach [20].
In the past several years, there have been many interesting works [4,5,6,7, 10,11,12,13, 23, 27] that have addressed the question of circular security (or more generally, key dependent message security), leading to circular secure encryption schemes under fairly standard assumptions such as bilinear decisional Diffie Hellman assumption (BDDH) and the Learning with Errors assumption (LWE)[29].
However, an important related question is whether any IND-CPA scheme is also circular secure. If so, circular security would come for free and no additional construction mechanisms would need to be designed (beyond what we already needed for IND-CPA security). Unfortunately, this is not true. For \(n=1\), there exists a trivial counterexample — an IND-CPA scheme where the encryption of the secret key is the secret key itself. The question for \(n>1\) was open for some time, and was resolved by Acar et al. [1]. They showed, under the SXDH assumption, an IND-CPA secure encryption scheme that was not 2-circular secure. A similar counterexample with additional features was proposed by Cash, Green and Hohenberger [16], also under the SXDH assumption. In a recent work, Bishop, Hohenberger and Waters [8] expanded the state-of-the-art for \(n = 2\) by showing counterexamples under the k-linear assumption and the LWE assumption. For arbitrary n, the first counterexamples were proposed by Koppula, Ramchen and Waters [24], and Marcedone and Orlandi [28]. Given any fixed integer n, Koppula, Ramchen and Waters showed how to construct an IND-CPA scheme that is not n-circular secure using indistinguishability obfuscation (iO). Marcedone and Orlandi concurrently achieved a similar result under the stronger notion of virtual black-box obfuscation (VBB). Recently, Alamati and Peikert [3], and Koppula and Waters [25] proved similar results using LWE assumption.
At first sight, these results might seem to shut the door on the prospect of getting circular security automatically from IND-CPA security. However, they miss an important distinction in the order of quantifiers. All prior works [3, 24, 25, 28] show that for every integer n, there exists an IND-CPA scheme which is not n-circular secure. In particular, the parameters of their schemes (i.e. the size of public parameters, secret keys and ciphertexts) depend on n. However, this leaves open the possibility that for every cryptosystem, there exists some polynomial function \(\alpha (\cdot )\), particular to that cryptosystem, such that the scheme is \(\alpha (\cdot )\)-circular secure. More formally, we are interested in the following question:
Is it possible that for every IND-CPA secure public key encryption scheme, there exists an integer \(\alpha \) such that the scheme is also \(\alpha \) -circular secure? Footnote 2
If this were true, then this would provide an automatic path to Gentry’s bootstrapping, and potentially other applications. For instance, suppose we have a bootstrappable homomorphic encryption scheme (that is, a homomorphic encryption scheme for circuit class \(\mathcal {C}\) where the decryption circuit is also in \(\mathcal {C}\)), and let us assume the scheme is \(\alpha \)-circular secure. Then, in order to get a homomorphic encryption scheme for all circuits, one simply needs to include an \(\alpha \) length key cycle as part of the public key. This key cycle can be used to reduce the amount of noise in homomorphically evaluated ciphertexts, thereby allowing us to perform arbitrary homomorphic evaluations.
With this motivation, we study the aforementioned question. Unfortunately, the answer is in the negative, and we show this by constructing a class of public key encryption schemes for which there does not exist any \(\alpha \) such that they are \(\alpha \)-circular secure. Our construction uses indistinguishability obfuscator (iO) for polynomial sized circuits, coupled with a leveled homomorphic encryption (LHE) scheme that is capable of homomorphically evaluating its own decryption circuitFootnote 3. Such LHE schemes [13, 21] are realizable from the LWE assumption. Current iO candidates [19, 32], on the other hand, rely on strong assumptions like multilinear maps [17, 18] and therefore, the reader might question the underlying security of current construction. However, we would like to emphasize that our result is a counterexample and it would hold as long as some iO scheme exists, thus the concern over reliability of current candidates is somewhat mitigated.
Our Approach. Below, we sketch an outline of our construction, which has the feature of being very intuitive. In our system, each public key consists of an LHE public key \(\texttt {PK}_\mathrm{HE}\) and an auxiliary program \(\mathsf {Prog}\) (to be described momentarily), whose purpose is to aid the circular security adversary. The secret key consists of the corresponding LHE secret key \(\texttt {SK}_\mathrm{HE}\). The encryption and decryption procedures are simply the LHE encryption and decryption algorithms. The program \(\mathsf {Prog}\) is the obfuscation of a program that on input an LHE ciphertext, under public key \(\texttt {PK}_\mathrm{HE}\), decrypts it using (hardwired) secret key \(\texttt {SK}_\mathrm{HE}\) and outputs 1 iff the plaintext is \(\texttt {SK}_\mathrm{HE}\) itself. In other words, \(\mathsf {Prog}\) acts as a publicly available self-cycle (1-cycle) tester.
Our idea for testing secret key cycles of any (unbounded) length is to iteratively reduce size of the cycle by homomorphically decrypting last ciphertext in the chain using the second-last ciphertext to generate a fresh ciphertext that will act as a new end of the chain. More formally, consider a key cycle of length n in which the last two ciphertexts \(\mathsf {ct}_{n - 1}\) and \(\mathsf {ct}_n\) are encryptions of \(\mathsf {sk}_n\) and \(\mathsf {sk}_1\) under public keys \(\mathsf {pk}_{n - 1}\) and \(\mathsf {pk}_n\) (respectively), and let \(C_{\mathsf {Dec}, n}\) be a circuit that takes an input x and uses it to decrypt \(\mathsf {ct}_n\). Our cycle tester will homomorphically evaluate circuit \(C_{\mathsf {Dec}, n}\) on input \(\mathsf {ct}_{n - 1}\). Since \(\mathsf {ct}_{n - 1}\) is an encryption of \(\mathsf {sk}_n\), the homomorphic evaluation will output a new ciphertext \(\mathsf {ct}'_{n - 1}\) which would be an encryption of \(\mathsf {sk}_1\) under public key \(\mathsf {pk}_{n - 1}\). Thus, this successfully reduces the length of key cycle from n to \(n - 1\), and iteratively applying this procedure would eventually reduce the cycle size to 1. At this point, we could use the program \(\mathsf {Prog}_1\) which is part of first public key \(\mathsf {pk}_1\) to test for a self-cycle. The crucial idea in our cycle tester is that we start slicing the cycle from the end, thus existence of a leveled homomorphic encryption scheme suffices, and we do not require a fully homomorphic scheme for testing unbounded length key cycles.
Now let us move on to the IND-CPA security proof. Ideally we would like to directly leverage the IND-CPA security of LHE scheme to prove IND-CPA security of our construction because intuitively, the obfuscated program \(\mathsf {Prog}\) should not reveal the hardwired LHE secret key. However, indistinguishability obfuscation is a relatively weak notion of program obfuscation, therefore using it directly is a bit tricky so we need to tweak our scheme slightly as in [24]. In our modified scheme, our secret key also contains a random string s, and the program \(\mathsf {Prog}\) has both \(\texttt {SK}_\mathrm{HE}\) and t hardwired, where \(t = \mathrm {PRG}(s)\). On any input ciphertext \(\mathsf {ct}\), it first decrypts using \(\texttt {SK}_\mathrm{HE}\) to recover (a, b) and then checks if \(a = \texttt {SK}_\mathrm{HE}\) and \(t = \mathrm {PRG}(b)\).
In order to use the IND-CPA security of the LHE scheme, we first need to modify program \(\mathsf {Prog}\) such that it does not contain \(\texttt {SK}_\mathrm{HE}\) anymore. To remove \(\texttt {SK}_\mathrm{HE}\) from \(\mathsf {Prog}\), we make a hybrid jump in which we choose t randomly instead of setting it as \(t = \mathrm {PRG}(s)\). This hybrid jump is indistinguishable due to the security of the pseudorandom generator. Note that if t is chosen uniformly at random, then with high probability, this program outputs \(\perp \) on all inputs. As a result, by the security of \(i\mathcal {O}\), this program is indistinguishable from one that always outputs \(\perp \). In this manner, we can remove the secret key \(\texttt {SK}_\mathrm{HE}\) from \(\mathsf {Prog}\). Once this is done, we can directly reduce a successful attack on our construction to a successful attack on IND-CPA security of LHE scheme. Our construction is described in detail in Sect. 4.
Organization. In Sect. 2, we describe the required notations and preliminaries. The definition of circular security can be found in Sect. 3. In Sect. 4, we describe our counterexample scheme. The circular security attack is included in Sect. 4.1 and the corresponding IND-CPA security proof in Sect. 4.2. Finally, in Sect. 5, we discuss (informally) how our construction can be modified to achieve a stronger negative result.
2 Preliminaries
Notation. Let \(\mathcal {R}\) be a ring, and let \(\mathcal {C}_{\mathcal {R}, \lambda ,k}\) denote the set of circuits of size at most \(\mathsf {poly}(\lambda )\) and depth at most k, with domain and co-domain being \(\mathcal {R}\). For simplicity of notation, we will skip the dependence of \(\mathcal {C}_{\mathcal {R}, \lambda , \ell }\) on \(\mathcal {R}\), \(\lambda \) when it is clear from the context.
2.1 Public Key Encryption
A public key encryption scheme \(\mathcal {PKE}\) with message space \(\mathcal {M}\) consists of three algorithms \(\mathsf {Setup}\), \(\mathsf {Enc}\) and \(\mathsf {Dec}\) with the following syntax:
-
\(\mathsf {Setup}(1^\lambda ) \rightarrow (\mathsf {pk}, \mathsf {sk})\) The setup algorithm takes as input the security parameter \(1^\lambda \) and outputs a public key \(\mathsf {pk}\) and secret key \(\mathsf {sk}\).
-
\(\mathsf {Enc}(\mathsf {pk}, m \in \mathcal {M}) \rightarrow \mathsf {ct}\) The encryption algorithm takes as input a public key \(\mathsf {pk}\) and a message \(m\in \mathcal {M}\) and outputs a ciphertext \(\mathsf {ct}\).
-
\(\mathsf {Dec}(\mathsf {sk}, \mathsf {ct}) \rightarrow x \in \mathcal {M}\cup \{\perp \}\) The decryption algorithm takes as input a secret key \(\mathsf {sk}\), ciphertext \(\mathsf {ct}\) and outputs \(x \in \mathcal {M}\cup \{\perp \}\).
Correctness: For correctness, we require that for all security parameters \(\lambda \), \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {Setup}(1^\lambda )\) and messages \(m\in \mathcal {M}\), \(\mathsf {Dec}(\mathsf {sk}, \mathsf {Enc}(\mathsf {pk}, m)) = m\).
Definition 1
(
\({\mathsf{IND}}\text {-}{\mathsf{CPA}}\) Security). A public key encryption scheme \(\mathcal {PKE}=(\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec})\) is said to be \({\mathsf{IND}}\text {-}{\mathsf{CPA}}\) secure if for all security parameters \(\lambda \), stateful PPT adversaries  ,
,  is negligible in \(\lambda \), where advantage of
is negligible in \(\lambda \), where advantage of  is defined as
is defined as  , and
, and  is defined in Fig. 1.
is defined in Fig. 1.
2.2 Homomorphic Encryption
Homomorphic encryption [20, 30] is a powerful extension of public key encryption that allows one to evaluate functions on ciphertexts. In this work, we will be using leveled homomorphic encryption schemes. Let \(\mathcal {R}\) be a ring. A leveled homomorphic encryption scheme \(\mathcal {HE}\) with message space \(\mathcal {R}\) consists of four algorithms \(\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec}, \mathsf {Eval}\) with the following syntax:
-
1.
\(\mathsf {Setup}(1^{\lambda }, 1^\ell ) \rightarrow (\mathsf {pk}, \mathsf {sk})\) The setup algorithm takes as input the security parameter \(\lambda \), bound on circuit depth \(\ell \) and outputs a public key \(\mathsf {pk}\) and secret key \(\mathsf {sk}\).
-
2.
\(\mathsf {Enc}(\mathsf {pk}, m \in \mathcal {R}) \rightarrow \mathsf {ct}\) The encryption algorithm takes as input a public key \(\mathsf {pk}\), message \(m \in \mathcal {R}\) and outputs a ciphertext \(\mathsf {ct}\).
-
3.
\(\mathsf {Eval}(C\in \mathcal {C}_{\ell }, \mathsf {ct}) \rightarrow \mathsf {ct}'\) The evaluation algorithm takes as input a circuit \(C \in \mathcal {C}_{\ell }\), a ciphertext \(\mathsf {ct}\) and outputs a ciphertext \(\mathsf {ct}'\).
-
4.
\(\mathsf {Dec}(\mathsf {sk}, \mathsf {ct}) \rightarrow x\) The decryption algorithm takes as input a secret key \(\mathsf {sk}\) and ciphertext \(\mathsf {ct}\) and outputs \(x\in \mathcal {R}\cup \{\perp \}\).
We will now define some properties of leveled homomorphic encryption schemes. Let \(\mathcal {HE}\) be any homomorphic encryption scheme with message space \(\mathcal {R}\). First, we have the correctness property, which states that the decryption of a homomorphic evaluation on a ciphertext must be equal to the evaluation on the underlying message.
Definition 2
(Correctness). The scheme \(\mathcal {HE}\) is said to be perfectly correct if for all security parameter \(\lambda \), circuit-depth bound \(\ell \), \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {Setup}(1^\lambda , 1^\ell )\), circuit \(C \in \mathcal {C}_{\ell }\) and message \(m \in \mathcal {R}\), \(\mathsf {Dec}(\mathsf {sk}, \mathsf {Eval}(C, \mathsf {Enc}(\mathsf {pk}, m))) = C(m)\).
Next, we have the compactness property which requires that the size of the output of an evaluation on a ciphertext must not depend upon the evaluation circuit. In particular, we require that there exists one decryption circuit such that this circuit can decrypt any bounded-depth evaluations on ciphertexts.
Definition 3
(Compactness). The scheme \(\mathcal {HE}\) is said to be compact if for all \(\lambda \), \(\ell \) there is a decryption circuit \(C^{\mathsf {Dec}}_{\lambda , \ell }\) such that for all \((\mathsf {pk}, \mathsf {sk}) \leftarrow \mathsf {Setup}(1^{\lambda }, 1^{\ell })\), \(m\in \mathcal {R}\), \(C\in \mathcal {C}_{\ell }\), \(C^{\mathsf {Dec}}_{\lambda , \ell }(\mathsf {sk}, \mathsf {Eval}(C, \mathsf {Enc}(\mathsf {pk}, m))) = C(m)\).
Finally, we define the notion of bootstrappability. Gentry [20] showed that if the decryption circuit is of low depth, then a homomorphic encryption scheme for low depth circuits can be bootstrapped to a homomorphic encryption scheme for polynomial depth circuits where the polynomial is apriori defined. We will use this property for constructing our unbounded circular security counterexample. We would like to emphasize that the following notion of bootstrappability does not directly imply fully homomorphic encryption since an FHE scheme must successfully evaluate a ciphertext on all polynomial depth circuits, and not just on apriori defined polynomials.
Definition 4
A compact homomorphic encryption scheme \(\mathcal {HE}\) is said to be bootstrappable if for all security parameters \(\lambda \), there exists a depth bound \(D = D(\lambda )\) such that for all \(\ell \ge D\), \(\mathsf {depth}(C^{\mathsf {Dec}}_{\lambda , \ell }) \le \ell \).
Security: For security, we require that the underlying scheme is \({\mathsf{IND}}\text {-}{\mathsf{CPA}}\) secure.
Definition 5
The scheme \(\mathcal {HE}\) is secure if \(\varGamma = (\mathsf {Setup}, \mathsf {Enc}, \mathsf {Dec})\) is \({\mathsf{IND}}\text {-}{\mathsf{CPA}}\) secure (as per Definition 1).
2.3 Indistinguishability Obfuscation
Next, we recall the definition of indistinguishability obfuscation from [31].
Definition 6
(Indistinguishability Obfuscation). A uniform PPT machine \(i\mathcal {O}\) is called an indistinguishability obfuscator for a circuit class \(\{\mathcal {C}_{\lambda }\}_\lambda \) if it satisfies the following conditions:
-
(Preserving Functionality) For all security parameters \(\lambda \in \mathbb {N}\), for all \({C} \in \mathcal {C}_{\lambda }\), for all inputs x, we have that \({C}'(x) = {C}(x)\) where \({C}' \leftarrow i\mathcal {O}(C)\).
-
(Indistinguishability of Obfuscation) For any (not necessarily uniform) PPT distinguisher (Samp, D), there exists a negligible function \(\text {negl}(\cdot )\) such that the following holds: if for all security parameters \(\lambda \in \mathbb {N}, \Pr [ \forall x,C_0(x) = C_1(x) : ({C}_0; {C}_1; \sigma ) \leftarrow Samp(1^{\lambda })] > 1-\text {negl}(\lambda )\), then
$$\begin{aligned} |&\Pr [D(\sigma , i\mathcal {O}(C_0))=1 : ({C}_0; {C}_1; \sigma ) \leftarrow Samp(1^{\lambda })] -\\&\Pr [D(\sigma , i\mathcal {O}(C_1))=1 : ({C}_0; {C}_1; \sigma ) \leftarrow Samp(1^{\lambda })] | \le \text {negl}(\lambda ) \end{aligned}$$
[19] showed a candidate indistinguishability obfuscator for the circuit class P / poly.
3 Circular Security
In this section, we define the notion of n-circular security. At a high level, n-circular security deals with the following question: “What additional information can a PPT adversary learn given an n-length encryption cycle (that is, a sequence of n ciphertexts where the \(i^{th}\) ciphertext is an encryption of the \((i + 1)^{th}\) secret key using the \(i^{th}\) public key)?”. In this work, we consider the following notion of circular security, where the adversary must distinguish between an n-encryption cycle and n encryptions of \(\varvec{\mathrm {0}}\) (where the \(i^{th}\) encryption is computed using the \(i^{th}\) public key).
Definition 7
A public key cryptosystem \(\mathcal {PKE}\) is said to n-circular secure if for all security parameters \(\lambda \), PPT adversaries  ,
,  is negligible in \(\lambda \), where advantage of
is negligible in \(\lambda \), where advantage of  is defined as
is defined as  , and
, and  is defined in Fig. 2.
is defined in Fig. 2.
3.1 Separating IND-CPA and Circular Security
First, let us recall the theorem statement from [24].
Theorem 1
([24]). If there exists a secure indistinguishability obfuscator for polynomial size circuits (Defintion 6) and a secure pseudorandom generator, then for every positive integer n, there exists a public key encryption scheme \(\mathcal {PKE}\) such that
-
For all PPT adversaries
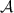 , there exists a negligible function \(\text {negl}_1(\cdot )\) and \(\lambda _0\) such that for all security parameters \(\lambda > \lambda _0\),
, there exists a negligible function \(\text {negl}_1(\cdot )\) and \(\lambda _0\) such that for all security parameters \(\lambda > \lambda _0\),  , and
, and -
There exists a PPT algorithm \(\mathsf {Test}\) and a negligible function \(\text {negl}_2(\cdot )\) such that for all security parameters \(\lambda \), \(\mathsf {Adv}_{\mathsf {Test}, \mathcal {PKE}}^{\mathsf {circ}}(\lambda , n) \ge 1/2 - \text {negl}_2(\lambda )\).
We observe that the counterexample provided by Koppula, Ramchen, and Waters could be trivially extended to prove the following (slightly stronger) statement.
Theorem 2
If there exists a secure indistinguishability obfuscator for polynomial size circuits (Defintion 6) and a secure pseudorandom generator, then there exists a public key encryption scheme \(\mathcal {PKE}\) such that
-
For all PPT adversaries
 , there exists a negligible function \(\text {negl}_1(\cdot )\) and \(\lambda _0\) such that for all security parameters \(\lambda > \lambda _0\),
, there exists a negligible function \(\text {negl}_1(\cdot )\) and \(\lambda _0\) such that for all security parameters \(\lambda > \lambda _0\),  , and
, and -
There exists a PPT algorithm \(\mathsf {Test}\), polynomial \(p(\cdot )\) and a negligible function \(\text {negl}_2(\cdot )\) such that for all security parameters \(\lambda \) and \(n\le p(\lambda )\), \(\mathsf {Adv}_{\mathsf {Test}, \mathcal {PKE}}^{\mathsf {circ}}(\lambda , n) \ge 1/2 - \text {negl}_2(\lambda )\).
The KRW counterexample could be extended as follows — For security parameter \(\lambda \) and polynomial \(p(\cdot )\), instantiate \(p(\lambda )\) copies of KRW scheme where each scheme is designed to be insecure for a certain length key cycle.
Our result proves a stronger statement which is not implied by the KRW counterexample. It is formally stated below.
Theorem 3
If there exists a secure indistinguishability obfuscator for polynomial size circuits (Defintion 6), secure bootstrappable homomorphic encryption scheme (Definitions 4 and 5), and a secure pseudorandom generator, then there exists a public key encryption scheme \(\mathcal {PKE}\) such that
-
For all PPT adversaries
 , there exists a negligible function \(\text {negl}_1(\cdot )\) and \(\lambda _0\) such that for all security parameters \(\lambda > \lambda _0\),
, there exists a negligible function \(\text {negl}_1(\cdot )\) and \(\lambda _0\) such that for all security parameters \(\lambda > \lambda _0\),  , and
, and -
There exists a PPT algorithm \(\mathsf {Test}\), a negligible function \(\text {negl}_2(\cdot )\) such that for all security parameters \(\lambda \) and positive integers \(\alpha \), \(\mathsf {Adv}_{\mathsf {Test}, \mathcal {PKE}}^{\mathsf {circ}}(\lambda , \alpha ) \ge 1/2 - \text {negl}_2(\lambda )\).
4 Unbounded Circular Insecure Public Key Encryption Scheme
In this section, we prove Theorem 3 by constructing a public key encryption scheme \(\mathcal {PKE}\) \(= (\textsf {Setup}_\mathrm{PKE},\) \(\textsf {Enc}_\mathrm{PKE},\) \(\textsf {Dec}_\mathrm{PKE})\) that breaks circular security with unbounded length key cycles. Let \(\mathcal {HE}\) \(= (\textsf {Setup}_\mathrm{HE},\) \(\textsf {Enc}_\mathrm{HE},\) \(\textsf {Eval}_\mathrm{HE},\) \(\textsf {Dec}_\mathrm{HE})\) be a secure bootstrappable homomorphic encryption scheme, \(i\mathcal {O}\) be a secure indistinguishability obfuscator and \(\mathrm {PRG}\) be a secure pseudorandom generator that maps \(\ell \) bit inputs to \(2\ell \) bit outputs. The construction is described as follows:
-
\(\textsf {Setup}_\mathrm{PKE}(1^{\lambda }):\) It runs HE setup algorithm to obtain a public and secret key pair as \((\texttt {PK}_\mathrm{HE}, \texttt {SK}_\mathrm{HE}) \leftarrow \textsf {Setup}_\mathrm{HE}(1^{\lambda }, 1^D)\), where D is a depth such that \(\mathsf {depth}(C^{\textsf {Dec}_\mathrm{HE}}_{\lambda , D}) \le D\).Footnote 4 It uniformly samples \(s \leftarrow \{0, 1\}^{\ell }\), sets \(t = \mathrm {PRG}(s)\), and computes the obfuscation of program \(\mathrm {SelfCycleTest}\) (described in Fig. 3) as \(\mathsf {Prog}\leftarrow i\mathcal {O}(\mathrm {SelfCycleTest})\). It sets the public key and secret key as \(\texttt {PK}_\mathrm{PKE}= (\texttt {PK}_\mathrm{HE}, \mathsf {Prog}), \texttt {SK}_\mathrm{PKE}= (\texttt {SK}_\mathrm{HE}, s)\).
-
\(\textsf {Enc}_\mathrm{PKE}(\texttt {PK}_\mathrm{PKE}, m; r)\): It computes ciphertext as \(\mathsf {ct}= \textsf {Enc}_\mathrm{HE}(\texttt {PK}_\mathrm{HE}, m; r)\), where \(\texttt {PK}_\mathrm{PKE}= (\texttt {PK}_\mathrm{HE}, \mathsf {Prog})\).
-
\(\textsf {Dec}_\mathrm{PKE}(\texttt {SK}_\mathrm{PKE}, \mathsf {ct})\): It outputs \(\textsf {Dec}_\mathrm{HE}(\texttt {SK}_\mathrm{HE}, \mathsf {ct})\), where \(\texttt {SK}_\mathrm{PKE}= (\texttt {SK}_\mathrm{HE}, s)\).
The proof of Theorem 3 is described in two parts. First, we show a poly-time attack on circular security of \(\mathcal {PKE}\) in Sect. 4.1. Next, we prove it to be IND-CPA secure in Sect. 4.2.
4.1 Attack on Unbounded Circular Security
We construct a PPT adversary \(\mathcal {A}\) which breaks unbounded circular security of above construction as follows:
-
1.
Challenger generates n public and secret key pairs as \(\left\{ \left( \mathsf {pk}_i, \mathsf {sk}_i \right) \right\} _{i = 1}^n\) by independently running the setup algorithm n times \(\big ((\mathsf {pk}_i, \mathsf {sk}_i) \leftarrow \textsf {Setup}_\mathrm{PKE}(1^{\lambda })\) \(\text { for } i \le n\big )\). It uniformly chooses a bit \(b \leftarrow \{0,1\}\), and computes ciphertexts \(\mathsf {ct}_i \leftarrow \textsf {Enc}_\mathrm{PKE}(\mathsf {pk}_i, m_{i, b}) \text { for } i \le n\), where \(m_{i, 0} = \mathsf {sk}_{(i \text { mod } n) + 1}\) and \(m_{i, 1} = 0^{|m_{i, 0}|}\). Finally, it sends \(\left\{ \left( \mathsf {pk}_i, \mathsf {ct}_i \right) \right\} _{i = 1}^n\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) receives n public key and ciphertext pairs \(\left\{ \left( \mathsf {pk}_i, \mathsf {ct}_i \right) \right\} _{i = 1}^n\), and proceeds as follows:
-
It sets \(\mathsf {ct}'_n = \mathsf {ct}_n\).
-
For \(i = n - 1\) to \(i = 1:\)
-
–
Compute \(\mathsf {ct}_i' = \textsf {Eval}_\mathrm{HE}(C_i, \mathsf {ct}_i)\), where \(C_i\) is the HE decryption circuit \(C^{\textsf {Dec}_\mathrm{HE}}\) with \(\mathsf {ct}'_{i + 1}\) hardwired as the its second input, i.e. \(C_i(x) = C^{\textsf {Dec}_\mathrm{HE}}(x, \mathsf {ct}'_{i + 1})\).Footnote 5
-
–
-
\(\mathcal {A}\) runs program \(\mathsf {Prog}_1\) on input \(\mathsf {ct}'_1\), and outputs \(b' = \mathsf {Prog}_1(\mathsf {ct}'_1)\) as its guess, where \(\mathsf {pk}_1 = (\mathsf {pk}'_1, \mathsf {Prog}_1)\).
-
-
3.
\(\mathcal {A}\) wins if its guess is correct \((b' = b)\).
Lemma 1
If \(\mathrm {PRG}\) is a secure pseudorandom generator, then there exists a negligible function \(\text {negl}(\cdot )\) such that for all security parameters \(\lambda \) and positive integers n, \(\mathsf {Adv}_{\mathcal {A}, \mathcal {PKE}}^{\mathsf {circ}}(\lambda , n) \ge 1/2 - \text {negl}(\lambda )\).
Proof
We prove this lemma in two parts. First, we consider a length n key cycle and show that adversary \(\mathcal {A}\) always correctly guesses challenger’s bit b as 1. Next, we show that, with all but negligible probability, \(\mathcal {A}\) correctly guesses b as 0.
As we described earlier, the basic idea is to slice the ring structure of n ciphertexts by iteratively reducing an n-circular attack to an \((n - 1)\)-circular attack and finally, reducing it to a 1-circular attack. For slicing the ring of ciphertexts, we use bootstrappability of the underlying scheme. The correctness of the above reduction is proven by induction over cycle length n. The base case \(n = 1\) follows directly from the correctness of program \(\mathsf {Prog}_1\). For the induction step, assume that \(\mathcal {A}\) correctly identifies a length k key cycle. To prove that \(\mathcal {A}\) also identifies length \(k + 1\) key cycle, we only need to show that \(\mathcal {A}\) correctly reduces a \((k + 1)\)-circular instance to a k-circular instance. Note that given \(k + 1\) public key, ciphertext pairs \((\left\{ \left( \mathsf {pk}_i, \mathsf {ct}_i \right) \right\} _{i = 1}^{k + 1})\). \(\mathcal {A}\) computes \(\mathsf {ct}_k'\) as \(\mathsf {ct}_k' = \textsf {Eval}_\mathrm{HE}(C_k, \mathsf {ct}_k)\). If \(\mathsf {ct}_{k + 1}\) is an encryption of \(\mathsf {sk}_1\) under \(\mathsf {pk}_{k + 1}\), and \(\mathsf {ct}_k\) is an encryption of \(\mathsf {sk}_{k + 1}\) under \(\mathsf {pk}_k\), then \(\mathsf {ct}_k'\) will be an encryption of \(\mathsf {sk}_1\) under \(\mathsf {pk}_{k}\) as the scheme \(\mathcal {HE}\) is bootstrappable satisfying Definition 4. Therefore, using inductive hypothesis, we can conclude that \(\mathcal {A}\) correctly identifies length \(k + 1\) key cycle. Thus, the above reduction correctly reduces circular instances with unbounded length key cycles to 1-circular instances, and therefore \(\mathcal {A}\) guesses the bit b as 1 with probability 1.
To conclude our proof we just need to show that if the cycle is encryption of all zeros, then \(\mathcal {A}\) outputs 0 with all but negligible probability. This follows from the fact that \(\mathrm {PRG}\) is a secure pseudorandom generator. Consider a hybrid experiment in which the value \(t_1\) is sampled uniformly at random instead of being computed as \(t_1 = \mathrm {PRG}(s_1)\). Since \(\mathrm {PRG}\) is a length doubling pseudorandom generator, we can claim that in the hybrid experiment (with all but negligible probability) \(\mathsf {Prog}_1\) outputs 0 because there does not exist any pre-image s for \(t_1\). Therefore, if \(\mathrm {PRG}\) is a secure pseudorandom generator, \(\mathcal {A}\) will always output 0 with all but negligible probability. Thus, \(\mathcal {A}\) wins the n-circular security game with all but negligible probability.
4.2 IND-CPA Security
Lemma 2
If \(i\mathcal {O}\) is a secure indistinguishability obfuscator for polynomial size circuits (Definition 6), \(\mathcal {HE}\) is a secure bootstrappable homomorphic encryption scheme (Definitions 4 and 5), and \(\mathrm {PRG}\) is a secure pseudorandom generator, then public key encryption scheme \(\mathcal {PKE}\) is IND-CPA secure (Definition 1).
Proof
We prove above lemma by contradiction. Let \(\mathcal {A}\) be any PPT adversary that wins the IND-CPA security game against \(\mathcal {PKE}\) with non-negligible advantage. We argue that such an adversary must break security of at least one underlying primitive. To formally prove security, we construct a series of hybrid games as follows.
Game 1: This game is the original IND-CPA security game described in Definition 1.
-
1.
Challenger runs HE setup algorithm to obtain a public and secret key pair as \((\texttt {PK}_\mathrm{HE}, \texttt {SK}_\mathrm{HE}) \leftarrow \textsf {Setup}_\mathrm{HE}(1^{\lambda })\). It uniformly samples \(s \leftarrow \{0, 1\}^{\ell }\), sets \(t = \mathrm {PRG}(s)\), and computes the obfuscation of program \(\mathrm {SelfCycleTest}\) (described in Fig. 3) as \(\mathsf {Prog}\leftarrow i\mathcal {O}(\mathrm {SelfCycleTest})\). It sets the public key and secret key as \(\texttt {PK}_\mathrm{PKE}= (\texttt {PK}_\mathrm{HE}, \mathsf {Prog}), \texttt {SK}_\mathrm{PKE}= (\texttt {SK}_\mathrm{HE}, s)\). Finally, it sends \(\texttt {PK}_\mathrm{PKE}\) to \(\mathcal {A}\).
-
2.
\(\mathcal {A}\) receives \(\texttt {PK}_\mathrm{PKE}\) from challenger, and computes messages \(m_0, m_1\). It sends \((m_0, m_1)\) to the challenger.
-
3.
Challenger chooses bit \(b \leftarrow \{0,1\}\), computes \(\mathsf {ct}^{*}\leftarrow \textsf {Enc}_\mathrm{PKE}(\texttt {PK}_\mathrm{PKE}, m_b)\), and sends \(\mathsf {ct}^{*}\) to \(\mathcal {A}\).
-
4.
\(\mathcal {A}\) receives challenge ciphertext \(\mathsf {ct}^{*}\) from challenger, and outputs its guess \(b'\).
-
5.
\(\mathcal {A}\) wins if it guesses correctly, that is if \(b = b'\).
Game 2: Game 2 is same as Game 1, except challenger uniformly samples t from \(\{0, 1\}^{2\ell }\) instead of computing it as \(t = \mathrm {PRG}(s)\).
-
1.
Challenger runs HE setup algorithm to obtain a public and secret key pair as \((\texttt {PK}_\mathrm{HE}, \texttt {SK}_\mathrm{HE}) \leftarrow \textsf {Setup}_\mathrm{HE}(1^{\lambda })\). It uniformly samples \(s \leftarrow \{0, 1\}^{\ell }\),
 , and computes the obfuscation of program \(\mathrm {SelfCycleTest}\) (described in Fig. 3) as \(\mathsf {Prog}\leftarrow i\mathcal {O}(\mathrm {SelfCycleTest})\). It sets the public key and secret key as \(\texttt {PK}_\mathrm{PKE}= (\texttt {PK}_\mathrm{HE}, \mathsf {Prog}), \texttt {SK}_\mathrm{PKE}= (\texttt {SK}_\mathrm{HE}, s)\). Finally, it sends \(\texttt {PK}_\mathrm{PKE}\) to \(\mathcal {A}\).
, and computes the obfuscation of program \(\mathrm {SelfCycleTest}\) (described in Fig. 3) as \(\mathsf {Prog}\leftarrow i\mathcal {O}(\mathrm {SelfCycleTest})\). It sets the public key and secret key as \(\texttt {PK}_\mathrm{PKE}= (\texttt {PK}_\mathrm{HE}, \mathsf {Prog}), \texttt {SK}_\mathrm{PKE}= (\texttt {SK}_\mathrm{HE}, s)\). Finally, it sends \(\texttt {PK}_\mathrm{PKE}\) to \(\mathcal {A}\). -
2–5.
Same as before.
Game 3: Game 3 is same as Game 2, except challenger computes \(\mathsf {Prog}\) as obfuscation of program \(\mathrm {Zero}\).
-
1.
Challenger runs HE setup algorithm to obtain a public and secret key pair as \((\texttt {PK}_\mathrm{HE}, \texttt {SK}_\mathrm{HE}) \leftarrow \textsf {Setup}_\mathrm{HE}(1^{\lambda })\). It uniformly samples \(s \leftarrow \{0, 1\}^{\ell }\), \(t \leftarrow \{0, 1\}^{2 \ell }\), and
 \(\mathsf {Prog}\)
\(\mathsf {Prog}\)  Footnote 6. It sets the public key and secret key as \(\texttt {PK}_\mathrm{PKE}= (\texttt {PK}_\mathrm{HE}, \mathsf {Prog}),\) \(\texttt {SK}_\mathrm{PKE}= (\texttt {SK}_\mathrm{HE}, s)\). Finally, it sends \(\texttt {PK}_\mathrm{PKE}\) to \(\mathcal {A}\).
Footnote 6. It sets the public key and secret key as \(\texttt {PK}_\mathrm{PKE}= (\texttt {PK}_\mathrm{HE}, \mathsf {Prog}),\) \(\texttt {SK}_\mathrm{PKE}= (\texttt {SK}_\mathrm{HE}, s)\). Finally, it sends \(\texttt {PK}_\mathrm{PKE}\) to \(\mathcal {A}\). -
2–5.
Same as before.
We now establish via a sequence of claims that the adversary’s advantage between each adjacent game is negligible. Let \(\mathsf {Adv}_i = \left| \Pr [b' = b] - 1/2 \right| \) denote the advantage of adversary \(\mathcal {A}\) in Game i of guessing the bit b.
Claim 1
If \(\mathrm {PRG}\) is a secure pseudorandom generator, then for all PPT \(\mathcal {A}\), \(\left| \mathsf {Adv}_1 - \mathsf {Adv}_2 \right| \le \text {negl}(\lambda )\) for some negligible function \(\text {negl}(\cdot )\).
Proof
We describe and analyze a PPT reduction algorithm \(\mathcal {B}\) that plays the pseudorandom generator security game. \(\mathcal {B}\) first receives a PRG challenge \(T \in \{0, 1\}^{2 \ell }\). It then plays the security game with \(\mathcal {A}\) as described in Game 1 with the exception that in step 1 it lets \(t = T\). If \(\mathcal {A}\) wins (i.e. \(b' = b\)), then \(\mathcal {B}\) guesses ‘1’ to indicate that T was chosen in the image space of \(\mathrm {PRG}(\cdot )\); otherwise, it outputs ‘0’ to that T was chosen randomly.
We observe that when T is generated as \(T = \mathrm {PRG}(r)\), then \(\mathcal {B}\) gives exactly the view of Game 1 to \(\mathcal {A}\). Otherwise if T is chosen randomly the view is of Game 2. Therefore if \(\left| \mathsf {Adv}_1 - \mathsf {Adv}_2 \right| \) is non-negligble, \(\mathcal {B}\) must also have non-negligible advantage against the pseudorandom generator.
Claim 2
If \(i\mathcal {O}\) is a secure indistinguishability obfuscator, then for all PPT \(\mathcal {A}\), \(\left| \mathsf {Adv}_2- \mathsf {Adv}_3 \right| \le \text {negl}(\lambda )\) for some negligible function \(\text {negl}(\cdot )\).
Proof
We describe and analyze a PPT reduction algorithm \(\mathcal {B}\) that plays the indistinguishability obfuscation security game with \(\mathcal {A}\). \(\mathcal {B}\) runs steps 1 as in Game 2, except it creates two programs as \(C_0 = \mathrm {SelfCycleTest}\) and \(C_1 = \mathrm {Zero}\). It submits both of these to the IO challenger and receives back a program P. It sets \(\mathsf {Prog}= P\) and finishes step 1. It executes steps 2–5 as in Game 2. If the attacker wins (i.e. \(b' = b\)), then \(\mathcal {B}\) guesses ‘0’ to indicate that P was and obfuscation of \(C_0\); otherwise, it guesses ‘1’ to indicate it was an obfuscation of \(C_1\).
We observe that when P is generated as an obfuscation of \(C_0\), then \(\mathcal {B}\) gives exactly the view of Game 2 to \(\mathcal {A}\). Otherwise if P is chosen as an obfuscation of \(C_1\) the view is of Game 2. In addition, the programs are functionally equivalent with all but negligible probability. The reason is that t is outside the image of the pseudorandom generator with probability at least \(1 - 2^\ell \). Therefore if \(\left| \mathsf {Adv}_2 - \mathsf {Adv}_3 \right| \) is non-negligble, \(\mathcal {B}\) must also have non-negligible advantage against the indisguishability obfuscation game.
Claim 3
If \(\mathcal {HE}\) is a secure bootstrappable homomorphic encryption scheme, then for all PPT \(\mathcal {A}\), \(\mathsf {Adv}_3 \le \text {negl}(\lambda )\) for some negligible function \(\text {negl}(\cdot )\).
Proof
We describe and analyze a PPT reduction algorithm \(\mathcal {B}\) that plays the IND-CPA security game with \(\mathcal {HE}\) challenger. \(\mathcal {B}\) receives public key \(\texttt {PK}_\mathrm{HE}\) from \(\mathcal {HE}\) challenger. It runs step 1 as described in Game 3 with the exception that it uses \(\texttt {PK}_\mathrm{HE}\) generated by \(\mathcal {HE}\) challenger instead of running the setup algorithm. \(\mathcal {B}\) forwards the challenge messages \((m_0, m_1)\) it receives from \(\mathcal {A}\) to \(\mathcal {HE}\) challenger as its challenge, and receives \(\mathsf {ct}^{*}\) as the challenge ciphertext, which it then forwards to \(\mathcal {A}\). Finally, \(\mathcal {B}\)outputs the same bit as \(\mathcal {A}\).
We observe that if \(\mathcal {A}\) wins (i.e. \(b' = b\)), then \(\mathcal {B}\) also wins because it exactly simulates the view of Game 3 for \(\mathcal {A}\). Therefore if \(\mathsf {Adv}_3\) is non-negligble, \(\mathcal {B}\) must also have non-negligible advantage against \(\mathcal {HE}\) challenger.
5 Unbounded Counterexamples with Mixed Cryptosystems
We conclude by making the following observation pertaining to our counterexample. In our construction, we started slicing the key cycle from the end, and after every cycle length reduction iteration, the new (homomorphically) evaluated ciphertext is encrypted under a different public key. Concretely, if we consider an n-length key cycle, then after \(i^{th}\) cycle reduction iteration, the ciphertext \(\mathsf {ct}'_{n - i}\) generated is encrypted under public key \(\mathsf {pk}_{n - i}\). Therefore, the cycle testing algorithm works in the presence of a LHE scheme. We observe that if we instantiate our idea with an unbounded fully homomorphic encryption (FHE) scheme as opposed to a leveled one, then the cycle testing algorithm could be alternatively evaluated by slicing the key cycle from the start. More formally, in the first iteration, our new cycle tester would homomorphically evaluate circuit \(C_{\mathsf {Dec}, 2}\) on \(\mathsf {ct}_1\), where \(C_{\mathsf {Dec}, 2}\) is a circuit that takes an input x and uses it to decrypt \(\mathsf {ct}_2\). Since \(\mathsf {ct}_1\) and \(\mathsf {ct}_2\) are encryptions of \(\mathsf {sk}_2\) and \(\mathsf {sk}_3\) under public keys \(\mathsf {pk}_1\) and \(\mathsf {pk}_2\) (respectively), the homomorphic evaluation would generate a new ciphertext \(\mathsf {ct}'_2\) that would be an encryption of \(\mathsf {sk}_3\) under public key \(\mathsf {pk}_1\). Note that this also reduces the key cycle length by one, but in the forward direction and it requires the encryption scheme to be fully homomorphic. Therefore, iteratively applying this procedure would finally generate a ciphertext \(\mathsf {ct}'_1\) which encrypts secret key \(\mathsf {sk}_1\) under public key \(\mathsf {pk}_1\), and as before, the self-cycle could be tested using \(\mathsf {Prog}_1\).
The crucial observation in the alternative cycle testing procedure is that we require only one encryption scheme to be homomorphic encryption scheme. This opens up the possibility of creating a counterexample for circular security under mixed public key encryption (PKE) framework, where the cycle could comprise of distinct and variegated PKE schemes with a universal message and key space. In particular, this shows that just one “bad” key could poison the circular security for any arbitrary length cycle.
Notes
- 1.
The \(n^{th}\) ciphertext is an encryption of the first secret key using the \(n^{th}\) public key.
- 2.
In comparison, the previous works addressed the following question: “Is it possible that there exists an integer n such that every IND-CPA secure public key encryption scheme is also n-circular secure?”.
- 3.
Recently, [15] provided constructions for LHE from sub-exponentially hard indistinguishability obfuscation, one-way functions, and re-randomizable encryption schemes.
- 4.
Note that such a depth D exists since our HE scheme is bootstrappable (Definition 4).
- 5.
Actually, the circuits \(C_i\) are not standard HE decryption circuits because ciphertexts \(\mathsf {ct}_i\) are encryptions of \((i + 1)^{th}\) secret key and an extra element, therefore the circuit must ignore the second element during homomorphic decryption.
- 6.
Note that program \(\mathrm {Zero}\) must be padded such that it is of same size as program \(\mathrm {SelfCycleTest}\).
References
Acar, T., Belenkiy, M., Bellare, M., Cash, D.: Cryptographic agility and its relation to circular encryption. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 403–422. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_21
Adão, P., Bana, G., Herzog, J., Scedrov, A.: Soundness and completeness of formal encryption: the cases of key cycles and partial information leakage. J. Comput. Secur. 17(5), 737–797 (2009)
Alamati, N., Peikert, C.: Three’s compromised too: circular insecurity for any cycle length from (ring-)LWE. Cryptology ePrint Archive, Report 2016/110 (2016)
Alperin-Sheriff, J., Peikert, C.: Circular and KDM security for identity-based encryption. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 334–352. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30057-8_20
Applebaum, B.: Key-dependent message security: generic amplification and completeness. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 527–546. Springer, Heidelberg (2011). doi:10.1007/978-3-642-20465-4_29
Applebaum, B., Cash, D., Peikert, C., Sahai, A.: Fast cryptographic primitives and circular-secure encryption based on hard learning problems. In: Halevi, S. (ed.) CRYPTO 2009. LNCS, vol. 5677, pp. 595–618. Springer, Heidelberg (2009). doi:10.1007/978-3-642-03356-8_35
Barak, B., Haitner, I., Hofheinz, D., Ishai, Y.: Bounded key-dependent message security. In: Gilbert, H. (ed.) EUROCRYPT 2010. LNCS, vol. 6110, pp. 423–444. Springer, Heidelberg (2010). doi:10.1007/978-3-642-13190-5_22
Bishop, A., Hohenberger, S., Waters, B.: New circular security counterexamples from decision linear and learning with errors. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 776–800. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48800-3_32
Black, J., Rogaway, P., Shrimpton, T.: Encryption-scheme security in the presence of key-dependent messages. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 62–75. Springer, Heidelberg (2003). doi:10.1007/3-540-36492-7_6
Boneh, D., Halevi, S., Hamburg, M., Ostrovsky, R.: Circular-secure encryption from decision diffie-hellman. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 108–125. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_7
Brakerski, Z., Goldwasser, S.: Circular and leakage resilient public-key encryption under subgroup indistinguishability (or: Quadratic residuosity strikes back). IACR Cryptology ePrint Archive 2010/226 (2010)
Brakerski, Z., Goldwasser, S., Kalai, Y.T.: Black-box circular-secure encryption beyond affine functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 201–218. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_13
Brakerski, Z., Vaikuntanathan, V.: Efficient fully homomorphic encryption from (standard) LWE. In: IEEE 52nd Annual Symposium on Foundations of Computer Science, FOCS 2011, Palm Springs, CA, USA, 22–25 October, 2011, pp. 97–106 (2011)
Camenisch, J., Lysyanskaya, A.: An efficient system for non-transferable anonymous credentials with optional anonymity revocation. IACR Cryptology ePrint Archive 2001/19 (2001)
Canetti, R., Lin, H., Tessaro, S., Vaikuntanathan, V.: Obfuscation of probabilistic circuits and applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 468–497. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_19
Cash, D., Green, M., Hohenberger, S.: New definitions and separations for circular security. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 540–557. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30057-8_32
Coron, J.-S., Lepoint, T., Tibouchi, M.: Practical multilinear maps over the integers. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 476–493. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_26
Garg, S., Gentry, C., Halevi, S.: Candidate multilinear maps from ideal lattices. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 1–17. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_1
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indstinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013)
Gentry, C.: Fully homomorphic encryption using ideal lattices. In: Proceedings of the 41st Annual ACM Symposium on Theory of Computing, STOC 2009, Bethesda, MD, USA, 31 May–2 June, 2009, pp. 169–178 (2009)
Gentry, C., Sahai, A., Waters, B.: Homomorphic encryption from learning with errors: conceptually-simpler, asymptotically-faster, attribute-based. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8042, pp. 75–92. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40041-4_5
Goldwasser, S., Micali, S.: Probabilistic encryption. J. Comput. Syst. Sci. 28(2), 270–299 (1984)
Haitner, I., Holenstein, T.: On the (im)possibility of key dependent encryption. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 202–219. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_13
Koppula, V., Ramchen, K., Waters, B.: Separations in circular security for arbitrary length key cycles. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 378–400. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_15
Koppula, V., Waters, B.: Circular security separations for arbitrary length cycles from lWE. Cryptology ePrint Archive, Report 2016/117 (2016)
Laud, P.: Encryption cycles and two views of cryptography. In: NORDSEC 2002 - Proceedings of the 7th Nordic Workshop on Secure IT Systems (Karlstad University Studies 2002:31, pp. 85–100 (2002)
Malkin, T., Teranishi, I., Yung, M.: Efficient circuit-size independent public key encryption with KDM security. In: Paterson, K.G. (ed.) EUROCRYPT 2011. LNCS, vol. 6632, pp. 507–526. Springer, Heidelberg (2011). doi:10.1007/978-3-642-20465-4_28
Marcedone, A., Orlandi, C.: Obfuscation \(\Rightarrow \) (IND-CPA Security \(\nRightarrow \) Circular Security). In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 77–90. Springer, Cham (2014). doi:10.1007/978-3-319-10879-7_5
Regev, O.: On lattices, learning with errors, random linear codes, and cryptography. In: Proceedings of the 37th Annual ACM Symposium on Theory of Computing, Baltimore, MD, USA, 22–24 May, 2005, pp. 84–93 (2005)
Rivest, R.L., Adleman, L., Dertouzos, M.L.: On data banks and privacy homomorphisms. In: Foundations of Secure Computation, pp. 169–179. Academia Press (1978)
Sahai, A., Waters, B.: How to use indistinguishability obfuscation: deniable encryption, and more. In: Symposium on Theory of Computing, STOC 2014, New York, NY, USA, 31 May–03 June, 2014, pp. 475–484 (2014)
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_15
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2017 International Association for Cryptologic Research
About this paper
Cite this paper
Goyal, R., Koppula, V., Waters, B. (2017). Separating IND-CPA and Circular Security for Unbounded Length Key Cycles. In: Fehr, S. (eds) Public-Key Cryptography – PKC 2017. PKC 2017. Lecture Notes in Computer Science(), vol 10174. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-54365-8_10
Download citation
DOI: https://doi.org/10.1007/978-3-662-54365-8_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-54364-1
Online ISBN: 978-3-662-54365-8
eBook Packages: Computer ScienceComputer Science (R0)







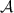 , there exists a negligible function
, there exists a negligible function  , and
, and , there exists a negligible function
, there exists a negligible function  , and
, and , there exists a negligible function
, there exists a negligible function  , and
, and
 , and computes the obfuscation of program
, and computes the obfuscation of program 

