Abstract
Garbled circuits is a cryptographic technique, which has been used among other things for the construction of two and three-party secure computation, private function evaluation and secure outsourcing. Garbling schemes is a primitive which formalizes the syntax and security properties of garbled circuits. We define a generalization of garbling schemes called reactive garbling schemes. We consider functions and garbled functions taking multiple inputs and giving multiple outputs. Two garbled functions can be linked together: an encoded output of one garbled function can be transformed into an encoded input of the other garbled function without communication between the parties. Reactive garbling schemes also allow partial evaluation of garbled functions even when only some of the encoded inputs are provided. It is possible to further evaluate the linked garbled functions when more garbled inputs become available. It is also possible to later garble more functions and link them to the ongoing garbled evaluation. We provide rigorous definitions for reactive garbling schemes. We define a new notion of security for reactive garbling schemes called confidentiality. We provide both simulation based and indistinguishability based notions of security. We also show that the simulation based notion of security implies the indistinguishability based notion of security. We present an instantiation of reactive garbling schemes. We finally present an application of reactive garbling schemes to reactive two-party computation secure against a malicious, static adversary.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Garbled circuits is a technique originating in the work of Yao and later formalised by Bellare, Hoang and Rogaway [2], who introduced the notion of a garbling scheme along with an instantiation. Garbling schemes have found a wide range of applications. However, many of these applications are using specific constructions of garbled circuits instead of the abstract notion of a garbling scheme. One possible explanation is that the notion of a garbling scheme falls short of capturing many of the current uses. In the notion of a garbling scheme, the constructed garbled function can only be used for a single evaluation and the garbled function has no further use. In contrast, many of the most interesting current applications of garbled circuits have a more granular look at garbling, where several components are garbled, dynamically glued together and possibly evaluated at different points in time. We now give a few examples of this.
In the standard cut-and-choose paradigm for two-party computation, Alice sends s copies of a garbled function to Bob. Half of the garblings (chosen by Bob) are opened to check that they were correctly constructed. This guarantees that the majority of the remaining instances were correctly constructed. Alice and Bob then use the remaining garblings for evaluation. Bob takes the majority output of these evaluations as his output. Although conceptually simple, this introduces a number of problems: Bob must ensure that Alice uses consistent inputs. It is also required that the probability that Bob aborts does not depend on his choice of input. Previous protocols solve these problems by doing white-box modifications of the underlying garbling scheme. We will show how to solve these problems by using reactive garbling schemes in a black-box manner.
In [18], Lindell presents a very efficient protocol for achieving active secure two-party computation from garbled circuits. In the scheme of Lindell, first s circuits are sent. Then a random subset of them are opened up to test that they were correctly constructed and the rest, the so-called evaluation circuits, are then evaluated in parallel. If the evaluations don’t all give the same output, then the evaluator can construct a certificate of cheating which can be fed into a small corrective garbled circuit. Another example is a technique introduced simultaneously by Krater, shelat and Shen [16] and Frederiksen, Jakobsen and Nielsen [6], where a part of the circuit which checks the so-called input consistency of one of the parties is constructed after the main garbled circuit has been constructed and after Alice has given her input. We use a similar technique in our example application, showing that this trick can be applied to (reactive) garbling schemes in general. Another example is the work of Huang, Katz, Kolesnikov, Kumaresan and Malozemoff [14] on amortising garbled circuits, where one of the analytic challenges is a setting where many circuits are garbled prior to inputs being given. Our security notion allows this behaviour and this part of their protocol could therefore be cast as using a general (reactive) garbling scheme. Another example is the work of Huang, Evans, Katz and Malka [13] on fast secure two-party computation using garbled circuits, where they use pipelining: the circuit is garbled and evaluated in blocks for efficiency. Finally, we remark that sometimes the issue of garbling many circuits and gluing them together and having them interact with other security components can also lead to subtle insecurity problems, as demonstrated by the notion of a garbled RAM as introduced by Lu and Ostrovsky in [19], where the construction was later proven to be insecure by Gentry, Halevi, Lu, Ostrovsky, Raykova and Wichs [10]. We believe that having well founded abstract notions of partial garbling and gluing will make it harder to overlook security problems.
Our goal is to introduce a notion of reactive garbling schemes, which is general enough to capture the use of garbled circuits in most of the existing applications and which will hopefully form a foundation for many future applications of garbling schemes. Reactive garbling schemes generalize garbling schemes in several ways. First of all, we allow a garbled evaluation to save a state and use it in further computations. Specifically, when garbling a function f one can link it to a previous garbling of some function g and as a result get a garbling of \(f \circ g\). Even more, given two independent garblings of f and g, it is possible to do a linking which will produce a garbling of \(f \circ g\) or \(g \circ f\). The linking depends only on the output encoding and input encoding of the linked garblings. We also allow garbling of a single function which allows partial evaluation and which allows dynamic input selection based on partial outputs. This can be mixed with linking, so that the choice of which functions to garble and link can be based on partial outputs. This can be important in reactive secure computation which allows inputs to arrive gradually and allows branching based on public partial outputs. We introduce the syntax and security definitions for this notion. We give an instantiation of reactive garbling schemes in the random oracle model. We also construct a reactive, maliciously UC secure two-party computation protocol based on reactive garbling schemes in a black-box manner.
1.1 Discussion and Motivation
In this section, we describe the purpose of our framework and why certain design choices were made for the framework in this paper.
One of the main goals of garbling schemes was to define a primitive that would be used in constructions without relying on the underlying instantiation. Unfortunately, most secure two-party computation protocols still rely on garbled circuits to provide security. In some sense, the notion of garbling schemes is not able to achieve this goal for the given task. One way of thinking of our result is to note that many techniques that previously only worked for garbled circuits, now work for reactive garbling schemes.
More precisely, to achieve reactive secure computation, the protocol for reactive computation shows how three issues which typically are solved using the underlying instantiation of garbled circuits in cut-and-choose protocols can be solved using reactive garbling schemes. These issues are Alice’s input consistency, selective failure attacks and how to run the simulator against a corrupted Bob. We solve these three issues by using the notion of reactive garbling schemes. This means that many protocols in the literature can easily be modified to achieve security by only relying on the properties of reactive garbling schemes.
We now discuss why certain design choices were made. In particular, why we included notions such as linking multiple output wires to a single input wire, partial evaluation and output encoding. The reason that we allow multiple output wires to link to a single input wire is that otherwise we would exclude important constructions such as Minilego [7] and Lindell’s reduced circuit optimization [18].
Output encodings are important for many reasons. First, it provides a method for defining linking. Roughly because of this notion, it is easy to define a linking as information which allows an encoded output to be converted into an encoded input. Secondly, in certain cases, constructions based on garbling schemes require a special property of the encoded output which otherwise cannot be described. This is the case of [11] where the encoded input has to be the same size as the encoded output. It is also useful for output reuse, covers pipelining and has applications to protocols where the receiver can use a proof of cheating to extract the sender’s input.
We included partial evaluation for two main reasons, first we consider that it can be an important feature for reactive computation, secure outsourcing and secure computation where a partial output would be valuable. A partial output could be used to determine what future computation to run on data. In addition, we could garble blocks of functions and decide to link certain blocks together based on partial outputs.
In addition, many schemes in the literature inherently allow partial evaluation and not allowing partial evaluation imposes artificial restrictions on the constructions. For example, fine-grained privacy in [1] cannot be realized by standard schemes precisely because those schemes give out partial outputs.
1.2 Recasting Previous Constructions
The concept of using output encoding and linking has been implicitly used in many previous works. In particular, in cut-and-choose protocols, it has been used in [5, 6, 17, 23] to enforce sender input consistency (ensure that the sender uses the same input in each instance) and to prevent selective failure attacks (an attack that works by having the probability that the receiver aborts depend on his choice of input). These concepts have also been used for different optimizations. Pipelining [13, 16] and output reuse [11, 20] are examples of direct optimizations. Linking has also been employed to reduce the number of circuits that need to be sent in protocols that apply cut-and-choose at the circuit level [4, 18]. This is done by adding a phase where a receiver can extract the input of a cheating sender. Another example is gate soldering [7, 21]. This technique works by employing cut-and-choose at the gate level. The gates are then randomly split among different buckets and soldered together. This optimization reduces the replication factor for a security \(\ominus (s)\) to \(\ominus (\frac{s}{\log (n)})\) where n is the number of non-xor gates. There are many applications that benefit from output encoding and linking in garbling schemes. In addition, if we allow sequences where the input is chosen as a function of the garbling, reactive garbling schemes are also adaptive. The constructions of [9, 12] require adaptive garbling.
1.3 Structure of the Paper
In Sect. 2, we give the preliminaries. In Sect. 3, we define the syntax and security of reactive garbling schemes. In Sect. 4, we describe an instantiation of a reactive garbling scheme. In Sect. 4.1, we give a full description of the reactive garbling scheme. In Sect. 5, we give an intuitive description of the reactive two-party computation protocol based on reactive garbling schemes. In Sect. 5.1, we provide a full description of the reactive two-party computation protocol. We note that the techniques that we introduce in Sect. 5 can be applied to previous secure two-party computation protocol to convert them into constructions that only use reactive garbling schemes in a black-box manner. There is a full version of the paper with more details. [22] In the full version there is a detailed simulation proof that our reactive computation protocol is secure, a proof of security of our reactive garbling scheme using the indistinguishability based notion of security, we recast Lindell’s construction using reactive garbling schemes, we describe Minilego’s garbling and soldering as a reactive garbling scheme, and we prove security of our garbling scheme using the simulation based definition of confidentiality. We also show that simulation based definition implies the indistinguishability based definition of security.
2 Preliminaries
Let \(\mathbb {N}\) be the set of natural numbers. For \(n \in \mathbb {N}\), let \(\{0,1\}^n\) be the set of n-bit strings. Let \(\{0,1\}^* = \underset{n \in \mathbb {N}}{\cup } \{0,1\}^{n}\). We use \(\top \) and \(\bot \) as the syntax for true and false and we assume that \(\top , \bot \not \in \{0,1\}^*\). We use () to denote the empty sequence. For a sequence \(\sigma \), we use \(x \in \sigma \) to denote that x is in the sequence. When we iterate over \(x \in \sigma \) in a for-loop, we do it from left to right. For a sequence \(\sigma \) and an element x we use  to denote that we append x to \(\sigma \). We use
to denote that we append x to \(\sigma \). We use  to denote concatenation of sequences. When unambiguous, we also use juxtaposition for concatenating and appending. We use \(x {{\mathrm{{\smash [t]{\mathop {\leftarrow }\limits ^{\,_{\$}}}}}}}X\) to denote sampling a uniformly random x from a finite set X. We use [A] to denote the possible legal outputs of an algorithm A. This is just the set of possible outputs, with \(\bot \) removed.
to denote concatenation of sequences. When unambiguous, we also use juxtaposition for concatenating and appending. We use \(x {{\mathrm{{\smash [t]{\mathop {\leftarrow }\limits ^{\,_{\$}}}}}}}X\) to denote sampling a uniformly random x from a finite set X. We use [A] to denote the possible legal outputs of an algorithm A. This is just the set of possible outputs, with \(\bot \) removed.
We prove security of protocols in the UC framework and we assume that the reader is familiar with the framework. When we specify entities for the UC framework, ideal functionalities, parties in protocol, adversaries and simulators we give them by a set of rules of the form \(\textsc {Example}\) (which sends \((x_1, x_2)\) to the adversary in its last line). In Fig. 1, we give an example of a rule. A line of the form “send m to \(\mathcal {F}\).R”, where \(\mathcal {F}\) is another entity and R the name of a rule, the entity will send \((\textsc {R}, id, m)\) to \(\mathcal {F}\), where id is a unique identifier of the rule that is sending, including the session and sub-session identifier, in case many copies of the same rule are currently in execution. We then give \((\textsc {R}, id, ?)\) to the adversary and let the adversary decide when to deliver the message. Here ? is just a special reserved string indicating that the real input has been removed. When a message of the form \((\textsc {R}, id, m)\) arrives from an entity \(\mathsf {A}\), the receiver stores \((\textsc {R}, \mathsf {A}, id, m)\) in a pool of pending messages and turns the activation over to the adversary. A line of the form “on P from \(\mathsf {A}\)” executed in a rule named R running with identifier id and where P is a pattern, is executed as follows. The entity executing the rule stores \((\textsc {R}, \mathsf {A}, id, P)\) in a pool of pending receives and turns over the activation to the adversary. We say that a pending message \((\textsc {R}, \mathsf {A}, id, m)\) matches pending receive \((\textsc {R}, \mathsf {A}, id, P)\) if m can be parsed on the form P. Whenever an entity turns over the activation to the adversary it sends along \((\textsc {R}, \mathsf {A}, id, ?)\) for all matched \((\textsc {R}, \mathsf {A}, id, P)\), where ? is just a special reserved bit-string. There is a special procedure \(\textsc {Initialize}\) which is executed once, when the entity is created. All other rules begin with an on-command. The rule is considered ready for id if the first line is of the form “on P from \(\mathsf {A}\)” and \((\textsc {R}, \mathsf {A}, id, P)\) is matched and the rule was never executed with identifier id. In that case \((\textsc {R}, \mathsf {A}, id, P)\) is considered to be in the set of pending receives. If the adversary sends \((\textsc {R}, \mathsf {A}, id, ?)\) to an entity that has some pending receive \((\textsc {R}, \mathsf {A}, id, P)\) matched by some pending message \((\textsc {R}, \mathsf {A}, id, m)\), then the entity parses m using P and starts executing right after the line “on P from \(\mathsf {A}\)” which added \((\textsc {R}, \mathsf {A}, id, P)\) to the list of pending receives. A line of the form “await P” where P is a predicate on the state of the entity works like the on-command. The line turns activation over to the adversary along with an identifier, and the entity will report to the adversary which predicates have become true. The adversary can instruct the entity to resume execution right after any “await P” where P is true on the state of the entity. If an entity executes a rule which terminates, it turns the activation over to the adversary. The keyword abort makes an entity terminate and ignore all future inputs. A line of the form “verify P” makes the entity abort if P is not true on the state of the entity. We use \(\mathcal {A}\) to denote the adversary and \(\mathcal {Z}\) to denote the environment. A line of the form “on P” is equivalent to “on P from \(\mathcal {Z}\)”. When specifying ideal functionalities we use \({\mathsf {{Corrupt}}}\) to denote the set of corrupted parties.
We define security of cryptographic schemes via code-based games [3]. The game is given by a set of procedures. There is a special procedure \(\textsc {Initialize}\) which is called once, as the first call. There is another special procedure \(\textsc {Finalize}\) which may be called by the adversary. The output is true or false, \(\top \) or \(\bot \), where \(\top \) indicates that the adversary won the game. In between \(\textsc {Initialize}\) and \(\textsc {Finalize}\), the adversary might call the other procedures at will. The other procedures might also output \(\bot \) or \(\top \) at which point the game ends with that output. Other outputs go back to the adversary.
3 Syntax and Security of Reactive Garbling Schemes
Section overview. We will start by defining the notion of gradual function, this will allow us to describe the type of functions that can be garbled. The functions that we define, in contrast to standard garbling schemes allow multiple inputs and outputs as well as partial evaluation.
Next, we will define the syntax of a reactive garbling scheme in the same way that a garbling scheme was described before. We will describe tags, a way of assigning identities to garbled functions, so that we can refer to them later. We will then describe different algorithms: how to encode inputs, decode outputs, link garblings together and other algorithms. Next, we will define correctness. The work of [2] defined the notion of correctness by comparing it to a plaintext evaluation. We define the notion of garbling sequences which is the equivalent of plaintext evaluation but for reactive garbling. Some garbling sequences don’t make sense, for example producing an encoded input for a function that has not been defined. As a result, we will define the concept of legal garbling sequences to avoid sequences that are nonsensical. Finally, we can define correctness by comparing the plaintext evaluation of a garbling sequence with the evaluation of a garbling sequence by applying the algorithms define before. We then use the notion of garbling sequence to define the side-information function for reactive garbling. This is necessary to describe our notion of security which we call confidentiality.
Gradual Functions. We first define the notion of a gradual function. A gradual function is an extension of the usual notion of a function \(f: A_1 \times \cdots \times A_n \rightarrow B_1 \times \cdots \times B_m\), where we allow to partially evaluate the function on a subset of the input components. Some output components might become available before all input components have arrived. We require that when an output component has become available, it cannot become unavailable or change as more input components arrive. We also require that the set of available outputs depends only on which inputs are ready, not on the exact value of the inputs. In our framework, we only allow garblings of gradual functions. This allows us to define partial evaluation and to avoid issues such as circular evaluation and determining when outputs are defined. These issues would make our framework more complex. The access function will be the function describing which outputs are available when a given set of inputs is ready. We will use \(\bot \) to denote that an input is not yet specified and that an output is not yet available. We therefore require that \(\bot \) is not a usual input or output of the function. We now formalize these notions. For a function \(f: A_1 \times \cdots \times A_n \rightarrow B_1 \times \cdots \times B_m\) we use the following notation. \(f.n := n\) and \(f.m := m\), \(f.A := A_1 \times \cdots \times A_n\), \(f.B := B_1 \times \cdots \times B_m\), and \(f.A_{i} := A_{i}\) and \(f.B_{i} := B_{i}\).
Definition 1
We use component to denote a set \(C = \{0,1\}^{\ell } \cup \{ \bot \}\) for some \(\ell \in \mathbb {N}\), where \(\bot \not \in \{0,1\}^*\). We call \(\ell \) the length of C and we write \({\text {len}}(C) = \ell \). Let \(C_1, \ldots , C_n\) be components and let \(x', x \in {C}_1 \times \cdots \times {C}_n\).
-
We say that \(x'\) is an extension of x, written \(x \sqsubset x'\) if \(x_i \ne \bot \) implies that \(x_i = x'_i\) for \(i = 1, \ldots , n\).
-
We say that x and \(x'\) are equivalently undefined, written \(x \bowtie x'\), if for all \(i = 1, \ldots , n\) it holds that \(x_i = \bot \) iff \(x'_i = \bot \).
Definition 2 (Gradual Function)
Let \(A_1, \ldots , A_n, B_1, \ldots , B_m\) be components and let \(f: A_1 \times \cdots \times A_n \rightarrow B_1 \times \cdots \times B_m\). We say that f is a gradual function if it is monotone and variable defined.
-
It is monotone if for all \(x,x' \in {A}_1 \times \cdots \times {A}_m\) it holds that \(x \sqsubset x'\) implies that \(f(x) \sqsubset f(x')\).
-
It is variable defined if \(x \bowtie x'\) then \(f(x) \bowtie f(x')\).
We say that an algorithm computes a gradual function \(f: A_1 \times \cdots \times A_n \rightarrow B_1 \times \cdots \times B_m\) if on all inputs \(x \in A_1 \times \cdots \times A_m\) it accepts with output f(x) and on all other inputs it rejects. We define a notion of access function which specifies which outputs components will be available given that a given subset of input components are available.
Definition 3 (Access Function)
The access function of a gradual function \(f: A_1 \times \cdots \times A_n \rightarrow B_1 \times \cdots \times B_m\) is a function \({\mathsf {{access}}}(f): \{ \bot , \top \}^n \rightarrow \{ \bot , \top \}^m\) defined as follows. For \(j=1,\ldots ,m\), let \(q_j: B_j \rightarrow \{ \bot , \top \}\) be the function where \(q_j(\bot ) = \bot \) and \(q_j(y) = \top \) otherwise. Let \(q: B_1 \times \cdots \times B_m \rightarrow \{ \bot , \top \}^m\) be the function \((y_1, \ldots , y_m) \mapsto (q_1(y_1), \ldots , q_m(y_m))\). For \(i = 1, \ldots , n\), let \(p_i: \{ \bot , \top \}\rightarrow A_i\) be the function with \(p_i(\bot ) = \bot \) and \(p_i(\top ) = 0^{{\text {len}}(A_i)}\). Let \(p: \{ \bot , \top \}^n \rightarrow A_1 \times \cdots \times A_n\) be the function \((x_1, \ldots , x_n) \mapsto (p_1(x_1), \ldots , p_n(x_n))\). Then \({\mathsf {{access}}}(f) = q \circ f \circ p\).
Definition 4 (Gradual functional similarity)
Let f,g be gradual functions. We say that f is similar to g (\(f \sim g\)) if \(f.n = g.n\), \(f.m = g.m\), \(f.A = g.A\), \(f.B = g.B\) and \({\mathsf {{access}}}(f) = {\mathsf {{access}}}(g)\).
In the following, if we use a function at a place where a gradual function is expected and nothing else is explicitly mentioned, we extend it to be a gradual function by adding \(\bot \) to all input and output components and letting all outputs be undefined until all inputs are defined.
Syntax of Algorithms. A reactive garbling scheme consists of seven algorithms \(\mathcal {G}= ({\mathsf {{St}}}, {\mathsf {{Gb}}}, {\mathsf {{En}}}, {\mathsf {{li}}}, {\mathsf {{Ev}}}, {\mathsf {{ev}}}, {\mathsf {{De}}})\). The algorithms \({\mathsf {{St}}}\), \({\mathsf {{Gb}}}\) and \({\mathsf {{Li}}}\) are randomized and the other algorithms are deterministic. Gradual functions are described by strings f. We call f the original gradual function. For each such description, we require that \({\mathsf {{ev}}}(f, \cdot )\) computes some gradual function \({\mathsf {{ev}}}(f, \cdot ): A_1 \times \cdots \times A_n \rightarrow B_1 \times \cdots \times B_m\). This is the function that f describes. We often use f also to denote the gradual function \({\mathsf {{ev}}}(f, \cdot )\).
-
On input of a security parameter \(k \in \mathbb {N}\), the setup algorithm outputs a pair of parameters \((\mathsf {sps}, \mathsf {pps}) \leftarrow {\mathsf {{St}}}(1^k)\), where \(\mathsf {sps}\in \{0,1\}^*\) is the secret parameters and \(\mathsf {pps}\in \{0,1\}^*\) is the public parameters. All other algorithms will also receive \(1^k\) as their first input, but we will stop writing that explicitly.
-
On input f, a tagFootnote 1 \(t \in \{0,1\}^*\) and the secret parameters \(\mathsf {sps}\) the garbling algorithm \({\mathsf {{Gb}}}\) produces as output a quadruple of strings (F, e, o, d), where F is the garbled function, e is the input encoding function, d is the output decoding function, which is of the form \(d = (d_1, \ldots , d_m)\), and o is the output encoding function. When \((F, e, o, d) \leftarrow {\mathsf {{Gb}}}(\mathsf {sps}, f, t)\) we use \(F_t\) to denote F, we use \(d_{t,i}\) to denote the \(i^{\mathrm {th}}\) entry of d, and similarly for the other components. This naming is unique by the function-tag uniqueness and garble-tag uniqueness conditions described later.
-
The encoding algorithm \({\mathsf {{En}}}\) takes input (e, t, i, x) and produces encoded input \(X_{t,i}\).
-
The linking algorithm \({\mathsf {{li}}}\) takes input of the form \((t_1, i_{1},t_2,i_2, o, e)\) and produces an output \(L_{t_1, i_{1},t_2,i_2}\) called the encoded linking information. Think of this as information which allows to take an encoded output \(Y_{t_1, i_1}\) for \(F_{t_1}\) and turn it into an encoded input \(X_{t_2, i_2}\) for \(F_{t_2}\). In other words, we link the output wire with index \(i_1\) of the garbling with tag \(t_1\) to the input wire with index \(i_2\) of the garbling with tag \(t_2\).
-
The garbled evaluation algorithm \({\mathsf {{Ev}}}\) takes as input a set \(\mathcal {F}\) of pairs \((t, F_t)\) where t is a tag and \(F_t\) a garbled function (let T be the set of tags t occurring in \(\mathcal {F}\)), a set \(\mathcal {X}\) of triples \((t, i, X_{t,i})\) where \(t \in T\), \(i \in [F_t.n]\) and \(X_{i,j} \ne \bot \) is an encoded input, and a set \(\mathcal {L}\) of tuples \((t_1, i_1, t_2, i_2, L_{t_1, i_1, t_2, i_2})\) with \(t_1, t_2 \in T\) and \(i_1 \in [F_{t_1}.m]\) and \(i_2 \in [F_{t_2}.n]\) and \(L_{t_1, i_1, t_2, i_2} \ne \bot \) an encoded linking information. It outputs a set \(\mathcal {Y}= \{ (t, i, Y_{t,i}) \}_{t \in T, i \in [F_t.m]}\), where each \(Y_{t,i}\) is an encoded output. It might be that \(Y_{t,i} = \bot \) if the corresponding output is not ready.
-
The decoding algorithm takes input \((t,i,d_{t,i},Y_{t,i})\), and produces a final output \(y_{t,i}\). We require that \({\mathsf {{De}}}(\cdot , \cdot , \cdot , \bot ) = \bot \). The reason for this is that \(Y_{t,i} = \bot \) is used to signal that the encoded output cannot be computed yet, and we want this to decode to \(y_{t,i} = \bot \). We extend the decoding algorithm to work on sets of decoding functions and sets of encoded outputs, by simply decoding each encoded output for which the corresponding output decoding function is given, as follows. For a set \(\delta \), called the overall decoding function, consisting of triples of the form \((t, i, d_{t,i})\), and a set \(\mathcal {Y}\) of triples of the form \((t, i, Y_{t,i})\), we let \({\mathsf {{De}}}(\delta , \mathcal {Y})\) output the set of \((t, i, {\mathsf {{De}}}(t,i,d_{t,i}, Y_{t,i}))\) for which \((t, i, d_{t,i}) \in \delta \) and \((t, i, Y_{t,i}) \in \mathcal {Y}\).
Basic requirements. We require that f.n and f.m can be computed in linear time from a function description f. We require that \({\text {len}}(f.A_i)\) and \({\text {len}}(f.B_j)\) can be computed in linear time for \(i = 1, \ldots , n\) and \(j = 1, \ldots , m\). We require that the same numbers can be computed in linear time from any garbling F of f. We finally require that one can compute \({\mathsf {{access}}}(f)\) in polynomial time given a garbling F of f. We do not impose the length condition and the non-degeneracy condition from [2], i.e., e and d might depend on f. Our security definitions ensure that the dependency does not leak unwarranted information (Fig. 2).
Projective Schemes. Following [2], we call a scheme projective (on input component i) if all \(X \in \{\; En(e,t,i,x) \; | \; x \in \{0,1\}^n \;\}\) are of the form \(\{X_{1,0},X_{1,1}\} \times \ldots \times \{X_{c,0},X_{c,1}\}\), where \(c = {\text {len}}(f.X_i)\), and \(En(e,t,i,x) = (X_{1,x[1]},...,X_{c,x[c]})\). This should hold for all k, f, t, \(\ell \), \(x \in \{0,1\}^c\) and \((\mathsf {sps},\mathsf {pps}) \in [{\mathsf {{St}}}(1^k)]\) and \((F,e,o,d) \in [{\mathsf {{Gb}}}(\mathsf {sps}, f, t, \ell )]\). As in [2] being projective is defined only relative to the input encodings. One can define a similar notion for output decodings. Having projective output decodings is needed for capturing some applications using reactive garbling scheme, for instance [18].
Correctness. To define correctness, we need a notion of calling the algorithms of a garbling scheme in a meaningful order. For this purpose, we define a notion of garbling sequence \(\sigma \). A garbling sequence is a sequence of garbling commands, each command has one of the following forms:  ,
,  ,
,  ,
,  ,
,  . In the rest of the paper, we will use \(\sigma \) to refer to a garbling sequence. A garbling sequence is called legal if the following conditions hold.
. In the rest of the paper, we will use \(\sigma \) to refer to a garbling sequence. A garbling sequence is called legal if the following conditions hold.
- Function uniqueness::
-
\(\sigma \) does not contain distinct commands
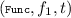 and
and  .
. - Garble uniqueness::
-
Each command
 occurs at most once in \(\sigma \).
occurs at most once in \(\sigma \). - Garble legality::
-
If
 occurs in \(\sigma \), it is preceded by
occurs in \(\sigma \), it is preceded by  .
. - Linkage legality::
-
If the command
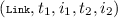 occurs in \(\sigma \), then the command is preceded by commands of the forms
occurs in \(\sigma \), then the command is preceded by commands of the forms 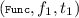 ,
,  ,
, 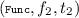 and
and 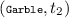 , and \(1 \le i_1 \le f_1.m\), \(1 \le i_2 \le f_2.n\) and \(f_1.B_{i_1} = f_2.A_{i_2}\).
, and \(1 \le i_1 \le f_1.m\), \(1 \le i_2 \le f_2.n\) and \(f_1.B_{i_1} = f_2.A_{i_2}\). - Input legality::
-
If
 occurs in \(\sigma \) it is preceded by
occurs in \(\sigma \) it is preceded by 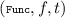 and
and  and \(x \in f.A_{i} \setminus \{\bot \}\).
and \(x \in f.A_{i} \setminus \{\bot \}\). - Output legality::
-
If
 occurs in a sequence it is preceded by
occurs in a sequence it is preceded by  and
and  and \(1 \le i \le f.m\).
and \(1 \le i \le f.m\).
Note that if a sequence is legal, then so is any prefix of the sequence. We call a garbling sequence illegal if it is not legal. Since we allow to link several output components onto the same input component we have to deal with the case where they carry different values. We consider this an error, and to catch it, we use the following safe assignment operator.

We now define an algorithm \({\mathsf {{eval}}}\), which takes as input a legal garbling sequence \(\sigma \) and outputs a set of tuples \((t, i, y_{t,i})\), one for each command  , where possibly \(y_{t,i} = \bot \). The values are computed by taking the least fix point of the evaluation of all the gradual functions, see Fig. 3. We call this the plain evaluation of \(\sigma \). We extend the definition of a legal sequence to include the requirement that
, where possibly \(y_{t,i} = \bot \). The values are computed by taking the least fix point of the evaluation of all the gradual functions, see Fig. 3. We call this the plain evaluation of \(\sigma \). We extend the definition of a legal sequence to include the requirement that
- Input uniqueness:
-
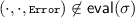 .
.
Therefore the use of the safe assignment in \({\mathsf {{eval}}}\) is only to conveniently define the notion of legal sequence. In the rest of the paper we assume that all inputs to \({\mathsf {{eval}}}\) are legal. The values \(y_{t,i} \ne \bot \) are by definition the values that are ready in \(\sigma \), i.e., \({\mathsf {{ready}}}(\sigma ) = \{ (t, i) \vert \exists (t, i, y_{t,i}) \in {\mathsf {{eval}}}(\sigma ) (y_{t,i} \ne \bot ) \}\). Note that since the gradual functions are variable defined, which outputs are ready does not depend on the values of the inputs, except via whether they are \(\bot \) or not.
The procedure \({\mathsf {{Eval}}}\) in Fig. 4 demonstrates how a legal garbling sequence is intended to be translated into calls to the algorithms of the garbling scheme. We call the procedure executed by \({\mathsf {{Eval}}}\) garbled evaluation of \(\sigma \).
Lemma 1
For a function description f, let T(f) be the worst case running time of \({\mathsf {{ev}}}(f, \cdot )\). The algorithm \({\mathsf {{eval}}}\) will terminate in time \({\text {poly}}(T \vert \sigma \vert (n + m))\), where  ,
,  , and
, and  .
.
Proof
By monotonicity, if the loop in \({\mathsf {{eval}}}\) does not terminate, another variable \(y_{t,i}\) has changed from \(\bot \) to \(\ne \bot \) and can never change value again. This bounds the number of iterations as needed.
Side-Information Functions. We use the same notion of side-information functions as in [2]. A side information function \(\varPhi \) maps function descriptions f into the side information \(\varPhi = \varPhi (f) \in \{0,1\}^*\). Intuitively, a garbling of f should not leak more than \(\varPhi (f)\). The exact meaning of the side information functions are given by our security definition. We extend a side information function \(\varPhi \) to the set of garbling sequences. For the empty sequence \(\sigma = ()\) we let \(\varPhi (\sigma ) = ()\).
For a sequence \(\sigma \), we define the side-information as \(\varPhi (\sigma ) := \varPhi _{\sigma }(\sigma )\) where for a sequence \(\bar{\sigma }\) and a command c:  , where
, where  ,
,  ,
,  ,
,  and
and  , where \(y_{t,i}\) is defined by \({\mathsf {{eval}}}(\sigma )\).
, where \(y_{t,i}\) is defined by \({\mathsf {{eval}}}(\sigma )\).
Legal Sequence Classes. We define the notion of a legal sequence class \(\mathbb {L}\) (relative to a given side-information function \(\varPhi \)). It is a subset of the legal garbling sequences which additionally has these five properties:
- Monotone::
-
If
 , then \(\sigma ' \in \mathbb {L}\).
, then \(\sigma ' \in \mathbb {L}\). - Input independent::
-
If
 , then
, then 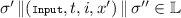 for all \(x' \in \{0,1\}^{\vert x \vert }\).
for all \(x' \in \{0,1\}^{\vert x \vert }\). - Function independent::
-
If
 , then
, then  for all f with \(\varPhi (f') = \varPhi (f)\).
for all f with \(\varPhi (f') = \varPhi (f)\). - Name invariant::
-
If \(\sigma \in \mathbb {L}\) and \(\sigma '\) is \(\sigma \) with all tags t replaced by \(t' = \pi (t)\) for an injection \(\pi \), then \(\sigma ' \in \mathbb {L}\).
- Efficient::
-
Finally, the language \(\mathbb {L}\) should be in \({\text {P}}\), i.e., in polynomial time.
It is easy to see that the set of all legal garbling sequences is a legal sequence class.
Definition 5 (Correctness)
For a legal sequence class \(\mathbb {L}\) and a reactive garbling scheme \(\mathcal {G}\) we say that \(\mathcal {G}\) is \(\mathbb {L}\)-correct if for all \(\sigma \in \mathbb {L}\), it holds that \({\mathsf {{De}}}({\mathsf {{Eval}}}(\sigma )) \subseteq {\mathsf {{eval}}}(\sigma )\) for all choices of randomness by the randomized algorithms.
Function Individual Garbled Evaluation. The garbled evaluation function \({\mathsf {{Ev}}}\) just takes as input sets of garbled functions, inputs and linking information and then somehow produces a set of garbled outputs. It is often convenient to have more structure to the garbled evaluation than this.
We say that garbled evaluation is function individual if each garbled function F is evaluated on its own. Specifically there exist deterministic poly-time algorithms \({\mathsf {{EvI}}}\) and \({\mathsf {{Li}}}\) called the individual garbled evaluation algorithm and the garbled linking algorithm. The input to \({\mathsf {{EvI}}}\) is a garbled function and some garbled inputs. For each fixed garbled function F with \(n = F.n\) and \(m = F.m\) the algorithm computes a gradual function \({\mathsf {{EvI}}}(F): A_1 \times \cdots \times A_n \rightarrow B_1 \times \cdots \times B_m\) and \((X_1, \ldots , X_n) \mapsto {\mathsf {{EvI}}}(F,X_1, \ldots , X_n)\), with \({\mathsf {{access}}}({\mathsf {{EvI}}}(F)) = {\mathsf {{access}}}(f)\), where f is the function garbled by F. We denote the output by \((Y_1, \ldots , Y_m) = {\mathsf {{EvI}}}(F,X_1,\ldots ,X_n)\). The intention is that the \(Y_j\) are garbled outputs (or \(\bot \)). To say that \({\mathsf {{Ev}}}\) has individual garbling we then require that it is defined from \({\mathsf {{EvI}}}\) and \({\mathsf {{Li}}}\) as in Fig. 5.
Security of Reactive Garbling. We define a notion of security that we call confidentiality, which unifies privacy and obliviousness as defined in [2]. Obliviousness says that if the evaluator is given a garbled function and garbled inputs but no output decoding function it can learn a garbled output of the function but learns no information on the plaintext value of the output. Privacy says that if the evaluator is given a garbled function, garbled inputs and the output decoding function it can learn the plaintext value of the function, but no other information, like intermediary values from the evaluation. It is necessary to synthesise these properties as we envision protocols where the receiver of the garbled functions might receive the output decoding function for some of the output components but not all of them. Obliviousness does not cover this case, since the adversary has some of the decoding keys. It is not covered by privacy either, as the receiver should not gain any information about outputs for which he does not have a decoding function.
In the confidentiality (indistinguishability) game, the adversary feeds two sequences \(\sigma _0\) and \(\sigma _1\) to the game, which produces a garbling of one of the two sequences, \(\sigma _b\) for a uniform bit b. The adversary wins if it can guess which sequence was garbled. It is required that the two sequences are not trivially distinguishable. For instance, the two commands at position i in the two sequences should have the same type, the side information of functions at the same positions in the sequences should be the same, and all outputs produced by the sequences should be the same. This is formalized by requiring that the side information of the sequences are the same. This is done by checking that \(\varPhi (\sigma _0)=\varPhi (\sigma _1)\) in the rule \(\textsc {Finalize}\). If one considers garbling sequences with only one function command, one garbling command, one input command per input component, no linking and where no output command is given, then confidentiality implies obliviousness. If in addition an output command is given for each output component, then confidentiality implies privacy.
In the confidentiality (simulation) game, the adversary feeds a sequence \(\sigma \) to the game. The game samples a uniform bit b. If \(b=0\), then the game uses the reactive garbling scheme to produce values for the sequence. Otherwise, if the bit \(b=1\), the game feeds the output of the side-information function to the simulator and forwards any response to the adversary. The simulation-based notion of confidentiality implies the indistinguishability-based notion of indistinguishability [22].
Definition 6 (Confidentiality)
For a legal sequence class \(\mathbb {L}\) relative to side-information function \(\varPhi \) and a reactive garbling scheme \(\mathcal {G}\), we say that \(\mathcal {G}\) is \((\mathbb {L},\varPhi )\)-confidential if for all PPT \(\mathcal {A}\) it holds that \(\mathbf {Adv}_{\mathcal {G},\mathbb {L}',\varPhi ,\mathcal {A}}^{\mathrm {adp.ind.con}}(1^k)\) is negligible, where \(\mathbf {Adv}_{\mathcal {G},\mathbb {L}',\varPhi ,\mathcal {A}}^{\mathrm {adp.ind.con}}(1^k) = \Pr [\mathbf {Game}_{\mathcal {G},\mathbb {L}',\varPhi ,\mathcal {A}}^{\mathrm {adp.ind.con}}(1^k) = \top ] - \smash {\frac{1}{2}}\) and \(\mathbf {Game}^{\mathrm {adp.ind.con}}_{\mathcal {G},\mathbb {L}',\varPhi }\) is given in Fig. 6.
Notice that this security definition is indistinguishability based, which is known to be very weak in some cases for garbling (cf. [2]). Consider for instance garbling a function f where the input x is secret and \(y = f(x)\) is made a public output. The security definition then only makes a requirement on the garbling scheme in the case where the adversary inputs two sequences where in sequence one the input is \(x_1\) and in sequence two the input is \(x_2\) and where \(f(x_1) = f(x_2)\). Consider then what happens if f is collision resistant. Since no adversary can compute such \(x_1\) and \(x_2\) where \(x_1 \ne x_2\), it follows that \(x_1 = x_2\) in all pairs of sequences that the adversary can submit to the game. It can then be seen that it would be secure to “garble” collision resistant functions f by simply sending f in plaintext. Despite this weak definition, we later manage to prove that it is sufficient for building secure two-party computation. Looking ahead, when we need to securely compute f, we will garble a function \(f'\) which takes an additional input p which is the same length as the output of f and where \(f'(x,p) = p \oplus f(x)\) and ask the party that supplies p to always let p be the all-zero string. Our techniques for ensuring active security in general is used to enforce that even a corrupted party does this. Correctness is thus preserved. Clearly \(f'\) is not collision resistant even if f is collision resistant. This prevents a secure garbling scheme from making insecure garblings of \(f'\). In fact, note that this trick ensures that \(f'\) has the efficient invertibility property defined by [2], which means that the indistinguishability and simulation based security coincide.
The game \(\mathbf {Game}^{\mathrm {adp.ind.con}}_{\mathcal {G},\mathbb {L},\varPhi }(1^k)\) defining adaptive indistinguishability confidentiality. In \(\textsc {Finalize}\) we check that \(\sigma _0 \in \mathbb {L}\) and the adversary loses if this is not the case. It is easy to see that when \(\mathbb {L}\) is a legal sequence class and \(\varPhi (\sigma _0) = \varPhi (\sigma _1)\), then \(\sigma _0 \in \mathbb {L}\) iff \(\sigma _1 \in \mathbb {L}\). We can therefore by monotonicity assume that the game returns \(\bot \) as soon as it happens that \(\sigma _c \not \in \mathbb {L}\). We use a number of notational conventions from above. Tags are used to name objects relative to \(\sigma _c\), which is assumed to be legal. As an example, in  , the function \(f_t\) refers to the function \(f_c\) occurring in the command
, the function \(f_t\) refers to the function \(f_c\) occurring in the command  which was added to \(\sigma _c\) in \(\textsc {Func}\) by Garble Legality. For another example, the \(d_{t,i}\) in \(\textsc {Output}(t,i)\) refers to the \(i^\text {th}\) component of the \(d_t\) component output by \({\mathsf {{Gb}}}(\mathsf {sps},f_t,t)\) in the execution of \(\textsc {Garble}(t,\pi )\) which must have been executed by Output Legality.
which was added to \(\sigma _c\) in \(\textsc {Func}\) by Garble Legality. For another example, the \(d_{t,i}\) in \(\textsc {Output}(t,i)\) refers to the \(i^\text {th}\) component of the \(d_t\) component output by \({\mathsf {{Gb}}}(\mathsf {sps},f_t,t)\) in the execution of \(\textsc {Garble}(t,\pi )\) which must have been executed by Output Legality.
4 Instantiating a Confidential Reactive Garbling Scheme
We show that the instantiation of garbling schemes in [2] can be extended to a reactive garbling scheme in the random-oracle (RO) model. We essentially implement the dual-key cipher construction from [2] using the RO. To link a wire with 0-token \(T_0\) and 1-token \(T_1\) to an input wire with tokens \(I_0\) and \(I_1\), we provide the linking information \(L_0 = RO(T_0) \oplus I_0\) and \(L_1 = RO(T_1) \oplus I_1\) in a random order with each value tagged by the permutation bits of their corresponding input wires and output wires. Evaluation is done using function individual evaluation. Evaluation of a single garbled circuit is done as in [2]. Evaluation of a linking is: given \(T_b\) and a permutation bit, the bit is used to retrieve \(L_b\) from which \(I_b = L_b \oplus RO(T_b)\) is computed. We provide the details in Sect. 4.1. We use the RO because reactive garbling schemes run into many of the same subtle security problems as adaptive garbling schemes [1], which are conveniently handled by being able to program the RO. We leave as an open problem the construction of (efficient) reactive garbling schemes in the standard model.
4.1 A Reactive Garbling Scheme
We will now give the details of the construction of a confidential reactive garbling scheme based on a random oracle. The protocol is inspired by the construction of garbling schemes from dual-key ciphers presented in [2]. The pseudocode for our reactive garbling scheme is shown in Figs. 7 and 8.
To simplify notation, we define \({\mathsf {{lsb}}}\) as the least significant bit, \({\mathsf {{slsb}}}\) as the second least significant bit. The operation \({\mathsf {{Root}}}\) removes the last two bits of a string. The symbol \({\mathsf {{H}}}\) denotes the random oracle.
We use the notation of [2] to represent a circuit. A circuit is a 6-tuple \(f = (n,m,q,A,B,G)\). Here \(n \ge 2\) is the number of inputs, \(m \ge 1\) is the number of outputs and \(q \ge 1\) is the number of gates. We let \(r = n + q\) be the number of wires. We let \({\text {Inputs}} = \{1,\ldots ,n\}\), \({\text {Wire}} = \{1,\ldots ,n+q\}\), \({\text {OutputWires}} = \{n+q-m+1,\ldots ,n+q\}\) and \({\text {Gates}} = \{n,\ldots ,n+q\}\). Then \(A:{\text {Gates}} \rightarrow {\text {Wires}} \backslash {\text {OutputWires}}\) is a function to identify each gate’s first incoming wire and \(B:{\text {Gates}} \rightarrow {\text {Wires}}{\backslash }{\text {OutputWires}}\) is a function to identify each gate’s second incoming wire. Finally, \(G:{\text {Gates}} \times \{0,1\}^2 \rightarrow \{0,1\}\) is a function that determines the functionality of each gate. We require that \(A(g)< B(g) < g\) for all \(g \in {\text {Gates}}\).
Our protocol will also follow the approach of [2]. To garble a circuit, two tokens are selected for each wire, one denoted by \(X_{t,i,0}\) which shall encode the value 0 and the other denoted by \(X_{t,i,1}\) which will encode the value 1, we refer to this mapping as the semantic of a token.
The encoding of an input for a value x is simply the token of the given wire with semantic x. The decoding of an output is the mask for that wire. We decouple the decoding from the linking to simplify the proof of security. The simulator will be able to produce linking without having to worry about the semantics of the output encoding.
For each wire, the two associated tokens will be chosen such that the least significant bit (the type of a token) will differ. It is important to note that the semantics and type of a token are independent. The second least significant bit is called the mask and will have a special meaning later when the tokens are output tokens. We use \({\mathsf {{root}}}(X)\) to denote the part of a token that is not the type bit or the mask bit.
Each gate g will be garbled by producing a garbled table. A garbled table will consist of four ciphertexts p[g, a, b] where \(a,b \in \{0,1\}\), The ciphertext P[g, a, b] will be produced in the following way: first find the token associated to the left input wire (\(i_1\)) with type a, denote the semantic of this token as x. Secondly, find the token associated to the right input wire (\(i_2\)) with type b, denote the semantic of this token as y. The ciphertext will be an encryption of the token of \(z \leftarrow G(g,x,y)\). We will denote  . The encryption will be
. The encryption will be 
For each non-output wire, the token with semantic 0 will be chosen randomly and the token with semantic 1 will be chosen uniformly at random except for the last bit which will be chosen to be the negation of the least significant bit of the token with semantic 0 for the same wire.
For each output wire, the first token will also be chosen uniformly at random. The token with semantic 0 will be chosen randomly and the token with semantic 1 will be chosen uniformly at random except for the least significant bit and the second least significant bit. For both of these positions, the second token will be chosen so that they differ from the value in the 0-token for the same position. We refer to the second least significant bit of the 0-token of an output token as the mask of an output wire.
A linking between output \((t_1,i_1)\) and input \((t_2,i_2)\) consists of two ciphertexts: let c be the type of the 0-token for the output wire. In this case, we set  . The linking is simply
. The linking is simply
where \(E^{T}_{k}(z) = {\mathsf {{H}}}(T || k) \oplus z\). Converting an encoded output into an encoded input follows naturally.
In [22] we prove the following theorem.
Theorem 1
Let \(\mathbb {L}\) be the set of all legal garbling sequence, let \(\varPhi \) denote the circuit topology of a function. Then RGS is \((\mathbb {L},\varPhi )\)-confidential in the random oracle model.
5 Application to Secure Reactive Two-Party Computation
We now show how to implement reactive two-party computation secure against a malicious, static adversary using a projective reactive garbling scheme. For simplicity we assume that \(\mathbb {L}\) is the set of all legal sequences. It can, however, in general consist of a set of sequences closed under the few augmentations we do of the sequence in the protocol. The implementation could be optimized using contemporary tricks for garbling based protocols, but we have chosen to not do this, as the purpose of this section is to demonstrate the use of our security definition, not efficiency.
We implement the ideal functionality in Fig. 9. The inputs to the parties will be a garbling sequence. The commands are received one-by-one, to have a well defined sequence, but can be executed in parallel. We assume that at any point in time the input sequence received by a party is a prefix or suffix of the input sequence of the other parties, except that when a party receives a secret input by receiving input  , then the other party receives
, then the other party receives  , to not leak the secret x, where we use ? to denote a special reserved input indicating that the real input has been removed. We also assume that the sequence of inputs given to any party is in \(\mathbb {L}\). If not, the ideal functionality will simply stop operating. We only specify an ideal functionality for static security. To correctly handle adaptive security a party should sometimes be allowed to replace its input when becoming adaptively corrupted. Since we only prove static security, we chose to not add these complication to the specification.
, to not leak the secret x, where we use ? to denote a special reserved input indicating that the real input has been removed. We also assume that the sequence of inputs given to any party is in \(\mathbb {L}\). If not, the ideal functionality will simply stop operating. We only specify an ideal functionality for static security. To correctly handle adaptive security a party should sometimes be allowed to replace its input when becoming adaptively corrupted. Since we only prove static security, we chose to not add these complication to the specification.
The implementation will be based on the idea of a watchlist [15]. Alice and Bob will run many instances of a base protocol where Alice is the garbler and Bob is the evaluator. Alice will in each instance provide Bob with garbled functions, linking information, encoded inputs for Alice’s inputs and encoded inputs for Bob’s inputs, and decoding information. For all Bob’s input bits, Alice computes encodings of both 0 and 1, and Bob uses an oblivious transfer to pick the encoding he wants. For a given input bit, the same oblivious transfer instance is used to choose the appropriate encodings in all the instances. This forces Bob to use the same input in all instances. Bob then does a garbled evaluation and decodes to get a plaintext output. Bob therefore gets one possible value of the output from each instance. If Alice cheats by sending incorrect garblings or using different inputs in different instances, the outputs might be different. We combat this by using a watchlist. For a random subset of the instances, Bob will learn all the randomness used by Alice to run the algorithms of the garbling scheme and Bob can therefore check whether Alice is sending the expected values in these instances. The instances inspected by Bob are called the watchlist instances. The other instances are called the evaluation instances. The watchlist is random and unknown to Alice. The number of instances and the size of the watchlist is set up such that except with negligible probability, either a majority of the evaluation instances are correct or Bob will detect that Alice cheated without leaking information about his input. Bob can therefore take the output value that appears the most often among the evaluation instances as his output. There are several issues with this general approach that must be handled.
-
1.
We cannot allow Bob to learn the encoded inputs of Alice in watchlist instances, as Bob also knows the input encoding functions for the watchlist instances. This is handled by letting Alice send her random tape \(r_i\) for each instance i to Bob in an oblivious transfer, where the other message is a key that will be used by Alice to encrypt the encodings of her input. That way Bob can choose to either make instance i a watchlist instance, by choosing \(r_i\), or learn the encoded inputs of Alice, but not both.
-
2.
Alice might not send correct input encodings of her own inputs, in which case correctness is not guaranteed. This is not caught by the watchlist mechanism as Bob does not learn Alice’s input encodings for the watchlist instances. To combat this attack, Alice must for all input bits of Alice, in all instances, commit to both the encoding of 0 and 1, in a random order, and send along with her input encodings an opening of one of the commitments. The randomness used to commit is picked from the random tape that Bob knows in the watchlist instances. That way Bob can check in the watchlist instances that the commitments were computed correctly, and hence the check in the evaluation position that the encoding sent by Alice opens one of the commitments will ensure that most evaluation instances were run with correct input encodings, except with negligible probability.
-
3.
We have to ensure that Alice uses the same input for herself in all instances. For the same reason as item 2, this cannot be caught by the watchlist mechanism. Instead, it is done by revealing in all instances a privacy-preserving message digest of Alice’s input. Bob can then check that this digest is the same in all instances. For efficiency, the digest is computed using a two-universal hash function. This is a common trick by now, see [6, 8, 23]. However, all previous work used garbled circuits in a white box manner to make this trick work. We can do it by a black box use of reactive garbling, as follows. First Alice garbles the function f to be evaluated producing the garbling F where Alice is to provide some input component x. Then Alice garbles the function g which takes as input a mask m, an index c for a family h of two-universal hash functions and an input x for the hash function and which outputs x and \(y = h_c(x) \oplus m\). Alice then randomly samples a mask m and then sends encodings of m and x to Bob as well as the output decoding function for y. Bob then samples an index c at random and makes it public. Then Alice sends the encoding of c to Bob. Alice then links the output component x of G into the input component x of F. This lets Bob compute y and an encoding X of the input x of f.
-
4.
As usual Alice can mount a selective attack by for example offering Bob a correct encoding of 0 and an incorrect encoding of 1 in one of the OTs used for picking Bob’s input. This will not be caught by the watchlist mechanism if Bob’s input is 0. As usual this is combated by encoding Bob’s input and instead using the encoding as input. The encoding is such that any s positions are uniformly random and independent of the input of Bob. Hence if Alice learns up to s bits of the encoding, it gives her no information on the input of Bob, and if she mounts more than s selective attacks, she will get caught except with probability \(2^{-s}\). This is again a known trick used in a white box manner in previous works, and again we use linking to generalize this technique to (reactive) garbling schemes. First, Alice will garble an identity function for which Bob will get an encoding of a randomly chosen input \(x'\) via OT. Then Bob selects a random hash function h from a two-universal family of hash functions such that \(h(x') = x\) where x is Bob’s real input. Bob sends h to Alice. Alice then garbles the hash function and links the output of the identity function to the input of the hash function and she links the output of the hash function to the encoded function which Bob is providing an input for.
With the above augmentations which solves obvious security problems, along with an augmentation described below, addressing a problem with simulation, the protocol is UC secure against a static adversary. We briefly sketch how to achieve simulation security.
Simulating corrupted Alice is easy. The simulator can cheat in the OTs used to set up the watchlist and learn both the randomness \(r_i\) and the input encodings of Alice in all the evaluation instances. The mechanisms described above ensure that in a majority of evaluation instances Alice correctly garbled and also used the same correct input encoding. Since the input encoding is projective, the input x of Alice can be computed from the input encoding function and her garbled input. By correctness of the garbling scheme, it follows that all correct evaluation instances would give the same output z consistent with x. Hence the simulator can use x as the input of Alice in the simulation.
As usual simulating corrupted Bob is more challenging. To get a feeling for the problem, assume that Alice has to send a garbled circuit F of the function f to be computed before Bob gives inputs. When Bob then gives input, the input y of Bob can be extracted in the simulation by cheating in the OTs and inspecting the choice bits used by Bob. The simulator then inputs y to the ideal functionality and gets back the output \(z = f(x,y)\) that Bob is to learn. However, the simulator then in addition has to make F output z in the simulated execution of the protocol. This in general would require finding an input \(x'\) of Alice such that \(z = f(x',y)\), which could be computationally hard. Previous papers have used white-box modifications of the garbled circuit or the output decoding function to facilitate enough cheating to make F hit z without having to compute \(x'\). We show how to do it in a very simple and elegant way in a black-box manner from any reactive garbling scheme which can garble the exclusive-or function. In our protocol Alice will not send to Bob the decoding key for the encoded output Z. Instead, she garbles a masking function \((\psi (z,m) = z \oplus m)\) and links the output of the function f to the first argument of the masking function. Then she produces an encoding M of the all-zero string for m and sends M to Bob along with the output decoding function for \(\psi \). Bob can then compute and decode from Z and M the value \(z \oplus 0 = z\). In the simulation, the simulator of corrupted Bob knows the watchlist and can hence behave honestly in the watchlist instances and use the freedom of m to make the output \(z \oplus m\) hit the desired output from the ideal functionality in the evaluation positions. This will be indistinguishable from the real world because of the confidentiality property. Since this trick does not require modifying the garbled function, our protocol will only require a projective garbling scheme which is confidential. It will work for any side-information function. Earlier protocols required that the side-information be the topology of the circuit to hide the modification of the function f needed for simulation, or they needed to do white box modifications of the output decoding function to make the needed cheating occur as part of the output decoding.
5.1 Details of the Reactive 2PC Protocol
We now give more details on the protocol. The different instances will be indexed by \(j \in I = \{1,\ldots ,s\}\). The watchlist is given by \(\mathbf {w} = (w_1, \ldots , w_s) \in \{0,1\}^s\), where \(w_j = 1\) iff j is a watchlist instance. In the protocol s instances are run in parallel. When a copy of a variable v is used in each instance, the copy used in instance j is denoted by \(v^j\). In most cases the code for an instance does not depend on j explicitly but only on whether the instance is on the watchlist or the evaluation list, in which case we will write the code generically using the variable name v. The convention is that all s copies \(v^1, \ldots , v^s\) are manipulated the same way, in single instruction multiple data program style. For instance, \(w = 1\) will mean \(w^j = 1\), such that \(w = 1\) is true iff the instance is in the watchlist.
We will use commitments and oblivious transfer within the protocol. We work in the OT hybrid model. We use \({\mathsf {{OT}}}.{\mathsf {{send}}}(m_0,m_1)\) to mean that Alice sends two messages via the oblivious-transfer functionality and we use the notation \({\mathsf {{OT}}}.{\mathsf {{choose}}}(b)\) to say that Bob chooses to receive \(m_b\). We use a perfect binding and computationally hiding commitment scheme. If a public key is needed, it could be generated by Alice and sent to Bob in initialization. A commitment to a message m produced with randomness r is denoted by \({\mathsf {{com}}}(m;r)\), sending (m, r) constitutes an opening of the commitment.
If we write A(x; r) for a randomized algorithm, where r is not bound before, then it means that we make a random run of A on input x and that we use r in the following to denote the randomness used by A. If we send a set \(\{ x, y \}\), then it is sent as a vector with the bit strings x and y sorted lexicographically, such that all information extra to the elements is removed before sending. When rules are called, tags t are provided. It follows from the input sequences being legal that these tags are unique, except when referring to a legal previous occurrence. We further assume that all tags provided as inputs are of the form \(0 \Vert \{0,1\}^{*}\), which allows us to use tags of the form \(1 \Vert \{0,1\}^{*}\) for internal book keeping. Tags for internal use will be derived from the tags given as input and the name of the rule creating the new tag. For a garbling scheme \(\mathcal {G}\), a commitment scheme \({\mathsf {{com}}}\) and an encryption scheme \(\mathcal {E}\), we use \(\pi _{\mathcal {G},{\mathsf {{com}}},\mathcal {E}}\) to denote protocol given by the set of rules in Figs. 10, 11, 12 13, 14 and 15. We add a few remarks to the figures.
In the \(\textsc {Initialize}\)-rules Alice and Bob setup the watchlist. They use a (symmetric) encryption scheme \(\mathcal {E}= ({\mathsf {{E}}}, {\mathsf {{D}}})\) with k-bit keys. For each instance j, Alice sends two keys via the oblivious transfer functionality, the watchlist key \(\mathsf {wk}^j\) and the evaluation key \(\mathsf {ek}^j\). Alice will later encrypt and send the information Bob is to learn for watchlist (evaluation) instances with the key \(\mathsf {wk}\) (\(\mathsf {ek}\)). In the \(\textsc {Func}\)-rules they simply associate a function to a tag. In the \(\textsc {Garble}\)-rules Alice garbles the function and sends the garbling to Bob, she also sends an encryption using the watchlist key of the randomness used to produce this garbling. This allows Bob, for the watchlist positions to check that Alice produced a correct garbling and to store the result of garbling. This knowledge will be used in other rules. In the \(\textsc {Link}\)-rules Alice sends linking information. Bob can for all watchlist positions check that the information is correct, since he knows the randomness used to garble. In the \(\textsc {Output}\)-rules Alice awaits that she has sent to Bob the encoded inputs and linkings to produce the encoded output associated to this rule. She produces a garbling of \(\psi \). She will link the output to \(\psi \) and produce an encoding of the zero-string for the second component, she also sends an encryption of the randomness used to produce the garbling of \(\psi \) to Bob. Bob awaits that he has received the garbling, linking and encoding to produce the encoded output in question. For each instance of the watchlist, he uses the randomness to check that the linking was done correctly, that \(\psi \) was garbled correctly and that an encoding of an all zero-string was sent for the second component of \(\psi \). He then evaluates each instance in the evaluation set and takes the majority value as his output.
In the  -rules Alice commits to both her input encodings and encrypts the openings of the commitments using the watchlist key. The opening of Alice’s input encoding will be encrypted using the evaluation key. To verify Alice’s input, we first pass Alice’s input through an auxiliary function which combines the identity function with an additional verification function which forces Alice to use the same input in different instances. We then link the output of the identity function to the appropriate input. We denoted the auxiliary function by \(g_{l}:A_1 \times A_2 \times A_3 \rightarrow B_1 \times B_2\) and \(g_{\ell }(x,m,c) = (x,v_{\ell }(x,m,c))\) where \(A_1 = A_2 = B_1 = \{0,1\}^{\ell } \cup \{\bot \} \) and \(v_{\ell }:A_1 \times A_2 \times A_3 \rightarrow B_2\). Efficient such functions with the properties needed for the security of the protocol can be based on universal hash functions, see for instance [6, 23].
-rules Alice commits to both her input encodings and encrypts the openings of the commitments using the watchlist key. The opening of Alice’s input encoding will be encrypted using the evaluation key. To verify Alice’s input, we first pass Alice’s input through an auxiliary function which combines the identity function with an additional verification function which forces Alice to use the same input in different instances. We then link the output of the identity function to the appropriate input. We denoted the auxiliary function by \(g_{l}:A_1 \times A_2 \times A_3 \rightarrow B_1 \times B_2\) and \(g_{\ell }(x,m,c) = (x,v_{\ell }(x,m,c))\) where \(A_1 = A_2 = B_1 = \{0,1\}^{\ell } \cup \{\bot \} \) and \(v_{\ell }:A_1 \times A_2 \times A_3 \rightarrow B_2\). Efficient such functions with the properties needed for the security of the protocol can be based on universal hash functions, see for instance [6, 23].
In the  -rules Alice first garbles the identity function. Bob then randomly samples a value \(x'\) and gets an encoding of that value via oblivious transfer for the garbled identity function. Then Bob samples uniformly at random a function h from a two-universal family of hash functions such that \(h(x') = x\) where x is the input of Bob. Alice will then garble the hash function. She will link the garbling of the identity function to the garbling of the hash function. She will then link the garbled hash function to the garbled function. We will denote by \(\mathcal {H}_{\ell }\) a two-universal family of hash functions \(h:\{0,1\}^{\ell + 2s +1} \rightarrow \{0,1\}^{\ell }\). We use \({\mathsf {{id}}} : A \rightarrow A\) to denote the identify function on A.
-rules Alice first garbles the identity function. Bob then randomly samples a value \(x'\) and gets an encoding of that value via oblivious transfer for the garbled identity function. Then Bob samples uniformly at random a function h from a two-universal family of hash functions such that \(h(x') = x\) where x is the input of Bob. Alice will then garble the hash function. She will link the garbling of the identity function to the garbling of the hash function. She will then link the garbled hash function to the garbled function. We will denote by \(\mathcal {H}_{\ell }\) a two-universal family of hash functions \(h:\{0,1\}^{\ell + 2s +1} \rightarrow \{0,1\}^{\ell }\). We use \({\mathsf {{id}}} : A \rightarrow A\) to denote the identify function on A.
In [22] we prove the following theorem.
Theorem 2
Let \(\mathbb {L}\) be the set of all legal sequences and let \(\varPhi \) be a side-information function. Let \(\mathcal {G}\) be a reactive garbling scheme. Let \({\mathsf {{com}}}\) be a commitment scheme and \(\mathcal {E}\) an encryption scheme. If \(\mathcal {G}\) is \(\mathbb {L}\)-correct and \((\mathbb {L}, \varPhi )\)-confidential and \({\mathsf {{com}}}\) is computationally hiding and perfect binding and \(\mathcal {E}\) is IND-CPA secure, then \(\pi _{\mathcal {G},{\mathsf {{com}}},\mathcal {E}}\) UC securely realizes  in the
in the  -hybrid model against a static, malicious adversary.
-hybrid model against a static, malicious adversary.
Notes
- 1.
Some of the algorithms will take as input values output by other algorithms. To identify where these inputs originate from we use tags.
References
Bellare, M., Hoang, V.T., Rogaway, P.: Adaptively secure garbling with applications to one-time programs and secure outsourcing. In: Wang, X., Sako, K. (eds.) ASIACRYPT 2012. LNCS, vol. 7658, pp. 134–153. Springer, Heidelberg (2012). doi:10.1007/978-3-642-34961-4_10
Bellare, M., Hoang, V.T., Rogaway, P.: Foundations of garbled circuits. In: Yu, T., Danezis, G., Gligor, V.D. (eds.) The ACM Conference on Computer and Communications Security, CCS 2012, Raleigh, NC, USA, 16–18 October 2012, pp. 784–796. ACM (2012)
Bellare, M., Rogaway, P.: The security of triple encryption and a framework for code-based game-playing proofs. In: Vaudenay, S. (ed.) EUROCRYPT 2006. LNCS, vol. 4004, pp. 409–426. Springer, Heidelberg (2006). doi:10.1007/11761679_25
Brandão, L.T.A.N.: Secure two-party computation with reusable bit-commitments, via a cut-and-choose with forge-and-lose technique. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 441–463. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_23
Carter, H., Lever, C., Traynor, P.: Whitewash: Outsourcing garbled circuit generation for mobile devices (2014)
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B.: Faster maliciously secure two-party computation using the GPU. In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 358–379. Springer, Heidelberg (2014). doi:10.1007/978-3-319-10879-7_21
Frederiksen, T.K., Jakobsen, T.P., Nielsen, J.B., Nordholt, P.S., Orlandi, C.: MiniLEGO: efficient secure two-party computation from general assumptions. In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 537–556. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_32
Frederiksen, T.K., Nielsen, J.B.: Fast and maliciously secure two-party computation using the GPU. IACR Cryptology ePrint Archive 2013, p. 46 (2013)
Gennaro, R., Gentry, C., Parno, B.: Non-interactive verifiable computing: outsourcing computation to untrusted workers. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 465–482. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_25
Gentry, C., Halevi, S., Lu, S., Ostrovsky, R., Raykova, M., Wichs, D.: Garbled RAM revisited. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 405–422. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_23
Gentry, C., Halevi, S., Vaikuntanathan, V.: i-hop homomorphic encryption and rerandomizable yao circuits. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 155–172. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_9
Goldwasser, S., Kalai, Y.T., Rothblum, G.N.: One-time programs. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 39–56. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_3
Huang, Y., Evans, D., Katz, J., Malka, L.: Faster secure two-party computation using garbled circuits. In: 20th USENIX Security Symposium, Proceedings, San Francisco, CA, USA, 8–12 August 2011. USENIX Association (2011)
Huang, Y., Katz, J., Kolesnikov, V., Kumaresan, R., Malozemoff, A.J.: Amortizing garbled circuits. In: Garay, J.A., Gennaro, R. (eds.) CRYPTO 2014. LNCS, vol. 8617, pp. 458–475. Springer, Heidelberg (2014). doi:10.1007/978-3-662-44381-1_26
Ishai, Y., Prabhakaran, M., Sahai, A.: Founding cryptography on oblivious transfer – efficiently. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 572–591. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_32
Kreuter, B., Shelat, A., Shen, C.H.: Billion-gate secure computation with malicious adversaries. Cryptology ePrint Archive, Report 2012/179 (2012). http://eprint.iacr.org/
Kreuter, B., Shelat, A., Shen, C.-H.: Billion-gate secure computation with malicious adversaries. In: USENIX Security Symposium, pp. 285–300 (2012)
Lindell, Y.: Fast cut-and-choose based protocols for malicious and covert adversaries. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 1–17. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_1
Lu, S., Ostrovsky, R.: How to garble RAM programs? In: Johansson, T., Nguyen, P.Q. (eds.) EUROCRYPT 2013. LNCS, vol. 7881, pp. 719–734. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38348-9_42
Mood, B., Gupta, D., Butler, K., Feigenbaum, J.: Reuse it or lose it: more efficient secure computation through reuse of encrypted values. In: Proceedings of the 2014 ACM SIGSAC Conference on Computer and Communications Security, pp. 582–596. ACM (2014)
Nielsen, J.B., Orlandi, C.: LEGO for two-party secure computation. In: Reingold, O. (ed.) TCC 2009. LNCS, vol. 5444, pp. 368–386. Springer, Heidelberg (2009). doi:10.1007/978-3-642-00457-5_22
Nielsen, J.B., Ranellucci, S.: Foundations of reactive garbling schemes. IACR Cryptology ePrint Archive 2015, p. 693 (2015)
Shelat, A., Shen, C.: Fast two-party secure computation with minimal assumptions. In: 2013 ACM SIGSAC Conference on Computer and Communications Security, CCS 2013, Berlin, Germany, 4–8 November 2013, pp. 523–534 (2013)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Nielsen, J.B., Ranellucci, S. (2016). Reactive Garbling: Foundation, Instantiation, Application. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10032. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53890-6_34
Download citation
DOI: https://doi.org/10.1007/978-3-662-53890-6_34
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53889-0
Online ISBN: 978-3-662-53890-6
eBook Packages: Computer ScienceComputer Science (R0)







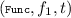 and
and  .
. occurs at most once in
occurs at most once in  occurs in
occurs in  .
.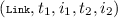 occurs in
occurs in 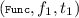 ,
,  ,
, 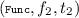 and
and 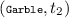 , and
, and  occurs in
occurs in 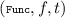 and
and  and
and  occurs in a sequence it is preceded by
occurs in a sequence it is preceded by  and
and  and
and 
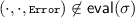 .
.
 , then
, then  , then
, then 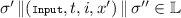 for all
for all  , then
, then  for all f with
for all f with 




 (only suitable for static security). For each line of the form, “on c from
(only suitable for static security). For each line of the form, “on c from 





