Abstract
In light of security challenges that have emerged in a world with complex networks and cloud computing, the notion of functional encryption has recently emerged. In this work, we show that in several applications of functional encryption (even those cited in the earliest works on functional encryption), the formal notion of functional encryption is actually not sufficient to guarantee security. This is essentially because the case of a malicious authority and/or encryptor is not considered. To address this concern, we put forth the concept of verifiable functional encryption, which captures the basic requirement of output correctness: even if the ciphertext is maliciously generated (and even if the setup and key generation is malicious), the decryptor is still guaranteed a meaningful notion of correctness which we show is crucial in several applications.
We formalize the notion of verifiable function encryption and, following prior work in the area, put forth a simulation-based and an indistinguishability-based notion of security. We show that simulation-based verifiable functional encryption is unconditionally impossible even in the most basic setting where there may only be a single key and a single ciphertext. We then give general positive results for the indistinguishability setting: a general compiler from any functional encryption scheme into a verifiable functional encryption scheme with the only additional assumption being the Decision Linear Assumption over Bilinear Groups (DLIN). We also give a generic compiler in the secret-key setting for functional encryption which maintains both message privacy and function privacy. Our positive results are general and also apply to other simpler settings such as Identity-Based Encryption, Attribute-Based Encryption and Predicate Encryption. We also give an application of verifiable functional encryption to the recently introduced primitive of functional commitments. Finally, in the context of indistinguishability obfuscation, there is a fundamental question of whether the correct program was obfuscated. In particular, the recipient of the obfuscated program needs a guarantee that the program indeed does what it was intended to do. This question turns out to be closely related to verifiable functional encryption. We initiate the study of verifiable obfuscation with a formal definition and construction of verifiable indistinguishability obfuscation.
A. Sahai—Research supported in part from a DARPA/ARL SAFEWARE award, NSF Frontier Award 1413955, NSF grants 1228984, 1136174, and 1065276, a Xerox Faculty Research Award, a Google Faculty Research Award, an equipment grant from Intel, and an Okawa Foundation Research Grant. This material is based upon work supported by the Defense Advanced Research Projects Agency through the ARL under Contract W911NF-15-C-0205. The views expressed are those of the author and do not reflect the official policy or position of the Department of Defense, the National Science Foundation, or the U.S. Government.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Encryption has traditionally been seen as a way to ensure confidentiality of a communication channel between a unique sender and a unique receiver. However, with the emergence of complex networks and cloud computing, recently the cryptographic community has been rethinking the notion of encryption to address security concerns that arise in these more complex environments.
In particular, the notion of functional encryption (FE) was introduced[29, 30], with the first comprehensive formalizations of FE given in [13, 26]. In FE, there is an authority that sets up public parameters and a master secret key. Encryption of a value x can be performed by any party that has the public parameters and x. Crucially, however, the master secret key can be used to generate limited “function keys.” More precisely, for a given allowable function f, using the master secret key, it is possible to generate a function key \(SK_f\). Applying this function key to an encryption of x yields only f(x). In particular, an adversarial entity that holds an encryption of x and \(SK_f\) learns nothing more about x than what is learned by obtaining f(x). It is not difficult to imagine how useful such a notion could be – the function f could enforce access control policies, or more generally only allow highly processed forms of data to be learned by the function key holder.
Our work: The case of dishonest authority and encryptor. However, either implicitly or explicitly, almostFootnote 1 all known prior work on FE has not considered the case where either the authority or the encryptor, or both, could be dishonest. This makes sense historically, since for traditional encryption, for example, there usually isn’t a whole lot to be concerned about if the receiver that chooses the public/secret key pair is herself dishonest. However, as we now illustrate with examples, there are simple and serious concerns that arise for FE usage scenarios when the case of a dishonest authority and encryptor is considered:
-
Storing encrypted images: Let us start with a motivating example for FE given in the paper of Boneh, Sahai, and Waters [13] that initiated the systematic study of FE. Suppose that there is a cloud service on which customers store encrypted images. Law enforcement may require the cloud to search for images containing a particular face. Thus, customers would be required to provide to the cloud a restrictive decryption key which allows the cloud to decrypt images containing the target face (but nothing else). Boneh et al. argued that one could use functional encryption in such a setting to provide these restricted decryption keys.
However, we observe that if we use functional encryption, then law enforcement inherently has to trust the customer to be honest, because the customer is acting as both the authority and the encryptor in this scenario. In particular, suppose that a malicious authority could create malformed ciphertexts and “fake” decryption keys that in fact do not provide the functionality guarantees required by law enforcement. Then, for example, law enforcement could be made to believe that there are no matching images, when in fact there might be several matching images.
A similar argument holds if the cloud is storing encrypted text or emails (and law enforcement would like to search for the presence of certain keywords or patterns).
-
Audits: Next, we consider an even older example proposed in the pioneering work of Goyal, Pandey, Sahai, and Waters [21] to motivate Attribute-Based Encryption, a special case of FE. Suppose there is a bank that maintains large encrypted databases of the transactions in each of its branches. An auditor is required to perform a financial audit to certify compliance with various financial regulations such as Sarbanes-Oxley. For this, the auditor would need access to certain types of data (such as logs of certain transactions) stored on the bank servers. However the bank does not wish to give the auditors access to the entire data (which would leak customer personal information, etc.). A natural solution is to have the bank use functional encryption. This would enable it to release a key to the auditor which selectively gives him access to only the required data.
However, note that the entire purpose of an audit is to provide assurances even in the setting where the entity being audited is not trusted. What if either the system setup, or the encryption, or the decryption key generation is maliciously done? Again, with the standard notions of FE, all bets are off, since these scenarios are simply not considered.
Surprisingly, to the best of our knowledge, this (very basic) requirement of adversarial correctness has not been previously captured in the standard definitions of functional encryption. Indeed, it appears that many previous works overlooked this correctness requirement while envisioning applications of (different types of) functional encryption. The same issue also arises in the context of simpler notions of functional encryption such as identity based encryption (IBE), attribute based encryption (ABE), and predicate encryption (PE), which have been studied extensively [11, 17, 18, 21, 23, 29, 32].
In order to solve this problem, we define the notion of Verifiable Functional Encryption Footnote 2 (VFE). Informally speaking, in a VFE scheme, regardless of how the system setup is done, for each (possibly maliciously generated) ciphertext C that passes a publicly known verification procedure, there must exist a unique message m such that: for any allowed function description f and function key \(SK_f\) that pass another publicly known verification procedure, it must be that the decryption algorithm given C, \(SK_f\), and f is guaranteed to output f(m). In particular, this also implies that if two decryptions corresponding to functions \(f_1\) and \(f_2\) of the same ciphertext yield \(y_1\) and \(y_2\) respectively, then there must exist a single message m such that \(y_1 = f_1(m)\) and \(y_2 = f_2(m)\).
We stress that even the public parameter generation algorithm can be corrupted. As illustrated above, this is critical for security in many applications. The fact that the public parameters are corrupted means that we cannot rely on the public parameters to contain an honestly generated Common Random String or Common Reference String (CRS). This presents the main technical challenge in our work, as we describe further below.
1.1 Our Contributions for Verifiable Functional Encryption
Our work makes the following contributions with regard to VFE:
-
We formally define verifiable functional encryption and study both indistinguishability and simulation-based security notions. Our definitions can adapt to all major variants and predecessors of FE, including IBE, ABE, and predicate encryption.
-
We show that simulation based security is unconditionally impossible to achieve by constructing a one-message zero knowledge proof system from any simulation secure verifiable functional encryption scheme. Interestingly, we show the impossibility holds even in the most basic setting where there may only be a single key and a single ciphertext that is queried by the adversary (in contrast to ordinary functional encryption where we know of general positive results in such a setting from minimal assumptions [27]). Thus, in the rest of our work, we focus on the indistinguishability-based security notion.
-
We give a generic compiler from any public-key functional encryption scheme to a verifiable public-key functional encryption scheme, with the only additional assumption being Decision Linear Assumption over Bilinear Groups (DLIN). Informally, we show the following theorem.
Theorem 1
(Informal) Assuming there exists a secure public key functional encryption scheme for the class of functions \({\mathcal {F}}\) and DLIN is true, there exists an explicit construction of a secure verifiable functional encryption scheme for the class of functions \({\mathcal {F}}\).
-
In the above, the DLIN assumption is used only to construct non-interactive witness indistinguishable (NIWI) proof systems. We show that NIWIs are necessary by giving an explicit construction of a NIWI from any verifiable functional encryption scheme. This compiler gives rise to various verifiable functional encryption schemes under different assumptions. Some of them have been summarized in Table 1.
-
We next give a generic compiler for the secret-key setting. Namely, we convert from any secret-key functional encryption scheme to a verifiable secret-key functional encryption scheme with the only additional assumption being DLIN. Informally, we show the following theorem:
Theorem 2
(Informal) Assuming there exists a message hiding and function hiding secret-key functional encryption scheme for the class of functions \({\mathcal {F}}\) and DLIN is true, there exists an explicit construction of a message hiding and function hiding verifiable secret-key functional encryption scheme for the class of functions \({\mathcal {F}}\).
An Application: Non-Interactive Functional Commitments: In a traditional non-interactive commitment scheme, a committer commits to a message m which is revealed entirely in the decommitment phase. Analogous to the evolution of functional encryption from traditional encryption, we consider the notion of functional commitments which were recently studied in [24] as a natural generalization of non-interactive commitments. In a functional commitment scheme, a committer commits to a message m using some randomness r. In the decommitment phase, instead of revealing the entire message m, for any function f agreed upon by both parties, the committer outputs a pair of values (a, b) such that using b and the commitment, the receiver can verify that \(a = f(m)\) where m was the committed value. Similar to a traditional commitment scheme, we require the properties of hiding and binding. Roughly, hiding states that for any pair of messages \((m_0,m_1)\), a commitment of \(m_0\) is indistinguishable to a commitment of \(m_1\) if \(f(m_0) = f(m_1)\) where f is the agreed upon function. Informally, binding states that for every commitment c, there is a unique message m committed inside c.
We show that any verifiable functional encryption scheme directly gives rise to a non-interactive functional commitment scheme with no further assumptions.
Verifiable iO: As shown recently [3, 4, 10], functional encryption for general functions is closely tied to indistinguishability obfuscation [6, 14]. In obfuscation, aside from the security of the obfuscated program, there is a fundamental question of whether the correct program was obfuscated. In particular, the recipient of the obfuscated program needs a guarantee that the program indeed does what it was intended to do.
Indeed, if someone hands you an obfuscated program, and asks you to run it, your first response might be to run away. After all, you have no idea what the obfuscated program does. Perhaps it contains backdoors or performs other problematic behavior. In general, before running an obfuscated program, it makes sense for the recipient to wait to be convinced that the program behaves in an appropriate way. More specifically, the recipient would want an assurance that only certain specific secrets are kept hidden inside it, and that it uses these secrets only in certain well-defined ways.
In traditional constructions of obfuscation, the obfuscator is assumed to be honest and no correctness guarantees are given to an honest evaluator if the obfuscator is dishonest. To solve this issue, we initiate a formal study of verifiability in the context of indistinguishability obfuscation, and show how to convert any iO scheme into a usefully verifiable iO scheme.
We note that verifiable iO presents some nontrivial modeling choices. For instance, of course, it would be meaningless if a verifiable iO scheme proves that a specific circuit C is being obfuscated – the obfuscation is supposed to hide exactly which circuit is being obfuscated. At the same time, of course every obfuscated program does correspond to some Boolean circuit, and so merely proving that there exists a circuit underlying an obfuscated program would be trivial. To resolve this modeling, we introduce a public predicate P, and our definition will require that there is a public verification procedure that takes both P and any maliciously generated obfuscated circuit \(\tilde{C}\) as input. If this verification procedure is satisfied, then we know that there exists a circuit C equivalent to \(\tilde{C}\) such that \(P(C)=1\). In particular, P could reveal almost everything about C, and only leave certain specific secrets hidden. (We also note that our VFE schemes can also be modified to also allow for such public predicates to be incorporated there, as well.)
iO requires that given a pair \((C_0, C_1)\) of equivalent circuits, the obfuscation of \(C_0\) should be indistinguishable from the obfuscation of \(C_1\). However, in our construction, we must restrict ourselves to pairs of circuits where this equivalence can be proven with a short witness. In other words, there should be an NP language L such that \((C_0, C_1) \in L\) implies that \(C_0\) is equivalent to \(C_1\). We leave removing this restriction as an important open problem. However, we note that, to the best of our knowledge, all known applications of iO in fact only consider pairs of circuits where proving equivalence is in fact easy given a short witnessFootnote 3.
1.2 Technical Overview
At first glance, constructing verifiable functional encryption may seem easy. One naive approach would be to just compile any functional encryption (FE) system with NIZKs to achieve verifiability. However, note that this doesn’t work, since if the system setup is maliciously generated, then the CRS for the NIZK would also be maliciously generated, and therefore soundness would not be guaranteed to hold.
Thus, the starting point of our work is to use a relaxation of NIZK proofs called non-interactive witness indistinguishable proof (NIWI) systems, that do guarantee soundness even without a CRS. However, NIWIs only guarantee witness indistinguishability, not zero-knowledge. In particular, if there is only one valid witness, then NIWIs do not promise any security at all. When using NIWIs, therefore, it is typically necessary to engineer the possibility of multiple witnesses.
A failed first attempt and the mismatch problem: Two parallel FE schemes. A natural initial idea would be to execute two FE systems in parallel and prove using a NIWI that at least one of them is fully correct: that is, its setup was generated correctly, the constituent ciphertext generated using this system was computed correctly and the constituent function secret key generated using this system was computed correctly. Note that the NIWI computed for proving correctness of the ciphertext will have to be separately generated from the NIWI computed for proving correctness of the function secret key.
This yields the mismatch problem: It is possible that in one of the FE systems, the ciphertext is maliciously generated, while in the other, the function secret key is! Then, during decryption, if either the function secret key or the ciphertext is malicious, all bets are off. In fact, several known FE systems [14, 15] specifically provide for programming either the ciphertext or the function secret key to force a particular output during decryption.
Could we avoid the mismatch problem by relying on majority-based decoding? In particular, suppose we have three parallel FE systems instead of two. Here, we run into the following problem: If we prove that at least two of the three ciphertexts are honestly encrypting the same message, the NIWI may not hide this message at all: informally speaking, the witness structure has too few “moving parts”, and it is not known how to leverage NIWIs to argue indistinguishability. On the other hand, if we try to relax the NIWI and prove only that at least two of the three ciphertexts are honestly encrypting some (possibly different) message, each ciphertext can no longer be associated with a unique message, and the mismatch problem returns, destroying verifiability.
Let’s take a look at this observation a bit more in detail in the context of functional commitments, which is perhaps a simpler primitive. Consider a scheme where the honest committer commits to the same message m thrice using a non-interactive commitment scheme. Let \(\mathsf {Z}_1,\mathsf {Z}_2,\mathsf {Z}_3\) be these commitments. Note that in the case of a malicious committer, the messages being committed \(m_0,m_1,m_2\), may all be potentially different. In the decommitment phase, the committer outputs a and a \(\mathsf {NIWI}\) proving that two out of the three committed values (say \(m_i\) and \(m_j\)) are such that \(a=f(m_i)=f(m_j)\). With such a NIWI, it is possible to give a hybrid argument that proves the hiding property (which corresponds to indistinguishability in the FE setting). However, binding (which corresponds to verifiability) is lost: One can maliciously commit to \(m_0,m_1,m_2\) such that they satisfy the following property: there exists functions f, g, h for which it holds that \(f(m_0)=f(m_1)\ne f(m_2)\), \(g(m_0)\ne g(m_1)= g(m_2)\) and \(h(m_0)= h(m_2)\ne h(m_1)\). Now, if the malicious committer runs the decommitment phase for these functions separately, there is no fixed message bound by the commitment.
As mentioned earlier, one could also consider a scheme where in the decommitment phase, the committer outputs f(m) and a \(\mathsf {NIWI}\) proving that two out of the three commitments correspond to the same message m (i.e. there exists i, j such that \(m_i=m_j\)) and \(f(m_i)=a\). The scheme is binding but does not satisfy hiding any more. This is because there is no way to move from a hybrid where all three commitments correspond to message \(m^*_0\) to one where all three commitments correspond to message \(m^*_1\), since at every step of the hybrid argument, two messages out of three must be equal.
This brings out the reason why verifiability and security are two conflicting requirements. Verifiability seems to demand a majority of some particular message in the constituent ciphertexts whereas in the security proof, we have to move from a hybrid where the majority changes (from that of \(m^*_0\) to that of \(m^*_1\)). Continuing this way it is perhaps not that hard to observe that having any number of systems will not solve the problem. Hence, we have to develop some new techniques to solve the problem motivated above. This is what we describe next.
Our solution: Locked trapdoors. Let us start with a scheme with five parallel FE schemes. Our initial idea will be to commit to the challenge constituent ciphertexts as part of the public parameters, but we will need to introduce a twist to make this work, that we will mention shortly. Before we get to the twist, let’s first see why having a commitment to the challenge ciphertext doesn’t immediately solve the problem. Let’s introduce a trapdoor statement for the relation used by the \(\mathsf {NIWI}\) corresponding to the VFE ciphertexts. This trapdoor statement states that two of the constituent ciphertexts are encryptions of the same message and all the constituent ciphertexts are committed in the public parameters. Initially, the \({\mathsf {NIWI}}\) in the challenge ciphertext uses the fact that the trapdoor statement is correct with the indices 1 and 2 encrypting the same message \(m_0^*\). The \({\mathsf {NIWI}}\)s in the function secret keys use the fact that the first four indices are secret keys for the same function. Therefore, this leaves the fifth index free (not being part of the \({\mathsf {NIWI}}\) in any function secret key or challenge ciphertext) and we can switch the fifth constituent challenge ciphertext to be an encryption of \(m_1^*\). We can switch the indices used in the \({\mathsf {NIWI}}\) for the function secret keys (one at a time) appropriately to leave some other index free and transform the challenge ciphertext to encrypt \(m_0^*\) in the first two indices and \(m_1^*\) in the last three. We then switch the proof in the challenge ciphertext to use the fact that the last two indices encrypt the same message \(m_1^*\). After this, in the same manner as above, we can switch the first two indices (one by one) of the challenge ciphertext to also encrypt \(m_1^*\). This strategy will allow us to complete the proof of indistinguishability security.
Indeed, such an idea of committing to challenge ciphertexts in the public parameters has been used in the FE context before, for example in [14]. However, observe that if we do this, then verifiability is again lost, because recall that even the public parameters of the system are under the adversary’s control! If a malicious authority generates a ciphertext using the correctness of the trapdoor statement, he could encrypt the tuple \((m,m,m_1,m_2,m_3)\) as the set of messages in the constituent ciphertexts and generate a valid \({\mathsf {NIWI}}\). Now, for some valid function secret key, decrypting this ciphertext may not give rise to a valid function output. The inherent problem here is that any ciphertext for which the \({\mathsf {NIWI}}\) is proved using the trapdoor statement and any honestly generated function secret key need not agree on a majority (three) of the underlying systems.
To overcome this issue, we introduce the idea of a guided locking mechanism. Intuitively, we require that the system cannot have both valid ciphertexts that use the correctness of the trapdoor statement and valid function secret keys. Therefore, we introduce a new “lock” in the public parameters. The statement being proved in the function secret key will state that this lock is a commitment of 1, while the trapdoor statement for the ciphertexts will state that the lock is a commitment of 0. Thus, we cannot simultaneously have valid ciphertexts that use the correctness of the trapdoor statement and valid function secret keys. This ensures verifiability of the system. However, while playing this cat and mouse game of ensuring security and verifiability, observe that we can no longer prove that the system is secure! In our proof strategy, we wanted to switch the challenge ciphertext to use the correctness of the trapdoor statement which would mean that no valid function secret key can exist in the system. But, the adversary can of course ask for some function secret keys and hence the security proof wouldn’t go through.
We handle this scenario by introducing another trapdoor statement for the relation corresponding to the function secret keys. This trapdoor statement is similar to the honest one in the sense that it needs four of the five constituent function secret keys to be secret keys for the same function. Crucially, however, additionally, it states that if you consider the five constituent ciphertexts committed to in the public parameters, decrypting each of them with the corresponding constituent function secret key yields the same output. Notice that for any function secret key that uses the correctness of the trapdoor statement and any ciphertext generated using the correctness of its corresponding trapdoor statement, verifiability is not lost. This is because of the condition that all corresponding decryptions yield the same output. Indeed, for any function secret key that uses the correctness of the trapdoor statement and any ciphertext generated using the correctness of its non-trapdoor statement, verifiability is maintained. Thus, this addition doesn’t impact the verifiability of the system.
Now, in order to prove security, we first switch every function secret key to be generated using the correctness of the trapdoor statement. This is followed by changing the lock in the public parameter to be a commitment of 1 and then switching the \({\mathsf {NIWI}}\) in the ciphertexts to use their corresponding trapdoor statement. The rest of the security proof unravels in the same way as before. After the challenge ciphertext is transformed into an encryption of message \(m_1^*\), we reverse the whole process to switch every function secret key to use the real statement (and not the trapdoor one) and to switch the challenge ciphertext to use the corresponding real statement. Notice that the lock essentially guides the sequence of steps to be followed by the security proof as any other sequence is not possible. In this way, the locks guide the hybrids that can be considered in the security argument, hence the name “guided” locking mechanism for the technique. In fact, using these ideas, it turns out that just having four parallel systems suffices to construct verifiable functional encryption in the public key setting.
In the secret key setting, to achieve verifiability, we also have to commit to all the constituent master secret keys in the public parameters. However, we need an additional system (bringing the total back to five) because in order to switch a constituent challenge ciphertext from an encryption of \(m_0^*\) to that of \(m_1^*\), we need to puncture out the corresponding master secret key committed in the public parameters. We observe that in the secret key setting, ciphertexts and function secret keys can be seen as duals of each other. Hence, to prove function hiding, we introduce indistinguishable modes and a switching mechanism. At any point in time, the system can either be in function hiding mode or in message hiding mode but not both. At all stages, verifiability is maintained using similar techniques.
Organisation: In Sect. 2 we define the preliminaries used in the paper. In Sect. 3, we give the definition of a verifiable functional encryption scheme. This is followed by the construction and proof of a verifiable functional encryption scheme in Sect. 4. In Sect. 5, we give the construction of a secret key verifiable functional encryption scheme. Section 6 is devoted to the study of verifiable obfuscation. An application of verifiable functional encryption is in achieving functional commitments. Due to lack of space, this has been discussed in the full version [5].
2 Preliminaries
Throughout the paper, let the security parameter be \(\lambda \) and let PPT denote a probabilistic polynomial time algorithm. We assume that reader is familiar with the concept of public key encryption and non-interactive commitment schemes.
2.1 One Message WI Proofs
We will be extensively using one message witness indistinguishable proofs \(\mathsf {NIWI}\) as provided by [22].
Definition 1
A pair of PPT algorithms \((\mathcal {P},\mathcal {V})\) is a \(\mathsf {NIWI}\) for an NP relation \(\mathcal {R}_{\mathcal {L}}\) if it satisfies:
-
1.
Completeness: for every \((x,w)\in \mathcal {R}_{\mathcal {L}} \), \(Pr[\mathcal {V}(x,\pi )=1: \pi \leftarrow \mathcal {P}(x,w)]=1\).
-
2.
(Perfect) Soundness: Proof system is said to be perfectly sound if there for every \(x \notin L\) and \(\pi \in \{ 0,1 \}^{*}\) \(Pr[\mathcal {V}(x,\pi )=1]=0\).
-
3.
Witness indistinguishability: for any sequence \(\mathcal {I}= \lbrace (x,w_{1},w_{2}):w_{1},w_{2}\in \mathcal {R}_{\mathcal {L}}(x)\rbrace \) \(\lbrace \pi _{1} : \pi _{1} \leftarrow \mathcal {P}(x,w_{1}) \rbrace _{(x,w_{1},w_{2})\in \mathcal {I}} \approx _{c}\lbrace \pi _{2} : \pi _{2} \leftarrow \mathcal {P}(x,w_{2}) \rbrace _{(x,w_{1},w_{2})\in \mathcal {I}}\)
[22] provides perfectly sound one message witness indistinguishable proofs based on the decisional linear (DLIN) assumption. [7] also provides perfectly sound proofs (although less efficient) under a complexity theoretic assumption, namely that Hitting Set Generators against co-non deterministic circuits exist. [9] construct \(\mathsf {NIWI}\) from one-way permutations and indistinguishability obfuscation.
3 Verifiable Functional Encryption
In this section we give the definition of a (public-key) verifiable functional encryption scheme. Let \(\mathcal {X}=\lbrace \mathcal {X}_{\lambda } \rbrace _{\lambda \in \mathbb {N}}\) and \(\mathcal {Y} = \lbrace \mathcal {Y}_{\lambda }\rbrace _{\lambda \in \mathbb {N}}\) denote ensembles where each \(\mathcal {X}_{\lambda }\) and \(\mathcal {Y}_{\lambda }\) is a finite set. Let \(\mathcal {F}=\lbrace \mathcal {F}_{\lambda } \rbrace _{\lambda \in \mathbb {N}}\) denote an ensemble where each \(\mathcal {F}_{\lambda }\) is a finite collection of functions, and each function \(f \in \mathcal {F}_{\lambda }\) takes as input a string \(x \in \mathcal {X}_{\lambda }\) and outputs \(f(x) \in \mathcal {Y}_{\lambda }\). A verifiable functional encryption scheme is similar to a regular functional encryption scheme with two additional algorithms \((\mathsf {VerifyCT},\mathsf {VerifyK})\). Formally, \(\mathsf {VFE}=(\mathsf {Setup},\mathsf {Enc},\mathsf {KeyGen},\mathsf {Dec},\mathsf {VerifyCT},\mathsf {VerifyK})\) consists of the following polynomial time algorithms:
-
\(\mathsf {Setup}(1^{\lambda })\). The setup algorithm takes as input the security parameter \(\lambda \) and outputs a master public key-secret key pair \((\mathsf {MPK},\mathsf {MSK})\).
-
\(\mathsf {Enc}(\mathsf {MPK},x)\rightarrow \mathsf {CT}\). The encryption algorithm takes as input a message \(x \in \mathcal {X}_{\lambda }\) and the master public key \({\mathsf {MPK}}\). It outputs a ciphertext \({\mathsf {CT}}\).
-
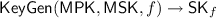 . The key generation algorithm takes as input a function \(f\in \mathcal {F}_{\lambda }\), the master public key \({\mathsf {MPK}}\) and the master secret key \({\mathsf {MSK}}\). It outputs a function secret key \(\mathsf {SK}_f\).
. The key generation algorithm takes as input a function \(f\in \mathcal {F}_{\lambda }\), the master public key \({\mathsf {MPK}}\) and the master secret key \({\mathsf {MSK}}\). It outputs a function secret key \(\mathsf {SK}_f\). -
\(\mathsf {Dec}(\mathsf {MPK},f,\mathsf {SK}_f,\mathsf {CT})\) \(\rightarrow y \) or \(\bot \). The decryption algorithm takes as input the master public key \({\mathsf {MPK}}\), a function f, the corresponding function secret key \(\mathsf {SK}_f\) and a ciphertext \(\textsf {CT}\). It either outputs a string \(y \in \mathcal {Y}\) or \(\bot \). Informally speaking, \({\mathsf {MPK}}\) is given to the decryption algorithm for verification purpose.
-
\(\mathsf {VerifyCT}(\mathsf {MPK},\mathsf {CT})\rightarrow 1/0\). Takes as input the master public key \({\mathsf {MPK}}\) and a ciphertext \({\mathsf {CT}}\). It outputs 0 or 1. Intuitively, it outputs 1 if \({\mathsf {CT}}\) was correctly generated using the master public key \({\mathsf {MPK}}\) for some message x.
-
\(\mathsf {VerifyK}(\mathsf {MPK},f,\mathsf {SK})\rightarrow 1/0\). Takes as input the master public key \({\mathsf {MPK}}\), a function f and a function secret key \(\mathsf {SK}_f\). It outputs either 0 or 1. Intuitively, it outputs 1 if \(\mathsf {SK}_f\) was correctly generated as a function secret key for f.
The scheme has the following properties:
Definition 2
(Correctness) A verifiable functional encryption scheme \({\mathsf {VFE}}\) for \({\mathcal {F}}\) is correct if for all \(f \in \mathcal {F}_\lambda \) and all \(x \in \mathcal {X}_\lambda \)
Definition 3
(Verifiability) A verifiable functional encryption scheme \({\mathsf {VFE}}\) for \({\mathcal {F}}\) is verifiable if, for all  , for all
, for all  , there exists \(x \in \mathcal {X}\) such that for all \(f \in \mathcal {F}\) and
, there exists \(x \in \mathcal {X}\) such that for all \(f \in \mathcal {F}\) and  , if
, if
then
Remark. Intuitively, verifiability states that each ciphertext (possibly associated with a maliciously generated public key) should be associated with a unique message and decryption for a function f using any possibly maliciously generated key \({\mathsf {SK}}\) should result in f(x) for that unique message f(x) and nothing else (if the ciphertext and keys are verified by the respective algorithms).
We also note that a verifiable functional encryption scheme should satisfy perfect correctness. Otherwise, a non-uniform malicious authority can sample ciphertexts/keys from the space where it fails to be correct. Thus, the primitives that we will use in our constructions are assumed to have perfect correctness. Such primitives have been constructed before in the literature.
3.1 Indistinguishability Based Security
The indistinguishability based security for verifiable functional encryption is similar to the security notion of a functional encryption scheme. For completeness, we define it below. We also consider a {full/selective} CCA secure variant where the adversary, in addition to the security game described below, has access to a decryption oracle which takes a ciphertext and a function as input and decrypts the ciphertext with an honestly generated key for that function and returns the output. The adversary is allowed to query this decryption oracle for all ciphertexts of his choice except the challenge ciphertext itself.
We define the security notion for a verifiable functional encryption scheme using the following game (\(\mathsf {Full-IND}\)) between a challenger and an adversary.
Setup Phase: The challenger \(\mathsf {(MPK,MSK)\leftarrow vFE.Setup(1^{\lambda })}\) and then hands over the master public key \(\mathsf {MPK}\) to the adversary.
Key Query Phase 1: The adversary makes function secret key queries by submitting functions \(\mathsf {f} \in \mathcal {F}_\lambda \). The challenger responds by giving the adversary the corresponding function secret key \(\mathsf {SK_{f}\leftarrow vFE.KeyGen(\mathsf {MPK},\mathsf {MSK},f)}\).
Challenge Phase: The adversary chooses two messages \(\mathsf {(m_{0}, m_{1})}\) of the same size (each in \(\mathcal {X_\lambda )}\)) such that for all queried functions \(\mathsf {f}\) in the key query phase, it holds that \(\mathsf {f(m_{0})=f(m_{1})}\). The challenger selects a random bit \(\mathsf {b}\in \{ 0,1 \}\) and sends a ciphertext \(\mathsf {CT\leftarrow vFE.Enc(\mathsf {MPK},m_{b})}\) to the adversary.
Key Query Phase 2: The adversary may submit additional key queries \(\mathsf {f\in } \mathcal {F}_\lambda \) as long as they do not violate the constraint described above. That is, for all queries f, it must hold that \(\mathsf {f(m_{0})=f(m_{1})}\).
Guess: The adversary submits a guess \(b^{'}\) and wins if \(b^{'}=b\). The adversary’s advantage in this game is defined to be \(\mathsf {2*\vert Pr[b=b^{'}]-1/2\vert }\).
We also define the selective security game, which we call \((\mathsf {sel-IND})\) where the adversary outputs the challenge message pair even before seeing the master public key.
Definition 4
A verifiable functional encryption scheme \(\mathsf {VFE}\) is { selective, fully} secure if all polynomial time adversaries have at most a negligible advantage in the \(\mathsf {\lbrace Sel-IND,Full-IND \rbrace }\) security game.
Functional Encryption: In our construction, we will use functional encryption as an underlying primitive. Syntax of a functional encryption scheme is defined in [14]. It is similar to the syntax of a verifiable functional encryption scheme except that it doesn’t have the \({\mathsf {VerifyCT}}\) and \({\mathsf {VerifyK}}\) algorithms, the \({\mathsf {KeyGen}}\) algorithm does not take as input the master public key and the decryption algorithm does not take as input the master public key and the function. Other than that, the security notions and correctness are the same. However, in general any functional encryption scheme is not required to satisfy the verifiability property.
3.2 Simulation Based Security
Many variants of simulation based security definitions have been proposed for functional encryption. In general, simulation security (where the adversary can request for keys arbitrarily) is shown to be impossible [2]. We show that even the weakest form of simulation based security is impossible to achieve for verifiable functional encryption.
Theorem 3
There exists a family of functions, each of which can be represented as a polynomial sized circuit, for which there does not exist any simulation secure verifiable functional encryption scheme.
Proof
Let L be a \(\mathsf {NP}\) complete language. Let \(\mathcal {R}\) be the relation for this language. \(\mathcal {R}: \{ 0,1 \}^{*} \times \{ 0,1 \}^{*}\rightarrow \{ 0,1 \}\), takes as input a string x and a polynomial sized (in the length of x) witness w and outputs 1 iff \(x\in L\) and w is a witness to this fact. For any security parameter \(\lambda \), let us define a family of functions \(\mathcal {F}_{\lambda }\) as a family indexed by strings \(y \in \{ 0,1 \}^{\lambda }\). Namely, \(\mathcal {F}_{\lambda }=\lbrace \mathcal {R}(y,\cdot )\text { }\forall y \in \{ 0,1 \}^{\lambda }\rbrace \).
Informally speaking, any verifiable functional encryption scheme that is also simulation secure for this family implies the existence of one message zero knowledge proofs for L. The proof system is described as follows: the prover, who has the witness for any instance x of length \(\lambda \), samples a master public key and master secret key pair for a verifiable functional encryption scheme with security parameter \(\lambda \). Using the master public key, it encrypts the witness and samples a function secret key for the function \(\mathcal {R}(x,\cdot )\). The verifier is given the master public key, the ciphertext and the function secret key. Informally, simulation security of the verifiable functional encryption scheme provides computational zero knowledge while perfect soundness and correctness follow from verifiability. A formal proof is can be found in the fullversion [5].
In a similar manner, we can rule out even weaker simulation based definitions in the literature where the simulator also gets to generate the function secret keys and the master public key. Interestingly, IND secure \(\mathsf {VFE}\) for the circuit family described in the above proof implies one message witness indistinguishable proofs(\(\mathsf {NIWI}\)) for \(\mathsf {NP}\) and hence it is intuitive that we will have to make use of \(\mathsf {NIWI}\) in our constructions.
Theorem 4
There exists a family of functions, each of which can be represented as a polynomial sized circuit, for which (selective) IND secure verifiable functional encryption implies the existence of one message witness indistinguishable proofs for \(\mathsf {NP}\) (\(\mathsf {NIWI}\)).
We prove the theorem in the full version [5].
The definition for verifiable secret key functional encryption and verifiable multi-input functional encryption can be found in the full version [5].
4 Construction of Verifiable Functional Encryption
In this section, we give a compiler from any \(\mathsf {Sel-IND}\) secure public key functional encryption scheme to a \(\mathsf {Sel-IND}\) secure verifiable public key functional encryption scheme. The techniques used in this construction have been elaborated upon in Sect. 1.2. The resulting verifiable functional encryption scheme has the same security properties as the underlying one - that is, the resulting scheme is q-query secure if the original scheme that we started out with was q-query secure and so on, where q refers to the number of function secret key queries that the adversary is allowed to make. We prove the following theorem:
Theorem 5
Let \(\mathcal {F}= \{\mathcal {F}_\lambda \}_{\lambda \in \mathbb {N}}\) be a parameterized collection of functions. Then, assuming there exists a \(\mathsf {Sel-IND}\) secure public key functional encryption scheme \({\mathsf {FE}}\) for the class of functions \({\mathcal {F}}\), a non-interactive witness indistinguishable proof system, a non-interactive perfectly binding and computationally hiding commitment scheme, the proposed scheme \({\mathsf {VFE}}\) is a \(\mathsf {Sel-IND}\) secure verifiable functional encryption scheme for the class of functions \({\mathcal {F}}\) according to Definition 3.
Notation: Without loss of generality, let’s assume that every plaintext message is of length \(\lambda \) where \(\lambda \) denotes the security parameter of our scheme. Let \((\mathsf {Prove},\mathsf {Verify})\) be a non-interactive witness-indistinguishable (\({\mathsf {NIWI}}\)) proof system for NP, \(\mathsf {FE}= (\mathsf {FE.Setup},\mathsf {FE.Enc},\mathsf {FE.KeyGen},\mathsf {FE.Dec})\) be a \(\mathsf {Sel-IND}\) secure public key functional encryption scheme, \({\mathsf {Com}}\) be a statistically binding and computationally hiding commitment scheme. Without loss of generality, let’s say \({\mathsf {Com}}\) commits to a string bit-by-bit and uses randomness of length \(\lambda \) to commit to a single bit. We denote the length of ciphertexts in \({\mathsf {FE}}\) by  . Let
. Let  .
.
Our scheme \(\mathsf {VFE}= (\mathsf {VFE.Setup},\mathsf {VFE.Enc},\mathsf {VFE.KeyGen},\mathsf {VFE.Dec},\mathsf {VFE.VerifyCT},\)
\(\mathsf {VFE.VerifyK})\) is as follows:
-
Setup \(\mathsf {VFE.Setup}(1^\lambda )\) :
The setup algorithm does the following:
-
1.
For all \(i \in [4]\), compute \((\mathsf {MPK}_i,\mathsf {MSK}_i) \leftarrow \mathsf {FE.Setup}(1^\lambda ;s_i)\) using randomness \(s_i\).
-
2.
Set \(\mathsf {Z}= \mathsf {Com}(0^\mathsf {len};u)\) and \(\mathsf {Z}_1 = \mathsf {Com}(1;u_1)\) where u,\(u_1\) represent the randomness used in the commitment.
The master public key is
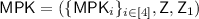 . The master secret key is \(\mathsf {MSK}= ( \{ {\mathsf {MSK}}_{i}\}_{i\in [4]},\{s_i\}_{i\in [4]},u,u_1)\).
. The master secret key is \(\mathsf {MSK}= ( \{ {\mathsf {MSK}}_{i}\}_{i\in [4]},\{s_i\}_{i\in [4]},u,u_1)\).
-
1.
-
Encryption \(\mathsf {VFE.Enc}(\mathsf {MPK},m)\) :
To encrypt a message m, the encryption algorithm does the following:
-
1.
For all \( i \in [4]\), compute \(\mathsf {CT}_i = \mathsf {FE.Enc}(\mathsf {MPK}_i,m;r_i)\).
-
2.
Compute a proof \(\pi \leftarrow \mathsf {Prove}(y,w)\) for the statement that \(y \in L\) using witness w where:
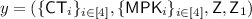 , \(w = (m,\{r_i\}_{i\in [4]},0,0,0^{|u|},0^{|u_1|})\).
, \(w = (m,\{r_i\}_{i\in [4]},0,0,0^{|u|},0^{|u_1|})\).L is defined corresponding to the relation R defined below.
-
1.
-
Relation R:
Instance:
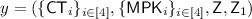 Witness: \(w = (m,\{r_i\}_{i\in [4]},i_1,i_2,u,u_1)\)
Witness: \(w = (m,\{r_i\}_{i\in [4]},i_1,i_2,u,u_1)\)
\(R_1(y,w)=1\) if and only if either of the following conditions hold:
-
1.
All 4 constituent ciphertexts encrypt the same message. That is,
\(\forall i \in [4]\), \(\mathsf {CT}_i = \mathsf {FE.Enc}(\mathsf {MPK}_i,m;r_i)\)
(OR)
-
2.
2 constituent ciphertexts (corresponding to indices \(i_1,i_2\)) encrypt the same message, \({\mathsf {Z}}\) is a commitment to all the constituent ciphertexts and \(\mathsf {Z}_1\) is a commitment to 0. That is,
-
(a)
\(\forall i \in \{\i _1,i_2\}\), \(\mathsf {CT}_{i} = \mathsf {FE.Enc}(\mathsf {MPK}_{i},m;r_{i})\).
-
(b)
\(\mathsf {Z}= \mathsf {Com}( \{ {\mathsf {CT}}_{i}\}_{i\in [4]};u).\)
-
(c)
\(\mathsf {Z}_1 = \mathsf {Com}(0;u_1).\) The output of the algorithm is the ciphertext \(\mathsf {CT}= ( \{ {\mathsf {CT}}_{i}\}_{i\in [4]},\pi )\).
\(\pi \) is computed for statement 1 of relation R.
-
(a)
-
1.
-
Key Generation \(\mathsf {VFE.KeyGen}(\mathsf {MPK},\mathsf {MSK},f)\) :
To generate the function secret key \({\mathsf {K}^f}\) for a function f, the key generation algorithm does the following:
-
1.
\(\forall i \in [4]\), compute \(\mathsf {K}^f_i = \mathsf {FE.KeyGen}(\mathsf {MSK}_i,f;r_i)\).
-
2.
Compute a proof \(\gamma \leftarrow \mathsf {Prove}(y,w)\) for the statement that \(y \in L_1\) using witness w where:
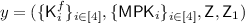 , \(w = (f, \{ {\mathsf {MSK}}_{i}\}_{i\in [4]},\{s_i\}_{i\in [4]},\{r_i\}_{i\in [4]},0^3,0^{|u|},u_1)\).
, \(w = (f, \{ {\mathsf {MSK}}_{i}\}_{i\in [4]},\{s_i\}_{i\in [4]},\{r_i\}_{i\in [4]},0^3,0^{|u|},u_1)\).\(L_1\) is defined corresponding to the relation \(R_1\) defined below.
-
1.
-
Relation \(R_1\):
Instance:
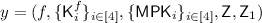 . Witness: \(w = ( \{ {\mathsf {MSK}}_{i}\}_{i\in [4]},\{s_i\}_{i\in [4]},\{r_i\}_{i\in [4]},i_1,i_2,i_3,u,u_1)\)
. Witness: \(w = ( \{ {\mathsf {MSK}}_{i}\}_{i\in [4]},\{s_i\}_{i\in [4]},\{r_i\}_{i\in [4]},i_1,i_2,i_3,u,u_1)\)
\(R_1(y,w)=1\) if and only if either of the following conditions hold:
-
1.
\(\mathsf {Z}_1\) is a commitment to 1, all 4 constituent function secret keys are secret keys for the same function and are constructed using honestly generated public key-secret key pairs.
-
(a)
\(\forall i \in [4]\), \(\mathsf {K}^f_i = \mathsf {FE.KeyGen}(\mathsf {MSK}_i,f;r_i)\).
-
(b)
\(\forall i \in [4]\), \((\mathsf {MPK}_i,\mathsf {MSK}_i) \leftarrow \mathsf {FE.Setup}(1^\lambda ;s_i)\).
-
(c)
\(\mathsf {Z}_1 = \mathsf {Com}(1;u_1)\).
(OR)
-
(a)
-
2.
3 of the constituent function secret keys (corresponding to indices \(i_1,i_2,i_3\)) are keys for the same function and are constructed using honestly generated public key-secret key pairs, \({\mathsf {Z}}\) is a commitment to a set of ciphertexts \({\mathsf {CT}}\) such that each constituent ciphertext in \({\mathsf {CT}}\) when decrypted with the corresponding function secret key gives the same output. That is,
-
(a)
\(\forall i \in \{i_1,i_2,i_3\}\), \(\mathsf {K}^f_{i} = \mathsf {FE.KeyGen}(\mathsf {MSK}_{i},f;r_{i})\).
-
(b)
\(\forall i \in \{i_1,i_2,i_3\}\), \((\mathsf {MPK}_{i},\mathsf {MSK}_{i}) \leftarrow \mathsf {FE.Setup}(1^\lambda ;s_{i})\).
-
(c)
\(\mathsf {Z}= \mathsf {Com}( \{ {\mathsf {CT}}_{i}\}_{i\in [4]};u).\)
-
(d)
\(\exists x \in \mathcal {X}_\lambda \) such that \(\forall i \in [4]\), \(\mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}^f_i) = x\)
The output of the algorithm is the function secret key \(\mathsf {K}^f= ( \{\mathsf {K}^f_i\} _{i\in [4]},\gamma )\).
\(\gamma \) is computed for statement 1 of relation \(R_1\).
-
(a)
-
1.
-
Decryption \(\mathsf {VFE.Dec}(\mathsf {MPK},f,\mathsf {K}^f,\mathsf {CT})\) :
This algorithm decrypts the ciphertext \(\mathsf {CT}= ( \{ {\mathsf {CT}}_{i}\}_{i\in [4]},\pi )\) using function secret key \(\mathsf {K}^f= ( \{\mathsf {K}^f_i\} _{i\in [4]},\gamma )\) in the following way:
-
1.
Let
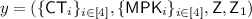 be the statement corresponding to proof \(\pi \). If \(\mathsf {Verify}(y,\pi )=0\), then stop and output \(\bot \). Else, continue to the next step.
be the statement corresponding to proof \(\pi \). If \(\mathsf {Verify}(y,\pi )=0\), then stop and output \(\bot \). Else, continue to the next step. -
2.
Let
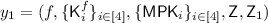 be the statement corresponding to proof \(\gamma \). If \(\mathsf {Verify}(y_1,\gamma )=0\), then stop and output \(\bot \). Else, continue to the next step.
be the statement corresponding to proof \(\gamma \). If \(\mathsf {Verify}(y_1,\gamma )=0\), then stop and output \(\bot \). Else, continue to the next step. -
3.
For \(i \in [4]\), compute \(m_i = \mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}^f_i)\). If at least 3 of the \(m_i\)’s are equal (let’s say that value is m), output m. Else, output \(\bot \).
-
1.
-
VerifyCT \(\mathsf {VFE.VerifyCT}(\mathsf {MPK},\mathsf {CT})\) :
Given a ciphertext \(\mathsf {CT}=( \{ {\mathsf {CT}}_{i}\}_{i\in [4]},\pi )\), this algorithm checks whether the ciphertext was generated correctly using master public key \({\mathsf {MPK}}\). Let
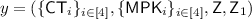 be the statement corresponding to proof \(\pi \). If \(\mathsf {Verify}(y,\pi )=1\), it outputs 1. Else, it outputs 0.
be the statement corresponding to proof \(\pi \). If \(\mathsf {Verify}(y,\pi )=1\), it outputs 1. Else, it outputs 0. -
VerifyK \(\mathsf {VFE.VerifyK}(\mathsf {MPK},f,\mathsf {K})\) :
Given a function f and a function secret key \(\mathsf {K}= ( \{{\mathsf {K}}_i\} _{i\in [4]},\gamma )\), this algorithm checks whether the key was generated correctly for function f using the master secret key corresponding to master public key \({\mathsf {MPK}}\). Let
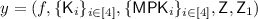 be the statement corresponding to proof \(\gamma \). If \(\mathsf {Verify}(y,\gamma )=1\), it outputs 1. Else, it outputs 0.
be the statement corresponding to proof \(\gamma \). If \(\mathsf {Verify}(y,\gamma )=1\), it outputs 1. Else, it outputs 0.
Correctness: Correctness follows directly from the correctness of the underlying FE scheme, correctness of the commitment scheme and the completeness of the \({\mathsf {NIWI}}\) proof system.
4.1 Verifiability
Consider any master public key \({\mathsf {MPK}}\) and any ciphertext \(\mathsf {CT}=( \{ {\mathsf {CT}}_{i}\}_{i\in [4]},\pi )\) such that
\(\mathsf {VFE.VerifyCT}(\mathsf {MPK},\mathsf {CT})=1\). Now, there are two cases possible for the proof \(\pi \).
-
1.
Statement 1 of relation R is correct:
Therefore, there exists \(m \in \mathcal {X}_\lambda \) such that \(\forall i \in [4]\), \(\mathsf {CT}_i = \mathsf {FE.Enc}(\mathsf {MPK}_i,m;r_i)\) where \(r_i\) is a random string. Consider any function f and function secret key \(\mathsf {K}=( \{{\mathsf {K}}_i\} _{i\in [4]},\gamma )\) such that \(\mathsf {VFE.VerifyK}(\mathsf {MPK},f,\mathsf {K})=1\). There are two cases possible for the proof \(\gamma \).
-
(a)
Statement 1 of relation \(R_1\) is correct:
Therefore, \(\forall i \in [4]\), \(\mathsf {K}_i\) is a function secret key for the same function - f. That is, \(\forall i \in [4]\), \(\mathsf {K}_i = \mathsf {FE.KeyGen}(\mathsf {MSK}_i,f;r'_i)\) where \(r'_i\) is a random string. Thus, for all \(i \in [4]\), \(\mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}_i) = f(m)\). Hence, \(\mathsf {VFE.Dec}(\mathsf {MPK},f,\mathsf {K},\mathsf {CT}) = f(m)\).
-
(b)
Statement 2 of relation \(R_1\) is correct:
Therefore, there exists 3 indices \(i_1,i_2,i_3\) such that \(\mathsf {K}_{i_1},\mathsf {K}_{i_2},\mathsf {K}_{i_3}\) are function secret keys for the same function - f. That is, \(\forall i \in \{i_1,i_2,i_3\}\), \(\mathsf {K}_{i} = \mathsf {FE.KeyGen}(\mathsf {MSK}_{i},f;r'_{i})\) where \(r'_i\) is a random string Thus, for all \(i \in \{i_1,i_2,i_3\}\), \(\mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}_i) = f(m)\). Hence, \(\mathsf {VFE.Dec}(\mathsf {MPK},f,\mathsf {K},\mathsf {CT}) = f(m)\).
-
(a)
-
2.
Statement 2 of relation R is correct:
Therefore, \(\mathsf {Z}_1 = \mathsf {Com}(0;u_1)\) and \(\mathsf {Z}= \mathsf {Com}( \{ {\mathsf {CT}}_{i}\}_{i\in [4]};u)\) for some random strings \(u,u_1\). Also, there exists 2 indices \(i_1,i_2\) and a message \(m \in \mathcal {X}_{\lambda }\) such that for \(i \in \{i_1,i_2\}\), \(\mathsf {CT}_{i} = \mathsf {FE.Enc}(\mathsf {MPK}_{i},m;r_{i})\) where \(r_i\) is a random string. Consider any function f and function secret key \(\mathsf {K}=( \{{\mathsf {K}}_i\} _{i\in [4]},\gamma )\) such that \(\mathsf {VFE.VerifyK}(\mathsf {MPK},f,\mathsf {K})=1\). There are two cases possible for the proof \(\gamma \).
-
(a)
Statement 1 of relation \(R_1\) is correct:
Then, it must be the case that \(\mathsf {Z}_1=\mathsf {Com}(1;u'_1)\) for some random string \(u'_1\). However, we already know that \(\mathsf {Z}_1 = \mathsf {Com}(0;u_1)\) and \({\mathsf {Com}}\) is a perfectly binding commitment scheme. Thus, this scenario isn’t possible. That is, both \(\mathsf {VFE.VerifyCT}(\mathsf {MPK},\mathsf {CT})\) and \(\mathsf {VFE.VerifyK}(\mathsf {MPK},f,\mathsf {K})\) can’t be equal to 1.
-
(b)
Statement 2 of relation \(R_1\) is correct:
Therefore, there exists 3 indices \(i'_1,i'_2,i'_3\) such that \(\mathsf {K}_{i'_1},\mathsf {K}_{i'_2},\mathsf {K}_{i'_3}\) are function secret keys for the same function - f. That is, \(\forall i \in \{i'_1,i'_2,i'_3\}\), \(\mathsf {K}_{i} = \mathsf {FE.KeyGen}(\mathsf {MSK}_{i},f;r'_i)\) where \(r'_i\) is a random string. Thus, by pigeonhole principle, there exists \(i^* \in \{i'_1,i'_2,i'_3\}\) such that \(i^* \in \{i_1,i_2\}\) as well. Also, \(\mathsf {Z}= \mathsf {Com}( \{ {\mathsf {CT}}_{i}\}_{i\in [4]};u)\) and \(\forall i \in [4]\), \(\mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}_i)\) is the same. Therefore, for the index \(i^*\), \(\mathsf {FE.Dec}(\mathsf {CT}_{i^*},\mathsf {K}_{i^*}) = f(m)\). Hence, \(\forall i \in [4]\), \(\mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}_i) = f(m)\). Therefore, \(\mathsf {VFE.Dec}(\mathsf {MPK},f,\mathsf {K},\mathsf {CT}) = f(m)\).
-
(a)
4.2 Security Proof
We now prove that the proposed scheme \({\mathsf {VFE}}\) is \(\mathsf {Sel-IND}\) secure. We will prove this via a series of hybrid experiments \(\mathsf {H}_1,\ldots ,\mathsf {H}_{16}\) where \(\mathsf {H}_1\) corresponds to the real world experiment with challenge bit \(b=0\) and \(\mathsf {H}_{16}\) corresponds to the real world experiment with challenge bit \(b=1\). The hybrids are summarized below in Table 2.
We briefly describe the hybrids below. A more detailed description can be found in the full version [5].
-
Hybrid \(\mathsf {H}_1\): This is the real experiment with challenge bit \(b=0\). The master public key is
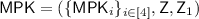 such that \(\mathsf {Z}= \mathsf {Com}(0^\mathsf {len};u)\) and \(\mathsf {Z}_1 = \mathsf {Com}(1;u_1)\) for random strings \(u,u_1\). The challenge ciphertext is \(\mathsf {CT}^*=( \{{\mathsf {CT}}^*_i\}_{i\in [4]},\pi ^*)\), where for all \(i \in [4]\), \(\mathsf {CT}^*_i = \mathsf {FE.Enc}(\mathsf {MPK}_i,m_0;r_i)\) for some random string \(r_i\). \(\pi ^*\) is computed for statement 1 of relation R.
such that \(\mathsf {Z}= \mathsf {Com}(0^\mathsf {len};u)\) and \(\mathsf {Z}_1 = \mathsf {Com}(1;u_1)\) for random strings \(u,u_1\). The challenge ciphertext is \(\mathsf {CT}^*=( \{{\mathsf {CT}}^*_i\}_{i\in [4]},\pi ^*)\), where for all \(i \in [4]\), \(\mathsf {CT}^*_i = \mathsf {FE.Enc}(\mathsf {MPK}_i,m_0;r_i)\) for some random string \(r_i\). \(\pi ^*\) is computed for statement 1 of relation R. -
Hybrid \(\mathsf {H}_2\): This hybrid is identical to the previous hybrid except that \({\mathsf {Z}}\) is computed differently. \(\mathsf {Z}= \mathsf {Com}( \{{\mathsf {CT}}^*_i\}_{i\in [4]};u)\).
-
Hybrid \(\mathsf {H}_3\): This hybrid is identical to the previous hybrid except that for every function secret key \(\mathsf {K}^f\), the proof \(\gamma \) is now computed for statement 2 of relation \(R_1\) using indices \(\{1,2,3\}\) as the set of 3 indices \(\{i_1,i_2,i_3\}\) in the witness. That is, the witness is \(w=( \mathsf {MSK}_1,\mathsf {MSK}_2,\mathsf {MSK}_3,0^{|\mathsf {MSK}_4|},s_1,s_2,s_3,\) \(0^{|s_4|},r_1,r_2,r_3,0^{|r_4|},1,2,3,u,0^{|u_1|})\).
-
Hybrid \(\mathsf {H}_4\): This hybrid is identical to the previous hybrid except that \(\mathsf {Z}_1\) is computed differently. \(\mathsf {Z}_1 = \mathsf {Com}(0;u_1)\).
-
Hybrid \(\mathsf {H}_5\): This hybrid is identical to the previous hybrid except that the proof \(\pi ^*\) in the challenge ciphertext is now computed for statement 2 of relation R using indices \(\{1,2\}\) as the 2 indices \(\{i_1,i_2\}\) in the witness. That is, the witness is \(w = (m,r_1,r_2,0^{|r_3|},0^{|r_4|},1,2,u,u_1)\).
-
Hybrid \(\mathsf {H}_6\): This hybrid is identical to the previous hybrid except that we change the fourth component \(\mathsf {CT}^*_4\) of the challenge ciphertext to be an encryption of the challenge message \(m_1\) (as opposed to \(m_0\)). That is, \(\mathsf {CT}^*_4 = \mathsf {FE.Enc}(\mathsf {MPK}_4,m_1;r_4)\) for some random string \(r_4\). Note that the proof \(\pi ^*\) is unchanged and is still proven for statement 2 of relation R.
-
Hybrid \(\mathsf {H}_7\): This hybrid is identical to the previous hybrid except that for every function secret key \(\mathsf {K}^f\), the proof \(\gamma \) is now computed for statement 2 of relation \(R_1\) using indices \(\{1,2,4\}\) as the set of 3 indices \(\{i_1,i_2,i_3\}\) in the witness. That is, the witness is \(w=( \mathsf {MSK}_1,\mathsf {MSK}_2,0^{|\mathsf {MSK}_3|},\mathsf {MSK}_4,s_1,s_2,0^{|s_3|},\) \(s_4,r_1,r_2,0^{|r_3|},r_4,1,2,4,u,0^{|u_1|})\).
-
Hybrid \(\mathsf {H}_8\): This hybrid is identical to the previous hybrid except that we change the third component \(\mathsf {CT}^*_3\) of the challenge ciphertext to be an encryption of the challenge message \(m_1\) (as opposed to \(m_0\)). That is, \(\mathsf {CT}^*_3 = \mathsf {FE.Enc}(\mathsf {MPK}_3,m_1;r_3)\) for some random string \(r_3\).
Note that the proof \(\pi ^*\) is unchanged and is still proven for statement 2 of relation R.
-
Hybrid \(\mathsf {H}_9\): This hybrid is identical to the previous hybrid except that the proof \(\pi ^*\) in the challenge ciphertext is now computed for statement 2 of relation R using message \(m_1\) and indices \(\{3,4\}\) as the 2 indices \(\{i_1,i_2\}\) in the witness. That is, the witness is \(w = (m_1,0^{|r_1|},0^{|r_2|},r_3,r_4,3,4,u,u_1)\). Also, for every function secret key \(\mathsf {K}^f\), the proof \(\gamma \) is now computed for statement 2 of relation \(R_1\) using indices \(\{1,3,4\}\) as the set of 3 indices \(\{i_1,i_2,i_3\}\) in the witness. That is, the witness is \(w=( \mathsf {MSK}_1,0^{|\mathsf {MSK}_2|},\mathsf {MSK}_3,\mathsf {MSK}_4,s_1,\) \(0^{|s_2|},s_3,s_4,r_1,0^{|r_2|},r_3,r_4,1,3,4,u,0^{|u_1|})\).
-
Hybrid \(\mathsf {H}_{10}\): This hybrid is identical to the previous hybrid except that we change the second component \(\mathsf {CT}^*_2\) of the challenge ciphertext to be an encryption of the challenge message \(m_1\) (as opposed to \(m_0\)). That is, \(\mathsf {CT}^*_2 = \mathsf {FE.Enc}(\mathsf {MPK}_2,m_1;r_2)\) for some random string \(r_2\).
Note that the proof \(\pi ^*\) is unchanged and is still proven for statement 2 of relation R.
-
Hybrid \(\mathsf {H}_{11}\): This hybrid is identical to the previous hybrid except that for every function secret key \(\mathsf {K}^f\), the proof \(\gamma \) is now computed for statement 2 of relation \(R_1\) using indices \(\{2,3,4\}\) as the set of 3 indices \(\{i_1,i_2,i_3\}\) in the witness. That is, the witness is \(w=( 0^{|\mathsf {MSK}_1|},\mathsf {MSK}_2,\mathsf {MSK}_3,\mathsf {MSK}_4,0^{|s_1|},s_2,s_3,\) \(s_4,0^{|r_1|},r_2,r_3,r_4,2,3,4,u,0^{|u_1|})\).
-
Hybrid \(\mathsf {H}_{12}\): This hybrid is identical to the previous hybrid except that we change the first component \(\mathsf {CT}^*_1\) of the challenge ciphertext to be an encryption of the challenge message \(m_1\) (as opposed to \(m_0\)). That is, \(\mathsf {CT}^*_1 = \mathsf {FE.Enc}(\mathsf {MPK}_1,m_1;r_1)\) for some random string \(r_1\). Note that the proof \(\pi ^*\) is unchanged and is still proven for statement 2 of relation R.
-
Hybrid \(\mathsf {H}_{13}\): This hybrid is identical to the previous hybrid except that the proof \(\pi ^*\) in the challenge ciphertext is now computed for statement 1 of relation R. The witness is \(w = (m_1,\{r_i\}_{i\in [4]},0,0,0^{|u|},0^{|u_1|})\).
-
Hybrid \(\mathsf {H}_{14}\): This hybrid is identical to the previous hybrid except that \(\mathsf {Z}_1\) is computed differently. \(\mathsf {Z}_1 = \mathsf {Com}(1;u_1)\).
-
Hybrid \(\mathsf {H}_{15}\): This hybrid is identical to the previous hybrid except that for every function secret key \(\mathsf {K}^f\), the proof \(\gamma \) is now computed for statement 1 of relation \(R_1\). The witness is \(w=( \{ {\mathsf {MSK}}_{i}\}_{i\in [4]},\{s_i\}_{i\in [4]},\{r_i\}_{i\in [4]},0^3,0^{|u|},u_1)\).
-
Hybrid \(\mathsf {H}_{16}\): This hybrid is identical to the previous hybrid except that \({\mathsf {Z}}\) is computed differently. \(\mathsf {Z}= \mathsf {Com}(0^{\mathsf {len}};u)\). This hybrid is identical to the real experiment with challenge bit \(b=1\).
Below we will prove that \((\mathsf {H}_1 \approx _c\mathsf {H}_2)\) and \((\mathsf {H}_5 \approx _c\mathsf {H}_6)\). The indistinguishability of other hybrids will follow along the same lines and is described in the full version [5].
Lemma 1
(\(\mathsf {H}_1 \approx _c\mathsf {H}_2).\) Assuming that \({\mathsf {Com}}\) is a (computationally) hiding commitment scheme, the outputs of experiments \(\mathsf {H}_1\) and \(\mathsf {H}_2\) are computationally indistinguishable.
Proof
The only difference between the two hybrids is the manner in which the commitment \({\mathsf {Z}}\) is computed. Let’s consider the following adversary \(\mathcal {A}_{\mathsf {Com}}\) that interacts with a challenger \(\mathcal {C}\) to break the hiding of the commitment scheme. Also, internally, it acts as the challenger in the security game with an adversary \({\mathcal {A}}\) that tries to distinguish between \(\mathsf {H}_1\) and \(\mathsf {H}_2\). \(\mathcal {A}_\mathsf {Com}\) executes the hybrid \(\mathsf {H}_1\) except that it does not generate the commitment \({\mathsf {Z}}\) on it’s own. Instead, after receiving the challenge messages \((m_0,m_1)\) from \({\mathcal {A}}\), it computes \(\mathsf {CT}^* = ( \{{\mathsf {CT}}^*_i\}_{i\in [4]},\pi ^*)\) as an encryption of message \(m_0\) by following the honest encryption algorithm as in \(\mathsf {H}_1\) and \(\mathsf {H}_2\). Then, it sends two strings, namely \((0^\mathsf {len})\) and \(( \{{\mathsf {CT}}^*_i\}_{i\in [4]})\) to the outside challenger \(\mathcal {C}\). In return, \(\mathcal {A}_\mathsf {Com}\) receives a commitment \({\mathsf {Z}}\) corresponding to either the first or the second string. It then gives this to \({\mathcal {A}}\). Now, whatever bit b \({\mathcal {A}}\) guesses, \(\mathcal {A}_\mathsf {Com}\) forwards the same guess to the outside challenger \(\mathcal {C}\). Clearly, \(\mathcal {A}_\mathsf {Com}\) is a polynomial time algorithm and breaks the hiding property of \({\mathsf {Com}}\) unless \(\mathsf {H}_1 \approx _c\mathsf {H}_2.\)
Lemma 2
(\(\mathsf {H}_5 \approx _c\mathsf {H}_6).\) Assuming that \({\mathsf {FE}}\) is a \(\mathsf {Sel-IND}\) secure functional encryption scheme, the outputs of experiments \(\mathsf {H}_5\) and \(\mathsf {H}_6\) are computationally indistinguishable.
Proof
The only difference between the two hybrids is the manner in which the challenge ciphertext is created. More specifically, in \(\mathsf {H}_5\), the fourth component of the challenge ciphertext \(\mathsf {CT}^*_4\) is computed as an encryption of message \(m_0\), while in \(\mathsf {H}_6\), \(\mathsf {CT}^*_4\) is computed as an encryption of message \(m_1\). Note that the proof \(\pi ^*\) remains same in both the hybrids.
Let’s consider the following adversary \(\mathcal {A}_{\mathsf {FE}}\) that interacts with a challenger \(\mathcal {C}\) to break the security of the underlying \({\mathsf {FE}}\) scheme. Also, internally, it acts as the challenger in the security game with an adversary \({\mathcal {A}}\) that tries to distinguish between \(\mathsf {H}_5\) and \(\mathsf {H}_6\). \(\mathcal {A}_\mathsf {FE}\) executes the hybrid \(\mathsf {H}_5\) except that it does not generate the parameters \((\mathsf {MPK}_4,\mathsf {MSK}_4)\) itself. It sets \((\mathsf {MPK}_4)\) to be the public key given by the challenger \(\mathcal {C}\). After receiving the challenge messages \((m_0,m_1)\) from \({\mathcal {A}}\), it forwards the pair \((m_0,m_1)\) to the challenger \(\mathcal {C}\) and receives a ciphertext \({\mathsf {CT}}\) which is either an encryption of \(m_0\) or \(m_1\) using public key  . \(\mathcal {A}_\mathsf {FE}\) sets \(\mathsf {CT}^*_4 = \mathsf {CT}\) and computes \(\mathsf {CT}^* = ( \{{\mathsf {CT}}^*_i\}_{i\in [4]},\pi ^*)\) as the challenge ciphertext as in \(\mathsf {H}_5\). Note that proof \(\pi ^*\) is proved for statement 2 of relation R. It then sets the public parameter \(\mathsf {Z}= \mathsf {Com}( \{{\mathsf {CT}}^*_i\}_{i\in [4]};u)\) and sends the master public key \({\mathsf {MPK}}\) and the challenge ciphertext \(\mathsf {CT}^*\) to \({\mathcal {A}}\).
. \(\mathcal {A}_\mathsf {FE}\) sets \(\mathsf {CT}^*_4 = \mathsf {CT}\) and computes \(\mathsf {CT}^* = ( \{{\mathsf {CT}}^*_i\}_{i\in [4]},\pi ^*)\) as the challenge ciphertext as in \(\mathsf {H}_5\). Note that proof \(\pi ^*\) is proved for statement 2 of relation R. It then sets the public parameter \(\mathsf {Z}= \mathsf {Com}( \{{\mathsf {CT}}^*_i\}_{i\in [4]};u)\) and sends the master public key \({\mathsf {MPK}}\) and the challenge ciphertext \(\mathsf {CT}^*\) to \({\mathcal {A}}\).
Now, whatever bit b \({\mathcal {A}}\) guesses, \(\mathcal {A}_\mathsf {FE}\) forwards the same guess to the outside challenger \(\mathcal {C}\). Clearly, \(\mathcal {A}_\mathsf {FE}\) is a polynomial time algorithm and breaks the security of the functional encryption scheme \({\mathsf {FE}}\) unless \(\mathsf {H}_5 \approx _c\mathsf {H}_6.\)
5 Construction of Verifiable Secret Key Functional Encryption
In this section, we give a compiler from any \(\mathsf {Sel-IND}\) secure message hiding and function hiding secret key functional encryption scheme to a \(\mathsf {Sel-IND}\) secure message hiding and function hiding verifiable secret key functional encryption scheme. The resulting verifiable functional encryption scheme has the same security properties as the underlying one - that is, the resulting scheme is q-query secure if the original scheme that we started out with was q-query secure and so on, where q refers to the number of function secret key queries (or encryption queries) that the adversary is allowed to make. We prove the following theorem.
Theorem 6
Let \(\mathcal {F}= \{\mathcal {F}_\lambda \}_{\lambda \in \mathbb {N}}\) be a parameterized collection of functions. Then, assuming there exists a \(\mathsf {Sel-IND}\) secure message hiding and function hiding secret key functional encryption scheme \({\mathsf {FE}}\) for the class of functions \({\mathcal {F}}\), a non-interactive witness indistinguishable proof system, a non-interactive perfectly binding and computationally hiding commitment scheme, the proposed scheme \({\mathsf {VFE}}\) is a \(\mathsf {Sel-IND}\) secure message hiding and function hiding verifiable secret key functional encryption scheme for the class of functions \({\mathcal {F}}\) according to Definition 3.
Notation: Without loss of generality, let’s assume that every plaintext message is of length \(\lambda \) where \(\lambda \) denotes the security parameter of our scheme and that the length of every function in \(\mathcal {F}_\lambda \) is the same. Let \((\mathsf {Prove},\mathsf {Verify})\) be a non-interactive witness-indistinguishable (\({\mathsf {NIWI}}\)) proof system for NP, \(\mathsf {FE}= (\mathsf {FE.Setup},\mathsf {FE.Enc},\mathsf {FE.KeyGen},\mathsf {FE.Dec})\) be a \(\mathsf {Sel-IND}\) secure message hiding and function hiding secret key functional encryption scheme, \({\mathsf {Com}}\) be a statistically binding and computationally hiding commitment scheme. Without loss of generality, let’s say \({\mathsf {Com}}\) commits to a string bit-by-bit and uses randomness of length \(\lambda \) to commit to a single bit. We denote the length of ciphertexts in \({\mathsf {FE}}\) by  . Let the length of every function secret key in \({\mathsf {FE}}\) be
. Let the length of every function secret key in \({\mathsf {FE}}\) be  . Let
. Let  and
and  .
.
Our scheme \(\mathsf {VFE}= (\mathsf {VFE.Setup},\mathsf {VFE.Enc},\mathsf {VFE.KeyGen},\mathsf {VFE.Dec},\mathsf {VFE.VerifyCT},\)
\(\mathsf {VFE.VerifyK})\) is as follows:
-
Setup \(\mathsf {VFE.Setup}(1^\lambda )\) : The setup algorithm does the following:
-
1.
For all \(i \in [5]\), compute \((\mathsf {MSK}_i) \leftarrow \mathsf {FE.Setup}(1^\lambda ;p_i)\) and \(\mathsf {S}_i = \mathsf {Com}(\mathsf {MSK}_i;s_i)\) using randomness \(s_i\).
-
2.
Set \(\mathsf {Z_{CT}}= \mathsf {Com}(0^\mathsf {len}_{CT};a)\) and \(\mathsf {Z_{f}}= \mathsf {Com}(0^\mathsf {len}_f;b)\) where a, b represents the randomness used in the commitments.
-
3.
For all \(i \in [3]\), set \(\mathsf {Z}_i = \mathsf {Com}(1;u_i)\) where \(u_i\) represents the randomness used in the commitment. Let’s denote
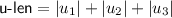 .
.
The public parameters are \(\mathsf {PP}= (\{\mathsf {S}_i\}_{i\in [5]},\mathsf {Z_{CT}},\mathsf {Z_{f}},\{\mathsf {Z}_i\}_{i\in [3]})\). The master secret key is \(\mathsf {MSK}= ( \{ {\mathsf {MSK}}_i\}_{i\in [5]},\{p_i\}_{i\in [5]},\{s_i\}_{i\in [5]},a,b,\{u_i\}_{i\in [3]})\).
-
1.
-
Encryption \(\mathsf {VFE.Enc}(\mathsf {PP},\mathsf {MSK},m)\) : To encrypt a message m, the encryption algorithm does the following:
-
1.
For all \( i \in [5]\), compute \(\mathsf {CT}_i = \mathsf {FE.Enc}(\mathsf {MSK}_i,m;r_i)\).
-
2.
Compute a proof \(\pi \leftarrow \mathsf {Prove}(y,w)\) for the statement that \(y \in L\) using witness w where: \(y= ( \{ {\mathsf {CT}}_i\} _{i\in [5]},\mathsf {PP})\), \(w = (m,\mathsf {MSK},\{r_i\}_{i\in [5]},0^2,5,0)\). L is defined corresponding to the relation R defined below.
-
1.
-
Relation R: Instance: \(y=( \{ {\mathsf {CT}}_i\} _{i\in [5]},\mathsf {PP})\) Witness: \(w = (m,\mathsf {MSK},\{r_i\}_{i\in [5]},i_1,i_2,j,k)\) \(R_1(y,w)=1\) if and only if either of the following conditions hold:
-
1.
4 out of the 5 constituent ciphertexts (except index j) encrypt the same message and are constructed using honestly generated secret keys. Also, \(\mathsf {Z}_1\) is a commitment to 1. That is,
-
(a)
\(\forall i \in [5]/\{j\}\), \(\mathsf {CT}_i = \mathsf {FE.Enc}(\mathsf {MSK}_i,m;r_i)\).
-
(b)
\(\forall i \in [5]/\{j\}\), \(\mathsf {S}_i = \mathsf {Com}(\mathsf {MSK}_i;s_i)\) and \(\mathsf {MSK}_i \leftarrow \mathsf {FE.Setup}(1^\lambda ;p_i)\)
-
(c)
\(\mathsf {Z}_1 = \mathsf {Com}(1;u_1)\)
(OR)
-
(a)
-
2.
2 constituent ciphertexts (corresponding to indices \(i_1,i_2\)) encrypt the same message and are constructed using honestly generated secret keys. \({\mathsf {Z_{CT}}}\) is a commitment to all the constituent ciphertexts, \(\mathsf {Z}_2\) is a commitment to 0 and \(\mathsf {Z}_3\) is a commitment to 1. That is,
-
(a)
\(\forall i \in \{\i _1,i_2\}\), \(\mathsf {CT}_{i} = \mathsf {FE.Enc}(\mathsf {MSK}_{i},m;r_{i})\).
-
(b)
\(\forall i \in \{\i _1,i_2\}\), \(\mathsf {S}_i = \mathsf {Com}(\mathsf {MSK}_i;s_i)\) and \(\mathsf {MSK}_i \leftarrow \mathsf {FE.Setup}(1^\lambda ;p_i)\)
-
(c)
\(\mathsf {Z_{CT}}= \mathsf {Com}( \{ {\mathsf {CT}}_i\} _{i\in [5]};a).\)
-
(d)
\(\mathsf {Z}_2 = \mathsf {Com}(0;u_2).\)
-
(e)
\(\mathsf {Z}_3 = \mathsf {Com}(1;u_3).\)
(OR)
-
(a)
-
3.
4 out of 5 constituent ciphertexts (except for index k) encrypt the same message and are constructed using honestly generated secret keys. \({\mathsf {Z_{f}}}\) is a commitment to a set of function secret keys \({\mathsf {K}}\) such that each constituent function secret key in \({\mathsf {K}}\) when decrypted with the corresponding ciphertext gives the same output . That is,
-
(a)
\(\forall i \in [5]/\{k\}\), \(\mathsf {CT}_{i} = \mathsf {FE.Enc}(\mathsf {MSK}_{i},m;r_{i})\).
-
(b)
\(\forall i \in [5]/\{k\}\), \(\mathsf {S}_i = \mathsf {Com}(\mathsf {MSK}_i;s_i)\) and \(\mathsf {MSK}_i \leftarrow \mathsf {FE.Setup}(1^\lambda ;p_i)\)
-
(c)
\(\mathsf {Z_{f}}= \mathsf {Com}( \{{\mathsf {K}}_i\} _{i\in [5]};b).\)
-
(d)
\(\exists x \in \mathcal {X}_\lambda \) such that \(\forall i \in [5]\), \(\mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}_i) = x\)
-
(a)
The output of the algorithm is the ciphertext \(\mathsf {CT}= ( \{ {\mathsf {CT}}_i\} _{i\in [5]},\pi )\). \(\pi \) is computed for statement 1 of relation R.
-
1.
-
Key Generation \(\mathsf {VFE.KeyGen}(\mathsf {PP},\mathsf {MSK},f)\) :
To generate the function secret key \({\mathsf {K}^f}\) for a function f, the key generation algorithm does the following:
-
1.
\(\forall i \in [5]\), compute \(\mathsf {K}^f_i = \mathsf {FE.KeyGen}(\mathsf {MSK}_i,f;r_i)\).
-
2.
Compute a proof \(\gamma \leftarrow \mathsf {Prove}(y,w)\) for the statement that \(y \in L_1\) using witness w where: \(y=( \{{\mathsf {K}}^f_i\} _{i\in [5]},\mathsf {PP})\), \(w = (f,\mathsf {MSK},\{r_i\}_{i\in [5]},0^3,5,0)\). \(L_1\) is defined corresponding to the relation \(R_1\) defined below.
-
1.
-
Relation \(R_1\): Instance: \(y=( \{{\mathsf {K}}^f_i\} _{i\in [5]},\mathsf {PP})\). Witness: \(w = (f,\mathsf {MSK},\{r_i\}_{i\in [5]},i_1,i_2,j,k)\) \(R_1(y,w)=1\) if and only if either of the following conditions hold:
-
1.
4 out of 5 constituent function secret keys (except index j) are keys for the same function and are constructed using honestly generated secret keys. Also, \(\mathsf {Z}_2\) is a commitment to 1. That is,
-
(a)
\(\forall i \in [5]/\{j\}\), \(\mathsf {K}^f_i = \mathsf {FE.KeyGen}(\mathsf {MSK}_i,f;r_i)\).
-
(b)
\(\forall i \in [5]/\{j\}\), \(\mathsf {S}_i = \mathsf {Com}(\mathsf {MSK}_i;s_i)\) and \(\mathsf {MSK}_i \leftarrow \mathsf {FE.Setup}(1^\lambda ;p_i)\)
-
(c)
\(\mathsf {Z}_2 = \mathsf {Com}(1;u_1)\)
(OR)
-
(a)
-
2.
4 out of 5 constituent function secret keys (except index k) are keys for the same function and are constructed using honestly generated secret keys. \({\mathsf {Z_{CT}}}\) is a commitment to a set of ciphertexts \({\mathsf {CT}}\) such that each constituent ciphertext in \({\mathsf {CT}}\) when decrypted with the corresponding function secret key gives the same output . That is,
-
(a)
\(\forall i \in [5]/\{k\}\), \(\mathsf {K}^f_{i} = \mathsf {FE.KeyGen}(\mathsf {MSK}_{i},f;r_{i})\).
-
(b)
\(\forall i \in [5]/\{k\}\), \(\mathsf {S}_i = \mathsf {Com}(\mathsf {MSK}_i;s_i)\) and \(\mathsf {MSK}_i \leftarrow \mathsf {FE.Setup}(1^\lambda ;p_i)\)
-
(c)
\(\mathsf {Z_{CT}}= \mathsf {Com}(\mathsf {CT};a).\)
-
(d)
\(\exists x \in \mathcal {X}_\lambda \) such that \(\forall i \in [5]\), \(\mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}^f_i) = x\)
(OR)
-
(a)
-
3.
2 constituent function secret keys (corresponding to indices \(i_1,i_2\)) are keys for the same function and are constructed using honestly generated secret keys. \({\mathsf {Z_{f}}}\) is a commitment to all the constituent function secret keys, \(\mathsf {Z}_1\) is a commitment to 0 and \(\mathsf {Z}_3\) is a commitment to 0. That is,
-
(a)
\(\forall i \in \{\i _1,i_2\}\), \(\mathsf {K}^f_{i} = \mathsf {FE.KeyGen}(\mathsf {MSK}_{i},f;r_{i})\).
-
(b)
\(\forall i \in \{\i _1,i_2\}\), \(\mathsf {S}_i = \mathsf {Com}(\mathsf {MSK}_i;s_i)\) and \(\mathsf {MSK}_i \leftarrow \mathsf {FE.Setup}(1^\lambda ;p_i)\)
-
(c)
\(\mathsf {Z_{f}}= \mathsf {Com}( \{{\mathsf {K}}^f_i\} _{i\in [5]};b).\)
-
(d)
\(\mathsf {Z}_1 = \mathsf {Com}(0;u_1).\)
-
(e)
\(\mathsf {Z}_3 = \mathsf {Com}(0;u_3).\)
-
(a)
The output of the algorithm is the function secret key \(\mathsf {K}^f= ( \{{\mathsf {K}}^f_i\} _{i\in [5]},\gamma )\). \(\gamma \) is computed for statement 1 of relation \(R_1\).
-
1.
-
Decryption \(\mathsf {VFE.Dec}(\mathsf {PP},\mathsf {K}^f,\mathsf {CT})\) : This algorithm decrypts the ciphertext \(\mathsf {CT}= ( \{ {\mathsf {CT}}_i\} _{i\in [5]},\pi )\) using function secret key \(\mathsf {K}^f= ( \{{\mathsf {K}}^f_i\} _{i\in [5]},\gamma )\) in the following way:
-
1.
Let \(y= ( \{ {\mathsf {CT}}_i\} _{i\in [5]},\mathsf {PP})\) be the statement corresponding to proof \(\pi \). If \(\mathsf {Verify}(y,\pi )=0\), then stop and output \(\bot \). Else, continue to the next step.
-
2.
Let \(y_1=( \{{\mathsf {K}}^f_i\} _{i\in [5]},\mathsf {PP})\) be the statement corresponding to proof \(\gamma \). If \(\mathsf {Verify}(y_1,\gamma )=0\), then stop and output \(\bot \). Else, continue to the next step.
-
3.
For \(i \in [5]\), compute \(m_i = \mathsf {FE.Dec}(\mathsf {CT}_i,\mathsf {K}^f_i)\). If at least 3 of the \(m_i\)’s are equal (let’s say that value is m), output m. Else, output \(\bot \).
-
1.
-
VerifyCT \(\mathsf {VFE.VerifyCT}(\mathsf {PP},\mathsf {CT})\) : Given a ciphertext \(\mathsf {CT}=( \{ {\mathsf {CT}}_i\} _{i\in [5]},\pi )\), this algorithm checks whether the ciphertext was generated correctly using the master secret key corresponding to the public parameters \({\mathsf {PP}}\). Let \(y= ( \{ {\mathsf {CT}}_i\} _{i\in [5]},\mathsf {PP})\) be the statement corresponding to proof \(\pi \). If \(\mathsf {Verify}(y,\pi )=1\), it outputs 1. Else, it outputs 0.
-
VerifyK \(\mathsf {VFE.VerifyK}(\mathsf {PP},\mathsf {K})\) : Given a function secret key \(\mathsf {K}= ( \{{\mathsf {K}}_i\} _{i\in [5]},\gamma )\), this algorithm checks whether the key was generated correctly for some function using the master secret key corresponding to public parameters \({\mathsf {PP}}\). Let \(y=( \{{\mathsf {K}}_i\} _{i\in [5]},\mathsf {PP})\) be the statement corresponding to proof \(\gamma \). If \(\mathsf {Verify}(y,\gamma )=1\), it outputs 1. Else, it outputs 0.
Correctness: Correctness follows directly from the correctness of the underlying FE scheme, correctness of the commitment scheme and the completeness of the \({\mathsf {NIWI}}\) proof system.
The proofs for verifiability and security can be found in the full version [5].
Verifiable Multi-Input Functional Encryption: We also study verifiability in the case of multi-input functional encryption. The construction (and proofs) of a verifiable multi-input functional encryption scheme are given in the full version [5].
6 Verifiable Indistinguishability Obfuscation
In this section, we first we recall the notion of indistinguishability obfuscation that was first proposed by [6] and then define the notion of verifiable indistinguishability obfuscation. For indistinguishability obfuscation, intuitively, we require that for any two circuits \(C_0\) and \(C_1\) that are “functionally equivalent" (i.e. for all inputs x in the domain, \(C_0(x) = C_1(x)\), the obfuscation of \(C_0\) must be computationally indistinguishable from the obfuscation of \(C_1\). Below, we present the formal definition following the syntax of [14].
Definition 5
(Indistinguishability Obfuscation). A uniform PPT machine \({\mathsf {i}\mathcal {O}}\) is called an indistinguishability obfuscator for a circuit class \(\{\mathcal {C}_\lambda \}_{\lambda \in \mathbb {N}}\) if the following conditions are satisfied:
-
Functionality:
For every \(\lambda \in \mathbb {N}\), every \(C \in \mathcal {C}_\lambda \) , every input x to C:
$$Pr[(\mathsf {i}\mathcal {O}(C))(x) \ne C(x)] <= negl(|C|),$$where the probability is over the coins of \({\mathsf {i}\mathcal {O}}\).
-
Polynomial Slowdown:
There exists a polynomial q such that for every \(\lambda \in \mathbb {N}\) and every \(C \in \mathcal {C}_\lambda \), we have that \(|\mathsf {i}\mathcal {O}(C)| <= q(|C|).\)
-
Indistinguishability:
For all PPT distinguishers \({\mathsf {D}}\), there exists a negligible function \(\alpha \) such that for every \(\lambda \in \mathbb {N}\), for all pairs of circuits \(C_0 , C_1 \in \mathcal {C}_\lambda \), we have that if \(C_0(x) = C_1(x)\) for all inputs x, then
$$ |Pr[D(\mathsf {i}\mathcal {O}(C_0))] - Pr[ D(\mathsf {i}\mathcal {O}(C_1))] | <= \alpha (\lambda ).$$
Definition 6
(\((L,\mathcal {C})-\)Restricted Verifiable Indistinguishability Obfuscation). Let \(\mathcal {C}=\lbrace \mathcal {C}_{\lambda } \rbrace _{\lambda \in \mathbb {N}}\) denote an ensemble where each \(\mathcal {C}_{\lambda }\) is a finite collection of circuits. Let L be any language in NP defined by a relation R satisfying the following two properties:
-
1.
For any two circuits \(C_0,C_1\in \mathcal {C}\), if there exists a string w such that \(R(C_0,C_1,w)=1\), then \(C_0\) is equivalent to \(C_1\).
-
2.
For any circuit \(C\in \mathcal {C}\), \(R(C,C,0)=1\).
Let \(\mathcal {X}_{\lambda }\) be the ensemble of inputs to circuits in \(\mathcal {C}_{\lambda }\). Let \(\mathcal {P}= \lbrace \mathcal {P}_{\lambda } \rbrace _{\lambda \in \mathbb {N}}\) be an ensemble where each \(\mathcal {P}_\lambda \) is a collection of predicates and each predicate \(\mathsf {P}\in \mathcal {P}_\lambda \) takes as input a circuit \(C \in \mathcal {C}_\lambda \) and outputs a bit. A verifiable indistinguishability obfuscation scheme consists of the following algorithms:
-
\(\mathsf {vi}\mathcal {O}(1^\lambda ,C,P\in \mathcal {P}_{\lambda }) \rightarrow \widehat{C}\). \({\mathsf {vi}\mathcal {O}}\) is a PPT algorithm that takes as input a security parameter \(\lambda \), a circuit \(C \in \mathcal {C}_\lambda \) and a predicate \({\mathsf {P}}\) in \(\mathcal {P}_\lambda \). It outputs an obfuscated circuit \(\widehat{C}\).
-
\(\mathsf {Eval}(\widehat{C},x,P\in \mathcal {P}_{\lambda }) \rightarrow y\). \(\mathsf {Eval}_{P}\) is a deterministic algorithm that takes as input an obfuscation \(\widehat{C}\), an input x and a predicate \({\mathsf {P}}\) in \(\mathcal {P}_\lambda \). It outputs a string y.
The scheme must satisfy the following properties:
-
Functionality:
For every \(\lambda \in \mathbb {N}\), every \(C \in \mathcal {C}_\lambda \), every \(\mathsf {P}\in \mathcal {P}_\lambda \) such that \(\mathsf {P}(C)=1\) and every input x to C:
$$Pr[\mathsf {Eval}(\mathsf {vi}\mathcal {O}(\lambda ,C,P),x,P) \ne C(x)] = 0 ,$$where the probability is over the coins of \({\mathsf {vi}\mathcal {O}}\).
-
Polynomial Slowdown:
There exists a polynomial q such that for every \(\lambda \in \mathbb {N}\), every \(C \in \mathcal {C}_\lambda \) and every \(\mathsf {P}\in \mathcal {P}_\lambda \), we have that \(|\mathsf {vi}\mathcal {O}(\lambda ,C,\mathsf {P})| <= q(|C|+|\mathsf {P}|+\lambda )\). We also require that the running time of Eval on input \((\widehat{C},x,\mathsf {P})\) is polynomially bounded in \(|P|+\lambda +|\widehat{C}|\)
-
Indistinguishability:
We define indistinguishability with respect to two adversaries \(\mathcal {A}=(\mathcal {A}_1,\mathcal {A}_2)\). We place no restriction on the running time of \(\mathcal {A}_1\). On input \(1^{\lambda }\) \(\mathcal {A}_1\) outputs two equivalent circuits \((C_0,C_1)\) in \(\mathcal {C}_{\lambda }\), such that \((C_0,C_1)\in L\). For all PPT distinguishers \(\mathcal {A}_2\), there exists a negligible function \(\alpha \) such that for every \(\lambda \in N\), for pairs of circuits \((C_0 , C_1)\) and for all predicates \(\mathsf {P}\in \mathcal {P}_\lambda \), we have that if \(C_0(x) = C_1(x)\) for all inputs x and \(\mathsf {P}(C_0) = \mathsf {P}(C_1)\), then
$$ |Pr[\mathcal {A}_2(\mathsf {vi}\mathcal {O}(\lambda ,C_0,P))] - Pr[ \mathcal {A}_2(\mathsf {vi}\mathcal {O}(\lambda ,C_1,P))] | \le \mathsf {negl}(\lambda )$$ -
Verifiability: In addition to the above algorithms, there exists an additional deterministic polynomial time algorithm \(\mathbf {VerifyO}\) that takes as input a string in \(\{ 0,1 \}^{*}\) and a predicate \(\mathsf {P}\in \mathcal {P}_\lambda \). It outputs 1 or 0. We say that the obfuscator \({\mathsf {vi}\mathcal {O}}\) is verifiable if: For any \(\mathsf {P}\in \mathcal {P}_\lambda \) and \(\widehat{C}\in \{0,1\}^*\) , if \(\mathbf {VerifyO}(\widehat{C},\mathsf {P})=1\), then there exists a circuit \(C \in \mathcal {C}_\lambda \) such that \(P(C)=1\) and for all \(x \in \mathcal {X}_\lambda \), \(\mathsf {Eval}(\widehat{C},x,\mathsf {P})=C(x)\).
6.1 Construction
Let \(\mathcal {C}=\{\mathcal {C}\}_\lambda \) be the set of all polynomial sized circuits and let \(L_{eq}\) be an NP language given by some relation \(\mathsf {R}_{eq}\).
Relation \(\mathsf {R_{eq}}\):
Instance: \(C',D'\)
Witness: \(\gamma \)
\(\mathsf {R}_{eq}(C',D',\pi )=1\) implies that:
-
1.
\(C'=D'\in \mathcal {C}_{\lambda }\) for some \(\lambda \in \mathbb {N}\). That is, both circuits are equal. (OR)
-
2.
\(C',D'\in \mathcal {C}_{\lambda }\), and there exists a witness \(\gamma \) of size \(\mathsf {poly}(|C'|,|D'|)\) proving that \(C'\) is functionally equivalent to \(D'\).
We now construct an \((L_{eq},\mathcal {C})-\)restricted verifiable indistinguishability obfuscation scheme. Let \({\mathsf {i}\mathcal {O}}\) be a perfectly correct indistinguishability obfuscator and \((\mathsf {Prove}, \mathsf {Verify})\) be a \(\mathsf {NIWI}\) for NP. Formally, we prove the following theorem:
Theorem 7
Assuming \(\mathsf {NIWI}\) is a witness indistinguishable proof system and \({\mathsf {i}\mathcal {O}}\) is a secure indistinguishability obfuscator for \(\mathcal {C}_{\lambda }\), the proposed scheme \({\mathsf {vi}\mathcal {O}}\) is a secure \((L_{eq},\mathcal {C})-\)restricted verifiable indistinguishability obfuscator.
 : The obfuscator does the following.
: The obfuscator does the following.
-
Compute \(C^i=\mathsf {i}\mathcal {O}(C;r_i)\) \(\forall i\in [3]\).
-
Compute a \(\mathsf {NIWI}\) proof \(\pi \) for the following statement \((\mathsf {P},C^1,C^2,C^3)\in L\) using witness \((1,2,C,C,r_1,r_2,0)\) where L is an NP language defined by the following relation \(\mathsf {R_1}\) where Relation \(\mathsf {R_1}\) Instance: \(y = (\mathsf {P},C^1,C^2,C^3)\) Witness: \(w = (i,j,C_i,C_j,r_i,r_j,\gamma )\) \(\mathsf {R_1}(y,w)=1\) if and only if:
-
1.
\(C^i=\mathsf {i}\mathcal {O}(C_i;r_i)\) and \(C^j=\mathsf {i}\mathcal {O}(C_j;r_j)\) where \(i\ne j\) and \(i,j\in [3]\). (AND)
-
2.
\(\mathsf {P}(C^i)=\mathsf {P}(C^j)=1\) (AND)
-
3.
\(R_{eq}(C_i,C_j,\gamma )=1\).
-
1.
-
Output \((C^1,C^2,C^3,\pi )\) as the obfuscation.
 To evaluate:
To evaluate:
-
Verify the proof \(\pi \). Output \(\bot \) if the verification fails.
-
Otherwise, output the majority of \(\{ C^i(x)\}_{i\in [3]}\).
We now investigate the properties of this scheme.
Correctness: By completeness of \(\mathsf {NIWI}\) and correctness of the obfuscator \({\mathsf {i}\mathcal {O}}\) it is straightforward to see that our obfuscator is correct.
Verifiability: We now present the algorithm \(\mathbf {VerifyO}\). It takes as input an obfuscation \((C^1,C^2,C^3,\pi )\) and a predicate \({\mathsf {P}}\). It outputs 1 if \(\pi \) verifies and 0 otherwise. Note that if \(\pi \) verifies then there are two indices \(i,j\in [3]\) such that \(C^i\) (\(C^j\)) is an \({\mathsf {i}\mathcal {O}}\) obfuscation of some circuit \(C_i\) (\(C_j\)) and it holds that \(\mathsf {P}(C_i)=\mathsf {P}(C_j)=1\). Also, either \(C_i=C_j\) or \(C_i\) is equivalent to \(C_j\) (due to the soundness of \(\mathsf {NIWI}\)). Hence, the evaluate algorithm always outputs \(C_i(x)\) on any input x due to perfect correctness of \({\mathsf {i}\mathcal {O}}\).
Security Proof: Let \({\mathsf {P}}\) be a predicate and \((C_0,C_1)\) be any two equivalent circuits in \(\mathcal {C}_{\lambda }\) such that \(P(C_0)=P(C_1)=1\) and there exists a string \(\gamma _1\) such that \(\mathsf {R_{eq}}(C_0,C_1,\gamma _1)=1\). Let \((C^1,C^2,C^3,\pi )\) be the challenge obfuscated circuit. We now define indistinguishable hybrids such that the first hybrid (\(\mathsf {Hybrid_0}\)) corresponds to the real world security game where the challenger obfuscates \(C_0\) and the final hybrid (\(\mathsf {Hybrid_5}\)) corresponds to the security game where the challenger obfuscates \(C_1\).
-
\(\mathbf {Hybrid_0:}\) In this hybrid, \(C^i=\mathsf {i}\mathcal {O}(C_0;r_i)\) \(\forall i\in [3]\) and \((1,2,C_0,C_0,r_1,r_2,0)\) is used as a witness to compute \(\pi \).
-
\(\mathbf {Hybrid_1:}\) This hybrid is same as the previous hybrid except that \(C^3\) is computed as \(C^3=\mathsf {i}\mathcal {O}(C_1;r_3)\).
-
\(\mathbf {Hybrid_2:}\) This hybrid is same as the previous hybrid except that the witness used to compute \(\pi \) is\((1,3,C_0,C_1,r_1,r_2,\gamma _1)\) where \(\gamma _1\) is the witness for the statement \((C_0,C_1)\in L_{eq}\).
-
\(\mathbf {Hybrid_3:}\) This hybrid is identical to the previous hybrid except that \(C^2\) is computed as \(C^2=\mathsf {i}\mathcal {O}(C_1;r_2)\).
-
\(\mathbf {Hybrid_4:}\) This hybrid is same as the previous hybrid except that the witness used to compute \(\pi \) is \((2,3,C_1,C_1,r_1,r_2,0)\).
-
\(\mathbf {Hybrid_5:}\) This hybrid is identical to the previous hybrid except that \(C^1=\mathsf {i}\mathcal {O}(C_1;r_1)\). This hybrid corresponds to the real world security game where the challenger obfuscates \(C_1\).
Now, we prove indistinguishability of the hybrids.
Lemma 3
Assuming \({\mathsf {i}\mathcal {O}}\) is a secure indistinguishability obfuscator for \(\mathcal {C}_{\lambda }\), \(\mathsf {Hybrid_0}\) is computationally indistinguishable from \(\mathsf {Hybrid_1}\).
Proof
Note that the only difference between \(\mathsf {Hybrid_0}\) and \(\mathsf {Hybrid_1}\) is the way \(C^3\) is generated. In \(\mathsf {Hybrid_0}\), it is generated as an obfuscation of \(C_0\), while in \(\mathsf {Hybrid_1}\) it is generated as an obfuscation of \(C_1\). Since \(C_0\) and \(C_1\) are equivalent the lemma now follows from the security of \({\mathsf {i}\mathcal {O}}\).
Lemma 4
Assuming \(\mathsf {NIWI}\) is a witness indistinguishable proof system, \(\mathsf {Hybrid_1}\) is computationally indistinguishable from \(\mathsf {Hybrid_2}\).
Proof
Note that the only difference between \(\mathsf {Hybrid_1}\) and \(\mathsf {Hybrid_2}\) is the way in which \(\pi \) is generated. In \(\mathsf {Hybrid_1}\) it uses \((1,2,C_0,C_0,r_1,r_2,0)\) as its witness while in \(\mathsf {Hybrid_2}\) it uses \((1,3,C_0,C_1,r_1,r_2,\gamma _1)\) as its witness where \(\gamma _1\) is the witness for the instance \((C_0,C_1)\) satisfying the relation \(\mathsf {R_{eq}}\). The lemma now follows due to the witness indistinguishability of \(\mathsf {NIWI}\).
Lemma 5
Assuming \({\mathsf {i}\mathcal {O}}\) is a secure indistinguishability obfuscator for \(\mathcal {C}_{\lambda }\), \(\mathsf {Hybrid_2}\) is computationally indistinguishable from \(\mathsf {Hybrid_3}\).
Proof
The only difference between the two hybrids is that \(C^2\) is generated as an obfuscation of \(C_0\) in \(\mathsf {Hybrid_2}\) and as an obfuscation of \(C_1\) in \(\mathsf {Hybrid_3}\). Since \(C_0\) and \(C_1\) are equivalent the lemma now follows from the security of \({\mathsf {i}\mathcal {O}}\).
Lemma 6
Assuming \(\mathsf {NIWI}\) is a witness indistinguishable proof system, \(\mathsf {Hybrid_3}\) is computationally indistinguishable from \(\mathsf {Hybrid_4}\).
Proof
Note that the only difference between \(\mathsf {Hybrid_3}\) and \(\mathsf {Hybrid_4}\) is the way \(\pi \) is generated. In \(\mathsf {Hybrid_3}\) it uses \((1,3,C_0,C_1,r_1,r_3,\gamma _1)\) as its witness while in \(\mathsf {Hybrid_4}\) it uses \((2,3,C_1,C_1,r_2,r_3,0)\) as its witness where \(\gamma _1\) is the witness for the instance \((C_0,C_1)\) satisfying the relation \(\mathbf {R_{eq}}\). The lemma now follows due to the witness indistinguishability of \(\mathsf {NIWI}\).
Lemma 7
Assuming \({\mathsf {i}\mathcal {O}}\) is a secure indistinguishability obfuscator for \(\mathcal {C}_{\lambda }\), \(\mathsf {Hybrid_4}\) is computationally indistinguishable from \(\mathsf {Hybrid_5}\).
Proof
The only difference between the two hybrids is that \(C^1\) is generated as an obfuscation of \(C_0\) in \(\mathsf {Hybrid_4}\) and as an obfuscation of \(C_1\) in \(\mathsf {Hybrid_5}\). Since \(C_0\) and \(C_1\) are equivalent the lemma now follows from the security of \({\mathsf {i}\mathcal {O}}\).
Notes
- 1.
- 2.
A primitive with the same name was also defined in [8]. However, their setting is entirely different to ours. They consider a scenario where the authority as well as the encryptor are honest. Their goal is to convince a weak client that the decryption (performed by a potentially malicious cloud service provider) was done correctly using the actual ciphertext and function secret key.
- 3.
For instance, suppose that \(C_0\) uses an ordinary GGM PRF key, but \(C_1\) uses a punctured GGM PRF key. It is easy to verify that these two keys are equivalent by simply verifying each node in the punctured PRF tree of keys by repeated application of the underlying PRG.
References
Abdalla, M., Raykova, M., Wee, H.: Multi-input inner-product functional encryption from pairings. IACR Cryptology ePrint Archive 2016, 425 (2016). http://eprint.iacr.org/2016/425
Agrawal, S., Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption: new perspectives and lower bounds. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 500–518. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_28
Ananth, P., Jain, A.: Indistinguishability obfuscation from compact functional encryption. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 308–326. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_15
Ananth, P., Jain, A., Sahai, A.: Achieving compactness generically: Indistinguishability obfuscation from non-compact functional encryption. IACR Cryptology ePrint Archive 2015, 730 (2015). http://eprint.iacr.org/2015/730
Badrinarayanan, S., Goyal, V., Jain, A., Sahai, A.: Verifiable functional encryption. IACR Cryptology ePrint Arch. 2016, 629 (2016)
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_1
Barak, B., Ong, S.J., Vadhan, S.P.: Derandomization in cryptography. SIAM J. Comput. 37(2), 380–400 (2007). http://dx.doi.org/10.1137/050641958
Barbosa, M., Farshim, P.: Delegatable homomorphic encryption with applications to secure outsourcing of computation. In: Dunkelman, O. (ed.) CT-RSA 2012. LNCS, vol. 7178, pp. 296–312. Springer, Heidelberg (2012). doi:10.1007/978-3-642-27954-6_19
Bitansky, N., Paneth, O.: ZAPs and non-interactive witness indistinguishability from indistinguishability obfuscation. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 401–427. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_16
Bitansky, N., Vaikuntanathan, V.: Indistinguishability obfuscation from functional encryption. In: FOCS (2015)
Boneh, D., Franklin, M.K.: Identity-based encryption from the weil pairing. SIAM J. Comput. 32(3), 586–615 (2003)
Boneh, D., Gentry, C., Gorbunov, S., Halevi, S., Nikolaenko, V., Segev, G., Vaikuntanathan, V., Vinayagamurthy, D.: Fully key-homomorphic encryption, arithmetic circuit abe and compact garbled circuits. In: Nguyen, P.Q., Oswald, E. (eds.) EUROCRYPT 2014. LNCS, vol. 8441, pp. 533–556. Springer, Heidelberg (2014). doi:10.1007/978-3-642-55220-5_30
Boneh, D., Sahai, A., Waters, B.: Functional encryption: definitions and challenges. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 253–273. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_16
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS (2013)
Goldwasser, S., Kalai, Y.T., Popa, R.A., Vaikuntanathan, V., Zeldovich, N.: Reusable garbled circuits and succinct functional encryption. In: STOC 2013 (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Functional encryption with bounded collusions via multi-party computation. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 162–179. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_11
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Attribute-based encryption for circuits. In: STOC 2013 (2013)
Gorbunov, S., Vaikuntanathan, V., Wee, H.: Predicate encryption for circuits from LWE. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 503–523. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_25
Goyal, V.: Reducing trust in the PKG in identity based cryptosystems. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 430–447. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74143-5_24
Goyal, V., Lu, S., Sahai, A., Waters, B.: Black-box accountable authority identity-based encryption. In: CCS (2008)
Goyal, V., Pandey, O., Sahai, A., Waters, B.: Attribute-based encryption for fine-grained access control of encrypted data. In: CCS (2006)
Groth, J., Ostrovsky, R., Sahai, A.: Non-interactive zaps and new techniques for NIZK. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 97–111. Springer, Heidelberg (2006). doi:10.1007/11818175_6
Katz, J., Sahai, A., Waters, B.: Predicate encryption supporting disjunctions, polynomial equations, and inner products. In: Smart, N. (ed.) EUROCRYPT 2008. LNCS, vol. 4965, pp. 146–162. Springer, Heidelberg (2008). doi:10.1007/978-3-540-78967-3_9
Libert, B., Ramanna, S., Yung, M.: Functional commitment schemes: From polynomial commitments to pairing-based accumulators from simple assumptions. In: ICALP 2016 (2016)
Okamoto, T., Takashima, K.: Fully secure functional encryption with general relations from the decisional linear assumption. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 191–208. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_11
O’Neill, A.: Definitional issues in functional encryption. IACR Cryptology ePrint Archive 2010, 556 (2010). http://eprint.iacr.org/2010/556
Sahai, A., Seyalioglu, H.: Worry-free encryption: functional encryption with public keys. In: CCS (2010)
Sahai, A., Seyalioglu, H.: Fully secure accountable-authority identity-based encryption. In: Catalano, D., Fazio, N., Gennaro, R., Nicolosi, A. (eds.) PKC 2011. LNCS, vol. 6571, pp. 296–316. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19379-8_19
Sahai, A., Waters, B.: Fuzzy identity-based encryption. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 457–473. Springer, Heidelberg (2005). doi:10.1007/11426639_27
Sahai, A., Waters, B.: Slides on functional encryption, powerpoint presentation (2008). http://www.cs.utexas.edu/~bwaters/presentations/files/functional.ppt
Takashima, K.: Expressive attribute-based encryption with constant-size ciphertexts from the decisional linear assumption. In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 298–317. Springer, Heidelberg (2014). doi:10.1007/978-3-319-10879-7_17
Waters, B.: Efficient identity-based encryption without random oracles. In: Cramer, R. (ed.) EUROCRYPT 2005. LNCS, vol. 3494, pp. 114–127. Springer, Heidelberg (2005). doi:10.1007/11426639_7
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Badrinarayanan, S., Goyal, V., Jain, A., Sahai, A. (2016). Verifiable Functional Encryption. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10032. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53890-6_19
Download citation
DOI: https://doi.org/10.1007/978-3-662-53890-6_19
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53889-0
Online ISBN: 978-3-662-53890-6
eBook Packages: Computer ScienceComputer Science (R0)





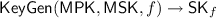 . The key generation algorithm takes as input a function
. The key generation algorithm takes as input a function 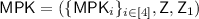 . The master secret key is
. The master secret key is 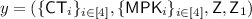 ,
, 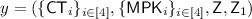 Witness:
Witness: 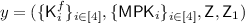 ,
, 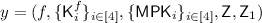 . Witness:
. Witness: 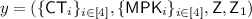 be the statement corresponding to proof
be the statement corresponding to proof 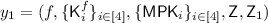 be the statement corresponding to proof
be the statement corresponding to proof 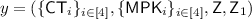 be the statement corresponding to proof
be the statement corresponding to proof 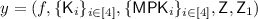 be the statement corresponding to proof
be the statement corresponding to proof 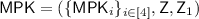 such that
such that 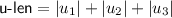 .
.