Abstract
We initiate the study of public-key encryption (PKE) secure against selective-opening attacks (SOA) in the presence of randomness failures, i.e., when the sender may (inadvertently) use low-quality randomness. In the SOA setting, an adversary can adaptively corrupt senders; this notion is natural to consider in tandem with randomness failures since an adversary may target senders by multiple means.
Concretely, we first treat SOA security of nonce-based PKE. After formulating an appropriate definition of SOA-secure nonce-based PKE, we provide efficient constructions in the non-programmable random-oracle model, based on lossy trapdoor functions.
We then lift our notion of security to the setting of “hedged” PKE, which ensures security as long as the sender’s seed, message, and nonce jointly have high entropy. This unifies the notions and strengthens the protection that nonce-based PKE provides against randomness failures even in the non-SOA setting. We lift our definitions and constructions of SOA-secure nonce-based PKE to the hedged setting as well.
You have full access to this open access chapter, Download conference paper PDF
Similar content being viewed by others
Keywords
These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.
1 Introduction
Imagine that an adversary wants to gain access to encrypted communication that various senders are transmitting to a receiver. There are various ways to go about doing this. One is to try to subvert the random-number generator used by the senders. Another is to break-in to the senders’ machines, possibly in an adaptive fashion. Encryption schemes resisting the first sort of attack have been studied in the context of security under randomness failures [3, 7, 10, 18, 23] while resistance to the second sort of attack corresponds to the notion of security against selective-opening attacks (SOA) [5, 9, 11, 14–16].Footnote 1 However, as far as we are aware, these notions have so far only been considered separately. We initiate the study of SOA-secure encryption in the presence of randomness failures, providing new definitions and constructions achieving these definitions in the public-key setting.
There are currently three main approaches in the literature to dealing with randomness failures for PKE: (1) deterministic PKE [2], which does not use randomness at all but guarantees security only if plaintexts have high entropy, (2) hedged PKE, which is randomized and guarantees security as long as plaintexts and the randomness jointly have high entropy, and (3) the recently introduced notion of nonce-based PKE by Bellare and Tackmann (BT) [10], where each sender uses a uniform seedFootnote 2 in addition to a nonce, and security is guaranteed if either the seed is secret and the nonces are unique, or the seed is revealed and the nonces have high entropy. Hedged PKE and nonce-based PKE are incomparable and are useful in different scenarios, and part of our contribution is to unify them into a single primitive. We start by adding consideration of SOA security to nonce-based PKE. We then lift the resulting notions to the setting of hedged PKE (which subsumes deterministic PKE) as well, thereby adding consideration of SOA to a unified primitive with the guarantees of both nonce-based and hedged PKE.
1.1 Our Results
Selective-opening security for nonce-based PKE. As explained above, the first notion we consider for protecting against randomness failures is nonce-based PKE, recently introduced by Bellare and Tackmann [10]. For consistency with the definitions of SOA security we introduce for later notions (where new technical challenges arise), we formulate an indistinguishability-based (rather than simulation-based) definition, which we call \(\text {N-SO-CPA}\), along the lines of the indistinguishability-based definition of SOA security for standard PKE [9]. Under our definition, the adversary can (i) learn the seeds of some senders, (ii) choose the nonces for all the other senders, as long as nonces of each individual sender do not repeat. Then, after seeing the ciphertexts, the adversary can adaptively corrupt some senders to learn their messages together with seeds and nonces. The definition asks that the adversary cannot distinguish between the plaintexts of the uncorrupted senders and a resampling of these plaintexts conditioned on the revealed plaintexts.
The next question is whether \(\text {N-SO-CPA}\) security is achievable. Throughout our work, we focus on constructions in the so-called non-programmable random-oracle model (NPROM) [20]. Intuitively, this means that in a security proof, the constructed adversary must honestly answer (i.e., cannot program) the random oracle queries of the assumed adversary. The NPROM is arguably closer to the standard (random oracle devoid) model than the programmable random oracle model (PROM), since real-world hash functions are not programmable. In this model, we give an efficient construction of \(\text {N-SO-CPA}\)-secureFootnote 3 nonce-based PKE based on any lossy trapdoor function [21]. The idea is to modify the nonce-based PKE scheme of Bellare and Tackmann, which encrypts a message m using public-key pk, seed xk, and nonce N by encrypting m using any standard (randomized) PKE scheme with public key pk and “synthetic” coins derived from a hash of (xk, N, m). Here, we use a specific randomized encryption scheme based on any lossy trapdoor function. The security proof of the resulting scheme, which we call \(\mathsf {NE1}\), relies on switching to the lossy key-generation algorithm and then using the random oracle to argue that the adversary’s choice of which senders to corrupt must be independent of the plaintexts.
SOA+hedged security for nonce-based PKE. Unlike nonce-based PKE, hedged PKE [3] guarantees security as long as the message and randomness used by the sender jointly have high entropy. Indeed, viewing the sender’s seed and nonce together as the sender’s randomness, nonce-based PKE as defined in [10] lacks such a guarantee. To get the best of both worlds, we would like to add such a guarantee to nonce-based PKE. This strengthens the protection provided against randomness failures even in the absence of SOA; however, sticking with the main theme of this work, we aim to achieve it in the SOA setting as well. This leads to a definition that we call \(\text {HN-SO-CPA}\), which incorporates both hedged and SOA security into the existing notion of nonce-based PKE.
Modeling SOA in the hedged setting is technically challenging. Indeed, Bellare et al. [4] recently showed that a simulation-based notion of SOA security for deterministic PKE (which is a special case of hedged PKE) is impossible to achieve. They also noted that a natural indistinguishability-based definition is (for different reasons) trivially impossible to achieve, and left open the problem of defining a meaningful (yet achievable) definition. To that end, we introduce a novel “comparison-based” definition of SOA for nonce-based PKE, inspired by the comparison-based definition of SOA for deterministic PKE [2, 6] combined with the indistinguishability-based definition of SOA for standard PKE [9]. Roughly, the definition requires that the adversary cannot predict any function of all the plaintexts (i.e., including those of the uncorrupted senders) with much better probability than by computing the same function on a resampling of all the plaintexts conditioned on the revealed plaintexts. For technical reasons, \(\text {HN-SO-CPA}\) does not protect partial information about the messages depending on the public key, so we still require \(\text {N-SO-CPA}\) to hold in addition.
We provide two approaches for achieving \(\text {HN-SO-CPA}+\text {N-SO-CPA}\)-secure nonce-based PKE. The first is a generic transform inspired by the “randomized-then-deterministic” transform of [3] in the setting of hedged security. Namely, we propose a “Nonce-then-Deterministic” (\(\mathsf {NtD}\)) transform in which one obtains a new nonce-based PKE scheme by composing an underlying nonce-based PKE scheme with a deterministic PKE scheme. We require that the underlying deterministic PKE scheme meet a corresponding special case of the \(\text {HN-SO-CPA}\) definition that we call \(\text {D-SO-CPA}\), and achieve it via a scheme \({\mathsf {DE1}}\) in the NPROM. Interestingly, the scheme \({\mathsf {DE1}}\) is exactly the recent construction of Bellare and Hoang [7], except that they assume the hash function is UCE-secure [8] and achieve standard security (not SOA). Again, the analysis is quite involved and deals with subtleties neither present in SOA for randomized PKE nor in prior work on deterministic PKE. Alternatively, we show that the scheme \(\mathsf {NE1}\) directly achieves both \(\text {HN-SO-CPA}\) and \(\text {N-SO-CPA}\) in the NPROM.
Separation results. Finally, to justify our developing new schemes in the setting of selective-opening security in the presence of randomness failures rather than using existing ones, we show that the \(\text {N-SO-CPA}\) and \(\text {D-SO-CPA}\) are not implied by the standard notions (non-SOA) of nonce-based PKE [10] and D-PKE [2], respectively. Our counter-examples rely on the recent result of Hofheinz, Rao, and Wichs (HRW) [15] that separates \(\mathrm {IND\text{- }CCA}\) security from SOA security for randomized PKE. We also show that \(\text {N-SO-CPA}\) does not imply \(\text {HN-SO-CPA}\) for nonce-based PKE, meaning the hedged security does strengthen the notion considered for nonce-based PKE in [10].
Open question. We leave obtaining standard-model (versus NPROM) schemes achieving our notions as an open question. Note that our \(\mathsf {NtD}\) transform is in the standard model, so if we had standard-model instantiations of the underlying primitives we would get a standard-model \(\text {HN-SO-CPA}+\text {N-SO-CPA}\)-secure nonce-based PKE as well.
1.2 Organization
In contrast to the order in which we explained the results above, in the main body of the paper we first present our results on SOA security for deterministic PKE, then move to our results on SOA security for nonce-based PKE, and then finally present our results on hedged security for SOA-secure nonce-based PKE. This is because the results for deterministic PKE constitute the technical core of our work, and form a basis for the results that follow.
2 Preliminaries
Notation and conventions. An adversary is an algorithm or tuple of algorithms. All algorithms may be randomized and are required to be efficient unless otherwise indicated; we let PPT stand for “probabilistic, polynomial time.” For an algorithm A we denote by  the experiment that runs A on the elided inputs with uniformly random coins and assigns the output to x, and
the experiment that runs A on the elided inputs with uniformly random coins and assigns the output to x, and  to denote the same experiment, but under the coins r instead of randomly chosen ones. If A is deterministic we denote this instead by
to denote the same experiment, but under the coins r instead of randomly chosen ones. If A is deterministic we denote this instead by  . We let \([A(\cdots )]\) denote the set of all possible outputs of A when run on the elided arguments. If S is a finite set then
. We let \([A(\cdots )]\) denote the set of all possible outputs of A when run on the elided arguments. If S is a finite set then  denotes choosing a uniformly random element from S and assigning it to s. We denote by \({\Pr }\left[ \, P(x)\,\, :\,\,\ldots \,\right] \) the probability that some predicate P is true of x after executing the elided experiment.
denotes choosing a uniformly random element from S and assigning it to s. We denote by \({\Pr }\left[ \, P(x)\,\, :\,\,\ldots \,\right] \) the probability that some predicate P is true of x after executing the elided experiment.
Let \({{\mathbb N}}\) denote the set of all non-negative integers. For any \(n \in {{\mathbb N}}\) we denote by [n] the set \(\{1,\ldots ,n\}\). For a vector \(\mathbf {x}\), we denote by \(|\mathbf {x}|\) its length (number of components) and by \(\mathbf {x}[i]\) its i-th component. For a vector \(\mathbf {x}\) of length n and any \(I \subseteq [n]\), we denote by \(\mathbf {x}[I]\) the vector of length |I| such that \(\mathbf {x}[I] = (\mathbf {x}[i])_{i \in I}\). For a string X, we let |X| denote its length. For any integer \(1 \le i \le j \le |X|\), we write X[i] to denote the ith bit of X, and X[i, j] the substring from the i-th to the j-th bit (inclusive) of X.
Public-key encryption. A public-key encryption scheme \({\mathsf {PKE}}\) with message space \({\mathsf {Msg}}\) is a tuple of algorithms \((\mathsf {Kg},\mathsf {Enc},\mathsf {Dec})\). The key-generation algorithm \(\mathsf {Kg}\) on input \(1^k\) outputs a public key \( pk \) and secret key \( sk \). The encryption algorithm \(\mathsf {Enc}\) on inputs a public key \( pk \) and message \(m \in {\mathsf {Msg}}(k)\) outputs a ciphertext c. The deterministic decryption algorithm \(\mathsf {Dec}\) on inputs a secret key \( sk \) and ciphertext c outputs a message m or \(\bot \). We require that for all \(( pk , sk ) \in [\mathsf {Kg}(1^k)]\) and all \(m \in {\mathsf {Msg}}(1^k)\), the probability that \(\mathsf {Dec}( sk ,(\mathsf {Enc}( pk ,m)) = m\) is 1. We say \({\mathsf {PKE}}\) is deterministic if \(\mathsf {Enc}\) is deterministic.
Lossy trapdoor function. A lossy trapdoor function [21] with domain \(\mathsf {LDom}\) and range \(\mathsf {LRng}\) is a tuple of algorithms \({\mathsf {LT}}= (\mathsf {LT.IKg}, \mathsf {LT.LKg}, \mathsf {LT.Eval}, \mathsf {LT.Inv})\) that work as follows. Algorithm \(\mathsf {LT.IKg}\) on input a unary encoding of the security parameter \(1^k\) outputs an “injective” evaluation key \( ek \) and matching trapdoor \( td \). Algorithm \(\mathsf {LT.LKg}\) on input \(1^k\) outputs a “lossy” evaluation key  . Algorithm \(\mathsf {LT.Eval}\) on inputs an (either injective or lossy) evaluation key \( ek \) and \(x \in \mathsf {LDom}(k)\) outputs \(y \in \mathsf {LRng}(1^k)\). Algorithm \(\mathsf {LT.Inv}\) on inputs a trapdoor \( td \) and a \(y' \in \mathsf {LRng}(k)\) outputs \(x' \in \mathsf {LDom}(k)\). We require the following properties.
. Algorithm \(\mathsf {LT.Eval}\) on inputs an (either injective or lossy) evaluation key \( ek \) and \(x \in \mathsf {LDom}(k)\) outputs \(y \in \mathsf {LRng}(1^k)\). Algorithm \(\mathsf {LT.Inv}\) on inputs a trapdoor \( td \) and a \(y' \in \mathsf {LRng}(k)\) outputs \(x' \in \mathsf {LDom}(k)\). We require the following properties.
Correctness: For all \(k \in {{\mathbb N}}\) and any \(( ek , td ) \in [\mathsf {LT.IKg}(1^k)]\), it holds that \(\mathsf {Inv}( td , \mathsf {LT.Eval}( ek ,x)) = x\) for every \(x \in \mathsf {LDom}(k)\).
Key indistinguishability: For every distinguisher D, the advantage \(\mathbf {Adv}^{\mathrm {ltdf}}_{{\mathsf {LT}},D}(k) =\)  is negligible.
is negligible.
Lossiness: The size of the co-domain of  is at most \(|\mathsf {LRng}(k)| / 2^{\tau (k)}\) for all \(k \in {{\mathbb N}}\) and all
is at most \(|\mathsf {LRng}(k)| / 2^{\tau (k)}\) for all \(k \in {{\mathbb N}}\) and all  . We call \(\tau \) the lossiness of \({\mathsf {LT}}\).
. We call \(\tau \) the lossiness of \({\mathsf {LT}}\).
If the function \(\mathsf {LT.Eval}( ek , \cdot )\) is a permutation for any \(k \in {{\mathbb N}}\) and any \(( ek , td ) \in [\mathsf {LT.IKg}(1^k)]\) then we call \({\mathsf {LT}}\) a lossy trapdoor permutation. Both RSA and Rabin are lossy trapdoor permutations under appropriate assumptions [19, 22].
Message samplers. A message sampler \({\mathcal M}\) is a PPT algorithm that takes as input \(1^k\) and a string  , and outputs a vector \(\mathbf {m}\) of messages and a vector \(\mathbf {a}\) of the same length. Each \(\mathbf {a}[i]\) is the auxiliary information that an adversary gains in addition to \(\mathbf {m}[i]\), if it breaks into the machine of the sender of \(\mathbf {m}[i]\). For example, if each \(\mathbf {m}[i]\) is a signature of some string \(\mathbf {x}[i]\), then the adversary may be able to obtain even \(\mathbf {x}[i]\) in its break-in. We require that \({\mathcal M}\) be associated with functions \(v(\cdot )\) and \(n(\cdot )\) such that for any
, and outputs a vector \(\mathbf {m}\) of messages and a vector \(\mathbf {a}\) of the same length. Each \(\mathbf {a}[i]\) is the auxiliary information that an adversary gains in addition to \(\mathbf {m}[i]\), if it breaks into the machine of the sender of \(\mathbf {m}[i]\). For example, if each \(\mathbf {m}[i]\) is a signature of some string \(\mathbf {x}[i]\), then the adversary may be able to obtain even \(\mathbf {x}[i]\) in its break-in. We require that \({\mathcal M}\) be associated with functions \(v(\cdot )\) and \(n(\cdot )\) such that for any  , for any \(k \in {{\mathbb N}}\), and any
, for any \(k \in {{\mathbb N}}\), and any  , we have \(|\mathbf {m}| = v(k)\) and \(|\mathbf {m}[i]| = n(k)\), for every \(i \le |\mathbf {m}|\).
, we have \(|\mathbf {m}| = v(k)\) and \(|\mathbf {m}[i]| = n(k)\), for every \(i \le |\mathbf {m}|\).
A message sampler \({\mathcal M}\) is \((\mu , d)\)-entropic if
-
For any \(k \in {{\mathbb N}}\), any \(I \subseteq \{1, \ldots , v(k)\}\) such that \(|I| \le d\), any
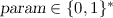 , and
, and 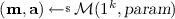 , conditioning on messages \(\mathbf {m}[I]\) and their auxiliary information \(\mathbf {a}[I]\) and
, conditioning on messages \(\mathbf {m}[I]\) and their auxiliary information \(\mathbf {a}[I]\) and 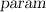 , each other message \(\mathbf {m}[j]\) (with \(j \in \{1, \ldots , v(k) \} \backslash I\)) must have conditional min-entropy at least \(\mu \). Note that here \((\mathbf {m}, \mathbf {a})\) is sampled independent of the set I.
, each other message \(\mathbf {m}[j]\) (with \(j \in \{1, \ldots , v(k) \} \backslash I\)) must have conditional min-entropy at least \(\mu \). Note that here \((\mathbf {m}, \mathbf {a})\) is sampled independent of the set I. -
Messages \(\mathbf {m}[1], \ldots , \mathbf {m}[|\mathbf {m}|]\) must be distinct, for any
 and any
and any  .
.
In this definition d can be \(\infty \), which corresponds to a message sampler in which the conditional distribution of each message, given  and all other messages and their corresponding auxiliary information, has at least \(\mu \) bits of min-entropy.
and all other messages and their corresponding auxiliary information, has at least \(\mu \) bits of min-entropy.
Resampling. Following [9], let \(\mathsf {Coins}[k]\) be the set of coins for \({\mathcal M}(1^k, \cdot )\), and  . Let
. Let  be the algorithm that first samples
be the algorithm that first samples  , then runs
, then runs  , and then returns \(\mathbf {m}'\). (Note that \(\mathsf {Resamp}_{\mathcal M}\) may run in exponential time.) A resampling algorithm of \({\mathcal M}\) is an algorithm \(\mathsf {Rsmp}\) such that
, and then returns \(\mathbf {m}'\). (Note that \(\mathsf {Resamp}_{\mathcal M}\) may run in exponential time.) A resampling algorithm of \({\mathcal M}\) is an algorithm \(\mathsf {Rsmp}\) such that  and
and  are identically distributed.Footnote 4 A message sampler \({\mathcal M}\) is fully resamplable if it admits a PPT resampling algorithm.
are identically distributed.Footnote 4 A message sampler \({\mathcal M}\) is fully resamplable if it admits a PPT resampling algorithm.
Partial resampling. We also introduce a new notion of “partial resampling.” Let \(\delta \) be a function and let  be the algorithm that samples
be the algorithm that samples  , runs
, runs  , and then returns
, and then returns  . We say that \({\mathcal M}\) is \(\delta \)
-partially resamplable if there is a PT algorithm \(\mathsf {Rsmp}\) such that
. We say that \({\mathcal M}\) is \(\delta \)
-partially resamplable if there is a PT algorithm \(\mathsf {Rsmp}\) such that  is identically distributed as
is identically distributed as  . Such an algorithm \(\mathsf {Rsmp}\) is called a \(\delta \)
-partial resampling algorithm of \({\mathcal M}\). If a message sampler is already fully resamplable then it’s \(\delta \)-partially resamplable for any PT function \(\delta \).
. Such an algorithm \(\mathsf {Rsmp}\) is called a \(\delta \)
-partial resampling algorithm of \({\mathcal M}\). If a message sampler is already fully resamplable then it’s \(\delta \)-partially resamplable for any PT function \(\delta \).
3 Selective-Opening Security for D-PKE
3.1 Security Notions
Bellare, Dowsley, and Keelveedhi [4] were the first to consider selective-opening security of deterministic PKE (D-PKE). They propose a “simulation-based” semantic security notion, but then show that this definition is unachievable in both the standard model and the non-programmable random-oracle model (NPROM), even if the messages are uniform and independent. To address this, we introduce an alternative, “comparison-based” semantic-security notion that generalizes the original PRIV definition for D-PKE of Bellare, Boldyreva, and O’Neill [2]. In particular, our notion follows the \(\text {IND-SO-CPA}\) notion of Bellare, Hofheinz, and Yilek (BHY) [9] in the sense that we compare what partial information the adversary learns from the unopened messages, versus messages resampled from the same conditional distribution.
\(\text {D-SO-CPA}1\) security. Let \({\mathsf {PKE}}= (\mathsf {Kg},\mathsf {Enc},\mathsf {Dec})\) be a D-PKE scheme. To a message sampler \({\mathcal M}\) and an adversary \(A = (A.\mathrm {pg}, A.\mathrm {cor}, A.\mathrm {g}, A.\mathrm {f})\), we associate the experiment in Fig. 1 for every \(k \in {{\mathbb N}}\). We say that \({\mathsf {DE}}\) is \(\text {D-SO-CPA}1\) secure for a class \(\mathscr {M}\) of resamplable message samplers and a class \(\mathscr {A}\) of adversaries if for every \({\mathcal M}\in \mathscr {M}\) and any \(A\in \mathscr {A}\),
is negligible. In these games, the adversary \(A.\mathrm {pg}\) first creates some parameter  to feed the message sampler \({\mathcal M}\). Note that \(A.\mathrm {pg}\) is not given the public key, and thus messages \(\mathbf {m}_1\) created by \({\mathcal M}\) are independent of the public key, a necessary restriction of D-PKE pointed out by Bellare et al. [2]. Next, adversary \(A.\mathrm {cor}\) will be given both the public key and the ciphertexts \(\mathbf {c}\), and decides which set I of indices that it’d like to open \(\mathbf {c}[I]\). It then passes its state to adversary \(A.\mathrm {g}\). The latter is also given \((\mathbf {m}_1[I], \mathbf {a}[I])\) and has to output some partial information \(\omega \) of the message vector \(\mathbf {m}_1\).
to feed the message sampler \({\mathcal M}\). Note that \(A.\mathrm {pg}\) is not given the public key, and thus messages \(\mathbf {m}_1\) created by \({\mathcal M}\) are independent of the public key, a necessary restriction of D-PKE pointed out by Bellare et al. [2]. Next, adversary \(A.\mathrm {cor}\) will be given both the public key and the ciphertexts \(\mathbf {c}\), and decides which set I of indices that it’d like to open \(\mathbf {c}[I]\). It then passes its state to adversary \(A.\mathrm {g}\). The latter is also given \((\mathbf {m}_1[I], \mathbf {a}[I])\) and has to output some partial information \(\omega \) of the message vector \(\mathbf {m}_1\).
Game \(\text {D-CPA1-REAL}^{A, {\mathcal M}}_{\mathsf {DE}}\) returns 1 if the string \(\omega \) above matches the output of  which is the partial information of interest to the adversary. On the other hand, game \(\text {D-CPA1-IDEAL}^{A, {\mathcal M}}_{\mathsf {DE}}\) returns 1 if \(\omega \) is matches the output of
which is the partial information of interest to the adversary. On the other hand, game \(\text {D-CPA1-IDEAL}^{A, {\mathcal M}}_{\mathsf {DE}}\) returns 1 if \(\omega \) is matches the output of  , where \(\mathbf {m}_0\) is the resampled message vector by
, where \(\mathbf {m}_0\) is the resampled message vector by  . Note that in both games, \(A.\mathrm {f}\) is not given the public key \( pk \), otherwise it can encrypt the messages it receives and output the resulting ciphertexts, while \(A.\mathrm {g}\) outputs \(\mathbf {c}\). Again, this issue is pointed out in [2]: since encryption is deterministic, the ciphertexts themselves are some partial information about the messages. D-PKE can only hope to protect partial information of \(\mathbf {m}\) that is independent of \( pk \), and \(A.\mathrm {f}\) is therefore stripped of access to \( pk \).
. Note that in both games, \(A.\mathrm {f}\) is not given the public key \( pk \), otherwise it can encrypt the messages it receives and output the resulting ciphertexts, while \(A.\mathrm {g}\) outputs \(\mathbf {c}\). Again, this issue is pointed out in [2]: since encryption is deterministic, the ciphertexts themselves are some partial information about the messages. D-PKE can only hope to protect partial information of \(\mathbf {m}\) that is independent of \( pk \), and \(A.\mathrm {f}\) is therefore stripped of access to \( pk \).
Discussion. For selective-opening attacks against a D-PKE scheme in which an adversary can open \(d\) messages, it is clear that the message sampler must be \((\mu , d)\)-entropic, where \(2^{-\mu (\cdot )}\) is a negligible function, for any meaningful privacy to be achievable. For convenience of discussion, let’s say that a scheme is \(\text {D-SO-CPA}1[d]\) secure if it’s \(\text {D-SO-CPA}1\) secure for all \((\mu , d)\)-entropic, fully resamplable message samplers and all PT adversaries that open at most d ciphertexts, for any \(\mu \) such that \(2^{-\mu (\cdot )}\) is a negligible function. (The resamplability restriction is dropped for \(d = 0\).) The \(\text {D-SO-CPA}1[0]\) security corresponds to the PRIV notion of Bellare et al. [2].Footnote 5
We note that it is unclear if \(\text {D-SO-CPA}1[\infty ]\) security implies the classic PRIV security: the latter doesn’t allow opening, but it can handle a broader class of message samplers. Our goal is to find D-PKE schemes that offer \(\text {D-SO-CPA}1[d]\) security for any value of d, including the important special cases \(d = 0\) (PRIV security) and \(d = \infty \) (unbounded opening).
Separation. In the full version, we show that the standard PRIV notion of D-PKE doesn’t imply \(\text {D-SO-CPA}1\). Our construction relies on the recent result of Hofheinz, Rao, and Wichs [15] that separates the standard IND-CPA notion and \(\text {IND-SO-CPA}\) of randomized PKE. Specifically, we build a contrived D-PKE scheme that is PRIV-secure in the standard model, but subject to the following \(\text {D-SO-CPA}1\) attack. The message sampler picks a string  and then secret-share it to v(k) shares \(\mathbf {x}[1], \ldots , \mathbf {x}[v(k)]\) such that any t(k) shares reveal no information about the secret s. Let
and then secret-share it to v(k) shares \(\mathbf {x}[1], \ldots , \mathbf {x}[v(k)]\) such that any t(k) shares reveal no information about the secret s. Let  for every \(i \in \{1, \ldots , v(k)\}\), where
for every \(i \in \{1, \ldots , v(k)\}\), where  . Since s is uniform, any \(t + 1\) shares \(\mathbf {x}[i]\) are uniform and independent. Thus, this message sampler is \((3\ell , t)\)-entropic. We show that it is also efficiently resamplable. Surprisingly, there is an efficient SOA adversary \((A.\mathrm {cor}, A.\mathrm {g})\) that opens just t ciphertexts and can recover all strings \(\mathbf {x}[i]\). Next, \(A.\mathrm {g}\) outputs \(\mathbf {x}[1] {\oplus }\cdots {\oplus }\mathbf {x}[v(k)]\), and \(A.\mathrm {f}\) outputs the checksum of the first \(\ell \) bits of the given messages. The adversary \(A\) thus wins with advantage \(1 - 2^{\ell (k)}\).
. Since s is uniform, any \(t + 1\) shares \(\mathbf {x}[i]\) are uniform and independent. Thus, this message sampler is \((3\ell , t)\)-entropic. We show that it is also efficiently resamplable. Surprisingly, there is an efficient SOA adversary \((A.\mathrm {cor}, A.\mathrm {g})\) that opens just t ciphertexts and can recover all strings \(\mathbf {x}[i]\). Next, \(A.\mathrm {g}\) outputs \(\mathbf {x}[1] {\oplus }\cdots {\oplus }\mathbf {x}[v(k)]\), and \(A.\mathrm {f}\) outputs the checksum of the first \(\ell \) bits of the given messages. The adversary \(A\) thus wins with advantage \(1 - 2^{\ell (k)}\).
\(\text {D-SO-CPA}2\) security. The \(\text {D-SO-CPA}1\) security notion only guarantees to protect messages that are fully resamplable. The \(\text {D-SO-CPA}2\) notion strengthens that protection, requiring privacy of  for any entropic message sampler \({\mathcal M}\) and any \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable. In Sect. 5, we’ll see a concrete use of this extra protection, where (i) we have a sampler \({\mathcal M}\) that is not fully resamplable, but (ii) each message itself is a ciphertext, and there’s a function \(\delta \) such that the plaintexts underneath
for any entropic message sampler \({\mathcal M}\) and any \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable. In Sect. 5, we’ll see a concrete use of this extra protection, where (i) we have a sampler \({\mathcal M}\) that is not fully resamplable, but (ii) each message itself is a ciphertext, and there’s a function \(\delta \) such that the plaintexts underneath  and \({\mathcal M}\) is \(\delta \)-partially resamplable. Formally, let
and \({\mathcal M}\) is \(\delta \)-partially resamplable. Formally, let
where games \(\text {D-CPA2-REAL}^{A, {\mathcal M}, \delta }_{\mathsf {DE}}\) and \(\text {D-CPA2-IDEAL}^{A, {\mathcal M}, \delta }_{\mathsf {DE}}\) are defined in Fig. 2. In these games, adversary \(A.\mathrm {f}\) is given either \(\delta (\mathbf {m}_1)\) in the real game, or the output of  in the ideal game. We say that \({\mathsf {DE}}\) is \(\text {D-SO-CPA}2\) secure if \(\mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},A, {\mathcal M}, \delta }(\cdot )\) is negligible for any \((\mu , d)\)-entropic message sampler \({\mathcal M}\) such that \(2^{-\mu }\) is a negligible function, any PT adversary \(A\) that opens at most d ciphertexts, and any PT functions \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable.
in the ideal game. We say that \({\mathsf {DE}}\) is \(\text {D-SO-CPA}2\) secure if \(\mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},A, {\mathcal M}, \delta }(\cdot )\) is negligible for any \((\mu , d)\)-entropic message sampler \({\mathcal M}\) such that \(2^{-\mu }\) is a negligible function, any PT adversary \(A\) that opens at most d ciphertexts, and any PT functions \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable.
Weak equivalence. Clearly, the \(\text {D-SO-CPA}2\) notion implies \(\text {D-SO-CPA}1\): the latter is the special case of the former for fully resamplable samplers, and for a specific function  that simply returns \(\mathbf {m}\). Below, we’ll show that if we just restrict to fully resamplable samplers, the \(\text {D-SO-CPA}1\) notion actually implies \(\text {D-SO-CPA}2\). This is expected, because on an entropic, fully resamplable \({\mathcal M}\), both notions promise to protect any partial information of \(\mathbf {m}\) that is independent of the public key.
that simply returns \(\mathbf {m}\). Below, we’ll show that if we just restrict to fully resamplable samplers, the \(\text {D-SO-CPA}1\) notion actually implies \(\text {D-SO-CPA}2\). This is expected, because on an entropic, fully resamplable \({\mathcal M}\), both notions promise to protect any partial information of \(\mathbf {m}\) that is independent of the public key.
Proposition 1
Let \({\mathcal M}\) be a fully resamplable sampler, and let \(\delta \) be a PT function. Then for any adversary \(A\), there is an adversary \(B\) such that
The adversary \(B\) opens as many ciphertexts as \(A\), and its running time is about that of \(A\) plus the time to run \(\delta \).
Proof
Let \(B\) be the adversary that is identical to \(A\), but \(B.\mathrm {f}\) behaves as follows. When it’s given a vector \(\mathbf {m}\) and parameter  , it’ll run
, it’ll run  and then outputs
and then outputs  . Then \(\mathbf {Adv}^{\text {d-so-cpa}1}_{{\mathsf {DE}},B, {\mathcal M}}(\cdot ) = \mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},A, {\mathcal M}, \delta }(\cdot )\). \(\square \)
. Then \(\mathbf {Adv}^{\text {d-so-cpa}1}_{{\mathsf {DE}},B, {\mathcal M}}(\cdot ) = \mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},A, {\mathcal M}, \delta }(\cdot )\). \(\square \)
In the remainder of the paper, we’ll have 6 other notions. Any notion \(\mathrm {xxx}\) considers an arbitrary message sampler \({\mathcal M}\) with a function \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable. One can consider a variant \(\mathrm {xxx}1\) of \(\mathrm {xxx}\), in which the message sampler is fully resamplable and only the specific function  is considered, and then establish a weak equivalence between \(\mathrm {xxx}1\) and \(\mathrm {xxx}\). However, it will lead to a proliferation of 12 definitions. We therefore choose to present just the stronger notion \(\mathrm {xxx}\).
is considered, and then establish a weak equivalence between \(\mathrm {xxx}1\) and \(\mathrm {xxx}\). However, it will lead to a proliferation of 12 definitions. We therefore choose to present just the stronger notion \(\mathrm {xxx}\).
CCA extension. To add a CCA flavor to \(\text {D-SO-CPA}2\), a notion which we call \(\text {D-SO-CCA}\), one would allow adversaries \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) oracle access to \(\mathsf {Dec}( sk , \cdot )\) with the restriction that they are forbidden from querying a ciphertext in the given \(\mathbf {c}\) to this oracle. Let \(\text {D-CCA-REAL}\) and \(\text {D-CCA-IDEAL}\) be the corresponding experiments, and define
We say that \({\mathsf {DE}}\) is \(\text {D-SO-CCA}\) secure if \(\mathbf {Adv}^{\text {d-so-cca}}_{{\mathsf {DE}},A, {\mathcal M}, \delta }(\cdot )\) is negligible for any \((\mu , d)\)-entropic message sampler \({\mathcal M}\) such that \(2^{-\mu }\) is a negligible function, any PT adversary \(A\) that opens at most d ciphertexts, and any PT functions \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable.
3.2 Achieving \(\text {D-SO-CPA}2\) Security
While the simulation-based definition of Bellare et al. [4] is impossible to achieve even in the non-programmable random-oracle model (NPROM), we show that it is possible to build a \(\text {D-SO-CPA}2\) secure scheme in the NPROM. A close variant of our scheme is shown to be PRIV-secure in the standard model [7]. Our scheme can handle messages of any length, and is highly efficient: the asymmetric cost is fixed and thus the amortized cost is about as cheap as a symmetric encryption. It’s also highly practical on short messages. The only public-key primitive that it uses is a lossy trapdoor function [21], which has practical instantiations, e.g., both Rabin and RSA are lossy [19, 22].
Achieving \(\text {D-SO-CPA}2\) security. To handle arbitrary-length messages, we use a hash function H of arbitrary input and output length. On input \((x, \ell ) \in \{0,1\}^* \times {{\mathbb N}}\), the hash returns \(y = H(x, \ell ) \in \{0,1\}^{\ell }\). Our scheme \({\mathsf {DE1}}[H, {\mathsf {LT}}]\) is shown in Fig. 3, where \({\mathsf {LT}}\) is a lossy trapdoor function with domain \(\{0,1\}^{\mathsf {LT.il}}\). Theorem 2 below shows that \({\mathsf {DE1}}\) is \(\text {D-SO-CPA}2\) secure in the NPROM. The proof is in the full version. We stress that for \((\mu , \infty )\)-entropic message samplers, our scheme allows the adversary to open as many ciphertexts as it wishes.
Theorem 2
Let \({\mathsf {LT}}\) be a lossy trapdoor function with lossiness \(\tau \). Let \({\mathcal M}\) be a \((\mu , d)\)-entropic message sampler, and let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let \({\mathsf {DE1}}[H, {\mathsf {LT}}]\) be as above. In the NPROM, for any adversary \(A\) opening at most \(d\) ciphertexts, there is an adversary D such that
where q(k) is the total number of random-oracle queries of \(A\) and \({\mathcal M}\), and v(k) is the number of messages that \({\mathcal M}\) produces. The running time of D is about that of \(A\) plus the time to run \(\delta \) and an efficient \(\delta \)-partial resampling algorithm of \({\mathcal M}\) plus the time to run \({\mathsf {DE1}}[H, {\mathsf {LT}}]\) to encrypt \({\mathcal M}\)’s messages. Adversary D makes at most q random-oracle queries.
Proof ideas. Let \(\textsc {RO}_1, \textsc {RO}_2, \textsc {RO}_3,\) and \(\textsc {RO}_4\) denote the oracle interface of \((A.\mathrm {pg}, {\mathcal M}), A.\mathrm {cor}, A.\mathrm {g}\), and \(A.\mathrm {f}\) respectively. Initially, each interface simply calls \(\textsc {RO}\). In game-based proofs of ROM-based D-PKE constructions, one often considers the event that \(A.\mathrm {pg}\) or \({\mathcal M}\) queries  to \(\textsc {RO}_1\), and then let the interface lies, instead of calling
to \(\textsc {RO}_1\), and then let the interface lies, instead of calling  . This allows the coins
. This allows the coins  to be independent of the messages \(\mathbf {m}\). The discrepancy due to the lying is tiny, since the chance that \(A.\mathrm {pg}\) or \({\mathcal M}\) can make such a query is at most \(q(k) / 2^k\). However, in the SOA setting, this strategy creates the following subtlety. For the resampling algorithm to behave correctly, one has to give it access to \(\textsc {RO}_1\). Yet the adversary \(A.\mathrm {cor}\) can embed some information of
to be independent of the messages \(\mathbf {m}\). The discrepancy due to the lying is tiny, since the chance that \(A.\mathrm {pg}\) or \({\mathcal M}\) can make such a query is at most \(q(k) / 2^k\). However, in the SOA setting, this strategy creates the following subtlety. For the resampling algorithm to behave correctly, one has to give it access to \(\textsc {RO}_1\). Yet the adversary \(A.\mathrm {cor}\) can embed some information of  in I, and therefore it’s well possible that the resampling algorithm queries
in I, and therefore it’s well possible that the resampling algorithm queries  . This issue is unique to SOA security of D-PKE: prior papers of SOA security for randomized PKE never have to deal with this. While getting around the subtlety above is not too difficult, it shows that a rigorous proof for Theorem 2 is not as simple as one might expect.
. This issue is unique to SOA security of D-PKE: prior papers of SOA security for randomized PKE never have to deal with this. While getting around the subtlety above is not too difficult, it shows that a rigorous proof for Theorem 2 is not as simple as one might expect.
Suppose that \(A.\mathrm {pg}\) and \({\mathcal M}\) never query  . The first step in the proof is to move from an injective key \( ek \) of \({\mathsf {LT}}\) to a lossy key
. The first step in the proof is to move from an injective key \( ek \) of \({\mathsf {LT}}\) to a lossy key  . Next, recall that the adversary \(A.\mathrm {cor}\) is given
. Next, recall that the adversary \(A.\mathrm {cor}\) is given  . Since each synthetic coin \(\mathbf {r}[i]\) is uniformly random and \({\mathsf {LT}}\) has lossiness \(\tau \), in the view of \(A.\mathrm {cor}\), each \(\mathbf {r}[i]\) has min-entropy at least \(\tau (k)\). Suppose that \(A.\mathrm {cor}\) doesn’t make any query in
. Since each synthetic coin \(\mathbf {r}[i]\) is uniformly random and \({\mathsf {LT}}\) has lossiness \(\tau \), in the view of \(A.\mathrm {cor}\), each \(\mathbf {r}[i]\) has min-entropy at least \(\tau (k)\). Suppose that \(A.\mathrm {cor}\) doesn’t make any query in  ; this happens with probability at least \(1 - q(k) v(k) / 2^{\mu (k)} - q(k) v(k) / 2^{\tau (k)}\). Then \(A.\mathrm {cor}\) knows nothing about \(\mathbf {m}\), and thus I is conditionally independent of \(\mathbf {m}\), given
; this happens with probability at least \(1 - q(k) v(k) / 2^{\mu (k)} - q(k) v(k) / 2^{\tau (k)}\). Then \(A.\mathrm {cor}\) knows nothing about \(\mathbf {m}\), and thus I is conditionally independent of \(\mathbf {m}\), given  . Hence in the view of \(A.\mathrm {g}\), each \(\mathbf {m}[i]\) (for \(i \not \in I\)) still has min-entropy \(\mu \), and thus the chance that \(A.\mathrm {g}\) can make a query in
. Hence in the view of \(A.\mathrm {g}\), each \(\mathbf {m}[i]\) (for \(i \not \in I\)) still has min-entropy \(\mu \), and thus the chance that \(A.\mathrm {g}\) can make a query in  .
.
The core of the proof is to bound the probability that the adversary \(A.\mathrm {g}\) can make a query in  . Let \(X_i\) be the random variable for the number of pre-images of
. Let \(X_i\) be the random variable for the number of pre-images of  . Although in the view of \(A.\mathrm {cor}\), the average conditional min-entropy of each \(\mathbf {r}[i]\) is \(\tau (k)\), the same claim may not hold in the view of \(A.\mathrm {g}\). For example, the adversary \(A.\mathrm {cor}\) may choose to open all but the ciphertext of \(\mathbf {m}[j]\), where j is chosen so that \(X_j = \min \{X_1, \ldots , X_{v(k)}\}\): while \(\mathbf {E}(1 / X_i) \le 2^{-\tau (k)}\) for each fixed \(i \in \{1, \ldots , v(k)\}\), the same bound doesn’t work for \(\mathbf {E}(1 / {\min \{X_1, \ldots , X_{v(k)}\}} )\). To get around this, note that the chance that \(A.\mathrm {g}\) can make a query in
. Although in the view of \(A.\mathrm {cor}\), the average conditional min-entropy of each \(\mathbf {r}[i]\) is \(\tau (k)\), the same claim may not hold in the view of \(A.\mathrm {g}\). For example, the adversary \(A.\mathrm {cor}\) may choose to open all but the ciphertext of \(\mathbf {m}[j]\), where j is chosen so that \(X_j = \min \{X_1, \ldots , X_{v(k)}\}\): while \(\mathbf {E}(1 / X_i) \le 2^{-\tau (k)}\) for each fixed \(i \in \{1, \ldots , v(k)\}\), the same bound doesn’t work for \(\mathbf {E}(1 / {\min \{X_1, \ldots , X_{v(k)}\}} )\). To get around this, note that the chance that \(A.\mathrm {g}\) can make a query in  is at most
is at most
Finally, if I is conditionally independent of \(\mathbf {m}\) given  , then the re-sampled string z is identically distributed as
, then the re-sampled string z is identically distributed as  , even conditioning on
, even conditioning on  , I, and
, I, and  .Footnote 6 Hence
.Footnote 6 Hence  with probability at most \(q(k) / 2^{k}\). If all bad events above don’t happen then (i) in the joint view of \(A.\mathrm {g}\) and \(A.\mathrm {f}\), the strings
with probability at most \(q(k) / 2^{k}\). If all bad events above don’t happen then (i) in the joint view of \(A.\mathrm {g}\) and \(A.\mathrm {f}\), the strings  and z are identically distributed, and (ii) the output of \(A.\mathrm {f}\) will be conditionally independent of the ciphertexts and the public key, given
and z are identically distributed, and (ii) the output of \(A.\mathrm {f}\) will be conditionally independent of the ciphertexts and the public key, given  . This means the \(\text {d-so-cpa}2\) advantage of \(A\) is 0.
. This means the \(\text {d-so-cpa}2\) advantage of \(A\) is 0.
3.3 Achieving \(\text {D-SO-CCA}\) Security
To achieve \(\text {D-SO-CCA}\) security, we modify \({\mathsf {DE1}}\) construction as follows: In the decryption, once we recover the message m, we’ll re-encrypt it and return \(\bot \) if the resulting ciphertext doesn’t match the given one, or the hash image of the message doesn’t match the string obtained via inverting the trapdoor function. The resulting construction \({\mathsf {DE2}}\) is shown in Fig. 4. The scheme \({\mathsf {DE}}= {\mathsf {DE2}}[H, {\mathsf {LT}}]\) is unique-ciphertext, as formalized by Bellare and Hoang [7]: for every \(k \in {{\mathbb N}}\), every \(( pk , sk ) \in [\mathsf {DE.Kg}(1^k)]\), and every \(m \in \{0,1\}^*\), there is at most a string c such that \(\mathsf {DE.Dec}( sk , c) = m\). Theorem 3 below shows that \({\mathsf {DE2}}\) is \(\text {D-SO-CCA}\) secure in the NPROM. The re-encrypting trick for lifting CPA to CCA security in the random-oracle model dates back to a paper of Fujisaki and Okamoto [13], but that work only considers randomized PKE and there’s no opening. Still, the proof ideas are quite similar.
Theorem 3
Let \({\mathsf {LT}}\) be a lossy trapdoor function with lossiness \(\tau \). Let \({\mathcal M}\) be a \((\mu , d)\)-entropic message sampler and let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let \({\mathsf {DE2}}[H, {\mathsf {LT}}]\) be as above. In the NPROM, for any adversary \(A\) opening at most \(d\) ciphertexts, there is an adversary D such that
where p(k) is the number of decryption-oracle queries of \(A\), q(k) is the total number of random-oracle queries of \(A\) and \({\mathcal M}\), and v(k) is the number of messages that \({\mathcal M}\) produces. The running time of D is about that of \(A\) plus the time to run \(\delta \) and an efficient \(\delta \)-partial resampling algorithm of \({\mathcal M}\), plus the time to run \({\mathsf {DE2}}[H, {\mathsf {LT}}]\) to encrypt \({\mathcal M}\)’s messages and decrypt \(A\)’s decryption queries. Adversary D makes at most 2q random-oracle queries.
Proof
Let \(\mathsf {Rsmp}\) be an efficient \(\delta \)-partial resampling algorithm for \({\mathcal M}\). Consider games \(G_1\) and \(G_2\) in Fig. 5. Then
Game \(G_2\) is identical to game \(G_1\), except for the following. In procedure \(\textsc {Dec}(c)\), instead of using the decryption of \({\mathsf {DE2}}\) to decrypt c, we maintain the set \(\mathsf {Dom}\) of the suffixes of random-oracle queries \((x, \ell )\) that \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) make such that  and \(\ell = \mathsf {LT.il}(k)\). If there’s \(m \in \mathsf {Dom}\) such that the corresponding ciphertext of m is c then we return m; otherwise return \(\bot \). Wlog, assume that \(A.\mathrm {cor}\) stores all random-oracle queries/answers in its state; that is, both \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) also can track \(\mathsf {Dom}\) and implement the \(\textsc {Dec}\) procedure of game \(G_2\) on their own, without calling the decryption oracle.Footnote 7 Let \(\mathsf {Range}= \{ {\mathsf {DE2}}.\mathsf {Enc}( pk , m) \mid m \in \mathsf {Dom}\}\). On a query \(c \in \mathsf {Range}\), the procedures \(\textsc {Dec}\) of both games have the same behavior, due to the correctness of the decryption of \({\mathsf {DE2}}\). Wlog, assume that both \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) never query \(c \in \mathsf {Range}\) to the decryption oracle. (Adversaries \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) are thus assumed to maintain the corresponding ciphertexts of messages in \(\mathsf {Dom}\). But this needs additional queries to the random oracle, so the total random-oracle queries of these two adversaries is now at most 2q.)
and \(\ell = \mathsf {LT.il}(k)\). If there’s \(m \in \mathsf {Dom}\) such that the corresponding ciphertext of m is c then we return m; otherwise return \(\bot \). Wlog, assume that \(A.\mathrm {cor}\) stores all random-oracle queries/answers in its state; that is, both \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) also can track \(\mathsf {Dom}\) and implement the \(\textsc {Dec}\) procedure of game \(G_2\) on their own, without calling the decryption oracle.Footnote 7 Let \(\mathsf {Range}= \{ {\mathsf {DE2}}.\mathsf {Enc}( pk , m) \mid m \in \mathsf {Dom}\}\). On a query \(c \in \mathsf {Range}\), the procedures \(\textsc {Dec}\) of both games have the same behavior, due to the correctness of the decryption of \({\mathsf {DE2}}\). Wlog, assume that both \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) never query \(c \in \mathsf {Range}\) to the decryption oracle. (Adversaries \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) are thus assumed to maintain the corresponding ciphertexts of messages in \(\mathsf {Dom}\). But this needs additional queries to the random oracle, so the total random-oracle queries of these two adversaries is now at most 2q.)
Games \(G_1\) and \(G_2\) of the proof of Theorem 3. Their procedures \(\textsc {Dec}\) are in the bottom-left and bottom-right panels, respectively.
Assume that \(A.\mathrm {pg}\) and \({\mathcal M}\) never make a random-oracle query \((x, \ell )\) such that the k-bit suffix of x is  . This happens with probability at least \(1 - q(k) / 2^k\). The adversaries can distinguish the games if and only if they can trigger \(\textsc {Dec}\) of game \(G_1\) to produce non-\(\bot \) output. Let
. This happens with probability at least \(1 - q(k) / 2^k\). The adversaries can distinguish the games if and only if they can trigger \(\textsc {Dec}\) of game \(G_1\) to produce non-\(\bot \) output. Let  be a decryption-oracle query. Let
be a decryption-oracle query. Let  and
and  . Due to the unique-ciphertext property of \({\mathsf {DE2}}\), if this can trigger the \(\textsc {Dec}\) procedure of game \(G_1\) to return a non-\(\bot \) answer, we must have \(m \not \in \{\mathbf {m}[1], \ldots , \mathbf {m}[|\mathbf {m}|]\} \cup \mathsf {Dom}\). Then there is no prior random-oracle query \((x, \mathsf {LT.il}(k))\) such that
. Due to the unique-ciphertext property of \({\mathsf {DE2}}\), if this can trigger the \(\textsc {Dec}\) procedure of game \(G_1\) to return a non-\(\bot \) answer, we must have \(m \not \in \{\mathbf {m}[1], \ldots , \mathbf {m}[|\mathbf {m}|]\} \cup \mathsf {Dom}\). Then there is no prior random-oracle query \((x, \mathsf {LT.il}(k))\) such that  . Hence procedure \(\textsc {Dec}\) of game \(G_1\) will return a non-\(\bot \) answer only if
. Hence procedure \(\textsc {Dec}\) of game \(G_1\) will return a non-\(\bot \) answer only if  , which happens with probability \(2^{-\mathsf {LT.il}(k)}\). Multiplying for p(k) decryption-oracle queries,
, which happens with probability \(2^{-\mathsf {LT.il}(k)}\). Multiplying for p(k) decryption-oracle queries,
Now in game \(G_2\), the decryption oracle always return \(\bot \), and thus wlog, assume that the adversaries never make a decryption query, meaning that they only launch a \(\text {D-SO-CPA}2\) attack. Hence
But \({\mathsf {DE2}}\) and \({\mathsf {DE1}}\) only differ in the decryption algorithms, which doesn’t affect the \(\text {D-SO-CPA}\) security. Hence from Theorem 2, we can construct a distinguisher D of the claimed running time such that
(Note that the bound above is for adversaries who make at most 2q random-oracle queries.) Summing up,
\(\square \)
4 Selective-Opening Security for Nonce-Based PKE
Recall that D-PKE protects only unpredictable messages, but in practice, messages often have very limited entropy [12]. Hedge PKE tries to improve this situation by adding the unpredictability of coins. However, the coins generated by Dual EC are completely determined by Big Brother, and those by the buggy Debian RNG have only about 15 bits of min-entropy. In a recent work, Bellare and Tackmann (BT) [10] propose the notion of nonce-based PKE to address this limitation, supporting arbitrary messages. In this section, we extend the notion of nonce-based PKE for SOA setting, and then show how to achieve this.
4.1 Security Notions
Nonce generators. A nonce generator \(\mathsf {NG}\) with nonce space \(\mathcal {N}\) is an algorithm that takes as input the unary encoding \(1^k\) of the security parameter, a current state \( St \), and a nonce selector \(\sigma \). It then probabilistically produces a nonce \(N \in \mathcal {N}\) together with an updated state \( St \). That is,  . A good nonce generator needs to satisfy the following properties: (i) nonces should never repeat, and (ii) each nonce is unpredictable, even if all nonce selectors are adversarially chosen. Formally, let \(\mathbf {Adv}^{\mathrm {rp}}_{\mathsf {NG}, A}(k) = \Pr [\mathrm {RP}_{\mathsf {NG}}^{A}(k)]\), where game \(\mathrm {RP}\) is defined in Fig. 6. We say that \(\mathsf {NG}\) is \(\mathrm {RP}\)-secure if for any PT adversary \(A\), \(\mathbf {Adv}^{\mathrm {rp}}_{\mathsf {NG}, A}(\cdot )\) is a negligible function.
. A good nonce generator needs to satisfy the following properties: (i) nonces should never repeat, and (ii) each nonce is unpredictable, even if all nonce selectors are adversarially chosen. Formally, let \(\mathbf {Adv}^{\mathrm {rp}}_{\mathsf {NG}, A}(k) = \Pr [\mathrm {RP}_{\mathsf {NG}}^{A}(k)]\), where game \(\mathrm {RP}\) is defined in Fig. 6. We say that \(\mathsf {NG}\) is \(\mathrm {RP}\)-secure if for any PT adversary \(A\), \(\mathbf {Adv}^{\mathrm {rp}}_{\mathsf {NG}, A}(\cdot )\) is a negligible function.
Nonce-based PKE. A nonce-based PKE with nonce space \(\mathcal {N}\) is a tuple \({\mathsf {NE}}= ({\mathsf {NE}}.{\mathsf {Kg}}, {\mathsf {NE}}.{\mathsf {Sg}}, {\mathsf {NE}}.{\mathsf {Enc}}, {\mathsf {NE}}.{\mathsf {Dec}})\). The key generator \({\mathsf {NE}}.{\mathsf {Kg}}(1^k)\) generates a public key \( pk \) and an associated secret key \( sk \). The seed generator \({\mathsf {NE}}.{\mathsf {Sg}}(1^k)\) produces a sender seed \( xk \). The encryption algorithm \({\mathsf {NE}}.{\mathsf {Enc}}\) takes as input a public key \( pk \), a sender seed \( xk \), a nonce \(N \in \mathcal {N}\), and a message m, and then deterministically returns a ciphertext c. The decryption algorithm \({\mathsf {NE}}.{\mathsf {Dec}}( sk , \cdot )\) plays the same role as in traditional randomized PKE; it’s not given the nonce or the sender seed.
Nonce-based PKE can be viewed as a way to harden the randomness at the sender side; the receiver is oblivious to this change. Security of nonce-based PKE should hold when either (i) the seed \( xk \) is secret and the nonces are unique, or (ii) the seed is leaked to the adversary, but the nonces are unpredictable to the adversary.Footnote 8
Discussion. To formalize security of nonce-based PKE, BT define two notions, NBP1 and NBP2. Both notions are in the single-sender setting and use nonces generated from a nonce generator \(\mathsf {NG}\). The former notion considers the situation when the seed \( xk \) is secret, and there’s no security requirement from \(\mathsf {NG}\), except the uniqueness of nonces. The latter notion considers the case when the seed \( xk \) is given to the adversary; now nonces generated from \(\mathsf {NG}\) have to satisfy \(\mathrm {RP}\) security.
When we bring SOA extension to nonce-based PKE below, there will be many changes. First, since there are multiple senders and only some of them can keep their seeds secret, one has to merge the SOA variants of NBP1 and NBP2 into a single definition. Next, because the adversary learns the seeds of some senders, the nonce generator \(\mathsf {NG}\) must be \(\mathrm {RP}\)-secure. If we let senders whose seeds are secret use unpredictable nonces from \(\mathsf {NG}\) then our notion will fail to model the possibility that the adversary can corrupt the nonce generator. Therefore, in our notion, for senders whose seeds are secret, we’ll let the adversary specify their nonces. We require the adversary to be nonce-respecting, meaning that the nonces of every single sender must be distinct.
\(\text {N-SO-CPA}\). Let \({\mathsf {NE}}\) be a nonce-based PKE scheme and \(\mathsf {NG}\) be a nonce generator of the same nonce space \(\mathcal {N}\). Let \({\mathcal M}\) be a message sampler, but the generated messages don’t have to be distinct or unpredictable. Let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. The game \(\text {N-SO-CPA}\) defining the \(\text {N-SO-CPA}\) security is specified in Fig. 7.
Initially, the game picks seed  and sets state
and sets state  for sender j, with \(j = 1, 2, \ldots \). The adversary is then given the public key \( pk \) and has to specify the list J of senders that it wishes to get the seeds. It’s then granted \(\varvec{xk}[J]\) and then has to provide some parameter
for sender j, with \(j = 1, 2, \ldots \). The adversary is then given the public key \( pk \) and has to specify the list J of senders that it wishes to get the seeds. It’s then granted \(\varvec{xk}[J]\) and then has to provide some parameter  for generating
for generating  , together with a vector \(\varvec{N}\) of nonces, a map \(U\) that specifies message \(\mathbf {m}[i]\) belongs to sender \(U[i]\), and a vector \(\varvec{\sigma }\) of nonce selectors for \(\mathsf {NG}\). Note that the messages \(\mathbf {m}\) here can depend on the public key. We require that the adversary be nonce-respecting, meaning that \((\varvec{N}[1], U[1]), (\varvec{N}[2], U[2]), \ldots \) are distinct.
, together with a vector \(\varvec{N}\) of nonces, a map \(U\) that specifies message \(\mathbf {m}[i]\) belongs to sender \(U[i]\), and a vector \(\varvec{\sigma }\) of nonce selectors for \(\mathsf {NG}\). Note that the messages \(\mathbf {m}\) here can depend on the public key. We require that the adversary be nonce-respecting, meaning that \((\varvec{N}[1], U[1]), (\varvec{N}[2], U[2]), \ldots \) are distinct.
The game then iterates over \(i = 1, \ldots , |\mathbf {m}|\) to encrypt each message \(\mathbf {m}[i]\). If \(i \in J\) then \(\varvec{N}[i]\) is overwritten by a nonce N generated by \(\mathsf {NG}\) as follows. Let  . The nonce generator \(\mathsf {NG}\) will read the current state \(\varvec{st}[j]\) of sender j and the nonce selector \(\varvec{\sigma }[i]\) for the message \(\mathbf {m}[i]\), to generate a nonce N and update \(\varvec{st}[j]\). The adversary then is given the ciphertexts and has to output a set I to indicate which ciphertexts it wants to open. Note that opening \(\mathbf {c}[i]\) returns not only \((\mathbf {m}[i], \mathbf {a}[i])\) but also the associated nonce and sender seed. Moreover, if the adversary opens a message belonging to sender j, then any other messages of this sender are considered open. Finally, the game resamples \(z_0\), and let
. The nonce generator \(\mathsf {NG}\) will read the current state \(\varvec{st}[j]\) of sender j and the nonce selector \(\varvec{\sigma }[i]\) for the message \(\mathbf {m}[i]\), to generate a nonce N and update \(\varvec{st}[j]\). The adversary then is given the ciphertexts and has to output a set I to indicate which ciphertexts it wants to open. Note that opening \(\mathbf {c}[i]\) returns not only \((\mathbf {m}[i], \mathbf {a}[i])\) but also the associated nonce and sender seed. Moreover, if the adversary opens a message belonging to sender j, then any other messages of this sender are considered open. Finally, the game resamples \(z_0\), and let  . It picks
. It picks  , and gives the adversary \(z_b\) and \((\mathbf {m}[I], \mathbf {a}[I], \varvec{xk}[U[I]], \varvec{N}[I])\). The adversary has to guess the challenge bit b. Define
, and gives the adversary \(z_b\) and \((\mathbf {m}[I], \mathbf {a}[I], \varvec{xk}[U[I]], \varvec{N}[I])\). The adversary has to guess the challenge bit b. Define
We say that \({\mathsf {NE}}\) is \(\text {N-SO-CPA}\) secure, with respect to \(\mathsf {NG}\), if for any message sampler \({\mathcal M}\) and any PT adversary \(A\), and any PT function \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable, \(\mathbf {Adv}^{\text {n-so-cpa}}_{{\mathsf {NE}}, \mathsf {NG}, A, {\mathcal M}, \delta }(\cdot )\) is a negligible function.
\(\text {N-SO-CCA}\). To add a CCA flavor to \(\text {N-SO-CPA}\), one would give the adversary oracle access to \(\mathsf {Dec}( sk , \cdot )\). Once it’s given the ciphertexts \(\mathbf {c}\), it’s not allowed to query any \(\mathbf {c}[i]\) to the decryption oracle. Let \(\text {N-SO-CCA}\) be the corresponding game, and define \(\mathbf {Adv}^{\text {n-so-cca}}_{{\mathsf {NE}}, \mathsf {NG}, A, {\mathcal M}, \delta }(k) = 2 \Pr [\text {N-SO-CCA}_{{\mathsf {NE}}, \mathsf {NG}}^{A, \mathcal{M}, \delta }(k)] - 1\).
Simulation-based security. One could also define an appropriate simulation-based notion of SOA security for nonce-based PKE, which unlike \(\text {N-SO-CPA}\) would not require the unrevealed messages to be efficiently resampleable, analogously to the SIM-SOA definition for randomized PKE in [9]. However, we conjecture that such a definition is impossible to achieve. We leave this as an open question. In any case, a simulation-based definition of SOA security for nonce-based PKE will indeed be impossible to achieve later when we lift the primitive to the hedged setting, where an existing impossibility result for a simulation-based notion of SOA security for deterministic PKE [4] applies (because hedged PKE generalizes deterministic PKE).
4.2 Separation
We now show that the standard notions for nonce-based PKE of BT [10] do not imply \(\text {N-SO-CPA}\). Our separation is based on the recent result of Hofheinz, Rao, and Wichs (HRW) [15] to show that \(\mathrm {IND\text{- }CCA}\) doesn’t imply the notion \(\text {IND-SO-CPA}\) for randomized PKE.
HRW construction. Our counterexample is based on the recent (contrived) construction \({\mathsf {RE}}_{{\mathsf {bad}}}= ({\mathsf {RE}}_{{\mathsf {bad}}}.{\mathsf {Kg}}, {\mathsf {RE}}_{{\mathsf {bad}}}.{\mathsf {Enc}}, {\mathsf {RE}}_{{\mathsf {bad}}}.{\mathsf {Dec}})\) of HRW. The scheme \({\mathsf {RE}}_{{\mathsf {bad}}}\) is IND-CCA secure, but is vulnerable to the following SOA attack. The message sampler  ignores
ignores  , picks a secret
, picks a secret  and then secret-shares it to v(k) messages \(\mathbf {m}[1], \ldots , \mathbf {m}[v(k)]\) so that any t(k) shares reveal no information of the secret s. In other words, it picks \(a_0, a_1, \ldots , a_{t}\) uniformly from \(\mathsf {GF}(2^{\ell })\), the finite field of size \(2^{\ell }\), and computes
and then secret-shares it to v(k) messages \(\mathbf {m}[1], \ldots , \mathbf {m}[v(k)]\) so that any t(k) shares reveal no information of the secret s. In other words, it picks \(a_0, a_1, \ldots , a_{t}\) uniformly from \(\mathsf {GF}(2^{\ell })\), the finite field of size \(2^{\ell }\), and computes  for every \(i \in \{1, \ldots , v(k)\}\), where \(f(x) = a_0 + a_1 x + \cdots + a_t x^t\) is the corresponding polynomial in \(\mathsf {GF}(2^\ell )[X]\). Recall that any \(t + 1\) shares will uniquely determine the polynomial f (via polynomial interpolation), and thus any \(t + 1\) shares are uniformly and independently random. The auxiliary information is empty. Surprisingly, there’s an efficient adversary that opens only t ciphertexts and can recover all messages. We note that HRW’s counter-example is based on public-coin differing-inputs obfuscation [17], which is a very strong assumption.
for every \(i \in \{1, \ldots , v(k)\}\), where \(f(x) = a_0 + a_1 x + \cdots + a_t x^t\) is the corresponding polynomial in \(\mathsf {GF}(2^\ell )[X]\). Recall that any \(t + 1\) shares will uniquely determine the polynomial f (via polynomial interpolation), and thus any \(t + 1\) shares are uniformly and independently random. The auxiliary information is empty. Surprisingly, there’s an efficient adversary that opens only t ciphertexts and can recover all messages. We note that HRW’s counter-example is based on public-coin differing-inputs obfuscation [17], which is a very strong assumption.
Results. Let H be a hash function. One can model it as a random oracle, or, for a standard-model result, a primitive that BT call hedged extractor. BT show that one can build a nonce-based PKE achieving their notions from an arbitrary \(\mathrm {IND\text{- }CCA}\) secure PKE \({\mathsf {RE}}\) as follows. Given seed \( xk \), nonce N, and message m, one uses \(H(( xk , N, m))\) to extract synthetic coins r, and then encrypt m via \({\mathsf {RE}}\) under coins r. Now, use the scheme \({\mathsf {RE}}_{{\mathsf {bad}}}\) above to instantiate \({\mathsf {RE}}\), and let \(\mathsf {NE_{bad}}[H, {\mathsf {RE}}_{{\mathsf {bad}}}]\) be the resulting nonce-based PKE. This \(\mathsf {NE_{bad}}[H, {\mathsf {RE}}_{{\mathsf {bad}}}]\) achieves BT’s notions.
We now break the \(\text {N-SO-CPA}\) security of \(\mathsf {NE_{bad}}\). The message sampler \({\mathcal M}\) is as described in HRW attack, and let \(A\) be the adversary attacking \({\mathsf {RE}}_{{\mathsf {bad}}}\) as above. Note that \({\mathcal M}\) is fully resamplable, and let  . Consider the following adversary \(B\) attacking \(\mathsf {NE_{bad}}\). It specifies \(J = \emptyset \), meaning that it doesn’t want to get any sender seed before the opening. It then lets \(\varvec{N}[i] = U[i] = i\), for every i. That is, each sender has only a single message. Then, when \(B\) gets the ciphertexts \(\mathbf {c}\), it runs \(A\) on those \(\mathbf {c}\). Note that \(\mathbf {c}\) are ciphertexts of \({\mathsf {RE}}_{{\mathsf {bad}}}\), although the coins are only pseudorandom. Still, adversary \(A\) can recover all messages by opening just t ciphertexts. When \(B\) is given the messages (real or resampled), it compares that with what \(A\) recovers. Then \(\mathbf {Adv}^{\text {n-so-cpa}}_{{\mathsf {NE}}, \mathsf {NG}, B, {\mathcal M}, \delta }(k) \ge 1 - 2^{-\ell (k)}\), where \(\ell \) is the length of each message.
. Consider the following adversary \(B\) attacking \(\mathsf {NE_{bad}}\). It specifies \(J = \emptyset \), meaning that it doesn’t want to get any sender seed before the opening. It then lets \(\varvec{N}[i] = U[i] = i\), for every i. That is, each sender has only a single message. Then, when \(B\) gets the ciphertexts \(\mathbf {c}\), it runs \(A\) on those \(\mathbf {c}\). Note that \(\mathbf {c}\) are ciphertexts of \({\mathsf {RE}}_{{\mathsf {bad}}}\), although the coins are only pseudorandom. Still, adversary \(A\) can recover all messages by opening just t ciphertexts. When \(B\) is given the messages (real or resampled), it compares that with what \(A\) recovers. Then \(\mathbf {Adv}^{\text {n-so-cpa}}_{{\mathsf {NE}}, \mathsf {NG}, B, {\mathcal M}, \delta }(k) \ge 1 - 2^{-\ell (k)}\), where \(\ell \) is the length of each message.
4.3 Achieving \(\text {N-SO-CPA}\) Security
BT’s construction of nonce-based PKE is simple. To encrypt a message m under a seed \( xk \), a nonce N, and public key \( pk \), we hash \(( xk , N, m)\) to derive a string r, and then uses a traditional randomized PKE to encrypt m under the synthetic coins r and public key \( pk \). Here we’ll use BT’s construction, but the underlying randomized PKE is a randomized counterpart of the D-PKE scheme \({\mathsf {DE1}}\) in Sect. 3.2.
Formally, let H be a hash of arbitrary input and output length, meaning that \(H(x, \ell )\) returns an \(\ell \)-bit string. Let \({\mathsf {LT}}\) be a lossy trapdoor function. Our nonce-based PKE \(\mathsf {NE1}[H, {\mathsf {LT}}]\) is described in Fig. 8; it has nonce space \(\{0,1\}^*\) and message space \(\{0,1\}^*\). Theorem 4 below shows that \(\mathsf {NE1}[H, {\mathsf {LT}}]\) is \(\text {N-SO-CPA}\) secure in the NPROM; the proof is in the full version.
Theorem 4
Let \({\mathsf {LT}}\) be a lossy trapdoor function with lossiness \(\tau \). Let \({\mathcal M}\) be a message sampler and let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let \(\mathsf {NE1}[H, {\mathsf {LT}}]\) be as above, and let \(\mathsf {NG}\) be a nonce generator. In the NPROM, for any adversary A, there are adversaries B and D such that
where v is the number of messages that \({\mathcal M}\) generates, and q bounds the total number of random-oracle queries that \(A\) and \({\mathcal M}\) make. The running time of B or D is about the time to run game \(\text {N-SO-CPA}_{{\mathsf {NE}}, \mathsf {NG}}^{A, \mathcal{M}, \delta }\), but using an efficient \(\delta \)-partial resampling algorithm of \({\mathcal M}\) instead of \(\mathsf {Resamp}_{{\mathcal M}, \delta }\). Each of B and D makes at most q random-oracle queries.
4.4 Achieving \(\text {N-SO-CCA}\) Security
To strengthen \(\mathsf {NE1}\) with CCA capability, in the encryption, we append to the ciphertext a hash image of \(r {\,\Vert \,}m\). When we decrypt a ciphertext, we’ll recover both r and m, and check if the hash image of \(r {\,\Vert \,}m\) matches with what’s given in the ciphertext. The resulting scheme \(\mathsf {NE2}[H, {\mathsf {LT}}]\) is shown in Fig. 9. The underlying randomized PKE of \(\mathsf {NE2}\) is a textbook IND-CCA construction in the ROM (but \({\mathsf {LT}}\) just needs to be an ordinary trapdoor function). Theorem 5 below shows that \(\mathsf {NE2}[H, {\mathsf {LT}}]\) is \(\text {N-SO-CCA}\) secure in the NPROM; the proof is in the full version.
Theorem 5
Let \({\mathsf {LT}}\) be a lossy trapdoor function with lossiness \(\tau \). Let \({\mathcal M}\) be a message sampler and let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let \(\mathsf {NE2}[H, {\mathsf {LT}}]\) be as above, and let \(\mathsf {NG}\) be a nonce generator. In the NPROM, for any adversary A, there are adversaries B and D such that
where v is the number of messages that \({\mathcal M}\) generates, p is the number of A’s queries to the decryption oracle, q bounds the total number of random-oracle queries that \(A\) and \({\mathcal M}\) make, and \(Q = q + 2p + v\). The running time of B or D is about the time to run game \(\text {N-SO-CCA}_{{\mathsf {NE}}, \mathsf {NG}}^{A, \mathcal{M}, \delta }\), but using an efficient \(\delta \)-partial resampling algorithm of \({\mathcal M}\) instead of \(\mathsf {Resamp}_{{\mathcal M}, \delta }\). Each of B and D makes at most \(q + 2p\) random-oracle queries.
5 Hedged Security for Nonce-Based PKE
Recall that the security of nonce-based PKE relies on the assumption that the adversary cannot obtain the secret seeds and corrupt the nonce generator simultaneously. Still, this assumption may fail in practice, and it’s desirable to retain some security guarantee when seeds and nonces are bad. We capture this via the notion \(\text {HN-SO-CPA}\) that is a variant of the notion \(\text {D-SO-CPA}2\), adapted for the nonce-based setting. A good nonce-based PKE thus has to satisfy both \(\text {N-SO-CPA}\) and \(\text {HN-SO-CPA}\) simultaneously. We then extend this treatment to the CCA setting.
5.1 Security Notions
Unpredictable samplers. Let \({\mathcal M}\) be a message sampler. We say that \({\mathcal M}\) is \((\mu , d)\)
-unpredictable if for any  ,
,
-
(i)
For any
 , each \(\mathbf {a}[i]\) is a tuple \((a_i, xk _i, N_i)\), where \( xk _i\) is a seed and \(N_i\) is a nonce. Moreover, \(( xk _1, N_1, \mathbf {m}[1]), ( xk _2, N_2, \mathbf {m}[2]), \ldots \) must be distinct.
, each \(\mathbf {a}[i]\) is a tuple \((a_i, xk _i, N_i)\), where \( xk _i\) is a seed and \(N_i\) is a nonce. Moreover, \(( xk _1, N_1, \mathbf {m}[1]), ( xk _2, N_2, \mathbf {m}[2]), \ldots \) must be distinct. -
(ii)
For any \(I \subseteq \{1, \ldots , v(k)\}\) such that \(|I| \le d\), and any \(i \in \{1, \ldots , v(k)\} \backslash I\), for
 the conditional min-entropy of \((\mathbf {m}[i], xk _i, N_i)\) given
the conditional min-entropy of \((\mathbf {m}[i], xk _i, N_i)\) given 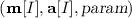 is at least \(\mu \), where v(k) is the number of messages that \({\mathcal M}\) produces and \( xk _i\) and \(N_i\) are the seed and nonce specified by \(\mathbf {a}[i]\).
is at least \(\mu \), where v(k) is the number of messages that \({\mathcal M}\) produces and \( xk _i\) and \(N_i\) are the seed and nonce specified by \(\mathbf {a}[i]\).
Defining unpredictable samplers allows us to model the situation when the seeds, nonces, and messages are related, and quantify security based on the combined min-entropy of each message with its nonce and seed.
\(\text {HN-SO-CPA}\) security. Let \({\mathsf {NE}}\) be a nonce-based PKE scheme, and let \({\mathcal M}\) be an unpredictable message sampler. Let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let \(A= (A.\mathrm {pg}, A.\mathrm {cor}, A.\mathrm {g}, A.\mathrm {f})\) be an adversary. Define
where the games are defined in Fig. 10.
\(\text {HN-SO-CCA}\) security. To add a CCA flavor to \(\text {HN-SO-CPA}\), one would give \(A.\mathrm {cor}\) and \(A.\mathrm {g}\) oracle access to \(\mathsf {Dec}( sk , \cdot )\). They are not allowed to query any \(\mathbf {c}[i]\) to the decryption oracle. Let \(\text {HN-CCA-REAL}\) and \(\text {HN-CCA-IDEAL}\) be the corresponding games, and define
Separation. We now show that \(\text {N-SO-CCA}\) doesn’t imply \(\text {HN-SO-CPA}\), even if \({\mathcal M}\) picks  and \(\mathbf {a}[i] = (i, i, i)\), and there’s no opening. Note that \({\mathcal M}\) is fully resamplable, and consider the function \(\delta \) such that
and \(\mathbf {a}[i] = (i, i, i)\), and there’s no opening. Note that \({\mathcal M}\) is fully resamplable, and consider the function \(\delta \) such that  . Let H be a hash and \({\mathsf {LT}}\) be a lossy trapdoor function. Let \(\mathsf {NE_{bad}}[H, {\mathsf {LT}}]\) be the following variant of \(\mathsf {NE2}[H, {\mathsf {LT}}]\). To encrypt message m under public key pk, seed \( xk \) and nonce N, instead of hashing \(( xk , N, m)\) to derive synthetic coins r, we just hash \(( xk , N)\). The proof of Theorem 5 can be recast to justify the \(\text {N-SO-CCA}\) security \(\mathsf {NE_{bad}}\). However, without even opening, one can trivially break \(\text {HN-SO-CPA}\) security of \(\mathsf {NE_{bad}}\) as follows. First, adversary \(A.\mathrm {pg}\) outputs an arbitrary
. Let H be a hash and \({\mathsf {LT}}\) be a lossy trapdoor function. Let \(\mathsf {NE_{bad}}[H, {\mathsf {LT}}]\) be the following variant of \(\mathsf {NE2}[H, {\mathsf {LT}}]\). To encrypt message m under public key pk, seed \( xk \) and nonce N, instead of hashing \(( xk , N, m)\) to derive synthetic coins r, we just hash \(( xk , N)\). The proof of Theorem 5 can be recast to justify the \(\text {N-SO-CCA}\) security \(\mathsf {NE_{bad}}\). However, without even opening, one can trivially break \(\text {HN-SO-CPA}\) security of \(\mathsf {NE_{bad}}\) as follows. First, adversary \(A.\mathrm {pg}\) outputs an arbitrary  . Next, adversary \(A.\mathrm {cor}\) stores the ciphertexts and the public key in its state, and outputs
. Next, adversary \(A.\mathrm {cor}\) stores the ciphertexts and the public key in its state, and outputs  . Adversary \(A.\mathrm {g}\) computes
. Adversary \(A.\mathrm {g}\) computes  , parses
, parses  , and outputs
, and outputs  . Finally, adversary
. Finally, adversary  simply outputs \(\mathbf {m}^*[1]\). The adversaries win with advantage \(1 - 2^{-k}\).
simply outputs \(\mathbf {m}^*[1]\). The adversaries win with advantage \(1 - 2^{-k}\).
5.2 Achieving \(\text {HN-SO-CPA}\) Security
\(\mathsf {NtD}\) transform. We first give a transform Nonce-then-Deterministic (\(\mathsf {NtD}\)). Let \({\mathsf {DE}}\) be a \(\text {D-SO-CPA}2\) secure D-PKE and \({\mathsf {NE}}\) be an \(\text {N-SO-CPA}\) secure nonce-based PKE. Then \(\mathsf {NtD}[{\mathsf {NE}}, {\mathsf {DE}}]\) achieves both \(\text {HN-SO-CPA}\) and \(\text {N-SO-CPA}\) security simultaneously. The resulting nonce-based PKE \(\mathsf {\overline{NE}}\) is a double encryption: it first encrypts via \({\mathsf {NE}}\), and then uses \({\mathsf {DE}}\) to encrypt the resulting ciphertext.Footnote 9 The transform \(\mathsf {NtD}\) is shown in Fig. 11, and Theorem 6 below confirms that it works as claimed.
Discussion. To explain why \(\mathsf {NtD}\) works, note that using an outer D-PKE on the ciphertext of \({\mathsf {NE}}\) doesn’t affect its \(\text {N-SO-CPA}\) security, and thus \(\mathsf {\overline{NE}}= \mathsf {NtD}[{\mathsf {NE}}, {\mathsf {DE}}]\) inherits the \(\text {N-SO-CPA}\) security of \({\mathsf {NE}}\). For \(\text {HN-SO-CPA}\) security, there are some subtle points as follows.
First, the “messages” for \({\mathsf {DE}}\) are the ciphertexts produced by \({\mathsf {NE}}\). Now, the \(\text {D-SO-CPA}2\) security demands that those “messages” must have good min-entropy, but we only know that the combined min-entropy of each message with its nonce and seed is \(\mu \). We need a bound, call it \({\mathsf {NE}}.{\mathsf {Guess}}(\mu )\), to quantify the min-entropy of the ciphertexts of \({\mathsf {NE}}\). Therefore, let \({\mathsf {NE}}.{\mathsf {Guess}}(\mu (k))\) be biggest number that, for any seed \( xk \), any nonce N, any message m, and any random variable X such that the conditional min-entropy of \((m, xk , N)\) given X is at least \(\mu (k)\), and  independent of \((m, xk , N, X)\), the conditional min-entropy of \({\mathsf {NE}}.{\mathsf {Enc}}( pk , xk , N, m)\) given X is at least \({\mathsf {NE}}.{\mathsf {Guess}}(\mu (k))\). We say that \({\mathsf {NE}}\) is entropy-preserving if for any \(\mu \) such that \(2^{-\mu }\) is negligible, so is \(2^{-{\mathsf {NE}}.{\mathsf {Guess}}(\mu )}\). For example, one can show that \(\mathsf {NE1}[H, {\mathsf {LT}}].{\mathsf {Guess}}(\mu (k)) \ge \min \{k, \mu (k) / 2\} - 1\), by modeling
independent of \((m, xk , N, X)\), the conditional min-entropy of \({\mathsf {NE}}.{\mathsf {Enc}}( pk , xk , N, m)\) given X is at least \({\mathsf {NE}}.{\mathsf {Guess}}(\mu (k))\). We say that \({\mathsf {NE}}\) is entropy-preserving if for any \(\mu \) such that \(2^{-\mu }\) is negligible, so is \(2^{-{\mathsf {NE}}.{\mathsf {Guess}}(\mu )}\). For example, one can show that \(\mathsf {NE1}[H, {\mathsf {LT}}].{\mathsf {Guess}}(\mu (k)) \ge \min \{k, \mu (k) / 2\} - 1\), by modeling  as a universal hash function, and using the Generalized Leftover Hash Lemma [1, Lemma 3.4]. Hence \(\mathsf {NE1}\) is entropy-preserving.
as a universal hash function, and using the Generalized Leftover Hash Lemma [1, Lemma 3.4]. Hence \(\mathsf {NE1}\) is entropy-preserving.
Next, we need to build an adversary \(B\) attacking \({\mathsf {DE}}\) from an adversary \(A\) that attacks \(\mathsf {\overline{NE}}\). Then \(B.\mathrm {pg}\) will run  , pick
, pick  , and outputs
, and outputs  , asking its sampler \(\overline{{\mathcal M}}\) to run \({\mathcal M}\) and encrypt the resulting messages, nonces, and seeds under \( pk \). At some point, \(A.\mathrm {cor}\) will asks to open some ciphertexts \(\mathbf {c}[I]\) to get the corresponding \(\mathbf {m}[I], \varvec{xk}[I], \varvec{N}[I]\), but the opened “messages” that \(B.\mathrm {g}\) receives are \({\mathsf {NE}}.{\mathsf {Enc}}( pk , \varvec{xk}[i, \varvec{N}[i], \mathbf {m}[i])\). Although \(B.\mathrm {g}\) knows the secret key \( sk \) of \({\mathsf {NE}}\), if we use \(\mathsf {NE1}\) to instantiate \({\mathsf {NE}}\) then one can’t recover \((\varvec{N}[i], \varvec{xk}[i])\) from just \(c_i = {\mathsf {NE}}.{\mathsf {Enc}}( pk , \varvec{xk}[i], \varvec{N}[i], \mathbf {m}[i])\) and \( sk \). Thanks to our explicit modeling of the auxiliary information, adversary \(B\) does get \((\varvec{xk}[i], \varvec{N}[i])\) when it opens \(\mathbf {c}[i]\).
, asking its sampler \(\overline{{\mathcal M}}\) to run \({\mathcal M}\) and encrypt the resulting messages, nonces, and seeds under \( pk \). At some point, \(A.\mathrm {cor}\) will asks to open some ciphertexts \(\mathbf {c}[I]\) to get the corresponding \(\mathbf {m}[I], \varvec{xk}[I], \varvec{N}[I]\), but the opened “messages” that \(B.\mathrm {g}\) receives are \({\mathsf {NE}}.{\mathsf {Enc}}( pk , \varvec{xk}[i, \varvec{N}[i], \mathbf {m}[i])\). Although \(B.\mathrm {g}\) knows the secret key \( sk \) of \({\mathsf {NE}}\), if we use \(\mathsf {NE1}\) to instantiate \({\mathsf {NE}}\) then one can’t recover \((\varvec{N}[i], \varvec{xk}[i])\) from just \(c_i = {\mathsf {NE}}.{\mathsf {Enc}}( pk , \varvec{xk}[i], \varvec{N}[i], \mathbf {m}[i])\) and \( sk \). Thanks to our explicit modeling of the auxiliary information, adversary \(B\) does get \((\varvec{xk}[i], \varvec{N}[i])\) when it opens \(\mathbf {c}[i]\).
Finally, one has to reason about the resamplability of the constructed sampler \(\overline{{\mathcal M}}\). Had we restricted our notions to fully resamplable samplers and the function  , we would have run into problem here. Why so? The resampling algorithm \(\overline{\mathsf {Rsmp}}\) of \(\overline{{\mathcal M}}\) has to generate \({\mathsf {NE}}.{\mathsf {Enc}}( pk , \varvec{xk}'[i], \varvec{N}'[i], \mathbf {m}'[i])\), but it only knows \( pk \) and another algorithm \(\mathsf {Rsmp}\) to generate \(\mathbf {m}'\). That is, it’s unclear how to resample the seeds \(\varvec{xk}'\) and nonces \(\varvec{N}'\). Using partial resamplability solves this issue. To justify this, suppose that we need to justify the \(\text {HN-SO-CPA}\) security of \(\mathsf {\overline{NE}}\) with respect to function \(\delta \). Then, we’ll find another function \(\overline{\delta }\) such that \(\mathbf {Adv}^{\text {hn-so-cpa}}_{\mathsf {\overline{NE}}, A, {\mathcal M}, \delta }(\cdot ) \le \mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},B, \overline{{\mathcal M}}, \overline{\delta }}(\cdot )\), and at the same time, \(\overline{{\mathcal M}}\) is \(\overline{\delta }\)-partially resamplable. The function
, we would have run into problem here. Why so? The resampling algorithm \(\overline{\mathsf {Rsmp}}\) of \(\overline{{\mathcal M}}\) has to generate \({\mathsf {NE}}.{\mathsf {Enc}}( pk , \varvec{xk}'[i], \varvec{N}'[i], \mathbf {m}'[i])\), but it only knows \( pk \) and another algorithm \(\mathsf {Rsmp}\) to generate \(\mathbf {m}'\). That is, it’s unclear how to resample the seeds \(\varvec{xk}'\) and nonces \(\varvec{N}'\). Using partial resamplability solves this issue. To justify this, suppose that we need to justify the \(\text {HN-SO-CPA}\) security of \(\mathsf {\overline{NE}}\) with respect to function \(\delta \). Then, we’ll find another function \(\overline{\delta }\) such that \(\mathbf {Adv}^{\text {hn-so-cpa}}_{\mathsf {\overline{NE}}, A, {\mathcal M}, \delta }(\cdot ) \le \mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},B, \overline{{\mathcal M}}, \overline{\delta }}(\cdot )\), and at the same time, \(\overline{{\mathcal M}}\) is \(\overline{\delta }\)-partially resamplable. The function  works as follows. It first parses
works as follows. It first parses  as
as  , runs \(\mathbf {m}[i] \leftarrow {\mathsf {NE}}.{\mathsf {Dec}}( sk , \mathbf {x}[i])\), and then outputs
, runs \(\mathbf {m}[i] \leftarrow {\mathsf {NE}}.{\mathsf {Dec}}( sk , \mathbf {x}[i])\), and then outputs  . We stress that the \(\mathsf {NtD}\) transform works in both the standard model and the NPROM. (Of course, this assumes that there are standard-model \(\text {D-SO-CPA}2\) secure D-PKE and \(\text {N-SO-CPA}\) secure entropy-preserving nonce-based PKE.)
. We stress that the \(\mathsf {NtD}\) transform works in both the standard model and the NPROM. (Of course, this assumes that there are standard-model \(\text {D-SO-CPA}2\) secure D-PKE and \(\text {N-SO-CPA}\) secure entropy-preserving nonce-based PKE.)
Theorem 6
Let \({\mathsf {NE}}\) be a nonce-based PKE, and let \({\mathsf {DE}}\) be a D-PKE scheme such that the ciphertext length of the former is a plaintext length of the latter. Let \(\mathsf {\overline{NE}}= \mathsf {NtD}[{\mathsf {NE}}, {\mathsf {DE}}]\).
\(\text {N-SO-CPA}\) adversary \(B\) in the proof of Theorem 6.
\(\underline{\text {N-SO-CPA}\ {\textsf {security:}}}\) For any adversary \(A\), any message sampler \({\mathcal M}\), any function \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable, and any nonce generator \(\mathsf {NG}\), there is an adversary \(B\) such that
The running time of \(B\) is about that of \(A\) plus the running time of \(\mathsf {DE.Kg}\) plus the time to run \(\mathsf {DE.Enc}\) on the messages that \({\mathcal M}\) produces.
\(\underline{\text {HN-SO-CPA}\ {\textsf {security:}}}\) For any \((\mu , d)\)-unpredictable message sampler \({\mathcal M}\), any function \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable, and any adversary \(A\), there are an adversary \(B\) that opens the same number of ciphertexts, another function \(\overline{\delta }\), and another \(({\mathsf {NE}}.{\mathsf {Guess}}(\mu ), d)\)-entropic, \(\overline{\delta }\)-partially resamplable message sampler \(\overline{{\mathcal M}}\) such that
The running time of \(B\) is about that of \(A\) plus the running time of \(\mathsf {\overline{NE}}.{\mathsf {Kg}}\) plus the time to run \(\mathsf {\overline{NE}}.{\mathsf {Dec}}\) on v ciphertexts, where v is the number of messages that \({\mathcal M}\) produces. The running time of \(\overline{{\mathcal M}}\) is about that of \({\mathcal M}\) plus the time to run \({\mathsf {NE}}.{\mathsf {Enc}}\) on v messages.
Proof
For the first part, consider an arbitrary adversary \(A\). Consider the adversary \(B\) in Fig. 12 attacking \({\mathsf {NE}}\). Then game \(\text {N-SO-CPA}_{{\mathsf {NE}}, \mathsf {NG}}^{B, {\mathcal M}, \delta }\) coincides with game \(\text {N-SO-CPA}_{\mathsf {\overline{NE}}, \mathsf {NG}}^{A, {\mathcal M}, \delta }\), and thus \(\mathbf {Adv}^{\text {n-so-cpa}}_{\mathsf {\overline{NE}}, \mathsf {NG}, A,{\mathcal M}, \delta }(\cdot ) = \mathbf {Adv}^{\text {n-so-cpa}}_{{\mathsf {NE}}, \mathsf {NG}, B, {\mathcal M}, \delta }(\cdot ).\)
For the second part, consider an arbitrary adversary \(A\) and a message sampler \({\mathcal M}\). Consider the following message sampler  . It parses
. It parses  as a triple
as a triple  , where \( pk _{\mathrm {n}}\) and \( sk _{\mathrm {n}}\) are public and secret keys for \({\mathsf {NE}}\). It then runs
, where \( pk _{\mathrm {n}}\) and \( sk _{\mathrm {n}}\) are public and secret keys for \({\mathsf {NE}}\). It then runs  to generate \((\mathbf {m}, \mathbf {a})\). Since \({\mathcal M}\) is unpredictable, each \(\mathbf {a}[i]\) can be parsed as \((a_i, xk _i, N_i)\). Now the “messages” of \({\mathcal M}\) is the vector \(\mathbf {y}\), where each \(\mathbf {y}[i] = {\mathsf {NE}}.{\mathsf {Enc}}( pk _{\mathrm {n}}, xk _i, N_i, \mathbf {m}[i])\), and the corresponding auxiliary information is still \(\mathbf {a}[i]\). The code of \(\overline{{\mathcal M}}\) is given in Fig. 13. Since \({\mathcal M}\) is \((\mu , d)\)-unpredictable, \(\overline{{\mathcal M}}\) is \(({\mathsf {NE}}.{\mathsf {Guess}}(\mu ), d)\)-entropic. Let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let
to generate \((\mathbf {m}, \mathbf {a})\). Since \({\mathcal M}\) is unpredictable, each \(\mathbf {a}[i]\) can be parsed as \((a_i, xk _i, N_i)\). Now the “messages” of \({\mathcal M}\) is the vector \(\mathbf {y}\), where each \(\mathbf {y}[i] = {\mathsf {NE}}.{\mathsf {Enc}}( pk _{\mathrm {n}}, xk _i, N_i, \mathbf {m}[i])\), and the corresponding auxiliary information is still \(\mathbf {a}[i]\). The code of \(\overline{{\mathcal M}}\) is given in Fig. 13. Since \({\mathcal M}\) is \((\mu , d)\)-unpredictable, \(\overline{{\mathcal M}}\) is \(({\mathsf {NE}}.{\mathsf {Guess}}(\mu ), d)\)-entropic. Let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let  be the following function. It parses
be the following function. It parses  as
as  , decrypts \(\mathbf {m}[i] \leftarrow {\mathsf {NE}}.{\mathsf {Dec}}( sk _{\mathrm {n}}, \mathbf {y}[i])\), and then returns
, decrypts \(\mathbf {m}[i] \leftarrow {\mathsf {NE}}.{\mathsf {Dec}}( sk _{\mathrm {n}}, \mathbf {y}[i])\), and then returns  . Then \(\overline{{\mathcal M}}\) is \(\overline{\delta }\)-partially resamplable: given any \(\delta \)-partial resampling algorithm \(\mathsf {Rsmp}\) for \({\mathcal M}\), we can construct a \(\overline{\delta }\)-partial resampling algorithm \(\overline{\mathsf {Rsmp}}\) for \(\overline{{\mathcal M}}\) as in Fig. 13.
. Then \(\overline{{\mathcal M}}\) is \(\overline{\delta }\)-partially resamplable: given any \(\delta \)-partial resampling algorithm \(\mathsf {Rsmp}\) for \({\mathcal M}\), we can construct a \(\overline{\delta }\)-partial resampling algorithm \(\overline{\mathsf {Rsmp}}\) for \(\overline{{\mathcal M}}\) as in Fig. 13.
\(\text {D-SO-CPA}2\) adversary \(B\), constructed sampler \(\overline{{\mathcal M}}\), and its partial resampling algorithm \(\overline{\mathsf {Rsmp}}\) in the proof of Theorem 6.
Now, consider the adversary \(B\) attacking \({\mathsf {DE}}\) as given in Fig. 13. It targets message sampler \(\overline{{\mathcal M}}\), with respect to function \(\overline{\delta }\). Initially, \(B.\mathrm {pg}(1^k)\) runs  , and then generates public and secret keys \( pk _{\mathrm {n}}\) and \( sk _{\mathrm {n}}\) for \({\mathsf {NE}}\). It then outputs
, and then generates public and secret keys \( pk _{\mathrm {n}}\) and \( sk _{\mathrm {n}}\) for \({\mathsf {NE}}\). It then outputs  . When \(B.\mathrm {g}\) receives its “messages” \(\mathbf {y}^*\), it extracts the secret key \( sk _{\mathrm {n}}\) from its state and decrypts \(\mathbf {m}^*[i] \leftarrow {\mathsf {NE}}.{\mathsf {Dec}}( sk _{\mathrm {n}}, \mathbf {y}^*[i])\), and then gives \(\mathbf {m}^*\) to \(A.\mathrm {g}\) together with the auxiliary information \(\mathbf {a}^*\). Then game \(\text {HN-CPA-REAL}_{\mathsf {\overline{NE}}}^{A, {\mathcal M}, \delta }\) coincides with game \(\text {D-CPA2-REAL}_{{\mathsf {DE}}}^{B, \overline{{\mathcal M}}, \overline{\delta }}\). Moreover, game \(\text {HN-CPA-IDEAL}_{\mathsf {\overline{NE}}}^{A, {\mathcal M}, \delta }\) coincides with \(\text {D-CPA2-IDEAL}_{{\mathsf {DE}}}^{B, \overline{{\mathcal M}}, \overline{\delta }}\). Hence \(\mathbf {Adv}^{\text {hn-so-cpa}}_{\mathsf {\overline{NE}}, A, {\mathcal M}, \delta }(\cdot ) \le \mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},B, \overline{{\mathcal M}}, \overline{\delta }}(\cdot )\). \(\square \)
. When \(B.\mathrm {g}\) receives its “messages” \(\mathbf {y}^*\), it extracts the secret key \( sk _{\mathrm {n}}\) from its state and decrypts \(\mathbf {m}^*[i] \leftarrow {\mathsf {NE}}.{\mathsf {Dec}}( sk _{\mathrm {n}}, \mathbf {y}^*[i])\), and then gives \(\mathbf {m}^*\) to \(A.\mathrm {g}\) together with the auxiliary information \(\mathbf {a}^*\). Then game \(\text {HN-CPA-REAL}_{\mathsf {\overline{NE}}}^{A, {\mathcal M}, \delta }\) coincides with game \(\text {D-CPA2-REAL}_{{\mathsf {DE}}}^{B, \overline{{\mathcal M}}, \overline{\delta }}\). Moreover, game \(\text {HN-CPA-IDEAL}_{\mathsf {\overline{NE}}}^{A, {\mathcal M}, \delta }\) coincides with \(\text {D-CPA2-IDEAL}_{{\mathsf {DE}}}^{B, \overline{{\mathcal M}}, \overline{\delta }}\). Hence \(\mathbf {Adv}^{\text {hn-so-cpa}}_{\mathsf {\overline{NE}}, A, {\mathcal M}, \delta }(\cdot ) \le \mathbf {Adv}^{\text {d-so-cpa}2}_{{\mathsf {DE}},B, \overline{{\mathcal M}}, \overline{\delta }}(\cdot )\). \(\square \)
\(\mathsf {NE1}\) alone is enough. Constructions via \(\mathsf {NtD}\) transform will be at least twice slower than \(\mathsf {NE1}\), because we need to run public primitives twice. But in the NPROM, \(\mathsf {NE1}[H, {\mathsf {LT}}]\) alone achieves both \(\text {N-SO-CPA}\) and \(\text {HN-SO-CPA}\) security simultaneously. In Theorem 7 below, we’ll show that \(\mathsf {NE1}\) is \(\text {HN-SO-CPA}\) secure. See the full version for the proof. We stress that for \((\mu , \infty )\)-unpredictable message samplers, \(\mathsf {NE1}\) allows the adversary to open as many ciphertexts as it wishes.
Theorem 7
Let \({\mathsf {LT}}\) be a lossy trapdoor function with lossiness \(\tau \). Let \({\mathcal M}\) be a \((\mu , d)\)-unpredictable resamplable message sampler, and let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let \(\mathsf {NE1}[H, {\mathsf {LT}}]\) be as above. In the NPROM, for any adversary \(A\) opening at most \(d\) ciphertexts, there is an adversary D such that
where q(k) is the total number of random-oracle queries of \(A\) and \({\mathcal M}\), and v(k) is the number of messages that \({\mathcal M}\) produces. The running time of D is about that of \(A\) plus the time to run \(\delta \) and an efficient \(\delta \)-partial resampling algorithm of \({\mathcal M}\) plus the time to run \(\mathsf {NE1}[H, {\mathsf {LT}}]\) to encrypt \({\mathcal M}\)’s messages. Adversary D makes at most q random-oracle queries.
5.3 Achieving \(\text {HN-SO-CCA}\) Security
In proving that \(\mathsf {NtD}[{\mathsf {NE}}, {\mathsf {DE}}]\) achieves \(\text {HN-SO-CPA}\) security, we don’t need any property of the D-PKE scheme \({\mathsf {DE}}\). This no longer holds for \(\text {HN-SO-CCA}\). Indeed, consider a scheme \({\mathsf {DE_{bad}}}\) such that \(\mathsf {DE_{bad}.Enc}\) appends 0 to the ciphertexts, and \(\mathsf {DE_{bad}.Dec}\) ignores the last bit of the ciphertexts. An adversary thus can obtain the plaintexts by modifying the last bits of the ciphertexts, and querying those to the decryption oracle. Hence to obtain \(\text {HN-SO-CCA}\), one has to exploit some property of \({\mathsf {DE}}\). We’ll need \({\mathsf {DE}}\) to be unique-ciphertext, a property formalized by Bellare and Hoang [7].
Formally, a D-PKE scheme \({\mathsf {DE}}\) is unique-ciphertext if for every \(k \in {{\mathbb N}}\), every \(( pk , sk ) \in [\mathsf {DE.Kg}(1^k)]\), and every \(m \in \{0,1\}^*\), there is at most a string c such that \(\mathsf {DE.Dec}( sk , c) = m\). The D-PKE scheme \({\mathsf {DE_{bad}}}\) above is not unique-ciphertext. The unique-ciphertext property of \({\mathsf {DE}}\) ensures that if one modifies a ciphertext of \(\mathsf {NtD}[{\mathsf {NE}}, {\mathsf {DE}}]\), the underneath ciphertext of \({\mathsf {NE}}\) will be changed.
Bellare and Hoang also show how to efficiently transform a D-PKE scheme \({\mathsf {DE}}\) to a unique-ciphertext one \(\mathsf {UE}\): in the decryption, we first recover the message, and then re-encrypt it and return \(\bot \) if the newly constructed ciphertext doesn’t match the given one. The transform \(\mathsf {UniqueCtx}\) is given in Fig. 14. Note that this transform doesn’t affect the \(\text {D-SO-CCA}\) security of \({\mathsf {DE}}\). Indeed, for any message sampler \({\mathcal M}\), any PT adversary \(A\) attacking \(\mathsf {UE}= \mathsf {UniqueCtx}[{\mathsf {DE}}]\), it’s trivial to construct another PT adversary \(B\) attacking \({\mathsf {DE}}\) such that \(\mathbf {Adv}^{\text {d-so-cca}}_{\mathsf {UE},B, {\mathcal M}}(\cdot ) \le \mathbf {Adv}^{\text {d-so-cca}}_{{\mathsf {DE}}, A, {\mathcal M}}(\cdot )\).
Let \({\mathsf {DE}}\) be unique-ciphertext and \(\text {D-SO-CCA}\) secure D-PKE and \({\mathsf {NE}}\) be an \(\text {N-SO-CCA}\) secure, entropy-preserving nonce-based PKE. Then, Theorem 8 confirms \(\mathsf {NtD}[{\mathsf {NE}}, {\mathsf {DE}}]\) achieves both \(\text {HN-SO-CCA}\) and \(\text {N-SO-CCA}\) security simultaneously; the proof is in the full version. To instantiate \({\mathsf {DE}}\), one can either apply the \(\mathsf {UniqueCtx}\) transform on a \(\text {D-SO-CCA}\) secure D-PKE scheme, or directly use our construction \({\mathsf {DE2}}\) in Sect. 3.3.
Theorem 8
Let \({\mathsf {NE}}\) be a nonce-based PKE as above, and let \({\mathsf {DE}}\) be a unique-ciphertext D-PKE scheme such that the ciphertext length of the former is a plaintext length of the latter. Let \(\mathsf {\overline{NE}}= \mathsf {NtD}[{\mathsf {NE}}, {\mathsf {DE}}]\).
\(\underline{\text {N-SO-CCA}\ {\textsf {security:}}}\) For any adversary \(A\), any message sampler \({\mathcal M}\), any function \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable, and any nonce generator \(\mathsf {NG}\), there is an adversary \(B\) such that
The running time of \(B\) is about that of \(A\) plus the running time of \(\mathsf {DE.Kg}\) plus the time to run \(\mathsf {DE.Enc}\) on the messages that \(A\) produces, and the time to run \(\mathsf {DE.Dec}\) on the decryption queries of \(A\). Adversary \(B\) makes as many decryption-oracle queries as \(A\).
\(\underline{\text {HN-SO-CCA}\ {\textsf {security:}}}\) For any adversary \(A\), any \((\mu , d)\)-unpredictable message sampler \({\mathcal M}\), and any function \(\delta \) such that \({\mathcal M}\) is \(\delta \)-partially resamplable, there are an adversary \(B\) that opens the same number of ciphertexts, a function \(\overline{\delta }\), and an \(({\mathsf {NE}}.{\mathsf {Guess}}(\mu ), d)\)-entropic, \(\overline{\delta }\)-partially resamplable message sampler \(\overline{{\mathcal M}}\) such that
The running time of \(B\) is about that of \(A\) plus the running time of \(\mathsf {\overline{NE}}.{\mathsf {Kg}}\) plus the time to run \(\mathsf {\overline{NE}}.{\mathsf {Dec}}\) on \(v + p\) ciphertexts, where v is the number of messages that \({\mathcal M}\) produces and p is the number of \(A\)’s decryption-oracle queries. Adversary \(B\) makes as many decryption-oracle queries as \(A\). The running time of \(\overline{{\mathcal M}}\) is about that of \({\mathcal M}\) plus the time to run \({\mathsf {NE}}.{\mathsf {Enc}}\) on v messages.
Alternatively, we can use \(\mathsf {NE2}\) directly. In Theorem 9 below, we’ll show that \(\mathsf {NE2}\) is \(\text {HN-SO-CCA}\) secure. See the full version for the proof.
Theorem 9
Let \({\mathsf {LT}}\) be a lossy trapdoor function with lossiness \(\tau \). Let \({\mathcal M}\) be a \((\mu , d)\)-unpredictable message sampler, and let \(\delta \) be a function such that \({\mathcal M}\) is \(\delta \)-partially resamplable. Let \(\mathsf {NE2}[H, {\mathsf {LT}}]\) be as above. In the NPROM, for any adversary \(A\) opening at most \(d\) ciphertexts, there is an adversary D such that
where q(k) is the total number of random-oracle queries of \(A\) and \({\mathcal M}\), v(k) is the number of messages that \({\mathcal M}\) produces, and p(k) is the number of decryption queries of \(A\), and \(Q(k) = q(k) + 2p(k)\). The running time of D is about that of \(A\) plus the time to run \(\delta \) and a \(\delta \)-partial resampling algorithm of \({\mathcal M}\) plus the time to run \(\mathsf {NE2}[H, {\mathsf {LT}}]\) to encrypt \({\mathcal M}\)’s messages. Adversary D makes at most Q random-oracle queries.
Notes
- 1.
There are two forms of SOA security, called coin-revealing (corresponding to sender corruption) and key-revealing (corresponding to receiver corruption). This paper concerns the first one.
- 2.
The idea is that because a seed is chosen infrequently, it can be generated using high-quality randomness.
- 3.
In the main body of the paper we treat both CPA and CCA security. For simplicity, we do not discuss CCA here.
- 4.
Here for simplicity, we only consider \({\mathcal M}\) and \(\mathsf {Rsmp}\) such that the distributions of
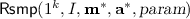 and
and  are identical. Following [9], one might also consider \({\mathcal M}\) and \(\mathsf {Rsmp}\) such that the two distributions above are statistically close.
are identical. Following [9], one might also consider \({\mathcal M}\) and \(\mathsf {Rsmp}\) such that the two distributions above are statistically close. - 5.
A technical difference is that, to be consistent with [4], we require the “partial information” to be an efficiently computable function of the messages. This formulation can be shown equivalent to a definition in the style of [2] up to a difference of one in the size of the message vectors output by \({\mathcal M}\), following [6, Appendix A].
- 6.
Even for the simple case that \({\mathcal M}\) is fully resamplable and outputs empty auxiliary information, and
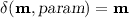 , note that if I is correlated to \(\mathbf {m}\) then \(\mathbf {m}\) and the re-sampled \(\mathbf {m}'\) may have completely different distributions. For example, consider \({\mathcal M}\) that outputs \((m_1, m_2)\), with
, note that if I is correlated to \(\mathbf {m}\) then \(\mathbf {m}\) and the re-sampled \(\mathbf {m}'\) may have completely different distributions. For example, consider \({\mathcal M}\) that outputs \((m_1, m_2)\), with  and
and  . Since \(m_1\) and \(m_2\) are independent, \({\mathcal M}\) is fully resamplable. Let \(I = \{1\}\) if \(m_1 = 00\), and \(I = \{2\}\) otherwise. Then \(\Pr [\mathbf {m}' = (00, 11)] = 3/8\), whereas \(\Pr [\mathbf {m}= (00, 11)]= 1/4\).
. Since \(m_1\) and \(m_2\) are independent, \({\mathcal M}\) is fully resamplable. Let \(I = \{1\}\) if \(m_1 = 00\), and \(I = \{2\}\) otherwise. Then \(\Pr [\mathbf {m}' = (00, 11)] = 3/8\), whereas \(\Pr [\mathbf {m}= (00, 11)]= 1/4\). - 7.
This assumption crucially relies on our use of a domain separation in hashing the coins r and the messages m: we employ
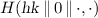 for m, but
for m, but 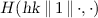 for r. In contrast, BH’s variant [7] doesn’t use domain separation, and one can’t make this assumption anymore: building the corresponding ciphertexts may create additional queries to
for r. In contrast, BH’s variant [7] doesn’t use domain separation, and one can’t make this assumption anymore: building the corresponding ciphertexts may create additional queries to  , leading to a possible exponential blowup on the number of random-oracle queries.
, leading to a possible exponential blowup on the number of random-oracle queries. - 8.
The definition of BT [10] requires that if the seed \( xk \) is secret then security should hold as long as the message/nonce pairs are unique. If one directly extends this to the SOA setting, there will be some pesky issue, as the adversary can detect equality within the message vectors by repeating the nonces. Here for simplicity, we only demand that nonces should be unique, which is analogous to nonce-based symmetric encryption. Nevertheless, our constructions are specific instantiations of BT construction, and thus meet their requirement.
- 9.
For simplicity, we assume that the ciphertext length of \(\mathsf {\overline{NE}}\) is the plaintext length of \({\mathsf {DE}}\). One may also consider a more generalized setting in which the ciphertext length of \({\mathsf {NE}}\) is smaller than the plaintext length of \({\mathsf {DE}}\). In this case one needs to pad \(10^*\) to the ciphertexts of \({\mathsf {NE}}\) before feeding them to \({\mathsf {DE}}\).
References
Barak, B., Dodis, Y., Krawczyk, H., Pereira, O., Pietrzak, K., Standaert, F.-X., Yu, Y.: Leftover hash lemma, revisited. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 1–20. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22792-9_1
Bellare, M., Boldyreva, A., O’Neill, A.: Deterministic and efficiently searchable encryption. In: Menezes, A. (ed.) CRYPTO 2007. LNCS, vol. 4622, pp. 535–552. Springer, Heidelberg (2007). doi:10.1007/978-3-540-74143-5_30
Bellare, M., Brakerski, Z., Naor, M., Ristenpart, T., Segev, G., Shacham, H., Yilek, S.: Hedged public-key encryption: how to protect against bad randomness. In: Matsui, M. (ed.) ASIACRYPT 2009. LNCS, vol. 5912, pp. 232–249. Springer, Heidelberg (2009). doi:10.1007/978-3-642-10366-7_14
Bellare, M., Dowsley, R., Keelveedhi, S.: How secure is deterministic encryption? In: Katz, J. (ed.) PKC 2015. LNCS, vol. 9020, pp. 52–73. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46447-2_3
Bellare, M., Dowsley, R., Waters, B., Yilek, S.: Standard security does not imply security against selective-opening. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 645–662. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_38
Bellare, M., Fischlin, M., O’Neill, A., Ristenpart, T.: Deterministic encryption: definitional equivalences and constructions without random oracles. In: Wagner, D. (ed.) CRYPTO 2008. LNCS, vol. 5157, pp. 360–378. Springer, Heidelberg (2008). doi:10.1007/978-3-540-85174-5_20
Bellare, M., Hoang, V.T.: Resisting randomness subversion: fast deterministic and hedged public-key encryption in the standard model. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 627–656. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_21
Bellare, M., Hoang, V.T., Keelveedhi, S.: Instantiating random oracles via UCEs. In: Canetti, R., Garay, J.A. (eds.) CRYPTO 2013. LNCS, vol. 8043, pp. 398–415. Springer, Heidelberg (2013). doi:10.1007/978-3-642-40084-1_23
Bellare, M., Hofheinz, D., Yilek, S.: Possibility and impossibility results for encryption and commitment secure under selective opening. In: Joux, A. (ed.) EUROCRYPT 2009. LNCS, vol. 5479, pp. 1–35. Springer, Heidelberg (2009). doi:10.1007/978-3-642-01001-9_1
Bellare, M., Tackmann, B.: Nonce-based cryptography: retaining security when randomness fails. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9665, pp. 729–757. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49890-3_28
Böhl, F., Hofheinz, D., Kraschewski, D.: On definitions of selective opening security. In: Fischlin, M., Buchmann, J., Manulis, M. (eds.) PKC 2012. LNCS, vol. 7293, pp. 522–539. Springer, Heidelberg (2012). doi:10.1007/978-3-642-30057-8_31
Cash, D., Grubbs, P., Perry, J., Ristenpart, T.: Leakage-abuse attacks against searchable encryption. In CCS, pp. 668–679 (2015)
Fujisaki, E., Okamoto, T.: How to enhance the security of public-key encryption at minimum cost. In: Imai, H., Zheng, Y. (eds.) PKC 1999. LNCS, vol. 1560, pp. 53–68. Springer, Heidelberg (1999). doi:10.1007/3-540-49162-7_5
Heuer, F., Kiltz, E., Pietrzak, K.: Standard security does imply security against selective opening for markov distributionss. Cryptology ePrint Archive, Report 2015/853 (2015). http://eprint.iacr.org/2015/853
Hofheinz, D., Rao, V., Wichs, D.: Standard security does not imply indistinguishability under selective opening. Cryptology ePrint Archive, Report 2015/792 (2015). http://eprint.iacr.org/2015/792
Hofheinz, D., Rupp, A.: Standard versus selective opening security: separation and equivalence results. In: Lindell, Y. (ed.) TCC 2014. LNCS, vol. 8349, pp. 591–615. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54242-8_25
Ishai, Y., Pandey, O., Sahai, A.: Public-coin differing-inputs obfuscation and its applications. In: Dodis, Y., Nielsen, J.B. (eds.) TCC 2015. LNCS, vol. 9015, pp. 668–697. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46497-7_26
Kamara, S., Katz, J.: How to encrypt with a malicious random number generator. In: Nyberg, K. (ed.) FSE 2008. LNCS, vol. 5086, pp. 303–315. Springer, Heidelberg (2008). doi:10.1007/978-3-540-71039-4_19
Kiltz, E., O’Neill, A., Smith, A.: Instantiability of RSA-OAEP under chosen-plaintext attack. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 295–313. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_16
Nielsen, J.B.: Separating random oracle proofs from complexity theoretic proofs: the non-committing encryption case. In: Yung, M. (ed.) CRYPTO 2002. LNCS, vol. 2442, pp. 111–126. Springer, Heidelberg (2002). doi:10.1007/3-540-45708-9_8
Peikert, C., Waters, B.: Lossy trapdoor functions and their applications. In: Ladner, R.E., Dwork, C. (eds.), 40th ACM STOC, pp. 187–196, Victoria, British Columbia, Canada, May 17–20. ACM Press (2008)
Seurin, Y.: On the lossiness of the rabin trapdoor function. In: Krawczyk, H. (ed.) PKC 2014. LNCS, vol. 8383, pp. 380–398. Springer, Heidelberg (2014). doi:10.1007/978-3-642-54631-0_22
Yilek, S.: Resettable public-key encryption: how to encrypt on a virtual machine. In: Pieprzyk, J. (ed.) CT-RSA 2010. LNCS, vol. 5985, pp. 41–56. Springer, Heidelberg (2010). doi:10.1007/978-3-642-11925-5_4
Acknowledgments
We thank the Asiacrypt reviewers for their insightful comments. This work was supported in part by NSF awards CNS-1223623, CNS-1423566, and CNS-1553758 (CAREER), as well as the Glen and Susanne Culler Chair. The work of Viet Tung Hoang was done while at the University of Maryland, Georgetown University, and UC Santa Barbara.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Hoang, V.T., Katz, J., O’Neill, A., Zaheri, M. (2016). Selective-Opening Security in the Presence of Randomness Failures. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10032. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53890-6_10
Download citation
DOI: https://doi.org/10.1007/978-3-662-53890-6_10
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53889-0
Online ISBN: 978-3-662-53890-6
eBook Packages: Computer ScienceComputer Science (R0)





 , and
, and 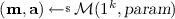 , conditioning on messages
, conditioning on messages  , each other message
, each other message  and any
and any  .
.



 and the check
and the check  can be omitted.
can be omitted.




 , each
, each  the conditional min-entropy of
the conditional min-entropy of 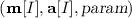 is at least
is at least 




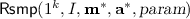 and
and  are identical. Following [
are identical. Following [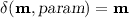 , note that if I is correlated to
, note that if I is correlated to 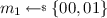 and
and 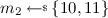 . Since
. Since 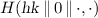 for m, but
for m, but 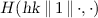 for r. In contrast, BH’s variant [
for r. In contrast, BH’s variant [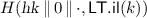 , leading to a possible exponential blowup on the number of random-oracle queries.
, leading to a possible exponential blowup on the number of random-oracle queries.