Abstract
We present the Balloon password-hashing algorithm. This is the first practical cryptographic hash function that: (i) has proven memory-hardness properties in the random-oracle model, (ii) uses a password-independent access pattern, and (iii) meets—and often exceeds—the performance of the best heuristically secure password-hashing algorithms. Memory-hard functions require a large amount of working space to evaluate efficiently and, when used for password hashing, they dramatically increase the cost of offline dictionary attacks. In this work, we leverage a previously unstudied property of a certain class of graphs (“random sandwich graphs”) to analyze the memory-hardness of the Balloon algorithm. The techniques we develop are general: we also use them to give a proof of security of the scrypt and Argon2i password-hashing functions, in the random-oracle model. Our security analysis uses a sequential model of computation, which essentially captures attacks that run on single-core machines. Recent work shows how to use massively parallel special-purpose machines (e.g., with hundreds of cores) to attack memory-hard functions, including Balloon. We discuss these important attacks, which are outside of our adversary model, and propose practical defenses against them. To motivate the need for security proofs in the area of password hashing, we demonstrate and implement a practical attack against Argon2i that successfully evaluates the function with less space than was previously claimed possible. Finally, we use experimental results to compare the performance of the Balloon hashing algorithm to other memory-hard functions.
The full version of this paper is available online at https://eprint.iacr.org/2016/027.
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
The staggering number of password-file breaches in recent months demonstrates the importance of cryptographic protection for stored passwords. In 2015 alone, attackers stole files containing users’ login names, password hashes, and contact information from many large and well-resourced organizations, including LastPass [79], Harvard [47], E*Trade [62], ICANN [45], Costco [41], T-Mobile [76], the University of Virginia [74], and a large number of others [65]. In this environment, systems administrators must operate under the assumption that attackers will eventually gain access to sensitive authentication information, such as password hashes and salts, stored on their computer systems. After a compromise, the secrecy of user passwords rests on the cost to an attacker of mounting an offline dictionary attack against the stolen file of hashed passwords.
An ideal password-hashing function has the property that it costs as much for an attacker to compute the function as it does for the legitimate authentication server to compute it. Standard cryptographic hashes completely fail in this regard: it takes \(100\,000\times \) more energy to compute a SHA-256 hash on a general-purpose x86 CPU (as an authentication server would use) than it does to compute SHA-256 on special-purpose hardware (such as the ASICs that an attacker would use) [21]. Iterating a standard cryptographic hash function, as is done in bcrypt [66] and PBKDF2 [43], increases the absolute cost to the attacker and defender, but the attacker’s \(100\,000\times \) relative cost advantage remains.
Memory-hard functions help close the efficiency gap between the attacker and defender in the setting of password hashing [8, 18, 37, 56, 60]. Memory-hard functions exploit the observation that on-chip memory is just as costly to power on special-purpose hardware as it is on a general-purpose CPU. If evaluating the password-hashing function requires large amounts of memory, then an attacker using special-purpose hardware has little cost advantage over the legitimate authentication server (using a standard x86 machine, for example) at running the password-hashing computation. Memory consumes a large amount of on-chip area, so the high memory requirement ensures that a special-purpose chip can only contain a small number of hashing engines.
An optimal memory-hard function, with security parameter n, has a space-time product that satisfies \(S \cdot T \in \varOmega (n^2)\), irrespective of the strategy used to compute the function [60]. The challenge is to construct a function that provably satisfies this bound with the largest possible constant multiple on the \(n^2\) term.
In this paper, we introduce the Balloon memory-hard function for password hashing. This is the first practical password-hashing function to simultaneously satisfy three important design goals [56]:
-
Proven memory-hard. We prove, in the random-oracle model [13], that computing the Balloon function with space S and time T requires \(S\cdot T \ge n^2/8\) (approximately). As the adversary’s space usage decreases, we prove even sharper time-space lower bounds.
To motivate our interest in memory-hardness proofs, we demonstrate in Sect. 4 an attack against the Argon2i password hashing function [18], winner of a recent password-hashing design competition [56]. The attack evaluates the function with far less space than claimed without changing the time required to compute the function. We also give a proof of security for Argon2i in the random-oracle model, which demonstrates that significantly more powerful attacks against Argon2i are impossible under our adversary model.
-
Password-independent memory-access pattern. The memory-access pattern of the Balloon algorithm is independent of the password being hashed. Password-hashing functions that lack this property are vulnerable to a crippling attack in the face of an adversary who learns the memory-access patterns of the hashing computation, e.g., via cache side-channels [23, 54, 77]. The attack, which we describe in the full version of this paper, makes it possible to run a dictionary attack with very little memory. A hashing function with a password-independent memory-access pattern eliminates this threat.
-
Performant. The Balloon algorithm is easy to implement and it matches or exceeds the performance of the fastest comparable password-hashing algorithms, Argon2i [18] and Catena [37], when instantiated with standard cryptographic primitives (Sect. 6).
We analyze the memory-hardness properties of the Balloon function using pebble games, which are arguments about the structure of the data-dependency graph of the underlying computation [48, 57, 59, 72, 75]. Our analysis uses the framework of Dwork, Naor, and Wee [32]—later applied in a number of cryptographic works [6, 8, 33, 34, 37]—to relate the hardness of pebble games to the hardness of certain computations in the random-oracle model [13].
The crux of our analysis is a new observation about the properties of “random sandwich graphs,” a class of graphs studied in prior work on pebbling [6, 8]. To show that our techniques are broadly applicable, we apply them in the full version of this paper to give simple proofs of memory-hardness, in the random-oracle model, for the Argon2i and scrypt functions. We prove stronger memory-hardness results about the Balloon algorithm, but these auxiliary results about Argon2i and scrypt may be of independent interest to the community.
The performance of the Balloon hashing algorithm is surprisingly good, given that our algorithm offers stronger proven security properties than other practical memory-hard functions with a password-independent memory access patterns. For example, if we configure Balloon to use Blake2b as the underlying hash function [10], run the construction for five “rounds” of hashing, and set the space parameter to require the attacker to use 1 MiB of working space to compute the function, then we can compute Balloon Hashes at the rate of 13 hashes per second on a modern server, compared with 12.8 for Argon2i, and 2.1 for Catena DBG (when Argon2i and Catena DBG are instantiated with Blake2b as the underlying cryptographic hash function).Footnote 1
Caveat: Parallel Attacks. The definition of memory-hardness we use puts a lower-bound on the time-space product of computing a single instance of the Balloon function on a sequential (single-core) computer. In reality, an adversary mounting a dictionary attack would want to compute billions of instances of the Balloon function, perhaps using many processors running in parallel. Alwen and Serbinenko [8], formalizing earlier work by Percival [60], introduce a new computational model— the parallel random-oracle model (pROM)—and a memory-hardness criterion that addresses the shortcomings of the traditional model. In recent work, Alwen and Blocki prove the surprising result that no function that uses a password-independent memory access pattern can be optimally memory-hard in the pROM [3]. In addition, they give a special-purpose pROM algorithm for computing Argon2i, Balloon, and other practical (sequential) memory-hard functions with some space savings. We discuss this important class of attacks and the relevant related work in Sect. 5.1.
Contributions. In this paper, we
-
introduce and analyze the Balloon hashing function, which has stronger provable security guarantees than prior practical memory-hard functions (Sect. 3),
-
present a practical memory-saving attack against the Argon2i password-hashing algorithm (Sect. 4), and
-
explain how to ameliorate the danger of massively parallel attacks against memory-hard functions with a password-independent access pattern (Sect. 5.1)
-
prove the first known time-space lower bounds for Argon2i and an idealized variant of scrypt, in the random-oracle model. (See the full version of this paper for these results.)
With the Balloon algorithm, we demonstrate that it is possible to provide provable protection against a wide class of attacks without sacrificing performance.
Notation. Throughout this paper, Greek symbols (\(\alpha \), \(\beta \), \(\gamma \), \(\lambda \), etc.) typically denote constants greater than one. We use \(\log _2(\cdot )\) to denote a base-two logarithm and \(\log (\cdot )\) to denote a logarithm when the base is not important. For a finite set S, the notation  indicates sampling an element of S uniformly at random and assigning it to the variable x.
indicates sampling an element of S uniformly at random and assigning it to the variable x.
2 Security Definitions
This section summarizes the high-level security and functionality goals of a password hashing function in general and the Balloon hashing algorithm in particular. We draw these aims from prior work on password hashing [60, 66] and also from the requirements of the recent Password Hashing Competition [56].
2.1 Syntax
The Balloon password hashing algorithm takes four inputs: a password, salt, time parameter, and space parameter. The output is a bitstring of fixed length (e.g., 256 or 512 bits). The password and salt are standard [52], but we elaborate on the role of the latter parameters below.
Space Parameter (Buffer Size). The space parameter, which we denote as “n” throughout, indicates how many fixed-size blocks of working space the hash function will require during the course of its computation, as in scrypt [60]. At a high level, a memory-hard function should be “easy” to compute with n blocks of working space and should be “hard” to compute with much less space than that. We make this notion precise later on.
Time Parameter (Number of Rounds). The Balloon function takes as input a parameter r that determines the number of “rounds” of computation it performs. As in bcrypt [66], the larger the time parameter, the longer the hash computation will take. On memory-limited platforms, a system administrator can increase the number of rounds of hashing to increase the cost of computing the function without increasing the algorithm’s memory requirement. The choice of r has an effect on the memory-hardness properties of the scheme: the larger r is, the longer it takes to compute the function in small space.
2.2 Memory-Hardness
We say that a function \(f_n\) on space parameter n is memory-hard in the (sequential) random-oracle model [13] if, for all adversaries computing \(f_n\) with high probability using space S and T random oracle queries, we have that \(S \cdot T \in \varOmega (n^2)\). This definition deserves a bit of elaboration. Following Dziembowski et al. [34] we say that an algorithm “uses space S” if the entire configuration of the Turing Machine (or RAM machine) computing the algorithm requires at least S bits to describe. When, we say that an algorithm computes a function “with high probability,” we mean that the probability that the algorithm computes the function is non-negligible as the output size of the random oracle and the space parameter n tend to infinity. In practice, we care about the adversary’s concrete success probability, so we avoid asymptotic notions of security wherever possible. In addition, as we discuss in the evaluation section (Sect. 6), the exact value of the constant hidden inside the \(\varOmega (\cdot )\) is important for practical purposes, so our analysis makes explicit and optimizes these constants.
A function that is memory-hard under this definition requires the adversary to use either a lot of working space or a lot of execution time to compute the function. Functions that are memory-hard in this way are not amenable to implementation in special-purpose hardware (ASIC), since the cost to power a unit of memory for a unit of time on an ASIC is the same as the cost on a commodity server. An important limitation of this definition is that it does not take into account parallel or multiple-instance attacks, which we discuss in Sect. 5.1.
2.3 Password-Independent Access Pattern
A first-class design goal of the Balloon algorithm is to have a memory access pattern that is independent of the password being hashed. (We allow the data-access pattern to depend on the salt, since the salts can be public.) As mentioned above, employing a password-independent access pattern reduces the risk that information about the password will leak to other users on the same machine via cache or other side-channels [23, 54, 77]. This may be especially important in cloud-computing environments, in which many mutually distrustful users share a single physical host [69].
Creating a memory-hard function with a password-independent access pattern presents a technical challenge: since the data-access pattern depends only upon the salt—which an adversary who steals the password file knows—the adversary can compute the entire access pattern in advance of a password-guessing attack. With the access pattern in hand, the adversary can expend a huge amount of effort to find an efficient strategy for computing the hash function in small space. Although this pre-computation might be expensive, the adversary can amortize its cost over billions of subsequent hash evaluations. A function that is memory-hard and that uses a password-independent data access pattern must be impervious to all small-space strategies for computing the function so that it maintains its strength in the face of these pre-computation attacks. (Indeed, as we discuss in Sect. 5.1, Alwen and Blocki show that in some models of computation, memory-hard functions with password-independent access patterns do not exist [3].)
2.4 Collision Resistance, etc.
If necessary, we can modify the Balloon function so that it provides the standard properties of second-preimage resistance and collision resistance [51]. It is possible to achieve these properties in a straightforward way by composing the Balloon function B with a standard cryptographic hash function H as
Now, for example, if H is collision-resistant, then \(H_B\) must also be.Footnote 2 That is because any inputs \((x_p, x_s) \ne (y_p, y_s)\) to \(H_B\) that cause \(H_B(x_p, x_s) = H_B(y_p, y_s)\) immediately yield a collision for H as:
no matter how the Balloon function B behaves.
3 Balloon Hashing Algorithm
In this section, we present the Balloon hashing algorithm.
3.1 Algorithm
The algorithm uses a standard (non-memory-hard) cryptographic hash function \(H: \mathbb {Z}_N \times \{0,1\}^{2k} \rightarrow \{0,1\}^k\) as a subroutine, where N is a large integer. For the purposes of our analysis, we model the function H as a random oracle [13].
The Balloon algorithm uses a large memory buffer as working space and we divide this buffer into contiguous blocks. The size of each block is equal to the output size of the hash function H. Our analysis is agnostic to the choice of hash function, except that, to prevent pitfalls described in the full version of this paper, the internal state size of H must be at least as large as its output size. Since H maps blocks of 2k bits down to blocks of k bits, we sometimes refer to H as a cryptographic compression function.
The Balloon function operates in three steps (Fig. 1):
-
1.
Expand. In the first step, the Balloon algorithm fills up a large buffer with pseudo-random bytes derived from the password and salt by repeatedly invoking the compression function H on a function of the password and salt.
-
2.
Mix. In the second step, the Balloon algorithm performs a “mixing” operation r times on the pseudo-random bytes in the memory buffer. The user-specified round parameter r determines how many rounds of mixing take place. At each mixing step, for each block i in the buffer, the routine updates the contents of block i to be equal to the hash of block \((i-1) \bmod n\), block i, and \(\delta \) other blocks chosen “at random” from the buffer. (See Theorem 1 for an illustration of how the choice of \(\delta \) affects the security of the scheme.)
Since the Balloon functions are deterministic functions of their arguments, the dependencies are not chosen truly at random but are sampled using a pseudorandom stream of bits generated from the user-specific salt.
-
3.
Extract. In the last step, the Balloon algorithm outputs the last block of the buffer.
Multi-core Machines. A limitation of the Balloon algorithm as described is that it does not allow even limited parallelism, since the value of the ith block computed always depends on the value of the \((i-1)\)th block. To increase the rate at which the Balloon algorithm can fill memory on a multi-core machine with M cores, we can define a function that invokes the Balloon function M times in parallel and XORs all the outputs. If \(\textsf {Balloon}(p, s)\) denotes the Balloon function on password p and salt s, then we can define an M-core variant \(\textsf {Balloon}_M(p, s)\) as:

A straightforward argument shows that computing this function requires computing M instances of the single-core Balloon function. Existing password hashing functions deploy similar techniques on multi-core platforms [18, 37, 60, 61].
3.2 Main Security Theorem
The following theorem demonstrates that attackers who attempt to compute the Balloon function in small space must pay a large penalty in computation time. The complete theorem statement is given in the full version of this paper.
Theorem 1 (informal)
Let \(\mathcal {A}\) be an algorithm that computes the n-block r-round Balloon function with security parameter \(\delta \ge 3\), where H is modeled as a random oracle. If \(\mathcal {A}\) uses at most S blocks of buffer space then, with overwhelming probability, \(\mathcal {A}\) must run for time (approximately) T, such that
Moreover, under the stated conditions, one obtains the stronger bound:
The theorem shows that, when the adversary’s space usage falls below a certain threshold (parameterized by \(\delta \)), the computation time increases exponentially in the number of rounds r. For example, when \(\delta = 7\) and the space S is less than n/8, the time to evaluate Balloon is at least \(2^r\) times the time to evaluate it with space n. Thus, attackers who attempt to compute the Balloon function in very small space must pay a large penalty in computation time.
The proof of the theorem is given in the full version of this paper.
Here we sketch the main ideas in the proof of Theorem 1.
Proof idea. The proof makes use of pebbling arguments, a classic technique for analyzing computational time-space trade-offs [42, 48, 59, 63, 72, 78] and memory-hard functions [8, 32, 33, 37]. We apply pebbling arguments to the data-dependency graph corresponding to the computation of the Balloon function (See Fig. 2 for an example graph). The graph contains a vertex for every random oracle query made during the computation of Balloon: vertex \(v_i\) in the graph represents the response to the ith random-oracle query. An edge \((v_i, v_j)\) indicates that the input to the jth random-oracle query depends on the response of the ith random-oracle query.
The data-dependency graph for a Balloon computation naturally separates into \(r+1\) layers—one for each round of mixing (Fig. 3). That is, a vertex on level \(\ell \in \{1, \dots , r\}\) of the graph represents the output of a random-oracle query made during the \(\ell \)th mixing round.
The first step in the proof shows that the data-dependency graph of a Balloon computation satisfies certain connectivity properties, defined below, with high probability. The probability is taken over the choice of random oracle H, which determines the data-dependency graph. Consider placing a pebble on each of a subset of the vertices of the data-dependency graph of a Balloon computation. Then, as long as there are “not too many” pebbles on the graph, we show that the following two properties hold with high probability:
-
Well-Spreadedness. For every set of k consecutive vertices on some level of the graph, at least a quarter of the vertices on the prior level of the graph are on unpebbled paths to these k vertices.
-
Expansion. All sets of k vertices on any level of the graph have unpebbled paths back to at least 2k vertices on the prior level. The value of k depends on the choice of the parameter \(\delta \).
The next step is to show that every graph-respecting algorithm computing the Balloon function requires large space or time. We say that an adversary \(\mathcal {A}\) is graph respecting if for every i, adversary \(\mathcal {A}\) makes query number i to the random-oracle only after it has in storage all of the values that this query takes as input.Footnote 3
We show, using the well-spreadedness and expansion properties of the Balloon data-dependency graph, that every graph-respecting adversary \(\mathcal {A}\) must use space S and time T satisfying \(S \cdot T \ge n^2/8\), with high probability over the choice of H. We use the graph structure in the proof as follows: fix a set of k values that the adversary has not yet computed. Then the graph properties imply that these k values have many dependencies that a space-S adversary cannot have in storage. Thus, making progress towards computing the Balloon function in small space requires the adversary to undertake a huge amount of recomputation.
The final step uses a technique of Dwork, Naor, and Wee [32]. They use the notion of a graph labeling to convert a directed acyclic graph G into a function \(f_G\). They prove that if G is a graph that is infeasible for time-T space-S graph-respecting pebbling adversaries to compute, then it is infeasible for time-\(T'\) space-\(S'\) arbitrary adversaries to compute the labeling function \(f_G\), with high probability in the random-oracle model, where \(T' \approx T\) and \(S' \approx S\).
We observe that Balloon computes the function \(f_G\) where G is the Balloon data-dependency graph. We then directly apply the technique of Dwork, Naor, and Wee to obtain a upper bound on the probability that an arbitrary adversary can compute the Balloon function in small time and space. \(\square \)
4 Attacking and Defending Argon2
In this section, we analyze the Argon2i password hashing function [18], which won the recent Password Hashing Competition [56].
An Attack. We first present an attack showing that it possible for an attacker to compute multi-pass Argon2i (the recommended version) saving a factor of \(e \approx 2.72\) in space with no increase in computation time.Footnote 4 Additionally, we show that an attacker can compute the single-pass variant of Argon2i, which is also described in the specification, saving more than a factor of four in space, again with no increase in computation time. These attacks demonstrate an unexpected weakness in the Argon2i design, and show the value of a formal security analysis.
A Defense. In the full version of this paper we give the first proof of security showing that, with high probability, single-pass n-block Argon2i requires space S and time T to compute, such that \(S \cdot T \ge n^2/192\), in the sequential random-oracle model. Our proof is relatively simple and uses the same techniques we have developed to reason about the Balloon algorithm. The time-space lower bound we can prove about Argon2i is weaker than the one we can prove about Balloon, since the Argon2i result leaves open the possibility of an attack that saves a factor of 192 factor in space with no increase in computation time. If Argon2i becomes a standard algorithm for password hashing, it would be a worthwhile exercise to try to improve the constants on both the attacks and lower bounds to get a clearer picture of its exact memory-hardness properties.
4.1 Attack Overview
Our Argon2i attacks require a linear-time pre-computation operation that is independent of the password and salt. The attacker need only run the pre-computation phase once for a given choice of the Argon2i public parameters (buffer size, round count, etc.). After running the pre-computation step once, it is possible to compute many Argon2i password hashes, on different salts and different passwords using our small-space computation strategy. Thus, the cost of the pre-computation is amortized over many subsequent hash computations.
The attacks we demonstrate undermine the security claims of the Argon2i (version 1.2.1) design documents [18]. The design documents claim that computing n-block single-pass Argon2i with n/4 space incurs a \(7.3\times \) computational penalty [18, Table 2]. Our attacks show that there is no computational penalty. The design documents claim that computing n-block three-pass Argon2i with n/3 space incurs a \(16,384\times \) computational penalty [18, Sect. 5.4]. We compute the function in \(n/2.7 \approx n/3\) space with no computational penalty.
We analyze a idealized version the Argon2i algorithm, which is slightly simpler than that proposed in the Argon2i v1.2.1 specification [18]. Our idealized analysis underestimates the efficacy of our small-space computation strategy, so the strategy we propose is actually more effective at computing Argon2i than the analysis suggests. The idealized analysis yields an expected n/4 storage cost, but as Fig. 4 demonstrates, empirically our strategy allows computing single-pass Argon2i with only n/5 blocks of storage. This analysis focuses on the single-threaded instantiation of Argon2i—we have not tried to extend it to the many-threaded variant.
4.2 Background on Argon
At a high level, the Argon2i hashing scheme operates by filling up an n-block buffer with pseudo-random bytes, one 1024-byte block at a time. The first two blocks are derived from the password and salt. For \(i \in \{3, \dots , n\}\), the block at index i is derived from two blocks: the block at index \((i-1)\) and a block selected pseudo-randomly from the set of blocks generated so far. If we denote the contents of block i as \(x_i\), then Argon2i operates as follows:
Here, H is a non-memory-hard cryptographic hash function mapping two blocks into one block. The random index \(r_i\) is sampled from a non-uniform distribution over \(S_i = \{1, \dots , i-1\}\) that has a heavy bias towards blocks with larger indices. We model the index value \(r_i\) as if it were sampled from the uniform distribution over \(S_i\). Our small-space computation strategy performs better under a distribution biased towards larger indices, so our analysis is actually somewhat conservative.
The single-pass variant of Argon2i computes \((x_1, \dots , x_{n})\) in sequence and outputs bytes derived from the last block \(x_{n}\). Computing the function in the straightforward way requires storing every generated block for the duration of the computation— n blocks total.
The multiple-pass variant of Argon2i works as above except that it computes pn blocks instead of just n blocks, where p is a user-specified integer indicating the number of “passes” over the memory the algorithm takes. (The number of passes in Argon2i is analogous to number of rounds r in Balloon hashing.) The default number of passes is three. In multiple-pass Argon2i, the contents of block i are derived from the prior block and one of the most recent n blocks. The output of the function is derived from the value \(x_{pn}\). When computing the multiple-pass variant of Argon2i, one need only store the latest n blocks computed (since earlier blocks will never be referenced again), so the storage cost of the straightforward algorithm is still roughly n blocks.
Our analysis splits the Argon2i computation into discrete time steps, where time step t begins at the moment at which the algorithm invokes the compression function H for the tth time.
4.3 Attack Algorithm
Our strategy for computing p-pass Argon2i with fewer than n blocks of memory is as follows:
-
Pre-computation Phase. We run the entire hash computation once—on an arbitrary password and salt—and write the memory access pattern to disk. For each memory block i, we pre-compute the time \(t_i\) after which block i is never again accessed and we store \(\{t_1, \dots , t_{pn}\}\) in a read-only array. The total size of this table on a 64-bit machine is at most 8pn bytes.Footnote 5
Since the Argon2i memory-access pattern does not depend on the password or salt, it is possible to use this same pre-computed table for many subsequent Argon2i hash computations (on different salts and passwords).
-
Computation Phase. We compute the hash function as usual, except that we delete blocks that will never be accessed again. After reading block i during the hash computation at time step t, we check whether the current time \(t \ge t_i\). If so, we delete block i from memory and reuse the space for a new block.
The expected space required to compute n-block single-pass Argon2i is n/4. The expected space required to compute n-block many-pass Argon2i tends to \(n/e \approx 2.7\) as the number of passes tends to infinity. We analyze the space usage of the attack algorithm in detail in Appendix A.
5 Discussion
In this section, we discuss parallel attacks against memory-hard functions and compare Balloon to other candidate password-hashing functions.
5.1 Memory Hardness Under Parallel Attacks
The Balloon Hashing algorithm achieves the notion of memory-hardness introduced in Sect. 2.2: an algorithm for computing Balloon must, with high probability in the random-oracle model, use (roughly) time T and space S that satisfy \(S \cdot T \in \varOmega (n^2)\). Using the time-space product in this way as a proxy metric for computation cost is natural, since it approximates the area-time product required to compute the function in hardware [60].
As Alwen and Serbinenko [8] point out, there are two key limitations to the standard definition of memory-hardness in which we prove security. First, the definition yields a single-instance notion of security. That is, our definition of memory-hardness puts a lower-bound on the ST cost of computing the Balloon function once, whereas in a password-guessing attack, the adversary potentially wants to compute the Balloon function billions of times.Footnote 6 Second, the definition treats a sequential model of computation—in which the adversary can make a single random-oracle query at each time step. In contrast, a password-guessing adversary may have access to thousands of computational cores operating in parallel.
To address the limitations of the conventional single-instance sequential adversary model, which we use for our analysis of the Balloon function, Alwen and Serbinenko introduce a new adversary model and security definition. Essentially, they allow the adversary to make many parallel random-oracle queries at each time step. In this “parallel random-oracle model” (pROM), they attempt to put a lower bound on the sum of the adversary’s space usage over time: \(\sum _t S_t \in \varOmega (n^2)\), where \(S_t\) is the number of blocks of space used in the t-th computation step. We call a function that satisfies this notion of memory-hardness in the pROM an amortized memory-hard function.Footnote 7
To phrase the definition in different terms: Alwen and Serbinenko look for functions f such that computing f requires a large amount of working space at many points during the computation of f. In contrast, the traditional definition (which we use) proves the weaker statement that the adversary computing f must use a lot of space at some point during the computation of f.
An impressive recent line of work has uncovered many new results in this model:
-
Alwen and Blocki [3, 4] show that, in the pROM, there does not exist a perfectly memory-hard function (in the amortized sense) that uses a password-independent memory-access pattern. In the sequential setting, Balloon and other memory-hard functions require space S and time T to compute such that \(S \cdot T \in \varOmega (n^2)\). In the parallel setting, Alwen and Blocki show that the best one can hope for, in terms of amortized space usage is \(\varOmega (n^2/\log n)\). Additionally, they give special-case attack algorithms for computing many candidate password-hashing algorithms in the pROM. Their algorithm computes Balloon, for example, using an amortized time-space product of roughly \(O(n^{7/4})\).Footnote 8
-
Alwen et al. [6] show that the amortized space-time complexity of the single-round Balloon function is at least \(\tilde{\varOmega }(n^{5/3})\), where the \(\tilde{\varOmega }(\cdot )\) ignores logarithmic factors of n. This result puts a limit on the effectiveness of parallel attacks against Balloon.
-
Alwen et al. [5] construct a memory-hard function with a password-independent access pattern and that has an asymptotically optimal amortized time-space product of \(S\cdot T \in \varOmega (n^2/\log n)\). Whether this construction is useful for practical purposes will depend heavily on value of the constant hidden in the \(\varOmega (\cdot )\). In practice, a large constant may overwhelm the asymptotic improvement.
-
Alwen et al. [6] prove, under combinatorial conjecturesFootnote 9 that scrypt is near-optimally memory-hard in the pROM. Unlike Balloon, scrypt uses a data-dependent access pattern—which we would like to avoid—and the data-dependence of scrypt’s access pattern seems fundamental to their security analysis.
As far as practical constructions go, these results leave the practitioner with two options, each of which has a downside:
-
Option 1. Use scrypt, which seems to protect against parallel attacks, but which uses a password-dependent access pattern and is weak in the face of an adversary that can learn memory access information. (We describe the attack in the full version of the paper)
-
Option 2. Use Balloon Hashing, which uses a password-independent access pattern and is secure against sequential attacks, but which is asymptotically weak in the face of a massively parallel attack.
A good practical solution is to hash passwords using a careful composition of Balloon and scrypt: one function defends against memory access pattern leakage and the other defends against massively parallel attacks. For the moment, let us stipulate that the pROM attacks on vanilla Balloon (and all other practical password hashing algorithms using data-independent access patterns) make these algorithms less-than-ideal to use on their own. Can we somehow combine the two constructions to get a “best-of-both-worlds” practical password-hashing algorithm? The answer is yes: compose a data-independent password-hashing algorithm, such as Balloon, with a data-dependent scheme, such as scrypt. To use the composed scheme, one would first run the password through the data-independent algorithm and next run the resulting hash through the data-dependent algorithm.Footnote 10
It is not difficult to show that the composed scheme is memory-hard against either: (a) an attacker who is able to learn the function’s data-access pattern on the target password, or (b) an attacker who mounts an attack in the pROM using the parallel algorithm of Alwen and Blocki [3]. The composed scheme defends against the two attacks separately but does not defend against both of them simultaneously: the composed function does not maintain memory-hardness in the face of an attacker who is powerful enough to get access-pattern information and mount a massively parallel attack. It would be even better to have a practical construction that could protect against both attacks simultaneously, but the best known algorithms that do this [5, 8] are likely too inefficient to use in practice.
The composed function is almost as fast as Balloon on its own—adding the data-dependent hashing function call is effectively as costly as increasing the round count of the Balloon algorithm by one.
5.2 How to Compare Memory-Hard Functions
If we restrict ourselves to considering memory-hard functions in the sequential setting, there are a number of candidate constructions that all can be proven secure in the random-oracle model: Argon2i [19],Footnote 11 Catena BRG, Catena DBG [37], and Balloon. There is no widely accepted metric with which one measures the quality of a memory-hard function, so it is difficult to compare these functions quantitatively.
In this section, we propose one such metric and compare the four candidate functions under it. The metric we propose captures the notion that a good memory-hard function is one that makes the attacker’s job as difficult as possible given that the defender (e.g., the legitimate authentication server) still needs to hash passwords in a reasonable amount of time. Let \(\mathsf {T}_f(\mathcal {A})\) denote the expected running time of an algorithm \(\mathcal {A}\) computing a function f and let \(\mathsf {ST}_f(\mathcal {A})\) denote its expected space-time product. Then we define the quality Q of a memory-hard function against a sequential attacker \(\mathcal {A}_S\) using space S to be the ratio:
We can define a similar notion of quality in the amortized/parallel setting: just replace the quantity in the numerator (the adversary’s space-time product) with the sum of a pROM adversary’s space usage over time: \(\sum _t S_t\) of \(\mathcal {A}_S\).
We can now use the existing memory-hardness proofs to put lower bounds on the quality (in the sequential model) of the candidate memory-hard functions. We show in the full version of the paper that Argon2i has a sequential time-space lower bound of the form \(S\cdot T \ge n^2/192\), for \(S < n/24\). The n-block r-round Balloon function has a time-space lower-bound of the form \(S \cdot T \ge (2^r - 1)n^2/8\) for \(S < n/64\) when the parameter \(\delta = 3\). The n-block Catena BRG function has a time-space lower bound of the form \(S \cdot T \ge n^2/16\) (Catena BRG has no round parameter). The r-round n-block Catena DBG function has a claimed time-space lower bound of the form \(S \cdot T \ge n(\frac{r n}{64 S})^r\), when \(S \le n/20\). These lower-bounds yield the following quality figures against an adversary using roughly n/64 space:
From these quality ratios, we can draw a few conclusions about the protection these functions provide against one class of small-space attackers (using \(S \approx n/64\)):
-
In terms of provable memory-hardness properties in the sequential model, one-round Balloon always outperforms Catena-BRG and Argon2i.
-
When the buffer size n grows and the number of rounds r is held fixed, Balloon outperforms Catena-DBG as well.
-
When the buffer size n is fixed and the number of rounds r grows large, Catena-DBG provides the strongest provable memory-hardness properties in the sequential model.
-
For many realistic choices of r and n (e.g., \(r= 5\), \(n= 2^{18}\)), r-round Balloon outperforms the other constructions in terms of memory-hardness properties.
6 Experimental Evaluation
In this section, we demonstrate experimentally that the Balloon hashing algorithm is competitive performance-wise with two existing practical algorithms (Argon2i and Catena), when all are instantiated with standard cryptographic primitives.
6.1 Experimental Set-Up
Our experiments use the OpenSSL implementation (version 1.0.1f) of SHA-512 and the reference implementations of three other cryptographic hash functions (Blake2b, ECHO, and SHA-3/Keccak). We use optimized versions of the underlying cryptographic primitives where available, but the core Balloon code is written entirely in C. Our source code is available at https://crypto.stanford.edu/balloon/ under the ISC open-source license. We used a workstation running an Intel Core i7-6700 CPU (Skylake) at 3.40 GHz with 8 GiB of RAM for our performance benchmarks. We compiled the code for our timing results with gcc version 4.8.5 using the \(\texttt {-O3}\) option. We average all of our measurements over 32 trials. We compare the Balloon functions against Argon2i (v.1.2.1) [18] and Catena [37]. For comparison purposes, we implemented the Argon2i, Catena BRG, and Catena DBG memory-hard algorithms in C.
On the Choice of Cryptographic Primitives. The four memory-hard functions we evaluate (Argon2i, Balloon, Catena-BRG, Catena-DBG) are all essentially modes of operation for an underlying cryptographic hash function. The choice of the underlying hash function has implications for the performance and the security of the overall construction. To be conservative, we instantiate all of the algorithms we evaluate with the Blake2b as the underlying hash function [10].
Memory-hard functions going back at least as far as scrypt [60] have used reduced-round hash functions as their underlying cryptographic building block. Following this tradition, the Argon2i specification proposes using a new and very fast reduced-round hash function as its core cryptographic primitive. Since the Argon2i hash function does not satisfy basic properties of a traditional cryptographic hash function (e.g., it is not collision resistant), modeling it as a random oracle feels particularly problematic. Since our goal in this work is to analyze memory-hard functions with provable security guarantees, we instantiate the memory-hard functions we evaluate with traditional cryptographic hashes for the purposes of this evaluation.
That said, we stress that the Balloon construction is agnostic to the choice of underlying hash function—it is a mode of operation for a cryptographic hash function—and users of the Balloon construction may instantiate it with a faster reduced-round hash function (e.g., scrypt’s BlockMix or Argon2i’s compression function) if they so desire.
6.2 Authentication Throughput
The goal of a memory-hard password hash function is to use as much working space as possible as quickly as possible over the course of its computation. To evaluate the effectiveness of the Balloon algorithm on this metric, we measured the rate at which a server can check passwords (in hashes per second) for various buffer sizes on a single core.
Figure 5 shows the minimum buffer size required to compute each memory-hard function with high probability with no computational slowdown, for a variety of password hashing functions. We set the block size of the construction to be equal to the block size of the underlying compression function, to avoid the issues discussed in the full version of this paper. The charted results for Argon2i incorporate the fact that an adversary can compute many-pass Argon2i (v.1.2.1) in a factor of \(e \approx 2.72\) less working space than the defender must allocate for the computation and can compute single-pass Argon2i with a factor of four less space (see Sect. 4). For comparison, we also plot the space usage of two non-memory-hard password hashing functions, bcrypt [66] (with \(\text {cost} = 12\)) and PBKDF2-SHA512 [43] (with \(10^5\) iterations).
If we assume that an authentication server must perform 100 hashes per second per four-core machine, Fig. 5 shows that it would be possible to use one-round Balloon hashing with a 2 MiB buffer or eight-round Balloon hashing with a 256 KiB buffer. At the same authentication rate, Argon2i (instantiated with Blake2b as the underlying cryptographic hash function) requires the attacker to use a smaller buffer—roughly 1.5 MiB for the one-pass variant. Thus, with Balloon hashing we simultaneously get better performance than Argon2i and stronger memory-hardness guarantees.
6.3 Compression Function
Finally, Fig. 6 shows the result of instantiating the Balloon algorithm construction with four different standard cryptographic hash functions: SHA-3 [17], Blake2b [10], SHA-512, and ECHO (a SHA-3 candidate that exploits the AES-NI instructions) [14]. The SHA-3 function (with \(\text {rate} = 1344\)) operates on 1344-bit blocks, and we configure the other hash functions to use 512-bit blocks.
On the x-axis, we plot the buffer size used in the Balloon function and on the y-axis, we plot the rate at which the Balloon function fills memory, in bytes of written per second. As Fig. 6 demonstrates, Blake2b and ECHO outperform the SHA functions by a bit less than a factor of two.
7 Related Work
Password Hashing. The problem of how to securely store passwords on shared computer systems is nearly as old as the systems themselves. In a 1974 article, Evans et al. described the principle of storing passwords under a hard-to-invert function [35]. A few years later, Robert Morris and Ken Thompson presented the now-standard notion of password salts and explained how to store passwords under a moderately hard-to-compute one-way function to increase the cost of dictionary attacks [52]. Their DES-based “crypt” design became the standard for password storage for over a decade [49] and even has a formal analysis by Wagner and Goldberg [80].
In 1989, Feldmeier and Karn found that hardware improvements had driven the cost of brute-force password guessing attacks against DES crypt down by five orders of magnitude since 1979 [36, 46]. Poul-Henning Kamp introduced the costlier md5crypt to replace crypt, but hardware improvements also rendered that design outmoded [27].
Provos and Mazières saw that, in the face of ever-increasing processor speeds, any fixed password hashing algorithm would eventually become easy to compute and thus ineffective protection against dictionary attacks. Their solution, bcrypt, is a password hashing scheme with a variable “hardness” parameter [66]. By periodically ratcheting up the hardness, a system administrator can keep the time needed to compute a single hash roughly constant, even as hardware improves. A remaining weakness of bcrypt is that it exercises only a small fraction of the CPU’s resources—it barely touches the L2 and L3 caches during its execution [50]. To increase the cost of custom password-cracking hardware, Reinhold’s HEKS hash [67] and Percival’s popular scrypt routine consume an adjustable amount of storage space [60], in addition to time, as they compute a hash. Balloon, like scrypt, aims to be hard to compute in little space. Unlike scrypt, however, we require that our functions’ data access pattern be independent of the password to avoid leaking information via cache-timing attacks [23, 54, 77] (see also the attack in the full version of this paper). The Dogecoin and Litecoin [22] crypto-currencies have incorporated scrypt as an ASIC-resistant proof-of-work function.
The recent Password Hashing Competition motivated the search for memory-hard password-hashing functions that use data-independent memory access patterns [56]. The Argon2 family of functions, which have excellent performance and an appealingly simple design, won the competition [18]. The Argon2 functions lack a theoretical analysis of the feasible time-space trade-offs against them; using the same ideas we have used to analyze the Balloon function, we provide the first such result in the full version of this paper.
The Catena hash functions [37], which became finalists in the Password Hashing Competition, are memory-hard functions whose analysis applies pebbling arguments to classic graph-theoretic results of Lengauer and Tarjan [48]. The Balloon analysis we provide gives a tighter time-space lower bounds than Catena’s analysis can provide in many cases, and the Balloon algorithm outperforms the more robust of the two Catena algorithms (see Sect. 6). Biryokov and Khovratovich demonstrated a serious flaw in the security analysis of one of the Catena variants, and they provide a corresponding attack against that Catena variant [20].
The other competition finalists included a number of interesting designs that differ from ours in important ways. Makwa [64] supports offloading the work of password hashing to an untrusted server but is not memory-hard. Lyra [2] is a memory-hard function but lacks proven space-time lower bounds. Yescrypt [61] is an extension of scrypt and uses a password-dependent data access pattern.
Ren and Devadas [68] give an analysis of the Balloon algorithm using bipartite expanders, following the pebbling techniques of Paul and Tarjan [58]. Their results imply that an adversary that computes the n-block r-round Balloon function in n/8 space, must use at least \(2^r n/c\) time to compute the function (for some constant c), with high probability in the random-oracle model. We prove the stronger statement that an adversary’s space-time product must satisfy: \(S \cdot T \in \varOmega (n^2)\) for almost all values of S. Ren and Devadas also prove statements showing that algorithms computing the Balloon functions efficiently must use a certain amount of space at many points during their computation. Our time-space lower bounds only show that the adversary must use a certain amount of space a some point during the Balloon computation.
Other Studies of Password Protection. Concurrently with the design of hashing schemes, there has been theoretical work from Bellare et al. on new security definitions for password-based cryptography [12] and from Di Crescenzo et al. on an analysis of passwords storage systems secure against adversaries that can steal only a bounded number of bits of the password file [28]. Other ideas for modifying password hashes include the key stretching schemes of Kelsey et al. [44] (variants on iterated hashes), a proposal by Boyen to keep the hash iteration count (e.g., time parameter in bcrypt) secret [24], a technique of Canetti et al. for using CAPTCHAs in concert with hashes [25], and a proposal by Dürmuth to use password hashing to do meaningful computation [29].
Parallel Memory-Hardness. In a recent line of work [3–6, 8] has analyzed memory-hard functions from a number of angles in the parallel random-oracle model, introduced by Alwen and Serbinenko [8]. We discuss these very relevant results at length in Sect. 5.1.
Memory-Bound Functions. Abadi et al. [1] introduced memory-bound functions as more effective alternatives to traditional proofs-of-work in heterogeneous computing environments [11, 31]. These functions require many cache misses to compute and, under the assumption that memory latencies are consistent across computing platforms, they are roughly as hard to compute on a computationally powerful device as on a computationally weak one. The theoretical analysis of memory-bound functions represented one of the first applications of pebbling arguments to cryptography [30, 32].
Proofs of Space. Dziembowski et al. [33] and Ateniese et al. [9] study proofs-of-space. In these protocols, the prover and verifier agree on a large bitstring that the prover is supposed to store. Later on, the prover can convince the verifier that the prover has stored some large string on disk, even if the verifier does not store the string herself. Spacemint proposes building a cryptocurrency based upon a proof-of-space rather than a proof-of-work [55]. Ren and Devadas propose using the problem of pebbling a Balloon graph as the basis for a proof of space [68].
Time-Space Trade-Offs. The techniques we use to analyze Balloon draws on extensive prior work on computational time-space trade-offs. We use pebbling arguments, which have seen application to register allocation problems [72], to the analysis of the relationships between complexity classes [15, 26, 42, 75], and to prior cryptographic constructions [32–34, 37]. Pebbling has also been a topic of study in its own right [48, 59]. Savage’s text gives a clear introduction to graph pebbling [71] and Nordström surveys the vast body of pebbling results in depth [53].
8 Conclusion
We have introduced the Balloon password hashing algorithm. The Balloon algorithm is provably memory-hard (in the random-oracle model against sequential adversaries), exhibits a password-independent memory access pattern, and meets or exceeds the performance of the fastest heuristically secure schemes. Using a novel combinatorial pebbling argument, we have demonstrated that password-hashing algorithms can have memory-hardness proofs without sacrificing practicality.
This work raises a number of open questions:
-
Are there efficient methods to defend against cache attacks on scrypt? Could a special-purpose ORAM scheme help [39]?
-
Are there practical memory-hard functions with password-independent access patterns that retain their memory-hardness properties under parallel attacks [8]? The recent work of Alwen et al. [4] is promising, though it is still unclear whether the pROM-secure constructions will be competitive with Balloon for concrete settings of the parameters.
-
Is it possible to build hardware that effectively implements the pROM attacks [3–5] against Argon2i and Balloon at realistic parameter sizes? What efficiency gain would this pROM hardware have over a sequential ASIC at attacking these constructions? Are these parallel attacks still practical in hardware when the function’s memory-access pattern depends on the salt (as Balloon ’s access pattern does)?
Notes
- 1.
The relatively poor performance of Argon2i here is due to the attack we present in Sect. 4. It allows an attacker to save space in computing Argon2i with no increase in computation time.
- 2.
- 3.
This description is intentionally informal—see the full version of the paperor the precise statement.
- 4.
- 5.
On an FPGA or ASIC, this table can be stored in relatively cheap shared read-only memory and the storage cost can be amortized over a number of compute cores. Even on a general-purpose CPU, the table and memory buffer for the single-pass construction together will only require \(8n + 1024(n/4) = 8n + 256n\) bytes when using our small-space computation strategy. Argon2i normally requires 1024n bytes of buffer space, so our strategy still yields a significant space savings.
- 6.
Bellare, Ristenpart, and Tessaro consider a different type of multi-instance security [12]: they are interested in key-derivation functions f with the property that finding \((x_1, \dots , x_m)\) given \((f(x_1), \dots , f(x_m))\) is roughly m times as costly as inverting f once. Stebila et al. [73] and Groza and Warinschi [40] investigate a similar multiple-instance notion of security for client puzzles [31] and Garay et al. [38] investigate related notions in the context of multi-party computation.
- 7.
In the original scrypt paper, Percival [60] also discusses parallel attacks and makes an argument for the security of scrypt in the pROM.
- 8.
There is no consensus on whether it would be feasible to implement this parallel attack in hardware for realistic parameter sizes. That said, the fact that such pROM attacks exist at all are absolutely a practical concern.
- 9.
A recent addendum to the paper suggests that the combinatorial conjectures that underlie their proof of security may be false [7, Sect. 0].
- 10.
Our argument here gives some theoretical justification for the Argon2id mode of operation proposed in some versions of the Argon2 specification [19, Appendix B]. That variant follows a hashing with a password-independent access pattern by hashing with a password-dependent access pattern.
- 11.
We provide a proof of security for single-pass Argon2i in the full version of this paper.
- 12.
As described in Sect. 4.2, the contents of block i in Argon2i are derived from the contents of block \(i-1\) and a block chosen at random from the set
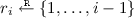 . Throughout our analysis, all probabilities are taken over the random choices of the \(r_i\) values.
. Throughout our analysis, all probabilities are taken over the random choices of the \(r_i\) values.
References
Abadi, M., Burrows, M., Manasse, M., Wobber, T.: Moderately hard, memory-bound functions. ACM Trans. Internet Technol. 5(2), 299–327 (2005)
Almeida, L.C., Andrade, E.R., Barreto, P.S.L.M., Simplicio Jr., M.A.: Lyra: password-based key derivation with tunable memory and processing costs. J. Cryptographic Eng. 4(2), 75–89 (2014)
Alwen, J., Blocki, J.: Efficiently computing data-independent memory-hard functions. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9815, pp. 241–271. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53008-5_9
Alwen, J., Blocki, J.: Towards practical attacks on Argon2i and Balloon Hashing. Cryptology ePrint Archive, Report 2016/759 (2016). http://eprint.iacr.org/2016/759
Alwen, J., Blocki, J., Pietrzak, K.: The pebbling complexity of depth-robust graphs. Manuscript (Personal Communication) (2016)
Alwen, J., Chen, B., Kamath, C., Kolmogorov, V., Pietrzak, K., Tessaro, S.: On the complexity of scrypt and proofs of space in the parallel random oracle model. In: Fischlin, M., Coron, J.-S. (eds.) EUROCRYPT 2016. LNCS, vol. 9666, pp. 358–387. Springer, Heidelberg (2016). doi:10.1007/978-3-662-49896-5_13
Alwen, J., Chen, B., Kamath, C., Kolmogorov, V., Pietrzak, K., Tessaro, S.: On the complexity of scrypt and proofs of space in the parallel random oracle model. Cryptology ePrint Archive, Report 2016/100 (2016). http://eprint.iacr.org/
Alwen, J., Serbinenko, V.: High parallel complexity graphs and memory-hard functions. In: STOC, pp. 595–603 (2015)
Ateniese, G., Bonacina, I., Faonio, A., Galesi, N.: Proofs of space: when space is of the essence. In: Abdalla, M., Prisco, R. (eds.) SCN 2014. LNCS, vol. 8642, pp. 538–557. Springer, Heidelberg (2014). doi:10.1007/978-3-319-10879-7_31
Aumasson, J.-P., Neves, S., Wilcox-O’Hearn, Z., Winnerlein, C.: BLAKE2: simpler, smaller, fast as MD5. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 119–135. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38980-1_8
Back, A.: Hashcash-a denial of service counter-measure, May 1997. http://www.cypherspace.org/hashcash/. Accessed 9 Nov 2015
Bellare, M., Ristenpart, T., Tessaro, S.: Multi-instance security and its application to password-based cryptography. In: Safavi-Naini, R., Canetti, R. (eds.) CRYPTO 2012. LNCS, vol. 7417, pp. 312–329. Springer, Heidelberg (2012). doi:10.1007/978-3-642-32009-5_19
Bellare, M., Rogaway, P.: Random oracles are practical: a paradigm for designing efficient protocols. In: CCS, pp. 62–73. ACM (1993)
Benadjila, R., Billet, O., Gilbert, H., Macario-Rat, G., Peyrin, T., Robshaw, M., Seurin, Y.: SHA-3 proposal: ECHO. Submission to NIST (updated) (2009)
Bennett, C.H.: Time/space trade-offs for reversible computation. SIAM J. Comput. 18(4), 766–776 (1989)
Bernstein, D.J., Lange, T.: Non-uniform cracks in the concrete: the power of free precomputation. In: Sako, K., Sarkar, P. (eds.) ASIACRYPT 2013. LNCS, vol. 8270, pp. 321–340. Springer, Heidelberg (2013). doi:10.1007/978-3-642-42045-0_17
Bertoni, G., Daemen, J., Peeters, M., Van Assche, G.: Keccak sponge function family. Submission to NIST (Round 2) (2009)
Biryukov, A., Dinu, D., Khovratovich, D.: Argon2 design document (version 1.2.1), October 2015
Biryukov, A., Dinu, D., Khovratovich, D.: Argon2 design document (version 1.3), February 2016
Biryukov, A., Khovratovich, D.: Tradeoff cryptanalysis of memory-hard functions. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 633–657. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48800-3_26
Bitcoin wiki - mining comparison. https://en.bitcoin.it/wiki/Mining_hardware_comparison
Bonneau, J., Miller, A., Clark, J., Narayanan, A., Kroll, J.A., Felten, E.W.: SoK: research perspectives and challenges for Bitcoin and cryptocurrencies. In: Symposium on Security and Privacy. IEEE, May 2015
Bonneau, J., Mironov, I.: Cache-collision timing attacks against AES. In: Goubin, L., Matsui, M. (eds.) CHES 2006. LNCS, vol. 4249, pp. 201–215. Springer, Heidelberg (2006). doi:10.1007/11894063_16
Boyen, X.: Halting password puzzles. In: USENIX Security (2007)
Canetti, R., Halevi, S., Steiner, M.: Mitigating dictionary attacks on password-protected local storage. In: Dwork, C. (ed.) CRYPTO 2006. LNCS, vol. 4117, pp. 160–179. Springer, Heidelberg (2006). doi:10.1007/11818175_10
Chan, S.M.: Just a pebble game. In: IEEE Conference on Computational Complexity, pp. 133–143. IEEE (2013)
CVE-2012-3287: md5crypt has insufficient algorithmic complexity (2012). http://cve.mitre.org/cgi-bin/cvename.cgi?name=CVE-2012-3287. Accessed 9 Nov 2015
Di Crescenzo, G., Lipton, R., Walfish, S.: Perfectly secure password protocols in the bounded retrieval model. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 225–244. Springer, Heidelberg (2006). doi:10.1007/11681878_12
Dürmuth, M.: Useful password hashing: how to waste computing cycles with style. In: New Security Paradigms Workshop, pp. 31–40. ACM (2013)
Dwork, C., Goldberg, A., Naor, M.: On memory-bound functions for fighting spam. In: Boneh, D. (ed.) CRYPTO 2003. LNCS, vol. 2729, pp. 426–444. Springer, Heidelberg (2003). doi:10.1007/978-3-540-45146-4_25
Dwork, C., Naor, M.: Pricing via processing or combatting junk mail. In: Brickell, E.F. (ed.) CRYPTO 1992. LNCS, vol. 740, pp. 139–147. Springer, Heidelberg (1993). doi:10.1007/3-540-48071-4_10
Dwork, C., Naor, M., Wee, H.: Pebbling and proofs of work. In: Shoup, V. (ed.) CRYPTO 2005. LNCS, vol. 3621, pp. 37–54. Springer, Heidelberg (2005). doi:10.1007/11535218_3
Dziembowski, S., Faust, S., Kolmogorov, V., Pietrzak, K.: Proofs of space. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9216, pp. 585–605. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48000-7_29
Dziembowski, S., Kazana, T., Wichs, D.: One-time computable self-erasing functions. In: Ishai, Y. (ed.) TCC 2011. LNCS, vol. 6597, pp. 125–143. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19571-6_9
Evans Jr., A., Kantrowitz, W., Weiss, E.: A user authentication scheme not requiring secrecy in the computer. Commun. ACM 17(8), 437–442 (1974)
Feldmeier, D.C., Karn, P.R.: UNIX password security - ten years later. In: Brassard, G. (ed.) CRYPTO 1989. LNCS, vol. 435, pp. 44–63. Springer, Heidelberg (1990). doi:10.1007/0-387-34805-0_6
Forler, C., Lucks, S., Wenzel, J.: Memory-demanding password scrambling. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 289–305. Springer, Heidelberg (2014). doi:10.1007/978-3-662-45608-8_16
Garay, J., Johnson, D., Kiayias, A., Yung, M.: Resource-based corruptions and the combinatorics of hidden diversity. In: ITCS, pp. 415–428. ACM (2013)
Goldreich, O., Ostrovsky, R.: Software protection and simulation on oblivious RAMs. J. ACM 43(3), 431–473 (1996)
Groza, B., Warinschi, B.: Revisiting difficulty notions for client puzzles and DoS resilience. In: Gollmann, D., Freiling, F.C. (eds.) ISC 2012. LNCS, vol. 7483, pp. 39–54. Springer, Heidelberg (2012). doi:10.1007/978-3-642-33383-5_3
Ho, S.: Costco, Sam’s Club, others halt photo sites over possible breach, July 2015. http://www.reuters.com/article/2015/07/21/us-cyberattack-retail-idUSKCN0PV00520150721. Accessed 9 Nov 2015
Hopcroft, J., Paul, W., Valiant, L.: On time versus space. J. ACM (JACM) 24(2), 332–337 (1977)
Kaliski, B.: PKCS #5: Password-based cryptography specification, version 2.0. IETF Network Working Group, RFC 2898, September 2000
Kelsey, J., Schneier, B., Hall, C., Wagner, D.: Secure applications of low-entropy keys. In: Okamoto, E., Davida, G., Mambo, M. (eds.) ISW 1997. LNCS, vol. 1396, pp. 121–134. Springer, Heidelberg (1998). doi:10.1007/BFb0030415
Kirk, J.: Internet address overseer ICANN resets passwords after website breach, August 2015. http://www.pcworld.com/article/2960592/security/icann-resets-passwords-after-website-breach.html. Accessed 9 Nov 2015
Klein, D.V.: Foiling the cracker: a survey of, and improvements to, password security. In: Proceedings of the 2nd USENIX Security Workshop, pp. 5–14 (1990)
Krantz, L.: Harvard says data breach occurred in June, July 2015. http://www.bostonglobe.com/metro/2015/07/01/harvard-announces-data-breach/pqzk9IPWLMiCKBl3IijMUJ/story.html. Accessed 9 Nov 2015
Lengauer, T., Tarjan, R.E.: Asymptotically tight bounds on time-space trade-offs in a pebble game. J. ACM 29(4), 1087–1130 (1982)
Leong, P., Tham, C.: UNIX password encryption considered insecure. In: USENIX Winter, pp. 269–280 (1991)
Malvoni, K., Designer, S., Knezovic, J.: Are your passwords safe: energy-efficient bcrypt cracking with low-cost parallel hardware. In: USENIX Workshop on Offensive Technologies (2014)
Menezes, A.J., Van Oorschot, P.C., Vanstone, S.A.: Handbook of Applied Cryptography. CRC Press, Boca Raton (1996)
Morris, R., Thompson, K.: Password security: a case history. Commun. ACM 22(11), 594–597 (1979)
Nordström, J.: New wine into old wineskins: a survey of some pebbling classics with supplemental results, March 2015. http://www.csc.kth.se/~jakobn/research/PebblingSurveyTMP.pdf. Accessed 9 Nov 2015
Osvik, D.A., Shamir, A., Tromer, E.: Cache attacks and countermeasures: the case of AES. In: Pointcheval, D. (ed.) CT-RSA 2006. LNCS, vol. 3860, pp. 1–20. Springer, Heidelberg (2006). doi:10.1007/11605805_1
Park, S., Pietrzak, K., Alwen, J., Fuchsbauer, G., Gazi, P.: Spacemint: a cryptocurrency based on proofs of space. Technical report, Cryptology ePrint Archive, Report 2015/528 (2015)
Password hashing competition. https://password-hashing.net/
Paterson, M.S., Hewitt, C.E.: Comparative schematology. In: Record of the Project MAC Conference on Concurrent Systems and Parallel Computation, pp. 119–127. ACM (1970)
Paul, W.J., Tarjan, R.E.: Time-space trade-offs in a pebble game. Acta Informatica 10(2), 111–115 (1978)
Paul, W.J., Tarjan, R.E., Celoni, J.R.: Space bounds for a game on graphs. Math. Syst. Theor. 10(1), 239–251 (1976)
Percival, C.: Stronger key derivation via sequential memory-hard functions. In: BSDCan, May 2009
Peslyak, A.: yescrypt, October 2015. https://password-hashing.net/submissions/specs/yescrypt-v2.pdf. Accessed 13 Nov 2015
Peterson, A.: E-Trade notifies 31,000 customers that their contact info may have been breached in 2013 hack, October 2015. https://www.washingtonpost.com/news/the-switch/wp/2015/10/09/e-trade-notifies-31000-customers-that-their-contact-info-may-have-been-breached-in-2013-hack/. Accessed 9 Nov 2015
Pippenger, N.: A time-space trade-off. J. ACM (JACM) 25(3), 509–515 (1978)
Pornin, T.: The Makwa password hashing function, April 2015. http://www.bolet.org/makwa/. Accessed 13 Nov 2015
Privacy Rights Clearinghouse: Chronology of data breaches. http://www.privacyrights.org/data-breach. Accessed 9 Nov 2015
Provos, N., Mazières, D.: A future-adaptable password scheme. In: USENIX Annual Technical Conference, pp. 81–91 (1999)
Reinhold, A.: HEKS: a family of key stretching algorithms (Draft G), July 2001. http://world.std.com/~reinhold/HEKSproposal.html. Accessed 13 Nov 2015
Ren, L., Devadas, S.: Proof of space from stacked expanders. Cryptology ePrint Archive, Report 2016/333 (2016). http://eprint.iacr.org/
Ristenpart, T., Tromer, E., Shacham, H., Savage, S.: Hey, you, get off of my cloud: exploring information leakage in third-party compute clouds. In: CCS, pp. 199–212. ACM (2009)
Rogaway, P.: Formalizing human ignorance. In: Nguyen, P.Q. (ed.) VIETCRYPT 2006. LNCS, vol. 4341, pp. 211–228. Springer, Heidelberg (2006). doi:10.1007/11958239_14
Savage, J.E.: Models of Computation: Exploring the Power of Computing. Addison-Wesley, New York (1998)
Sethi, R.: Complete register allocation problems. SIAM J. Comput. 4(3), 226–248 (1975)
Stebila, D., Kuppusamy, L., Rangasamy, J., Boyd, C., Gonzalez Nieto, J.: Stronger difficulty notions for client puzzles and denial-of-service-resistant protocols. In: Kiayias, A. (ed.) CT-RSA 2011. LNCS, vol. 6558, pp. 284–301. Springer, Heidelberg (2011). doi:10.1007/978-3-642-19074-2_19
Takala, R.: UVA site back online after chinese hack, August 2015. http://www.washingtonexaminer.com/uva-site-back-online-after-chinese-hack/article/2570383. Accessed 9 Nov 2015
Tompa, M.: Time-space tradeoffs for computing functions, using connectivity properties of their circuits. In: STOC, pp. 196–204. ACM (1978)
Tracy, A.: In wake of T-Mobile and Experian data breach, John Legere did what all CEOs should do after a hack, October 2015. http://www.forbes.com/sites/abigailtracy/2015/10/02/in-wake-of-t-mobile-and-experian-data-breach-john-legere-did-what-all-ceos-should-do-after-a-hack/. Accessed 9 Nov 2015
Tromer, E., Osvik, D.A., Shamir, A.: Efficient cache attacks on AES, and countermeasures. J. Cryptology 23(1), 37–71 (2010)
Valiant, L.G.: Graph-theoretic arguments in low-level complexity. In: Gruska, J. (ed.) MFCS 1977. LNCS, vol. 53, pp. 162–176. Springer, Heidelberg (1977). doi:10.1007/3-540-08353-7_135
Vaughan-Nichols, S.J.: Password site LastPass warns of data breach, June 2015. http://www.zdnet.com/article/lastpass-password-security-site-hacked/. Accessed 9 Nov 2015
Wagner, D., Goldberg, I.: Proofs of security for the unix password hashing algorithm. In: Okamoto, T. (ed.) ASIACRYPT 2000. LNCS, vol. 1976, pp. 560–572. Springer, Heidelberg (2000). doi:10.1007/3-540-44448-3_43
Acknowledgements
We would like to our anonymous reviewers for their helpful comments. We also thank Josh Benaloh, Joe Bonneau, Greg Hill, Ali Mashtizadeh, David Mazières, Yan Michalevsky, Bryan Parno, Greg Valiant, Riad Wahby, Keith Winstein, David Wu, Sergey Yekhanin, and Greg Zaverucha for comments on early versions of this work. This work was funded in part by an NDSEG Fellowship, NSF, DARPA, a grant from ONR, and the Simons Foundation. Opinions, findings and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of DARPA.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
A Details of the Attack on Argon2
A Details of the Attack on Argon2
In this section, we provide a detailed analysis of the attack on Argon2i that we introduced in Sect. 4.
The goal of the attack algorithm is to compute Argon2i in the same number of time steps as the naïve algorithm uses to compute the function, while using a constant factor less space than the naïve algorithm does. In this way, an attacker mounting a dictionary attack against a list of passwords hashed with Argon2i can do so at less cost (in terms of the space-time product) than the Argon2i specification claimed possible.
Argon2i has one-pass and many-pass variants and our attack applies to both; the many-pass variant is recommended in the specification. We first analyze the attack on the one-pass variant and then analyze the attack on the many-pass variant.
We are interested in the attack algorithm’s expected space usage at time step t—call this function S(t).Footnote 12
Analysis of One-Pass Argon2i. At each step of the one-pass Argon2i algorithm, the expected space usage S(t) is equal to the number of memory blocks generated so far minus the expected number of blocks in memory that will never be used after time t. Let \(A_{i,t}\) be the event that block i is never needed after time step t in the computation. Then \(S(t) = t - \sum _{i=1}^t \Pr [A_{i,t}]\).
To find S(t) explicitly, we need to compute the probability that block i is never used after time t. We know that the probability that block i is never used after time t is equal to the probability that block i is not used at time \(t+1\) and is not used at time \(t+2\) and [...] and is not used at time n. Let \(U_{i,t}\) denote the event that block i is unused at time t. Then:
The equality on the right-hand side comes from the fact that \(U_{i,t'}\) and \(U_{i,t''}\) are independent events for \(t' \ne t''\).
To compute the probability that block i is not used at time \(t'\), consider that there are \(t'-1\) blocks to choose from and \(t'-2\) of them are not block i: \(\Pr [U_{i,t'}] = \frac{t'-2}{t'-1}\). Plugging this back into Eq. 1, we get:
Now we substitute this back into our original expression for S(t):
Taking the derivative \(S'(t)\) and setting it to zero allows us to compute the value t for which the expected storage is maximized. The maximum is at \(t = n/2\) and the expected number of blocks required is \(S(n/2) \approx n/4\).
Larger in-degree. A straightforward extension of this analysis handles the case in which \(\delta \) random blocks—instead of one—are hashed together with the prior block at each step of the algorithm. Our analysis demonstrates that, even with this strategy, single-pass Argon2i is vulnerable to pre-computation attacks. The maximum space usage comes at \(t^* = n/(\delta +1)^{1/\delta }\), and the expected space usage over time S(t) is:
Analysis of Many-Pass Argon2i. One idea for increasing the minimum memory consumption of Argon2i is to increase the number of passes that the algorithm takes over the memory. For example, the Argon2 specification proposes taking three passes over the memory to protect against certain time-space tradeoffs. Unfortunately, even after many passes over the memory, the Argon2i algorithm sketched above still uses many fewer than n blocks of memory, in expectation, at each time step.
To investigate the space usage of the many-pass Argon2i algorithm, first consider that the space usage will be maximized at some point in the middle of its computation—not in the first or last passes. At some time step t in the middle of its computation the algorithm will have at most n memory blocks in storage, but the algorithm can delete any of these n blocks that it will never need after time t.
At each time step, the algorithm adds a new block to the end of the buffer and deletes the first block. At any one point in the algorithm’s execution, there will be at most n blocks of memory in storage. If we freeze the execution of the Argon2i algorithm in the middle of its execution, we can inspect the n blocks it has stored in memory. Call the first block “stored block 1” and the last block “stored block n.”
Let \(B_{i,t}\) denote the event that stored block i is never needed after time t. Then we claim \(\Pr [B_{i,t}] = (\frac{n-1}{n})^{i}\). To see the logic behind this calculation: notice that, at time t, the first stored block in the buffer can be accessed at time \(t+1\) but by time \(t+2\), the first stored block will have been deleted from the buffer. Similarly, the second stored block in the buffer at time t can be accessed at time \(t+1\) or \(t+2\), but not \(t+3\) (since by then stored block 2 will have been deleted from the buffer). Similarly, stored block i can be accessed at time steps \((t+1)\), \((t+2)\), ..., \((t+i)\) but not at time step \((t+i+1)\).
The total storage required is then:
Thus, even after many passes over the memory, Argon2i can still be computed in roughly n/e space with no time penalty.
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Boneh, D., Corrigan-Gibbs, H., Schechter, S. (2016). Balloon Hashing: A Memory-Hard Function Providing Provable Protection Against Sequential Attacks. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10031. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53887-6_8
Download citation
DOI: https://doi.org/10.1007/978-3-662-53887-6_8
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53886-9
Online ISBN: 978-3-662-53887-6
eBook Packages: Computer ScienceComputer Science (R0)








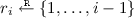 . Throughout our analysis, all probabilities are taken over the random choices of the
. Throughout our analysis, all probabilities are taken over the random choices of the