Abstract
In recent years there have been several attempts to build white-box block ciphers whose implementations aim to be incompressible. This includes the weak white-box ASASA construction by Bouillaguet, Biryukov and Khovratovich from Asiacrypt 2014, and the recent space-hard construction by Bogdanov and Isobe from CCS 2015. In this article we propose the first constructions aiming at the same goal while offering provable security guarantees. Moreover we propose concrete instantiations of our constructions, which prove to be quite efficient and competitive with prior work. Thus provable security comes with a surprisingly low overhead.
P.-A. Fouque, P. Karpman, P. Kirchner, B. Minaud—Partially supported by the French ANR project BRUTUS, ANR-14-CE28-0015.
P. Karpman—Partially supported by the Direction Générale de l’Armement and by the Singapore National Research Foundation Fellowship 2012 (NRF-NRFF2012-06).
You have full access to this open access chapter, Download conference paper PDF
1 Introduction
1.1 White-Box Cryptography
The notion of white-box cryptography was originally introduced by Chow et al. in the early 2000s [CEJO02a, CEJO02b]. The basic goal of white-box cryptography is to provide implementations of cryptographic primitives that offer cryptographic guarantees even in the presence of an adversary having direct access to the implementation. The exact content of these security guarantees varies, and different models have been proposed.
Ideally, white-box cryptography can be thought of as trying to achieve security guarantees similar to a Trusted Execution Environment [ARM09] or trusted enclaves [CD16], purely through implementation means—in so far as this is feasible. Of course this line of research finds applications in many situations where code containing secret information is deployed in non-trusted environments, such as software protection (DRM) [Wys09, Gil16].
Concretely, the initial goal in [CEJO02a, CEJO02b] was to offer implementations of the DES and AES block ciphers, such that an adversary having full access to the implementation would not be able to extract the secret keys. Unfortunately both the initial constructions and later variants aiming at the same goal (such as [XL09]) were broken [BGEC04, GMQ07, WMGP07, DMRP12]: to this day no secure white-box implementation of DES or AES is known.
Beside cryptanalytic weaknesses, defining white-box security as the impossibility to extract the secret key has some drawbacks. Namely, it leaves the door open to code lifting attacks, where an attacker simply extracts the encryption function as a whole and achieves the same functionality as if she had extracted the secret key: conceptually, the encryption function can be thought of as an equivalent secret keyFootnote 1.
This has led research on white-box cryptography into two related directions. One is to find new, sound and hopefully achievable definitions of white-box cryptography. The other is to propose new constructions fulfilling these definitions.
In the definitional line of work, various security goals have been proposed for white-box constructions. On the more theoretical end of the spectrum, the most demanding property one could hope to attain for a white-box construction would be that of virtual black-box obfuscation [BGI+01]. That is, an adversary having access to the implementation of a cipher would learn no more than they could from interacting with the cipher in a black-box way (i.e. having access to an oracle computing the output of the cipher). Tremendous progress has been made in recent years in the domain of general program obfuscation, starting with [GGH+13]. However the current state of the art is still far from practical use, both in terms of concrete security (see e.g. [Hal15]) and performance (see e.g. an obfuscation of AES in [Zim15]).
A less ambitious goal, proposed in [DLPR13, BBK14] is that an adversary having access to the implementation of an encryption scheme may be able to encrypt (at least via code lifting), but should remain unable to decrypt. This notion is called strong white-box in [BBK14] and one-wayness in [DLPR13]. Such a goal is clearly very similar to that of a trapdoor permutation, and indeed known constructions rely on public-key primitives. As a consequence they are no faster than public key encryption. An interesting way to partially circumvent this issue, proposed in [BBK14], is to use multivariate cryptography, where knowledge of the secret information allows encryption and decryption at a speed comparable to standard symmetric ciphers (although public key operations are quite slow). However multivariate cryptography lacks security reductions to well-established hard problems (although they are similar in flavor to \(\mathsf {MQ}\)), and numerous instantiations have been broken, including those of [BBK14]: see [GPT15, DDKL15, MDFK15].
Finally, on the more modest but efficiently achievable end of the spectrum, one can ask that an adversary having access to the white-box implementation cannot produce a functionally equivalent program of significantly smaller size. This notion has been called incompressibility in [DLPR13], weak white-box in [BBK14] and space-hardness in [BI15]Footnote 2. This definition implies in particular that it is difficult for an adversary to extract a short master key, which captures the goal of the original white-box constructions by Chow et al. In addition, the intent behind this approach is that large, incompressible code can more easily be made resistant to code lifting when combined with engineering obfuscation techniques [BBK14, BI15, Gil16]; and make code distribution more cumbersome for a potential attacker.
As mentioned earlier, there is no known implementation of AES or DES that successfully hides the encryption key. A fortiori there is no known way to achieve incompressibility for AES, DES or indeed any pre-existing cipher. However recent constructions have proposed new, ad-hoc, and quite efficient ciphers specifically designed to meet the incompressibility criterion [BBK14, BI15]. These constructions aim for incompressibility by relying on a large pseudo-random table hard-coded into the implementation of the cipher, with repeated calls to the table being made during the course of encryption. The idea is that, without knowledge of all or most of the table, most plaintexts cannot be encrypted. This enforces incompressibility.
In [BBK14], the table is used as an S-box in a custom block cipher design. This requires building the table as a permutation, which is achieved using an ASASA construction, alternating secret affine and non-linear layers. Unfortunately this construction was broken [DDKL15, MDFK15]. This type of attack is completely avoided in the new SPACE construction [BI15], where the table is built by truncating calls to AES. This makes it impossible for an adversary to recover the secret key used to generate the table, based solely on the security of AES. However this also implies that the table is no longer a permutation and cannot be used as an S-box. Accordingly, in SPACE, the table is used as a round function in a generalized Feistel network. While an adversary seeking to extract the key is defeated by the use of AES, there is no provable resistance against an adversary trying to compress the cipher.
We also remark that the standard formalization of white-box cryptography is very close to other models. For example, the bounded-storage model considers the problem of communicating securely given a long public random string which the adversary is unable to store. Indeed, up to renaming, it is essentially the same as the incompressibility of the key, and one of our design is inspired by a solution proposed to this problem [Vad04]. Another model, even stronger than incompressibility, is intrusion-resilience [Dzi06]. The goal is to communicate securely, even when a virus may output any data to the adversary during the computations of both parties, as long as the total data leaked is somewhat smaller than the key size. The disadvantage of this model is that it requires rounds of communication (e.g. 9 rounds in [CDD+07]), while white-box solutions need only add some computations.
1.2 Our Contribution
Both of the previously mentioned constructions in [BBK14, BI15] use ad-hoc designs. They are quite efficient, but cannot hope to achieve provable security. Our goal is to offer provable constructions, while retaining similar efficiency.
First, we introduce new formal definitions of incompressibility, namely weak and strong incompressibility. Weak incompressibility is very close to incompressibility definitions in previous work [BBK14, BI15], and can be regarded as a formalization of the space-hardness definition of [BI15]. Strong incompressibility on the other hand is a very demanding notion; in particular it is strictly stronger than the incompressibility definition of [DLPR13].
Our main contribution is to introduce two provably secure white-box constructions, named WhiteKey and WhiteBlock. We prove both constructions in the weak model. The bounds we obtain are close to a generic attack, and yield quite efficient parameters. Moreover we also prove WhiteKey in the strong model.
Previous work has concentrated on building white-box block ciphers. This was of course unavoidable when attempting to provide white-box implementations of AES or DES. However, it was already observed in the seminal work of Chow et al. that the use of white-box components could be limited to key encapsulation mechanisms [CEJO02a]. That is, the white-box component is used to encrypt and decrypt a symmetric key, which is then used to encrypt or decrypt the rest of the message. This is of course the same technique as hybrid encryption, and beneficial for the same reason: white-box component are typically slower than standard symmetric ciphers (albeit to a lesser extent than public-key schemes).
In this context, the white-box component need not be a block cipher, and our WhiteKey construction is in fact a key generator. That is, it takes a random string as input and outputs a key, which can then be used with any standard block cipher. Its main feature is that it is provably strongly incompressible. Roughly speaking, this implies it is unfeasible for an adversary, given full access to a white-box implementation of WhiteKey, to produce a significantly smaller implementation that is functionally equivalent on most inputs. In fact, an efficient adversary knowing this smaller implementation cannot even use it to distinguish, with noticeable probability, outputs of the original WhiteKey instance from random.
However, WhiteKey is not invertible, and in particular it is not a block cipher, unlike prior work. Nevertheless we also propose a white-box block cipher named WhiteBlock. WhiteBlock can be used in place of any 128-bit block cipher, and is not restricted to key generation. However this comes at some cost: WhiteBlock has a more complex design, and is slightly less efficient than WhiteKey. Furthermore, it is proved only in the weak incompressibility model (essentially the same model as that of SPACE [BI15]), using a heuristic assumption. Thus WhiteKey is a cleaner and more efficient solution, if the key generation functionality suffices (which is likely in most situations where a custom white-box design can be used).
Regarding the proof of WhiteKey in the strong incompressibility model, the key insight is that what we are trying to build is essentially an entropy extractor. Indeed, roughly speaking, the table can be regarded as a large entropy pool. If an adversary tries to produce an implementation significantly smaller than the table, then the table still has high (min-)entropy conditioned on the knowledge of the compressed implementation. Thus if the key generator functions as a good entropy extractor, then the output of the key generator looks uniform to an (efficient) adversary knowing only the compressed implementation.
Furthermore, for efficiency reasons, we want our extractor to be local, i.e. we want our white-box key generator to make as few calls to the table as possible. Hence a local extractor does precisely what we require, and as a result our proof relies directly on previous work on local extractors [Vad04]. Meanwhile our proofs in the weak incompressibility model use dedicated combinatorial arguments.
Finally, we provide concrete instantiations of WhiteKey and WhiteBlock, named PuppyCipher and CoureurDesBois respectively. Our implementations show that these instances are quite efficient, yielding performance comparable to previous ad-hoc designs such as SPACE. Like in previous work, our instances also offer various choices in terms of the desired size of the white-box implementation.
1.3 Related Work
We are aware of three prior incompressible white-box schemes [DLPR13, BBK14, BI15]. In the first of these papers, incompressibility is formally defined [DLPR13]. A public-key scheme is proven in the incompressible model: in a nutshell, the scheme consists in a standard RSA encryption, except for the fact that the public key is inflated by adding an arbitrary multiple of the group order. This provably results in an incompressible scheme, which is also one-way due to its public-key nature. However it is orders of magnitude slower than a symmetric scheme (note that it is also slower than standard RSA due to the size of the exponent).
On the other hand, the authors of [BBK14, BI15] propose symmetric encryption schemes aiming at incompressibility alone. These constructions naturally achieve higher performance. The white-box construction of [BBK14] was broken in [MDFK15, DDKL15]. The construction in [BI15] provides provable guarantees against an adversary attempting to recover the secret key used to generate the table. However no proof is given against an adversary merely attempting to compress the implementation. In fact the construction relies on symmetric building blocks, and any such proof seems out of reach.
An independent work by Bellare, Kane and Rogaway was recently published at Crypto 2016 [BKR16]; its underlying goal and techniques are similar to our strong incompressibility model, and the WhiteKey construction in particular. Although the setting of [BKR16] is different and no mention is made of white-box cryptography, the design objective is similar. The setting considered in [BKR16] is that of the bounded-retrieval model [ADW09], and the aim is to foil key exfiltration attempts by using a large encryption key. The point is that encryption should remain secure in the presence of an adversary having access to a bounded exfiltration of the big key. The exfiltrated data is modeled as the output of an adversarially-defined function of the key with bounded output.
The compressed implementation plays the same role in our definition of strong incompressibility: interestingly, our strong model almost matches big-key security in that sense (contrary to prior work on incompressible white-box cryptography, which is closer to our weak model). Relatively minor differences include the fact that we require a bound on the min-entropy of the table/big key relative to the output of the adversarially-defined function, rather than specifically the number of bits; and we can dispense with a random oracle at the output because we do not assume that the adversary is able to see generated keys directly, after the compression phase. A notable difference is how authenticity is treated: we require that the adversary is unable to encrypt most plaintexts, given the compressed implementation; whereas the authors of [BKR16] only enforce authenticity when there is no leakage. A word-based generalization of the main result in [BKR16], as mentioned in the discussion of that paper, would be very interesting from our perspective, likely allowing better bounds for WhiteKey in the strong incompressibility model. Proofs of weak incompressibility, the WhiteBlock construction, as well as the concrete design of the WhiteKey instance using a variant of the extractor from [CMNT11], are unrelated.
As mentioned earlier in the introduction, the design of local extractors is also directly related to our proof in the strong incompressibility model, most notably [Vad04].
2 Models
2.1 Context
As noted in the introduction, the term white-box cryptography encompasses a variety of models, aiming to achieve related, but distinct security goals. Here we are interested in the incompressibility model. The basic goal is to prevent an attacker who has access to the full implementation of a cipher to produce a more compact implementation.
Incompressibility has been defined under different names and with slight variations in prior work. It is formally defined as \((\lambda ,\delta )\)-Incompressibility in [DLPR13]. A very similar notion is called weak white-box in [BBK14], and space-hardness in [BI15]. In [BBK14], the weak white-box model asks that an efficient adversary, given full access to the cipher implementation, is unable to produce a new implementation of the same cipher of size less than some security parameter T. In [BI15], this notion is refined by allowing the adversary-produced implementation to be correct up to a negligible proportion \(2^{-Z}\) of the input space. Thus a scheme is considered (T, Z)-space-hard iff an efficient adversary is unable to produce an implementation of the cipher of size less than T, that is correct on all but a proportion \(2^{-Z}\) of inputs. This is essentially equivalent to the \((\lambda ,\delta )\)-incompressibility definition of [DLPR13], where \(\lambda \) and \(\delta \) play the respective roles of T and \(2^{-Z}\).
In this work, we introduce and use two main notions of incompressibility, which we call weak and strong incompressibility. Weak incompressibility may be regarded as a formalization of space-hardness from [BI15]. As the names suggest, strong incompressibility implies weak incompressibility (see the full version of this paper [FKKM16]). The point of strong incompressibility is that it provides stronger guarantees, and is a natural fit for the WhiteKey construction.
2.2 Preliminary Groundwork
To our knowledge, all prior work that has attempted to achieve white-box incompressibility using symmetric meansFootnote 3 has followed a similar framework. The general idea is as follows. The white-box implementation of the cipher is actually a symmetric cipher that uses a large table as a component. The table is hard-coded into the implementation. To an adversary looking at the implementation, the table looks uniformly random. An adversary attempting to compress the implementation would be forced to retain only part of the table in the compressed implementation. Because repeated pseudo-random calls to the table are made in the course of each encryption and decryption, any implementation that ignores a significant part of the table would be unable to encrypt or decrypt accurately most messages. This enforces incompressibility.
To a legitimate user in possession of the shared secret however, the table is not uniformly random. It is in fact generated using a short secret key. Of course this short master key should be hard to recover from the table, otherwise the scheme could be dramatically compressed.
Thus a white-box encryption scheme is made up of two components: an encryption scheme, which takes as input a short master secret key and uses it to encrypt data, and a white-box implementation, which is functionally equivalent, but does not use the short master secret key directly. Instead, it uses a large table (which can be thought of as an equivalent key) that has been derived from the master key. This situation is generally formalized by defining a white-box scheme as an encryption scheme together with a white-box compiler, which produces the white-box implementation of the scheme.
Definition 1 (Encryption Scheme)
An encryption scheme is a mapping \(E: \mathcal {K} \times \mathcal {R} \times \mathcal {P} \rightarrow \mathcal {C}\), taking as input a key \(K \in \mathcal {K}\), possibly some randomness \(r \in \mathcal {R}\), and a plaintext \(P \in \mathcal {P}\). It outputs a ciphertext \(C \in \mathcal {C}\). Furthermore it is required that the encryption scheme be invertible, in the sense that there exists a decryption function \(D: \mathcal {K} \times \mathcal {C} \rightarrow \mathcal {P}\) such that \(\forall K, R, P, D(K,E(K,R,P)) = P\).
Definition 2 (White-box Encryption Scheme)
A white-box encryption scheme is defined by a pair of two encryption schemes:
together with a white-box compiler \(C: \mathcal {K} \rightarrow \mathcal {T}\), such that for all \(K \in \mathcal {K}\), \(E_{1}(K,\cdot ,\cdot )\) is functionally equivalent to \(E_{2}(C(K),\cdot ,\cdot )\).
In the definition above, \(E_{1}\) can be thought of as a standard encryption scheme relying on a short (say, 128-bit) master key K, while \(E_{2}\) is its white-box implementation, relying on a large table T derived from K. To distinguish between \(E_{1}\) and \(E_{2}\), we will sometimes call the first scheme the cipher, and the second the (white-box) implementation.
2.3 Splitting the Adversaries
A white-box scheme is faced with two distinct adversaries:
-
The black-box adversary only has black-box access to the scheme. She attempts to attack the cipher with respect to some standard black-box security notion.
-
The white-box adversary has full access to the white-box implementation. She attempts to break incompressibility by producing a smaller implementation of the scheme.
The black-box adversary can be evaluated with respect to standard security notions such as IND-CCA. The specificity of white-box schemes is of course the second adversary, on which we now focus. The white-box adversary itself can be decomposed into two distinct adversaries:
-
The compiler adversary attempts to recover the master key K of \(E_{1}\) given the implementation \(E_{2}\). This is the adversary that succeeds in the cryptanalyses of many previous schemes, e.g. [BGEC04, GMQ07, DDKL15, MDFK15]. More generally this adversary attempts to distinguish C(K) for \(K \leftarrow ^{\$} \mathcal {K}\) from a uniform element of \(\mathcal {T}\).
-
Finally, the implementation adversary does not attempt to distinguish T, and instead regards T as uniformly random. She focuses purely on the white-box implementation \(E_{2}\). She attempts to produce a functionally equivalent (up to some error rate specified by the security parameters), but smaller implementation of \(E_{2}\).
Nicely enough, the three black-box, compiler and implementation adversaries target respectively the \(E_{1}\), C, and \(E_{2}\) components of the white-box scheme (hence their name). Of course the two white-box adversaries (targeting the compiler and implementation) break incompressibility, so they can be captured by the same security definition (as in [DLPR13]). However it is helpful to think of the two as separate adversaries, especially because they can be thwarted by separate mechanisms. Moreover it is clear that resistance to both adversaries implies incompressibility (the dichotomy being whether the table can be efficiently distinguished from random).
The authors of [BI15] introduce a new general method to make sure that the compiler adversary fails, i.e. C(T) is indistinguishable from uniform. Namely, they propose to generate the table T by truncating the output of successive calls to AES (or some other fixed block cipher). In this scenario the master key K of \(E_{1}\) is the AES key. Assuming AES cannot be distinguished from a uniformly random permutation, and the truncated output is (say) at most half of the original cipher, then the table T is indistinguishable from a random function.
2.4 Weak Incompressibility
As noted in the previous section, using the technique from [BI15], defeating the compiler adversary is quite easy, and relies directly and provably on the security of a standard cipher. As a result, our security definition (and indeed, our constructions) focus on the implementation adversary.
The weak incompressibility notion we define below is very close to the space-hardness notion of [BI15], indeed it is essentially a formalization of it. Like in [BBK14, BI15], the definition is specific to the case where the table T is actually a table (rather than an arbitrary binary string) which implements a function (or permutation) \(T: \mathcal {I} \rightarrow \mathcal {O}\), and can be queried on inputs \(i \in \mathcal {I}\).
We write weak incompressibility as ENC-TCOM: ENC reflects the fact that the adversary’s ultimate goal is to encrypt a plaintext. TCOM stands for table-compressed, as the adversary is given access to a compressed form of the table. This is of course weaker than being given access to a compressed implementation defined in an arbitrary adversarially-defined way, as will be the case in the next section.
In the following definition, the encryption scheme should be thought of as the white-box implementation \(E_{2}\) from the previous sections. In particular the “key” is a large table.
Definition 3 (Weak Incompressibility, ENC-TCOM)
Let \(E: \mathcal {T} \times \mathcal {R} \times \mathcal {P}\) denote an encryption scheme. Let \(s, \lambda \) denote security parameters. Let us further assume that the key \(T \in \mathcal {T}\) is a function \(T: \mathcal {I} \rightarrow \mathcal {O}\) for some input and output sets \(\mathcal {I}\) and \(\mathcal {O}\). The encryption scheme is said to be \(\tau \)-secure for \((s,\lambda ,\delta )\)-weak incompressibility iff, with probability at least \(1-2^{-\lambda }\) over the random choice of \(T \in \mathcal {T}\) (performed in the initial step of the game), the probability of success of an adversary running in time \(\tau \) and playing the following game is upper-bounded by \(\delta \).
-
1.
The challenger \(\mathcal {B}\) picks \(T \in \mathcal {T}\) uniformly at random.
-
2.
For \(0 \le i < s\), the adversary chooses \(q_{i} \in \mathcal {I}\), and receives \(T(q_{i})\) from the challenger. Note that the queries are adaptive.
At this point the adversary is tasked with trying to encrypt a random message:
-
3.
The challenger chooses \(P \in \mathcal {P}\) uniformly at random, and sends P to the adversary.
-
4.
The adversary chooses \(C \in \mathcal {C}\). The adversary wins iff C decrypts to P (for key T).
In other words, a scheme is \((s,\lambda ,\delta )\)-weakly incompressible iff any adversary allowed to adaptively query up to s entries of the table T can only correctly encrypt up to a proportion \(\delta \) of plaintexts (except with negligible probability \(2^{-\lambda }\) over the choice of T). Note that \((s,\lambda ,\delta )\)-weak incompressibility matches exactly with \((s,-\log (\delta ))\)-space-hardness in [BI15]. The only difference is that our definition is more formal, as is necessary since we wish to provide a security proof. In particular we specify that the adversary’s queries are adaptive.
It should also be noted that the adversary’s goal could be swapped for e.g. indistinguishability in the definition above. The reason we choose a weaker goal here is that it matches with prior white-box definitions, namely space-hardness [BI15] and weak white-box [BBK14]. Moreover it makes sense in white-box contexts such as DRM, where an attacker is attempting to create a rogue encryption or decryption algorithm: the point is that such an algorithm should fail on most inputs, unless the adversary has succeeded in extracting the whole table (or close to it), and the algorithm includes it.
It is noteworthy that in our definitions, “incompressibility” is captured as a power given to the adversary. The adversary’s goal, be it encryption or indistinguishability, can be set independently of the specific form of compressed implementation she is allowed to ask for. This makes the definition conveniently modular, in the spirit of standard security notions such as IND-CCA.
2.5 Strong Incompressibility
We now introduce a stronger notion of incompressibility. This definition is stronger in two significant ways.
-
1.
First, there is no more restriction on how the adversary can choose to compress the implementation. In the case of weak incompressibility, the adversary was only allowed to “compress” by learning a portion of the table. With strong incompressibility, she is allowed to compress the implementation in an arbitrary way, as long as the table T retains enough randomness from the point of view of the adversary (i.e. she does not learn the whole secret).
-
2.
Second, the adversary’s goal is to distinguish the output of the encryption function from random, rather than being able to encrypt. This requirement may be deemed too demanding for some applications, but can be thought of as the best form of incompressibility one can ask for.
We denote strong incompressibility by IND-COM because the ultimate goal of the adversary is to break an indistinguishability game (IND), given a compressed (or compact) implementation of their choice (COM). We actually give more power to the adversary than this would seem to imply, as the adversary is also given the power to query plaintexts of her choice after receiving the compressed implementation.
Note that in the following definitions, f is not computationally bounded, so generating the tables via a pseudorandom function is not possible.
Definition 4 (Strong Incompressibility, IND-COM)
Let \(E: \mathcal {T} \times \mathcal {R} \times \mathcal {P}\) denote an encryption scheme. Let \(\mu \) denote a security parameter. Let us further assume that the key \(T \in \mathcal {T}\) is chosen according to some distribution D (typically uniform). The scheme E is said to be \((\tau ,\epsilon )\)-secure for \(\mu \)-strong incompressibility iff the advantage of an adversary \(\mathcal {A}\) running in time \(\tau \) and playing the following game is upper-bounded by \(\epsilon \).
-
1.
The adversary chooses a set \(\mathcal {S}\) and a function \(f: \mathcal {T} \rightarrow \mathcal {S}\), subject only to the condition that for all \(s \in \mathcal {S}\), the min-entropy of the variable T conditioned on \(f(T) = s\) is at least \(\mu \). The function f should be thought of as a compression algorithm chosen by the adversary.
-
2.
Meanwhile the challenger \(\mathcal {B}\) picks \(T \in \mathcal {T}\) according to the distribution D (thus fixing an instance of the encryption scheme).
-
3.
The adversary receives f(T). At this point the adversary is tasked with breaking a standard IND-CPA game, namely:
-
4.
The adversary may repeatedly choose any plaintext \(P \in \mathcal {P}\), and learns E(T, R, P).
-
5.
The adversary chooses two plaintext messages \(P_{0}, P_{1} \in \mathcal {P}\), and sends \((P_{0},P_{1})\) to \(\mathcal {B}\).
-
6.
The challenger chooses a uniform bit \(b \in \{0,1\}\), randomness \(R \in \mathcal {R}\), and sends \(E(T,R,P_{b})\) to the adversary.
-
7.
The adversary computes \(b' \in \{0,1\}\) and wins iff \(b' = b\).
It may be tempting, in the previous definition, to allow the adversary to first query E, and choose f based on the answers. However it is not necessary to add such interactions to the definition: indeed, such interactions can be folded into the function f, which can be regarded as an arbitrary algorithm or protocol between the adversary and the challenger having access to T. The only limitation is that the min-entropy of T should remain above \(\mu \) from the point of view of the adversary. It is clear that a limitation of this sort is necessary, otherwise the adversary could simply learn T.
Furthermore, while a definition based on min-entropy may seem rather impractical, it encompasses as a special case the simpler space-hard notion of [BI15]. In that case the table T is a uniform function, and f outputs a fixed proportion 1/4 of the table. The min-entropy \(\mu \) is then simply the number of unknown output bits of the table (namely 3/4 of its output).
The WhiteKey construction that we define later on is actually a key generator. That is, it takes as input a uniformly random string and outputs a key. The strong incompressibility definition expects an encryption scheme. In order for the WhiteKey key generator to fulfill strong incompressibility, it needs to be converted into an encryption scheme. This is achieved generically by using the generated key (the output of WhiteKey) with a conventional symmetric encryption scheme, as in a standard hybrid cryptosystem. For instance, the plaintext can be XORed with the output of a pseudorandom generator whose input is the generated key. Strictly speaking, when we say that WhiteKey satisfies strong incompressibility, we mean that this is the case when WhiteKey is thus used as a key generator in combination with any conventional symmetric encryption process.
Note that this does not enforce authenticity. For instance, if the generated key is used as an input to a stream cipher, forgeries are trivial. More generally it is not possible to prevent existential forgeries, as the adversarially compressed implementation could include any fixed arbitrary valid ciphertext. However universal forgeries can be prevented. This is naturally expressed by the following model. The model actually captures the required goal in previous definitions of incompressibility, in fact the model as a whole is essentially equivalent to incompressibility in the sense of [DLPR13].
Definition 5 (Encryption Incompressibility, ENC-COM)
Let \(E: \mathcal {T} \times \mathcal {R} \times \mathcal {P}\) denote an encryption scheme. Let \(\mu \) denote a security parameter. Let us further assume that the key \(T \in \mathcal {T}\) is chosen according to some distribution D (typically uniform). The scheme E is said to be \((\tau ,\epsilon )\)-secure for \(\mu \)-strong incompressibility iff the advantage of an adversary \(\mathcal {A}\) running in time \(\tau \) and playing the following game is upper-bounded by \(\epsilon \).
-
1.
The adversary chooses a distribution \(\mathcal {D}\) with min-entropy at least \(\mu \) on \(\mathcal {P}\).
-
2.
The adversary chooses a set \(\mathcal {S}\) and a function \(f: \mathcal {T} \rightarrow \mathcal {S}\), subject only to the condition that for all \(s \in \mathcal {S}\), the min-entropy of the variable T conditioned on \(f(T) = s\) is at least \(\mu \). The function f should be thought of as a compression algorithm chosen by the adversary.
-
3.
Meanwhile the challenger \(\mathcal {B}\) picks \(T \in \mathcal {T}\) according to the distribution D (thus fixing an instance of the encryption scheme).
-
4.
The adversary receives f(T). At this point the adversary is tasked with forging a message, namely:
-
5.
The adversary samples a plaintext \(M \in \mathcal {P}\) from the distribution \(\mathcal {D}\).
-
6.
The adversary may repeatedly choose any plaintext \(P \in \mathcal {P}\), and learns E(T, R, P).
-
7.
The adversary wins iff she can compute a \(C\in \mathcal {C}\) such that \(D(T,C)=M\).
This model can also be fulfilled by the WhiteKey scheme, if we derive the required randomness from \(H(P)+r\) where H is a random oracle, P is the plaintext, and r is a uniform value of \(\mu \) bits added to the encryption. The decryption starts by recovering the key, and then checks if the randomness used came from \(H(P',r)\) where \(P'\) is the decrypted plaintext. This naturally makes any encryption scheme derived from a key generator resistant to universal forgeries.
Remark that it is necessary in the model to have the forged message generated independently of \(f(\mathcal {T})\), otherwise one can simply put an encryption of the message in f(T).
Finally, observe that ENC-COM is stronger than ENC-TCOM, as ENC-TCOM it is the special case of ENC-COM where the adversary’s chosen function f does nothing more than querying T on some adaptively chosen inputs, and returning the outputs.
3 Constructions
In this section, we present two constructions that are provably secure in the weak white-box model ENC-TCOM of Sect. 2 (cf. Definition 3): the WhiteBlock block cipher, and the WhiteKey key generator. WhiteKey is also provable in the strong model. We also propose PuppyCipher and CoureurDesBois as concrete instantiations of each construction, using the AES as underlying primitive.
3.1 The WhiteBlock Block Cipher
The general idea of WhiteBlock is to build a Feistel network whose round function uses calls to a large table T. An adversary who does not extract and store a large part of this table should be unable to encrypt most plaintexts. For that purpose, it is important that the inputs of table calls be pseudo-random, or at least not overly structured. Otherwise the adversary could attempt to store a structured subset of the table that exploits this lack of randomness. In WhiteBlock, the pseudo-randomness of table calls is enforced by interleaving calls to a block cipher between each Feistel round.
Concretely, WhiteBlock defines a family of block ciphers with blocks of size \(b=128\) bits, and a key of size \(\kappa =128\) bitsFootnote 4. The family is parameterized with a size parameter which corresponds to the targeted size of a white-box implementation. In principle, this size can be anything from a few dozen bytes up to \(\approx 2^{64}\) bytes, but we will mostly restrict this description to the smallest case considered in this article, which has an implementation of size \(2^{21}\) bytes.
Formally, we define one round of WhiteBlock (with tables of input size 16 bits) as follows. Let \({{\mathrm{\mathcal {A}}}}_k\) denote a call to the block cipher \({{\mathrm{\mathcal {A}}}}\) with key k, and \({{\mathrm{\mathcal {T}}}}_i : \{0,1\}^{16} \rightarrow \{0,1\}^{64}\) denote the i-th table. The Feistel round function is defined by:
and one round of WhiteBlock with key k is defined as:
A full instance of WhiteBlock is then simply the composition of a certain number of independently-keyed round functions, with the addition of one initial top call to \({{\mathrm{\mathcal {A}}}}\): \(\text {WhiteBlock} _{k_0,\ldots k_r} : \{0,1\}^{128} \rightarrow \{0,1\}^{128}, x \mapsto {{\mathrm{\mathcal {A}}}}_{k_r} \circ {{\mathrm{\mathcal {R}}}}_{k_{r-1}} \circ \cdots \circ {{\mathrm{\mathcal {R}}}}_{k_0}(x)\). We give an illustration of this construction (omitting the outer sandwiching calls to \({{\mathrm{\mathcal {A}}}}\)) in Fig. 1.
Constructing the Tables. For WhiteBlock instances with small tables, the most efficient way to implement the cipher is simply to use the white-box implementation, i.e. use a table-based implementation of \({{\mathrm{\mathcal {F}}}}\) (this will be clear from the results of Sect. 5). In that case, it is easy to generate the tables “perfectly” by drawing each entry uniformly at random, either by using a suitable source of randomness (in that case, no one may be able to compress the tables) or by using the output of a cryptographically-strong PRG seeded with a secret key. In the latter case, the owner of the secret knows how to compactly represent the tables, but this knowledge seems to be hard to exploit in a concrete implementation.
For larger instances, it is not true anymore that the fastest implementation is table-based, and it may be useful in some contexts to be able to compute the output of a table more efficiently than by querying it. Surely, if one knows how to compactly represent a table, it is desirable that he would be able to do so, at least for large tables. In that respect, drawing the tables at random would not be satisfactory anymore.
Consequently, the tables used in WhiteBlock are generated as follows. Let again \({{\mathrm{\mathcal {T}}}}_i : \{0,1\}^{16} \rightarrow \{0,1\}^{64}\) be such a table (in the 16-bit case), then an instance of it is defined with two parameters \(k \in \{0,1\}^{128}\), \(c \in \{0,1\}^{128-16}\) as  , with \(\lfloor \cdot \rfloor _{64}\) denoting the truncation to the 64 lowest bits.
, with \(\lfloor \cdot \rfloor _{64}\) denoting the truncation to the 64 lowest bits.
An instance of WhiteBlock can thus always be described and implemented compactly when knowing k and c. Of course this knowledge is not directly accessible in a white-box implementation, where a user would only be given the tables as a whole.
Concrete Parameters for Various Instances of WhiteBlock. We need to address two more points before finishing this high-level description of WhiteBlock: (1) given the size of the tables, how many rounds r are necessary to obtain a secure white-box construction; (2) how to generate the multiple round keys \(k_0,\ldots k_r\). The answer to (1) is provided by the analysis of the construction done in the full paper, specifically [FKKM16, Theorem 3]. By instantiating the formula from the theorem with concrete parameters, we obtain the results given in Table 1. As for (2), we simply suggest to use independent keys (as both their generation process and the cost of storing the precomputed subkeys are negligible w.r.t. the generation and storage of the tables). There is some flexibility in the framework and one can for instance consider using a tweakable block cipher instead, as we do in our actual instantiation of WhiteBlock presented next.
PuppyCipher: WhiteBlock in Practice. So far WhiteBlock has been described from an abstract point of view, where all components are derived from a block cipher \({{\mathrm{\mathcal {A}}}}\). In practice, we need to specify a concrete cipher; we thus define the PuppyCipher family as an instantiation of WhiteBlock using AES128 [DR02] for the underlying block cipher. Furthermore, though relying on a secure block cipher is an important argument in the proof of the construction, one can wish for a less expensive round function in practice. Hence we also define the lighter, more aggressive alternative “\(\textsc {Hound} \)” which trades provable security for speed. The only differences between PuppyCipher and \(\textsc {Hound} \) are:
-
1.
The calls to the full AES128 are traded for calls to AES128 reduced to five rounds (this excludes the calls in the table generation, which still use the full AES).
-
2.
The round keys \(k_r \ldots k_0\) used as input to \({{\mathrm{\mathcal {A}}}}\) are simply derived from a unique key K as
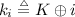 . Note that using a tweakable cipher such as KIASU-BC [JNP14] would also be possible here.
. Note that using a tweakable cipher such as KIASU-BC [JNP14] would also be possible here.
In Sect. 5, we discuss the efficiency of PuppyCipher and \(\textsc {Hound} \) implemented with the AES instructions, for tables of 16, 20, and 24-bit inputs.
3.2 The WhiteKey Key Generator
In WhiteBlock, we generated pseudo-random calls to a large table by interleaving a block cipher between table calls. If we are not restricted by the state size of a block cipher, generating pseudo-random inputs for the table is much easier: we can simply use a pseudo-random generator. From a single input, we are then able to generate a large number of pseudo-random values to be used as inputs for table calls. It then remains to combine the outputs of these table calls into a single output value of appropriate size. For this purpose, we use an entropy extractor. More details on our choice of extractor are provided in the design rationale below.
We now describe the WhiteKey function family, which can in some way be seen as an unrolled and parallel version of WhiteBlock, with some adjustments. As with WhiteBlock, we describe the main components of WhiteKey for use with a 128-bit block cipher and tables of 16-bit inputs, but this generalizes easily to other sizes.
Thus WhiteKey uses a table \(T: \{0,1\}^{16} \rightarrow \{0,1\}^{128}\). Let n denote the number of table calls (which will be determined later on by security proofs),  and
and  . At a high level, the construction of WhiteKey can be described by the following process: (1) from a random seed, generate t 128-bit values using a block cipher \({{\mathrm{\mathcal {A}}}}\) with key k in counter mode; (2) divide each such value into eight 16-bit words; (3) use these words as n inputs to the table T (possibly ignoring from one to seven of the last generated values), resulting in n 128-bit values \(Q_{i,j}, 0 \le i, j \le d = \lceil \sqrt{n}\rceil \) (if n is not a square, the remaining values \(Q_{i,j}\) are set to zero); (4) from a random seed, generate d 128-bit values \(a_i\) and d 128-bit values \(b_i\) using \({{\mathrm{\mathcal {A}}}}\) with key \(k'\) in counter mode; (5) the output of WhiteKey is \(\sum _{i,j} Q_{i,j}\cdot a_i \cdot b_j\), the operations being computed in \(\mathbb {F}_{2^{128}}\).
. At a high level, the construction of WhiteKey can be described by the following process: (1) from a random seed, generate t 128-bit values using a block cipher \({{\mathrm{\mathcal {A}}}}\) with key k in counter mode; (2) divide each such value into eight 16-bit words; (3) use these words as n inputs to the table T (possibly ignoring from one to seven of the last generated values), resulting in n 128-bit values \(Q_{i,j}, 0 \le i, j \le d = \lceil \sqrt{n}\rceil \) (if n is not a square, the remaining values \(Q_{i,j}\) are set to zero); (4) from a random seed, generate d 128-bit values \(a_i\) and d 128-bit values \(b_i\) using \({{\mathrm{\mathcal {A}}}}\) with key \(k'\) in counter mode; (5) the output of WhiteKey is \(\sum _{i,j} Q_{i,j}\cdot a_i \cdot b_j\), the operations being computed in \(\mathbb {F}_{2^{128}}\).
Let us now define this more formally. We write \({{\mathrm{\mathcal {A}}}}_k^t(s)\) for the t first 128-bit output blocks of \({{\mathrm{\mathcal {A}}}}\) in counter mode with key k and initial value s. We write \(\mathcal {C}_n\) for the parallel application of \(n \le 8\times t\) tables \({{\mathrm{\mathcal {T}}}}: \{0,1\}^{16} \rightarrow \{0,1\}^{128}\) (written here in the case \(n = 8 \times t\) for the sake of simplicity):
We write \({{\mathrm{\mathcal {S}}}}_n\) for the “matrixification” mapping; taking  (here with \(n = 57\), for a not too complex general case):
(here with \(n = 57\), for a not too complex general case):
Finally, we write \({{\mathrm{\mathcal {E}}}}\) the “product” mapping:
We can then describe an instance of WhiteKey parametered by \((k_1, s_1, k_2, s_2)\) over t and n values as  (using a Curried version of \({{\mathrm{\mathcal {E}}}}\) for simplicity of notations).
(using a Curried version of \({{\mathrm{\mathcal {E}}}}\) for simplicity of notations).
Constructing the Tables. The table used in an instance of WhiteKey is built in the same way as for WhiteBlock. The only difference is that the output of \({{\mathrm{\mathcal {A}}}}\) is not truncated and the full 128 bits are used.
Design Rationale of WhiteKey. The first part of the scheme consists in selecting a fraction of the secret that needs to be accessed, which is a necessary step. The fastest way to implement this part is to access the secret in parallel at locations that are thus determined independently.
The second part is to derive a short key from the table outputs, which are of high min-entropy. The standard way to build a key derivation function is to use a hash function [Kra10]. However it is slow, since even a fast hash function like BLAKE2b takes 3 cycles per byte on modern processors [ANWOW13]. Instead, we decided to use an extractor, which has also the advantage to be unconditionally secure for a uniform seed. The extractor literature focused primarily on reducing the number of seed bits and maximizing the number of extracted bits, because of their importance in theoretical computer science; see [Sha11] for a survey. In our case, we want to extract only a few bits and speed is the principal concern. The approach recommended by [BDK+11] is to generate pseudo-random elements in a large field using a standard pseudorandom generator (say, AES-CTR) and to compute a dot product with the input. The main problem of this extractor is that it uses a seed which is very large, and it takes about as much time to generate it (with AES-NI) as to use it. Hence, we decided to use the extractor introduced in [CMNT11], which has a seed length about the square root of the length of the input. Since we can evaluate \(\sum _{i,j} Q_{i,j}a_ib_j\) with about one multiplication and one addition in the field per input value, the computation of the extractor takes essentially the same time. Indeed, the complexity of the extractor is similar to GHASH.
Another possibility for the extractor is to increase the degree, for instance use \(\sum _{i,j,k} Q_{i,j,k}a_ib_jc_k\). While this approach, proposed by [CNT12], is indeed sound and allows to reduce the seed further, the best bound we know on the statistical distance of the output is about \(q^{-1/2}\) when working over \(\mathbb {F}_q\). The main problem is that the tensor decomposition of \(Q_{i,j,k}\) does not have the needed properties, so that Coron et al. use a generic bound on the number of zeroes, which must account for elliptic curves and therefore a deviation of \(q^{-1/2}\) is required. The specific case of \(\sum _{k=0}^1\sum _{i,j} Q_{i,j,k}a_ib_jc_k\) can probably be tackled using linear matrix pencil theory, at the cost of a much more difficult proof.
Concrete Parameters for Various Instances of WhiteKey. Once the size of an instance of WhiteKey has been chosen (i.e. the output size of the table \({{\mathrm{\mathcal {T}}}}\)), the only parameter that needs to be determined is the number of calls to the tables n, and thus the number of output blocks t of \({{\mathrm{\mathcal {A}}}}\). This is obtained by instantiating the formula of [FKKM16, Theorem 2] for a given white-box security. We give the parameters for instances of various sizes in Table 2. The tables used in these instances have the same input size as the ones of the WhiteBlock instances of Table 1, but they are twice as large because of their larger output size, which impacts the size of a white-box implementation similarly. On the other hand, a single table is used in WhiteKey, whereas up to four (for input sizes of 16 bits and more) are necessary in WhiteBlock.
CoureurDesBois: WhiteKey in Practice. Similarly to WhiteBlock and PuppyCipher, we define the CoureurDesBois family as a concrete instantiation of WhiteKey. It simply consists in using AES128 for \({{\mathrm{\mathcal {A}}}}\) and a specific representation for \(\mathbb {F}_{2^{128}}\), e.g. \(\mathbb {F}_2[x]/x^{128} + x^7 + x^2 + x + 1\) (the “GCM” field).
Unlike PuppyCipher, the components of CoureurDesBois are not cascaded multiple times; hence we cannot hope for a similar tradeoff of provable security against speed. However, the main advantage of CoureurDesBois compared to PuppyCipher is that it lends itself extremely well to parallelization. This allows to optimally hide the latency of the executions of AES and of the queries to the table in memory.
We further discuss the matter in Sect. 5, where we evaluate implementations of CoureurDesBois with AES instructions for tables of 16 to 24-bit inputs.
4 Security Proofs
For both the WhiteBlock and WhiteKey constructions, we provide proofs in the weak incompressibility model. These proofs provide concrete bounds, on which we base our implementations. This allows direct comparison to previous work [BBK14, BI15]. Moreover in the case of WhiteKey, we provide a proof in the strong incompressibility model. This proof shows the soundness of the general construction in a very demanding model. However we do not use it to derive the parameters of our constructions.
Recall that weak incompressibility (Definition 3) depends on three parameters s, \(\lambda \), \(\delta \): essentially if the number of outputs of the table known to the adversary is s, then \((s,\lambda ,\delta )\)-incompressibility says that with probability at least \(1-2^{-\lambda }\), the adversary is unable to encrypt more than a ratio \(\delta \) of plaintexts, no matter which s table outputs she chooses to learn. If inputs to the table are t-bit long, then \(\alpha = s2^{-t}\) is the fraction of the table known to the adversary. We can fix \(\alpha = 1/4\) as in [BI15], hence \(s = \alpha 2^{t}\). In that case weak incompressibility essentially matches \((s,-\log (\delta ))\)-space hardness from [BI15], and \(-\log (\delta )\) can be thought of as the number of bits of white-box security.
However we do not claim security for \(\delta = 2^{-128}\), which would express 128 bits of white-box security. Instead, we claim security for \(\delta = 2^{-128+t}\). Thus for larger table of size \(\approx 2^{28}\), white-box security drops to around \(2^{100}\). We believe this is quite acceptable.
The reason we claim only \(128-t\) bits of white-box security rather than 128 is a result of our security proofs, as we shall see. This should be compared with the fact that an adversary allowed to store s table inputs could use the same space to store s outputs of the whole scheme (within a small constant factor \(\lambda /t\) in the case of WhiteBlock). Such an adversary would naturally be able to encrypt a proportion \(s2^{-\lambda }\) of inputs. Since \(s = 2^{t}/4\), with a small constant factor 1 / 4, this yields the \(128-t\) bits of white-box security achieved by our proofs.
Our security claims are summarized in Tables 1 and 3.2.
4.1 Proofs of Weak Incompressibility
We provide proofs of both WhiteKey and WhiteBlock in the weak incompressibility model. In the case of WhiteKey, a proof is also available in the strong incompressibility model. However the proof of WhiteKey for weak incompressibility is fairly straightforward, yields better bounds (as one would expect), and also serves as a warm-up for the combinatorially more involved proof of WhiteBlock. The bulk of the proofs for WhiteKey and WhiteBlock are given in the full paper [FKKM16]. In this section, we provide some context and a brief outline.
Weak Incompressibility of WhiteKey. First note that if the AES in counter mode used in the initial layer of WhiteKey is modeled as a pseudo-random generator (PRG), the proof is quite straightforward. Indeed, we are then free to regard the inputs of table calls as uniformly random (after paying the PRG advantage of an adversary against counter mode AES). It follows that the adversary has probability \(\alpha \) of knowing the output of each individual table call, where \(\alpha \) is the proportion of the table she has queried, regardless of which particular inputs she chose to query. Since the extractor in the last layer of the scheme is linear, as soon as the adversary is missing one table output, the global output of the scheme is uniformly random from her point of view.
However we focus on a different route for the proof, where the initial layer of the scheme is modeled as a pseudo-random function (PRF) rather than a PRG. The main reason we do this is that the resulting proof will be much closer to the proof of WhiteBlock, and serve to prepare it.
We thus view the initial layer of WhiteKey as being comprised of a PRF generating the inputs of the table calls. Using standard arguments, this pseudo-random function can be replaced by a random function; the effect this has on the weak incompressibility adversary is upper-bounded by the distinguishing advantage of a real-or-random adversary against the PRF.
In the weak incompressibility game, the adversary learns the output of the table on some adaptively chosen inputs. By nature of white-box security, any keying material present in the PRF is known to the adversary (formally, in our definition of white-box encryption scheme this keying material would have to be appended to the table T of the white-box implementation, and could be recovered with a single or few queries). Hence the adversary can choose which table inputs she queries based on full knowledge of the initial PRF.
On the other hand, for a given PRF input, as soon as the adversary does not know a single output of the table, due to the linearity of the final layer of the construction, the output has full 128-bit entropy from the point of view of the adversary.
Thus the core of the proof, is to show that, with high probability over the random choice of the PRF, for the best possible choice of s table inputs the adversary chooses to queryFootnote 5, most PRF outputs still include at least one table input that is unknown to the adversary. We explicitly compute this upper bound in the complete proof.
More precisely, [FKKM16, Theorem 2] shows:
where:
-
\(n = 2^{\lambda }\) is the size of the input space of WhiteKey;
-
t is the number of bits at the input of a table;
-
s is the number of table entries stored by the adversary;
-
\(\rho = 2^{\lambda }(s/2^{t})^{m}\), with m the number of table calls in the construction;
-
k is the maximal number of inputs the adversary may be able to encrypt;
-
and \(\mu (s)\) is the maximal number of WhiteKey inputs that can be encrypted with storage size s; it is a random variable over the uniform choice of the initial PRF (\(\mathcal {A}\) in counter mode, in the previous description).
We want this bound to be below \(-\lambda \). We are now interested in what this implies, in terms of number of table calls m necessary to achieve a given security level. As noted earlier, the bound imposes \(k \approx 2^{t}\). For simplicity we let \(k = 2^{t}\), which means we achieve \(\lambda -t\) bits of white-box security (i.e. \(\delta = 2^{t-\lambda }\) in the sense of Definition 3). We can also fix \(s/2^{t} = 1/4\) for the purpose of being comparable to [BI15].
The term \(\left( n-k\right) \ln \left( ({n-k})/({n-\rho })\right) \) is equivalent to \(\rho -k\) as k / n tends to zeroFootnote 6. Since we are looking for an upper bound we can approximate it by k. This yields a probability:
In the end, we get that m only needs to be slightly larger than \(\frac{\lambda -\log (k)}{2}\). Indeed, as long as this is the case, the \(2^{t}\) factor will ensure that the bound is (much) lower than \(-128\).
This actually matches a generic attack. If the adversary just stores \(s = 2^{t}/4\) random outputs of the table, then on average she is able to encrypt a ratio \(2^{-2m}\) of inputs. This imposes \(2^{-2m} < k2^{-\lambda }\), so \(m > (\lambda -\log (k))/2\). When testing our parameter choices against Eq. 1, we find that it is enough to add a single table call beyond what the generic attack requires: in essence, [FKKM16, Theorem 2] implies that no strategy is significantly better than random choices.
Weak Incompressibility of WhiteBlock. The general approach of the proof is the same as above. However the combinatorial arguments are much trickier, essentially because table calls are no longer independent (they depend on table outputs in the previous round.). Nevertheless an explicit bound is proven in the full paper.
However, what we prove is only that w.h.p., for most inputs to WhiteBlock, during the computation of the output, at least two table calls at different rounds are unknown to the adversary. Since table outputs cover half a block, this implies that at two separate rounds during the course of the computation, 64 bits are unknown and uniform from the point of view of the adversary. At this point we heuristically assume that for an efficient adversary, this implies the output cannot be computed with probability significantly higher then \(2^{-128}\). In practice the bottleneck in the bound provided by the proof comes from other phenomena, namely we prove \(128-t\) bits of security for t-bit tables. Nevertheless this means our proof is heuristic.
More precisely, [FKKM16, Theorem 3] shows:
where:
-
\(\lambda \) is the input size of WhiteBlock;
-
t is the number of bits at the input of a table;
-
r is the number of rounds;
-
m is the total number of table calls in the construction (
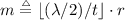 );
); -
s is the number of table entries stored by the adversary;
-
k is the maximal number of inputs the adversary may be able to encrypt;
and \(\mu (s)\) is the maximal number of WhiteBlock inputs that can be encrypted with storage size s; it is a random variable over the uniform choice of the round permutations \(\mathcal {A}_{k_{i}}\).
We are now interested in what this bound implies, in terms of number of rounds r to achieve a given security level. Observe that the bound requires \(k \approx 2^{t}\). For simplicity we let \(k = 2^{t}\), which means we achieve \(\lambda -t\) bits of white-box security (i.e. \(\delta = 2^{t-\lambda }\) in the sense of Definition 3). We can also fix \(s/2^{t} = 1/4\) for the purpose of being comparable to [BI15]. Observe that 1 / k is negligible compared to 1 / r. Let \(c = \lfloor (\lambda /2)/t\rfloor \) be the number of table calls per round. Then our bound asks:
Indeed, as long as this value is negative, the preceding \(k = 2^{t}\) factor will ensure that the bound is (much) lower than \(-128\). We get:
We can compare this bound with the previous generic attack, where the adversary stores table outputs at random. As we have seen, this attack implies \(m > (\lambda -\log (k))/2\), so \(r > (\lambda -\log (k))/(2c)\). Instead our proof requires \(r > \frac{\lambda }{2c} + 1\). Thus the extra number of rounds required by our security proof, compared to the lower bound coming from the generic attack, is less than \(\log (k)/(2c) + 1\): it is only a few extra rounds (and not, for instance, a multiplicative factor).
4.2 Proof of Strong Incompressibility
We first prove that \(\sum _{i,j} Q_{i,j}a_ib_j \in {{\mathrm{\mathbb {F}}}}_q\) is a strong extractor. This extractor comes mostly from Coron et al. [CMNT11, Sect. 4.2] but we tighten the proof.
Definition 6
A family \(\mathcal {H}\) of hash functions \(h:X\mapsto Y\) is \(\epsilon \)-pairwise independent if
The next lemma is a variant of the leftover hash lemma, proven in [Sti02, Theorem 8.1].
Lemma 1
Let \(h\in \mathcal {H}\) be uniformly sampled, and \(x\in X\) be an independent random variable with min-entropy at least k. Then, the statistical distance between (h(x), h) and the uniform distribution is at most
We now prove that our function is indeed pairwise independent.
Lemma 2
Let \(\mathcal {H}={{\mathrm{\mathbb {F}}}}_q^{2n}\), \(X=M_n({{\mathrm{\mathbb {F}}}}_q)\) and \(Y={{\mathrm{\mathbb {F}}}}_q\). Then, the function \(h_{a,b}(Q)=\sum _{i,j} Q_{i,j}a_ib_j=a^tQb\) is \(11q^{-n}\)-pairwise independent.
Proof
We first count the number of a, b such that \(\sum _{i,j} Q_{i,j}a_ib_j=a^tQb=0\). Let Q be a matrix of rank r. Then, there exist r vectors u, v such that \(Q=\sum _{k=0}^{r-1} u_iv_i^t\) and the \(u_i\) as well as the \(v_i\) are linearly independent. Thus,
and therefore, by a change of basis, this form has the same number of zeros as
which is \(q^{2n-1}+q^{2n-r}-q^{2n-r-1}\).
Now, there are \(\prod _{k=1}^{r-1} \frac{(q^n-q^k)^2}{q^r-q^k}\) matrices of rank r. We deduce:
\(\square \)
Hence, if the input of our extractor has at least \(2\mu \) bits of entropy, the generated key will be essentially uniform. The proof for the security of sampling the seed from a pseudorandom generator (from which we cannot build a public-key primitive) is in [BDK+11]. We now prove that the input has indeed a lot of entropy.
Lemma 3
Let \(f:[n]\mapsto [0;1]\) be of average \(\mu \). Then, the average of the image k uniform elements is at least \(\mu -\delta \), except with probability
Proof
This is the result of Bernstein’s inequality (see [BLB04, Theorem 3]), since the variance of all terms is at most 1 / 4 and they are all positive. \(\square \)
We now use a lemma of Vadhan [Vad04, Lemma 9]:
Lemma 4
Let S be a random variable over \([n]^t\) with distinct coordinates and \(\mu ,\delta ,\epsilon >0\), such that for any function \(f:[n]\mapsto [0;1]\) of average \((\delta -2\tau )/\log (1/\tau )\), we have that the probability that the average of the image of the t positions given by S is smaller than \((\delta -3\tau )/\log (1/\tau )\) is at most \(\epsilon \).
Then, for every X of min-entropy \(\delta n\) over \(\{0,1\}^n\), the variable \((S,X_S)\) where \(X_S\) is the subset of bits given by S is \(\epsilon +2^{-\varOmega (\tau n)}\) close to (A, B) where B conditioned on \(A=a\) has a min-entropy \((\delta -\tau )t\).
Finally, it is clear that if a sampling done with a pseudorandom generator instead of a uniform function leads to a low min-entropy key, we have a distinguisher on the pseudorandom generator.
5 Implementation
In this section, we evaluate the efficiency of PuppyCipher {16,20,24}, Hound {16,20,24} and CoureurDesBois {16,20,24}, when implemented with the AES and PCLMULQDQ instructions (the latter being only used for the finite field arithmetic of CoureurDesBois) on a recent Haswell CPU. For each algorithm, we tested table-based white-box implementations and “secret” implementations where one has the knowledge of the key used to generate the tables.
The number of rounds we choose was directly deduced from proofs in the weak model (cf. Sects. 3 and 4). Since this model essentially matches that of previous work [BBK14, BI15], this allows for a direct comparison.
The processor on our test machine was an Intel Xeon E5-1603v3, which has a maximal clock frequency of 2.8 GHz and a 10 MB cache (which is thus larger than the implementation sizes of the ‘16 instances). The machine has 32 GB of memory, in four sticks of 8 GB all clocked at 2133 MHz. All measurements were done on an idle system, without Turbo Boost activatedFootnote 7. As a reference, we first measured the performance of AES128 implemented with the AES instructions, given in Table 3. We give the average (Avg.) number of clock cycles and the standard deviation (Std. Dev.) for one execution, both in the transient and steady regime (in practice, when performing series of independent runs, the transient regime only corresponds to the first run of the series). The average and standard deviation are computed from 25 series of 11 runs. The figures obtained from this test are coherent with the theoretical performance of the AES instruction set (even if slightly better): on a Haswell architecture, the aesenc and aesenclast instructions are both given for a latency of 7 cycles, and the cost of a single full AES128 is dominated by the \(10 \times 7\) calls to perform the 10 rounds of encryption.
5.1 PuppyCipher
Writing a simple implementation of PuppyCipher is quite straightforward. The main potential for instruction-level parallelism (ILP) are the calls to the tables (or the analogous on-the-fly function calls); the rest of the cipher is chiefly sequential, especially the many intermediate calls to the (potentially reduced) AES. This parallelism is however somewhat limited, especially starting from PuppyCipher 24 where only two parallel calls to the tables can be made.
In all implementations, we precompute the sub-keys for the calls to AES (including calls potentially made to emulate the tables). Not doing so would only add a negligible overhead.
The performance measurements were done in a setting similar to the reference test on AES128 from above. We give the results for PuppyCipher {16,20,24} in Table 4 and for \(\textsc {Hound} \) {16,20,24} in Table 5. In both tables, we also express the performance in the steady regime as the number of equivalent AES128 calls (Eq. A) with AES instructions on the same platform (taken to be 68 cycles, as per Table 3) as it is a block cipher with similar expected (black-box) security, and as the number of equivalent ephemeral Diffie-Hellman key exchanges with the Four\(\mathbb {Q}\) elliptic curve (Eq. F), one of the fastest current implementation of ECDHE [CL15] (measured at 92000 cycles on the Haswell architecture), as there is some overlap in what white-box and public-key cryptography try to achieve.
Discussion. As it was mentioned in Sect. 3, for a small white-box implementation such as the one of PuppyCipher 16, table-based implementations may be the most efficient way of implementing the cipher, especially as the entire tables can usually fit in the cache. However, from a certain size on, the random RAM accesses inherent to such implementations cost more than recomputing the necessary outputs of the tables (when the secret is known).
It is quite easy to estimate how much time is spent in RAM accesses compared to the time spent in calls to the (potentially reduced) AES. Indeed, knowing the number of rounds and the cost of one AES execution, one can subtract this contribution to the total. For instance, based on the cycle counts in the steady and transient regimes, for PuppyCipher 24, at least \(2380 = 35 \times 68\) and at most \(2765 = 35 \times 79\) cycles are expected to be spent in AES instructions; the real figure in this case is about 2690 cycles, for an average cost per AES call of 77 cycles. All in all, this means that in steady regime, close to \(90\,\%\) of the time is spent in RAM accesses. This is understandingly slightly more for the \(\textsc {Hound} \) 24 variant, where RAM accesses represent about \(93\,\%\) of the execution time.
It is also interesting to look at how many RAM accesses can effectively be done in parallel. As two to four table calls are independent every round, we may hope to partially hide the latency of some of these. For PuppyCipher 24, removing one of the two table accesses decreases the cycle count to 19400 on average. This means that the second table call only adds less than 4000 cycles. Put another way, using a single table per round, one table access takes 490 cycles on average, but this goes down to an amortized 300 cycles when two tables are accessed per round. In the end, the 68 table access of PuppyCipher 24 only cost an equivalent 42 purely sequential accesses. A similar analysis can be performed for PuppyCipher 20 and PuppyCipher 16, where the 69 and 72 parallel accesses cost 31 and 23 equivalent accesses respectively.
Comparison with SPACE. We can compare the performance of PuppyCipher with the one of SPACE-(16,128) and SPACE-(24,128), which offer similar white-box implementation sizes as PuppyCipher 16 and PuppyCipher 24 respectively [BI15]. As the authors of SPACE do not provide cycle counts for their ciphers but only the number of necessary cache or RAM accesses, a few assumptions are needed for a brief comparison. Both SPACE instances need 128 table accesses, which is much more than the 72 of PuppyCipher 16 and 68 of PuppyCipher 24. However, there is an extra cost in PuppyCipher due to the many AES calls, which need to be taken into account. On the other hand, the table accesses in SPACE are necessarily sequential, which is not the case for PuppyCipher, and we have just seen that parallel accesses can bring a considerable gain. It is thus easiest to use our average sequential access times as a unit. In that respect, PuppyCipher 24 and \(\textsc {Hound} \) 24 cost on average \(48 = 23390 / 490\) and \(44 = 21790 / 490\) table accesses, which is significantly less than the 128 of SPACE-(24,128). Similarly, we measured one sequential table access for PuppyCipher 16 to take 59 cycles on average, and we thus have a cost of \(47 = 2800 / 59\) and \(37 = 2190 / 59\) for table accesses for PuppyCipher 16 and \(\textsc {Hound} \) 16.
The performance gap reduces slightly when one considers the case of “secret” implementations. As the tables of SPACE use the AES as a building block, the cost of a secret SPACE (24–128) implementation should correspond to approximately 128 sequential calls to AES; the corresponding PuppyCipher and Hound implementations cost an equivalent 97 and 79 AES respectively.
5.2 CoureurDesBois
The main advantage of CoureurDesBois compared to PuppyCipher (as far as efficiency is concerned) is the higher degree of parallelism that it offers. Unlike PuppyCipher, the calls to AES can be made in parallel, and there is no limit either in the potential parallelism of table accesses. Because the output of the tables are of a bigger size, there is also fewer accesses to be made. Consequently, we expect CoureurDesBois to be quite more efficient than PuppyCipher.
A consequence of the higher parallelism of CoureurDesBois is that there are more potential implementation tradeoffs than for PuppyCipher. In our implementations, we chose to parallelize the AES calls up to four calls at a time, and the table accesses (or equivalent secret computations) at the level of one block (i.e. from eight parallel accesses for CoureurDesBois 16 to five for CoureurDesBois 24). The final step of CoureurDesBois also offers some parallelism; we have similarly regrouped the calls to AES used for randomness generation by four, and the finite field multiplications are regrouped by rows of eight.
The results for CoureurDesBois {16,20,24} are given in Table 6.
Discussion. We can notice a few things from these results. First, CoureurDesBois is indeed more efficient than PuppyCipher; for instance, CoureurDesBois 24 is about twice as fast as \(\textsc {Hound} \) 24. Second, the performance gap between secret and white-box implementations is somewhat smaller for the smaller instances of CoureurDesBois; on the other hand, the gap between transient and steady regime performance is slightly bigger than for PuppyCipher.
As pointed out above, more tradeoffs are possible in implementing CoureurDesBois than for PuppyCipher. As a result, it would be interesting to evaluate alternatives in practice.
Implementations of our schemes will be made available at http://whitebox4.gforge.inria.fr/.
Notes
- 1.
This can be partially mitigated by the use of external encodings [CEJO02a].
- 2.
Here, we lump together very similar definitions, although they are technically distinct. More details are provided in Sect. 2.1.
- 3.
This excludes the incompressible construction from [DLPR13], which is based on a modified RSA.
- 4.
This generalizes well to other sizes.
- 5.
In this respect, the adversary we consider is computationally unbounded.
- 6.
In fact, simple functional analysis shows that we can bound the right-hand term by \(4(\rho -k)\) provided \(\alpha ^{m}<1/2\) and \(k<4n\), which will always be the case.
- 7.
As a matter of fact, this CPU does not have Turbo Boost support.
References
Alwen, J., Dodis, Y., Wichs, D.: Survey: leakage resilience and the bounded retrieval model. In: Kurosawa, K. (ed.) ICITS 2009. LNCS, vol. 5973, pp. 1–18. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14496-7_1
Aumasson, J.-P., Neves, S., Wilcox-O’Hearn, Z., Winnerlein, C.: BLAKE2: simpler, smaller, fast as MD5. In: Jacobson, M., Locasto, M., Mohassel, P., Safavi-Naini, R. (eds.) ACNS 2013. LNCS, vol. 7954, pp. 119–135. Springer, Heidelberg (2013). doi:10.1007/978-3-642-38980-1_8
ARM: Security Technology Building a Secure System Using Trust-Zone Technology. White paper (2009). http://infocenter.arm.com/help/topic/com.arm.doc.prd29-genc-009492c/
Biryukov, A., Bouillaguet, C., Khovratovich, D.: Cryptographic schemes based on the ASASA structure: black-box, white-box, and public-key (Extended Abstract). In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8873, pp. 63–84. Springer, Heidelberg (2014). doi:10.1007/978-3-662-45611-8_4
Barak, B., Dodis, Y., Krawczyk, H., Pereira, O., Pietrzak, K., Standaert, F.-X., Yu, Y.: Leftover hash lemma, revisited. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 1–20. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22792-9_1
Billet, O., Gilbert, H., Ech-Chatbi, C.: Cryptanalysis of a white box AES implementation. In: Handschuh, H., Hasan, M.A. (eds.) SAC 2004. LNCS, vol. 3357, pp. 227–240. Springer, Heidelberg (2004). doi:10.1007/978-3-540-30564-4_16
Barak, B., Goldreich, O., Impagliazzo, R., Rudich, S., Sahai, A., Vadhan, S., Yang, K.: On the (im)possibility of obfuscating programs. In: Kilian, J. (ed.) CRYPTO 2001. LNCS, vol. 2139, pp. 1–18. Springer, Heidelberg (2001). doi:10.1007/3-540-44647-8_1
Bogdanov, A., Isobe, T.: Revisited, white-box cryptography: space-hard ciphers. In: CCM 2015, pp. 1058–1069. ACM (2015)
Bellare, M., Kane, D., Rogaway, P.: Big-key symmetric encryption: resisting key exfiltration. In: Robshaw, M., Katz, J. (eds.) CRYPTO 2016. LNCS, vol. 9814, pp. 373–402. Springer, Heidelberg (2016). doi:10.1007/978-3-662-53018-4_14
Boucheron, S., Lugosi, G., Bousquet, O.: Concentration inequalities. In: Bousquet, O., Luxburg, U., Rätsch, G. (eds.) ML -2003. LNCS (LNAI), vol. 3176, pp. 208–240. Springer, Heidelberg (2004). doi:10.1007/978-3-540-28650-9_9
Costan, V., Devadas, S.: Intel SGX Explained. IACR Cryptology ePrint Archive 2016:86 (2016)
Cash, D., Ding, Y.Z., Dodis, Y., Lee, W., Lipton, R., Walfish, S.: Intrusion-resilient key exchange in the bounded retrieval model. In: Vadhan, S.P. (ed.) TCC 2007. LNCS, vol. 4392, pp. 479–498. Springer, Heidelberg (2007). doi:10.1007/978-3-540-70936-7_26
Chow, S., Eisen, P., Johnson, H., Oorschot, P.C.: White-box cryptography and an AES implementation. In: Nyberg, K., Heys, H. (eds.) SAC 2002. LNCS, vol. 2595, pp. 250–270. Springer, Heidelberg (2003). doi:10.1007/3-540-36492-7_17
Chow, S., Eisen, P., Johnson, H., Oorschot, P.C.: A white-box DES implementation for DRM applications. In: Feigenbaum, J. (ed.) DRM 2002. LNCS, vol. 2696, pp. 1–15. Springer, Heidelberg (2003). doi:10.1007/978-3-540-44993-5_1
Costello, C., Longa, P.: Four\(\mathbb{Q}\): four-dimensional decompositions on a \(\mathbb{Q}\)-curve over the mersenne prime. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9452, pp. 214–235. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48797-6_10
Coron, J.-S., Mandal, A., Naccache, D., Tibouchi, M.: Fully homomorphic encryption over the integers with shorter public keys. In: Rogaway, P. (ed.) CRYPTO 2011. LNCS, vol. 6841, pp. 487–504. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22792-9_28
Coron, J.-S., Naccache, D., Tibouchi, M.: Public key compression and modulus switching for fully homomorphic encryption over the integers. In: Pointcheval, D., Johansson, T. (eds.) EUROCRYPT 2012. LNCS, vol. 7237, pp. 446–464. Springer, Heidelberg (2012). doi:10.1007/978-3-642-29011-4_27
Dinur, I., Dunkelman, O., Kranz, T., Leander, G.: Decomposing the ASASA block cipher construction. IACR Cryptology ePrint Archive 2015:507 (2015)
Delerablée, C., Lepoint, T., Paillier, P., Rivain, M.: White-box security notions for symmetric encryption schemes. In: Lange, T., Lauter, K., Lisoněk, P. (eds.) SAC 2013. LNCS, vol. 8282, pp. 247–264. Springer, Heidelberg (2014). doi:10.1007/978-3-662-43414-7_13
Mulder, Y., Roelse, P., Preneel, B.: Cryptanalysis of the xiao – lai white-box AES implementation. In: Knudsen, L.R., Wu, H. (eds.) SAC 2012. LNCS, vol. 7707, pp. 34–49. Springer, Heidelberg (2013). doi:10.1007/978-3-642-35999-6_3
Daemen, J., Rijmen, V.: The Design of Rijndael: AES - The Advanced Encryption Standard. Information Security and Cryptography. Springer, Heidelberg (2002)
Dziembowski, S.: Intrusion-resilience via the bounded-storage model. In: Halevi, S., Rabin, T. (eds.) TCC 2006. LNCS, vol. 3876, pp. 207–224. Springer, Heidelberg (2006). doi:10.1007/11681878_11
Fouque, P.-A., Karpman, P., Kirchner, P., Minaud, B.: Efficient and Provable White-Box Primitives. IACR Cryptology ePrint Archive 2016:642 (2016)
Garg, S., Gentry, C., Halevi, S., Raykova, M., Sahai, A., Waters, B.: Candidate indistinguishability obfuscation and functional encryption for all circuits. In: FOCS 2013, pp. 40–49. IEEE (2013)
Gilbert, H.: On White-Box Cryptography. invited talk, Fast Software Encryption 2016 (2016). slides https://fse.rub.de/slides/wbc_fse2016_hg_2pp.pdf
Goubin, L., Masereel, J.-M., Quisquater, M.: Cryptanalysis of white box DES implementations. In: Adams, C., Miri, A., Wiener, M. (eds.) SAC 2007. LNCS, vol. 4876, pp. 278–295. Springer, Heidelberg (2007). doi:10.1007/978-3-540-77360-3_18
Gilbert, H., Plût, J., Treger, J.: Key-recovery attack on the ASASA cryptosystem with expanding S-boxes. In: Gennaro, R., Robshaw, M. (eds.) CRYPTO 2015. LNCS, vol. 9215, pp. 475–490. Springer, Heidelberg (2015). doi:10.1007/978-3-662-47989-6_23
Halevi, S.: Graded Encoding, Variations on a Scheme. IACR Cryptology ePrint Archive, 2015:866 (2015)
Jean, J., Nikolić, I., Peyrin, T.: Tweaks and keys for block ciphers: the TWEAKEY framework. In: Sarkar, P., Iwata, T. (eds.) ASIACRYPT 2014. LNCS, vol. 8874, pp. 274–288. Springer, Heidelberg (2014). doi:10.1007/978-3-662-45608-8_15
Krawczyk, H.: Cryptographic extraction and key derivation: the HKDF scheme. In: Rabin, T. (ed.) CRYPTO 2010. LNCS, vol. 6223, pp. 631–648. Springer, Heidelberg (2010). doi:10.1007/978-3-642-14623-7_34
Minaud, B., Derbez, P., Fouque, P.-A., Karpman, P.: Key-recovery attacks on ASASA. In: Iwata, T., Cheon, J.H. (eds.) ASIACRYPT 2015. LNCS, vol. 9453, pp. 3–27. Springer, Heidelberg (2015). doi:10.1007/978-3-662-48800-3_1
Shaltiel, R.: An introduction to randomness extractors. In: Aceto, L., Henzinger, M., Sgall, J. (eds.) ICALP 2011. LNCS, vol. 6756, pp. 21–41. Springer, Heidelberg (2011). doi:10.1007/978-3-642-22012-8_2
Stinson, D.R.: Universal hash families and the leftover hash lemma, and applications to cryptography and computing. J. Comb. Math. Comb. Comput. 42, 3–32 (2002)
Vadhan, S.P.: Constructing locally computable extractors and cryptosystems in the bounded-storage model. J. Cryptology 17(1), 43–77 (2004)
Wyseur, B., Michiels, W., Gorissen, P., Preneel, B.: Cryptanalysis of white-box DES implementations with arbitrary external encodings. In: Adams, C., Miri, A., Wiener, M. (eds.) SAC 2007. LNCS, vol. 4876, pp. 264–277. Springer, Heidelberg (2007). doi:10.1007/978-3-540-77360-3_17
Wyseur, B.: White-box cryptography. Ph.D. thesis, KU Leuven (2009)
Xiao, Y., Lai, X.: A secure implementation of white-box AES. In: CSA 2009, pp. 1–6. IEEE (2009)
Zimmerman, J.: How to obfuscate programs directly. In: Oswald, E., Fischlin, M. (eds.) EUROCRYPT 2015. LNCS, vol. 9057, pp. 439–467. Springer, Heidelberg (2015). doi:10.1007/978-3-662-46803-6_15
Acknowledgments
The authors would like to thank Florent Tardif for letting us use his test machine.
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2016 International Association for Cryptologic Research
About this paper
Cite this paper
Fouque, PA., Karpman, P., Kirchner, P., Minaud, B. (2016). Efficient and Provable White-Box Primitives. In: Cheon, J., Takagi, T. (eds) Advances in Cryptology – ASIACRYPT 2016. ASIACRYPT 2016. Lecture Notes in Computer Science(), vol 10031. Springer, Berlin, Heidelberg. https://doi.org/10.1007/978-3-662-53887-6_6
Download citation
DOI: https://doi.org/10.1007/978-3-662-53887-6_6
Published:
Publisher Name: Springer, Berlin, Heidelberg
Print ISBN: 978-3-662-53886-9
Online ISBN: 978-3-662-53887-6
eBook Packages: Computer ScienceComputer Science (R0)



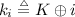 . Note that using a tweakable cipher such as KIASU-BC [
. Note that using a tweakable cipher such as KIASU-BC [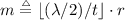 );
);